An Upper Bound Asymptotically Tight for the Connectivity of the Disjointness Graph of Segments in the Plane

Abstract

Let P be a set of $n\ge 3$ points in general position in the plane. The edge disjointness graph $D\left(P\right)$ of P is the graph whose vertices are the $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ closed straight line segments with endpoints in P, two of which are adjacent in $D\left(P\right)$ if and only if they are disjoint. In this paper we show that the connectivity of $D\left(P\right)$ is at most $\frac{7n^2}{18}+\Theta \left(n\right)$, and that this upper bound is asymptotically tight. The proof is based on the analysis of the connectivity of $D\left(Q_n\right)$, where $Q_n$ denotes an n-point set that is almost 3-symmetric.

1. Introduction

We call set in general position to any finite set of points in the Euclidean plane that does not contain three collinear elements. Let P be a set of $n\ge 3$ points in general position. A segment of P is a closed straight line segment with its two endpoints being elements of P. In this paper, we shall use $\mathcal{P}$ to denote the set of all $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ segments of P. The edge disjointness graph $D\left(P\right)$ of P is the graph whose vertex set is $\mathcal{P}$, and two elements of $\mathcal{P}$ are adjacent in $D\left(P\right)$ if and only if they are disjoint. We note that $\mathcal{P}$ naturally defines a rectilinear drawing in the plane of the complete graph $K_n$ on n vertices. See Figure 1.

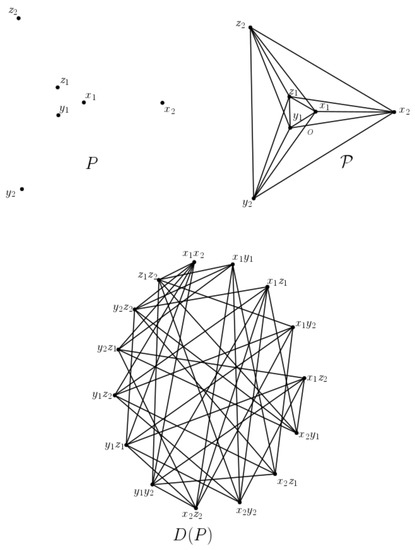
Figure 1. The point set $P=\{x_1,x_2,y_1,y_2,z_1,z_2\}$ on the upper left is a set in general position. In the upper right we have $\mathcal{P}$, which can be seen as the rectilinear drawing of $K_6$ induced by P. As the largest number of crossings on any segment of $\mathcal{P}$ is 1, then $\overline{lcr}\left(P\right)=1$. The graph on the bottom part is the edge disjointness graph $D\left(P\right)$ corresponding to P.

The class of edge disjointness graphs was introduced in 2005 by Araujo, Dumitrescu, Hurtado, Noy, and Urrutia [1], as a geometric version of the Kneser graphs. We recall that for $k,m\in {\mathbb{Z}}^{+}$ with $k\le m/2$, the Kneser graph $KG(m;k)$ is defined as the graph whose vertices are all the k–subsets of $\{1,2,\dots ,m\}$ and in which two k-subsets from an edge if and only if they are disjoint. In 1956, Kneser conjectured [2] that the chromatic number $\chi \left(KG\right(m;k\left)\right)$ of $KG(m;k)$ is equal to $m-2k+2$. This conjecture was proved by Lovász [3] and (independently) by Bárány [4] in 1978. For more results on Kneser graphs, we refer the reader to [5,6,7,8,9,10] and the references therein.

In [1] the effort was focussed on the estimation of the chromatic number $\chi \left(D\right(P\left)\right)$ of $D\left(P\right)$, and a general lower bound was established. The problem of determining the exact value of $\chi \left(D\right(P\left)\right)$ remains open in general. On the other hand, there are only two families of point sets for which the exact value of $\chi \left(D\right(P\left)\right)$ is known: when P is in convex position [11,12], and when P is the double chain [13]. The connectivity $\kappa \left(D\right(P\left)\right)$ of $D\left(P\right)$ was studied by Leaños, Ndjatchi, and Ríos-Castro in [14], where it was shown that $\kappa \left(D\left(P\right)\right)\ge \left(\genfrac{}{}{0pt}{}{\lfloor \frac{n-2}{2}\rfloor }{2}\right)+\left(\genfrac{}{}{0pt}{}{\lceil \frac{n-2}{2}\rceil }{2}\right)$. We remark that in this paper we give a complementary upper bound for $\kappa \left(D\right(P\left)\right)$.

Recently, Aichholzer, Kynčl, Scheucher, and Vogtenhuber [15] have established an asymptotic upper bound for the maximum size of certain independent sets of vertices of $D\left(P\right)$. In 2017 Pach, Tardos, and Tóth [16] studied the chromatic number and the clique number of $D\left(P\right)$ in the more general setting of ${\mathbb{R}}^d$ for $d\ge 2$, i.e., when P is a subset of ${\mathbb{R}}^d$. More precisely, in [16] was shown that the chromatic number of $D\left(P\right)$ is bounded by above by a polynomial function that depends on its clique number $\omega \left(D\right(P\left)\right)$, and that the problem of determining any of $\chi \left(D\right(P\left)\right)$ or $\omega \left(D\right(P\left)\right)$ is NP-hard. Two years later, Pach and Tomon [17] have shown that if G is the disjointness graph of a set of grounded x-monotone curves in ${\mathbb{R}}^2$ and $\omega \left(G\right)=k$, then $\chi \left(G\right)\le k+1$.

Another wide research area, which is closely related to this work, is the study of the combinatorial properties of geometric graphs. We recall that a geometric graph is a graph whose vertex set V is a finite set of points in general positions in the plane, and the edges are straight line segments connecting some pairs of V. Clearly, the sets of segments studied in this paper correspond to a class of the geometric graph, namely the class of complete geometric graphs. See [18] for an excellent survey on geometric graphs.

Following [14], if $x,y\in P$ and $x\ne y$, then $xy$ will be the element of $\mathcal{P}$ with endpoints x and y. Let $x_1{y}_2$ and $y_1{x}_2$ be two distinct elements of $\mathcal{P}$, and suppose that $x_1{y}_2\cap y_1{x}_2\ne \varnothing$. Then $x_1{y}_2\cap y_1{x}_2$ consists precisely of one point $o\in {\mathbb{R}}^2$, because P is a set in general position. If o is an interior point of both $x_1{y}_2$ and $y_1{x}_2$, then we say that they cross at o, and we will refer to o as a crossing of $\mathcal{P}$. See Figure 1 (upper right).

Let $H=\left(V\right(H),E(H\left)\right)$ be a (non-empty) simple connected graph. As usual, if $u,v\in V\left(H\right)$, then the distance between u and v in H will be denoted by $d_H(u,v)$, and we write $uv$ to mean that u and v are adjacent in H. We note that the $uv$ notation is similar to that used to denote the straight line segment $xy$ defined by the points $x,y\in P$. However, none of these notations should be a source of confusion, because the former objects are vertices of a graph, and the latter are points in the plane.

The neighborhood of v in H is the set $\{u\in V(H):uv\in E(H\left)\right\}$ and is denoted by $N_H\left(v\right)$. If $S\subseteq V\left(H\right)$, then $N_H\left(S\right):={\cup }_{v\in S}{N}_H\left(v\right)$. The degree ${deg}_H\left(v\right)$ of v is the number $|N_H\left(v\right)|$. The number $\delta \left(H\right):=min\{{deg}_H\left(v\right):v\in V\left(H\right)\}$ is the minimum degree of H. A $u-v$ path of H is a path of H having an endpoint in u and the other endpoint in v. Similarly, if U is a subgraph of H, then $H\backslash U$ is the subgraph of H that results by removing U from H.

We recall that if k is a nonnegative integer, then H is k–connected if $\left|V\right(H\left)\right|>k$ and $H\backslash W$ is connected for every set $W\subset V\left(H\right)$ with $\left|W\right|<k$. The connectivity $\kappa \left(H\right)$ of H is greatest integer k such that H is k-connected. See Figure 2.

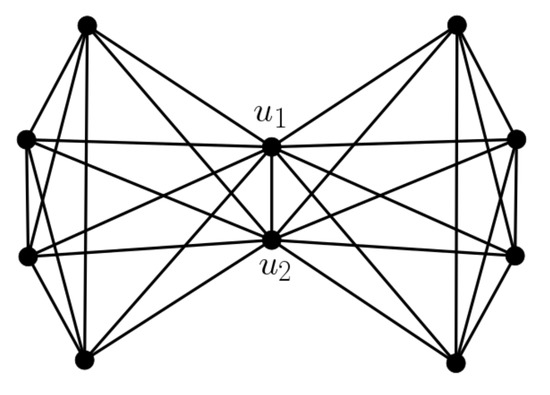
Figure 2. This graph is 2–connected, but not 3–connected. Indeed, if we remove any vertex, what remains is still connected. On the other hand, note that $U=\{u_1,u_2\}$ is vertex cut of order 2, and hence U is a vertex cut of minimum order.

Our aim in this paper is to show the following result.

Theorem 1.

Let P be a set of $n\ge 3$ points in general positions in the plane. Then $\kappa \left(D\left(P\right)\right)\le \frac{7}{18}{n}^2+\Theta \left(n\right)$, and this bound is asymptotically tight.

The rest of the paper is organized as follows. The validity of inequality in Theorem 1 is proved in Section 2, by making strong use of the main result of Ábrego and Fernández-Merchant in [19]. In Section 3 we briefly explain the strategy to prove Theorem 1 and present the key ingredients of our proof. Finally, in Section 4, we show that the upper bound in Theorem 1 is asymptotically tight, by proving that $\kappa \left(D\left(Q_n\right)\right)=\frac{7}{18}{n}^2-\Theta \left(n\right)$ for certain infinite family ${\left\{Q_n\right\}}_{n=3}^{\infty }$ of point sets in general position with certain symmetry property.

2. The Rectilinear Local Crossing Number of ${\mathit{K}}_{\mathit{n}}$ and the Validity of Inequality in Theorem 1

In what follows n is an integer with $n\ge 3$, and P is an n-point set in general position. Our aim in this section is to show that $\kappa \left(D\left(P\right)\right)\le \frac{7}{18}{n}^2+\Theta \left(n\right)$. In order to do that, we need to establish a straightforward, yet essential, relationship between the minimum degree $\delta \left(D\right(P\left)\right)$ of the graph $D\left(P\right)$ and the rectilinear local crossing number of the drawing $\mathcal{P}$ of $K_n$ induced by P.

We recall that the rectilinear local crossing number of P denoted by $\overline{lcr}\left(P\right)$, is the largest number of crossings on any element of $\mathcal{P}$, and that the rectilinear local crossing number of $K_n$ denoted by $\overline{lcr}\left(K_n\right)$, is the minimum of $\overline{lcr}\left(P\right)$ taken over all n-point sets P in general position. See Figure 1 (upper right).

Proposition 2.

The minimum degree $\delta \left(D\right(P\left)\right)$ of the graph $D\left(P\right)$ is equal to $\left(\genfrac{}{}{0pt}{}{n-2}{2}\right)-\overline{lcr}\left(P\right)$.

Proof. 

Let $e=xy$ be an element of $\mathcal{P}$, and let $\mathcal{E}$ be the subset of $\mathcal{P}$ consisting of all segments that cross e. From the definitions of e and $\mathcal{E}$ it follows that an element of $\mathcal{P}\backslash \left\{e\right\}$ is adjacent to e in $D\left(P\right)$ if and only if has both endpoints in $P\backslash \{x,y\}$ and does not belong to $\mathcal{E}$. Since $\left|P\right|=n$, then the degree of e in $D\left(P\right)$ is exactly $\left(\genfrac{}{}{0pt}{}{n-2}{2}\right)-\left|\mathcal{E}\right|$. The last fact and $\left|\mathcal{E}\right|\le \overline{lcr}\left(P\right)$ imply $\delta \left(D\left(P\right)\right)\ge \left(\genfrac{}{}{0pt}{}{n-2}{2}\right)-\overline{lcr}\left(P\right)$. On the other hand, from the definition of $\overline{lcr}\left(P\right)$ we know that $\mathcal{P}$ contains a segment, say g, that is crossed by exactly $\overline{lcr}\left(P\right)$ elements of $\mathcal{P}\backslash \left\{g\right\}$, and hence the degree of g in $D\left(P\right)$ is $\left(\genfrac{}{}{0pt}{}{n-2}{2}\right)-\overline{lcr}\left(P\right)$, as required. □

The following result was proved in [19] and is the key ingredient in the proof of Corollary 4.

Theorem 3

(Theorem 1 [19]). If n is a positive integer, then

$$\overline{lcr}\left(K_n\right)=\left\{\begin{array}{ccc}\frac{1}{9}{(n-3)}^2\hfill & if& n\equiv 0(mod3),\\ \\ \frac{1}{9}(n-1)(n-4)\hfill & if& n\equiv 1(mod3),\\ \\ \frac{1}{9}{(n-2)}^2-\lfloor \frac{n-2}{6}\rfloor \hfill & if& n\equiv 2(mod3),n\notin \{8,14\}.\end{array}\right.$$

(1)

In addition, $\overline{lcr}\left(K_8\right)=4$ and $\overline{lcr}\left(K_{14}\right)=15$.

Corollary 4.

Let P be an n-point set in general position, and let $n\ge 3$. Then $\kappa \left(D\left(P\right)\right)\le \frac{7}{18}{n}^2+\Theta \left(n\right)$.

Proof. 

It is well-known that $\kappa \left(D\right(P\left)\right)\le \delta \left(D\right(P\left)\right)$. Thus, it suffices to show that $\delta \left(D\left(P\right)\right)\le \frac{7}{18}{n}^2+\Theta \left(n\right)$. A trivial manipulation of Equation (1) allow us to see that $\overline{lcr}\left(K_n\right)=\frac{1}{9}{n}^2-\Theta \left(n\right)$. On the other hand, from Proposition 2 and the fact that $\overline{lcr}\left(K_n\right)\le \overline{lcr}\left(P\right)$, it follows that $\delta \left(D\left(P\right)\right)\le \left(\genfrac{}{}{0pt}{}{n-2}{2}\right)-\overline{lcr}\left(K_n\right)=\left(\genfrac{}{}{0pt}{}{n-2}{2}\right)-\left(\frac{1}{9}{n}^2-\Theta \left(n\right)\right)=\frac{7}{18}{n}^2+\Theta \left(n\right)$, as required. □

3. The Key Ingredients of the Proof of Theorem 1

Our strategy to prove that the upper bound in Theorem 1 is asymptotically tight is as follows. First, for any integer n with $n\ge 3$, we define a certain n-point set in a general position, which we denote by $Q_n$. The family ${\left\{Q_n\right\}}_{n=3}^{\infty }$ was originally defined by Lara, Rubio-Montiel and Zaragoza in [20], where it was shown that $\overline{lcr}\left(K_n\right)=\frac{1}{9}{n}^2-\Theta \left(n\right)$. More recently, Ábrego and Fernández-Merchant [19] showed that $\overline{lcr}\left(K_n\right)=\overline{lcr}\left(Q_n\right)$ for any $n\not\equiv 2(mod3)$. Then, we will give some notation and basic facts related to the connectivity of $D\left(Q_n\right)$, which will allow us to simplify the remaining part of the proof of Theorem 1. Finally, in Section 4.2, we will show that $\kappa \left(D\left(Q_n\right)\right)=\frac{7}{18}{n}^2-\Theta \left(n\right)$.

We now recall a couple of classical results in graph theory which are fundamental in our proof.

Theorem 5

(Hall’s theorem). Let H be a bipartite graph with bipartition $\{A,B\}$, and let C be an element of $\{A,B\}$ of minimum cardinality. Then H contains a matching of size $\left|C\right|$ if and only if $|N_H\left(S\right)|\ge |S|$ for any $S\subseteq C$.

Theorem 6

(Menger’s theorem). A graph is k-connected if and only if it contains k pairwise internally disjoint paths between any two distinct vertices.

It is straightforward to check that the graph $D\left(P\right)$ is connected for any n-point set P in general position with $n\ge 5$. In view of this, the following consequence of Menger’s theorem will be useful.

Corollary 7.

Let H be a connected graph. Then H is k-connected if and only if H has k pairwise internally disjoint $a-b$ paths, for any two vertices a and b of H such that $d_H(a,b)=2$.

Proof. 

The forward implication follows directly from Menger’s theorem. Conversely, let U be a vertex cut of H of minimum order. Let $H_1$ and $H_2$ be two distinct components of $H\backslash U$, and let $u\in U$. Since U is a minimum cut, then u has at least a neighbor $v_i$ in $H_i$, for $i=1,2$. Then $d_H(v_1,v_2)=2$. By hypothesis, H has k pairwise internally disjoint $v_1-v_2$ paths. Since each of these k paths intersects U, then we have that $\left|U\right|\ge k$, as required. □

Another ingredient that plays a central role in this work is the property of 3-symmetry of point sets in the plane, which is a recurrent concept in crossing number theory. A subset X in ${\mathbb{R}}^2$ is called 3-symmetric if X contains a subset $X_1$ such that $X=X_1\cup \rho \left(X_1\right)\cup {\rho }^2\left(X_1\right)$, where $\rho$ is a $2\pi /3$ clockwise rotation around a suitable point in the plane. The relationship between the concept of 3-symmetry and several variants of crossing number have been investigated by a number of authors [19,20,21,22]. If X is finite and $\left|X\right|\not\equiv 0(mod3)$, then we say that X is almost 3-symmetric if X contains a subset $X^{\prime }$ with at most two elements such that $X\backslash X^{\prime }$ is 3-symmetric. As we shall see in the next section, the main part of the proof of Theorem 1 is based on the estimation of the connectivity of $D\left(Q_n\right)$, where $Q_n$ is an almost 3-symmetric set with n points.

4. The Upper Bound in Theorem 1 Is Asymptotically Tight

For the rest of the paper, n is an integer with $n\ge 3$. We begin by introducing the family of point sets that we use in the proof of our main result, and some notation.

4.1. The Family ${\left\{Q_n\right\}}_{n=3}^{\infty }$ and Its Properties

Following [19], let $C_0$ be the arc of the circumference passing through the points $(1,0),(3,0)$, and $(2,ϵ)$, where $ϵ\in {\mathbb{R}}^{+}$ is close to zero. Let $C_1$ (resp. $C_2$) be the $2\pi /3$ (resp. $4\pi /3$) counterclockwise rotation of $C_0$ around the origin $O:=(0,0)$. We choose $ϵ$ small enough so that any straight line passing through two distinct points of $C_0$ separates $C_1$ from $C_2$. See Figure 3. Since $Y:=C_0\cup C_1\cup C_2$ is a 3-symmetric set, we can choose an almost 3-symmetric subset $Q_n$ of Y with exactly n points. For $i\in \{0,1,2\}$, let $n_i:=|Q_n\cap Y|$. Then, $n_0+n_1+n_2=n$, and $|n_i-n_j|\le 1$ for $i,j\in \{0,1,2\}$.

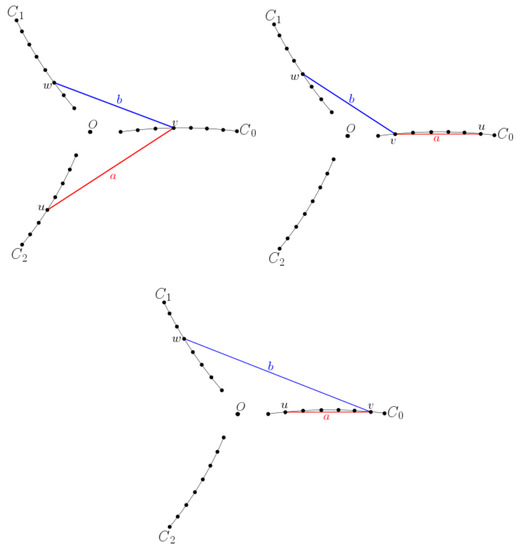
Figure 3. The underlying point set in these three drawings is $Q_{24}$. Note that $n_i=8$ for each $i=0,1,2$. The difference between these configurations is the way in which the endpoints of $a=uv$ and $b=vw$ are located on $C_0,C_1,$ and $C_2$.

For the rest of the paper, we use ${\mathcal{Q}}_n$ to denote the set of all $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ segments of $Q_n$, and $G_n:=D\left(Q_n\right)$. Similarly, if $a,b\in {\mathcal{Q}}_n$, then $\eta (Q_n;a,b)$ will denote the maximum number of pairwise internally-disjoint $a-b$ paths in $G_n$.

Remark 8.

Let $a,b$ be vertices of $G_n$ such that $d_{G_n}(a,b)=2$. By Corollary 7 and Menger’s theorem, in order to show the last assertion of Theorem 1 it is enough to show that $\eta (Q_n;a,b)=\frac{7}{18}{n}^2-\Theta \left(n\right)$.

In view of the previous remark, for the rest of the work, we can assume that a and b are two fixed vertices of $G_n$ such that $d_{G_n}(a,b)=2$. Then a and b are not adjacent in $G_n$, and hence $a\cap b\ne \varnothing$. This inequality and the fact that $Q_n$ is a set in general position imply that $a\cap b$ consists precisely of one point of ${\mathbb{R}}^2$, which will be denoted by o. Then either a and b cross at o or o is common endpoint of them.

We note that if $e\in {\mathcal{Q}}_n$, then there is a unique $i\in \{0,1,2\}$ such that e has an endpoint in $C_i$ and the other in $C_i\cup C_{i+2}$, where addition is taken $mod3$. We will say that such an i is the type of e. In particular, note that in any of the three cases of Figure 3, a and b are of type 0 and 1, respectively.

Clearly, there are only two possibilities for a and b with respect to their types: they have the same type, or they have different types. If a and b have the same type, then, by rotating $Q_n$ around O (if necessary) but not the labels $C_0,C_1$, and $C_2$, we may assume that a and b are both of type 0. Analogously, if a and b have different types, then, by rotating $Q_n$ (if necessary) we can assume that 0 and 1 are the types of a and b.

It is not hard to check that if a and b are of type 0 and 1, respectively, then the three configurations illustrated in Figure 3 are the only possibilities to put the endpoints of a and b on the arcs $C_0,C_1,$ and $C_2$. Similarly, if a and b are both of type 0, then ten configurations illustrated in Figure 4 are the only possibilities to put the endpoints of a and b on the arcs $C_0$ and $C_2$. Then, from now on, we can assume without any loss of generality that a and b are placed in ${\mathcal{Q}}_n$ according to some case of Figure 3 and Figure 4. We abuse notation and we shall use $C_i$ to refer to the subset of points of $Q_n$ that lies on the arc $C_i$. In particular, we will assume that $|C_i|=n_i$. For distinct $i,j\in \{0,1,2\}$, we let $C_{i,j}:=C_i\cup C_j$.

Figure 4. Except for rotations, these ten configurations together with those three in Figure 3, are the only possibilities to put the endpoints of a and b on $C_0,C_1,$ and $C_2$. The arcs here are not as flat as they should be; we have drawn them in this way for illustrative purposes only.

We now split the set of neighbours of a and b into three sets as follows.

$$\mathcal{A}:=\{e\in {\mathcal{Q}}_n|e\cap a=\varnothing \mathrm{and} e\cap b\ne \varnothing \},$$

$$\mathcal{B}:=\{e\in {\mathcal{Q}}_n|e\cap b=\varnothing \mathrm{and} e\cap a\ne \varnothing \},$$

$$\mathcal{D}:=\{e\in {\mathcal{Q}}_n|e\cap b=\varnothing \mathrm{and} e\cap a=\varnothing \}.$$

Clearly, $\mathcal{A},\mathcal{B},\mathcal{D},$ and $\{a,b\}$ are pairwise disjoint. We also note that $N_{G_n}\left(a\right)=\mathcal{A}\cup \mathcal{D},N_{G_n}\left(b\right)=\mathcal{B}\cup \mathcal{D}$, and hence

$$\eta (Q_n;a,b)\le \left|\mathcal{D}\right|+min\left\{\right|\mathcal{A}|,|\mathcal{B}\left|\right\}.$$

(2)

Keeping in mind the facts and the terminology given in this subsection, we now proceed to show the last assertion of our main result.

4.2. Constructing the Required $a-b$ Paths of $G_n$

As we have mentioned in Remark 8, all we need to finish the proof of Theorem 1 is to show the following lemma.

Lemma 9.

If a and b are as in Remark 8, then $\eta (Q_n;a,b)=\frac{7}{18}{n}^2-\Theta \left(n\right).$

We devote this section to show Lemma 9, and hence to complete the proof of Theorem 1. Our proof is constructive and uses two types of constructions, depending on whether a and b are located in ${\mathcal{Q}}_n$ according to some case of Figure 3 or Figure 4. In the interest of readability, we start by presenting several technical issues needed to define both types of constructions.

Since the equality in Lemma 9 is asymptotic, in what remains of this section, we assume that $n\ge 15$. Note that this assumption guarantees that each of $C_0,C_1,$ and $C_2$ has at least one point that does not belong to a or b. This will be used in Section 4.2.2.

4.2.1. Suppose That a and b Have Distinct Types

Then, a and b are located in ${\mathcal{Q}}_n$ according to some case of Figure 3, and so $a=uv,b=vw,v\in C_0,w\in C_1,$ and $u\in C_{0,2}\backslash \left\{v\right\}$. Let H be the bipartite subgraph of $G_n$ with bipartition $\{\mathcal{A},\mathcal{B}\}$ such that $f\in \mathcal{A}$ is adjacent to $g\in \mathcal{B}$ in H if and only if f and g are adjacent in $G_n$. Thus, H is an induced bipartite subgraph of $G_n$. If X and Y are nonempty subsets of $Q_n$, we will denote the set of all segments of ${\mathcal{Q}}_n$ that have an endpoint in X and the other in Y by $X\ast Y$.

A simple inspection of the several cases in which two elements of ${\mathcal{Q}}_n$ can cross each other yields the following assertion.

Observation 10.

If $f,g\in {\mathcal{Q}}_n$ cross each other, then f and g are of the same type.

A key fact that will allow us to construct the first class of paths is that H satisfies the Hall’s condition. We formalize this idea as follows.

Proposition 11.

Let $\mathcal{C}$ be an element of $\{\mathcal{A},\mathcal{B}\}$ of minimum cardinality. Then $|N_H\left(\mathcal{S}\right)|\ge |\mathcal{S}|$ for any $\mathcal{S}\subseteq \mathcal{C}$.

Proof. 

We break the proof into two cases, depending on whether $\left|\mathcal{A}\right|\le \left|\mathcal{B}\right|$ or $\left|\mathcal{A}\right|>\left|\mathcal{B}\right|$. We remark that Observation 10 is often used in this proof without explicit mention.

(A) Suppose that $\left|\mathcal{A}\right|\le \left|\mathcal{B}\right|$, and let $\mathcal{S}\subseteq \mathcal{A}$. We can assume that $\mathcal{S}\ne \varnothing$ and that $\mathcal{B}\backslash N_H\left(\mathcal{S}\right)\ne \varnothing$, as otherwise we are done. Let $e^{*}$ be a fixed segment of $\mathcal{B}\backslash N_H\left(\mathcal{S}\right)$, and assume that $e^{*}=pq$.

The next facts follow easily from the choice of $e^{*}$ and $\mathcal{S}$. (F1) $e^{*}$ intersects each element of $\mathcal{S}\cup \left\{a\right\}$, (F2) b intersects each element of $\mathcal{S}$, and (F3) each element of $\mathcal{S}$ has at least one endpoint in $C_1$.

(A1) Suppose that $p\in C_0$ and $q\in C_2$. Then (F1) and (F3) imply that $\mathcal{S}$ is a subset of ${\mathcal{A}}^{\prime }:=\mathcal{X}\cup \left\{qw\right\}$, where $\mathcal{X}$ denotes the set of all segments that intersect b and are in $\left\{p\right\}\ast C_1$. Note that if $\mathcal{S}=\left\{qw\right\}$, then $\left\{u\right\}\ast (C_0\backslash \{u,v\})\subseteq N_H\left(\mathcal{S}\right)$, and so $|N_H\left(\mathcal{S}\right)|\ge n_0-2\ge 1=\left|\mathcal{S}\right|$. Thus, we may assume that $\mathcal{X}\ne \varnothing$. This implies that if $qw\in \mathcal{S}$ (respectively, $qw\notin \mathcal{S}$), then ${\mathcal{B}}^{\prime }:=\left\{u\right\}\ast (C_{0,2}\backslash \{q,u,v\})$ (respectively, ${\mathcal{B}}^{\prime }:=\left\{u\right\}\ast (C_{0,2}\backslash \{p,u,v\})$) is a subset of $N_H\left(\mathcal{S}\right)$. Since $|{\mathcal{A}}^{\prime }|\le n_1+1,\left|{\mathcal{B}}^{\prime }\right|\ge n_0+n_2-3$ and $n_0+n_2\ge n_1+4$, we have $|N_H\left(\mathcal{S}\right)|\ge |\mathcal{S}|$.

(A2) Suppose that $p,q\in C_0$. Then (F1) and (F3) imply that $\mathcal{S}$ is a subset of the set ${\mathcal{A}}^{\prime }$, which consists of all segments that intersect b and are in $\{p,q\}\ast C_1$. Then, $\left|\mathcal{S}\right|\le |{\mathcal{A}}^{\prime }|\le 2n_1$. Let $e\in \mathcal{S}$, and assume without loss of generality that $p\in e$. Since $e\cap a=\varnothing$, then $p\notin \{u,v\}$ and ${\mathcal{B}}^{\prime }:=\left\{u\right\}\ast (C_{0,2}\backslash \{u,v,p\})$ is a subset of $N_H\left(e\right)$. Then, $|N_H\left(\mathcal{S}\right)|\ge |{\mathcal{B}}^{\prime }|=n_0+n_2-3$, and we can assume that $|{\mathcal{A}}^{\prime }|>n_0+n_2-3$, as otherwise we are done. This implies that there exists $g\in \mathcal{S}$ with $q\in g$.

Since $u\in C_2$ implies $|{\mathcal{A}}^{\prime }|\le n_1+1<n_0+n_2-3$, we can assume that $u\in C_0$. Let $I_0$ be the set of points of $C_0$ that are between u and v. From (F1) we know that at most one of p or q is in $I_0$. If $z\in \{p,q\}$ is a point of $I_0$, then ${\mathcal{B}}^{\prime }\cup (\left\{z\right\}\ast C_2)$ is a subset of $N_H\left(\{e,g\}\right)$. Then $|N_H\left(\mathcal{S}\right)|\ge (n_0+n_2-3)+n_2\ge 2n_1\ge \left|\mathcal{S}\right|$, as required. Then, neither p nor q is in $I_0$. Since $e^{*}\cap a\ne \varnothing$, we must have $u=q$. This implies that $\mathcal{S}\subseteq \left\{p\right\}\ast C_1$, and so $|N_H\left(\mathcal{S}\right)|\ge n_0+n_2-3\ge n_1\ge \left|\mathcal{S}\right|$.

(A3) Suppose that $p,q\in C_2$. Since $e^{*}$ is of type 2 and $e^{*}\cap a\ne \varnothing$, then u must be a common endpoint of $e^{*}$ and a, by Observation 10. Without loss of generality, suppose that $p=u$.

From (F1) and (F3) we know that $\mathcal{S}$ is a subset of $\left\{w\right\}\ast (Y\cup \{q\left\}\right)$, where Y denotes the set of all points of $C_2$ that lie between u and q. Note that if u and q are consecutive points of $C_2$, then $Y=\varnothing$. Let e be the segment of $\mathcal{S}$ whose endpoint $q^{\prime }\in Y\cup \left\{q\right\}$ is closest to q. Let $Y^{\prime }$ be the set of all points of $C_2$ that lie between u and $q^{\prime }$. Then $|Y^{\prime }|+1\ge |\mathcal{S}|$, and ${\mathcal{B}}^{\prime }:=\left\{u\right\}\ast (Y^{\prime }\cup C_0\backslash \left\{v\right\})$ is a subset of $N_H\left(e\right)$. Since $\left|\mathcal{S}\right|\le |Y^{\prime }|+1$ and $|{\mathcal{B}}^{\prime }|=(n_0-1)+\left|Y^{\prime }\right|$, then $n_0\ge 5$ implies $|N_H\left(\mathcal{S}\right)|\ge |\mathcal{S}|$.

(A4) Suppose that $e^{*}$ has an endpoint in $C_1$. We assume without loss of generality that $p\in C_1$. Clearly, $p\ne w$. Since $e^{*}\cap a\ne \varnothing$, then $q=u$, and so $q\in C_{0,2}\backslash \left\{v\right\}$.

(A4.1) Suppose that $q\in C_0\backslash \left\{v\right\}$. Then $e^{*},b\in C_1\ast \{u,v\}$, and $e^{*}\cap b=\varnothing$. Since $u,v\in C_0$, then $\left\{w\right\}\ast C_2\subseteq \mathcal{A}\backslash \mathcal{S}$ due to (F1). Let ${\mathcal{A}}^{\prime }:=\mathcal{A}\backslash (\left\{w\right\}\ast C_2)$, and let ${\mathcal{B}}^{\prime }$ be the set that results by removing any segment of $\left\{u\right\}\ast (C_1\backslash \left\{p\right\})$ from $\mathcal{B}$. Then, $|{\mathcal{B}}^{\prime }|\ge |{\mathcal{A}}^{\prime }|$ because $\left|\mathcal{B}\right|\ge \left|\mathcal{A}\right|$. We note that (F1) implies $\mathcal{S}\subseteq {\mathcal{A}}^{\prime }$. If $\mathcal{S}$ contains a segment e with both endpoints in $C_1$, then (F1) implies ${\mathcal{B}}^{\prime }\subseteq N_H\left(e\right)$, and hence $|N_H\left(\mathcal{S}\right)|\ge |{\mathcal{B}}^{\prime }|\ge |{\mathcal{A}}^{\prime }|\ge |\mathcal{S}|$, as required. Thus, we may assume that $\mathcal{S}\cap (C_1\ast C_1)=\varnothing$, and so $\mathcal{S}\subseteq C_0\ast C_1$.

Let $I_0$ be the set of points of $C_0$ that are between u and v (if u and v are contiguous, $I_0=\varnothing$), and let $J_0:=C_0\backslash (I_0\cup \left\{v\right\})$. By (F1) and (F2) we know that each segment of $\mathcal{S}$ intersects both $e^{*}$ and b. Since b and $e^{*}$ are disjoint, no segment of $\mathcal{S}$ can have an endpoint in $I_0\cup \left\{v\right\}$, and, on the other hand, each segment of ${\mathcal{B}}^{\prime }$ must have at least one endpoint in $I_0\cup \left\{u\right\}$. Note that if $J_0$ has at least two points being incident with segments of $\mathcal{S}$, then each segment of ${\mathcal{B}}^{\prime }$ is disjoint from at least one of these points of $J_0$, and hence ${\mathcal{B}}^{\prime }\subseteq N_H\left(\mathcal{S}\right)$, as required.

Thus, we can assume that all segments of $\mathcal{S}$ are incident with one point of $J_0$, say z. Then, $\mathcal{S}\subseteq \left\{z\right\}\ast (C_1\backslash \left\{p\right\})$ or $\mathcal{S}\subseteq \left\{z\right\}\ast (C_1\backslash \left\{w\right\})$, and so $\left|\mathcal{S}\right|\le n_1-1\le n_2$. On the other hand, note that $\left\{u\right\}\ast C_2\subseteq N_H\left(\mathcal{S}\right)$, and so $|N_H\left(\mathcal{S}\right)|\ge n_2$, as required.

(A4.2) Suppose now that $q\in C_2$. Then (F1), (F2), and (F3) imply that each segment of $\mathcal{S}$ must be incident with at least one of p or w. Then, $\mathcal{S}$ is the disjoint union ${\mathcal{S}}_p$ and ${\mathcal{S}}_w$, where ${\mathcal{S}}_p$ (respectively, ${\mathcal{S}}_w$) denotes the subset of $\mathcal{S}$ contained in $\left\{p\right\}\ast (C_{0,1}\backslash \{p,v\})$ (respectively, $\left\{w\right\}\ast (C_2\backslash \left\{u\right\}))$. Then, $\left|\mathcal{S}\right|=|{\mathcal{S}}_p|+|{\mathcal{S}}_w|\le (n_0+n_1-2)+(n_2-1)$.

Let ${\mathcal{B}}_u^1:=\left\{u\right\}\ast (C_1\backslash \{p,w\})$ and ${\mathcal{B}}_u^{0,2}:=\left\{u\right\}\ast (C_{0,2}\backslash \{u,v\})$. Clearly, ${\mathcal{B}}_u^1$ and ${\mathcal{B}}_u^{0,2}$ are disjoint sets. Moreover, by (A1) and (A3), we may assume that ${\mathcal{B}}_u^{0,2}\subset N_H\left(\mathcal{S}\right)$.

Suppose first that ${\mathcal{S}}_p$ has no segments in $\left\{p\right\}\ast (C_0\backslash \left\{v\right\})$. Then ${\mathcal{S}}_p\subseteq \left\{p\right\}\ast (C_1\backslash \left\{p\right\})$, and so $\left|\mathcal{S}\right|=|{\mathcal{S}}_p|+|{\mathcal{S}}_w|\le (n_1-1)+(n_2-1)$. We may assume that $n_0+n_2-2=|{\mathcal{B}}_u^{0,2}|\le |N_H\left(\mathcal{S}\right)|<|{\mathcal{S}}_p|+|{\mathcal{S}}_w|\le n_1+n_2-2$, as otherwise we are done. Since $n_0\ge n_1-1$, then we must have that $n_0=n_1-1,{\mathcal{S}}_p=\left\{p\right\}\ast (C_1\backslash \left\{p\right\}),$ and ${\mathcal{S}}_w=\left\{w\right\}\ast (C_2\backslash \left\{u\right\})$. From ${\mathcal{S}}_p=\left\{p\right\}\ast (C_1\backslash \left\{p\right\})$ it follows that $pw\in \mathcal{S}$, and hence ${\mathcal{B}}_u^1\subset N_H\left(pw\right)\subset N_H\left(\mathcal{S}\right)$. Since ${\mathcal{B}}_u^1$ and ${\mathcal{B}}_u^{0,2}$ are pairwise disjoint, $|N_H\left(\mathcal{S}\right)|\ge (n_0+n_2-2)+(n_1-2)>n_1+n_2-2\ge \left|\mathcal{S}\right|$, as required.

Suppose now that ${\mathcal{S}}_p$ has a segment e in $\left\{p\right\}\ast (C_0\backslash \left\{v\right\})$. Then ${\mathcal{B}}_u^1\subset N_H\left(e\right)\subset N_H\left(\mathcal{S}\right)$, and hence $|N_H\left(\mathcal{S}\right)|\ge |{\mathcal{B}}_u^{0,2}|+|{\mathcal{B}}_u^1|=(n_0+n_2-2)+(n_1-2)$. Thus, we may assume that $|{\mathcal{S}}_p|=n_0+n_1-2$ and $|{\mathcal{S}}_w|=n_2-1$, as otherwise we are done. Then, ${\mathcal{S}}_p=\left\{p\right\}\ast (C_{0,1}\backslash \{p,v\})$ and ${\mathcal{S}}_w=\left\{w\right\}\ast (C_2\backslash \left\{u\right\})$.

From ${\mathcal{S}}_p=\left\{p\right\}\ast (C_{0,1}\backslash \{p,v\})$ and (F2) it is not hard to see that $vp$ must be the segment of $C_0\ast C_1$ with either the smallest or the largest length. Let ${\mathcal{B}}^{\prime }:=(C_0\backslash \left\{v\right\})\ast (C_2\backslash \left\{u\right\})$. If $vp$ is the segment of $C_0\ast C_1$ with the smallest (respectively, largest) length, then ${\mathcal{S}}_w=\left\{w\right\}\ast (C_2\backslash \left\{u\right\})$ and (F1) imply that $pu$ must have the largest (respectively, smallest) length among all segments in $\left\{p\right\}\ast C_2$, and hence ${\mathcal{B}}^{\prime }\subset N_H\left(\mathcal{S}\right)$. Since ${\mathcal{B}}_u^1,B_u^{0,2},$ and ${\mathcal{B}}^{\prime }$ are pairwise disjoint and $|{\mathcal{B}}^{\prime }|\ge (n_0-1)(n_2-1)\ge 4$, then $|N_H\left(\mathcal{S}\right)|\ge (n_0+n_2-2)+(n_1-2)+4>\left|\mathcal{S}\right|$, as required.

(B) Suppose that $\left|\mathcal{B}\right|<\left|\mathcal{A}\right|$, and let $\mathcal{S}\subseteq \mathcal{B}$. We can assume that $\mathcal{S}\ne \varnothing$ and that $\mathcal{A}\backslash N_H\left(\mathcal{S}\right)\ne \varnothing$, as otherwise we are done. Let $d:{\mathbb{R}}^2\to {\mathbb{R}}_{\ge 0}$ denote the ordinary euclidean distance in ${\mathbb{R}}^2$. For $i\in \{0,1,2\}$ and $x\in C_i$, we let $C_i^{>x}:=\left\{y\right|y\in C_{i}andd(O,y)>d(O,x)\}$. The set $C_i^{<x}$ is defined analogously. It is not hard to see that $\mathcal{A}\subseteq \mathcal{F}$, where

$$\mathcal{F}:=(\left\{w\right\}\ast (Q_n\backslash \{u,v,w\}))\cup (C_0^{<v}\ast C_1^{>w})\cup (C_0^{>v}\ast C_1^{<w})\cup (C_1^{<w}\ast C_1^{>w}).$$

Note that ${\mathcal{F}}_w:=\left\{w\right\}\ast (Q_n\backslash \{u,v,w\})$ is a subset of $\mathcal{A}$. Since no segment of $\mathcal{B}$ intersects every segment of ${\mathcal{F}}_w$, then at least one segment of ${\mathcal{F}}_w$ is in $N_H\left(\mathcal{S}\right)$, and so $|N_H\left(\mathcal{S}\right)|\ge 1$. Thus $\left|\mathcal{S}\right|\ge 2$, as otherwise we are done.

(B1) Suppose that $\mathcal{S}$ has two distinct segments of type 0, say $e_1$ and $e_2$, so that $e_1\cap e_2\cap C_0=\varnothing$. Then $\mathcal{A}\subseteq N_H\left(\{e_1,e_2\}\right)\subseteq N_H\left(\mathcal{S}\right)$, unless $e_1\cap e_2=y\in C_2$. Since the former case contradicts $\mathcal{A}\backslash N_H\left(\mathcal{S}\right)\ne \varnothing$, we assume that $e_1\cap e_2=y\in C_2$. Then $\mathcal{A}\backslash \left\{yw\right\}\subseteq N_H\left(\{e_1,e_2\}\right)$, and hence $|N_H\left(\mathcal{S}\right)|\ge |N_H\left(\{e_1,e_2\}\right)|\ge |\mathcal{A}|-1\ge |\mathcal{B}|\ge |\mathcal{S}|$, as required.

(B2) Suppose now that each segment of $\mathcal{S}$ is incident with exactly one point $x\in C_0$. Clearly, $x\ne v$. If $x\ne u$, then $\mathcal{S}\subseteq \left\{x\right\}\ast (C_{0,2}\backslash \{x,v\})$, and hence $\left|\mathcal{S}\right|\le n_0+n_2-2$. Since $\left|\mathcal{S}\right|\ge 2$, then $C_{0,2}\backslash \{x,v\}$ has at least two points, say $z_1$ and $z_2$, such that $x{z}_1,x{z}_2\in \mathcal{S}$. We note that ${\mathcal{F}}_w\backslash \left\{wx\right\}\subseteq N_H\left(\{x{z}_1,x{z}_2\}\right)\subseteq N_H\left(\mathcal{S}\right)$, and so $|N_H\left(\mathcal{S}\right)|\ge |{\mathcal{F}}_w|-1\ge n_0+n_1+n_2-4$. Since $n_1\ge 3$, then $|N_H\left(\mathcal{S}\right)|\ge n_0+n_2-1\ge \left|\mathcal{S}\right|$.

Suppose now that $u=x$. Then $\mathcal{S}\subseteq \left\{u\right\}\ast (Q_n\backslash \{u,v,w\})$, and so $\left|\mathcal{S}\right|\le n_0+n_1+n_2-3$. If $\mathcal{S}$ has at least one segment in $\left\{u\right\}\ast C_2$, then $\left|\mathcal{S}\right|\ge 2$ implies that ${\mathcal{F}}_w\subseteq N_H\left(\mathcal{S}\right)$, and so $|N_H\left(\mathcal{S}\right)|\ge |{\mathcal{F}}_w|\ge n_0+n_1+n_2-3\ge \left|\mathcal{S}\right|$. Then, we may assume that $\mathcal{S}$ has no segments in $\left\{u\right\}\ast C_2$, and hence $\left\{w\right\}\ast C_2\subseteq N_H\left(\mathcal{S}\right)$.

Let $W_1$ be the subset of all points in $C_1$ that are incident with a segment of $\mathcal{S}$. Then $\mathcal{S}\subseteq \left\{u\right\}\ast (W_1\cup C_0\backslash \{u,v\})$, and so $\left|\mathcal{S}\right|\le |W_1|+n_0-2$. If $W_1=\varnothing$, then $\left|\mathcal{S}\right|\le n_0-2\le n_2=|\left\{w\right\}\ast C_2|\le |N_H\left(\mathcal{S}\right)|$, as required. Then we can assume that $W_1\ne \varnothing$. Let $w^{\prime }$ be the point in $W_1$ that is farthest from w. Since any segment in $\left\{w\right\}\ast (W_1\backslash \left\{w^{\prime }\right\})$ is disjoint from $u{w}^{\prime }$, then ${\mathcal{F}}_w^{\prime }:=\left\{w\right\}\ast (C_2\cup (W_1\backslash \left\{w^{\prime }\right\}))$ is a subset of $N_H\left(\mathcal{S}\right)$, and hence $|N_H\left(\mathcal{S}\right)|\ge |{\mathcal{F}}_w^{\prime }|\ge |W_1|-1+n_2\ge |W_1|+n_0-2\ge \left|\mathcal{S}\right|$.

(B3) Suppose that $u\in C_2$. Let ${\mathcal{S}}^{\prime }$ be the set of all segments of $\mathcal{S}$ that are not incident with u. Suppose first that ${\mathcal{S}}^{\prime }=\varnothing$. Then (B1) implies that $\mathcal{S}$ has at most one segment in $\left\{u\right\}\ast C_0$. If there exists $x\in C_0$ such that $ux\in \mathcal{S}$, then $\left|\mathcal{S}\right|\ge 2$ implies that $\mathcal{A}\subseteq N_H\left(\mathcal{S}\right)$, and hence $|N_H\left(\mathcal{S}\right)|\ge |\mathcal{A}|>|\mathcal{B}|\ge |\mathcal{S}|$. Thus, we may assume that $\mathcal{S}\subseteq \left\{u\right\}\ast (C_{1,2}\backslash \{u,w\})$. For $k=1,2$, let $W_k$ be the subset of all points in $C_k\backslash \{u,w\}$ that are incident with a segment of $\mathcal{S}$. Then $\mathcal{S}=\left\{u\right\}*(W_1\cup W_2)$, and so $\left|\mathcal{S}\right|=|W_1|+|W_2|$. If $W_k\ne \varnothing$, then we use $w_k$ to denote the point in $W_k$ that is closest to w if $k=1$ (resp. u if $k=2$). Since any segment in $\left\{w\right\}\ast (W_k\backslash \left\{w_k\right\})$ is disjoint from at least one of $u{w}_1$ or $u{w}_2$, then ${\mathcal{F}}_w^{\prime }:=\left\{w\right\}\ast ((C_0\cup W_1\cup W_2)\backslash \{v,w_1,w_2\})$ is a subset of $N_H\left(\mathcal{S}\right)$, and hence $|N_H\left(\mathcal{S}\right)|\ge |{\mathcal{F}}_w^{\prime }|\ge n_0+|W_1|+|W_2|-3\ge |W_1|+|W_2|\ge |\mathcal{S}|$.

Suppose now that ${\mathcal{S}}^{\prime }\ne \varnothing$. Then each segment of ${\mathcal{S}}^{\prime }$ crosses a, and has at least one endpoint in $C_0\backslash \left\{v\right\}$. From (B2) it follows that there is $x\in C_0\backslash \left\{v\right\}$ such that ${\mathcal{S}}^{\prime }\subseteq \left\{x\right\}\ast C_2$. This fact and (B2) imply the existence of $uy\in \mathcal{S}$ with $y\in C_{1,2}\backslash \{u,w\}$. Note that if $|{\mathcal{S}}^{\prime }|>1$, then $\mathcal{A}\backslash \left\{xy\right\}\subseteq N_H({\mathcal{S}}^{\prime }\cup \left\{uy\right\})\subseteq N_H\left(\mathcal{S}\right)$. On the other hand, if ${\mathcal{S}}^{\prime }=\left\{xz\right\}$ for some $z\in C_2\backslash \left\{u\right\}$, then $\mathcal{A}\backslash \left\{wz\right\}\subseteq N_H\left(\{xz,uy\}\right)\subseteq N_H\left(\mathcal{S}\right)$. In any case, we have $|N_H\left(\mathcal{S}\right)|\ge |\mathcal{A}|-1\ge |\mathcal{B}|\ge |\mathcal{S}|$.

(B4) Suppose that $u\in C_0$. Let ${\mathcal{S}}_u$ be the set of all segments of $\mathcal{S}$ in $\left\{u\right\}\ast (C_1\backslash \left\{w\right\})$, and let ${\mathcal{S}}^{\prime }=\mathcal{S}\backslash {\mathcal{S}}_u$. Then, any element in ${\mathcal{S}}^{\prime }$ is a segment of type 0. We may assume that ${\mathcal{S}}_u\ne \varnothing$, as otherwise we are in (B1) or (B2) due to $\left|\mathcal{S}\right|\ge 2$. Similarly, if ${\mathcal{S}}^{\prime }=\varnothing$, then $\left|\mathcal{S}\right|=|{\mathcal{S}}_u|\le n_1-1$. From ${\mathcal{S}}_u\ne \varnothing$ we have that $\left\{w\right\}\ast C_2\subseteq N_H\left(\mathcal{S}\right)$, and so $|N_H\left(\mathcal{S}\right)|\ge n_2\ge n_1-1\ge \left|\mathcal{S}\right|$. Thus, we also assume that ${\mathcal{S}}^{\prime }\ne \varnothing$.

From (B1) and ${\mathcal{S}}^{\prime }\ne \varnothing$ we know that there exists a point $x\in C_0\backslash \left\{v\right\}$ that is incident with any segment of ${\mathcal{S}}^{\prime }$. Since $\left\{w\right\}\ast C_2\subseteq N_H\left({\mathcal{S}}_u\right)$ and $\left\{w\right\}\ast (C_0\cup C_1\backslash \{u,v,x,w\})\subseteq N_H\left({\mathcal{S}}^{\prime }\right)$, then $|N_H\left(\mathcal{S}\right)|\ge n_0+n_1+n_2-4$. Seeking a contradiction, suppose that $\left|\mathcal{S}\right|\ge n_0+n_1+n_2-3$. Since $|{\mathcal{S}}_u|\le n_1-1$, then $|{\mathcal{S}}^{\prime }|\ge n_0+n_2-2$. From ${\mathcal{S}}^{\prime }\subseteq \left\{x\right\}\ast C_{0,2}\backslash \{x,v\}$ and $n_0\ge 3$ it follows that ${\mathcal{S}}^{\prime }$ has a segment $e=xy$ with $y\in C_0\backslash \{x,v\}$. Since e together with any other $e^{\prime }\in {\mathcal{S}}^{\prime }\backslash \left\{e\right\}$ satisfy the conditions of (B1), then we must have that ${\mathcal{S}}^{\prime }=\left\{e\right\}$, contradicting $|{\mathcal{S}}^{\prime }|\ge n_0+n_2-2$. □

4.2.2. Suppose That a and b Have The Same Type

Then, a and b are located in ${\mathcal{Q}}_n$ according to some case of Figure 4. For $i=0,1,2$ let $E_i$ be the set of points in $C_i$ that are endpoints of at least one of a and b, and let $C_i^{\prime }:=C_i\backslash E_i$. Then, $3\le |E_0|+|E_1|+|E_2|\le 4$. From a simple inspection of the ten cases in Figure 4 we can see that $|E_0|\in \{1,2,3,4\}$, $|E_1|=0$, and $|E_2|\in \{0,1,2\}$. Thus, for $i=0,1,2$ the following holds:

$$\lfloor n/3\rfloor +1\ge |C_i|\ge |C_i^{\prime }|\ge \lfloor n/3\rfloor -4\ge 1.$$

(3)

Let $G_n^{\prime }$ be the subgraph of $G_n$ induced by $C_{0,2}$, i.e., $G_n^{\prime }:=D\left(C_{0,2}\right)$. Similarly, let

$${\mathcal{D}}_1:=(C_1\ast C_1)\cup (C_1\ast C_0^{\prime })\cup (C_1\ast C_2^{\prime }).$$

It is easy to check that ${\mathcal{D}}_1$ and $G_n^{\prime }$ satisfy the following properties: (i) the three sets forming ${\mathcal{D}}_1$ are pairwise disjoint, (ii) no segment of ${\mathcal{D}}_1$ belongs to $G_n^{\prime }$, (iii) ${\mathcal{D}}_1\subseteq \mathcal{D}$, and (iv) a and b are vertices of $G_n^{\prime }$.

By applying the main result of [14] to $G_n^{\prime }$ we have that the connectivity of $G_n^{\prime }$ is at least

$${\kappa }_n^{\prime }:=\left(\genfrac{}{}{0pt}{}{\lfloor \frac{m-2}{2}\rfloor }{2}\right)+\left(\genfrac{}{}{0pt}{}{\lceil \frac{m-2}{2}\rceil }{2}\right),$$

(4)

where $m=|C_{0,2}|$.

We are finally ready to prove Lemma 9.

Proof of Lemma 9. 

We analyze two cases separately, depending on whether a and b are located in ${\mathcal{Q}}_n$ according to some case of Figure 3 or Figure 4. □

Case 1. Suppose that a and b are located in ${\mathcal{Q}}_n$ according to some case of Figure 3, and let $H\subseteq G_n$ be as in Section 4.2.1. From Proposition 11 and Hall’s theorem it follows that H has a matching M of size $m_1:=min\left\{\right|\mathcal{A}|,|\mathcal{B}\left|\right\}$. Suppose that $M=\left\{a_k{b}_k\right|a_k\in \mathcal{A},b_k\in \mathcal{B},\mathrm{and} k=1,2,\dots ,m_1\}.$ Then

$$\mathbb{L}:=\left\{a{a}_k{b}_{k}b|a_k{b}_k\in M\right\},$$

is a collection $a-b$ paths of $G_n$ of length 3. Furthermore, the paths in $\mathbb{L}$ are pairwise internally disjoint, because M is a matching of H. On the other hand, note that

$${\mathbb{L}}^{\prime }:=\left\{adb|d\in \mathcal{D}\right\},$$

is also a collection of pairwise internally disjoint $a-b$ paths of $G_n$ of length 2. Since $\mathcal{D}\cap (\mathcal{A}\cup \mathcal{B})=\varnothing$, then the paths in $\mathbb{L}\cup {\mathbb{L}}^{\prime }$ are pairwise internally disjoint. The existence of such $m_1+\left|\mathcal{D}\right|$ paths, and (2) imply

$$\eta (Q_n;a,b)=\left|\mathcal{D}\right|+m_1=\left|\mathcal{D}\right|+min\left\{\right|\mathcal{A}|,|\mathcal{B}\left|\right\}=min\{{deg}_{G_n}\left(a\right),{deg}_{G_n}\left(b\right)\}.$$

(5)

Combining Proposition 2 and Theorem 3 we obtain that $\delta \left(G_n\right)=\frac{7}{18}{n}^2+\Theta \left(n\right)$. Since $min\{{deg}_{G_n}\left(a\right),{deg}_{G_n}\left(b\right)\}\ge \delta \left(G_n\right)$, then (2) and (5) imply $\eta (Q_n;a,b)=\frac{7}{18}{n}^2+\Theta \left(n\right)=\frac{7}{18}{n}^2-\Theta \left(n\right)$, as required.

Case 2. Suppose now that a and b are located in ${\mathcal{Q}}_n$ according to some case of Figure 4, and let $G_n^{\prime },C_i^{\prime },{\mathcal{D}}_1,{\kappa }_n^{\prime },m,$ and Properties (i)–(iv) as in Section 4.2.2.

Since $2\lfloor \frac{n}{3}\rfloor \le m\le 2\lfloor \frac{n}{3}\rfloor +2$, a straightforward manipulation on (4) gives that $k_n^{\prime }=\frac{2}{18}{n}^2-\Theta \left(n\right)$. This last equality, (iv), and Menger’s theorem imply that $G_n^{\prime }$ has collection $\mathbb{T}$ of at least $\frac{2}{18}{n}^2-\Theta \left(n\right)$ pairwise internally disjoint $a-b$ paths. On the other hand, from (iii) it follows that

$${\mathbb{T}}^{\prime }:=\left\{adb|d\in {\mathcal{D}}_1\right\},$$

is a collection of $|{\mathcal{D}}_1|$ pairwise internally disjoint $a-b$ paths of $G_n$ of length 2. Moreover, by (ii) we have that $\mathbb{T}\cup {\mathbb{T}}^{\prime }$ is also a collection of pairwise internally disjoint $a-b$ paths of $G_n$. From (3), (i), and the definition of ${\mathbb{T}}^{\prime }$, it is not hard to see that

$$|{\mathbb{T}}^{\prime }|=|{\mathcal{D}}_1|=\left(\genfrac{}{}{0pt}{}{|C_1|}{2}\right)+|C_1\left|\right|C_0^{\prime }|+|C_1\left|\right|C_2^{\prime }|\ge \frac{5}{18}{n}^2-\Theta \left(n\right).$$

Thus, $\eta (Q_n;a,b)\ge |\mathbb{T}\cup {\mathbb{T}}^{\prime }|\ge \frac{7}{18}{n}^2-\Theta \left(n\right)$. This last and (2) imply $\eta (Q_n;a,b)=\frac{7}{18}{n}^2-\Theta \left(n\right)$, as required. □

5. Concluding Remarks

Let P be a set of $n\ge 3$ points in general position in the plane. We have observed that the minimum degree $\delta \left(D\right(P\left)\right)$ of the disjointness graph of segments defined by P can be expressed in terms of n and the rectilinear local crossing number of the rectilinear drawing $\mathcal{P}$ of $K_n$ induced by P. From this observation and the exact value of $\overline{lcr}\left(K_n\right)$ provided by Theorem 1 in [19], it is easy to see that $\left(\genfrac{}{}{0pt}{}{n}{2}\right)-\overline{lcr}\left(K_n\right)$ is an upper bound for $\delta \left(D\right(P\left)\right)$, which is tight for each n. Since the connectivity $\kappa \left(H\right)$ of a graph H is upper bounded by its minimum degree $\delta \left(H\right)$, then $\left(\genfrac{}{}{0pt}{}{n}{2}\right)-\overline{lcr}\left(K_n\right)$ is also a general upper bound for $\kappa \left(D\right(P\left)\right)$.

On the other hand, the main goal in this work is to estimate the connectivity of $D\left(Q_n\right)$, where ${\left\{Q_n\right\}}_{n=3}^{\infty }$ is one of the families of point sets best understood from the point of view of rectilinear crossing number. In particular, it is known that $Q_n$ is almost 3-symmetric and that $\overline{lcr}\left(K_n\right)=\overline{lcr}\left({\mathcal{Q}}_n\right)$ for each $n\not\equiv 2(mod3)$. The basic idea behind our approach is to show that $\delta \left(D\left(Q_n\right)\right)-\kappa \left(D\left(Q_n\right)\right)$ cannot be too large. In fact, we strongly believe that $\delta \left(D\left(Q_n\right)\right)=\kappa \left(D\left(Q_n\right)\right)$ holds, and that this equality can be verified by analogous arguments to those used in Section 4.2.1. We finally remark that Theorem 1 is an asymptotic solution for an open question posed in [14].