From the Quasi-Total Strong Differential to Quasi-Total Italian Domination in Graphs

Abstract

This paper is devoted to the study of the quasi-total strong differential of a graph, and it is a contribution to the Special Issue “Theoretical computer science and discrete mathematics” of Symmetry. Given a vertex $x\in V\left(G\right)$ of a graph G, the neighbourhood of x is denoted by $N\left(x\right)$. The neighbourhood of a set $X\subseteq V\left(G\right)$ is defined to be $N\left(X\right)={\bigcup }_{x\in X}N\left(x\right)$, while the external neighbourhood of X is defined to be $N_e\left(X\right)=N\left(X\right)\setminus X$. Now, for every set $X\subseteq V\left(G\right)$ and every vertex $x\in X$, the external private neighbourhood of x with respect to X is defined as the set $P_e(x,X)=\{y\in V\left(G\right)\setminus X:N\left(y\right)\cap X=\left\{x\right\}\}.$ Let $X_w=\{x\in X:P_e(x,X)\ne ⌀\}$. The strong differential of X is defined to be ${\partial }_s\left(X\right)=|N_e\left(X\right)|-|X_w|$, while the quasi-total strong differential of G is defined to be ${\partial }_{s^{*}}\left(G\right)=max\{{\partial }_s\left(X\right):X\subseteq V\left(G\right)\mathrm{and}{X}_w\subseteq N\left(X\right)\}.$ We show that the quasi-total strong differential is closely related to several graph parameters, including the domination number, the total domination number, the 2-domination number, the vertex cover number, the semitotal domination number, the strong differential, and the quasi-total Italian domination number. As a consequence of the study, we show that the problem of finding the quasi-total strong differential of a graph is NP-hard.

1. Introduction

Given a graph $G=\left(V\right(G),E(G\left)\right)$, the open neighbourhood of a vertex $x\in V\left(G\right)$ is defined to be $N\left(x\right)=\{y\in V(G):xy\in E(G\left)\right\}$. The open neighbourhood of a set $X\subseteq V\left(G\right)$ is defined by $N\left(X\right)={\bigcup }_{x\in X}N\left(x\right)$, while the external neighbourhood of X, or boundary of X, is defined as $N_e\left(X\right)=N\left(X\right)\setminus X$.

The differential of a subset $X\subseteq V\left(G\right)$ is defined as $\partial \left(X\right)=|N_e\left(X\right)|-|X|$ and the differential of a graph G is defined as

$$\partial \left(G\right)=max\{\partial (X):X\subseteq V(G\left)\right\}.$$

These concepts were introduced by Hedetniemi about twenty-five years ago in an unpublished paper, and the preliminary results on the topic were developed by Goddard and Henning [1]. The development of the topic was subsequently continued by several authors, including [2,3,4,5,6,7]. Currently, the study of differentials in graphs and their variants is of great interest because it has been observed that the study of different types of domination can be approached through a variant of the differential which is related to them. Specifically, we are referring to domination parameters that are necessarily defined through the use of functions, such as Roman domination, perfect Roman domination, Italian domination and unique response Roman domination. In each case, the main result linking the domination parameter to the corresponding differential is a Gallai-type theorem, which allows us to study these domination parameters without the use of functions. For instance, the differential is related to the Roman domination number [3], the perfect differential is related to the perfect Roman domination number [5], the strong differential is related to the Italian domination number [8], the 2-packing differential is related to the unique response Roman domination number [9]. Next, we will briefly describe the case of the strong differential and then introduce the study of the quasi-total strong differential. We refer the reader to the corresponding papers for details on the other cases.

For any $x\in X$, the external private neighbourhood of x with respect to X is defined to be

$$P_e(x,X)=\{y\in V\left(G\right)\setminus X:N\left(y\right)\cap X=\left\{x\right\}\}.$$

We define the set $X_w=\{x\in X:P_e(x,X)\ne ⌀\}$.

The strong differential of a set X is defined to be

$${\partial }_s\left(X\right)=|N_e\left(X\right)|-|X_w|,$$

while the strong differential of G is defined to be

$${\partial }_s\left(G\right)=max\{{\partial }_s\left(X\right):X\subseteq V\left(G\right)\}.$$

As shown in [8], the problem of finding the strong differential of a graph is NP-hard, and this parameter is closely related to several graph parameters. In particular, the theory of strong differentials allows us to develop the theory of Italian domination without the use of functions.

In this paper, we study the quasi-total strong differential of G, which is defined as

$${\partial }_{s^{*}}\left(G\right)=max\{{\partial }_s\left(X\right):X\subseteq V\left(G\right)\mathrm{and}{X}_w\subseteq N\left(X\right)\}.$$

We will show that this novel parameter is perfectly integrated into the theory of domination. In particular, we will show that the quasi-total strong differential is closely related to several graph parameters, including the domination number, the total domination number, the 2-domination number, the vertex cover number, the semitotal domination number, the strong differential, and the quasi-total Italian domination number. As a consequence of the study, we show that the problem of finding the quasi-total strong differential of a graph is NP-hard.

The paper is organised as follows. Section 2 is devoted to establish the main notation, terminology and tools needed to develop the remaining sections. In Section 3 we obtain several bounds on the quasi-total strong differential of a graph and we discuss the tightness of these bounds. In Section 4 we prove a Gallai-type theorem which shows that the theory of quasi-total strong differentials can be applied to develop the theory of Italian domination, provided that the Italian dominating functions fulfil an additional condition. Finally, in Section 5 we show that the problem of finding the quasi-total strong differential of a graph is NP-hard.

2. Notation, Terminology and Basic Tools

Throughout the paper, we will use the notation $G\cong H$ if G and H are isomorphic graphs. Given a set $X\subseteq V\left(G\right)$, the subgraph of G induced by X will be denoted by $G\left[X\right]$, while (for simplicity) the subgraph induced by $V\left(G\right)\setminus X$ will be denoted by $G-X$. The minimum degree, the maximum degree and the order of G will be denoted by $\delta \left(G\right)$, $\mathrm{\Delta }\left(G\right)$ and $n\left(G\right)$, respectively.

A leaf of G is a vertex of degree one. A support vertex of G is a vertex which is adjacent to a leaf, while a strong support vertex is a vertex which is adjacent to at least two leaves. The set of leaves, support vertices and strong support vertices of G will be denoted by $\mathcal{L}\left(G\right)$, $\mathcal{S}\left(G\right)$ and ${\mathcal{S}}_s\left(G\right)$, respectively.

A dominating set of G is a subset $D\subseteq V\left(G\right)$ such that $N\left(v\right)\cap D\ne ⌀$ for every $v\in V\left(G\right)\setminus D$. Let $\mathcal{D}\left(G\right)$ be the set of dominating sets of G. The domination number of G is defined to be,

$$\gamma \left(G\right)=min\left\{\right|D|:D\in \mathcal{D}(G\left)\right\}.$$

The domination number has been extensively studied. For instance, we cite the following books [10,11,12].

We define a $\gamma \left(G\right)$-set as a set $D\in \mathcal{D}\left(G\right)$ with $\left|D\right|=\gamma \left(G\right)$. The same agreement will be assumed for optimal parameters associated to other characteristic sets of a graph. For instance, a ${\partial }_{s^{*}}\left(G\right)$-set will be a set $X\subseteq V\left(G\right)$ such that $X_w\subseteq N\left(X\right)$ and ${\partial }_s\left(X\right)={\partial }_{s^{*}}\left(G\right)$.

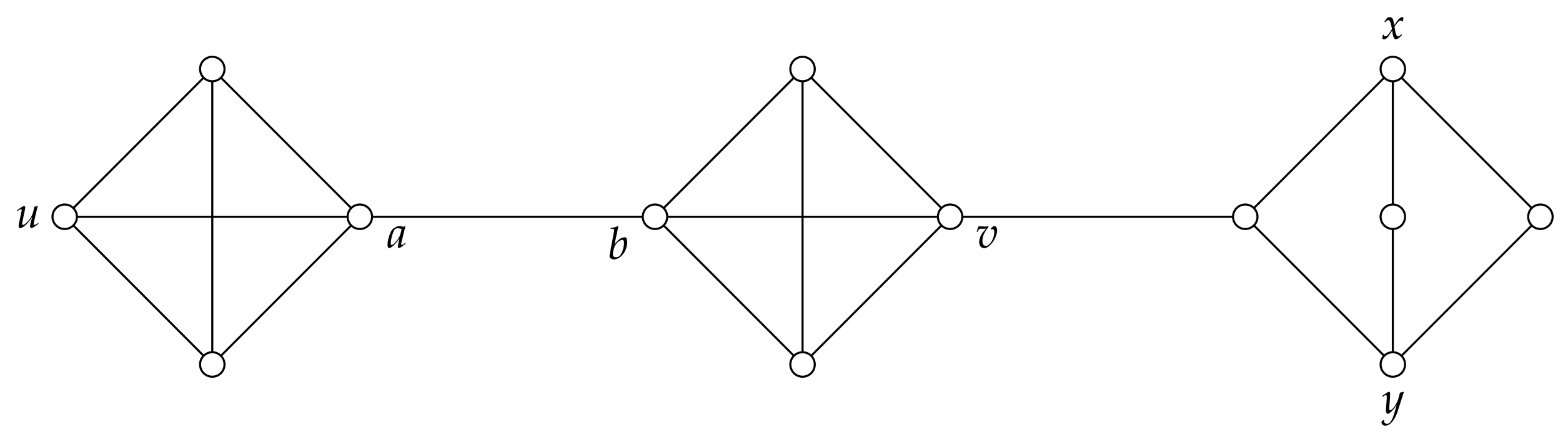
As described in Figure 1, $X=\{a,b,x,y\}$ is a ${\partial }_{s^{*}}\left(G\right)$-set while $X^{\prime }=\{u,v,x,y\}$ is not a ${\partial }_{s^{*}}\left(G\right)$-set, as $X_w^{\prime }=\{u,v\}\neg \subseteq N\left(X^{\prime }\right)$. In contrast, both X and $X^{\prime }$ are ${\partial }_s\left(G\right)$-sets. Another ${\partial }_{s^{*}}\left(G\right)$-sets are $Y=\{a,b,u,v,x,y\}$ and $Y^{\prime }=\{a,b,v,x,y\}$.

A total dominating set of G is a subset $D\subseteq V\left(G\right)$ such that $N\left(v\right)\cap D\ne ⌀$ for every vertex $v\in V\left(G\right)$. Let ${\mathcal{D}}_t\left(G\right)$ be the set of total dominating sets of G. The total domination number of G is defined to be,

$${\gamma }_t\left(G\right)=min\left\{\right|D|:D\in {\mathcal{D}}_t\left(G\right)\}.$$

The total domination number has been extensively studied. For instance, we cite the book [13].

A k-dominating set of G is a subset $D\subseteq V\left(G\right)$ such that $\left|N\right(v)\cap D|\ge k$ for every vertex $v\in V\left(G\right)\setminus D$. Let ${\mathcal{D}}_k\left(G\right)$ be the set of k-dominating sets of G. The k-domination number of G is defined to be,

$${\gamma }_{{}_k}\left(G\right)=min\left\{\right|D|:D\in {\mathcal{D}}_k\left(G\right)\}.$$

For a comprehensive survey on k-domination in graphs, we cite the book [10] published in 2020. In particular, there is a chapter, Multiple Domination, by Hansberg and Volkmann, where they put into context all relevant research results on multiple domination concerning k-domination that have been found up to 2020.

In particular, the following result will be useful in the study of quasi-total strong differentials.

Theorem 1

([14]). Let r and k be positive integers. For any graph G with $\delta \left(G\right)\ge \frac{r+1}{r}k-1$,

$${\gamma }_{{}_k}\left(G\right)\le \frac{r}{r+1}n\left(G\right).$$

A semitotal dominating set of a graph G with no isolated vertex, is a dominating set D of G such that every vertex in D is within distance two of another vertex in D. This concept was introduced in 2014 by Goddard et al. in [15]. Let ${\mathcal{D}}_{t2}\left(G\right)$ be the set of semitotal dominating sets of G. The semitotal domination number of G is defined to be

$${\gamma }_{{}_{t2}}\left(G\right)=min\left\{\right|D|:D\in {\mathcal{D}}_{t2}\left(G\right)\}.$$

By definition,

$$\gamma \left(G\right)\le {\gamma }_{{}_{t2}}\left(G\right)\le min\{{\gamma }_{{}_t}\left(G\right),{\gamma }_{{}_2}\left(G\right)\}.$$

A set $C\subseteq V\left(G\right)$ is a vertex cover of G if every edge of G is incident with at least one vertex in C. The vertex cover number of G, denoted by $\beta \left(G\right)$, is the minimum cardinality among all vertex covers of G. Recall that the largest cardinality of a set of vertices of G, no two of which are adjacent, is called the independence number of G and it is denoted by $\alpha \left(G\right)$. The following well-known result, due to Gallai, states the relationship between the independence number and the vertex cover number of a graph.

Theorem 2

(Gallai’s theorem, [16]). For any graph G,

$$\alpha \left(G\right)+\beta \left(G\right)=n\left(G\right).$$

The concept of a corona product graph was introduced in 1970 by Frucht and Harary [17]. Given two graphs $G_1$ and $G_2$, the corona product graph $G_1\odot G_2$ is the graph obtained from $G_1$ and $G_2$, by taking one copy of $G_1$ and $n\left(G_1\right)$ copies of $G_2$ and joining by an edge every vertex from the $i^{th}$-copy of $G_2$ with the $i^{th}$-vertex of $G_1$. Notice that $n(G_1\odot G_2)=n\left(G_1\right)(n\left(G_2\right)+1)$ and $\gamma (G_1\odot G_2)=n\left(G_1\right)$.

The following result will be one of our main tools.

Theorem 3

([8]). For any graph G, the following statements hold.

(i) 

There exists a ${\partial }_s\left(G\right)$-set which is a dominating set of G.

(ii) 

$n\left(G\right)-min\{2\gamma \left(G\right),{\gamma }_{{}_2}\left(G\right)\}\le {\partial }_s\left(G\right)\le n\left(G\right)-\gamma \left(G\right)-\left|{\mathcal{S}}_s\left(G\right)\right|.$

For the remainder of the paper, definitions will be introduced whenever a concept is needed. In particular, this is the case for concepts, notation and terminology that are used only once or only in a short section.

3. General Results

To begin this section we present some bounds on the quasi-total strong differential of a graph, and then we discuss the tightness of the bounds.

Theorem 4.

For any graph G, the following statements hold.

(i) 

${\partial }_s\left(G\right)-\gamma \left(G\right)\le {\partial }_{s^{*}}\left(G\right)\le {\partial }_s\left(G\right).$

(ii) 

$n\left(G\right)-min\{3\gamma \left(G\right),{\gamma }_{{}_2}\left(G\right)\}\le {\partial }_{s^{*}}\left(G\right)\le n\left(G\right)-\gamma \left(G\right)-\left|{\mathcal{S}}_s\left(G\right)\right|.$

Proof. 

The inequality ${\partial }_{s^{*}}\left(G\right)\le {\partial }_s\left(G\right)$ is straightforward, as for any ${\partial }_{s^{*}}\left(G\right)$-set X we have ${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(X\right)\le {\partial }_s\left(G\right)$.

We proceed to prove ${\partial }_{s^{*}}\left(G\right)\ge {\partial }_s\left(G\right)-\gamma \left(G\right)$. Let D be a ${\partial }_s\left(G\right)$-set such that $D\in \mathcal{D}\left(G\right)$, which exists by Theorem 3. Now, we define $D^{\prime \prime }\subseteq V\left(G\right)$ as a set of minimum cardinality among all supersets $D^{\prime }$ of D such that $N\left(v\right)\cap D^{\prime }\ne ⌀$ for every vertex $v\in D_w$. Since D is a dominating set, $D_w^{\prime \prime }\subseteq D_w$. Moreover, observe that $|D^{\prime \prime }\setminus D|\le \gamma \left(G\right)$, by the minimality of $D^{\prime \prime }$. Therefore,

$$\begin{array}{cc}\hfill {\partial }_{s^{*}}\left(G\right)& \ge {\partial }_s\left(D^{\prime \prime }\right)\hfill \\ \hfill & =|N_e\left(D^{\prime \prime }\right)|-|D_w^{\prime \prime }|\hfill \\ \hfill & \ge |N_e\left(D\right)|-|D^{\prime \prime }\setminus D|-|D_w^{\prime \prime }|\hfill \\ \hfill & \ge |N_e\left(D\right)|-|D_w|-|D^{\prime \prime }\setminus D|\hfill \\ \hfill & ={\partial }_s\left(G\right)-|D^{\prime \prime }\setminus D|\hfill \\ \hfill & \ge {\partial }_s\left(G\right)-\gamma \left(G\right),\hfill \end{array}$$

as required.

To prove lower bound ${\partial }_{s^{*}}\left(G\right)\ge n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$ we only need to observe that for any ${\gamma }_{{}_2}\left(G\right)$-set S we have ${\partial }_{s^{*}}\left(G\right)\ge {\partial }_s\left(S\right)=|N_e\left(S\right)|-|S_w|=|N_e\left(S\right)|=n\left(G\right)-|S|=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$.

Finally, to complete the proof of (ii) we only need to combine the previous bounds with Theorem 3. □

Corollary 1.

Let G be a graph. If ${\partial }_s\left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$ or there exists a ${\partial }_s\left(G\right)$-set which is a total dominating set, then ${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(G\right)$.

In order to show some classes of graphs with ${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(G\right)$ and ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-\gamma \left(G\right)-\left|{\mathcal{S}}_s\left(G\right)\right|$, we consider the case of corona graphs. It is not difficult to see that if $G_1$ has no isolated vertex and $G_2$ is a non trivial graph, then

$${\partial }_{s^{*}}(G_1\odot G_2)={\partial }_s(G_1\odot G_2)=n\left(G_1\right)(n\left(G_2\right)-1).$$

In addition, if $G_2$ is a graph with at least two isolated vertices, then

$$\begin{array}{cc}\hfill {\partial }_{s^{*}}(G_1\odot G_2)& =n\left(G_1\right)(n\left(G_2\right)-1)\hfill \\ \hfill & =n(G_1\odot G_2)-\gamma (G_1\odot G_2)-\left|{\mathcal{S}}_s(G_1\odot G_2)\right|.\hfill \end{array}$$

Next we discuss some cases where the lower bounds given in Theorem 4 are achieved.

Theorem 5.

For any graph G, the following statements are equivalent.

(i) 

${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(G\right)-\gamma \left(G\right)$.

(ii) 

${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-3\gamma \left(G\right)$.

Proof. 

Assume ${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(G\right)-\gamma \left(G\right)$. By Theorem 3, there exists a set $D\in \mathcal{D}\left(G\right)$ which is a ${\partial }_s\left(G\right)$-set. Now, we define $D^{\prime \prime }\subseteq V\left(G\right)$ as a set of minimum cardinality among all supersets $D^{\prime }$ of D such that $N\left(v\right)\cap D^{\prime }\ne ⌀$ for every vertex $v\in D_w$. Obviously, $|D^{\prime \prime }\setminus D|\le |D_w|\le |D|$. As we have shown in the proof of Theorem 4,

$${\partial }_{s^{*}}\left(G\right)\ge {\partial }_s\left(G\right)-|D^{\prime \prime }\setminus D|\ge {\partial }_s\left(G\right)-\gamma \left(G\right),$$

which implies that $\gamma \left(G\right)=|D^{\prime \prime }\setminus D|$, and so $\gamma \left(G\right)\le |D_w|\le |D|$. On the other side, ${\partial }_s\left(G\right)\ge n\left(G\right)-2\gamma \left(G\right)$, by Theorem 3. In summary,

$$n\left(G\right)-2\gamma \left(G\right)\le {\partial }_s\left(G\right)=n\left(G\right)-\left|D\right|-|D_w|\le n\left(G\right)-2\gamma \left(G\right),$$

Therefore, ${\partial }_s\left(G\right)=n\left(G\right)-2\gamma \left(G\right)$, and so ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-3\gamma \left(G\right)$.

Conversely, assume ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-3\gamma \left(G\right)$. By Theorems 3 and 4 we have

$$n\left(G\right)-3\gamma \left(G\right)={\partial }_{s^{*}}\left(G\right)\ge {\partial }_s\left(G\right)-\gamma \left(G\right)\ge n\left(G\right)-3\gamma \left(G\right).$$

Therefore, ${\partial }_s\left(G\right)=n\left(G\right)-2\gamma \left(G\right)$ and, as a result, ${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(G\right)-\gamma \left(G\right)$. □

To continue the study, we need to establish the following lemma.

Lemma 1.

For any graph G, there exists a ${\partial }_{s^{*}}\left(G\right)$-set X which is a dominating set of G and $|P_e(v,X)|\ge 2$ for every $v\in X_w$.

Proof. 

Let D be a ${\partial }_{s^{*}}\left(G\right)$-set and $D^{\prime }=V\left(G\right)\setminus N_e\left(D\right)$. Since $N_e\left(D^{\prime }\right)=N_e\left(D\right)$ and $D_w^{\prime }\subseteq D_w$,

$${\partial }_s\left(D^{\prime }\right)=|N_e\left(D^{\prime }\right)|-|D_w^{\prime }|\ge |N_e\left(D\right)|-|D_w|={\partial }_s\left(D\right)={\partial }_{s^{*}}\left(G\right),$$

which implies that $D^{\prime }$ is a ${\partial }_{s^{*}}\left(G\right)$-set, as $D_w^{\prime }\subseteq N\left(D^{\prime }\right)$. Obviously, $D^{\prime }$ is a dominating set.

Now, let $D_1\subseteq D_w^{\prime }$ such that $|P_e(v,D^{\prime })|=1$ for every $v\in D_1$ and $|P_e(v,D^{\prime })|\ge 2$ for every $v\in D_w^{\prime }\setminus D_1$. Let ${\displaystyle X=D^{\prime }\cup \left(\bigcup _{v\in D_1}{P}_e(v,D^{\prime })\right)}$. Since $|N_e\left(X\right)|=|N_e\left(D^{\prime }\right)|-|D_1|$ and $|X_w|\le |D_w^{\prime }|-|D_1|$,

$${\partial }_s\left(X\right)=|N_e\left(X\right)|-|X_w|\ge |N_e\left(D^{\prime }\right)|-|D_w^{\prime }|={\partial }_s\left(D^{\prime }\right)={\partial }_{s^{*}}\left(G\right).$$

Therefore, X is a ${\partial }_{s^{*}}\left(G\right)$-set, as $X_w\subseteq N\left(X\right)$. Clearly, $|P_e(v,X)|\ge 2$ for every $v\in X_w$. □

We are now able to characterize the graphs with ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-\gamma \left(G\right)$.

Theorem 6.

For any graph G, the following statements are equivalent.

(i) 

${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-\gamma \left(G\right)$.

(ii) 

${\gamma }_{{}_2}\left(G\right)=\gamma \left(G\right)$.

(iii) 

${\partial }_s\left(G\right)=n\left(G\right)-\gamma \left(G\right)$.

Proof. 

Assume ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-\gamma \left(G\right)$. By Lemma 1, there exists a set $D\in \mathcal{D}\left(G\right)$ which is a ${\partial }_{s^{*}}\left(G\right)$-set. Hence, $n\left(G\right)-\gamma \left(G\right)={\partial }_{s^{*}}\left(G\right)=|N_e\left(D\right)|-|D_w|=n\left(G\right)-|D|-|D_w|$, which implies that $\left|D\right|+|D_w|=\gamma \left(G\right)$. Since $\gamma \left(G\right)\le \left|D\right|$, we deduce that $\left|D\right|=\gamma \left(G\right)$ and $|D_w|=0$. Therefore, D is a 2-dominating set of G and so, ${\gamma }_{{}_2}\left(G\right)\le \left|D\right|=\gamma \left(G\right)\le {\gamma }_{{}_2}\left(G\right)$, which leads to ${\gamma }_{{}_2}\left(G\right)=\gamma \left(G\right)$.

Conversely, from Theorem 4 we deduce that ${\gamma }_{{}_2}\left(G\right)=\gamma \left(G\right)$ implies that ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-\gamma \left(G\right)$.

Finally, the equivalence (ii)⟷(iii) was previously established in [8]. □

By the result above we have that if ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-\gamma \left(G\right)$, then ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$. However, the converse does not hold. For instance, as we will see in Corollary 2, if G is a path or a cycle, then ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)<n\left(G\right)-\gamma \left(G\right)$.

We next consider some cases of graphs satisfying ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$.

Theorem 7.

Let G be a graph. If $\mathrm{\Delta }\left(G\right)\le 3$ or G is a claw-free graph, then

$${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right).$$

Proof. 

By Lemma 1, there exists $D\in \mathcal{D}\left(G\right)$ which is a ${\partial }_{s^{*}}\left(G\right)$-set and $|P_e(v,D)|\ge 2$ for every $v\in D_w$. Assume that $\mathrm{\Delta }\left(G\right)\le 3$. We define a set $D^{\prime }\subseteq V\left(G\right)$ as follows.

$$D^{\prime }=\left(D\setminus D_w\right)\cup \left(\bigcup _{v\in D_w}{P}_e(v,D)\right).$$

Notice that $N\left(v\right)\cap D\ne ⌀$ and $|N\left(v\right)\setminus D|=|P_e(v,D)|=2$ for every $v\in D_w$. Hence, $D^{\prime }\in \mathcal{D}\left(G\right)$ and $D_w^{\prime }=⌀$, which implies that $D^{\prime }$ is a 2-dominating set of G and

$$\begin{array}{cc}\hfill n\left(G\right)-|D^{\prime }|& =n\left(G\right)-\left|D\right|-|D_w|\hfill \\ \hfill & =|N_e\left(D\right)|-|D_w|\hfill \\ \hfill & ={\partial }_s\left(D\right)\hfill \\ \hfill & ={\partial }_{s^{*}}\left(G\right).\hfill \end{array}$$

Therefore, ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-\left|D^{\prime }\right|\le n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$, and we deduce the equality by the lower bound ${\partial }_{s^{*}}\left(G\right)\ge n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$ given in Theorem 4.

Now, assume that G is a claw-free graph. Observe that in this case $P_e(v,D)$ is a clique for every $v\in D_w$, as $N\left(v\right)\cap D\ne ⌀$. Let $X\subseteq V\left(G\right)\setminus D$ such that $\left|X\right|=|D_w|$ and $|X\cap P_e(v,D)|=1$ for every $v\in D_w$. Notice that $X^{\prime }=D\cup X$ is a 2-dominating set of G. Hence,

$${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(D\right)=|N_e\left(D\right)|-|D_w|=n\left(G\right)-|D|-|D_w|=n\left(G\right)-|X^{\prime }|\le n\left(G\right)-{\gamma }_{{}_2}\left(G\right).$$

Therefore, by the lower bound ${\partial }_{s^{*}}\left(G\right)\ge n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$ given in Theorem 4 we conclude the proof. □

The following result is a direct consequence of Theorem 7 and the well-known equalities ${\gamma }_{{}_2}\left(C_n\right)=\lceil \frac{n}{2}\rceil$ and ${\gamma }_{{}_2}\left(P_n\right)=\lceil \frac{n+1}{2}\rceil$ due to Fink and Jacobson [18].

Corollary 2.

For any integer $n\ge 3$,

$${\partial }_{s^{*}}\left(P_n\right)=⌊\frac{n-1}{2}⌋\mathrm{and}{\partial }_{s^{*}}\left(C_n\right)=⌊\frac{n}{2}⌋.$$

By Theorems 1 and 4 we derive the following result.

Theorem 8.

Given a graph G, the following statements hold.

(i) 

If $\delta \left(G\right)\ge 3$, then ${\partial }_{s^{*}}\left(G\right)\ge \frac{n\left(G\right)}{2}.$

(ii) 

If $\delta \left(G\right)=2$, then ${\partial }_{s^{*}}\left(G\right)\ge \frac{n\left(G\right)}{3}.$

For instance, for any cubic graph with ${\gamma }_{{}_2}\left(G\right)=\frac{n\left(G\right)}{2}$ we have ${\partial }_{s^{*}}\left(G\right)=\frac{n\left(G\right)}{2}$, and for any corona graph of the form $G\cong G_1\odot K_2$ we have ${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(G\right)=\frac{n\left(G\right)}{3}.$

We next discuss the relationship between the quasi-total strong differential and the semitotal domination number.

Theorem 9.

Given a graph G with no isolated vertex, the following statements hold.

(i) 

${\partial }_{s^{*}}\left(G\right)\le n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right).$

(ii) 

${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)$ if and only if ${\gamma }_{{}_{t2}}\left(G\right)={\gamma }_{{}_2}\left(G\right)$.

(iii) 

${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)-1$ if and only if one of the following conditions holds.

(a)

${\gamma }_{{}_2}\left(G\right)={\gamma }_{{}_{t2}}\left(G\right)+1$.

(b)

${\gamma }_{{}_2}\left(G\right)\ge {\gamma }_{{}_{t2}}\left(G\right)+1$ and there exist a ${\gamma }_{{}_{t2}}\left(G\right)$-set D and a vertex $v\in D\cap N\left(D\right)$ such that $P_e(v,D)\ne ⌀$ and D is a 2-dominating set of $G-P_e(v,D)$.

Proof. 

By Lemma 1, there exists a dominating set D which is a ${\partial }_{s^{*}}\left(G\right)$-set. In addition, since G has no isolated vertex, D is also a semitotal dominating set of G, which implies that $\left|D\right|\ge {\gamma }_{{}_{t2}}\left(G\right)$. Hence,

$${\partial }_{s^{*}}\left(G\right)=|N_e\left(D\right)|-|D_w|\le n\left(G\right)-|D|-|D_w|\le n\left(G\right)-|D|\le n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right).$$

Therefore, (i) follows and ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)$ if and only if D is a 2-dominating set and $\left|D\right|={\gamma }_{{}_{t2}}\left(G\right)$. Now, since ${\gamma }_{{}_{t2}}\left(G\right)\le {\gamma }_{{}_2}\left(G\right)$, every 2-dominating set of cardinality ${\gamma }_{{}_{t2}}\left(G\right)$ is a ${\gamma }_{{}_2}\left(G\right)$-set. Therefore, (ii) follows.

Finally, we proceed to prove (iii). We first assume that ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)-1$. By (i) we deduce that ${\gamma }_{{}_{t2}}\left(G\right)+1\le {\gamma }_{{}_2}\left(G\right)$. Also, notice that

$$n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)-1={\partial }_{s^{*}}\left(G\right)={\partial }_s\left(D\right)=n\left(G\right)-\left|D\right|-|D_w|,$$

which implies that $\left|D\right|+|D_w|={\gamma }_{{}_{t2}}\left(G\right)+1$. Since $\left|D\right|\ge {\gamma }_{{}_{t2}}\left(G\right)$, we obtain that $|D_w|\in \{0,1\}$. We distinguish these two cases.

Case 1. $|D_w|=0$. In this case, we have that D is a 2-dominating set of G of cardinality ${\gamma }_{{}_{t2}}\left(G\right)+1$, which implies that ${\gamma }_{{}_{t2}}\left(G\right)+1\le {\gamma }_{{}_2}\left(G\right)\le \left|D\right|={\gamma }_{{}_{t2}}\left(G\right)+1$. Therefore, ${\gamma }_{{}_2}\left(G\right)={\gamma }_{{}_{t2}}\left(G\right)+1$. Conversely, if ${\gamma }_{{}_2}\left(G\right)={\gamma }_{{}_{t2}}\left(G\right)+1$, then by (i) and Theorem 4 we have that $n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)-1\le {\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)$, and so (ii) leads to ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)-1$.

Case 2. $|D_w|=1$. If $D_w=\left\{v\right\}$, then $v\in D\cap N\left(D\right)$ and $P_e(v,D)\ne ⌀$. In addition, since $\left|D\right|+|D_w|=|D|+1={\gamma }_{{}_{t2}}\left(G\right)+1$, we have that D is a ${\gamma }_{{}_{t2}}\left(G\right)$-set and a 2-dominating set of $G-P_e(v,D)$. Therefore, (b) holds. Conversely, assume that (b) holds. Since ${\gamma }_{{}_2}\left(G\right)\ge {\gamma }_{{}_{t2}}\left(G\right)+1$, from (i) and (ii) we conclude that ${\partial }_{s^{*}}\left(G\right)\le n\left(G\right)-{\gamma }_{{}_{t2}}\left(G\right)-1$, and so the ${\gamma }_{{}_{t2}}\left(G\right)$-set satisfying (b) is a ${\partial }_{s^{*}}\left(G\right)$-set. □

Next we derive some lower bounds on ${\partial }_{s^{*}}\left(G\right)$.

Theorem 10.

For any graph G with every component of order at least three,

$${\partial }_{s^{*}}\left(G\right)\ge ⌈\frac{1}{2}\left(n\left(G\right)-\gamma \left(G\right)+\left|\mathcal{L}\left(G\right)\right|-2\left|\mathcal{S}\left(G\right)\right|-2|{\mathcal{S}}_s\left(G\right)|\right)⌉.$$

Proof. 

Let S be a $\gamma \left(G\right)$-set such that $\mathcal{S}\left(G\right)\subseteq S$ and $\overline{S}=V\left(G\right)\setminus S$.

Now, we define $S^{\prime \prime }\subseteq \overline{S}$ as a set of minimum cardinality among all subsets $S^{\prime }$ of $\overline{S}$ that satisfy the following conditions.

(a)

$N\left(v\right)\cap \mathcal{L}\left(G\right)\cap S^{\prime }\ne ⌀$ for every vertex $v\in \mathcal{S}\left(G\right)\setminus {\mathcal{S}}_s\left(G\right)$ or $v\in \mathcal{S}\left(G\right)$ with $N\left(v\right)\subseteq \mathcal{L}\left(G\right)$.

(b)

$(N\left(v\right)\cap S^{\prime })\setminus \mathcal{L}\left(G\right)\ne ⌀$ for every vertex $v\in {\mathcal{S}}_s\left(G\right)$ such that $N\left(v\right)\cap S=⌀$ and $N\left(v\right)\neg \subseteq \mathcal{L}\left(G\right)$.

Notice that $\left|\mathcal{S}\left(G\right)\right|-|{\mathcal{S}}_s\left(G\right)|\le |S^{\prime \prime }|\le |\mathcal{S}\left(G\right)|$. Now, let $I\subseteq \overline{S}\setminus S^{\prime \prime }$ the set of isolated vertices of the graph $G[\overline{S}\setminus S^{\prime \prime }]$. Hence, by definition of $S^{\prime \prime }$ we deduce that $\left|I\right|\ge \left|\mathcal{L}\left(G\right)\right|-\left|\mathcal{S}\left(G\right)\right|+|{\mathcal{S}}_s\left(G\right)|$.

Now, we define $X^{\prime \prime }\subseteq \overline{S}\setminus (I\cup S^{\prime \prime })$ as a set of minimum cardinality among all subsets $X^{\prime }$ of $\overline{S}\setminus (I\cup S^{\prime \prime })$ such that $N\left(v\right)\cap X^{\prime }\ne ⌀$ for every vertex $v\in \overline{S}\setminus (I\cup S^{\prime \prime }\cup X^{\prime })$. It is clear that if $\overline{S}=I\cup S^{\prime \prime }$, then $X^{\prime \prime }=⌀$, while if $\overline{S}\setminus (I\cup S^{\prime \prime })\ne ⌀$, then $X^{\prime \prime }$ is a $\gamma \left(G[\overline{S}\setminus (I\cup S^{\prime \prime })]\right)$-set. As $G[\overline{S}\setminus (I\cup S^{\prime \prime })]$ has no isolated vertex, we have that

$$|X^{\prime \prime }|\le \frac{1}{2}(n\left(G\right)-(\left|S\right|+\left|I\right|+|S^{\prime \prime }\left|\right))\le \frac{1}{2}(n\left(G\right)-\gamma \left(G\right)-|\mathcal{L}\left(G\right)\left|\right).$$

Hence, in any case $|X^{\prime \prime }|\le \frac{1}{2}(n\left(G\right)-\gamma \left(G\right)-|\mathcal{L}\left(G\right)\left|\right)$ because $\left|S\right|+\left|\mathcal{L}\right(G\left)\right|\le n\left(G\right)$.

Now, let $D=S\cup S^{\prime \prime }\cup X^{\prime \prime }$. Notice that $D\in \mathcal{D}\left(G\right)$, $D_w\subseteq {\mathcal{S}}_s\left(G\right)$ and $D_w\subseteq N\left(D\right)$. Hence,

$$\begin{array}{cc}\hfill {\partial }_{s^{*}}\left(G\right)& \ge {\partial }_s\left(D\right)\hfill \\ \hfill & =|N_e\left(D\right)|-|D_w|\hfill \\ \hfill & =n\left(G\right)-\left|D\right|-|D_w|\hfill \\ \hfill & =n\left(G\right)-\left|S\right|-|S^{\prime \prime }|-|X^{\prime \prime }|-|{\mathcal{S}}_s\left(G\right)|\hfill \\ \hfill & \ge n\left(G\right)-\gamma \left(G\right)-\left|\mathcal{S}\left(G\right)\right|-\frac{1}{2}(n\left(G\right)-\gamma \left(G\right)-|\mathcal{L}\left(G\right)\left|\right)-|{\mathcal{S}}_s\left(G\right)|\hfill \\ \hfill & =\frac{1}{2}(n\left(G\right)-\gamma \left(G\right)+|\mathcal{L}\left(G\right)|-2|\mathcal{S}\left(G\right)|-2|{\mathcal{S}}_s\left(G\right)\left|\right).\hfill \end{array}$$

Therefore, the result follows. □

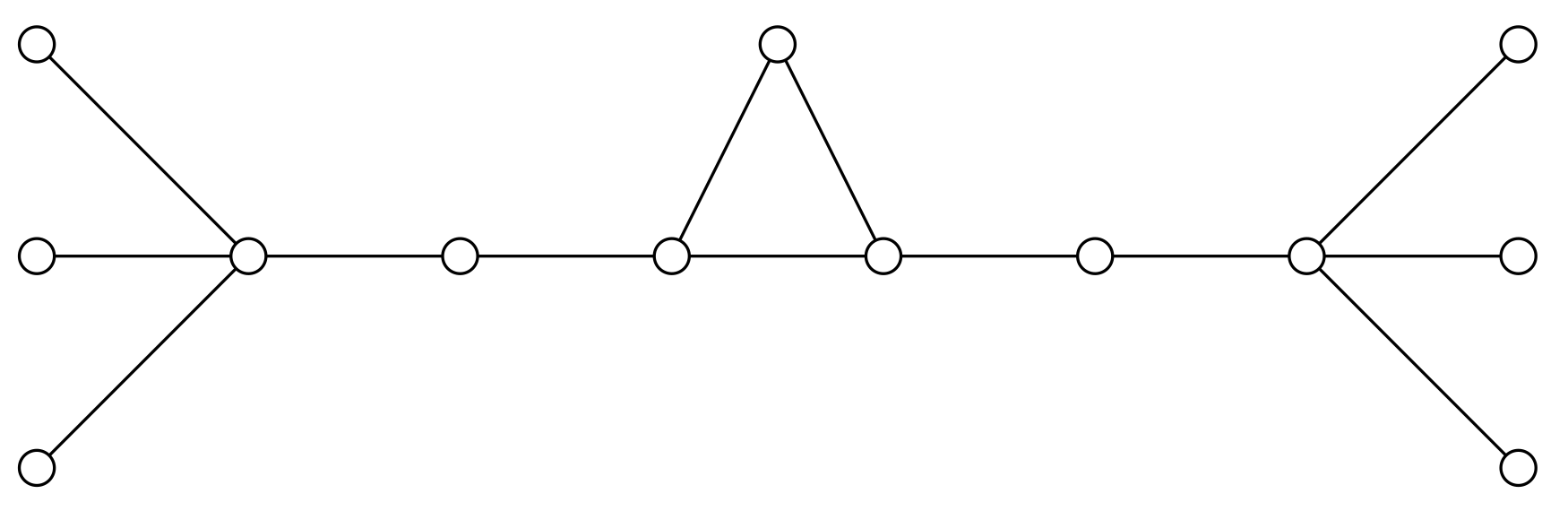
The bound above is tight. For instance, it is achieved by the graphs shown in Figure 2.

Corollary 3.

For any graph G with $\delta \left(G\right)=2$,

$${\partial }_{s^{*}}\left(G\right)\ge \frac{1}{2}\left(n\left(G\right)-\gamma \left(G\right)\right).$$

The bound above is achieved by any corona graph of the form $G\cong G_1\odot K_2$, where $G_1$ is a nontrivial graph. In this case, ${\partial }_{s^{*}}\left(G\right)={\partial }_s\left(G\right)=n\left(G_1\right)=\frac{1}{2}(n\left(G\right)-\gamma \left(G\right)).$

Theorem 11.

For any graph G with no isolated vertex,

$${\partial }_{s^{*}}\left(G\right)\ge n\left(G\right)-{\gamma }_t\left(G\right)-\gamma \left(G\right).$$

Proof. 

Let $S_1$ be a ${\gamma }_t\left(G\right)$-set and $S_2$ a $\gamma \left(G\right)$-set. Let $S=S_1\cup S_2$. As $S_1\in {\mathcal{D}}_t\left(G\right)$ and $S_2\in \mathcal{D}\left(G\right)$, we deduce that $S_w\subseteq N\left(S\right)$ and $S_w\subseteq S_1\cap S_2$. Hence,

$$\begin{array}{cc}\hfill {\partial }_{s^{*}}\left(G\right)& \ge {\partial }_s\left(S\right)\hfill \\ \hfill & =|N_e\left(S\right)|-|S_w|\hfill \\ \hfill & =n\left(G\right)-\left|S\right|-|S_w|\hfill \\ \hfill & \ge n\left(G\right)-|S_1|-|S_2|+|S_1\cap S_2|-|S_w|\hfill \\ \hfill & \ge n\left(G\right)-{\gamma }_t\left(G\right)-\gamma \left(G\right),\hfill \end{array}$$

as desired. □

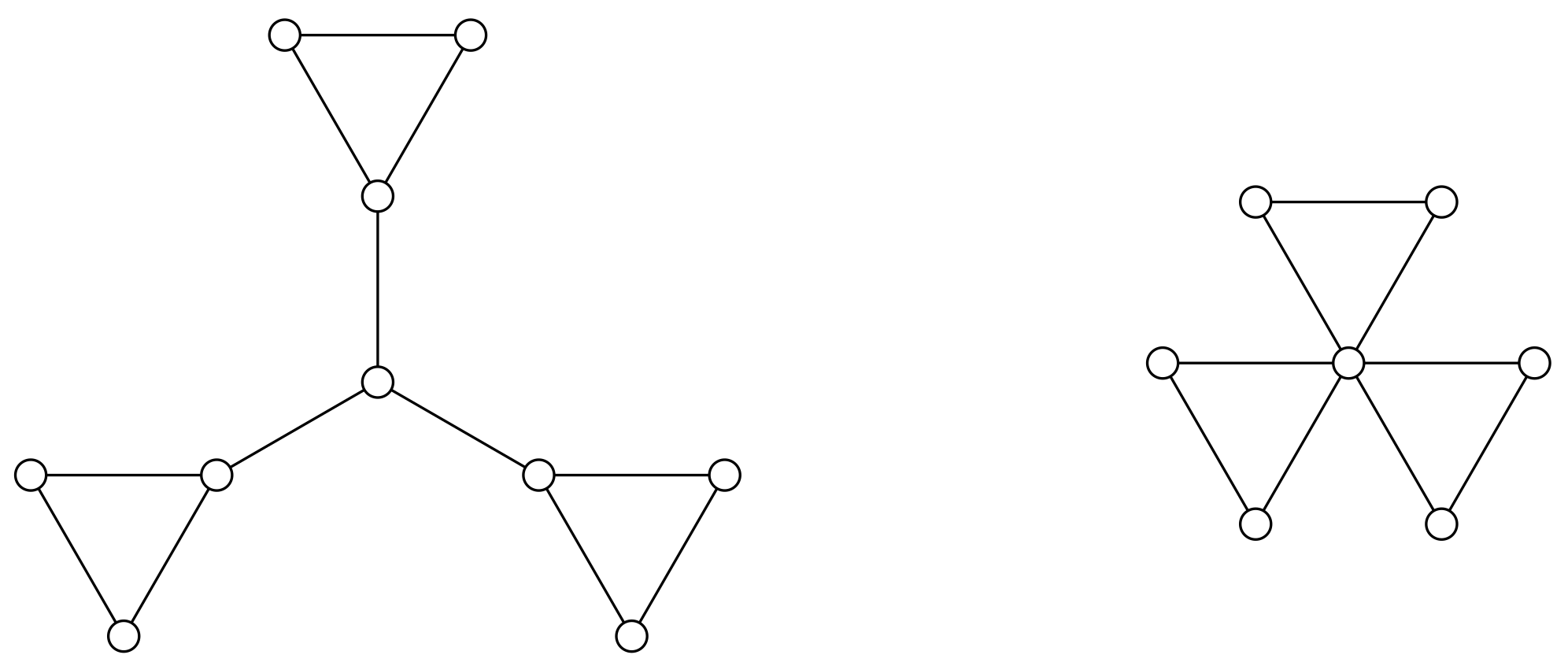
The bound above is tight. Figure 3 shows a graph G with $\gamma \left(G\right)<{\gamma }_t\left(G\right)$, where ${\partial }_{s^{*}}\left(G\right)=5=n\left(G\right)-{\gamma }_t\left(G\right)-\gamma \left(G\right).$

Theorem 12.

For any graph G with every component of order at least three,

$${\partial }_{s^{*}}\left(G\right)\ge n\left(G\right)-\beta \left(G\right)-\left|\mathcal{S}\left(G\right)\right|-|{\mathcal{S}}_s\left(G\right)|.$$

Proof. 

Let S be a $\beta \left(G\right)$-set such that $\mathcal{S}\left(G\right)\subseteq S$. Now, we define $S^{\prime }\subseteq \mathcal{L}\left(G\right)$ such that $|S^{\prime }|=|\mathcal{S}\left(G\right)|$ and $|N\left(v\right)\cap S^{\prime }|=1$ for every vertex $v\in \mathcal{S}\left(G\right)$. Hence, $S^{\prime \prime }=S\cup S^{\prime }$ is a dominating set, $S_w^{\prime \prime }\subseteq {\mathcal{S}}_s\left(G\right)$ and $S_w^{\prime \prime }\subseteq N\left(S^{\prime \prime }\right)$, which implies that

$$\begin{array}{cc}\hfill {\partial }_{s^{*}}\left(G\right)& \ge {\partial }_s\left(S^{\prime \prime }\right)\hfill \\ \hfill & =|N_e\left(S^{\prime \prime }\right)|-|S_w^{\prime \prime }|\hfill \\ \hfill & =n\left(G\right)-|S^{\prime \prime }|-|S_w^{\prime \prime }|\hfill \\ \hfill & \ge n\left(G\right)-\left|S\right|-\left|\mathcal{S}\left(G\right)\right|-|{\mathcal{S}}_s\left(G\right)|.\hfill \end{array}$$

Therefore, the result follows. □

The bound above is tight. For instance, Figure 3 shows a graph G with ${\partial }_{s^{*}}\left(G\right)=5=n\left(G\right)-\beta \left(G\right)-\left|\mathcal{S}\left(G\right)\right|-|{\mathcal{S}}_s\left(G\right)|=\alpha \left(G\right)-|\mathcal{S}\left(G\right)|-|{\mathcal{S}}_s\left(G\right)|.$

Notice that Theorems 2 and 12 lead to the following bound.

Theorem 13.

For any graph G with every component of order at least three,

$${\partial }_{s^{*}}\left(G\right)\ge \alpha \left(G\right)-\left|\mathcal{S}\left(G\right)\right|-|{\mathcal{S}}_s\left(G\right)|.$$

In particular, for graphs of minimum degree at least two we deduce the following result.

Theorem 14.

For any graph G with $\delta \left(G\right)\ge 2$, the following statements hold.

(i) 

${\partial }_{s^{*}}\left(G\right)\ge \alpha \left(G\right)$.

(ii) 

If ${\partial }_{s^{*}}\left(G\right)=\alpha \left(G\right)$, then $\alpha \left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$.

(iii) 

${\partial }_{s^{*}}\left(G\right)\ge \gamma \left(G\right).$

(iv) 

If ${\partial }_{s^{*}}\left(G\right)=\gamma \left(G\right)$, then $\gamma \left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$.

Proof. 

Obviously, (i) is an immediate consequence of Theorem 13 and (iii) is derived from the fact that $\alpha \left(G\right)\ge \gamma \left(G\right)$.

Now, since $\delta \left(G\right)\ge 2$, every vertex cover is a 2-dominating set, which implies that ${\gamma }_{{}_2}\left(G\right)\le \beta \left(G\right)=n\left(G\right)-\alpha \left(G\right)$. Thus, by Theorem 4, if ${\partial }_{s^{*}}\left(G\right)=\alpha \left(G\right)$, then

$$\alpha \left(G\right)={\partial }_{s^{*}}\left(G\right)\ge n\left(G\right)-{\gamma }_{{}_2}\left(G\right)\ge \alpha \left(G\right).$$

Therefore, (ii) follows, and by analogy we deduce that (iii) follows. □

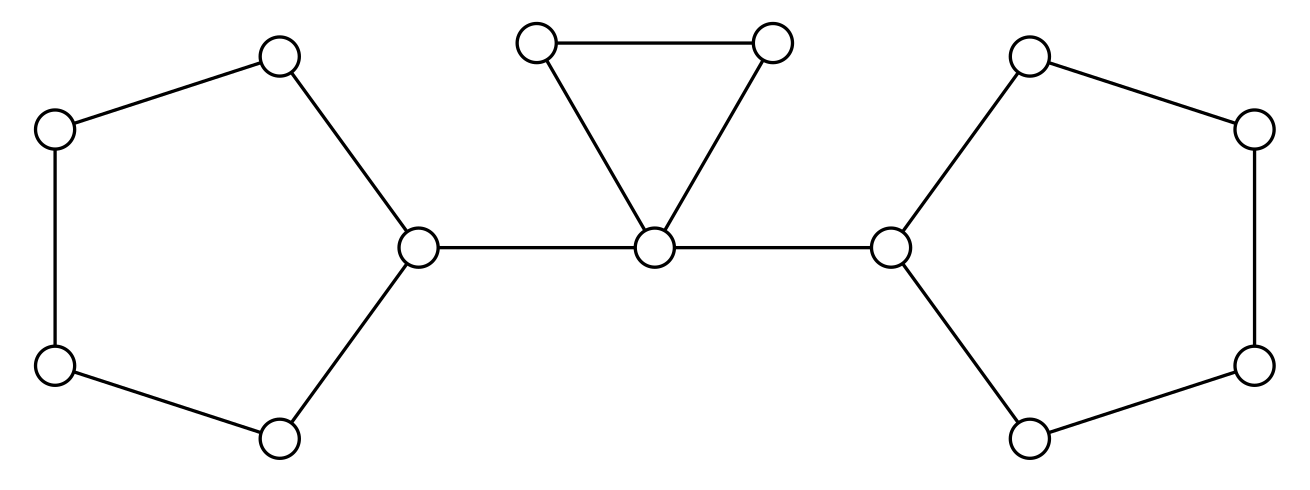
The graph shown in Figure 4, on the left, satisfies ${\partial }_{s^{*}}\left(G\right)=\alpha \left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)=4$. The converse of Theorem 14 (ii) does not hold. For instance, for the right hand side graph shown in Figure 4 we have $\alpha \left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)=3$, while ${\partial }_{s^{*}}\left(G\right)=4$.

The graph shown in Figure 5 satisfies ${\partial }_{s^{*}}\left(G\right)=\gamma \left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)=5$. We would point out that there are several cases of graphs of minimum degree one with ${\partial }_{s^{*}}\left(G\right)\le \gamma \left(G\right)-1.$

Next we discuss the trivial bounds on ${\partial }_{s^{*}}\left(G\right)$ and we characterize the extreme cases.

Proposition 1.

For any graph G of order $n\left(G\right)\ge 3$, the following statements hold.

(i) 

$max\{0,\mathrm{\Delta }\left(G\right)-2\}\le {\partial }_{s^{*}}\left(G\right)\le n\left(G\right)-2.$

(ii) 

${\partial }_{s^{*}}\left(G\right)=0$ if and only if $\mathrm{\Delta }\left(G\right)\le 1$.

(iii) 

${\partial }_{s^{*}}\left(G\right)=1$ if and only if $\mathrm{\Delta }\left(G\right)\in \{2,3\}$ and ${\gamma }_{{}_2}\left(G\right)=n\left(G\right)-1$.

(iv) 

${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-2$ if and only if ${\gamma }_{{}_2}\left(G\right)=2$.

(v) 

${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-3$ if and only if ${\gamma }_{{}_2}\left(G\right)=3$ or ${\gamma }_{{}_2}\left(G\right)\ne 2$ and $\gamma \left(G\right)=1$.

Proof. 

We first proceed to prove (i). If $\mathrm{\Delta }\left(G\right)\in \{0,1\}$, then it is straightforward that ${\partial }_{s^{*}}\left(G\right)=0$. We assume that $\mathrm{\Delta }\left(G\right)\ge 2$. Let $v\in V\left(G\right)$ be a vertex of maximum degree, $u\in N\left(v\right)$ and $S=\left\{u\right\}\cup \left(V\right(G)\setminus N(v\left)\right)$. Notice that either $S_w=⌀$ or $S_w=\left\{v\right\}$. Hence, ${\partial }_{s^{*}}\left(G\right)\ge {\partial }_s\left(S\right)=|N_e\left(S\right)|-|S_w|\ge \mathrm{\Delta }\left(G\right)-2$, as desired. Since $n\left(G\right)\ge 3$ every ${\partial }_{s^{*}}\left(G\right)$-set has cardinality at least two, and so ${\partial }_{s^{*}}\left(G\right)\le n\left(G\right)-2$.

We next proceed to prove (ii). if ${\partial }_{s^{*}}\left(G\right)=0$, then $\mathrm{\Delta }\left(G\right)\le 2$ by (i). Now, if $\mathrm{\Delta }\left(G\right)=2$, then for any vertex x of maximum degree we have that $V\left(G\right)\setminus \left\{x\right\}$ is a 2-dominating set, and so ${\partial }_{s^{*}}\left(G\right)\ge 1$, which is a contradiction. Therefore, $\mathrm{\Delta }\left(G\right)\le 1$. Obviously, if $\mathrm{\Delta }\left(G\right)\le 1$, then ${\partial }_{s^{*}}\left(G\right)=0$.

Now, we proceed to prove (iii). First, we assume that ${\partial }_{s^{*}}\left(G\right)=1$. By (i) and (ii) we deduce that $\mathrm{\Delta }\left(G\right)\in \{2,3\}$. Hence, Theorem 7 leads to ${\gamma }_{{}_2}\left(G\right)=n\left(G\right)-1$. Conversely, if $\mathrm{\Delta }\left(G\right)\in \{2,3\}$ and ${\gamma }_{{}_2}\left(G\right)=n\left(G\right)-1$, then Theorem 7 leads to ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)=1$. Therefore, (iii) follows.

To prove the remaining statements, we take a ${\partial }_{s^{*}}\left(G\right)$-set $D\in \mathcal{D}\left(G\right)$, which exists due to Lemma 1.

We next proceed to prove (iv). First, assume that ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-2$. In this case, we deduce that $\left|D\right|+|D_w|=2$, which implies that $\left|D\right|=2$ and $D_w=⌀$. Therefore, D is a ${\gamma }_{{}_2}\left(G\right)$-set and so, ${\gamma }_{{}_2}\left(G\right)=2$. On the other side, if ${\gamma }_{{}_2}\left(G\right)=2$, then by Theorem 4 and (i) we deduce that ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-2$.

Finally, we proceed to prove (v). If either ${\gamma }_{{}_2}\left(G\right)=3$ or ${\gamma }_{{}_2}\left(G\right)\ne 2$ and $\gamma \left(G\right)=1$, then by Theorem 4 and the statements (i) and (iv) we deduce that ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-3$. Conversely, assume that ${\partial }_{s^{*}}\left(G\right)=n\left(G\right)-3$. From (iv) we deduce that ${\gamma }_{{}_2}\left(G\right)\ge 3$. Moreover, we deduce that $\left|D\right|+|D_w|=3$, which implies that either $\left|D\right|=2$ and $|D_w|=1$ or $\left|D\right|=3$ and $|D_w|=0$. If $\left|D\right|=2$ and $|D_w|=1$, then $\gamma \left(G\right)=1$ as $D\in \mathcal{D}\left(G\right)$, while if $\left|D\right|=3$ and $|D_w|=0$, then D is a 2-dominating set, and so ${\gamma }_{{}_2}\left(G\right)=3$. □

To conclude this section, we discuss the case of join graphs.

Proposition 2.

For any two graphs G and H we have the following statements.

(i) 

$n\left(G\right)+n\left(H\right)-4\le {\partial }_{s^{*}}(G+H)\le n\left(G\right)+n\left(H\right)-2$.

(ii) 

${\partial }_{s^{*}}(G+H)=n\left(G\right)+n\left(H\right)-2$ if and only if $min\{{\gamma }_{{}_2}\left(G\right),{\gamma }_{{}_2}\left(H\right)\}=2$ or $\gamma \left(G\right)=\gamma \left(H\right)=1$.

(iii) 

${\partial }_{s^{*}}(G+H)=n\left(G\right)+n\left(H\right)-3$ if and only if one of the following holds.

• $min\{{\gamma }_{{}_2}\left(G\right),{\gamma }_{{}_2}\left(H\right)\}=3$ and $max\left\{\gamma \right(G),\gamma (H\left)\right\}\ge 2$.
• $min\{{\gamma }_{{}_2}\left(G\right),{\gamma }_{{}_2}\left(H\right)\}\ge 3$ and, in addition, $\gamma \left(G\right)=2$ or $\gamma \left(H\right)=2$.
• $min\left\{\gamma \right(G),\gamma (H\left)\right\}=1$ and $max\left\{\gamma \right(G),\gamma (H\left)\right\}\ge 2$ and $min\{{\gamma }_{{}_2}\left(G\right),{\gamma }_{{}_2}\left(H\right)\}$$\ge 3$.

(iv) 

${\partial }_{s^{*}}(G+H)=4$ if and only if $min\left\{\gamma \right(G),\gamma (H\left)\right\}\ge 3$ and $min\{{\gamma }_{{}_2}\left(G\right),{\gamma }_{{}_2}\left(H\right)\}\ge 4$.

Proof. 

By Proposition 1 (i) we deduce that ${\partial }_{s^{*}}(G+H)\le n\left(G\right)+n\left(H\right)-2$. For any set $D=\{u,v\}$, where $u\in V\left(G\right)$ and $v\in V\left(H\right)$, we have that ${\partial }_{s^{*}}(G+H)\ge |N_e\left(D\right)|-|D_w|=n\left(G\right)+n\left(H\right)-|D|-|D_w|\ge n\left(G\right)+n\left(H\right)-4$. Thus, (i) follows. Finally, by (i) and Proposition 1 (iv) and (v), we deduce the remaining statements, which completes the proof. □

4. A Gallai-Type Theorem

A Gallai-type theorem is a result of the form $a\left(G\right)+b\left(G\right)=n\left(G\right)$, where $a\left(G\right)$ and $b\left(G\right)$ are parameters defined on G. This terminology comes from Theorem 2, which is a well-known result stated by Gallai in 1959. The aim of this section is to identify the parameter $a\left(G\right)$ such that $a\left(G\right)+{\partial }_{s^{*}}\left(G\right)=n\left(G\right)$. We will show that this invariant, which is associated to a version of the Italian domination, is perfectly integrated into the theory of domination.

Let $f:V\left(G\right)⟶\{0,1,2\}$ be a function and $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$ for $i\in \{0,1,2\}$. We will identify the function f with these subsets of $V\left(G\right)$ induced by f, and write $f(V_0,V_1,V_2).$ The weight of f is defined to be

$$\omega \left(f\right)=f\left(V\left(G\right)\right)=\sum _{v\in V\left(G\right)}f\left(v\right)=\sum _{i}i\left|V_i\right|.$$

The theory of Roman domination was introduced by Cockayne et al. [19]. They defined a Roman dominating function on a graph G to be a function $f(V_0,V_1,V_2)$ satisfying the condition that every vertex in $V_0$ is adjacent to at least one vertex in $V_2$. Recently, Cabrera García et al. [20] defined a quasi-total Roman dominating function as a Roman dominating function $f(V_0,V_1,V_2)$ such that $N\left(v\right)\cap (V_1\cup V_2)\ne ⌀$ for every $v\in V_2$.

An Italian dominating function on a graph G is a function $f(V_0,V_1,V_2)$ satisfying that $f\left(N\left(v\right)\right)={\sum }_{u\in N\left(v\right)}f\left(u\right)\ge 2$ for every $v\in V_0$, i.e., $f(V_0,V_1,V_2)$ is an Italian dominating function if $N\left(v\right)\cap V_2\ne ⌀$ or $|N\left(v\right)\cap V_1|\ge 2$ for every $v\in V_0$. Hence, every Roman dominating function is an Italian dominating function. The concept of Italian domination was introduced by Chellali et al. in [21] under the name Roman $\left\{2\right\}$-domination. The term Italian Domination was later introduced by Henning and Klostermeyer [22,23]. The Italian domination number, denoted by ${\gamma }_{{}_I}\left(G\right)$, is the minimum weight among all dominating functions on G.

The following Gallai-type theorem for the strong differential and the Italian domination number was stated in [8].

Theorem 15

(Gallai-type theorem, [8]). For any graph G,

$${\gamma }_{{}_I}\left(G\right)+{\partial }_s\left(G\right)=n\left(G\right).$$

We say that an Italian dominating function $f(V_0,V_1,V_2)$ is a quasi-total Italian dominating function if $N\left(v\right)\cap (V_1\cup V_2)\ne ⌀$ for every $v\in V_2$. Clearly, every quasi-total Roman dominating function is a quasi-total Italian dominating function. The quasi-total Italian domination number, denoted by ${\gamma }_{{}_I*}\left(G\right)$, is the minimum weight among all quasi-total dominating functions on G.

Theorem 16

(Gallai-type theorem). For any graph G,

$${\gamma }_{{}_I*}\left(G\right)+{\partial }_{s^{*}}\left(G\right)=n\left(G\right).$$

Proof. 

By Lemma 1, there exists a ${\partial }_{s^{*}}\left(G\right)$-set D which is a dominating set of G. Hence, the function $g(W_0,W_1,W_2)$, defined from $W_1=D\setminus D_w$ and $W_2=D_w$, is a quasi-total Italian dominating function on G, which implies that

$$\begin{array}{cc}\hfill {\gamma }_{{}_I*}\left(G\right)& \le \omega \left(g\right)\hfill \\ \hfill & =2|D_w|+|D\setminus D_w|\hfill \\ \hfill & =|D_w|+|D|\hfill \\ \hfill & =n\left(G\right)-\left(\right|N_e\left(D\right)|-|D_w\left|\right)\hfill \\ \hfill & =n\left(G\right)-{\partial }_{s^{*}}\left(G\right).\hfill \end{array}$$

We proceed to show that ${\gamma }_{{}_I*}\left(G\right)\ge n\left(G\right)-{\partial }_{s^{*}}\left(G\right).$ Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{{}_I*}\left(G\right)$-function. It is readily seen that for $D^{\prime }=V_1\cup V_2$ we have that $D^{\prime }\setminus D_w^{\prime }=V_1$ and $D_w^{\prime }=V_2$. Thus,

$$\begin{array}{cc}\hfill {\partial }_{s^{*}}\left(G\right)& \ge {\partial }_s\left(D^{\prime }\right)\hfill \\ \hfill & =|N_e\left(D^{\prime }\right)|-|D_w^{\prime }|\hfill \\ \hfill & =|V\left(G\right)\setminus (V_1\cup V_2)|-|V_2|\hfill \\ \hfill & =n\left(G\right)-2|V_2|-|V_1|\hfill \\ \hfill & =n\left(G\right)-{\gamma }_{{}_I*}\left(G\right).\hfill \end{array}$$

Therefore, the result follows. □

5. Computational Complexity

In this section, we show that the problem of finding the quasi-total strong differential of graph is NP-hard. To this end, we need to establish the following result.

Theorem 17.

For any graph G,

$${\partial }_{s^{*}}(G\odot K_1)=n\left(G\right)-\gamma \left(G\right).$$

Proof. 

Given $x\in V\left(G\right)$, let $x^{\prime }$ be the vertex of the copy of $K_1$ associated to x in $G\odot K_1$, and let $V(G\odot K_1)=V\left(G\right)\cup X$, where ${\displaystyle X=\bigcup _{x\in V\left(G\right)}\left\{x^{\prime }\right\}}$.

By Lemma 1, there exists a ${\partial }_{s^{*}}(G\odot K_1)$-set A which is a dominating set and $|P_e(v,A)|\ge 2$ for every $v\in A_w$. Hence, $A_w\cap X=⌀$. Now, if there exists $x\in V\left(G\right)\cap A_w$, then there exists $u\in P_e(x,A)\cap V\left(G\right)$ such that $u^{\prime }\notin A$ and $N\left(u^{\prime }\right)\cap A=⌀$, which is a contradiction. Hence, $A_w=⌀$, which implies that A is a 2-dominating set of $G\odot K_1$. Thus,

$${\partial }_{s^{*}}(G\odot K_1)={\partial }_s\left(A\right)=n(G\odot K_1)-\left|A\right|\le n(G\odot K_1)-{\gamma }_{{}_2}(G\odot K_1).$$

Since Theorem 4 leads to ${\partial }_{s^{*}}(G\odot K_1)\ge n(G\odot K_1)-{\gamma }_{{}_2}(G\odot K_1),$ we conclude that

$${\partial }_{s^{*}}(G\odot K_1)=2n\left(G\right)-{\gamma }_{{}_2}(G\odot K_1).$$

Now, let D be a dominating set of G and $D^{\prime }=D\cup X$. Since $D^{\prime }$ is a 2-dominating set of $G\odot K_1$, we have that

$${\gamma }_{{}_2}(G\odot K_1)\le \left|D^{\prime }\right|=\gamma \left(G\right)+n\left(G\right).$$

Finally, for any ${\gamma }_{{}_2}(G\odot K_1)$-set $Y,$ we have that $X\subseteq Y$ and $Y\cap V\left(G\right)$ is a dominating set of G, which implies that

$${\gamma }_{{}_2}(G\odot K_1)=\left|Y\right|=\left|X\right|+|Y\cap V\left(G\right)|\ge |X|+\gamma \left(G\right)=n\left(G\right)+\gamma \left(G\right).$$

Therefore, ${\gamma }_{{}_2}(G\odot K_1)=n\left(G\right)+\gamma \left(G\right)$, and so the result follows. □

A direct consequence of the preceding result is the determination of computational complexity of finding the quasi-total strong differential. Given a graph G and a positive integer t, the domination problem is to decide whether there exists a dominating S in G such that $\left|S\right|$ is at most t. It is well known that the domination problem is NP-complete. Hence, the optimization problem of finding $\gamma \left(G\right)$ is NP-hard. Therefore, from Theorem 17, we derive the following result.

Corollary 4.

Given a graph G, the problem of finding ${\partial }_{s^{*}}\left(G\right)$ is NP-hard.

6. Conclusions and Open Problems

This article is a contribution to the theory differential of graphs. Particularly, we introduce the concept of the quasi-total strong differential of a graph. In our study, we show that the quasi-total strong differential is closely related to several graph parameters, including the domination number, the total domination number, the 2-domination number, the vertex cover number, the semitotal domination number, the strong differential, and the quasi-total Italian domination number. Finally, we proved that the problem of finding the quasi-total strong differential of a graph is NP-hard.

Some open problems have emerged from the study carried out. For instance, we highlight the following.

(a)

It would be interesting to obtain some Nordhaus-Gaddum type relations.

(b)

We have shown that if ${\partial }_{s^{*}}\left(G\right)=\alpha \left(G\right)$, then $\alpha \left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$. Likewise, we have shown that if ${\partial }_{s^{*}}\left(G\right)=\gamma \left(G\right)$, then $\gamma \left(G\right)=n\left(G\right)-{\gamma }_{{}_2}\left(G\right)$. However, the problem of characterizing all graphs such that ${\partial }_{s^{*}}\left(G\right)=\alpha \left(G\right)$ and ${\partial }_{s^{*}}\left(G\right)=\gamma \left(G\right)$ is still an open problem.

(c)

Since the optimization problem of finding ${\partial }_{s^{*}}\left(G\right)$ is NP-hard, it would be interesting to devise polynomial-time algorithm for simple families of graphs or to develop heuristics that allow to estimate as accurately as possible this parameter for any graph.

(d)

It would be interesting to investigate the quasi-total strong differential of product graphs, and try to express this invariant in terms of different parameters of the graphs involved in the product.