Optimization Models for Efficient (t, r) Broadcast Domination in Graphs

Abstract

Known to be NP-complete, domination number problems in graphs and networks arise in many real-life applications, ranging from the design of wireless sensor networks and biological networks to social networks. Initially introduced by Blessing et al., the $(t,r)$ broadcast domination number is a generalization of the distance domination number. While some theoretical approaches have been addressed for small values of $t,r$ in the literature; in this work, we propose an approach from an optimization point of view. First, the $(t,r)$ broadcast domination number is formulated and solved using linear programming. The efficient broadcast, whose wasted signals are minimized, is then found by a genetic algorithm modified for a binary encoding. The developed method is illustrated with several grid graphs: regular, slant, and king’s grid graphs. The obtained computational results show that the method is able to find the exact $(t,r)$ broadcast domination number, and locate an efficient broadcasting configuration for larger values of $t,r$ than what can be provided from a theoretical basis. The proposed optimization approach thus helps overcome the limitations of existing theoretical approaches in graph theory.

1. Introduction

Consider a connected graph $G=\left(V\left(G\right),E\left(G\right)\right)$ with a vertex set $V\left(G\right)$ and an edge set $E\left(G\right)$. A dominating set of the graph G is defined as a subset of vertices $D\subseteq V\left(G\right)$ such that every vertex $v\in V\left(G\right)\backslash D$ is adjacent to at least one vertex in D. The domination number of the graph G, denoted by $\gamma \left(G\right)$, is the minimum size of dominating sets. A variant of broadcast domination depending on two integer parameters t and r was introduced by Blessing et al. [1]. This class of domination is called the $(t,r)$ broadcast domination. We denote the distance between any two vertices $u,v\in V\left(G\right)$ by $d(u,v)$. For example, $d(u,v)$ can be defined as the number of edges in a shortest path connecting u and v. Let us now state required definitions:

Definition 1.

A vertex $v\in V\left(G\right)$ is called a broadcasting vertex or tower of transmission t if it broadcasts a transmission of strength $t-d(u,v)$ to its neighbor vertex u with $d(u,v)<t$.

Definition 2.

Given a set of broadcasting towers $S\subseteq V\left(G\right)$ of transmission strength t, the reception at any vertex $u\in V\left(G\right)$, denoted by $r\left(u\right)$, is the sum of transmissions that vertex u receives from all broadcasting neighbors $v\in S$ with $d(u,v)<t$, i.e., $r\left(u\right)={\sum }_{v\in S}max(t-d(v,u),0)$.

Definition 3.

We say that a subset of broadcasting towers $S\subseteq V\left(G\right)$ of transmission strength t is a $(t,r)$ broadcast dominating set of the graph G if every vertex $u\in V\left(G\right)$ receives the reception at least r, i.e., $r\left(u\right)\ge r,\forall u\in V\left(G\right)$.

Definition 4.

A minimum $(t,r)$ broadcast dominating set is a $(t,r)$ broadcast dominating set of smallest size for a given graph G. The $(t,r)$ broadcast domination number of the graph G, denoted by $\gamma (t,r)$, is the size of a minimum $(t,r)$ broadcast dominating set.

Over the last decade, there have been a few theoretical studies on the $(t,r)$ broadcast domination problems. This includes, for example, the work by Blessing et al. [1] that provided the exact $(t,r)$ broadcast domination numbers for small grid graphs, and identified upper bounds of the $(t,r)$ broadcast domination numbers for large grid graphs. Crepeau et al. [2] studied the $(t,r)$ broadcast domination numbers for finite 2-D grid, 3-D tower, slant and lattice graph types. Some studies have also extended the $(t,r)$ broadcast domination to infinite graphs such as the infinite ${\mathbb{Z}}^2$ grid [3,4] and a triangular lattice [5]. While a linear programming model has been applied to obtain some domination parameters, e.g., strong domination, restrained domination and strong restrained domination [6], weighted total domination [7], double roman domination [8], none of these work have applied the method to solve the $(t,r)$ broadcast domination number.

Through mathematical optimization, our contribution is therefore identifying the $(t,r)$ broadcast domination numbers for larger-scale graphs for which no solutions are known within the theoretical framework. We apply our proposed method to solve three types of finite grid graphs, namely, regular, slant and king’s grid graphs with various values of t and r. The difference between these graphs is mainly the diagonal edges as shown in Figure 1. In addition, an efficient broadcasting configuration will also be specified using a modified genetic algorithm for a binary encoding.

The remainder of this paper is structured as follows. Section 2 presents a mathematical model for the $(t,r)$ broadcast domination number problems. A description of an efficient broadcast and the optimization framework used to find an efficient broadcasting configuration are detailed in Section 3. Numerical experiments and results including some corrections to Blessing et al.’s results presented in [1] are discussed in Section 4. Finally, Section 5 gives the limitation of the research work and the future directions.

2. Linear Programming for the $(t,r)$ Broadcast Domination Number

Consider an $m\times n$ grid graph. Assigning an index to every vertex $i=1,2,\dots ,mn$ in the graph, we define $v_i$ as a binary decision variable: $v_i=1$ if the vertex i is chosen to place a broadcasting tower of transmission t, and zero otherwise. Let $\mathbf{R}$ be an $mn\times mn$ reception matrix whose row i column j element ${\mathbf{R}}_{ij}$ is a reception strength at vertex i obtained from a broadcasting tower of transmission strength t located at vertex j.

A linear programming model for the $(t,r)$ broadcast domination number can be formulated as follows:

$$\begin{array}{cc}\hfill \gamma (t,r):=& \mathrm{minimize}\sum _{i=1}^{mn}{v}_i\hfill \end{array}$$

(1)

$$\mathrm{subject}\mathrm{to}:\mathbf{R}\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_{mn}\end{array}\right]\ge \left[\begin{array}{c}r\\ r\\ ⋮\\ r\end{array}\right]$$

(2)

$$\begin{array}{cc}\hfill v_i\in \{0,1\}& \forall i=1,2,\dots ,mn.\hfill \end{array}$$

(3)

The objective (1) is to minimize the number of required broadcasting towers. Constraint (2) ensures that every vertex receives adequate reception of strength at least r (as defined in Definition 3). The optimal value to this linear programming problem is precisely the $(t,r)$ broadcast domination number defined in Definition 4.

3. Optimization Modelling for an Efficient Broadcast

Given a graph $G=\left(V\left(G\right),E\left(G\right)\right)$ and a subset of broadcasting towers $S\subseteq V\left(G\right)$, we define $O\left(S\right)$ to be an “overlapping” set containing those vertices $v\in V\left(G\right)$ which receive signals from more than one broadcasting towers.

An efficient broadcast, as defined in [2,5], can be any $(t,r)$ broadcast dominating set that minimizes total wasted signals at those vertices $v\in O\left(S\right)$, and not necessarily a minimum $(t,r)$ broadcast dominating set. That is, the number of broadcasting towers of an efficient broadcast does not need to be $\gamma (t,r)$. In this work, we are interested in finding an efficient broadcasting configuration when the number of broadcasting towers is also the $(t,r)$ broadcast domination number, $\gamma (t,r)$. This class of efficient broadcasting configurations is very well applicable, e.g., if the expense for installing one more tower dominates that of the waste at those vertices whose signal strength exceeds the level r by a small amount.

For this reason, we shall restrict our focus to the class of minimum $(t,r)$ broadcast dominating sets of the graph G denoted by ${\mathcal{B}}_{\gamma (t,r)}$.

Definition 5.

Consider a graph $G=\left(V\right(G),E(G\left)\right)$. We say that a configuration of broadcasting towers $S\subseteq V\left(G\right)$ is in the class ${\mathcal{B}}_{\gamma (t,r)}$ if it satisfies two properties:

(1)

S is a $(t,r)$ broadcast dominating set of G.

(2)

The number of broadcasting towers of S is $\gamma (t,r)$.

We now define a class of $\gamma (t,r)$ efficient broadcasts.

Definition 6.

A minimum $(t,r)$ broadcast dominating set of a graph G is said to be a $\gamma (t,r)$ efficient broadcast, denoted by $S_{\gamma (t,r)}^{*}$, if

$$S_{\gamma (t,r)}^{*}\in \underset{S\in {\mathcal{B}}_{\gamma (t,r)}}{arg\; min}\sum _{v\in O\left(S\right)}(r\left(v\right)-r).$$

(4)

Here, we search for an efficient broadcast among those configurations in the class ${\mathcal{B}}_{\gamma (t,r)}$. To find a $\gamma (t,r)$ efficient broadcasting configuration $S_{\gamma (t,r)}^{*}$, we convert the problem in (4) into an equivalent unconstrained minimization problem with the objective function

$$\begin{array}{c}\hfill f\left(S\right)=\sum _{v\in O\left(S\right)}max(r\left(v\right)-r,0)\\ \hfill +M\sum _{v\in V\left(G\right)}max\left(r-r\left(v\right),0\right)\\ \hspace{1em}+M|\#S-\gamma (t,r)|,\hfill \\ \hfill \mathrm{subject}\mathrm{to}S\in \mathcal{S}\end{array}$$

(5)

where the feasible set $\mathcal{S}$ contains all possible broadcast configurations without any restriction (with any number of towers), M is a sufficiently large positive number and $\#S$ denotes the number of towers in the configuration S.

The first term in (5) is the summation of wasted signals at those vertices in the overlapping set $O\left(S\right)$ whose reception exceeds the required level r. As our feasible region is ${\mathcal{B}}_{\gamma (t,r)}$, the second and third terms ensure that a configuration S possess properties 1 and 2 of Definition 5, respectively. Any violation is subjected to the penalty cost M. Note that if the last term, which forces the number of broadcasting towers in a configuration S to be exactly equal to $\gamma (t,r)$, is removed, the objective function can be used to find an efficient broadcast considered in [2,5].

4. Numerical Experiments and Results

In this section, we present the results of our studies on the linear programming problem for the $(t,r)$ broadcast domination number, followed by results of the $\gamma (t,r)$ efficient broadcast via a genetic algorithm modified for binary encoding.

4.1. Finding a $(t,r)$ Broadcast Domination Number

To solve the problem of $(t,r)$ broadcast domination number as detailed in Section 2, we define the distance between any two vertices, computed as part of the reception coefficient matrix $\mathbf{R}$ in (3), as the number of edges in a shortest path connecting them.

First, we consider those problems studied in Blessing et al. [1] where the values of $(t,r)$ are fixed to $(2,2)$ and $(3,1)$, and only a grid graph of varying sizes $m\times n$, $1\le m,n\le 10$ are considered. We use the notation $G_{m\times n}$ for an $m\times n$ regular grid graph. Note that the results of $(t,r)$ broadcast domination numbers in [1] were obtained by solving a dynamic programming algorithm coded in SAGE.

The compared results of $G_{m\times n}$ for $(t,r)$ equal to $(2,2)$ and $(3,1)$ are given in

Table 1. Results for the $(2,2)$ broadcast domination numbers of $G_{8\times 7}$, $G_{9\times 7}$, $G_{9\times 8}$, $G_{9\times 9}$, $G_{10\times 8}$ and $G_{10\times 9}$.

Blessing et al.’s Results											Our Results
m/n	n1	n2	n3	n4	n5	n6	n7	n8	n9	n10	m/n	n1	n2	n3	n4	n5	n6	n7	n8	n9	n10
m1	1										m1	1
m2	2	2									m2	2	2
m3	2	3	4								m3	2	3	4
m4	3	4	6	8							m4	3	4	6	8
m5	3	5	7	10	11						m5	3	5	7	10	11
m6	4	6	8	12	14	16					m6	4	6	8	12	14	16
m7	4	7	10	13	16	19	21				m7	4	7	10	13	16	19	21
m8	5	8	11	15	18	22	25	28			m8	5	8	11	15	18	22	24	28
m9	5	9	12	17	20	24	28	32	35		m9	5	9	12	17	20	24	27	31	34
m10	6	10	14	19	22	27	30	35	39	42	m10	6	10	14	19	22	27	30	34	38	42

and

Table 2. Results for the $(3,1)$ broadcast domination numbers of $G_{8\times 2}$ and $G_{10\times 10}$.

Blessing et al.’s Results											Our Results
m/n	n1	n2	n3	n4	n5	n6	n7	n8	n9	n10	m/n	n1	n2	n3	n4	n5	n6	n7	n8	n9	n10
m1	1										m1	1
m2	1	1									m2	1	1
m3	1	1	1								m3	1	1	1
m4	1	2	2	3							m4	1	2	2	3
m5	1	2	2	3	4						m5	1	2	2	3	4
m6	2	2	2	4	4	4					m6	2	2	2	4	4	4
m7	2	2	3	4	4	6	6				m7	2	2	3	4	4	6	6
m8	2	2	3	4	5	6	7	8			m8	2	3	3	4	5	6	7	8
m9	2	3	3	5	6	6	7	8	9		m9	2	3	3	5	6	6	7	8	9
m10	2	3	4	5	6	7	8	9	10	10	m10	2	3	4	5	6	7	8	9	10	11

, respectively. The left panel presents the results from Blessing et al. [1], and the right one illustrates our results obtained by solving the formulated LP model. Since swapping the two numbers $m,n$ simply means rotating a symmetric grid graph, we only provide results in the lower triangular table. This leads to finding $(t,r)$ broadcast domination numbers for 55 different grid-size problems.

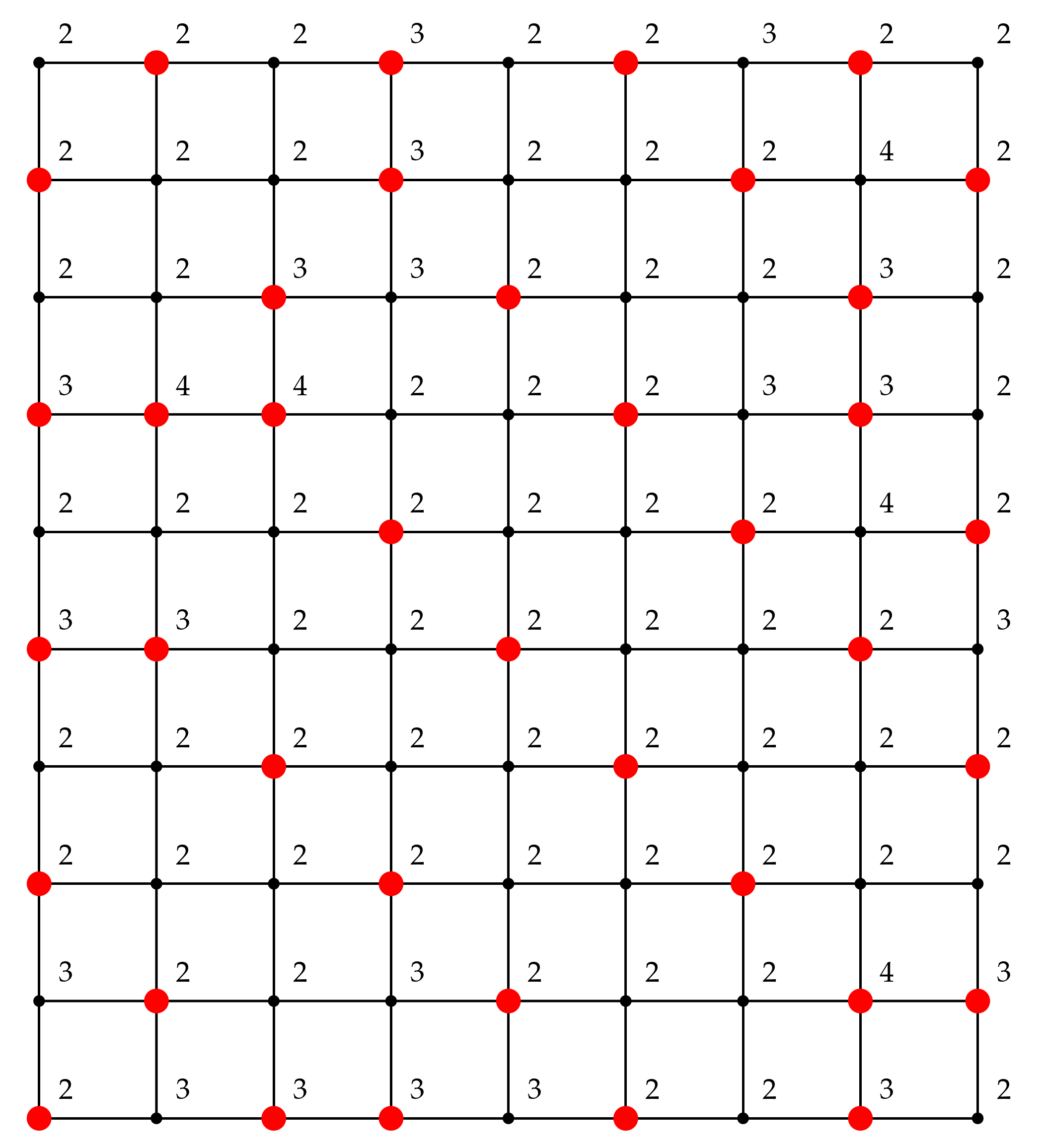
Compared to our results, we found inconsistencies in their reporting (6 boldface values in Table 1, and 2 values in Table 2). For example, in Table 1, the $(2,2)$ broadcast domination number of $G_{8\times 7}$ was reported as 25 in [1], but our results show that using only 24 broadcasting towers is sufficient as illustrated in Figure 2. The other five domination numbers found by [1] in Table 1 are also of higher values than ours. Verification examples, similar to Figure 2, that our optimal solutions are indeed the domination numbers are given in Appendix A for all these other cases.

On the other hand, the two boldface numbers in Table 2 indicate that the domination numbers found by Blessing et al. are smaller than ours. For example, for the $G_{8\times 2}$, the $(3,1)$ broadcast domination number was reported as 2 in [1], while our optimal solution from the LP was found to be 3. In this case, we carried out the exhaustive verification to confirm that all $\left(\genfrac{}{}{0pt}{}{16}{2}\right)=120$ possible configurations with 2 broadcasting towers on 16 vertices fail to be a broadcast dominating set for the $G_{8\times 2}$ graph. Thus, our optimal solution is actually the broadcast domination number. However, let us note that we could not perform exhaustive verification for the $(3,1)$ broadcast domination number of $G_{10\times 10}$ graph whose value was found to be 10 in [1], smaller than ours by 1 tower. This is because the size of all possible configurations with 10 broadcasting towers on 100 vertices of the $G_{10\times 10}$ graph is $\left(\genfrac{}{}{0pt}{}{100}{10}\right)>{10}^{13}$ exceeding our computational abilities.

As the proposed LP approach is applicable to any graph types, we provide additional results for $(t,r)$ broadcast domination numbers on other graph types not considered in [1], namely, slant and king’s grid graphs. For the sake of convenience, the notations $S_{m\times n}$ and $K_{m\times n}$ will be used to denote $m\times n$ slant and king’s grid graphs, respectively. Furthermore, since the LP approach is applicable to larger $t,r$ values than the settings considered in [1], we shall also vary the $t,r$ values from 1 to 10. A summary of problems we solved is given in

Table 3. A summary of additional problems considered for $(t,r)$ broadcast domination numbers.

Types	Problems
Regular	$G_{5\times 4}$, $G_{5\times 5}$, $G_{8\times 5}$, $G_{10\times 2}$, $G_{10\times 4}$, $G_{10\times 5}$, $G_{10\times 6}$, $G_{12\times 5}$
Slant	$S_{5\times 4}$, $S_{7\times 6}$, $S_{8\times 5}$, $S_{10\times 2}$, $S_{10\times 5}$, $S_{10\times 10}$, $S_{12\times 5}$, $S_{15\times 8}$
King	$K_{5\times 4}$, $K_{6\times 5}$, $K_{8\times 5}$, $K_{10\times 5}$, $K_{10\times 6}$, $K_{10\times 7}$, $K_{10\times 10}$, $K_{12\times 5}$

.

Here, we present two cases from each graph type: $G_{5\times 4}$ and $G_{10\times 5}$, $S_{5\times 4}$ and $S_{10\times 10}$, $K_{5\times 4}$ and $K_{12\times 5}$. The broadcast domination numbers for these graphs are provided in

Table 4. The $(t,r)$ broadcast domination numbers for regular grid types: (a) $G_{5\times 4}$ and (b) $G_{10\times 5}$.

(a) ${\mathit{G}}_{5\times 4}$											(b) ${\mathit{G}}_{10\times 5}$
t/r	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10	t/r	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10
t1	20	-	-	-	-	-	-	-	-	-	t1	50	-	-	-	-	-	-	-	-	-
t2	6	10	14	18	-	-	-	-	-	-	t2	13	22	32	42	-	-	-	-	-	-
t3	3	4	5	7	9	10	12	14	15	18	t3	6	8	12	16	19	22	26	30	33	38
t4	2	3	3	4	5	6	7	7	9	9	t4	4	5	6	8	10	12	13	15	17	19
t5	1	2	2	3	3	4	4	5	5	6	t5	2	3	4	5	6	7	8	9	10	11
t6	1	1	2	2	2	3	3	4	4	4	t6	2	2	3	4	4	5	6	6	7	8
t7	1	1	1	2	2	2	2	3	3	3	t7	2	2	2	3	3	4	4	5	5	6
t8	1	1	1	1	2	2	2	2	2	3	t8	1	2	2	2	2	3	3	4	4	4
t9	1	1	1	1	1	2	2	2	2	2	t9	1	1	2	2	2	2	3	3	3	4
t10	1	1	1	1	1	1	2	2	2	2	t10	1	1	1	2	2	2	2	3	3	3

,

Table 5. The $(t,r)$ broadcast domination numbers for slant types: (a) $S_{5\times 4}$ and (b) $S_{10\times 10}$.

(a) ${\mathit{S}}_{5\times 4}$											(b) ${\mathit{S}}_{10\times 10}$
t/r	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10	t/r	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10
t1	20	-	-	-	-	-	-	-	-	-	t1	100	-	-	-	-	-	-	-	-	-
t2	4	8	11	15	-	-	-	-	-	-	t2	18	30	46	61	-	-	-	-	-	-
t3	2	4	5	6	8	10	11	13	14	16	t3	8	11	16	22	27	32	38	43	48	54
t4	2	2	3	4	4	5	6	7	8	8	t4	5	6	8	11	13	16	18	21	24	26
t5	1	2	2	2	3	3	4	4	5	5	t5	4	4	5	6	8	9	11	12	14	15
t6	1	1	2	2	2	3	3	3	4	4	t6	3	3	4	4	6	6	7	8	9	10
t7	1	1	1	2	2	2	2	3	3	3	t7	2	2	3	4	4	5	6	6	7	8
t8	1	1	1	1	2	2	2	2	2	3	t8	2	2	2	3	3	4	4	5	5	6
t9	1	1	1	1	1	2	2	2	2	2	t9	2	2	2	2	3	3	4	4	4	5
t10	1	1	1	1	1	1	2	2	2	2	t10	1	2	2	2	2	2	3	3	3	4

and

Table 6. The $(t,r)$ broadcast domination numbers for king’s grid types: (a) $K_{5\times 4}$ and (b) $K_{12\times 5}$.

(a) ${\mathit{K}}_{5\times 4}$											(b) ${\mathit{K}}_{12\times 5}$
t/r	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10	t/r	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10
t1	20	-	-	-	-	-	-	-	-	-	t1	60	-	-	-	-	-	-	-	-	-
t2	4	7	10	12	18	-	-	-	-	-	t2	8	16	25	32	42	-	-	-	-	-
t3	1	2	4	5	6	8	9	10	12	13	t3	3	6	9	12	14	18	20	24	27	30
t4	1	1	2	2	3	4	4	5	5	6	t4	2	3	4	6	7	8	10	11	12	14
t5	1	1	1	2	2	2	3	3	4	4	t5	2	2	2	4	4	5	6	6	7	8
t6	1	1	1	1	2	2	2	2	3	3	t6	2	2	2	2	4	4	4	4	6	6
t7	1	1	1	1	1	2	2	2	2	2	t7	1	2	2	2	2	3	4	4	4	4
t8	1	1	1	1	1	1	2	2	2	2	t8	1	1	2	2	2	2	3	3	4	4
t9	1	1	1	1	1	1	1	2	2	2	t9	1	1	1	2	2	2	2	3	3	3
t10	1	1	1	1	1	1	1	1	2	2	t10	1	1	1	1	2	2	2	2	2	3

. Results for other cases can be found in Appendix B. Note that different from Table 1 and Table 2, a number in these tables is a $(t,r)$ broadcast domination number for a fixed graph size. A dash symbol (-) in the table indicates an infeasible situation as the reception parameter r is too large for the given transmission parameter t. Considering the three graph types of same size: $G_{5\times 4}$, $S_{5\times 4}$ and $K_{5\times 4}$, which correspond to panel (a) of each table, we can observe that a king’s grid graph requires fewest number of broadcasting towers followed by slant and grid graphs. This makes intuitive sense because additional diagonal edges allow signals to transmit to more neighbor vertices.

4.2. Locating an Efficient Broadcast

Having found $\gamma (t,r)$, the minimum size of a $(t,r)$ broadcast dominating set, we now identify a $\gamma (t,r)$ efficient broadcasting configuration $S_{\gamma (t,r)}^{*}$, as defined in Definition 6.

For a computational purpose, we consider an equivalent unconstrained binary optimization problem to the problem in (5). To that end, we define a binary vector $\mathbf{v}\in {\{0,1\}}^{mn}$ where each component $v_i$ corresponds to the vertex i of the graph G: $v_i=1$ if the vertex i is selected as a broadcasting tower of transmission t, and zero otherwise. We subsequently define a relation between a configuration S which is our decision variable in the original problem, and a binary vector $\mathbf{v}\in {\{0,1\}}^{mn}$ by

$$S:=\left\{i\right|v_i=1\},$$

(6)

and consider the equivalent problem with a binary vector input $\mathbf{v}$ instead. Once the optimal solution ${\mathbf{v}}^{*}$ to the latter is found, we can convert the solution back to the optimal configuration $S^{*}$ by using the predefined relation in (6).

To solve the unconstrained binary optimization problem, we apply the genetic algorithm (GA) with a binary input. To speed up the convergence and leverage the available information, we supply an optimal configuration, a solution of the LP problem in (1)–(3) (which is guaranteed to be in ${\mathcal{B}}_{\gamma (t,r)}$), to the initial population of the GA algorithm. The GA parameters which are the population size and the maximum number of iterations are set to 1000 and 3000, respectively. The algorithm stops when the optimal solution (efficient broadcasting configuration) is found. To determine the sufficiently large penalty $M>0$ used in (5), recall that our goal is to minimize the wasted signals. We thus consider the worst-case scenario, i.e., when all vertices are used as broadcasting towers, and set M as the resulting wasted signals.

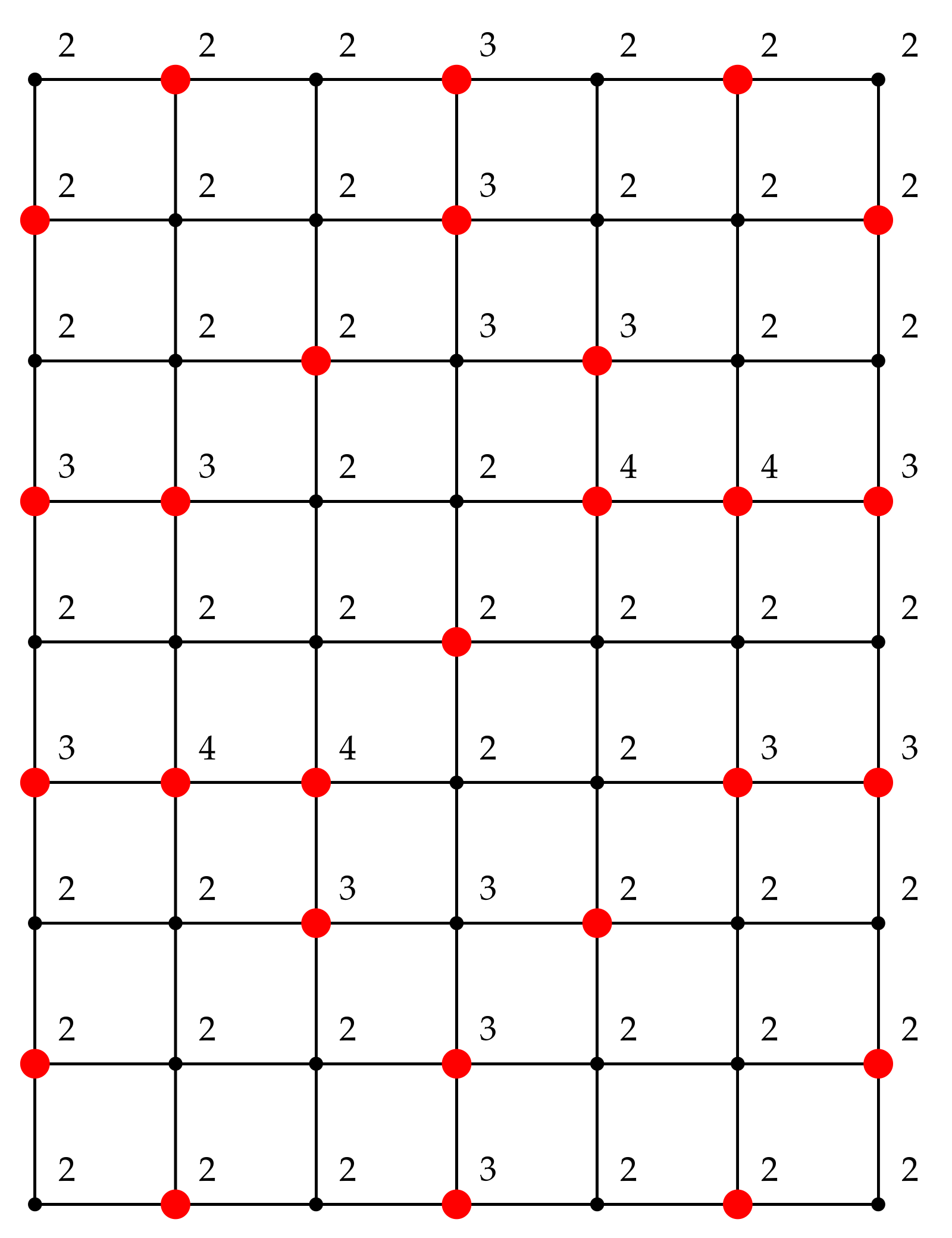
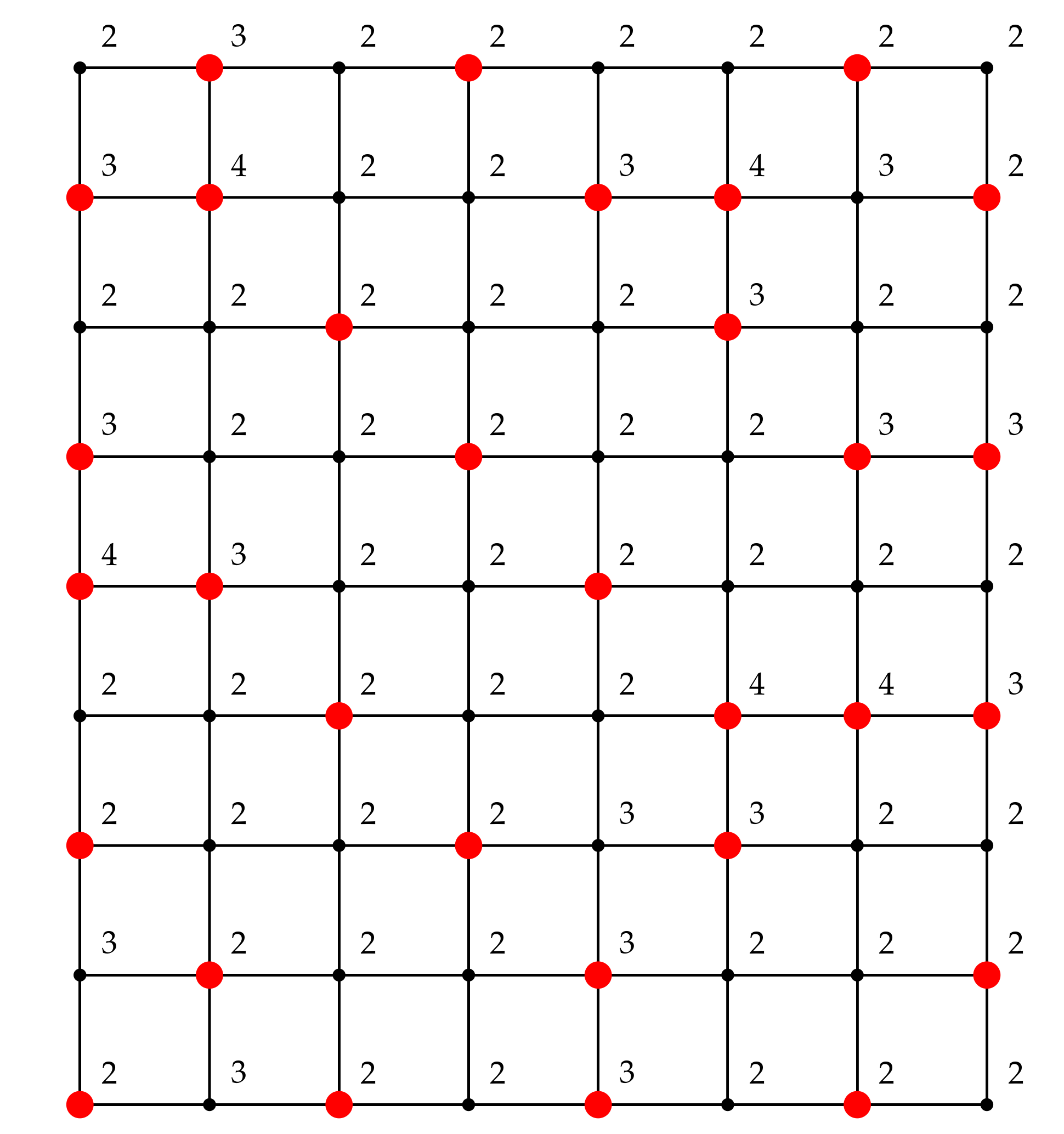
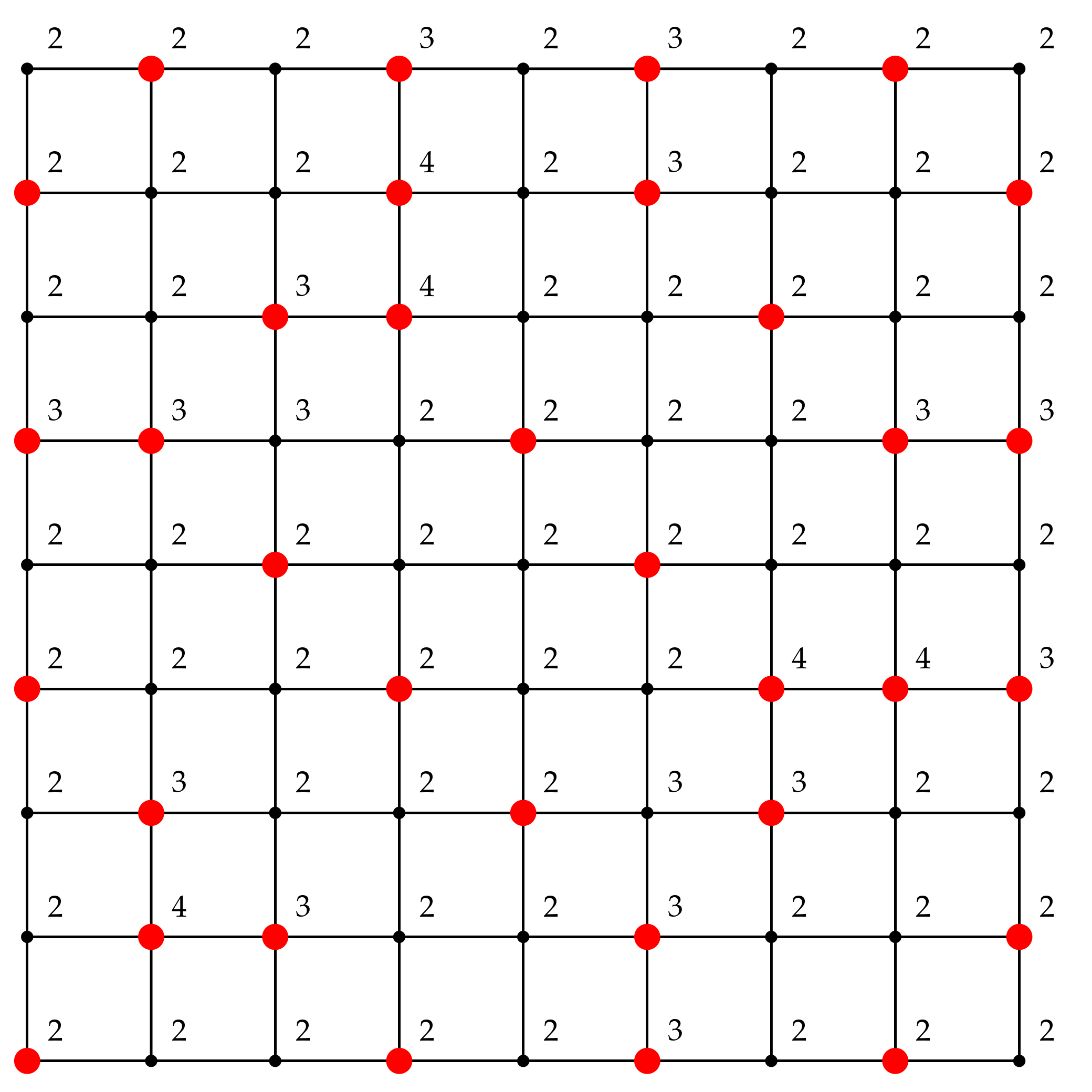
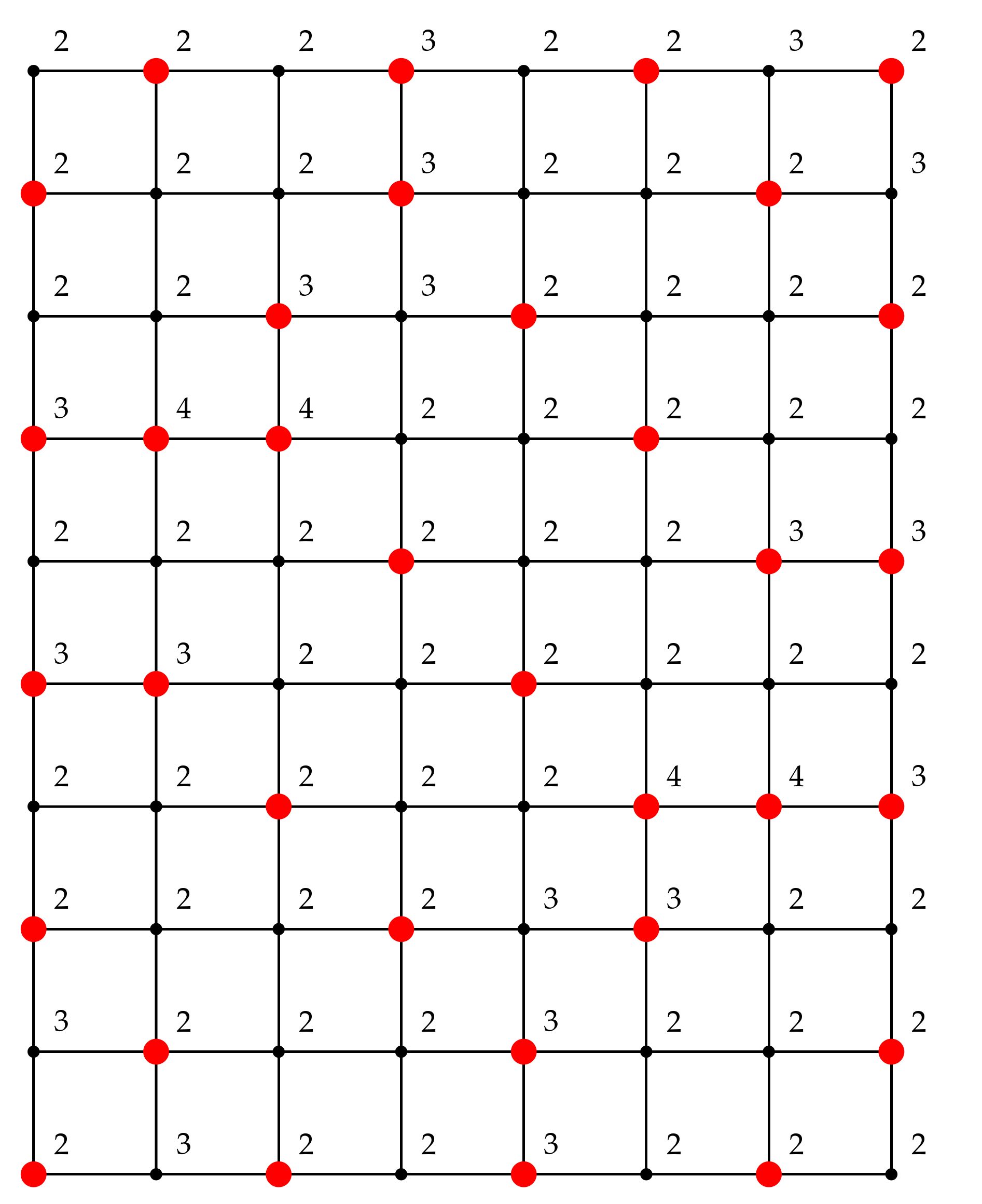
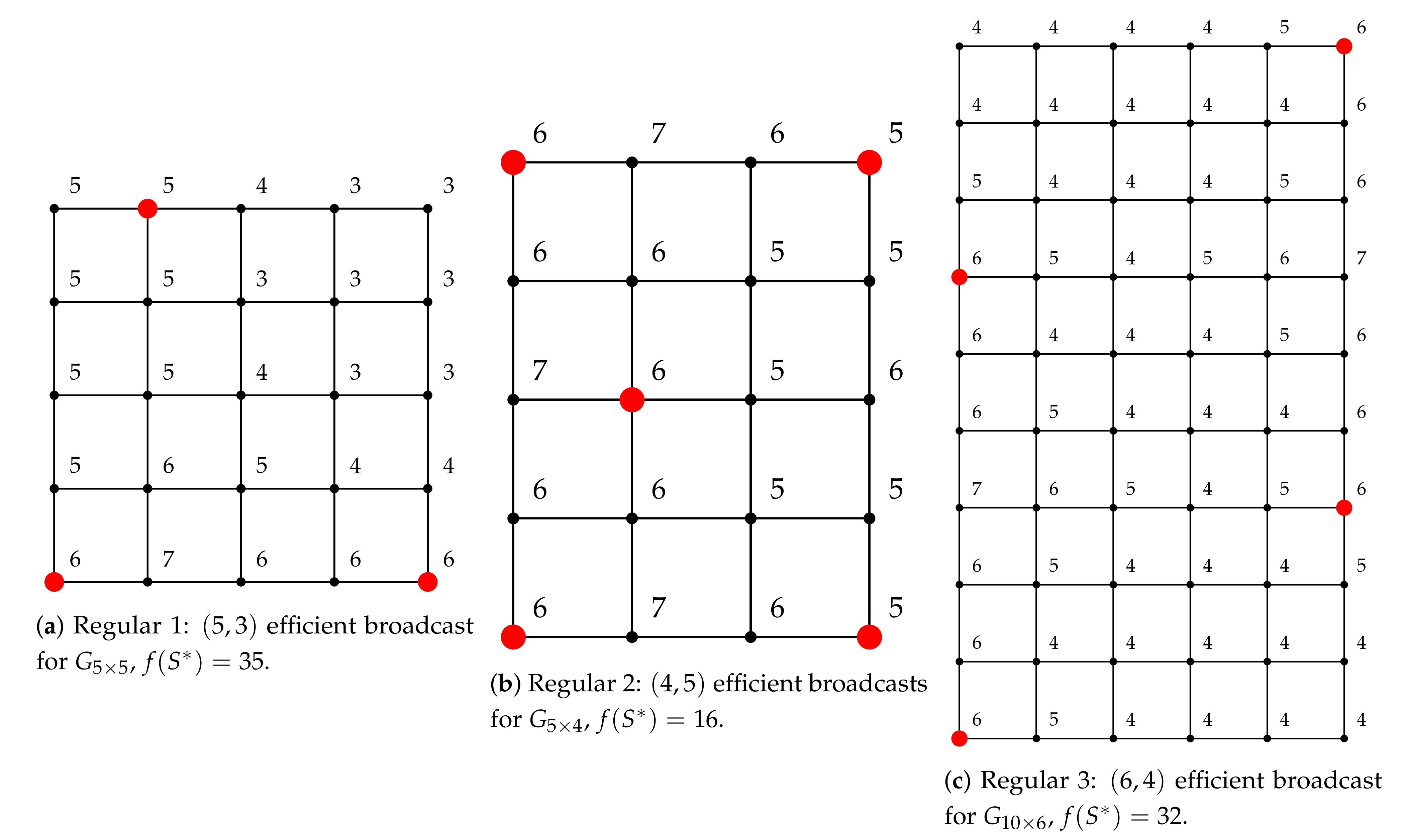
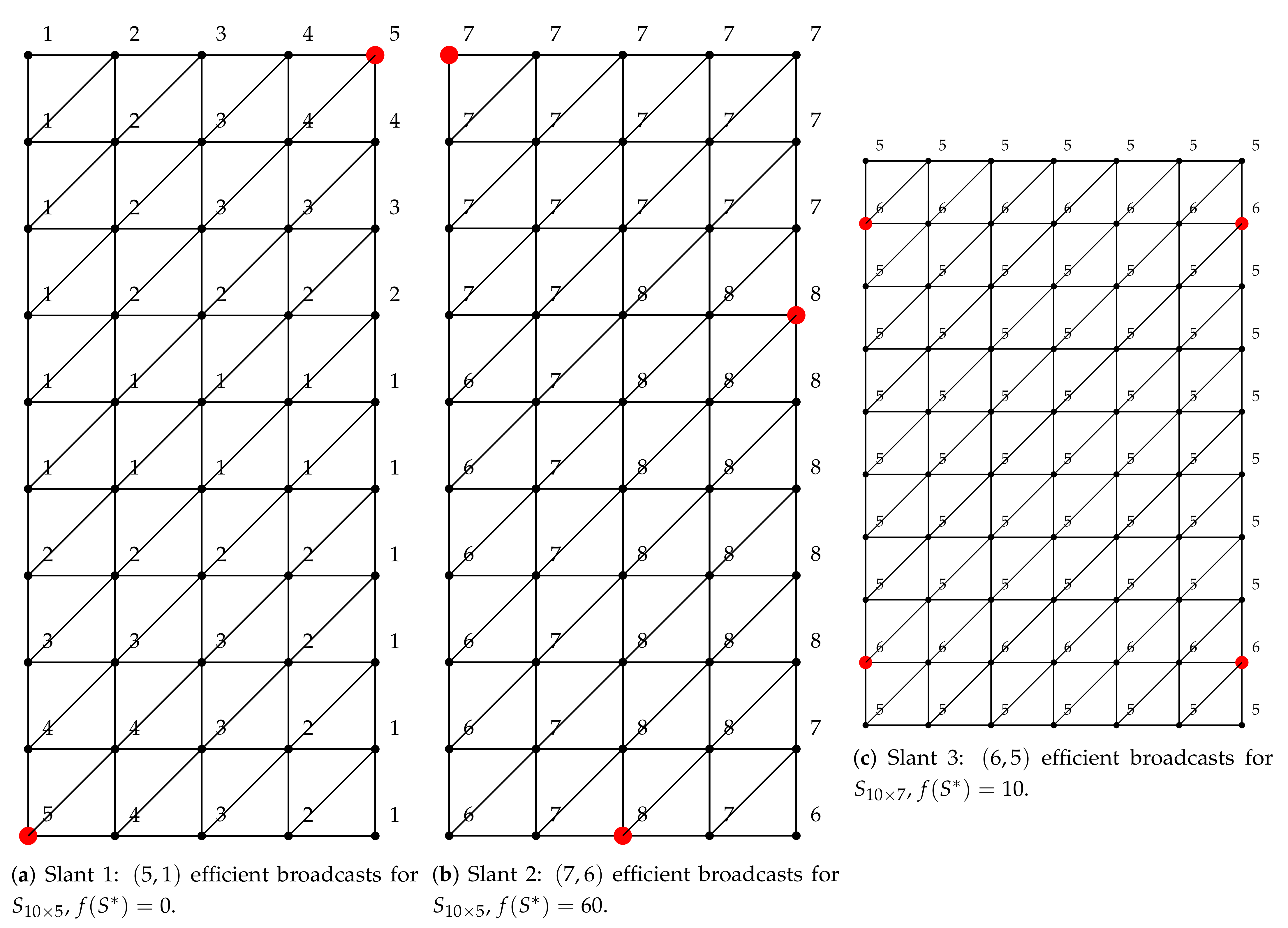
We demonstrate our approach on three problems for each graph type, resulting in 9 problems in total. The details of these problems are presented in

Table 7. Descriptions of problems considered in Section 4.2.

Problem	$(\mathit{m},\mathit{n})$	$(\mathit{t},\mathit{r})$	$\mathit{\gamma }(\mathit{t},\mathit{r})$
Regular 1	(5, 5)	(5, 3)	3
Regular 2	(5, 4)	(4, 5)	5
Regular 3	(10, 6)	(6, 4)	4
Slant 1	(10, 5)	(5, 1)	2
Slant 2	(10, 5)	(7, 6)	3
Slant 3	(10, 7)	(6, 5)	4
King 1	(10, 5)	(4, 2)	2
King 2	(7, 6)	(6, 8)	3
King 3	(12, 5)	(6, 6)	4

. Columns 2–3 of the table give specific parameter values of the graph size $(m,n)$, the transmission t, and the required reception strength r. Column 4 corresponds to the broadcast domination number which was found by solving the LP problem in Section 4.1.

Each experiment is repeated for 20 replications with different initial population. Examples of an optimal configuration of the efficient broadcast found by solving minimization problem in (5) with the stated values of M for the regular, slant and king’s grid graphs are illustrated in Figure 3, Figure 4 and Figure 5. The caption below each sub-figure provides also the optimal objective function value $f\left(S^{*}\right)$. Note that it is possible to have multiple optimal configurations with the same objective function value.

To validate our obtained results, we carried out a computationally expensive exhaustive search to get an efficient broadcasting configuration $S_{\mathrm{exact}}$, and calculate the value of $f\left(S_{\mathrm{exact}}\right)$ according to (5). Numerical results revealed that the GA algorithm could attain the same minimum value of $f\left(S_{\mathrm{exact}}\right)$ for all problems, implying that the proposed approach could efficiently locate the exact efficient broadcast.

5. Conclusions

From an optimization perspective, we formulated and solved a problem of finding the $(t,r)$ broadcast domination number via a linear programming model. We also implemented a meta-heuristic genetic algorithm to locate an efficient broadcasting configuration that minimizes overall wasted signals in a graph network. To validate our models, three types of grid graphs, namely regular, slant and king’s grid graphs with different sizes were considered. Some corrections of the results presented in [1] were also made according to our obtained results. Numerical results showed that optimization approaches we developed to find the exact $(t,r)$ broadcast domination number as well as efficient broadcasting configurations are very efficient, and can be used to obtain optimal solutions for problems with larger values of $t,r$ than what can be provided on a theoretical basis.

By modifying a reception matrix $\mathbf{R}$ appropriately, the proposed model can also be applied to solve other graph types as well as real-world applications, for example, the problem of installing mobile transmission towers. Using other heuristic or surrogate-based optimization methods to find a large-scale broadcast domination number might also be worth investigating when solving linear programming with the simplex method becomes infeasible, e.g., problems with larger graph sizes, or problems with small t, but relatively large r.