Comparative Analysis of Hybrid Fuzzy MCGDM Methodologies for Optimal Robot Selection Process
Abstract
1. Introduction
2. Literature Review
3. Preliminaries
4. GITrF-BW Method
4.1. Step 1. Selection of a Criteria Set
4.2. Step 2. Selection of Most Favorable Criterion and Least Favorable Criterion
4.3. Step 3. GITrF-RC of the Best Criterion over All Other Criteria
4.4. Step 4. GITrF-RC of All of the Other Criteria over the Worst Criterion
4.5. Step 5. Determine the GITrFWs of Criteria
5. GITrF-TOPSIS Method
5.1. Step 1. Experts’ Alternatives and Criteria Sets
5.2. Step 2. Aggregation of Group Decision
5.3. Step 3. Normalization Process
5.4. Step 4. GITrF-PIS and GITrF-NIS
5.5. Step 5. Ideal and Anti-Ideal Matrices
5.6. Step 6. Relative Closeness
5.7. Step 7. Ranking
6. GITrF-VIKOR Method
6.1. Step 5. Calculation of S and R
6.2. Step 6. Compute Q Value
6.3. Step 7. Ranking
7. Optimal Robot Selection Process
7.1. GITrF-TOPSIS Results
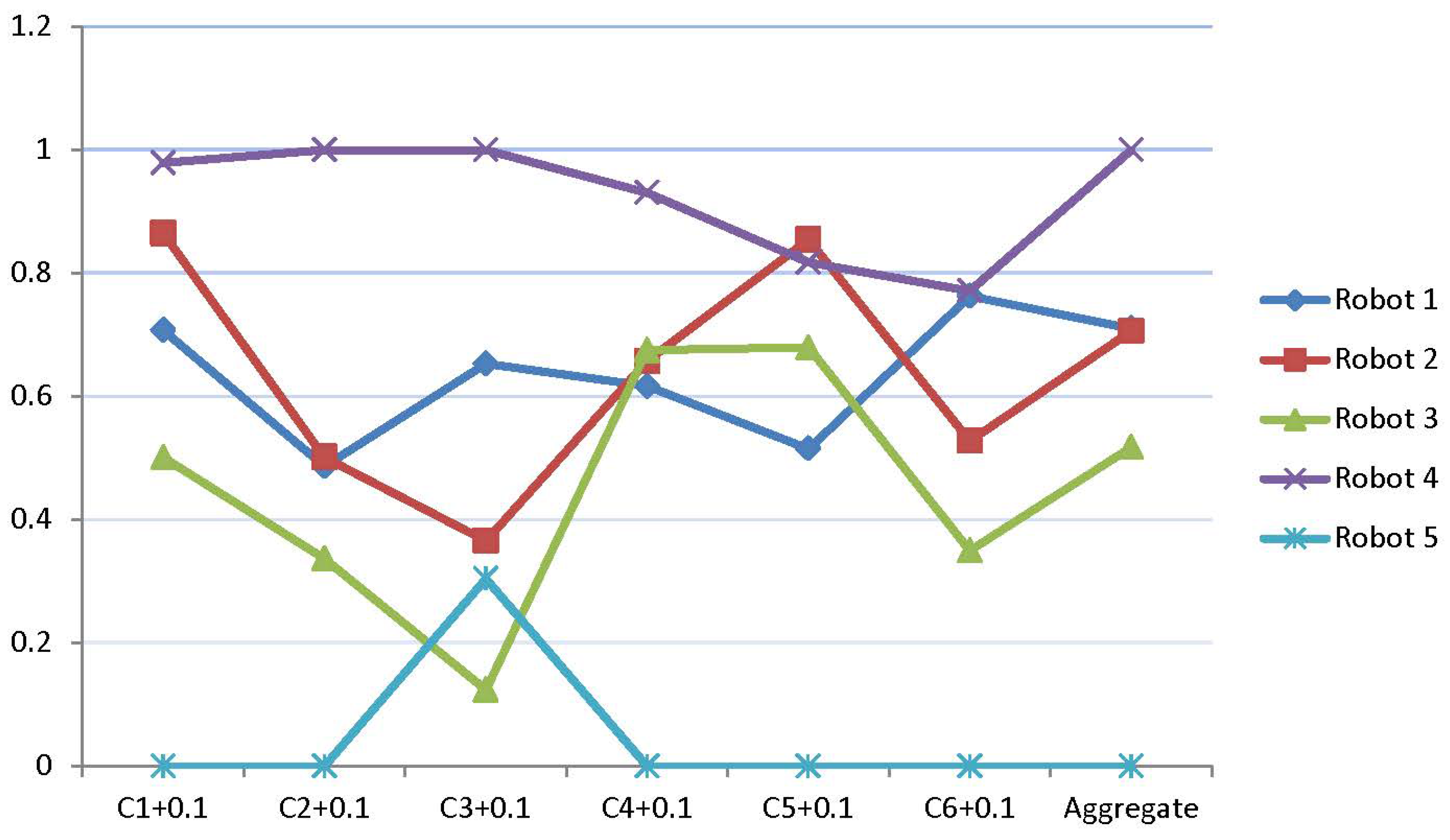
7.2. GITrF-VIKOR Results
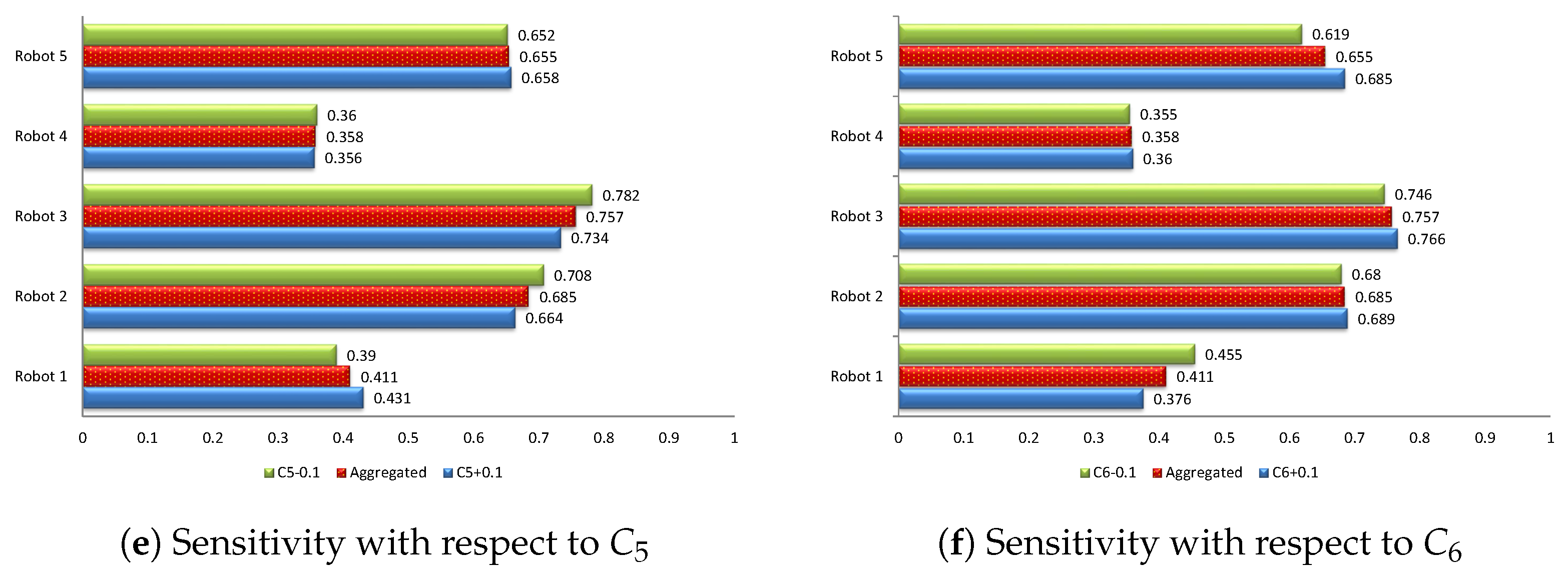
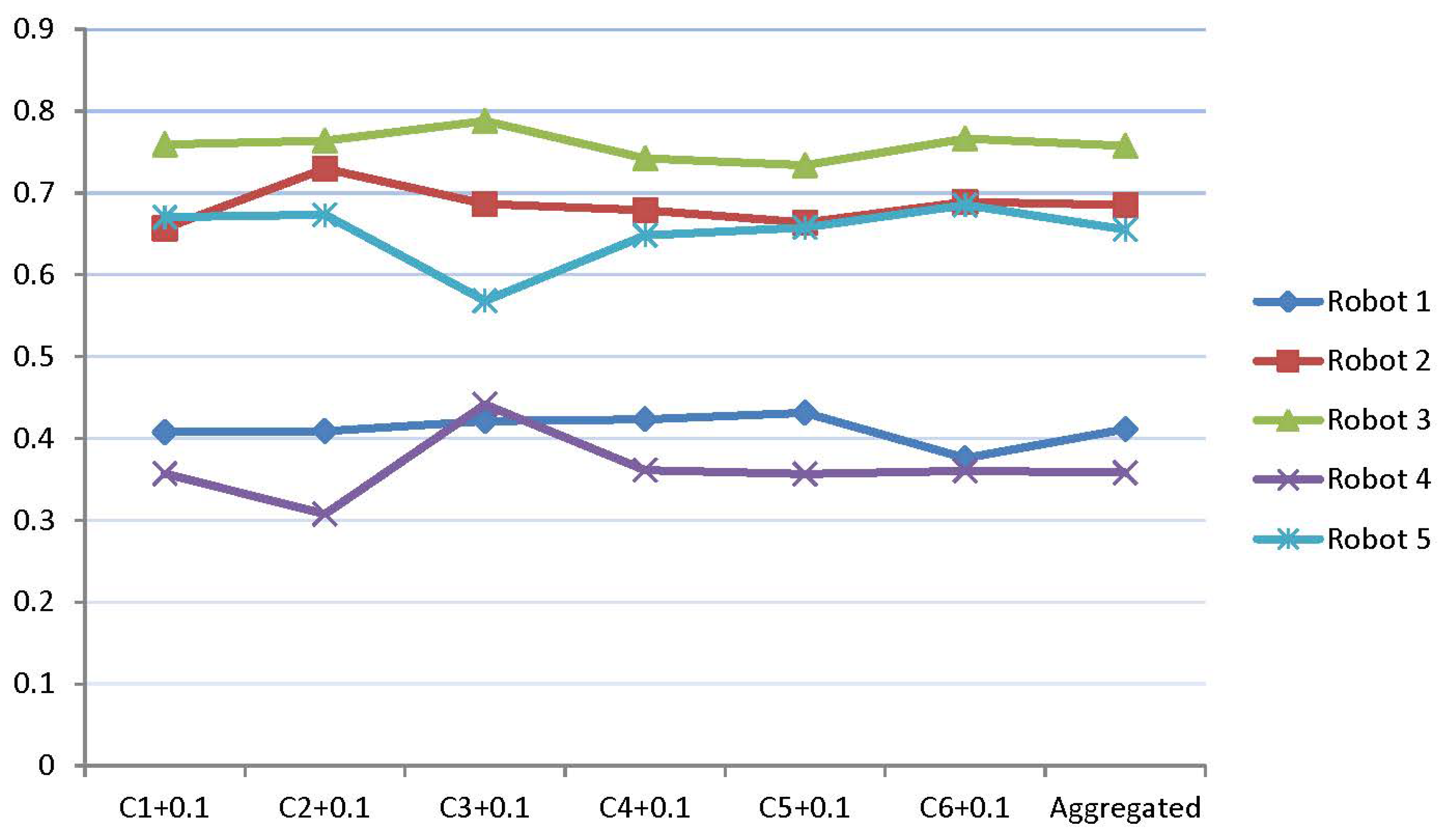
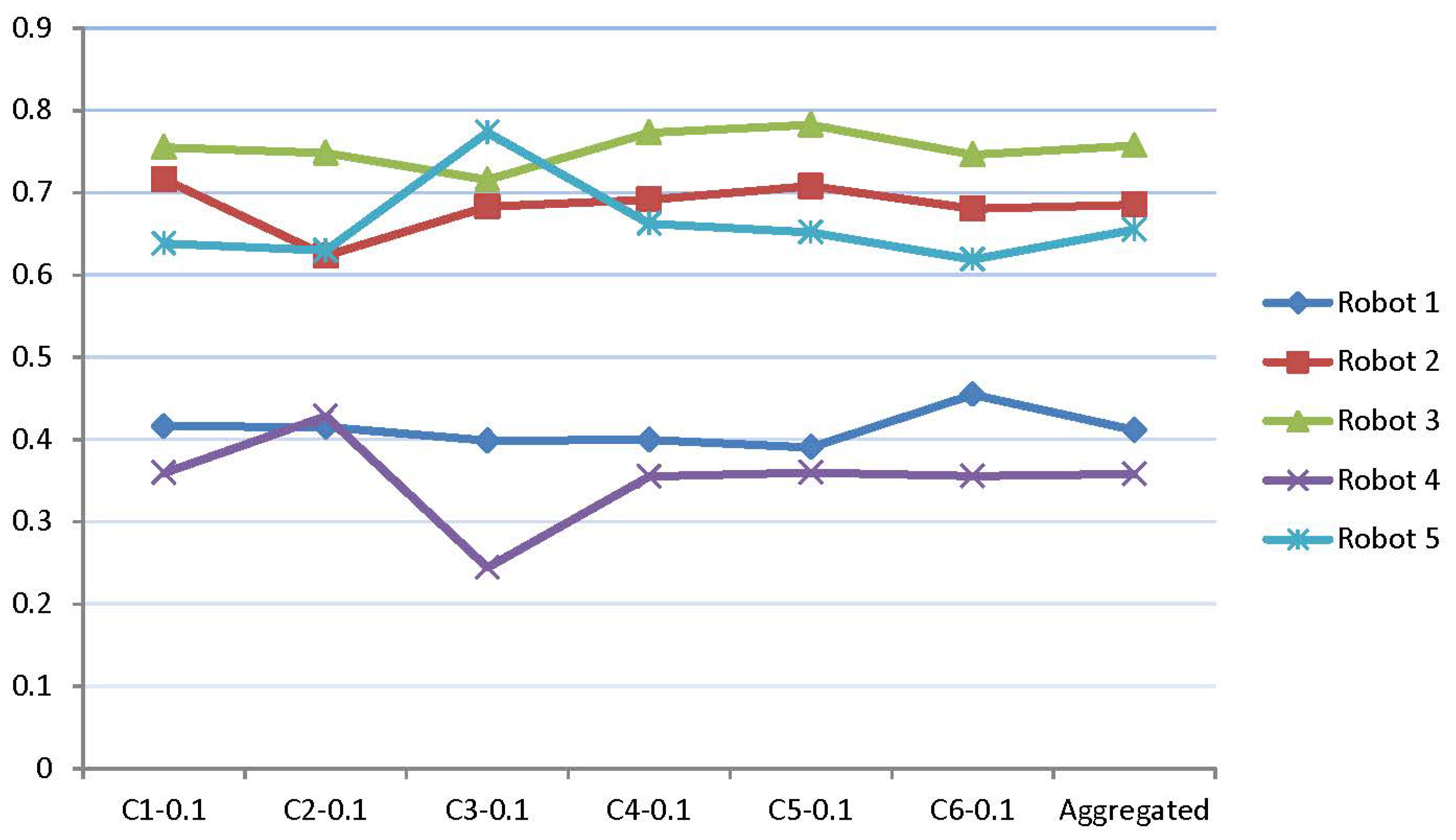
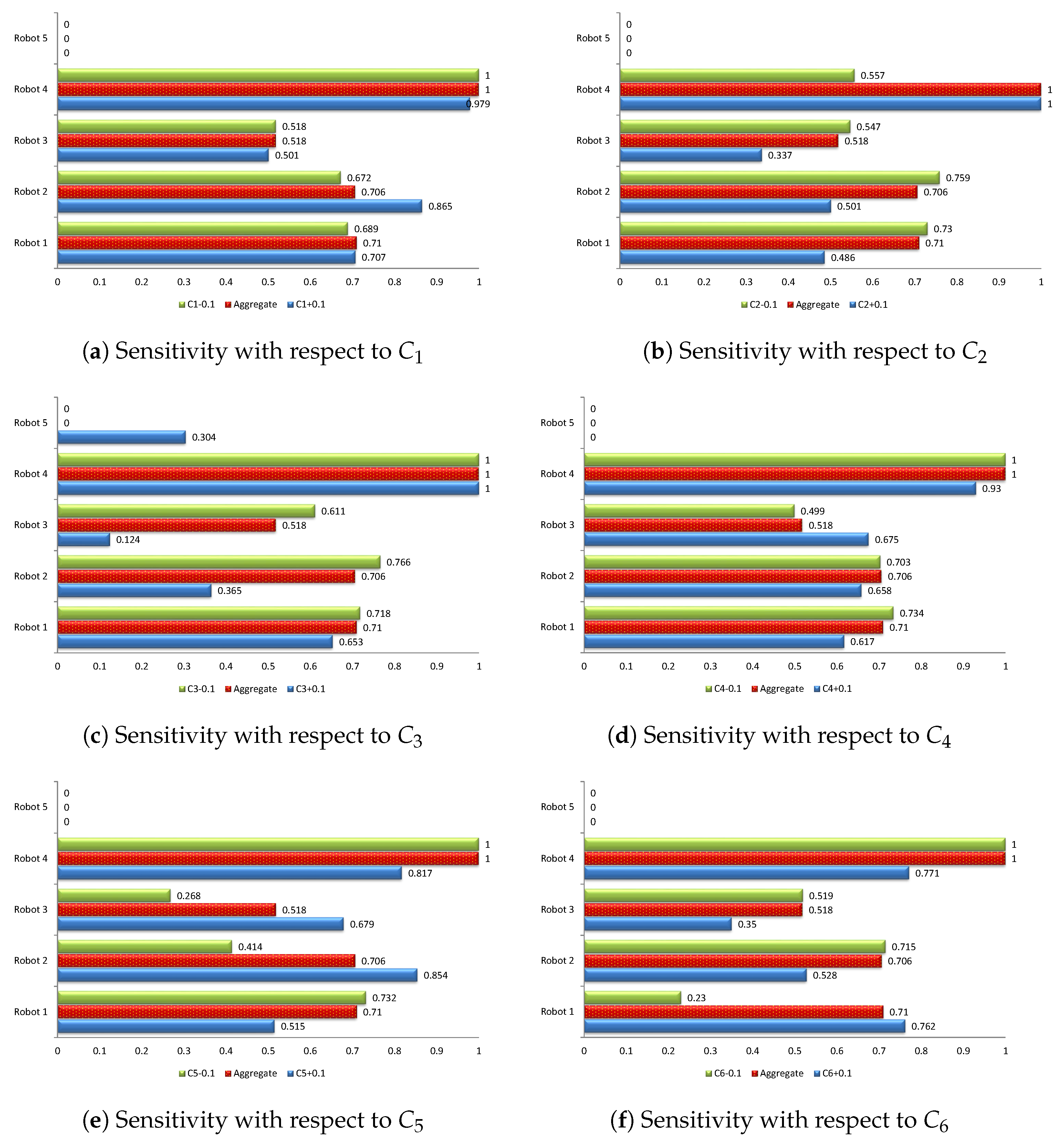
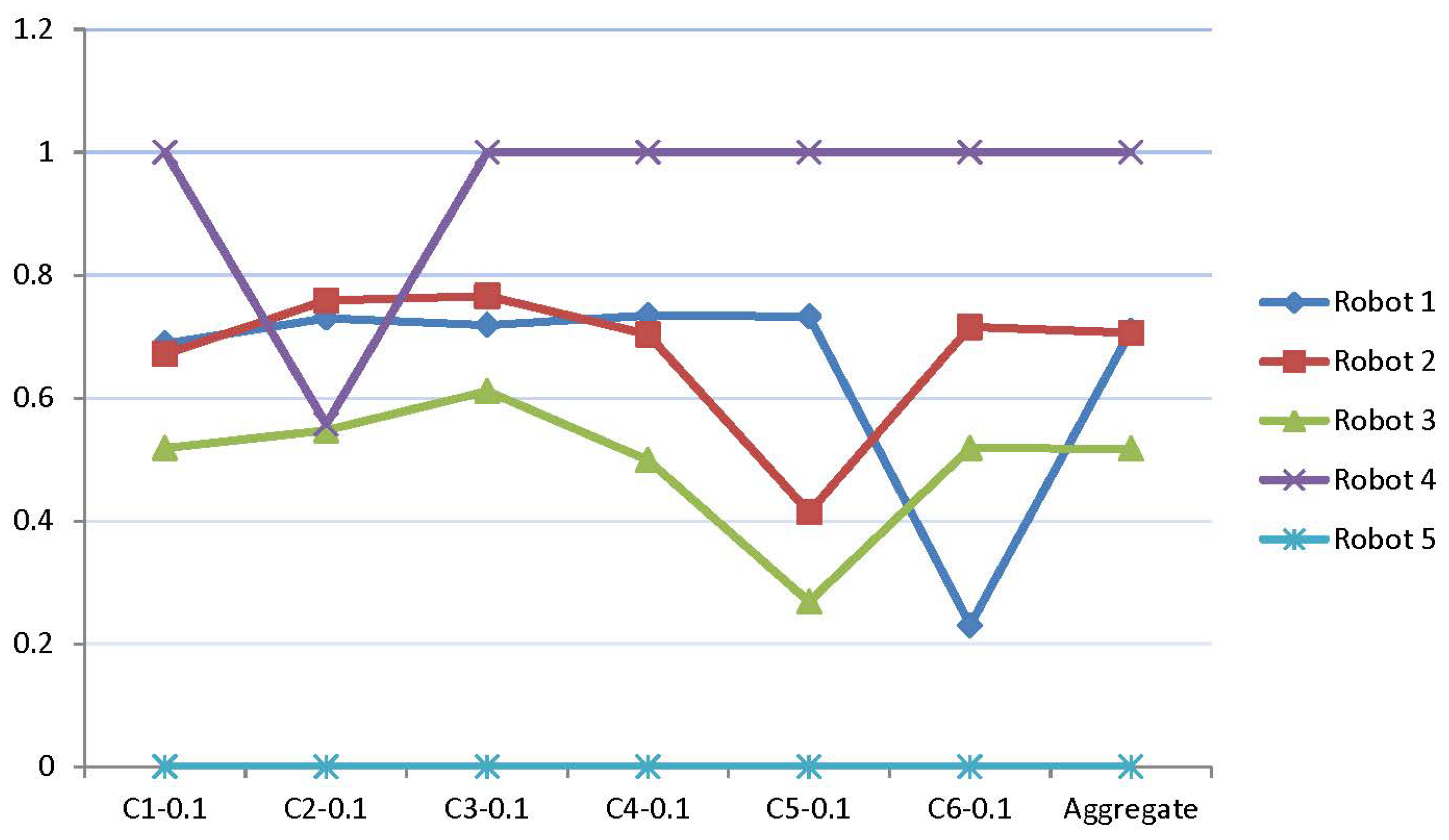
8. Sensitivity Analysis
9. Discussion
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BWM | Best-worst method |
| COPRAS-G | COmplex PRoportional ASsessment of alternatives with Grey relations |
| CoG | Center of gravity |
| DM | Decision maker |
| ELECTRE | ELimination Et Choice Translating REality |
| FAHP | Analytic hierarchy process |
| GITrFNs | Generalized interval-valued trapezoidal fuzzy numbers |
| GITrFWs | Generalized interval-valued trapezoidal fuzzy weights |
| GITrF-BWM | Generalized interval-valued trapezoidal fuzzy best-worst method |
| GITrFP | Generalized interval-valued trapezoidal fuzzy preference |
| GITrF-RC | Generalized interval-valued trapezoidal fuzzy reference comparison |
| GITrF-PIS | Generalized interval-valued trapezoidal fuzzy positive-ideal solution |
| GITrF-NIS | Generalized interval-valued trapezoidal fuzzy negative-ideal solution |
| GMIR | Graded mean integration representation |
| MCDM | Multi-criteria decision making |
| MCGDM | Multiple criteria group decision-making |
| TOPSIS | Technique for Order Preference by Similarity to the Ideal Solution |
| TPOP | Technique of Precise Order Preferences |
| VIKOR | VIsekriterijumska optimizacija i KOmpromisno Resenje |
References
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bellman, R.; Zadeh, L. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, B141–B273. [Google Scholar] [CrossRef]
- Wu, P.; Liu, S.; Zhou, L.; Chen, H. A fuzzy group decision making model with trapezoidal fuzzy preference relations based on compatibility measure and COWGA operator. Appl. Intell. 2018, 48, 46–67. [Google Scholar] [CrossRef]
- Wu, P.; Wu, Q.; Zhou, L.; Chen, H.; Zhou, H. A consensus model for group decision making under trapezoidal fuzzy numbers environment. Neural Comput. Appl. 2019, 31, 377–394. [Google Scholar] [CrossRef]
- Wu, P.; Zhou, L.; Zheng, T.; Chen, H. A fuzzy group decision making and its application based on compatibility with multiplicative trapezoidal fuzzy preference relations. Int. J. Fuzzy Syst. 2017, 19, 683–701. [Google Scholar] [CrossRef]
- Luo, M.; Long, H. Picture Fuzzy Geometric Aggregation Operators Based on a Trapezoidal Fuzzy Number and Its Application. Symmetry 2021, 13, 119. [Google Scholar] [CrossRef]
- Wei, S.H.; Chen, S.M. Fuzzy risk analysis based on interval-valued fuzzy numbers. Expert Syst. Appl. 2009, 36, 2285–2299. [Google Scholar] [CrossRef]
- Chen, S.H. Ranking fuzzy numbers with maximizing set and minimizing set. Fuzzy Sets Syst. 1985, 17, 113–129. [Google Scholar] [CrossRef]
- Wei, S.H.; Chen, S.M. A new similarity measure between interval-valued trapezoidal fuzzy numbers based on geometric distance and the center-of-gravity-points. In Proceedings of the IEEE 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; Volume 3, pp. 1412–1417. [Google Scholar]
- Liu, P. A weighted aggregation operators multi-attribute group decision-making method based on interval-valued trapezoidal fuzzy numbers. Expert Syst. Appl. 2011, 38, 1053–1060. [Google Scholar] [CrossRef]
- Liu, P.; Jin, F. A multi-attribute group decision-making method based on weighted geometric aggregation operators of interval-valued trapezoidal fuzzy numbers. Appl. Math. Model. 2012, 36, 2498–2509. [Google Scholar] [CrossRef]
- Ebrahimnejad, A. A simplified new approach for solving fuzzy transportation problems with generalized trapezoidal fuzzy numbers. Appl. Soft Comput. 2014, 19, 171–176. [Google Scholar] [CrossRef]
- Sulaiman, T.; Bulut, H.; Baskonus, H. On the exact solutions to some system of complex nonlinear models. Appl. Math. Nonlinear Sci. 2020, 6, 29–42. [Google Scholar] [CrossRef]
- Yu, J. A Model Study Based on Social Network Relational Dimensions and Structural Dimensions. Appl. Math. Nonlinear Sci. 2020, 5, 121–128. [Google Scholar] [CrossRef]
- Alghamd, M.; Alshaery, A. Mathematical Algorithm for Solving Two–Body Problem. Appl. Math. Nonlinear Sci. 2020, 5, 217–228. [Google Scholar] [CrossRef]
- Li, R.; Sun, T. Assessing factors for designing a successful B2C E–Commerce website using fuzzy AHP and TOPSIS–Grey methodology. Symmetry 2020, 12, 363. [Google Scholar] [CrossRef]
- de Assis, R.; Pazim, R.; Malavazi, M.; Petry, P.d.C.; de Assis, L.; Venturino, E. A mathematical model to describe the herd behaviour considering group defense. Appl. Math. Nonlinear Sci. 2020, 5, 11–24. [Google Scholar] [CrossRef]
- Zhu, P.; Fan, Q.; Zhu, J. Empirical Analysis on Environmental Regulation Performance Measurement in Manufacturing Industry: A Case Study of Chongqing, China. Appl. Math. Nonlinear Sci. 2020, 5, 25–34. [Google Scholar] [CrossRef]
- İnce, N.; Shamilov, A. An application of new method to obtain probability density function of solution of stochastic differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 337–348. [Google Scholar] [CrossRef]
- Çitil, H. Important notes for a fuzzy boundary value problem. Appl. Math. Nonlinear Sci. 2019, 4, 305–314. [Google Scholar] [CrossRef]
- Ruiz-Fernández, J.P.; Benlloch Marco, J.; López, M.A.; Valverde-Gascueña, N. Influence of seasonal factors in the earned value of construction. Appl. Math. Nonlinear Sci. 2019, 4, 21–34. [Google Scholar] [CrossRef]
- Rashid, T.; Beg, I.; Husnine, S. Robot selection by using generalized interval-valued fuzzy numbers with TOPSIS. Appl. Soft Comput. 2014, 21, 462–468. [Google Scholar] [CrossRef]
- Ali, A.; Rashid, T. Best–worst method for robot selection. Soft Comput. 2021, 25, 563–583. [Google Scholar] [CrossRef]
- Rashid, T.; Ali, A.; Chu, Y.M. Hybrid BW-EDAS MCDM methodology for optimal industrial robot selection. PLoS ONE 2021, 16, e0246738. [Google Scholar] [CrossRef]
- Opricovic, S. Multicriteria optimization of civil engineering systems. Fac. Civ. Eng. Belgrade 1998, 2, 5–21. [Google Scholar]
- Athawale, V.; Chatterjee, P.; Chakraborty, S. Selection of industrial robots using compromise ranking method. Int. J. Ind. Syst. Eng. 2012, 11, 3–15. [Google Scholar] [CrossRef]
- Chatterjee, P.; Athawale, V.; Chakraborty, S. Selection of industrial robots using compromise ranking and outranking methods. Robot. Comput.-Integr. Manuf. 2010, 26, 483–489. [Google Scholar] [CrossRef]
- Devi, K. Extension of VIKOR method in intuitionistic fuzzy environment for robot selection. Expert Syst. Appl. 2011, 38, 14163–14168. [Google Scholar] [CrossRef]
- Rao, R.; Patel, B.; Parnichkun, M. Industrial robot selection using a novel decision making method considering objective and subjective preferences. Robot. Auton. Syst. 2011, 59, 367–375. [Google Scholar] [CrossRef]
- İç, Y.T.; Yurdakul, M.; Dengiz, B. Development of a decision support system for robot selection. Robot. Comput.-Integr. Manuf. 2013, 29, 142–157. [Google Scholar]
- Bairagi, B.; Dey, B.; Sarkar, B.; Sanyal, S. Selection of robot for automated foundry operations using fuzzy multi-criteria decision making approaches. Int. J. Manag. Sci. Eng. Manag. 2014, 9, 221–232. [Google Scholar] [CrossRef]
- Liu, H.C.; Ren, M.L.; Wu, J.; Lin, Q.L. An interval 2-tuple linguistic MCDM method for robot evaluation and selection. Int. J. Prod. Res. 2014, 52, 2867–2880. [Google Scholar] [CrossRef]
- Lanbaran, N.; Celik, E.; Yigider, M. Evaluation of investment opportunities with interval–valued fuzzy TOPSIS method. Appl. Math. Nonlinear Sci. 2020, 5, 461–474. [Google Scholar] [CrossRef]
- Parameshwaran, R.; Kumar, S.; Saravanakumar, K. An integrated fuzzy MCDM based approach for robot selection considering objective and subjective criteria. Appl. Soft Comput. 2015, 26, 31–41. [Google Scholar] [CrossRef]
- Bairagi, B.; Dey, B.; Sarkar, B.; Sanyal, S. A De Novo multi-approaches multi-criteria decision making technique with an application in performance evaluation of material handling device. Comput. Ind. Eng. 2015, 87, 267–282. [Google Scholar] [CrossRef]
- Samantra, C.; Datta, S.; Mahapatra, S. Selection of industrial robot using interval–valued trapezoidal fuzzy numbers set combined with VIKOR method. Int. J. Technol. Intell. Plan. 2011, 7, 344–360. [Google Scholar] [CrossRef]
- Ghorabaee, M. Developing an MCDM method for robot selection with interval type-2 fuzzy sets. Robot. Comput.-Integr. Manuf. 2016, 37, 221–232. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, T.; Feng, Y. Identifying the Critical Factors of Sustainable Manufacturing Using the Fuzzy DEMATEL Method. Appl. Math. Nonlinear Sci. 2020, 5, 391–404. [Google Scholar] [CrossRef]
- Joshi, D.; Kumar, S. Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. Eur. J. Oper. Res. 2016, 248, 183–191. [Google Scholar] [CrossRef]
- Ziemba, P.; Becker, A.; Becker, J. A consensus measure of expert judgment in the fuzzy TOPSIS method. Symmetry 2020, 12, 204. [Google Scholar] [CrossRef]
- Wang, C.N.; Dang, T.T.; Tibo, H.; Duong, D.H. Assessing renewable energy production capabilities using DEA window and fuzzy TOPSIS model. Symmetry 2021, 13, 334. [Google Scholar] [CrossRef]
- Moslem, S.; Farooq, D.; Ghorbanzadeh, O.; Blaschke, T. Application of the AHP–BWM Model for evaluating driver behavior factors related to road safety: A case study for Budapest. Symmetry 2020, 12, 243. [Google Scholar] [CrossRef]
- Li, T.; Yang, W. Supply Chain Planning Problem Considering Customer Inventory Holding Cost Based on an Improved Tabu Search Algorithm. Appl. Math. Nonlinear Sci. 2020, 5, 557–564. [Google Scholar] [CrossRef]
- Sunarsih, S.; Pamurti, R.; Khabibah, S.; Hadiyanto, H. Analysis of Priority Scale for Watershed Reforestation Using Trapezoidal Fuzzy VIKOR Method: A Case Study in Semarang, Central Java Indonesia. Symmetry 2020, 12, 507. [Google Scholar] [CrossRef]
- Khan, M.; Kumam, P.; Alreshidi, N.; Shaheen, N.; Kumam, W.; Shah, Z.; Thounthong, P. The Renewable Energy Source Selection by Remoteness Index-Based VIKOR Method for Generalized Intuitionistic Fuzzy Soft Sets. Symmetry 2020, 12, 977. [Google Scholar] [CrossRef]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are MCDA Methods Benchmarkable? A Comparative Study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II Methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Chen, T.Y. Signed distance-based TOPSIS method for multiple criteria decision analysis based on generalized interval-valued fuzzy numbers. Int. J. Inf. Technol. Decis. Mak. 2011, 10, 1131–1159. [Google Scholar] [CrossRef]
- Chen, S.; Hsieh, C. Representation, ranking, distance, and similarity of LR type fuzzy number and application. Aust. J. Intell. Process. Syst. 2000, 6, 217–229. [Google Scholar]
- Liao, M.; Liang, G.H.; Chen, C.Y. Fuzzy grey relation method for multiple criteria decision-making problems. Qual. Quant. 2013, 47, 3065–3077. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S. Selecting green supplier of thermal power equipment by using a hybrid MCDM method for sustainability. Sustainability 2014, 6, 217–235. [Google Scholar] [CrossRef]
- Baležentis, T.; Zeng, S. Group multi-criteria decision making based upon interval-valued fuzzy numbers: An extension of the MULTIMOORA method. Expert Syst. Appl. 2013, 40, 543–550. [Google Scholar] [CrossRef]
- Ali, A.; Rashid, T. Generalized interval-valued trapezoidal fuzzy best-worst multiple criteria decision-making method with applications. J. Intell. Fuzzy Syst. 2020, 38, 1705–1719. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
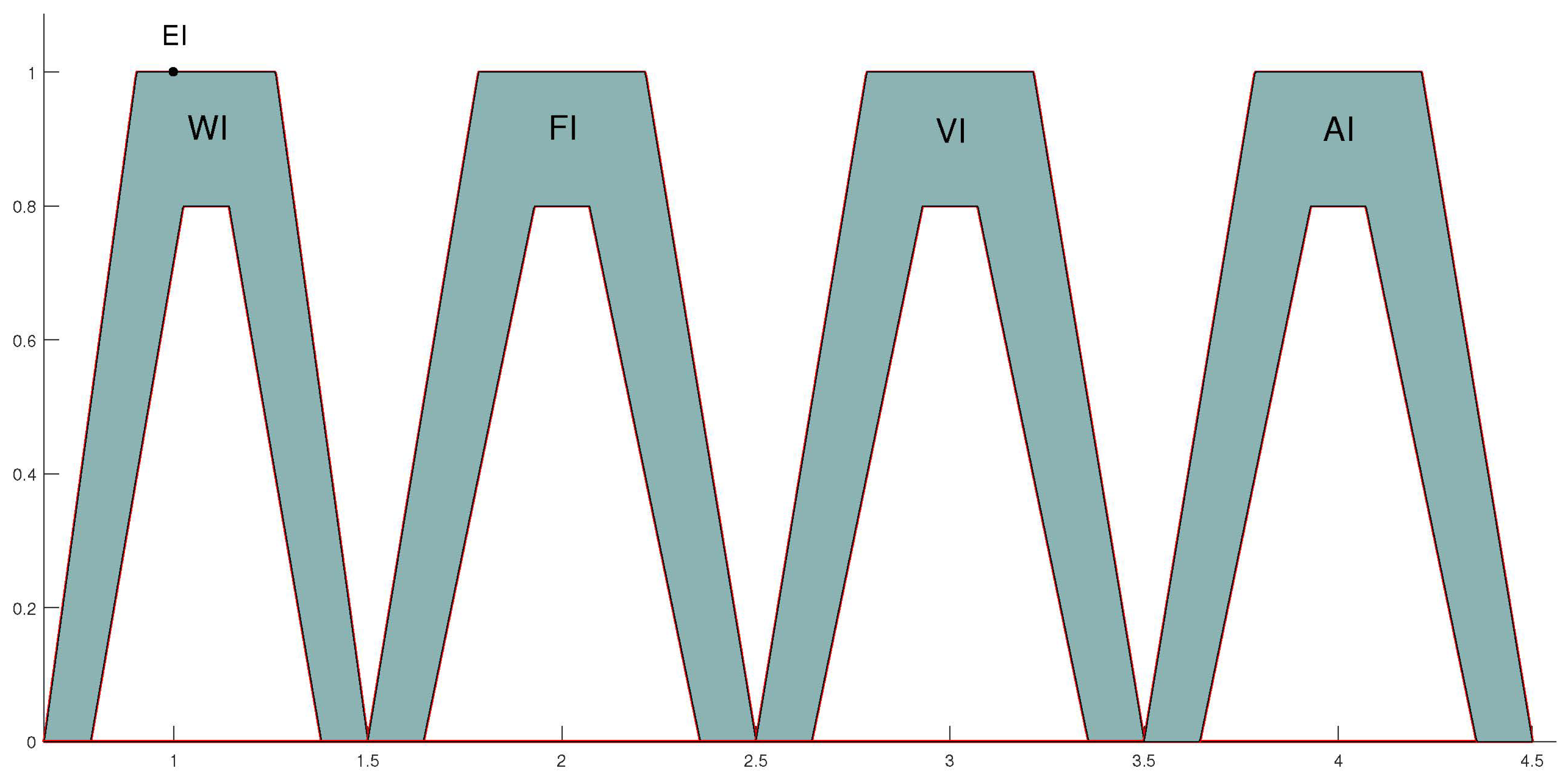

| GITrFNs Transformation | Linguistic Terms |
|---|---|
| Equally Important (EI) | |
| Weakly Important (WI) | |
| Fairly Important (FI) | |
| Very Important (VI) | |
| Absolutely Important (AI) |
| GITrFNs | Linguistic Terms |
|---|---|
| Absolutely poor (AP) | |
| Very poor (VP) | |
| Poor (P) | |
| Medium poor (MP) | |
| Medium (M) | |
| Medium good (MG) | |
| Good (G) | |
| Very good (VG) | |
| Absolutely good (AG) |
| DM1 | |||||||||
| WI | FI | AI | FI | WI | VI | FI | VI | VI | |
| DM2 | |||||||||
| WI | FI | AI | WI | FI | VI | FI | VI | VI | |
| DM3 | |||||||||
| WI | WI | FI | FI | AI | VI | FI | FI | VI | |
| DM4 | |||||||||
| AI | FI | VI | FI | WI | VI | WI | FI | VI |
| DMs | Weights | GITrFNs |
|---|---|---|
| DM1 | ||
| DM2 | ||
| DM3 | ||
| DM4 | ||
| Aggregate | ||
| Criteria | Rotots | Decision Makers | |||
|---|---|---|---|---|---|
| M | M | G | VG | ||
| M | G | M | G | ||
| G | M | VG | MG | ||
| VG | VG | MG | P | ||
| MG | MG | G | G | ||
| G | P | G | MG | ||
| VG | G | VG | G | ||
| G | M | VG | VG | ||
| P | MG | G | P | ||
| MG | VG | MG | G | ||
| M | M | G | G | ||
| G | M | VG | MG | ||
| G | G | G | VG | ||
| VG | VG | MG | G | ||
| MP | MG | P | MP | ||
| Criteria | Rotots | Rating of Criteria |
|---|---|---|
| Criteria | Robots | Normalized Rating Value of Criteria |
|---|---|---|
| Criteria | Robots | Weighted Normalized Rating Value of Criteria |
|---|---|---|
| Criteria | GITrF-PIS/GITrF-NIS | Normalized Rating Value of Criteria |
|---|---|---|
| GITrF-PIS | ||
| GITrF-NIS | ||
| GITrF-PIS | ||
| GITrF-NIS | ||
| GITrF-PIS | ||
| GITrF-NIS | ||
| GITrF-PIS | ||
| GITrF-NIS | ||
| GITrF-PIS | ||
| GITrF-NIS | ||
| GITrF-PIS | ||
| GITrF-NIS |
| Ranking | |||
|---|---|---|---|
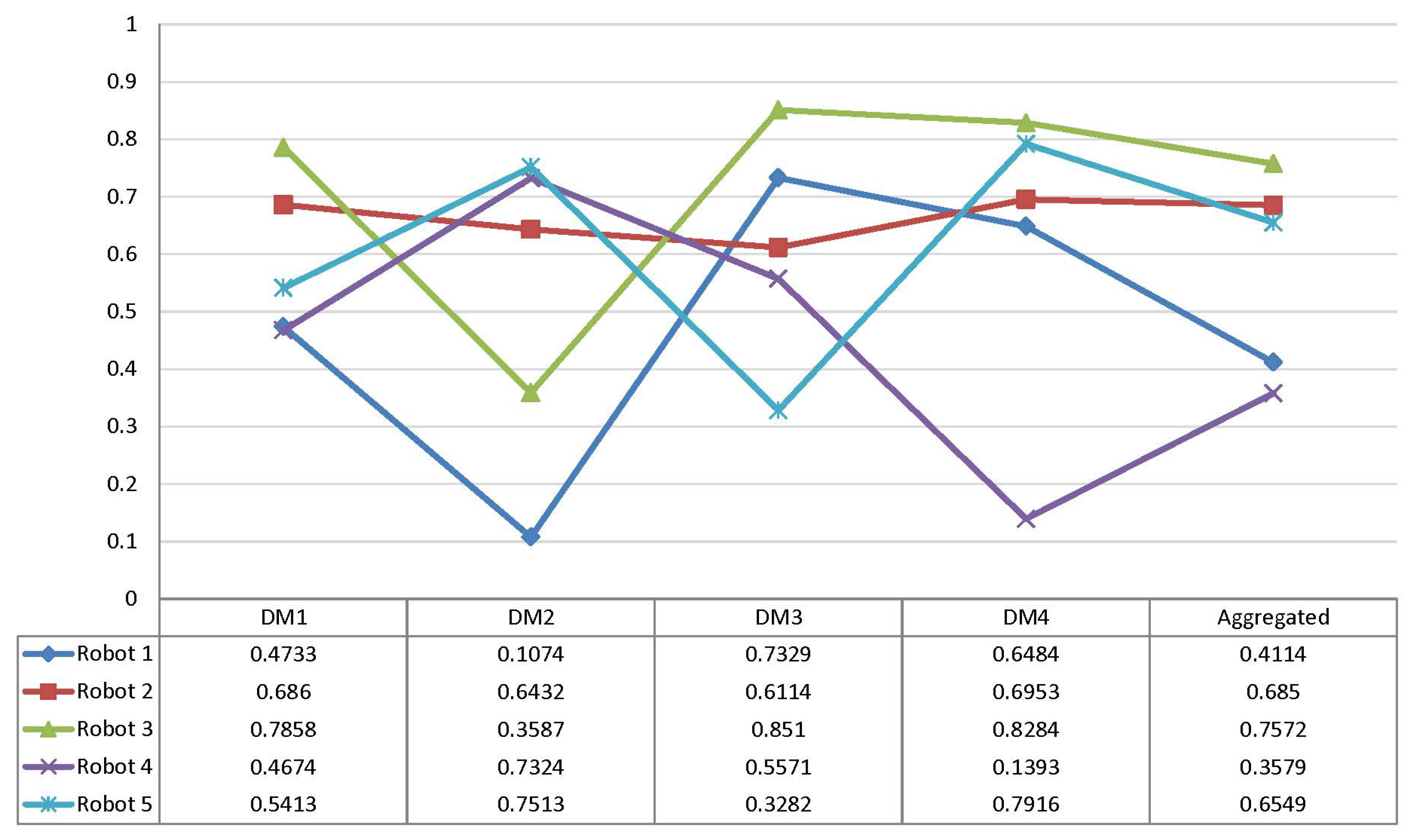
| 0.1485 | 0.1038 | 0.4114 | 4 |
| 0.0795 | 0.1728 | 0.6850 | 2 |
| 0.0613 | 0.1911 | 0.7572 | 1 |
| 0.1620 | 0.0903 | 0.3579 | 5 |
| 0.0871 | 0.1653 | 0.6549 | 3 |
| GITrF-TOPSIS Ranking | |
|---|---|
| DM1 | |
| DM2 | |
| DM3 | |
| DM4 | |
| Aggregated |
| Ranking | |||
|---|---|---|---|
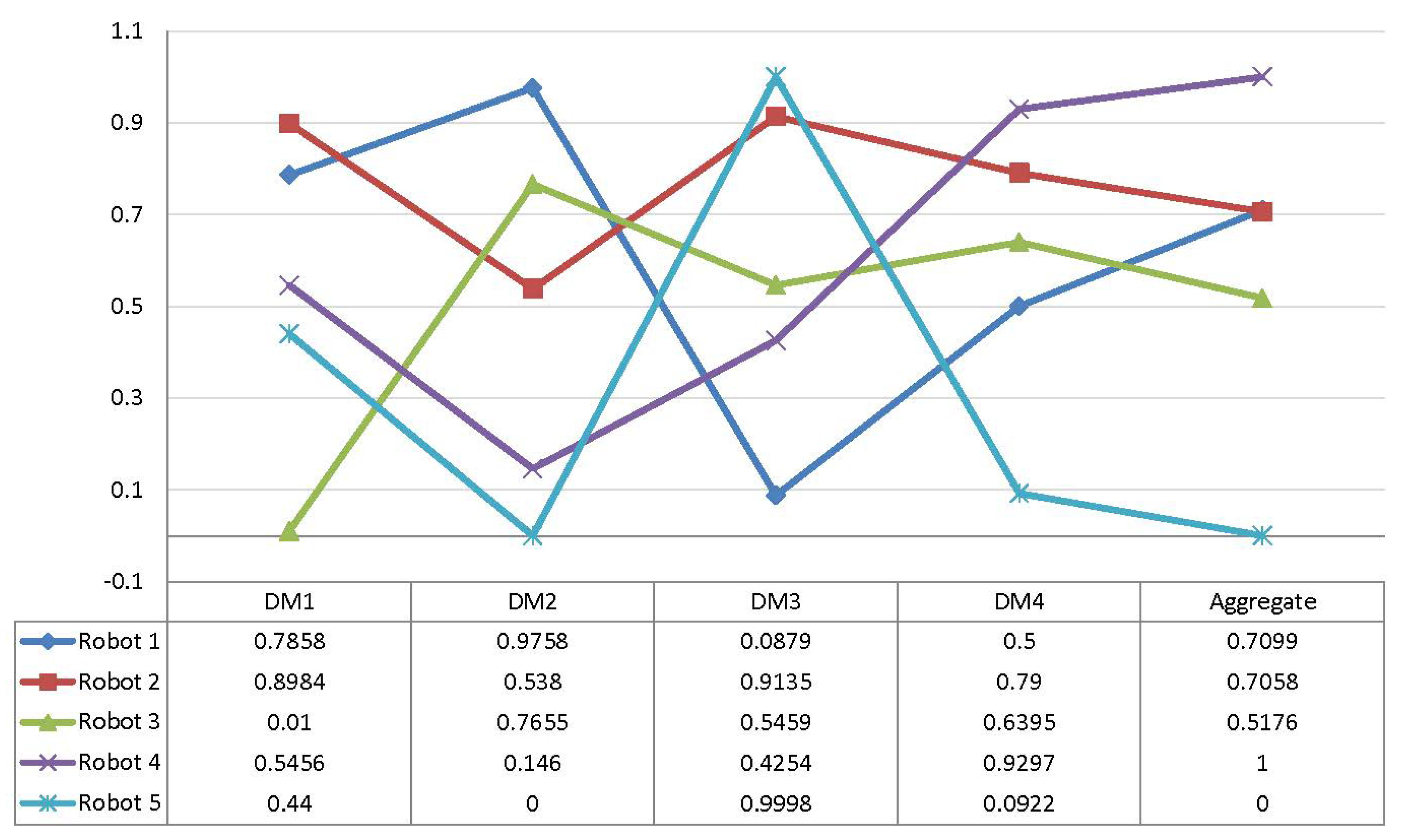
| 0.4760 | 0.1749 | 0.7099 | 4 |
| 0.5301 | 0.1693 | 0.7058 | 3 |
| 0.4381 | 0.1689 | 0.5176 | 2 |
| 0.6130 | 0.1761 | 1 | 5 |
| 0.3578 | 0.1505 | 0 | 1 |
| GITrF-VIKOR Ranking | |
|---|---|
| DM1 | |
| DM2 | |
| DM3 | |
| DM4 | |
| Aggregated |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, T.; Ali, A.; Guirao, J.L.G.; Valverde, A. Comparative Analysis of Hybrid Fuzzy MCGDM Methodologies for Optimal Robot Selection Process. Symmetry 2021, 13, 839. https://doi.org/10.3390/sym13050839
Rashid T, Ali A, Guirao JLG, Valverde A. Comparative Analysis of Hybrid Fuzzy MCGDM Methodologies for Optimal Robot Selection Process. Symmetry. 2021; 13(5):839. https://doi.org/10.3390/sym13050839
Chicago/Turabian StyleRashid, Tabasam, Asif Ali, Juan L. G. Guirao, and Adrián Valverde. 2021. "Comparative Analysis of Hybrid Fuzzy MCGDM Methodologies for Optimal Robot Selection Process" Symmetry 13, no. 5: 839. https://doi.org/10.3390/sym13050839
APA StyleRashid, T., Ali, A., Guirao, J. L. G., & Valverde, A. (2021). Comparative Analysis of Hybrid Fuzzy MCGDM Methodologies for Optimal Robot Selection Process. Symmetry, 13(5), 839. https://doi.org/10.3390/sym13050839







