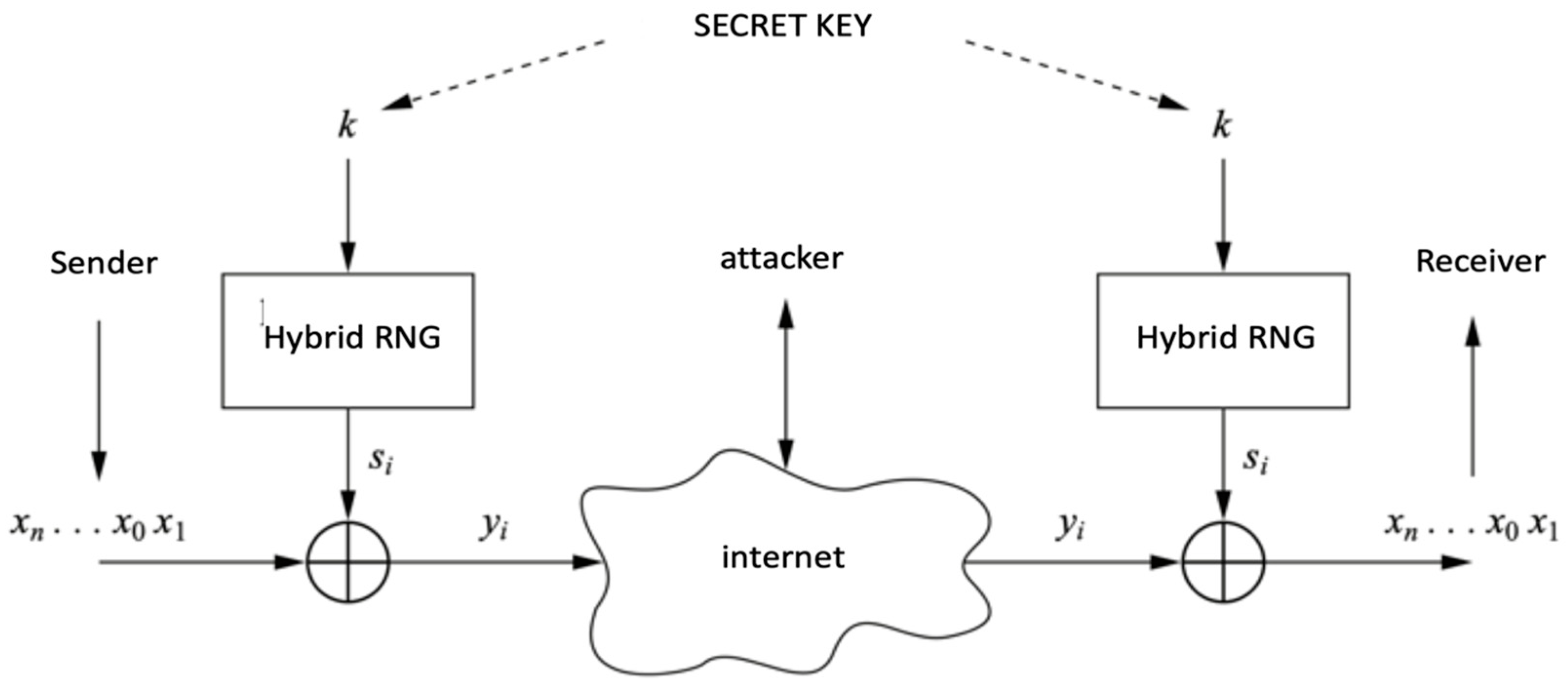
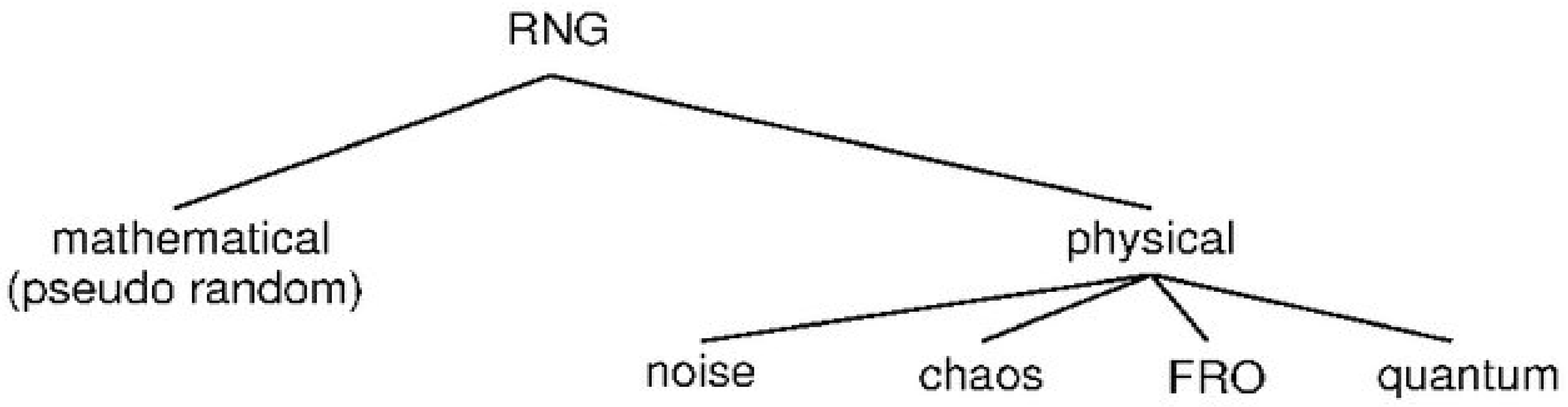
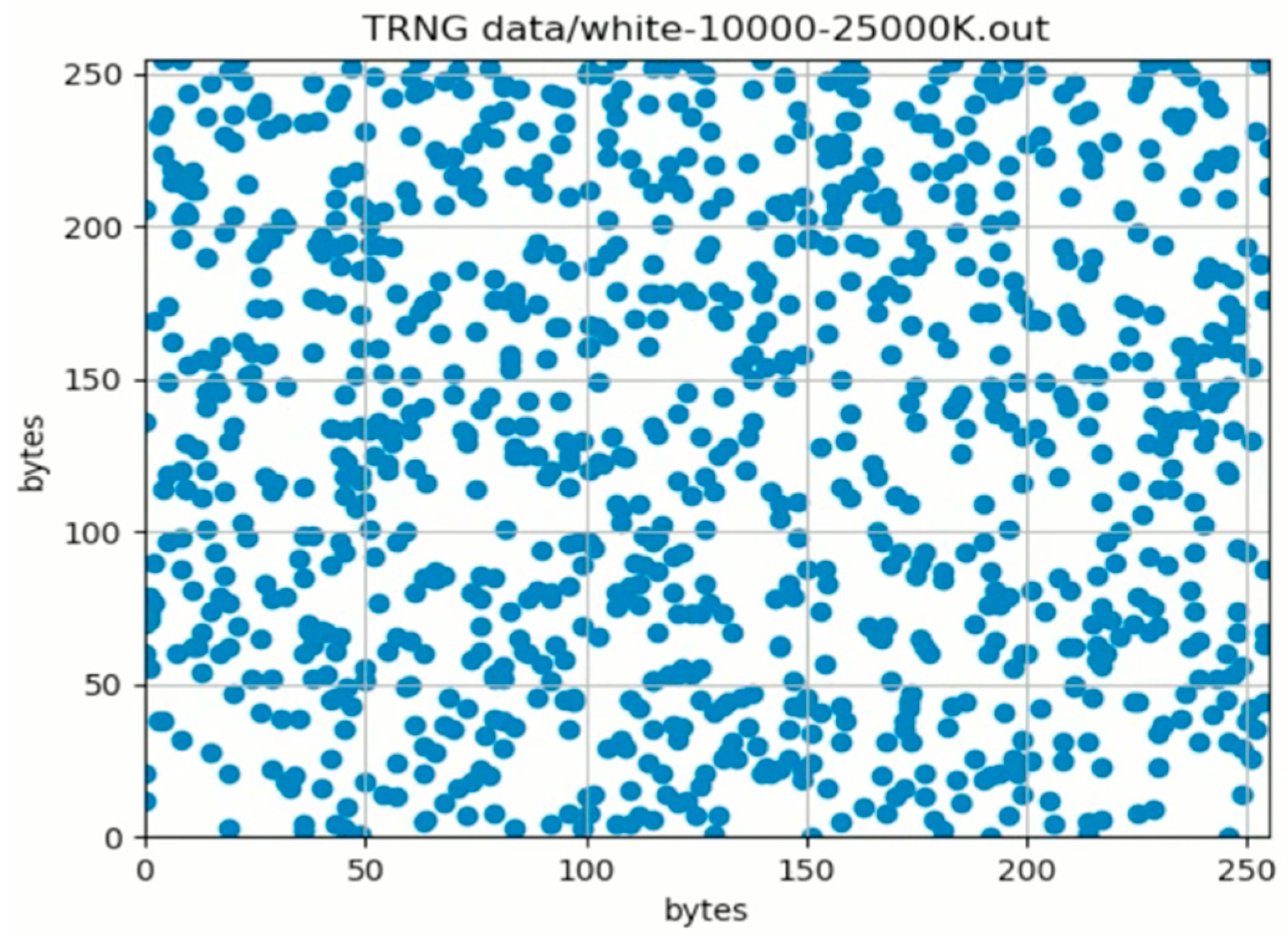
Abstract
One of the general problems in modern digital society is undoubtedly the information security topic. It is critical to ensure the security of information transferred, processed, and stored throughout digital channels. Among this information, digital images draw attention in terms of frequency of use in digital channels. In this study, a new image encryption algorithm is proposed to address the security problems of digital images. The aspect that differentiates the proposed algorithm from thousands of image encryption algorithms in the literature is that it is designed within the framework of the provable security design principle. The provable security design approach has ensured that the proposed algorithm is theoretically secure with mathematical proof techniques. In addition to addressing the proposed architecture security concerns, the hybrid random number generator used as the key generator constitutes another unique aspect. This generator, which was designed using chaotic systems, physical unclonable functions, and optimization algorithms, stands out as the innovative aspect of the study. The statistical randomness properties of the proposed random number generator were tested using the NIST SP 800-22 Statistical Test Suite. Successful results were obtained for 15 tests in the test package. In addition, the success of these outputs was tested on a new image encryption algorithm. The security of the proposed algorithm was tested from different angles using various experimental analyzes and a 12-step provable security analysis roadmap. Successful analysis results and performance measurements indicate that the proposed cryptographic components can be used in many information security applications and many future designs.
1. Introduction
Developments in digital transformation have significantly changed our lives [1]. The effect of this change continues to increase exponentially. This effect has changed and continues to change many processes [2]. Even wars are now associated with cyberattacks on critical infrastructures [3]. Thus, more than ever, information security concepts have gained importance. Therefore, how to ensure the security of the huge information set called big data is now a serious problem for everyone [4]. Strong cryptographic algorithms are needed to address this problem [5,6]. However, cryptology is a difficult discipline. It is not sufficient to simply demonstrate that certain security requirements are met. As new attacks are developed, new cryptographic algorithms and countermeasures should be constantly investigated [7]. One of the outstanding topics among these researches involves design studies based on nonlinear dynamics [8,9,10,11,12]. The number of studies on this subject in recent years is in the thousands [13]. Although this quantitative size is an indication of how hot the subject is, the security problems of these studies and the difficulties that may occur in practical applications reveal another aspect of the subject that should be addressed. The original aspect of this proposal is the development of a cryptographic key generator module and practical applications that can address security concerns in digital channels within the framework of provable security principles.
1.1. Related Works
The existence of chaos-based random number generators (CBRNGs) is known in the literature. In this section, some basic studies published in the last 3 years are discussed, and the general features of the CBRNG literature are discussed. The prominent feature of RNG proposed by Datcu et al. [14] is the shaping of the entropy source with chaotic systems. Hua et al. [15] implemented a new model and hardware realization in order to use the effect of chaotic systems on the quality of the entropy source more effectively. Yang and Chien [16] examined the success of the hardware realization of chaotic systems for the four-dimensional chaotic system and combined the obtained outputs with AES in an image encryption algorithm. Natiq et al. [17] proposed a random number generator based on the chaotic behavior of the plasma model. Özkaynak [18] has shown that, by using the fractional order model of the chaotic Chen system, the randomness requirements can be improved, and this can be a positive effect for cryptographic purposes. Li et al. [19] showed that the randomness requirements can be improved with white chaos and deep learning. Moysis et al. [20] aimed to improve the randomness properties by using a new two-parameter model for the logistics map. Stoller and Campbell [21] aimed to create a memristor-based entropy source for a more effective randomness. Demidova et al. [22] aimed to improve the randomness characteristics by using optimization algorithms. Chai et al. [23] proposed an image encoding system using automata and a chaos-based system. Tsafack et al. [24] proposed a design using a 4D chaotic circuit in the design of the image encryption algorithm. Ramasamy et al. [25] aimed to ensure the security of images on the basis of a system designed using a logistic and tent map.
1.2. Contribution of Proposed Method
The common point of all these studies is the use of chaotic systems as an entropy source in the center of the design. It can be observed that the joint effort of researchers has been to search for new alternatives to improve the statistical randomness characteristics of the entropy source. The most important innovation that distinguishes this proposal from similar ones is that the most appropriate entropy source is obtained in terms of cryptographical requirements with the help of optimization algorithms. Providing the requirements for randomness in the most appropriate way is an important challenge. The idea to consider this problem as an optimization problem was proposed by Tanyıldızı and Özkaynak. In [26], the initial conditions and control parameters describing all statistical tests for four different chaotic systems were determined using different heuristic optimization algorithms. A similar study was conducted by Jiang et al. [27] for chaotic systems. Açıkkapı and Özkaynak [28] showed how different initial conditions can be determined by presenting an approach with a simpler structure compared to the optimization algorithms. Using the approaches suggested in these studies, an ideal entropy pool was formed by obtaining many different initial conditions. Experimental studies were carried out using the initial conditions published in previous studies. Other initial conditions that can be used to feed the entropy pool are not shared, because they are covered by the patent application and there are a large number of them. References [26,28] can be examined in detail for alternative initial conditions for use in practical applications. The corresponding author can be contacted for initial conditions that can be selected for commercial or more professional needs.
It is an undeniable fact that both hardware and software generators designed using entropy resources based on chaotic systems have many advantages. Following the generation of the ideal entropy source, the strong building blocks of modern cryptology can be combined with the unique features of chaos theory, and the architecture to be designed can address security concerns with a provable security approach. The goal of our study was to most suitably improve the entropy source rather than show the shortcomings of CBRNGs, whose general properties were listed in Section 1.1. This output was merely the result of the study. Our main goal was to use this successful output in an effective image encryption algorithm, because even the most successful cryptographic components can be easily broken if used in a bad scenario. Since an attacker will always target the weakest point of the system, combining strong cryptographic components in a way that allows no openness is a difficult task. The architecture proposed in this study aimed to address this purpose. Transforming all these outputs into a practical application can provide an opportunity to evaluate the success of the outputs from a different perspective. An image encryption algorithm as a practical application was designed. This image encryption algorithm was designed to meet the requirements such as security level, speed, effective solution proposal for resource constrained platforms, and easy usability, representing further original contributions of the proposal.
The study is organized as follows: in Section 2, a detailed expression of the problem is given by presenting an analysis of the current literature. This section also emphasizes the original contributions of the proposed approach to address these problems. The details of the proposed architecture are explained in Section 3. In Section 4, analysis and test results are given. In the last section, the results are discussed and suggestions are made for future studies.
2. Statement of Problem
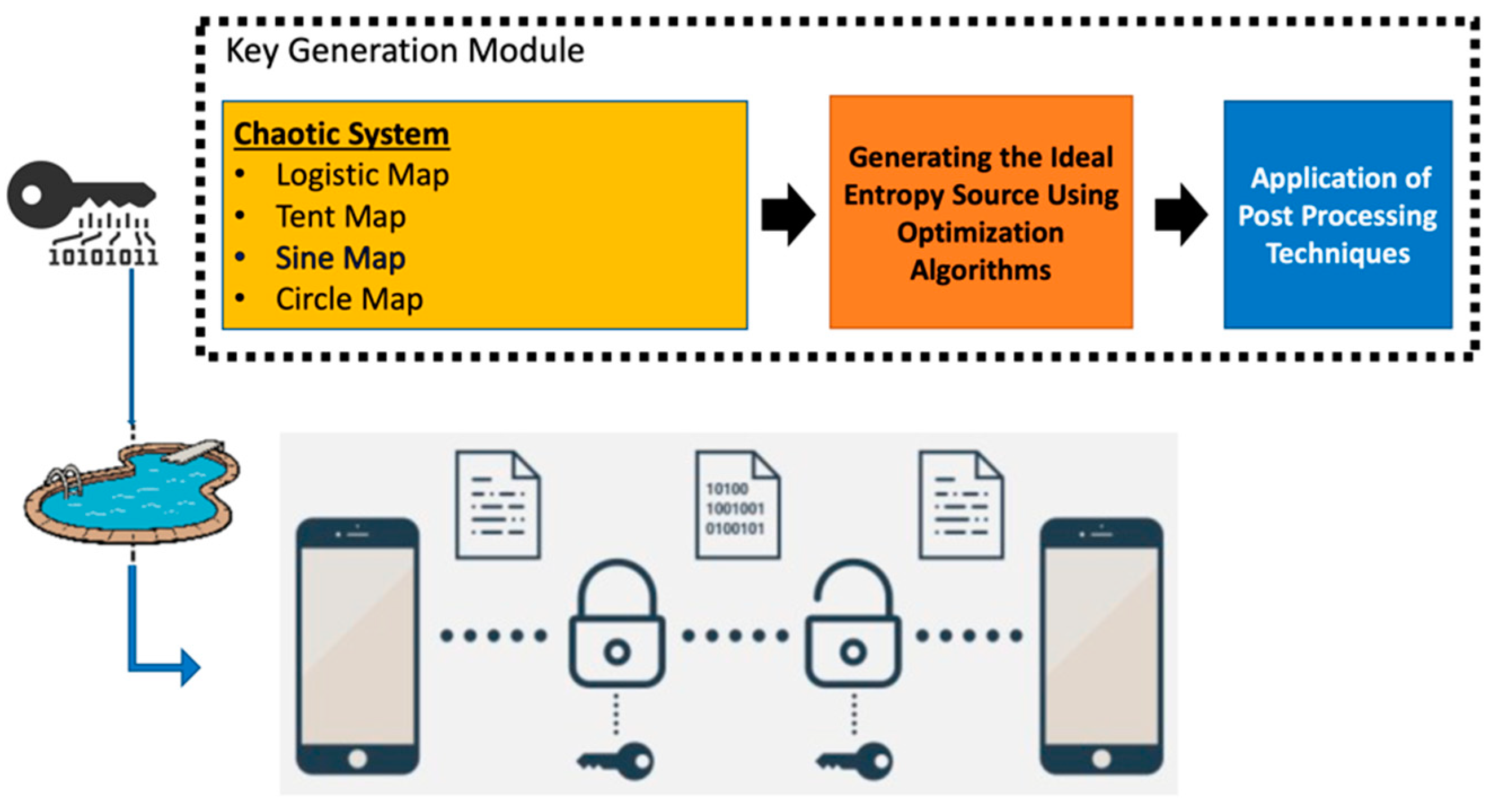
The basic components expressing the scope of the proposal are shown in Figure 1. For these three main components related to the proposal, the current problems in the literature, how these problems are addressed with the approach suggested in the proposal, and the original contributions of the proposal are detailed in this section.
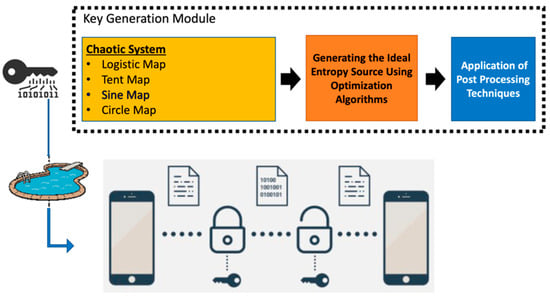
Figure 1.
The basic components expressing the scope of the proposal.
The first topic of the proposal is related to chaos theory. The basic element used to meet the cryptographic requirements in the proposed architecture constitutes chaotic systems. Chaotic systems are used in order to provide the need for confusion (mixing). The proposed architecture was developed with the assumption that the unpredictable nature of chaotic systems could be a very powerful element for shaping an ideal entropy source [29,30].
In the study, the ideal entropy source for four different discrete-time chaotic systems was obtained with the help of six different heuristic optimization algorithms. In a system, the necessary conditions for observing complex dynamics defined as strange attractors are as follows: (i) the system must contain nonlinear element(s), and (ii) the system must be sensitive to the initial condition. These conditions are necessary for the existence of chaos in a system. However, this is not enough. If the system is a continuous time system, the system grade must be at least three, because chaos is not observed in nonlinear systems with a system degree of less than three. Such a condition is not required for discrete-time systems. Chaos can be observed even in a first-order system (logistic map). Therefore, discrete-time chaotic systems are preferred in many practical applications of chaos. The most important reason for this type of preference is that discrete-time chaotic systems have a simpler structure compared to continuous-time and hyperchaotic systems [30]. In the preliminary study, four different discrete-time chaotic systems were used due to this simple structure [26].
The third topic that constitutes the proposal is related to the postprocessing techniques that can be used for true random number generators (TRNGs) to be used for cryptographical purposes [19,21,22]. Because strong key design is a difficult task, demonstrating that cryptographical applications meet the randomness requirements is not an easy process. These requirements can be grouped under two main headings: showing good statistical properties (R1) and unpredictability (R2). In some sources, these requirements are detailed in more detail under four main headings. Essentially, requirements expressed as R3 and R4 are detailed forms of the R2 requirement. The most widely accepted randomness requirements according to Werner Schindler [31] are briefly described below.
- R1: Random numbers should not show any statistical weakness.
- R2: Knowing the subsets of random numbers should not allow the calculation or prediction of predecessor and consecutive random numbers.
- R3: It should not be possible to calculate previous random numbers if the internal state value of RSU is known, even if the internal state value is not known.
- R4: It should not be possible to calculate future random numbers if the internal state value of RSU is known, even if the internal state value is unknown.
According to the level of security that different applications need, the requirements listed above may vary. For example, it is sufficient to meet the R1 requirement for applications such as simulation, modeling, and games of chance, while all requirements must be met in order to guarantee the confidentiality of sensitive information. However, it is not easy to guarantee unpredictability while providing good statistical features. For example, while random number generators such as linear congruential generator, middle square method, and linear feedback shift register (LFSR) show good statistical properties, the deterministic structures of these generators make them easier to predict. Designs such as radioactive decay, noise in electrical circuits, and chaotic systems do not show good statistical properties, but their predictability is difficult [32]. Developing a design that simultaneously meets all requirements is the main problem facing researchers working in this field.
Various statistical tests are available to check that the R1 requirement is met. These tests are used as the objective function of the optimization algorithm. It is ensured that the resulting entropy source has a uniform distribution and that any attacker will be unable to make a better statistical inference than a blind guess. However, as stated earlier, statistical randomness is only one of four requirements. It alone is not enough. Therefore, it has to be verified that the proposed generator has an unpredictable nature (R2 requirement). The sensitive nature of chaotic systems to the initial conditions and control parameters can guarantee a wide key space. In the process of determining this initial condition and control parameters, the use of physical unclonable functions specific to the device/hardware is another element that meets the R2 requirement of the generator. Although the condition that the previous and subsequent subsequences of random numbers are unpredictable, which are the other two requirements (R3 and R4) that random number generators must meet, is related to the second requirement, it is planned to use hash functions in the proposed architecture to guarantee these requirements. The one-way nature of hash functions mathematically makes invertibility impossible (requirement R3). Again, the additional physical unclonable inputs can provide additional security for the R4 requirement.
The second leg of the proposal is the practical application of the key generator module. The device (mobile phone or computer) provides feeding of an entropy pool by using device-dependent (physically unclonable) parameters. Allowing the entropy pool to be differentiated according to security requirements can provide an important advantage to ensure the security/ease of use balance. The strong cryptographical keys generated can be used in the image encryption algorithm of the proposed architecture. The advantage of the practical application presented herein is the use of the space-filling curve transformation approach to solve the correlation problem specific to digital images.
3. Details of Proposed Architecture
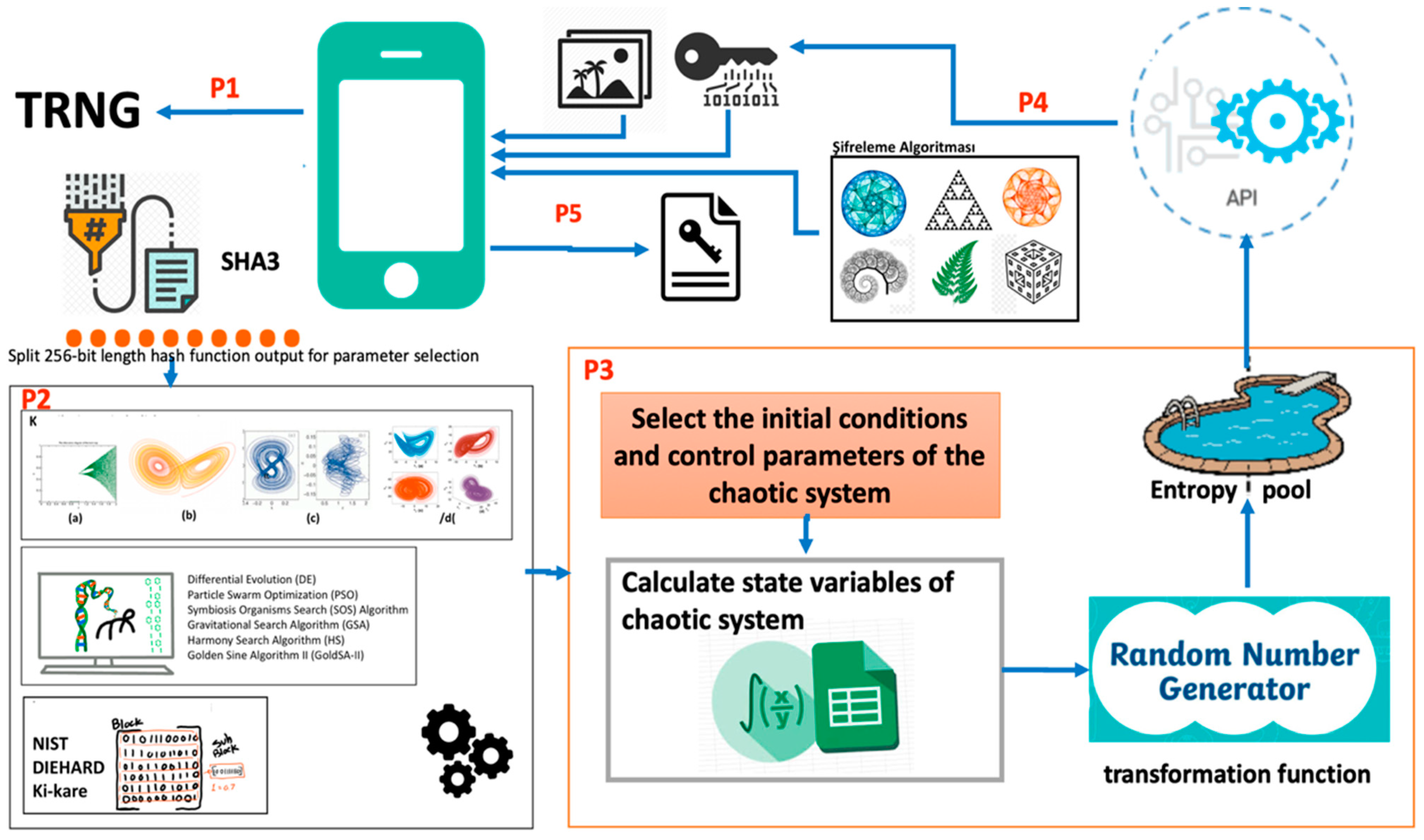
The proposed architecture consists of five main parts. In this section, the details of these parts are separately given. The general view of the proposed architecture is given in Figure 2.
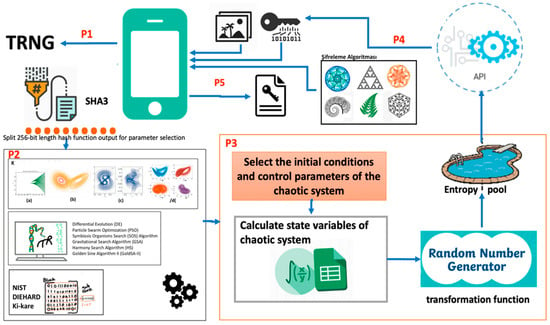
Figure 2.
The general view of the proposed architecture.
3.1. Part I: Physical Unclonable Function Module
True random number generators (TRNGs) are critical in cryptographic designs to ensure unpredictability. In the proposed architecture, the hardware as an entropy source shown in Figure 3 was chosen as the TRGN structure. There are many advantages to choosing this hardware. Low cost, easy integration into mobile devices via USB port, and meeting statistical randomness requirements are some of these advantages [33]. A mobile device or computer is used to feed this entropy source. Thus, the hardware is used as a physical unclonable function (PUF) in the proposed architecture. The PUF module is very important for the provable security perspective since, according to the cryptanalysis scenario, the user of a system is a potential privileged attacker [34,35,36]. For example, the user can reverse-engineer the logic of the algorithm by storing the single-use passwords that come to him. PUFs without user control have been used to address this attack scenario and contribute to the unpredictable nature of the generator. In fact, it is known in the literature that there are more effective PUF structures than the hardware in Figure 3. This hardware is used only to explain the design logic through an example. In future studies, different PUF structures will be used.

Figure 3.
(a) General view of Crowd Supply Infinite Noise TRNG hardware used as a PUF; (b) general view of architecture of PUF device [33].
Outputs of the PUF hardware are given as input to the cryptographic hash function. Hash functions are used to address cryptanalysis scenarios associated with chosen/known plaintext attacks. In the proposed architecture, it is planned to use the SHA3 algorithm [37]. Such a choice was made because it is the latest hash function standard, with a 256 bit value are the output. It was divided into seven sections with the help of a fragmentation algorithm to be used in parameter selection. It was converted into numerical values using the mod function for each part. These numerical values were used in determining the selection parameters required in other parts of proposed architecture.
3.2. Part II: Determination of Initial Conditions and Control Parameters of Chaotic Systems Module
Outputs of Part I of the proposed architecture can be used as selection parameters. By using the determined selection parameters, the chaotic system type, the optimization function to be used, the statistical test approach to be selected as the objective function, the population size, the number of iterations, and other necessary parameter values for the optimization algorithm are assigned. In the proposed architecture, four different chaotic systems, seven different optimization algorithms, and three different statistical test scenarios can be used. In Table 1, the main features of the probable options and their effects on system success are discussed.

Table 1.
Main features of probable options.
After determining the selection parameters for Part II, the initial conditions and control parameters of the chaotic system were determined for the selected statistical test requirements with the help of the optimization algorithm. The probable options listed in Table 1 provide ideas for different future studies. The reason for using discrete-time systems in experimental studies is their simple structure. Similarly, there are many different optimization algorithms that can be used in the literature. Different alternatives can be chosen instead of the optimization algorithms listed in Table 1. Ref. [26] can be examined for the effect of currently used algorithms on performance, design parameters, and other details.
3.3. Part III: Random Number Generator Module
Depending on the chaotic system type chosen, the chaotic system can have more than one state variable. In Figure 2, this detail is shown using the examples of a (a) discrete-time chaotic system, (b) continuous-time chaotic system, (c) hyperchaotic system, and (d) fractional-order chaotic system in the P2 block. If a generalization is made between chaotic system types, it is observed that the system complexity from (a) to (d) increases. It was analyzed in the literature that this complex structure positively affects the entropy source. In order to benefit from these differences of chaotic system classes in the best way, it is proposed to use three different scenarios at the beginning to determine which state variables are selected. Details of these possible scenarios are discussed in Table 2.

Table 2.
Scenarios to be used in the process of choosing state variables.
State variables of chaotic systems are rationally valuable. Therefore, the selected state variable must be converted to random bit values. Three different scenarios are proposed for this transformation process. Details of the scenarios are discussed in Table 3. The scenarios presented in these tables are presented for guidance only. It is planned to achieve a more stable model by analyzing both current and different scenarios in future studies.

Table 3.
State variable/random bit conversion scenarios.
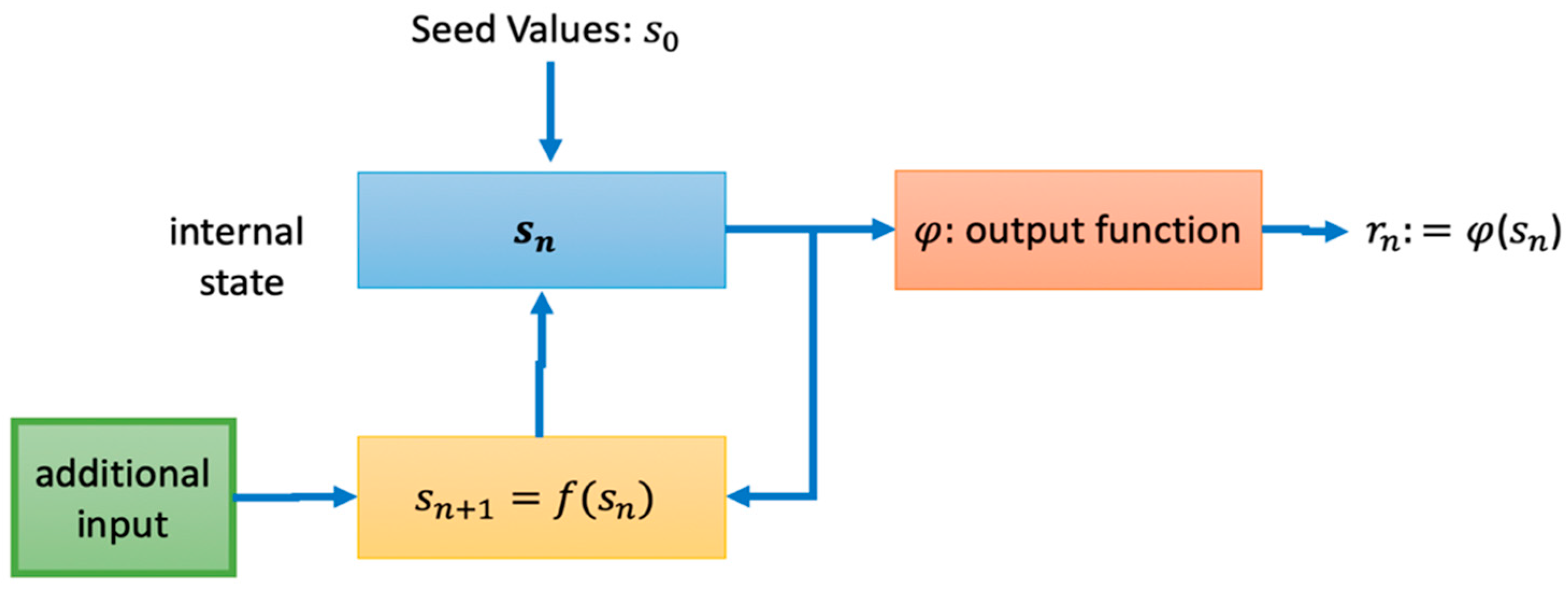
A more detailed representation of the random number generator (RNG) module in P3 is given in Figure 4. Actually, Figure 4 reflects the general architecture of hybrid RNGs [32].
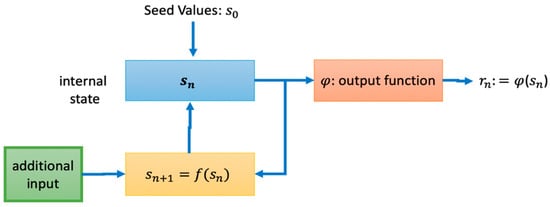
Figure 4.
Detailed representation of the random number generator (RNG) module.
Initial conditions and control parameters of the chaotic system are used as the seed value. The function f, shown as the state transition function, is related to which of the approaches suggested in Table 2 is used in connection with the mathematical model of the chaotic system. The output function represents the transformation function suggested in Table 3. The outputs obtained in addition to this function are passed through the cryptographical hash functions and transferred to the entropy pool. Depending on the security requirements of the application, it can be used for additional inputs when it comes to the security of sensitive data, with the help of these additional inputs to be obtained from PUF modules.
3.4. Part IV: Application Programming Interface
The API (application programming interface) performs the process of generating keys according to user requirements. One of the most important factors for the success of this module is the effective meeting of the security/ease-of-use balance. Selection parameters have an important role among the factors that affect this balance. For example, the chi-square test can be used as an objective function to generate faster key values. This choice indicates that only the chi-square test can be used instead of the NIST test in an optimization process where 15 tests are provided together for applications whose security level is not critical. Similarly, simple mathematical models of discrete-time chaotic systems can be used to quickly achieve the desired goals. On the other hand, when a security-critical image needs to be encrypted, prediction using additional structures can be carried out such as hyperchaotic or fractional-order chaotic systems, using PUF-based additional inputs in the RNG architecture, updating the seed value at regular intervals, state transition functions, and dynamic selection of output functions. The aim is to address security concerns by providing a structure that is more difficult to achieve.
3.5. Part V: Encryption Module
The image encryption module inputs consist of the key sent by the API module and the original image. It is ensured that both color and gray images are used in the encryption process. To meet this requirement, the selected image is transformed into a one-dimensional array. The value of each cell of the array ranges from 0–255. If the image to be encrypted is a gray-level image, it is in an array of (1 × MN) size, whereas a color image is in an array of (1 × 3MN) size. Here, M represents the number of rows and N represents the number of columns.
One of the most important problems arising in the encryption of digital images is the correlation problem. Therefore, classical encryption algorithms may fail in the encryption process. One of the most known examples of this is shown in Figure 5. Although the problem in Figure 5 is related to the processing modes of block ciphers, the fact that the values of neighboring pixels have similar numerical values creates a weakness in terms of cryptanalysis.

Figure 5.
Correlation problem in the process of encrypting digital images. (a) test image 1, (b) test image 2.
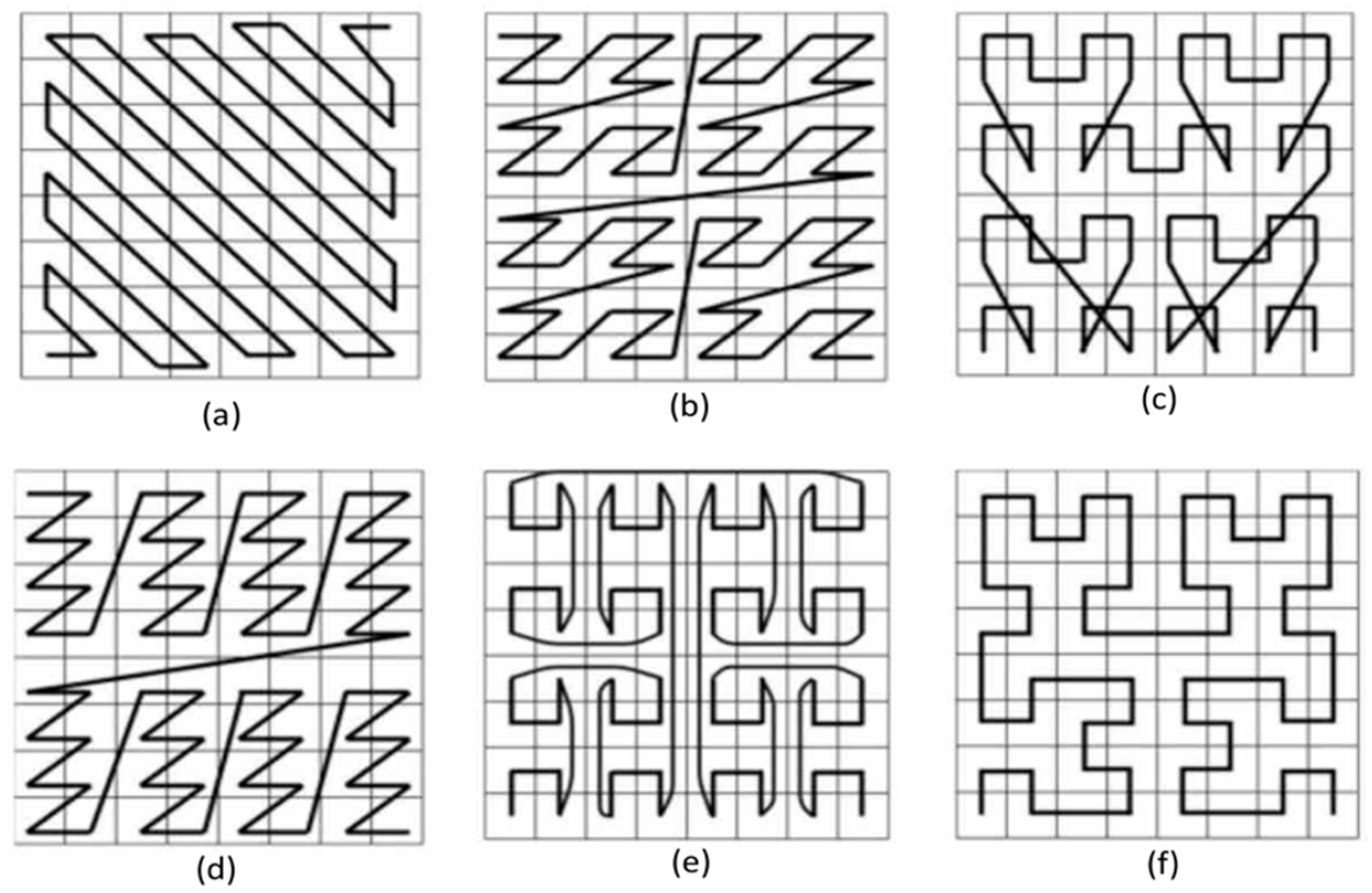
One of the most important original aspects of the proposal is that the space-filling curves approach has been proposed to overcome this correlation problem. The space-filling curve approach uses some patterns when transforming digital images into one-dimensional arrays. Some sample space-filling curves are shown in Figure 6 as an example. More effective suggestions have been used in the future studies.
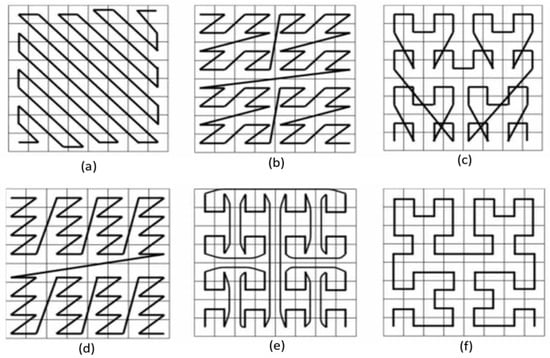
Figure 6.
Six different space-filling curves (a–f) that can be used in the transformation phase.
4. Analysis of Proposed Architecture
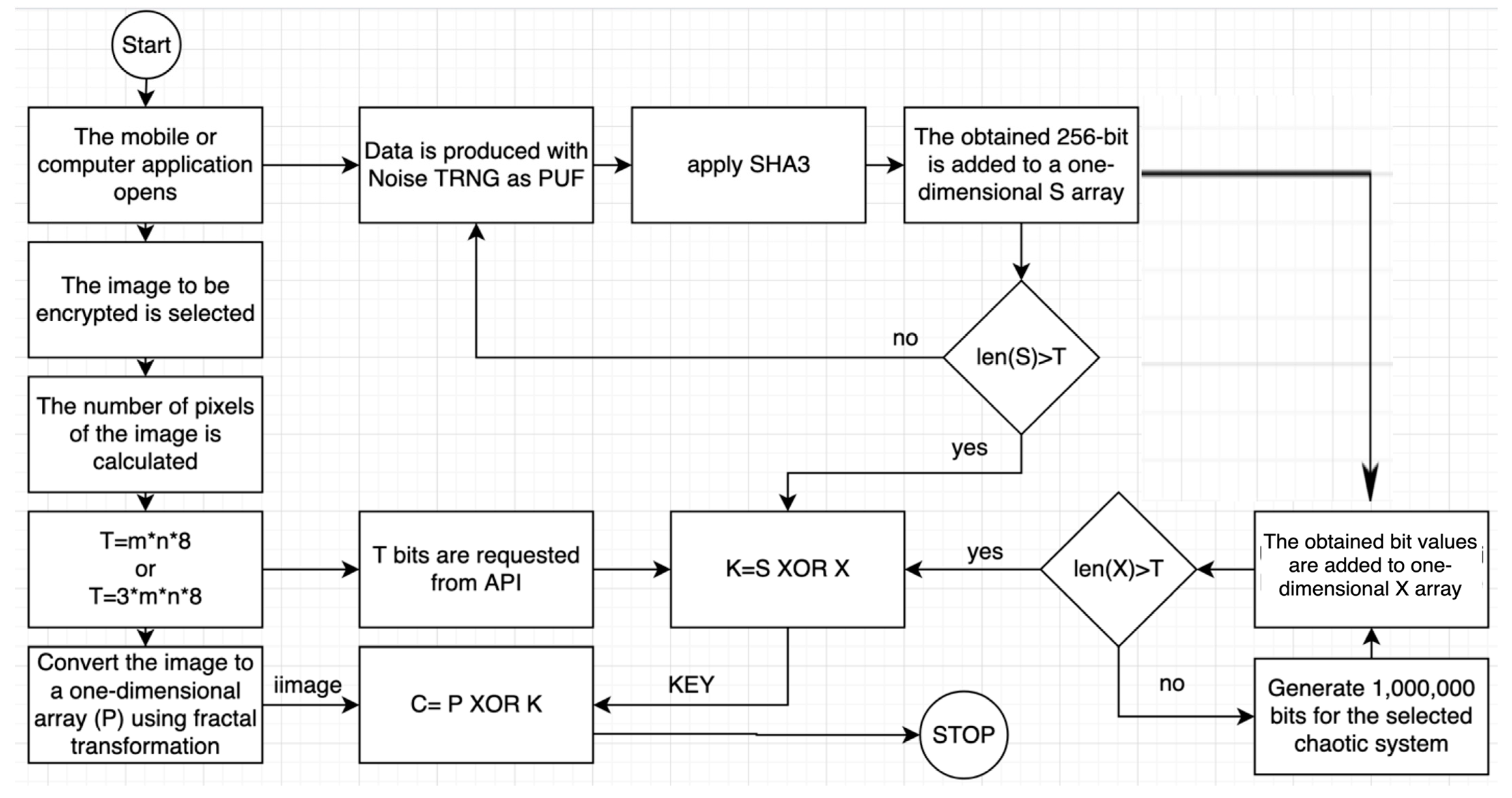
A flowchart is given in Figure 7 to better explain the working of the proposed encryption architecture. As stated in the flowchart, the three basic components of the proposed architecture are the PUF, chaotic system, and XOR operator. It is known that there are various suggestions in the literature designed based on these components. For example, various proposals that meet the confusion and diffusion requirements in the encryption process of an image using only chaotic permutations are some of the widely accepted design types [38,39,40,41,42,43]. Using the DNA encoding and shuffling approach in addition to chaotic permutations is another common type of alternative design [44,45,46,47,48]. Design types based on chaotic permutations are generally included in the classification known as secret key (symmetric) cryptography. Various design suggestions that make use of public key (asymmetric) encryption techniques were presented in some recent studies [49,50,51]. Similar to the design logic proposed in the study, other design studies have highlighted the key generator [52,53,54] and used best practices of modern cryptology science [55,56,57]. Quantum systems [58,59], fractional systems [60,61,62], and medical encryption algorithms [63,64,65], which have attracted attention recently, are other current topics related to design proposals.
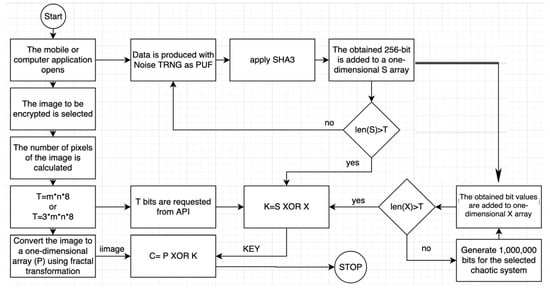
Figure 7.
The basic components expressing the scope of the proposal.
The encrypted images obtained for the sample test images in Figure 8 using the proposed algorithm are given in Figure 9. One of the most important advantages of the proposed algorithm is that it offers many options. The options listed in Table 4 were used in analyzing this section.

Figure 8.
The eight different sample test images (a–h).


Table 4.
Selected options of encryption algorithm.
4.1. Statistical Analysis
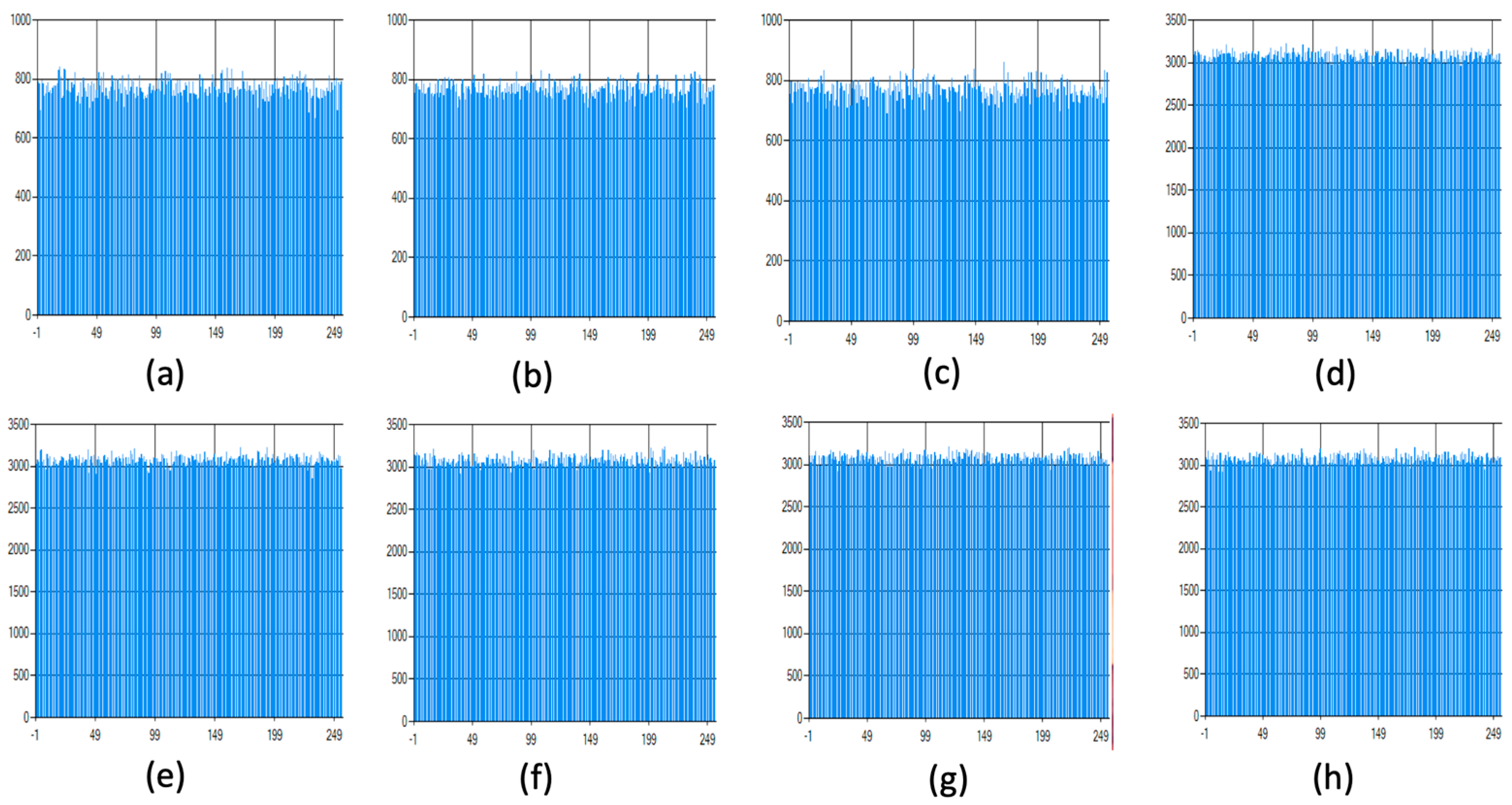
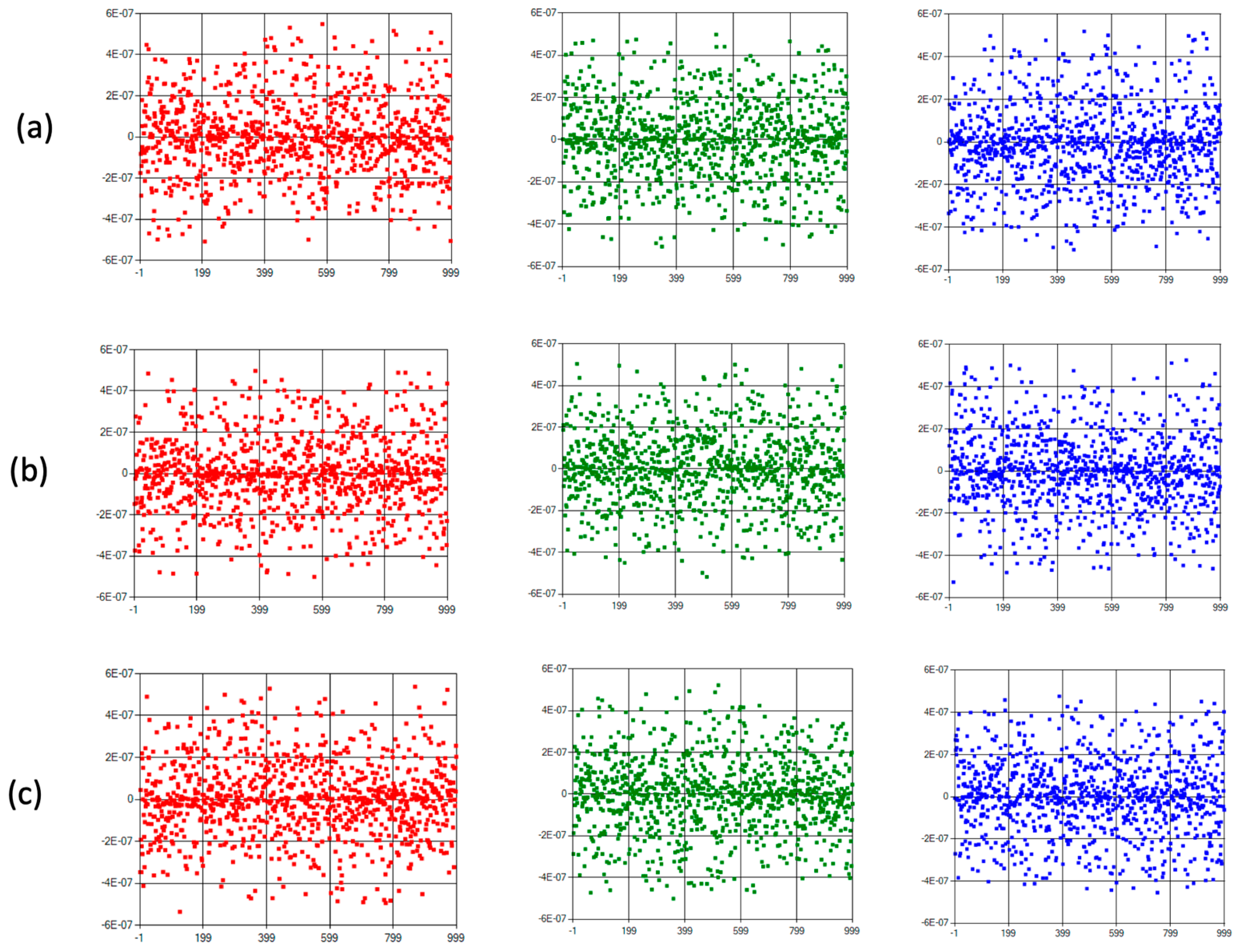
One of the analysis tools widely used in the cryptanalysis process of chaos-based encryption algorithms is statistical evaluation. In this section, first of all, various statistical analyses are presented, and the drawbacks of safety evaluations made using only these analyses are discussed. Various statistical tests are given in Figure 10 and Figure 11. While histogram analysis results are given in Figure 10, correlation analysis results are shown in Figure 11.
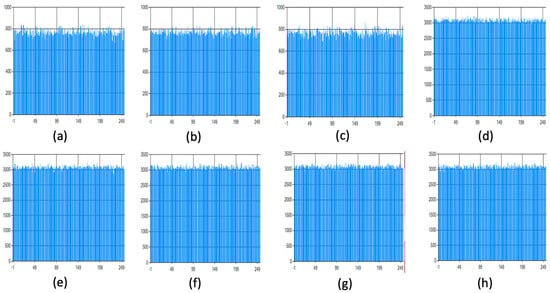
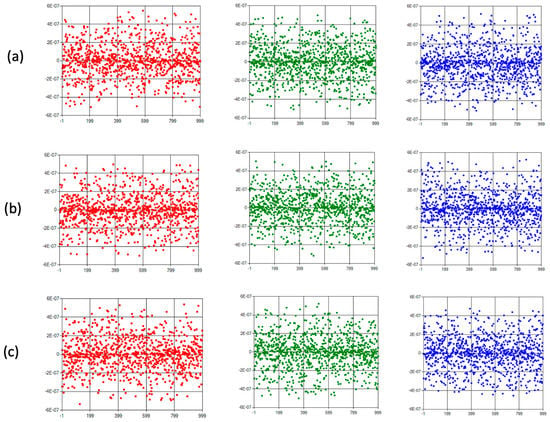
Figure 11.
Horizontal (a), vertical (b), and diagonal (c) axis correlation analysis of RGB components for Figure 9a.
It can be observed that the histogram analysis of the original images has a normal distribution, while the encrypted images have a uniform distribution. A similar inference can be made in correlation analysis. In addition to these two measurements, the results of NPCR (number of pixels change rate) and UACI (unified average changing intensity) analysis, which are other supplementary statistical tests, are shown in Table 5. Ref. [66] can be examined for further details on how the calculations are made for NPCR and UACI tests. A value of 0.99 for the NPCR test and a value of 0.33 for UACI are interpreted as success criteria. In many studies, such results are accepted as an indication that the encryption process does not allow statistical attacks (deductions).

Table 5.
NPCR and UACI test results for images in Figure 9.
In fact, this type of analysis is used as security analysis in many studies. For example, it was discussed in detail by Whu et al. [66] that the values accepted as successful test results in the literature for NPCR and UACI tests are actually open to misinterpretation. Therefore, statistical tests are required in the cryptanalysis scenario. However, this is not enough to qualify an encryption algorithm as secure. It has been shown in various studies that many studies based on such a false hypothesis can be easily broken. Since the aim of this study was to address security concerns in the most effective way, it focused on analyzing more comprehensive analysis scenarios rather than giving a more statistical test approach. For the security analysis of the proposed algorithm, the analysis roadmap proposed in [7] was used.
4.2. Provable Security Analysis
When designing a cryptographical algorithm in the provable security design approach [67], the boundaries of each component are shown mathematically. The algorithm is considered secure as long as the maximum computational capacity the attacker can reach is lower than the computational capacity required to break the cryptographic component [68]. However, this is not an easy process to demonstrate. In some studies, various analysis roadmaps were designed to overcome this difficulty [69,70,71,72,73,74]. A sample analysis roadmap was presented in [7]. This analysis roadmap consists of a 12-step attack scenario allowing a comprehensive evaluation of any encryption algorithm. Some steps consist of various subheadings. In this section, each of these steps (analysis questions) is analyzed, and the security level of the proposed encryption algorithm is discussed in detail.
Step 1: The encryption algorithm has to be expressed mathematically and analyzed.
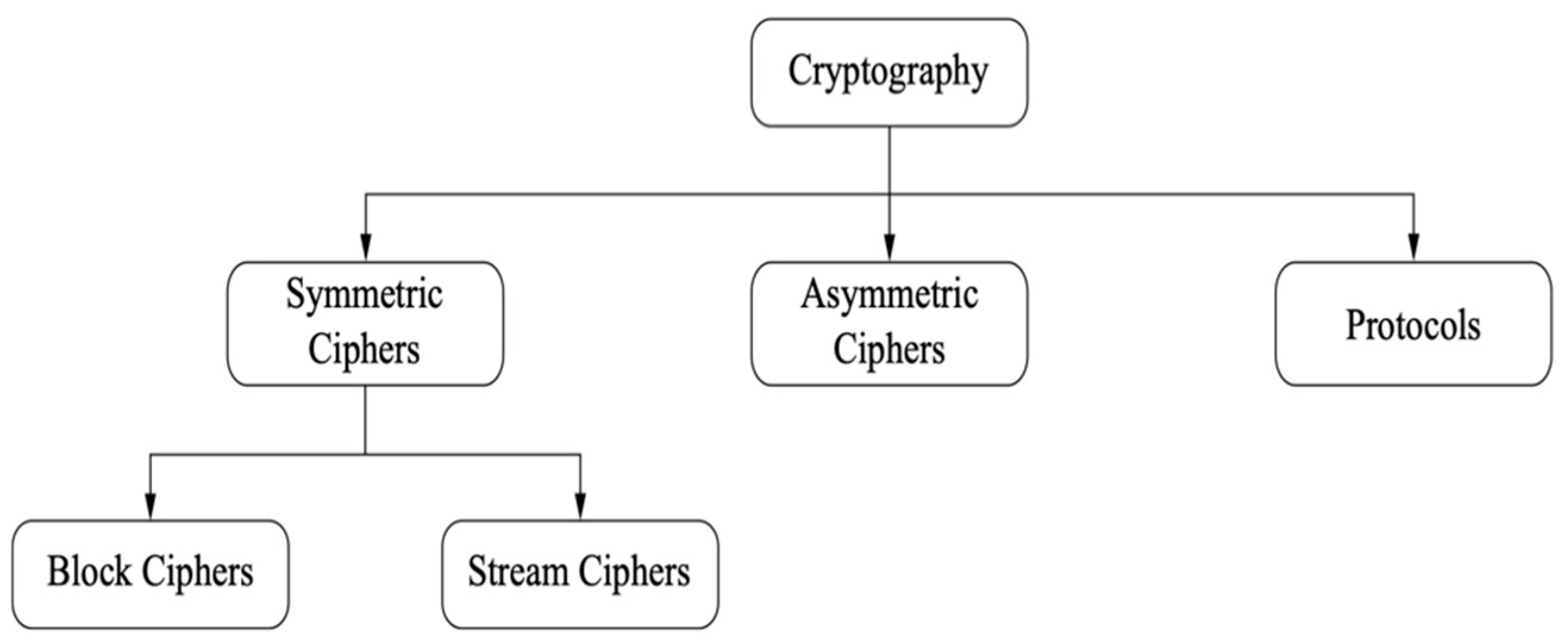
Analysis Step 1: The classification showing the general taxonomy of cryptology science is given in Figure 12. The proposed encryption algorithm is a stream encryption algorithm. The design architecture is based on the one-time password mechanism proposed by Vernam [75,76]. This architectural ward is known to be safe. It has a very simple mathematical model as expressed in Equation (1).
C = P XOR K.
Figure 12.
The general taxonomy of cryptology science [76].
This simple structure provides a great advantage in speed. As a result, the security of the algorithm is related to the quality of the keys to be produced. The analysis of the security of the key is discussed in detail in other stages.
Step 2: It is expected that the mathematical expression of the components in the algorithm is given.
Analysis of Step 2: As can be understood from the flowchart given in Figure 7, the general structure of the architecture is based on the XOR logic as given in Equation (1). Analysis of all other components is discussed in more detail in the later steps.
Step 3: Mathematical proof of the proposed architecture is required within the framework of the provable security approach.
Analysis of Step 3: A simplified representation of the proposed architecture from a different perspective is shown in Figure 13.
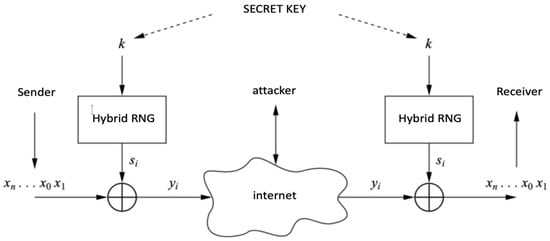
Figure 13.
A simplified representation of the proposed architecture [76].
The key generator and XOR function draw attention in this architecture. Analyses related to the key generator are given later. The XOR function has a special role in the design of cryptographical algorithms. Because the probability of the output values is 1/2, as can be deduced from the truth table, this process is similar to flipping a coin. Therefore, it is known that the proposed architecture is unconditionally secure, provided that a different key is used in each encryption process.
Step 4: In order to test whether it is compatible with the given mathematical expression, a flow chart of the proposed architecture should be given.
Analysis of Step 4: The flow chart of the algorithm is given in Figure 7. The flow chart and the mathematical expression given in Equation (1) are compatible. Any negatives during the analysis process were detected.
Step 5: The proposed architecture is expected to be designed in accordance with Kerckhoffs’s principle.
Analysis of Step 5: According to Kerckhoffs’s principle, there should not be any hidden parameters other than the secret key in the encryption architecture. Even if the attacker has the maximum computing power and maximum expert knowledge, they should not be able to break the architecture. As listed in Table 4, there are many options that can be used when creating the ciphertext to be obtained as a result of the algorithm. This wide range of options allows successfully fulfilling Kerckhoffs’s principle as it can guarantee different keys each time.
Step 6: Which design approach is used in the proposed architecture (cryptanalysis-driven design or provable security design approach)?
Analysis of Step 6: The provable security design approach was used.
Step 7: Which components are used to meet the confusion and diffusion properties?
Analysis of Step 7: The XOR function was used for the confusion properties. In the confusion requirement, the relationship between the key and the ciphertext is desired to be as complex as possible. The ciphertext is obtained as a result of applying the XOR operation to the key and plaintext. Hence, it is theoretically not possible to deduce the relationship between them because the probability of inference is exactly 1/2. Since this is no better than a blind guess, the proposed architecture is unconditionally safe if each key is used only once. Since the generated set of keys has a statistically uniform distribution, the ciphertext also has a uniform distribution after XOR processing. As a result, the diffusion feature is also guaranteed.
Step 8: What is the computational complexity of the proposed algorithm?
Analysis of Step 8: Since the proposed encryption algorithm is classified in the stream cipher category, the most important advantage over other encryption algorithm architectures is that the encryption process can be implemented quickly. This advantage is most clearly observed in complexity analysis. The encryption process of the algorithm is realized by applying two one-dimensional arrays of length T to the XOR operation. Thus, the overall complexity of the algorithm can be expressed as O(T) or O(n) in the commonly known form.
One point to be analyzed at this stage is the computational difficulty required for optimization algorithms and PUF structures in the key generator process of the algorithm. However, an entropy pool is proposed in the chosen design architecture. The ability to feed the entropy pool offline allows this calculative difficulty to be ignored.
Step 9: What is the algorithm’s complexity class?
Analysis of Step 9: The complexity class of the algorithm is P. The complexity class of the heuristic optimization algorithm used for the selection of control parameters and the initial conditions of chaotic systems in connection with the previous step is NP.
Step 10: Analysis of key generation module.
Analysis of Step 10: Since one of the unique aspects of the study is the key generator module, this analysis step was handled more comprehensively as a separate section.
Step 11: The numerical deterioration problem of chaotic systems must be analyzed.
Analysis of Step 11: The problem of numerical deterioration is related to the fact that the chaotic system state variables show a periodic behavior depending on the computational sensitivity of the computer where the encryption algorithm is implemented, and where the structure that is taken as the entropy source can no longer meet the randomness requirements. The initial conditions obtained through optimization algorithms must have a certain sensitivity value. Therefore, the proposed algorithm should have a configuration that can implement only the specified initial conditions. This dependency eliminates the numerical deterioration problem. In addition, since the use of hash functions at various stages of the proposed architecture allows mapping the output to a fixed length regardless of the input data, an additional measure is taken to address the problem of numerical deterioration. These choices indicate that possible attacks that can be associated with numerical deterioration are addressed.
Step 12: The effects of implementation attacks should be analyzed.
Analysis of Step 12: It was examined in previous studies that chaos-based designs can provide an advantage over algebraic techniques. It was evaluated that the presence of chaotic structures in the proposed architecture may provide an advantage against side-channel attacks.
4.3. Analysis of Key Generation
Random number generators (RNGs) have application areas not only in cryptology but also in games, modeling, and simulations. Each application area has its own specific requirements. There is a general classification for random numbers associated with these requirements. This classification is shown in Figure 14.
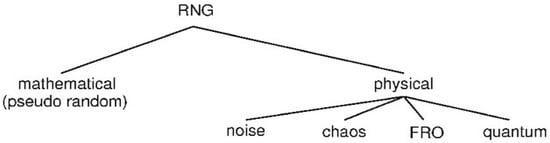
Figure 14.
A classification for random number generators [77].
The class known as DRNGs (mathematical/pseudo random) generates random numbers with the help of an algorithm. Good statistical properties and speed are the most important advantages of this class of generators. However, the predictability of these generators is an important problem. The TRNG (physical) class, which is an alternative to DRNG structures, has an advantage of low (may impossible) predictability; however, high cost and bad statistical properties are serious problems for researchers and designers.
The keys to be used in the process of encrypting sensitive information are required to have both good statistical properties and an unpredictable structure. Therefore, a hybrid generator architecture is proposed in this study. The unpredictable requirements of the proposed generator architecture are met by chaotic systems and PUF structures. In order to improve the statistical properties, the initial conditions and control parameters of chaotic systems were improved with optimization algorithms, while hash functions were applied to PUF outputs. The most widely accepted NIST randomness tests [78] were applied to analyze the success of the proposed approach. Here, 100,000,000 bit was generated as the PUF output. This output was divided into 100 pieces with a length of 1,000,000, because 1,000,000 bits are required to run NIST tests. A total of 84 of these 100 tests were successfully achieved. The remaining 16 pieces passed 14 tests and failed only one test. The analysis results of five randomly selected tests are given in Table 6. A comparison of the real random number generator used as the PUF structure with other TRNG structures is given in Table 7. The distribution of random values obtained after the seed values produced for the PUF hardware used in this study were processed through certain complex processes is given in Figure 15. The manufacturer’s web page states that “the driver allows application of a multiplier, which defines how many bits will be put out of the hashing function for each incoming bit of entropy. This enables generating over 50 megabytes of pure random numbers without measurable degradation of entropy.” Reference [33] can be examined for more details.

Table 6.
NIST test results for PUF outputs.

Table 7.
Comparisons for TRNG Structures.
Figure 15.
Distribution of random values after applying various postprocessing techniques to Crowd Supply Infinite Noise TRNG core values [33].
Chaotic systems constitute the other leg of the hybrid generator. The pseudo code of the chaotic generator is given in Algorithm 1. Optimization algorithms were used to determine the initial conditions of the chaotic system. Statistical properties were guaranteed, as the objective function of the optimization algorithm was chosen as NIST tests. NIST tests for the 1,000,000 bit value generated for the 0.187791210204038, 0.468326113906509, and 0.766654720925613 initial values of the logistic map are given in Table 8. Four control parameters of logistic maps were chosen. Since a hash function is applied to the output of the generated values, a countermeasure was established against numerical deterioration and/or known/chosen plaintext attacks. Obtaining the key as a result of applying XOR to the outputs produced from chaotic systems and PUF structures is considered as the last step positively affecting security. References [26,28] can be examined for more details.
| Algorithm 1 Pseudo code for chaotic bit generator for logistic map |
| Input: xValue, ControlParam Output: sequence 1. begin 2. sequence [1:1000000] 3. for i = 1 to 1000000 4. begin 5. xValue = ControlParam * xValue * (1 − xValue) 6. if (xValue < 0.5) 7. sequence[i] = 0 8. else 9. sequence[i] = 1 10. end if 11. end for 12. return sequence 13. end |

Table 8.
NIST test results for outputs of chaotic system.
5. Conclusions
The aim of this study was to realize a new cryptographic key generator algorithm and its practical application. As a practical application, the aim was to develop an image encryption algorithm that can eliminate security concerns. Analysis results showed that all goals were successfully achieved. This shows that the original aspects of the proposed architecture can be considered as cryptographical components in various security applications in the future.
- The proposed key generator module successfully meets all the requirements (R1, R2, R3 and R4) needed for cryptographical applications.
- The developed key generator module has a high bit output rate (1:1).
- It was shown that the most suitable initial conditions and control parameters that meet the statistical randomness requirements for chaotic systems can be determined with the help of optimization algorithms.
- A user-friendly image encryption algorithm was designed.
- It was shown that the correlation problem in digital images can be overcome by using the space-filling curve transformation method.
- The cryptanalysis of the image encryption algorithm was proven using not only statistical measurements, but also a provable security approach. This approach addressed security concerns via proof with mathematical techniques.
- The proposed encryption architecture is based on a key generator fed from two different entropy sources and cryptographic primitives such as the SHA3 mod function and XOR operator, whose security has been proven as a result of long-term cryptanalysis studies. These design choices specifically address critical security threats such as known-plaintext [79] and chosen-ciphertext [13] attacks.
Despite these advantages, it is thought that there are aspects of the proposed approach in future studies that need improvement. These aspects, which can be discussed as the limits of the proposed method, are listed below.
- Hardware was used as a PUF structure in the study. The dependency of this hardware can be a problem. This hardware dependency can be reduced by using alternative PUF resources in the future.
- The computing realization of chaotic systems is a critical issue, especially considering the problem of digital deterioration. In order to avoid this problem, the calculation sensitivity of the machine in the proposed study should be such that it does not cause this problem. This dependency can be considered as a disadvantage.
- Optimization algorithms are used to determine the initial conditions. It has been evaluated that the computational complexity of optimization algorithms can be interpreted as a disadvantage, although the process of determining the initial conditions with optimization algorithms can be operated offline.
- The cryptology science is a challenge between attacker and designer. Technological advances always keep the possibility of attack alive. Although the security of the proposed method has been proven from different angles, there is a need for a continuous cryptanalysis studies against vulnerabilities that may occur in the future.
Author Contributions
Conceptualization, A.S.M. and F.Ö.; methodology, F.Ö.; software, A.S.M. and F.Ö.; validation, A.S.M.; formal analysis, A.S.M.; investigation, A.S.M. and F.Ö.; resources, A.S.M. and F.Ö.; data curation, A.S.M. and F.Ö.; writing—original draft preparation, F.Ö.; writing—review and editing, F.Ö.; visualization, F.Ö.; supervision, F.Ö. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Please contact the corresponding author.
Acknowledgments
F.Ö. was supported in part by the Scientific and Technological Research Council of Turkey under Grant 120E444.
Conflicts of Interest
The authors declare no conflict of interest.
References
- She, R.; Liu, S.; Wan, S.; Xiong, K.; Fan, P. Importance of Small Probability Events in Big Data: Information Measures, Applications, and Challenges. IEEE Access 2019, 7, 100363–100382. [Google Scholar] [CrossRef]
- Yu, J.-Y.; Lee, E.; Oh, S.-R.; Seo, Y.-D.; Kim, Y.-G. A Survey on Security Requirements for WSNs: Focusing on the Characteristics Related to Security. IEEE Access 2020, 8, 45304–45324. [Google Scholar] [CrossRef]
- Son, J.; Choi, J.; Yoon, H. New Complementary Points of Cyber Security Schemes for Critical Digital Assets at Nuclear Power Plants. IEEE Access 2019, 7, 78379–78390. [Google Scholar] [CrossRef]
- Aljohani, M.; Ahmad, I.; Basheri, M.; Alassafi, M.O. Performance Analysis of Cryptographic Pseudorandom Number Generators. IEEE Access 2019, 7, 39794–39805. [Google Scholar] [CrossRef]
- Ahmad, M.; Al-Solami, E.; Alghamdi, A.M.; Yousaf, M.A. Bijective S-Boxes Method Using Improved Chaotic Map-Based Heuristic Search and Algebraic Group Structures. IEEE Access 2020, 8, 110397–110411. [Google Scholar] [CrossRef]
- Zahid, A.H.; Al-Solami, E.; Ahmad, M. A Novel Modular Approach Based Substitution-Box Design for Image Encryption. IEEE Access 2020, 8, 150326–150340. [Google Scholar] [CrossRef]
- Özkaynak, F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dyn. 2018, 92, 305–313. [Google Scholar] [CrossRef]
- Zhang, G.; Ding, W.; Li, L. Image Encryption Algorithm Based on Tent Delay-Sine Cascade with Logistic Map. Symmetry 2020, 12, 355. [Google Scholar] [CrossRef]
- Kang, Y.; Huang, L.; He, Y.; Xiong, X.; Cai, S.; Zhang, H. On a Symmetric Image Encryption Algorithm Based on the Peculiarity of Plaintext DNA Coding. Symmetry 2020, 12, 1393. [Google Scholar] [CrossRef]
- Thoai, V.P.; Kahkeshi, M.S.; Van Huynh, V.; Ouannas, A.; Pham, V.-T. A Nonlinear Five-Term System: Symmetry, Chaos, and Prediction. Symmetry 2020, 12, 865. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. A Novel Chaos-Based Color Image Encryption Scheme Using Bit-Level Permutation. Symmetry 2020, 12, 1497. [Google Scholar] [CrossRef]
- Zhang, R.; Yu, L.; Jiang, D.; Ding, W.; Song, J.; He, K.; Ding, Q. A Novel Plaintext-Related Color Image Encryption Scheme Based on Cellular Neural Network and Chen’s Chaotic System. Symmetry 2021, 13, 393. [Google Scholar] [CrossRef]
- Muhammad, Z.M.Z.; Ozkaynak, F. Security Problems of Chaotic Image Encryption Algorithms Based on Cryptanalysis Driven Design Technique. IEEE Access 2019, 7, 99945–99953. [Google Scholar] [CrossRef]
- Datcu, O.; Macovei, C.; Hobincu, R. Chaos Based Cryptographic Pseudo-Random Number Generator Template with Dynamic State Change. Appl. Sci. 2020, 10, 451. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine Chaotification Model for Enhancing Chaos and Its Hardware Implementation. IEEE Trans. Ind. Electron. 2019, 66, 1273–1284. [Google Scholar] [CrossRef]
- Yang, C.-H.; Chien, Y.-S. FPGA Implementation and Design of a Hybrid Chaos-AES Color Image Encryption Algorithm. Symmetry 2020, 12, 189. [Google Scholar] [CrossRef]
- Natiq, H.; Ariffin, M.; Asbullah, M.; Mahad, Z.; Najah, M. Enhancing Chaos Complexity of a Plasma Model through Power Input with Desirable Random Features. Entropy 2020, 23, 48. [Google Scholar] [CrossRef]
- Ozkaynak, F. A Novel Random Number Generator Based on Fractional Order Chaotic Chua System. Elektron. Elektrotechnika 2020, 26, 52–57. [Google Scholar] [CrossRef]
- Li, C.; Zhang, J.; Sang, L.; Gong, L.; Wang, L.; Wang, A.; Wang, Y. Deep Learning-Based Security Verification for a Random Number Generator Using White Chaos. Entropy 2020, 22, 1134. [Google Scholar] [CrossRef] [PubMed]
- Moysis, L.; Tutueva, A.; Volos, C.; Butusov, D.; Munoz-Pacheco, J.M.; Nistazakis, H. A Two-Parameter Modified Logistic Map and Its Application to Random Bit Generation. Symmetry 2020, 12, 829. [Google Scholar] [CrossRef]
- Stoller, S.; Campbell, K. Demonstration of Three True Random Number Generator Circuits Using Memristor Created Entropy and Commercial Off-the-Shelf Components. Entropy 2021, 23, 371. [Google Scholar] [CrossRef]
- Demidova, L.A.; Gorchakov, A.V. A Study of Chaotic Maps Producing Symmetric Distributions in the Fish School Search Optimization Algorithm with Exponential Step Decay. Symmetry 2020, 12, 784. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Zhang, Y.; Lu, Y.; Chen, Y. An efficient chaos-based image compression and encryption scheme using block compressive sensing and elementary cellular automata. Neural Comput. Appl. 2018, 32, 4961–4988. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J.; Abd-El-Atty, B.; Iliyasu, A.M.; Hirota, K.; El-Latif, A.A.A. Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf. Sci. 2020, 515, 191–217. [Google Scholar] [CrossRef]
- Ramasamy, P.; Ranganathan, V.; Kadry, S.; Damaševičius, R.; Blažauskas, T. An Image Encryption Scheme Based on Block Scrambling, Modified Zigzag Transformation and Key Generation Using Enhanced Logistic—Tent Map. Entropy 2019, 21, 656. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Ozkaynak, F. A New Chaotic S-Box Generation Method Using Parameter Optimization of One Dimensional Chaotic Maps. IEEE Access 2019, 7, 117829–117838. [Google Scholar] [CrossRef]
- Jiang, Y.; Lau, F.C.M.; Wang, S.; Tse, C.K. Parameter identification of chaotic systems by a novel dual particle swarm optimization. Int. J. Bifurc. Chaos 2016, 26, 1650024. [Google Scholar] [CrossRef]
- Acikkapi, M.S.; Ozkaynak, F. A Method to Determine the Most Suitable Initial Conditions of Chaotic Map in Statistical Randomness Applications. IEEE Access 2021, 9, 1482–1494. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Applications to Physics; Taylor & Francis: New York, NY, USA, 2014. [Google Scholar]
- Sprott, J. Elegant Chaos Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Schindler, W. Random Number Generators for Cryptographic Applications. In Cryptographic Engineering; Metzler, J.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Özkaynak, F. Cryptographically secure random number generator with chaotic additional input. Nonlinear Dyn. 2014, 78, 2015–2020. [Google Scholar] [CrossRef]
- Crowdsupply. Infinite Noise TRNG. Available online: https://www.crowdsupply.com/13-37/infinite-noise-trng (accessed on 7 May 2021).
- Kong, J.; Koushanfar, F. Processor-Based Strong Physical Unclonable Functions with Aging-Based Response Tuning. IEEE Trans. Emerg. Top. Comput. 2013, 2, 16–29. [Google Scholar] [CrossRef]
- Shamsoshoara, A.; Korenda, A.; Afghah, F.; Zeadally, S. A survey on physical unclonable function (PUF)-based security solutions for Internet of Things. Comput. Netw. 2020, 183, 107593. [Google Scholar] [CrossRef]
- Guajardo, J.; Gu, Q.; Paillier, P.; Lange, T.; Teske, E.; Hankerson, D.; Menezes, A.; Zhang, D.; Yue, F.; Zuo, W.; et al. Physical Unclonable Functions (PUFs). In Encyclopedia of Cryptography and Security; Springer: Boston, MA, USA, 2011; pp. 929–934. [Google Scholar]
- Dworkin, M.J. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions. In SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Liu, L.; Lei, Y.; Wang, D. A Fast Chaotic Image Encryption Scheme with Simultaneous Permutation-Diffusion Operation. IEEE Access 2020, 8, 27361–27374. [Google Scholar] [CrossRef]
- Jolfaei, A.; Wu, X.-W.; Muthukkumarasamy, V. On the Security of Permutation-Only Image Encryption Schemes. IEEE Trans. Inf. Forensics Secur. 2015, 11, 235–246. [Google Scholar] [CrossRef]
- Alshammari, B.M.; Guesmi, R.; Guesmi, T.; AlSaif, H.; AlZamil, A. Implementing a Symmetric Lightweight Cryptosystem in Highly Constrained IoT Devices by Using a Chaotic S-Box. Symmetry 2021, 13, 129. [Google Scholar] [CrossRef]
- Askar, S.; Al-Khedhairi, A.; Elsonbaty, A.; Elsadany, A. Chaotic Discrete Fractional-Order Food Chain Model and Hybrid Image Encryption Scheme Application. Symmetry 2021, 13, 161. [Google Scholar] [CrossRef]
- Lin, C.-H.; Hu, G.-H.; Chan, C.-Y.; Yan, J.-J. Chaos-Based Synchronized Dynamic Keys and Their Application to Image Encryption with an Improved AES Algorithm. Appl. Sci. 2021, 11, 1329. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, X.; Zhao, X.; Yu, H.; Zhang, L. Quadratic Function Chaotic System and its Application on Digital Image Encryption. IEEE Access 2020, 8, 55540–55549. [Google Scholar] [CrossRef]
- Elkamchouchi, D.H.; Mohamed, H.G.; Moussa, K.H. A Bijective Image Encryption System Based on Hybrid Chaotic Map Diffusion and DNA Confusion. Entropy 2020, 22, 180. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Chen, L.; Li, T. Hyper-Chaotic Color Image Encryption Based on Transformed Zigzag Diffusion and RNA Operation. Entropy 2021, 23, 361. [Google Scholar] [CrossRef]
- Khan, J.S.; Boulila, W.; Ahmad, J.; Rubaiee, S.; Rehman, A.U.; Alroobaea, R.; Buchanan, W.J. DNA and Plaintext Dependent Chaotic Visual Selective Image Encryption. IEEE Access 2020, 8, 159732–159744. [Google Scholar] [CrossRef]
- Wan, Y.; Gu, S.; Du, B. A New Image Encryption Algorithm Based on Composite Chaos and Hyperchaos Combined with DNA Coding. Entropy 2020, 22, 171. [Google Scholar] [CrossRef]
- Iqbal, N.; Hanif, M.; Abbas, S.; Khan, M.A.; Al Motiri, S.H.; Al Ghamdi, M.A. DNA Strands Level Scrambling Based Color Image Encryption Scheme. IEEE Access 2020, 8, 178167–178182. [Google Scholar] [CrossRef]
- Diaz, E.A.H.; Meana, H.M.P.; Garcia, V.M.S. Encryption of RGB Images by Means of a Novel Cryptosystem using Elliptic Curves and Chaos. IEEE Lat. Am. Trans. 2020, 18, 1407–1415. [Google Scholar] [CrossRef]
- Luo, Y.; Ouyang, X.; Liu, J.; Cao, L. An Image Encryption Method Based on Elliptic Curve Elgamal Encryption and Chaotic Systems. IEEE Access 2019, 7, 38507–38522. [Google Scholar] [CrossRef]
- Yousif, S.F.; Abboud, A.J.; Radhi, H.Y. Robust Image Encryption with Scanning Technology, the El-Gamal Algorithm and Chaos Theory. IEEE Access 2020, 8, 155184–155209. [Google Scholar] [CrossRef]
- Song, Y.; Zhu, Z.; Zhang, W.; Yu, H.; Zhao, Y. Efficient and Secure Image Encryption Algorithm Using a Novel Key-Substitution Architecture. IEEE Access 2019, 7, 84386–84400. [Google Scholar] [CrossRef]
- Li, H.; Deng, L.; Gu, Z. A Robust Image Encryption Algorithm Based on a 32-bit Chaotic System. IEEE Access 2020, 8, 30127–30151. [Google Scholar] [CrossRef]
- Rehman, A.U.; Firdous, A.; Iqbal, S.; Abbas, Z.; Shahid, M.M.A.; Wang, H.; Ullah, F. A Color Image Encryption Algorithm Based on One Time Key, Chaos Theory, and Concept of Rotor Machine. IEEE Access 2020, 8, 172275–172295. [Google Scholar] [CrossRef]
- Shah, T.; Haq, T.U.; Farooq, G. Improved SERPENT Algorithm: Design to RGB Image Encryption Implementation. IEEE Access 2020, 8, 52609–52621. [Google Scholar] [CrossRef]
- Muhammad, Z.M.Z.; Ozkaynak, F. An Image Encryption Algorithm Based on Chaotic Selection of Robust Cryptographic Primitives. IEEE Access 2020, 8, 56581–56589. [Google Scholar] [CrossRef]
- Boussif, M.; Aloui, N.; Cherif, A. Securing DICOM images by a new encryption algorithm using Arnold transform and Vigenère cipher. IET Image Process. 2020, 14, 1209–1216. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D.; Huang, W.; Liu, C. Quantum Block Image Encryption Based on Arnold Transform and Sine Chaotification Model. IEEE Access 2019, 7, 57188–57199. [Google Scholar] [CrossRef]
- Zhou, S. A Quantum Image Encryption Method Based on DNACNot. IEEE Access 2020, 8, 178336–178344. [Google Scholar] [CrossRef]
- Faragallah, O.S.; Afifi, A.; El-Shafai, W.; El-Sayed, H.S.; Naeem, E.A.; AlZain, M.A.; Al-Amri, J.F.; Soh, B.; El-Samie, F.E.A. Investigation of Chaotic Image Encryption in Spatial and FrFT Domains for Cybersecurity Applications. IEEE Access 2020, 8, 42491–42503. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Sun, K.; Cao, Y.; Jin, J. Color Image Compression-Encryption Algorithm Based on Fractional-Order Memristor Chaotic Circuit. IEEE Access 2019, 7, 58751–58763. [Google Scholar] [CrossRef]
- Neto, J.R.D.O.; Lima, J.B.; Panario, D. The Design of a Novel Multiple-Parameter Fractional Number-Theoretic Transform and Its Application to Image Encryption. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2489–2502. [Google Scholar] [CrossRef]
- Ibrahim, S.; Alhumyani, H.; Masud, M.; Alshamrani, S.S.; Cheikhrouhou, O.; Muhammad, G.; Hossain, M.S.; Abbas, A.M. Framework for Efficient Medical Image Encryption Using Dynamic S-Boxes and Chaotic Maps. IEEE Access 2020, 8, 160433–160449. [Google Scholar] [CrossRef]
- Li, T.; Du, B.; Liang, X. Image Encryption Algorithm Based on Logistic and Two-Dimensional Lorenz. IEEE Access 2020, 8, 13792–13805. [Google Scholar] [CrossRef]
- Ali, T.S.; Ali, R. A Novel Medical Image Signcryption Scheme Using TLTS and Henon Chaotic Map. IEEE Access 2020, 8, 71974–71992. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.; Again, S. Npcr and Uaci Randomness Tests for Image Encryption. JSAT 2011, 31–38. [Google Scholar]
- Bellare, M. Practice-Oriented Provable-Security. In Proceedings of the International Workshop on Information Security, Kuala Lumpur, Malaysia, 6–7 November 1999; pp. 1–15. [Google Scholar]
- Goldwasser, S.; Bellare, M. Lecture Notes on Cryptography Summer Course ‘Cryptography and Computer Security’; Massachusetts Institute of Technology: Cambridge, MA, USA, 1999. [Google Scholar]
- Feng, W.; He, Y.-G. Cryptanalysis and Improvement of the Hyper-Chaotic Image Encryption Scheme Based on DNA Encoding and Scrambling. IEEE Photon J. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lu, J. Cryptanalyzing an Image-Scrambling Encryption Algorithm of Pixel Bits. IEEE MultiMedia 2017, 24, 64–71. [Google Scholar] [CrossRef]
- Ozkaynak, F. Role of NPCR and UACI tests in security problems of chaos based image encryption algorithms and possible solution proposals. In Proceedings of the 2017 International Conference on Computer Science and Engineering (UBMK), London, UK, 5–7 July 2017. [Google Scholar]
- Feng, W.; He, Y.; Li, H.; Li, C. Cryptanalysis and Improvement of the Image Encryption Scheme Based on 2D Logistic-Adjusted-Sine Map. IEEE Access 2019, 7, 12584–12597. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Xie, E.Y. When an attacker meets a cipher-image in 2018: A year in review. J. Inf. Secur. Appl. 2019, 48. [Google Scholar] [CrossRef]
- Burhan, Y.; Artuger, F.; Ozkaynak, F. A Novel Hybrid Image Encryption Algorithm Based on Data Compression and Chaotic Key Planning Algorithms. In Proceedings of the 7th International Symposium on Digital Forensics and Security (ISDFS), Barcelos, Portugal, 10–12 June 2019; pp. 1–5. [Google Scholar]
- Wernam, B.; Steven, M. Frank Miller: Inventor of the One-Time Pad. Cryptologia 2021, 35, 203–222. [Google Scholar]
- Paar, C.; Pelzl, J. Understanding Cryptography: A Textbook for Students and Practitioners; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Stipčević, M.; Koç, K. True Random Number Generators. In Open Problems in Mathematics and Computational Science; Metzler, J.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 275–315. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Defense Technical Information Center: Fort Belvoir, VA, USA, 2010.
- Wei, W.; Woźniak, M.; Damaševičius, R.; Fan, X.; Li, Y. Algorithm Research of Known-plaintext Attack on Double Random Phase Mask Based on WSNs. J. Internet Technol. 2019, 20, 39–48. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).