Study of Parameters in the Genetic Algorithm for the Attack on Block Ciphers

Abstract

In recent years, the use of Genetic Algorithms (GAs) in symmetric cryptography, in particular in the cryptanalysis of block ciphers, has increased. In this work, the study of certain parameters that intervene in GAs was carried out, such as the time it takes to execute a certain number of iterations, so that a number of generations to be carried out in an available time can be estimated. Accordingly, the size of the set of individuals that constitute admissible solutions for GAs can be chosen. On the other hand, several fitness functions were introduced, and which ones led to better results was analyzed. The experiments were performed with the block ciphers AES(t), for $t\in \{3,4,7\}$.

1. Introduction

There are several methods and tools that are used as optimization methods and predictive tools. Several heuristic algorithms have been used in the context of cryptography; in [1], the Ant Colony Optimization (ACO) heuristic method was used, and a methodology with S-AES block encryption was tested, using two pairs of plain encrypted texts. In [2], a combination of GA and ACO methods was used for cryptanalysis of stream ciphers. In [3,4,5], the possibilities of combining and designing these analyzes using machine learning and deep learning tools were shown. In [6,7,8], the methods of the Artificial Neural Network (ANN), Support Vector Machine (SVM), and Gene-Expression Programming (GEP) were used as predictive tools in other contexts.

The Genetic Algorithm (GA) is an optimization method used in recent years in cryptography for various purposes, mainly to carry out attacks on various encryption types. Some of the research conducted in this direction is mentioned next. In [9], the authors presented a combination of the GA with particle swarm optimization (another heuristic method based on evolutionary techniques); they called their method genetic swarm optimization and applied it to attack the block cipher Data Encryption Standard (DES). Their experimental results showed that better results were obtained by applying their combined method than by using both methods separately. The proposal presented in [10] provided a preliminary exploration of GA’s use over a Permutation Substitution Network (SPN) cipher. The purpose of the scan was to determine how to find weak keys. Both works [9,10] used a known plaintext attack, i.e., given a plaintext T and the corresponding ciphertext C, one is interested in finding the key K. In [10], the fitness function evaluates the bitwise difference (Hamming distance) between C and the ciphertext of T, using a candidate for the key, whereas, on the contrary, in [9] the Hamming distance between T and the decryption of the ciphertext of C is measured. In [11], a ciphertext-only attack on simplified DES was shown, obtaining better results than by brute force. The authors used a fitness function that combined the relative frequency of monograms, digrams, and trigrams (for a particular language). Since the key length was very small, they were able to use this kind of function. The approach in [12] was similar to [11]; it used essentially the same fitness function, but with different parameters. It was also more detailed regarding the experiments and compared them concerning brute force and random search. For more details on the area of cryptanalysis using GAs, see [13,14,15].

As in all evolutionary algorithms, it is always a difficulty in the GA that, as the number of individuals in the space of admissible solutions grows, in this case, the set of keys, it is necessary to perform a greater number of generations in order to obtain the best results. It is clear that the greater the number of generations, the more time the algorithm consumes, so it is important to be able to estimate the time that may be necessary to execute a certain number of desired generations. On the other hand, it is necessary to analyze fitness functions that allow obtaining better results with the fittest individuals obtained.

Symmetry is omnipresent in the universe; in particular, it is present in symmetric cryptography, where the secret key is known for both authorized parts in the communication channel essentially by symmetry. We worked with block ciphers, an important primitive of symmetric cryptographic, where the key space (the population of admissible solutions for the GA in this case) is exponentially big, making it impossible in many cases to fully move in that space.

In the present work, the ideas to divide the key space that were started in [16,17] were followed. Both methodologies for dividing the key space allow the GA search space to be reduced over a subset of individuals. For this case, we studied the behavior of time and the introduction of various fitness functions. The structure of the work is as follows. In Section 2, the general ideas of the GA and two methodologies for partitioning the key space are presented; in Section 3, several parameters of the cryptanalysis for block ciphers using the GA are studied; in Section 3.1, the time it takes to execute a certain number of iterations is analyzed, so that a number of generations to be carried out in an available time can be estimated; and in Section 3.2, other fitness functions are proposed. Finally, Section 4 gives the conclusions.

2. Preliminaries

2.1. The Genetic Algorithm

The GA is a heuristic optimization method. We assume that the reader knows the general ideas of how the GA works; see Algorithm 1. In this section, we briefly describe the GA scheme used in this work.

Algorithm 1. Genetic algorithm.

Input:  m (quantity of individuals in the population), F (fitness function), g (number of generations). Output:  the individual with the highest fitness function as the best solution. 1: Randomly generate an initial population $P_i$ with m individuals (possible solutions). 2: Compute the fitness of each individual from $P_i$ with F. 3: while the solution is not found, or the g generations are not reached do 4:  Select parent pairs in $P_i$. 5:  Perform the crossover of the selected parents, and generate a pair of offspring. 6:  Mutate each of the resulting descendants. 7:  Compute the fitness of each of the descendants with F and their mutations. 8:  By the tournament method between two, based on the fitness of the parents and descendants, decide what is the new population $P_i$ for the next generation (selecting two individuals at random each time and choosing the one with the highest fitness). 9: end while

The individuals from the populations are elements of the key space taken as binary blocks. For Crossover, the crossing by two points was used, and the crossover probability was fixed to $0.6$. The Mutate operation consisted of interchanging the values of the bits of at most three random components of the binary block with a mutation rate of 0.2. The values of $0.6$ and $0.2$ were fixed for all experiments, and the study of the incidence of the variation of these values in the behavior of the GA was not addressed in this paper. An individual x is better adapted than another y, if it has greater fitness, i.e., if $F\left(x\right)>F\left(y\right)$. Fitness functions are studied in more detail in Section 3.2. For the specification of the GA to block ciphers, see Section 3 of [16].

2.2. Key Space Partition Methodologies

The methodologies introduced in [16,17] allow GAs to work on a certain subset of the set of admissible solutions as if it were the complete set. The importance of this fact is that it reduces the size of the search space and gives the heuristic method a greater chance of success, assuming that the most suitable individuals are found in the selected subset. Let ${\mathbb{F}}_2^{k_1}$ be the key space of length $k_1\in {\mathbb{Z}}_{>0}$. It is known that ${\mathbb{F}}_2^{k_1}$ has cardinality $2^{k_1}$, and therefore, there is a one-to-one correspondence between ${\mathbb{F}}_2^{k_1}$ and the range $\left[0,2^{k_1}-1\right]$. If an integer $k_2$ is set, ($1<k_2\le k_1$), then the key space can be represented by the numbers,

$$q{2}^{k_2}+r,$$

(1)

where $q\in \left[0,2^{k_1-k_2}-1\right]$ and $r\in \left[0,2^{k_2}-1\right]$. In this way, the key space is divided into $2^{k_1-k_2}$ blocks (determined by the quotient in the division algorithm dividing by $2^{k_2}$), and within each block, the corresponding key is determined by its position, which is given by the remainder r. The main idea is to stay in a block (given by q) and move within this block through the elements (given by r) using the GA. Note in this methodology that first q is set to choose a block, and then, r varies to be able to move through the elements of the block; however, the complete key in ${\mathbb{F}}_2^{k_1}$ is obtained from Expression (1). We refer to this methodology as BBM. For more details on the connection with GAs, see [16].

The following methodology is based on the definition of the quotient group of the keys $G_K$ whose objective is to make a partition of ${\mathbb{F}}_2^{k_1}$ in equivalence classes. It is known that ${\mathbb{F}}_2^{k_1}$, as an additive group, is isomorphic to ${\mathbb{Z}}_{2^{k_1}}$. Let h be the homomorphism defined as follows:

$$\begin{array}{ccc}\hfill h:{\mathbb{Z}}_{2^{k_1}}& ⟶& {\mathbb{Z}}_{2^{k_2}}\hfill \\ \hfill n& ⟶& n\left(mod{2}^{k_2}\right),\hfill \end{array}$$

(2)

where $k_2\in {\mathbb{Z}}_{>0}$ and $0<k_2<k_1$. We denote by N the kernel of h, i.e.,

$$N=\{x\in {\mathbb{Z}}_{2^{k_1}}|h\left(x\right)=0\in {\mathbb{Z}}_{2^{k_2}}\}.$$

(3)

Then, by the definition of h, we have that N is composed by the elements of ${\mathbb{Z}}_{2^{k_1}}$, which are multiples of $2^{k_2}$. It is known that N is an invariant subgroup; therefore, the main objective is to calculate the quotient group of ${\mathbb{Z}}_{2^{k_1}}$ by N, and in this way, the key space will be divided into $2^{k_2}$ equivalence classes. We denote by $G_K$ the quotient group of ${\mathbb{Z}}_{2^{k_1}}$ by N ($G_K={\mathbb{Z}}_{2^{k_1}}/N$). By Lagrange’s theorem, we have that $o\left(G_K\right)=o\left({\mathbb{Z}}_{2^{k_1}}\right)/o\left(N\right)$, but $o\left(G_K\right)=o\left({\mathbb{Z}}_{2^{k_2}}\right)=2^{k_2}$, then,

$$o\left(N\right)=o\left({\mathbb{Z}}_{2^{k_1}}\right)/o\left({\mathbb{Z}}_{2^{k_2}}\right)=2^{k_1-k_2}.$$

(4)

Now, N can be described, taking into account that its elements are multiples of $2^{k_2}$. For this, we take $Q=\{0,1,2,\dots ,2^{k_1-k_2}-1\}$, then:

$$\begin{array}{ccc}\hfill N& =& <2^{k_2}>=\{x\in {\mathbb{Z}}_{2^{k_1}}|\exists q\in Q,x=q{2}^{k_2}\}\hfill \\ & =& \{0,2^{k_2},2\ast 2^{k_2},3\ast 2^{k_2},\dots ,(2^{k_1-k_2}-1)\ast 2^{k_2}\}.\hfill \end{array}$$

(5)

On the other hand,

$$G_K=\{N,1+N,2+N,\dots ,(2^{k_2}-2)+N,(2^{k_2}-1)+N\}.$$

(6)

In this way, ${\mathbb{Z}}_{2^{k_1}}$ is divided into a partition of $2^{k_2}$ classes given by N. $G_K$ is called the quotient group of keys. Let,

$$E:{\{0,1\}}^m\times {\{0,1\}}^n\to {\{0,1\}}^n,m,n\in \mathbb{N},m\ge n,$$

(7)

be a block cipher, T a plaintext, K a key, and C the corresponding ciphertext, i.e., $C=E(K,T)$; $K^{\prime }$ is said to be a consistent key with E, T, and C, if $C=E(K^{\prime },T)$ (see [16]). The idea here is also to go through, from the total space, the elements that are in a class and then find one (or several) consisting of the keys of that class. To be able to go through the elements of each class, note that ${\mathbb{Z}}_{2^{k_2}}$ is isomorphic with $G_K$, and the isomorphism corresponds to each $r\in {\mathbb{Z}}_{2^{k_2}}$ its equivalence class $r+N$ in $G_K$; thus, selecting a class is setting an element $r\in {\mathbb{Z}}_{2^{k_2}}$. On the other hand, the elements of N are of the form $q{2}^{k_2}$ ($q\in Q$); therefore, the elements of the class $r+N$ are of the form,

$$q{2}^{k_2}+r,q\in Q.$$

(8)

Then, the problem of looping through each element of each equivalence class consists of first setting an element of ${\mathbb{Z}}_{2^{k_2}}$ and then looping through each element of the set Q, to find a key of $G_K$ using Equation (8). The elements of the set Q have block length $k_d=k_1-k_2$, and each class has $2^{k_d}$ elements. We refer to this methodology as TBB. Note that the TBB methodology is a kind of dual idea with respect to the BBM methodology, i.e., one first stays in the same class (given by r) and then moves within this class through the elements (given by q) using the GA. In this case, the length of the blocks is $2^{k_d}$ instead of $2^{k_2}$.

The main difficulty in these methodologies is the choice of $k_2$, since it is the parameter that determines the number of equivalence classes and, therefore, the number of elements within them. If in $G_K$, $k_2$ increases, the classes have fewer elements, but there are more classes; on the contrary, if it decreases, so does the number of classes, but the number of elements of each increases. Something similar happens in the first methodology. The operations of the space partitioning and going through the elements of each class are done with the decimal representation and the specific operations of the GA with the binary representation. For more details, see [16,17].

In Figure 1, the relationship of the content by subsections and the attack on block ciphers are shown in a flowchart.

3. Study of Parameters in the GA

3.1. Time Estimation

In GAs, less complex operations such as mutation and crossing are performed within each class, where the elements have block length $k_2\le k_1$ or $k_d\le k_1$ depending on the way of partitioning the space. However, despite the variation of these two parameters, the calculation of the fitness function, being the function of greater complexity within the GA, is carried out using (8), i.e., with the complete key of length $k_1$, and not with the part of it found in the class. This means that a variation in the number of elements in a class does not affect the fitness function’s cost. Moreover, if all the parameters remain the same, the GA’s time in each generation must be quite similar, even if $k_2$ varies. To check this, experiments were done with a PC with an Intel(R) Core (TM) i3-4160 CPU @ 3.60GHz (four CPUs), and 4GB of RAM. AES(t) encryption was used, a parametric version of AES, where $t\in \{3,4,5,6,7,8\}$ and also AES(8) = AES (see [18,19]). The experiment consisted of executing the GA with the BBM methodology and measuring the time (in minutes) that it took in a generation for different values of $k_2$ (keeping the other parameters fixed), then verifying if these data were used to forecast the time it would take in n generations. The size of the population was $m=100$ in all cases.

Table 1. Time estimation in AES(3).

${\mathit{k}}_2$	1 Gen	n Gen	${\mathit{t}}_{\mathit{r}}$	${\mathit{t}}_{\mathit{e}}$	${\mathit{E}}_{\mathit{p}}$
10	0.0355	2	0.0962	0.0871	0.0091
11	0.0518	20	0.7134	0.8711	0.1577
12	0.0429	27	1.0491	1.1760	0.1269
13	0.042	81	3.3475	3.5281	0.1806
14	0.0429	49	2.0863	2.1343	0.0481
15	0.0454	71	3.1606	3.0926	0.0680
16	0.0444	655	28.9312	28.5299	0.4012

,

Table 2. Time estimation in AES(4).

${\mathit{k}}_2$	1 Gen	n Gen	${\mathit{t}}_{\mathit{r}}$	${\mathit{t}}_{\mathit{e}}$	${\mathit{E}}_{\mathit{p}}$
10	0.0519	9	0.3739	0.4675	0.0936
11	0.0553	8	0.3838	0.4155	0.0318
12	0.0465	5	0.2756	0.2597	0.0159
13	0.0564	2	0.1303	0.1039	0.0264
14	0.0506	81	4.1554	4.2071	0.0517
15	0.0510	98	4.9621	5.0900	0.1279
16	0.0519	655	34.1330	34.0202	0.1128

and

Table 3. Time estimation in AES(7).

${\mathit{k}}_2$	1 Gen	n Gen	${\mathit{t}}_{\mathit{r}}$	${\mathit{t}}_{\mathit{e}}$	${\mathit{E}}_{\mathit{p}}$
17	0.1895	373	69.1909	70.8811	1.6902
18	0.1905	932	178.069	177.108	0.9610

summarize the results corresponding to AES(3), AES(4), and AES(7), respectively. The first column has the different values that were given to $k_2$. The second column is the average time $t_{k_2}$ that was obtained for a generation in 10 executions of each $k_2$. The general mean for all the $k_2$ values is $t_m=0.0435571$ minutes approximately in Table 1, $t_m=0.0519393$ in Table 2, and $t_m=0.1900297$ in Table 3. The third column represents the number of generations ($n_g$). The real-time that the algorithm takes, $t_r$, appears in the fourth column. The fifth column is the estimated time, $t_e$, that should be delayed, the calculation of which is based on:

$$t_e=t_m{n}_g.$$

(9)

Finally, the last column is the error of the prediction, $E_p=|t_r-t_e|.$ With these experiments, we wanted to check for the procedure whether if for a specific value of $k_2$ and having $n_g$ generations, then the approximate time (t) that the GA would take to complete those generations was $t\approx t_e.$

With a generation, or very few, the average time it took for the GA was slightly slower, decreasing and tending to stabilize at a limit as it performed more iterations. This was due to probabilistic functions that intervened in the GA and a set of operations to randomly create an initial population. Therefore, the criterion for calculating the average time $t_{k_2}$ was to let the GA finish executing in a certain number of generations, either because it found the key or because it reached the last iteration without finding it, and then calculate the average. Therefore, calculating $t_{k_2}$ in a few generations or setting the amount to one, would get longer times; however, doing so would be valid if the intention were to go over the top in estimating the time that the algorithm consumed.

In the case of AES(7) (Table 3), we only experimented with the values 17 and 18 of $k_2$, since considering all the previous (or higher) values would take a considerably longer time (given the greater strength of AES(7)).

Similar results were obtained if more values of $k_2$ were chosen to calculate $t_m$. For example, using a PC Laptop with a processor: Intel (R) Celeron (R) CPU N3050 @ 1.60GHz (two CPUs), ∼1.6 GHz, and 4 GB of RAM and going through all the values of $k_2$ from 10 to 48 (AES(3) key length), $t_m=0.2340212$ was obtained. Now, for $n_g=215$, we had $t_r=48.14715$ and $t_e=t_m{n}_g\approx 50.3145.$ In another test: $n_g=150$, $t_r=34.9565$, then $t_e\approx 35.1032$. Note that the PC used in this case had different characteristics and less computational capacity than the experiments in Table 1, Table 2 and Table 3. The interesting thing is that under these conditions, the results were as expected as well.

In a similar way, the GA was executed with the TBB methodology for the search in $G_K$, for values of $k_d$ equal to those of $k_2$ and different generations ($n_g$). It was observed that the time estimates behaved in a similar way to the results presented previously for the BBM methodology. Note that in the AES(t) family of ciphers, the length of the key increases from 48 for AES(3) to 128 for AES(8); however, regardless of the key length, the same behavior was seen in all of them.

Now, we showed with these experiments another application of this study on time estimation. In the GA scheme with the BBM methodology, the total number of generations (iterations) to perform for a given value of $k_2$ is:

$$g=⌊\frac{2^{k_2}}{m}⌋.$$

(10)

Taking $n_g=g$, by using $t_e$, then we can do an a priori estimation for a given value of $k_2$, of the total time it will take the GA to perform all the generations or a certain desired percent of them. For example, in AES(3), for $k_2=16$, in Expression (10), we have $g=655$; now, since $t_m=0.0435571$ in Table 1, then the approximate time that the GA will consume to perform 655 generations is $t_e\approx 655·0.0435571\approx 28.5299$, as can be seen in the table. Another example can be seen in Table 2, also for $k_2=16$.

On the other hand, supposing we have an available time $t_e$, to carry out the attack with this model, thus we may use (9) and (10), to compute an approximated value of $k_2$, which implies doing the corresponding partition of the space and computing the number of generations to perform for this time $t_e$ and the value of $k_2$. In this sense, doing $n_g=g$ in (9), we have:

$$k_2\approx ⌊{log}_2\frac{m{t}_e}{t_m}⌋.$$

(11)

We remark that the above is valid in the TBB methodology, only that $k_d$ is used instead of $k_2$.

As can be observed, the results on the estimation of time were favorable. In this sense, the following points can be summarized:

• Taking into account the estimation of time $t_e$ and its observed closeness to the real value $t_r$, a number of generations to be carried out in an available or desired time can be estimated (using Expression (9)), which can be taken as a starting point for the proper choice of $k_2$, or $k_d$ in $G_K$ (see Section 2). In this way, it is possible to adapt the size of the search space (to choose a proper value of $k_2$ using (11)) to the number of generations that it is estimated can be executed in a given time.
• The time $t_{k_2}$ could be used to perform the time estimation of its own $k_2$, but as can be seen in the tables, sometimes, it makes predictions with minor errors and other times greater than with $t_m$. Another drawback is that it cannot be used for other $k_2$. On the contrary, the main advantage of using $t_m$ is that it can be calculated for some sparse values of $k_2$ and be used to estimate the time even with values of this parameter whose $t_{k_2}$ has not been calculated.

3.2. Proposal of Other Fitness Functions

In the context of the BBM and TBB methodologies used in this work with the GA, we studied in this section which fitness functions provided a better response, in the sense that consistent keys were obtained as solutions in a greater percentage of occasions. Let E be a block cipher with length n of plaintext and ciphertext, defined as in Expression (7), T a plaintext, K a key, and C the corresponding ciphertext, that is $C=E(K,T)$. Let:

$$D:{\left\{0.1\right\}}^m\times {\left\{0.1\right\}}^n\to {\left\{0.1\right\}}^n,$$

(12)

be the function of decryption of E, such that $T=D(K,C)$. Then, the fitness function with which we have been working and based on the Hamming distance $d_H$, for a certain individual X of the population, is:

$$F_1\left(X\right)=\frac{n-d_H(C,E(X,T))}{n},$$

(13)

which measures the closeness between the encrypted texts C and the text obtained from encrypting T with the probable key X (see [16]). A similar function is the one that measures the closeness between plaintexts:

$$F_2\left(X\right)=\frac{n-d_H(T,D(X,C))}{n}.$$

(14)

Another function that follows the idea of comparing texts in binary with $d_H$ is the weighting of $F_1$ and $F_2$. Let $\alpha ,\beta \in [0,1]\subset \mathbb{R}$, such that $\alpha +\beta =1$, then this function would be defined as follows:

$$F_3\left(X\right)=\alpha F_1\left(X\right)+\beta F_2\left(X\right).$$

(15)

It is interesting to note that $F_3$ is more time consuming than each function separately, but the idea is to be more efficient in searching for the key.

The fitness functions proposed at this point are based on measuring the closeness of the plaintext and ciphertext, but in decimals. Let $Y_d$ be the corresponding conversion to decimals of the binary block Y. The first function is defined as follows,

$$F_4\left(X\right)=\frac{2^n-1-|C_d-E{(X,T)}_d|}{2^n-1}.$$

(16)

Note that if the encrypted texts are equal, $C_d=E{(X,T)}_d$, then $|C_d-E{(X,T)}_d|=0$, which implies that $F_4\left(X\right)=1$, i.e., if they are equal, then the fitness function takes the highest value. On the contrary, the greatest difference is the farthest they can be, i.e., $C_d=2^n-1$ and $E{(X,T)}_d=0$, and therefore, $F_4\left(X\right)=0$. The following is a weighting of the functions $F_1$ and $F_4$,

$$F_5\left(X\right)=\alpha F_1\left(X\right)+\beta F_4\left(X\right).$$

(17)

Both functions have in common that they measure the closeness between ciphertexts. This is not ambiguous since, for example, if C and $E(X,T)$ differ by two bits, the function $F_1$ will always have the same value no matter what these two bits are. On the contrary, it is not the same in $F_4$ if the bits are both more or less significant since the numbers are not the same in their decimal representation. The following function measures the closeness in decimals of plaintexts:

$$F_6\left(X\right)=\frac{2^n-1-|T_d-D{(X,C)}_d|}{2^n-1}.$$

(18)

Finally, the functions $F_7$, $F_8$, and $F_9$ are defined with respect to the previous ones as follows,

$$\begin{array}{ccc}\hfill F_7\left(X\right)& =& \alpha F_2\left(X\right)+\beta F_6\left(X\right),\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill F_8\left(X\right)& =& \alpha F_4\left(X\right)+\beta F_6\left(X\right),\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill F_9\left(X\right)& =& {\alpha }_1{F}_1\left(X\right)+{\alpha }_2{F}_2\left(X\right)+{\alpha }_3{F}_4\left(X\right)+{\alpha }_4{F}_6\left(X\right),\hfill \end{array}$$

(21)

where ${\alpha }_i\in [0,1]\subset \mathbb{R},i\in \{1,2,3,4\}$ and ${\displaystyle \sum _{i=1}^4}{\alpha }_i=1$. This guarantees that in general, each $F_j\left(X\right)\in [0,1]\subset \mathbb{R},j\in \{1,2,3,4,5,6,7,8,9\}$.

The idea behind the introduction of these functions lies mainly in the fact that there are changes that the Hamming distance does not detect, as opposed to the decimal distance. For example, suppose the key is $a={(1,1,1,1,1,1)}_2$, and $b={(0,0,0,0,0,1)}_2$ is the possible key, both in binary. It is clear that the Hamming distance is five, and the distance in decimals is 62 since $a=63$ and $b=1$; the fitness functions take the values $1-5/6=0.17$ for the binary version and $1-62/63=0.016$ for the decimal version. Now, if $b={(0,0,1,0,0,0)}_2$, the binary fitness function would still be 0.17 since there are still five different bits; on the other hand, $b=8$, so the decimal fitness function takes the value $1-55/63=0.13$. Finally, if we take $b={(1,0,0,0,0,0)}_2=32$, then the distance in binary remains the same value, but the decimal continues to change, therefore, the fitness function as well, and takes the value 0.49. Therefore, this shows that the change of b, the decimal distance, is always detected, unlike the binary distance, which remains the same for certain changes.

AES(3) encryption attack experiments were carried out for the two methodologies for partitioning the key space to compare these functions. The main idea is to find the key and not do a component percent match analysis between them, where the fitness functions with the Hamming distance would be more useful. A PC with an Inter (R) Core (TM) i3-4160 CPU @ 3.60GHz (four CPUs), and 4 GB of RAM was used. For the results, we took into account the average time it took to find the key, the average number of generations in which it was found, the percentage of failures (in many attacks carried out), and a parameter called efficiency, $E_{F_i}$, which resulted in a weighting of the three previous criteria.

Definition 1 

(Fitness functions’ efficiency). Let ${\mu }_1$, ${\mu }_2,{\mu }_3\in [0,1]\subset \mathbb{R},$${\mu }_1+{\mu }_2+{\mu }_3=1$, $t_{F_i}$, $i=\overline{1,\dots ,k}$, the time it takes the GA to find the key with $F_i$, on an average for $g_{F_i}$ generations, and $p_{F_i}$ the percent of attempts in that the GA did not find the key with $F_i$. Then, the efficiency, $E_{F_i}$, of the fitness function $F_i$ with respect to the other $k-1$ functions, $F_j,j\ne i$, is defined as,

$$E_{F_i}=1-\left({\mu }_1\frac{t_{F_i}}{{\displaystyle \sum _{\gamma =1}^k}{t}_{F_{\gamma }}}+{\mu }_2\frac{g_{F_i}}{{\displaystyle \sum _{\gamma =1}^k}{g}_{F_{\gamma }}}+{\mu }_3\frac{p_{F_i}}{{\displaystyle \sum _{\gamma =1}^k}{p}_{F_{\gamma }}}\right).$$

(22)

Note that the number of generations and the failure percentage are inversely proportional to the efficiency $E_{F_i}$ as the higher these parameters, the lower its efficiency fitness function.

Table 4. Comparison of fitness functions, with BBM.

${\mathit{F}}_{\mathit{i}}$	Times	Generations	Failures (%)	${\mathit{E}}_{{\mathit{F}}_{\mathit{i}}}$
$F_1$	5.233	121.2	60	0.8731
$F_2$	5.402	108.4	50	0.8870
$F_3$	11.101	117.4	50	0.8584
$F_4$	4.764	109.2	40	0.8995
$F_5$	9.451	109.8	30	0.8885
$F_6$	3.126	63.4	20	0.9433
$F_7$	12.424	121.3	50	0.8511
$F_8$	7.054	77.1	10	0.9309
$F_9$	15.811	87.7	30	0.8682

presents the results of the comparison of the different fitness functions for the BBM space partitioning methodology, in this case $k=9$. We took $\alpha =\beta =0.5$ and each ${\alpha }_i=0.25$. To calculate $E_{F_i}$ the values ${\mu }_1=0.33$, ${\mu }_2=0.33$ and ${\mu }_3=0.34$ were taken for $t_{F_i}$, $g_{F_i}$, and $p_{F_i}$, respectively. Sorting $F_i$ with respect to efficiency, the first five would be $F_6$, $F_8$, $F_4$, $F_5$, and $F_2$. It is noteworthy that of the first three that use only the Hamming distance, only $F_2$ appears.

In the comparison of these functions for the TBB methodology of partitioning the key space and searching in $G_K$, the experiment results are presented in

Table 5. Comparison of fitness functions, with TBB.

${\mathit{F}}_{\mathit{i}}$	Times	Generations	Failures (%)	${\mathit{E}}_{{\mathit{F}}_{\mathit{i}}}$
$F_1$	3.688	83.1	20	0.9278
$F_2$	5.353	109.1	60	0.8633
$F_3$	11.403	122.9	40	0.8536
$F_4$	3.226	67.8	30	0.9240
$F_5$	7.147	83.4	10	0.9235
$F_6$	4.871	96.2	40	0.8939
$F_7$	10.694	113.1	20	0.8840
$F_8$	8.354	92	20	0.9029
$F_9$	16.876	95.7	50	0.8270

. In this case, ordering the functions by their efficiency, the first five would be $F_1$, $F_4$, $F_5$, $F_8$, and $F_6$. Again, a single function appears from the first three, in this case $F_1$, and the others repeat. Note in particular that $F_8$ (the weight of the functions in decimals) is better than $F_3$ (the weight of the functions in binary) in each of the parameters measured in both methodologies.

It is interesting to see what happens if the values of the weights are changed in the functions $F_5$, $F_7$, and $F_9$, which combine the functions with distance in decimals and binary, keeping fixed ${\mu }_1$, ${\mu }_2$, and ${\mu }_3$ for the calculation of $E_{F_i}$. In this sense, in the following group of experiments, the weights were assigned as follows for each methodology: the values were 0.2 and 0.8; first, in each of these three functions, the subfunctions in binary were favored, from which $\alpha =0.8$, $\beta =0.2$ (in $F_5$, $F_7$), ${\alpha }_1={\alpha }_2=0.4$, and ${\alpha }_3={\alpha }_4=0.1$ (in $F_9$; note that this function has two subfunctions with the distance in binary and two in decimals); in this case, we identified the functions as $F_{5b}$, $F_{7b}$, and $F_{9b}$; then, we changed the order of these same weights, and the largest were given to the subfunctions whose distance was in decimals; and we identified the functions for this case as $F_{5d}$, $F_{7d}$, and $F_{9d}$.

For the BBM methodology, the results are presented in

Table 6. Comparison of functions $F_5$, $F_7$, and $F_9$, with BBM.

${\mathit{F}}_{\mathit{i}}$	Times	Generations	Failures (%)	${\mathit{E}}_{{\mathit{F}}_{\mathit{i}}}$
$F_{5b}$	10.247	115	50	0.772
$F_{7b}$	9.131	90.6	40	0.814
$F_{9b}$	20.053	107.4	50	0.728
$F_{5d}$	7.276	83.3	10	0.891
$F_{7d}$	5.921	61.3	0	0.933
$F_{9d}$	13.799	77.5	10	0.862

. Note that according to $E_{F_i}$, the first is $F_{7d}$, followed by $F_{5d}$ and $F_{9d}$.

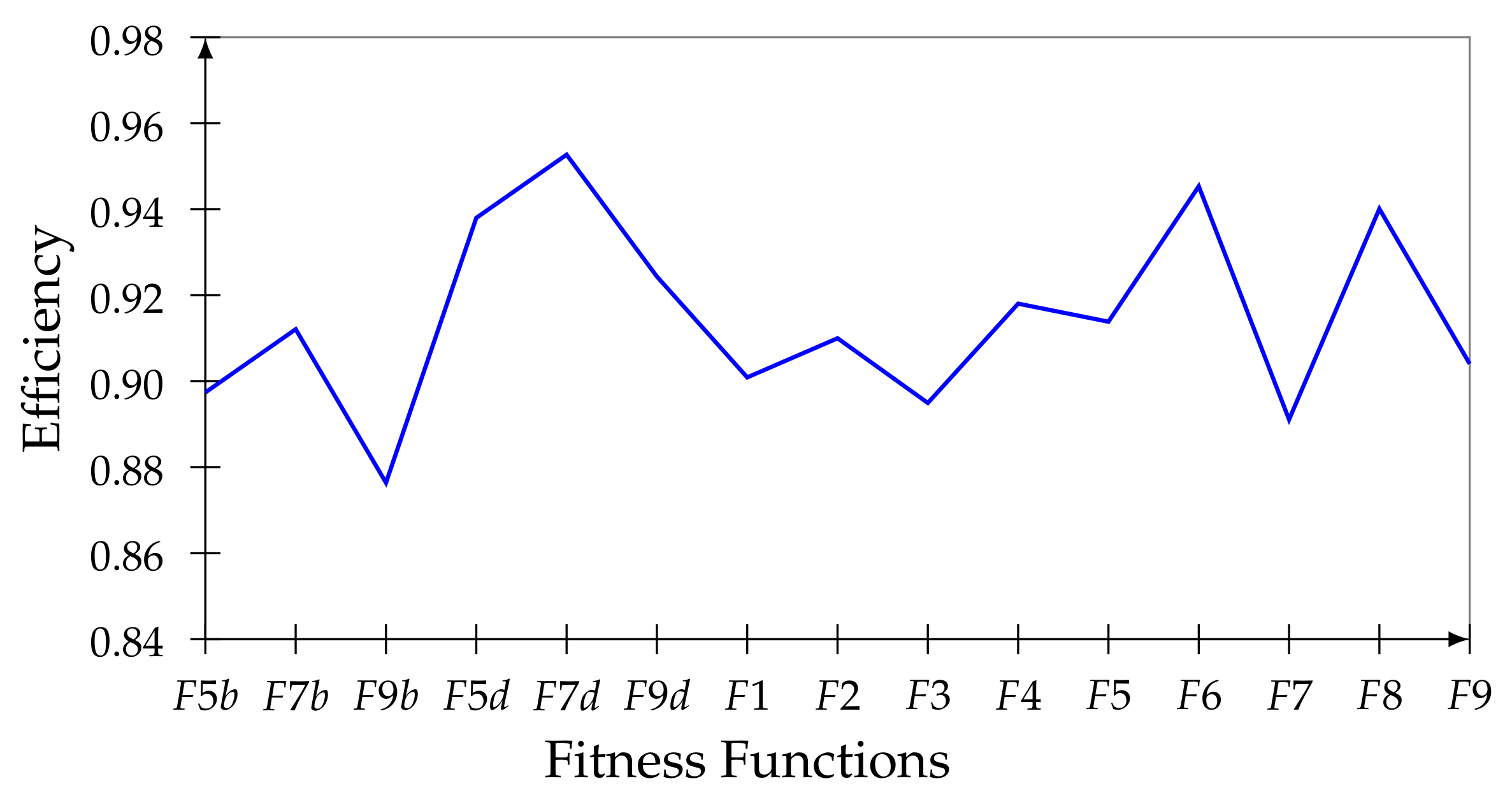
In Figure 2, these results are compared, according to $E_{F_i}$, with those of Table 4, also including the values of $F_5$, $F_7$, and $F_9$. Sorting the functions according to their efficiency, the first five are $F_{7d}$, $F_6$, $F_8$, $F_{5d}$, and $F_{9d}$.

Notice how the best results prevail in the functions with the distance in decimals. In this sense, $F_7$ and $F_9$ (now as $F_{7d}$ and $F_{9d}$) are incorporated into the first ones and three of those that already were in this group in the above experiments, $F_5$ (as $F_{5d})$, $F_6$, and $F_8$.

In the case of the TBB methodology, the results are presented in

Table 7. Comparison of functions $F_5$, $F_7$, and $F_9$, with TBB.

${\mathit{F}}_{\mathit{i}}$	Times	Generations	Failures (%)	${\mathit{E}}_{{\mathit{F}}_{\mathit{i}}}$
$F_{5b}$	9.987	111.5	40	0.845
$F_{7b}$	8.578	86.7	10	0.909
$F_{9b}$	22.500	119.1	50	0.777
$F_{5d}$	8.341	96.9	10	0.905
$F_{7d}$	13.623	141.8	80	0.754
$F_{9d}$	22.183	114.8	30	0.811

. According to efficiency, the first is $F_{7b}$, followed by $F_{5d}$ and $F_{5b}$.

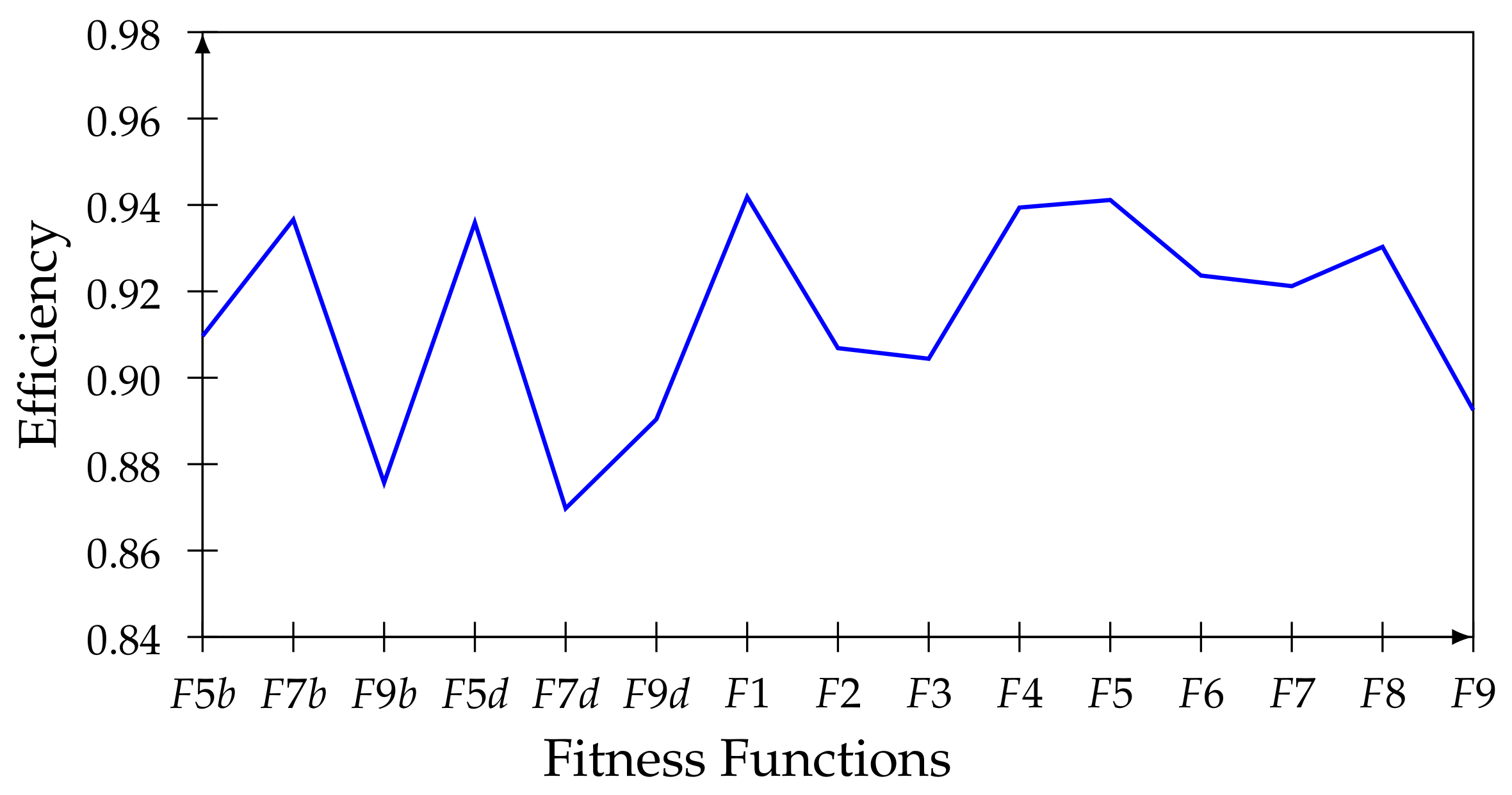
In Figure 3, these results are compared with those of all the functions of Table 5. The first five are now $F_1$, $F_5$, $F_4$, $F_{7b}$, and $F_{5d}$; notice how the functions that contain the distance prevail in decimals and this combined with binary. In the experiments, the best global behavior of the functions with the decimal distance is verified, and specifically in the BBM methodology, where the keys are grouped into intervals according to their decimal position in space, contrary to the other methodology, where the keys of each class are positioned throughout the space.

Note that when comparing Figure 2 and Figure 3, the values of $E_{F_i}$ that are in the tables are not directly compared, but rather, it is necessary to recalculate $E_{F_i}$ taking into account that there are 15 functions. We mean,

$$E_{F_{{\delta }_i}}=1-\left({\mu }_1\frac{t_{F_{{\delta }_i}}}{{\displaystyle \sum _{\gamma =1}^k}{t}_{F_{{\delta }_{\gamma }}}}+{\mu }_2\frac{g_{F_{{\delta }_i}}}{{\displaystyle \sum _{\gamma =1}^k}{g}_{F_{{\delta }_{\gamma }}}}+{\mu }_3\frac{p_{F_{{\delta }_i}}}{{\displaystyle \sum _{\gamma =1}^k}{p}_{F_{{\delta }_{\gamma }}}}\right),$$

(23)

where ${\delta }_i\in \{1,\dots ,9,5b,5d,7b,7d,9b,9d\}$, $i=\overline{1,\dots ,k}$, and, $k=15$.

4. Conclusions

In this article, various aspects of some parameters of the GA for the attack on block ciphers were studied. In the first place, a way of estimating the time that the GA takes in a given number of generations was proposed, having an average of the time that this algorithm takes in one generation. This study is important to jointly evaluate different parameters and make the best decisions according to the computational capacity, available time, and an adequate selection of the size of the search space when using the BBM and TBB methodologies. On the other hand, several fitness functions were proposed with favorable results in the experiments with respect to the fitness functions using only the Hamming distance. In this sense, it was found that the fitness functions that use the decimal distance, in general, are more efficient than those that use only the Hamming distance, especially in the methodology BBM.

As future work, several directions are possible. Similar studies can be carried out with the GA working with other parameters, such as varying the crossover probability and mutation rate and making comparisons regarding the percentage of success of the method. It is also recommended to explore other heuristic techniques and to evaluate the use of whole space partitioning methods so that the methods work closed on the subsets. In the same way, it is also recommended to investigate the combined use with some other tools such as machine learning, deep learning, ANN, SVM, and GEP.