Wigner Function Non-Classicality Induced in a Charge Qubit Interacting with a Dissipative Field Cavity
Abstract
:1. Introduction
2. Dissipative Qubit-Cavity System
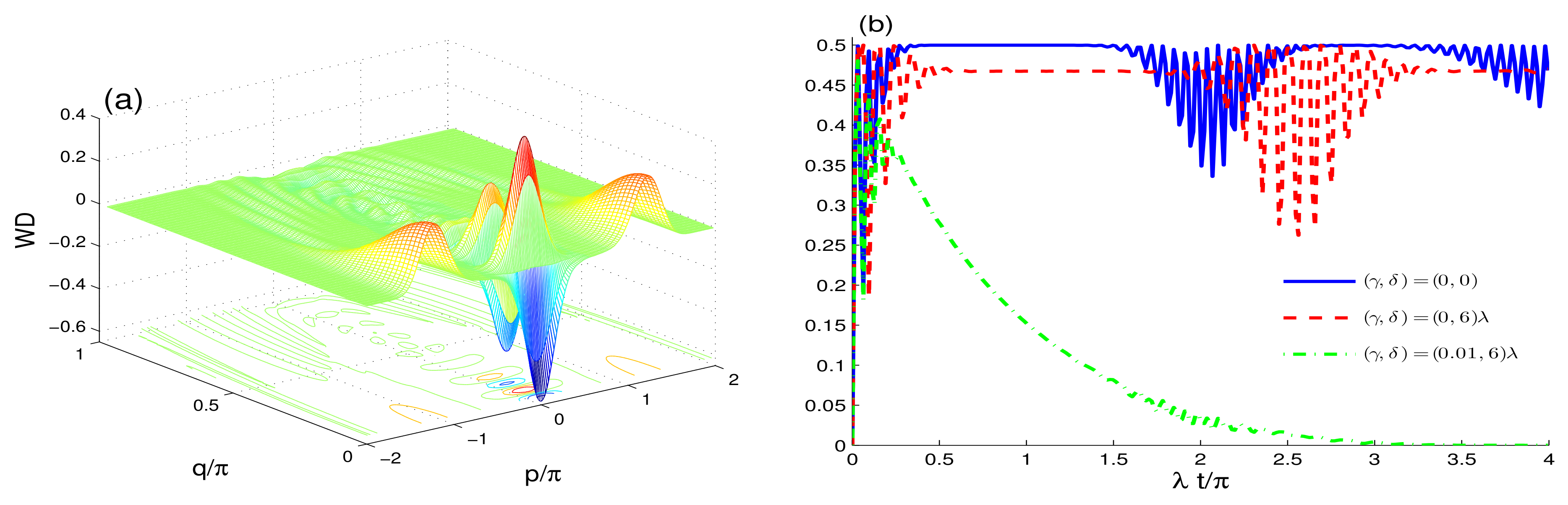
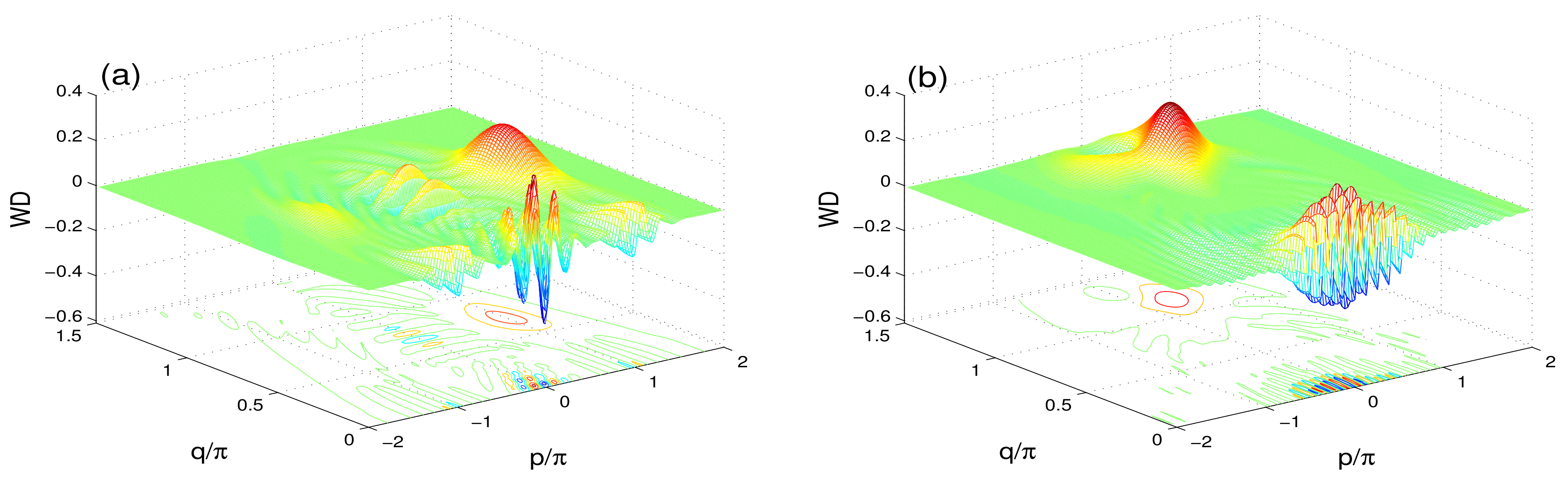
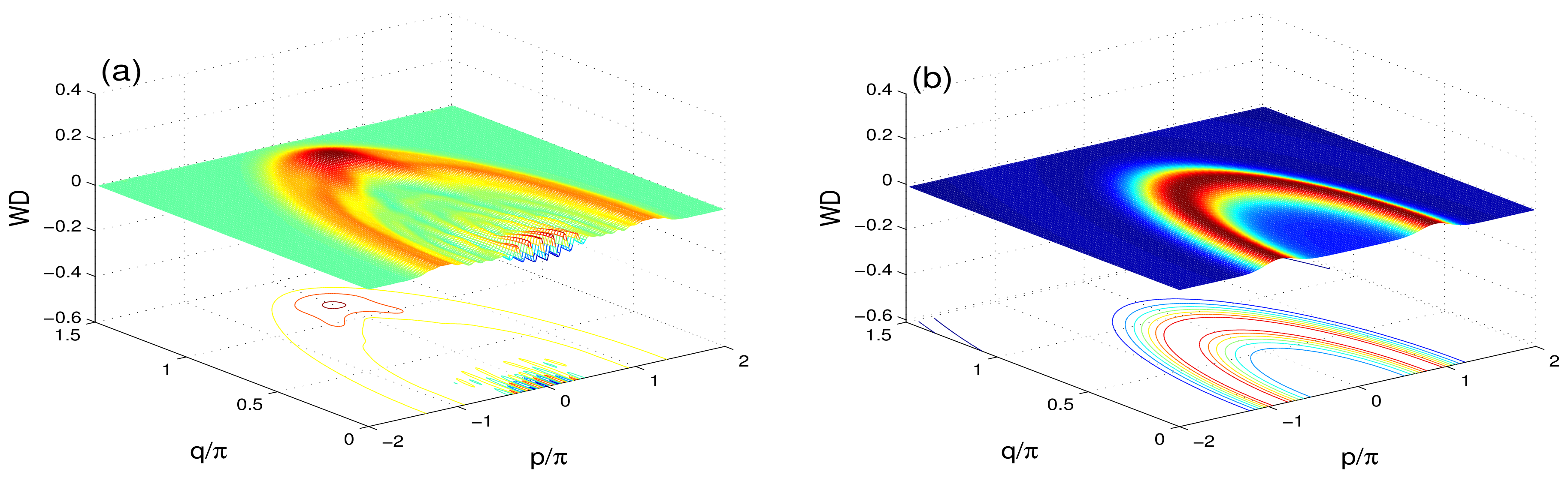
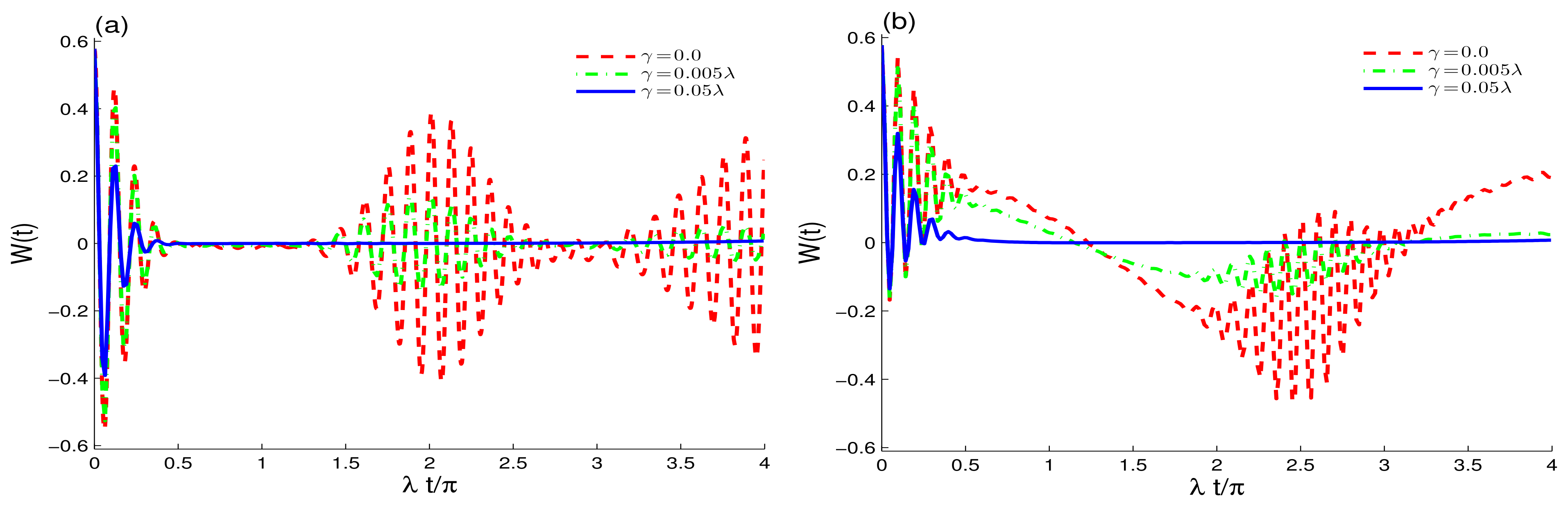
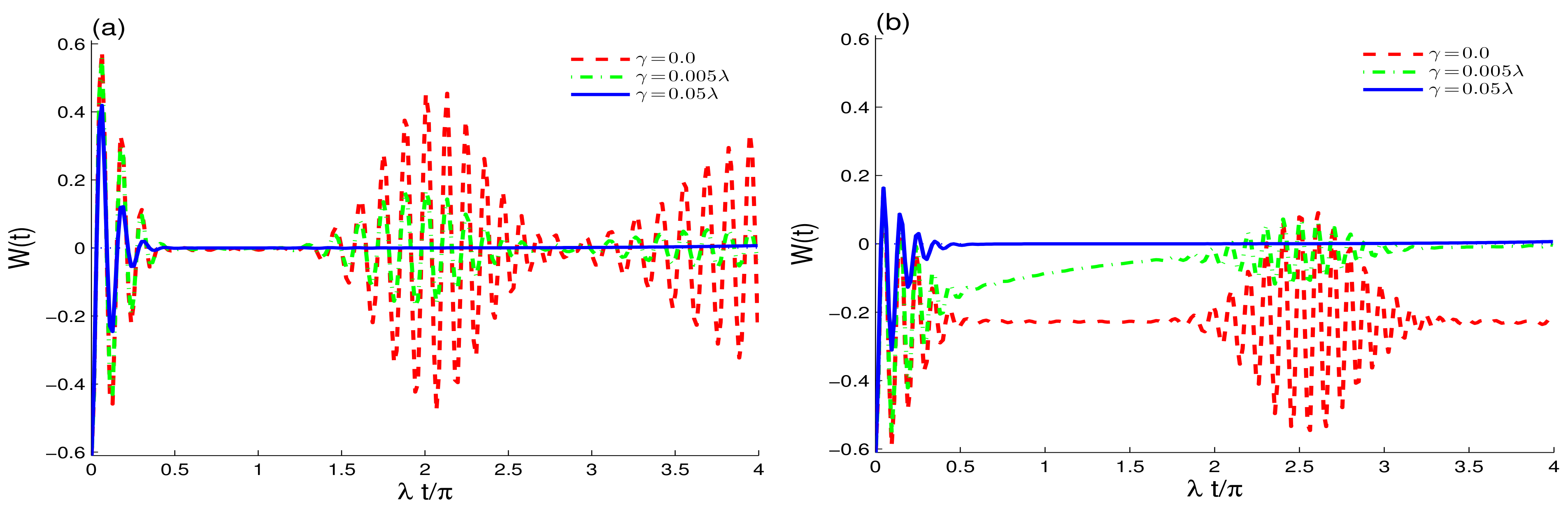
3. Wigner Distribution (WD)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roman, S.; Kossakowski, A.; Ohya, M. Information Dynamics and Open Systems: Classical and Quantum Approach; Springer: New York, NY, USA, 1997. [Google Scholar]
- Attal, S.; Joye, A.; Alain, P. Open Quantum Systems II: The Markovian Approach; Springe: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Pikovski, I.; Zych, M.; Costa, F.; Brukner, C. Time dilation in quantum systems and decoherence. New J. Phys. 2017, 19, 025011. [Google Scholar] [CrossRef]
- Eric, R.B.; Peter, J.R. Quantum decoherence in mixed quantum-classical systems: Nonadiabatic processes. J. Chem. Phys. 1995, 103, 8130. [Google Scholar]
- Eleuch, H.; Rotter, I. Clustering of exceptional points and dynamical phase transitions. Phys. Rev. A 2016, 93, 042116. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.-B.A.; Eleuch, H.; Ooi, C.H.R. Quantum coherence and entanglement partitions for two driven quantum dots inside a coherent micro cavity. Phys. Lett. A 2019, 383, 125905. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Hessian, H.A.; Eleuch, H. Robust correlations in a dissipative two-qubit system interacting with two coupled fields in a non-degenerate parametric amplifier. Quantum Inf. Process. 2019, 18, 327. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H.; Ooi, C.H.R. Non-locality Correlation in Two Driven Qubits Inside an Open Coherent Cavity: Trace Norm Distance and Maximum Bell Function. Sci. Rep. 2019, 9, 19632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sete, A.E.; Eleuch, H. High-efficiency quantum state transfer and quantum memory using a mechanical oscillator. Phys. Rev. A 2015, 91, 032309. [Google Scholar] [CrossRef] [Green Version]
- Ikram, M.; Li, F.L.; Zubairy, M.S. Disentanglement in a two-qubit system subjected to dissipation environments. Phys. Rev. A 2007, 75, 062336. [Google Scholar] [CrossRef] [Green Version]
- Brauner, T. Spontaneous Symmetry Breaking and Nambu-Goldstone Bosons in Quantum Many-Body Systems. Symmetry 2010, 2, 609–657. [Google Scholar] [CrossRef] [Green Version]
- Arraut, I. The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry 2019, 11, 803. [Google Scholar] [CrossRef] [Green Version]
- Nambu, Y. Spontaneous Breaking of Lie and Current Algebras. J. Stat. Phys. 2004, 115, 7. [Google Scholar] [CrossRef]
- Nambu, Y. From Yukawa’s Pion to Spontaneous Symmetry Breaking. J. Phys. Soc. Jpn. 2007, 76, 111002. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasrniot, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246. [Google Scholar] [CrossRef]
- Wilming, H.; Kastoryano, M.J.; Werner, A.H.; Eisert, J. Emergence of spontaneous symmetry breaking in dissipative lattice systems. J. Math. Phys. 2017, 58, 033302. [Google Scholar] [CrossRef] [Green Version]
- Hannukainen, J.; Larson, J. Dissipation-driven quantum phase transitions and symmetry breaking. Phys. Rev. A 2018, 98, 042113. [Google Scholar] [CrossRef] [Green Version]
- Booker, C.; Buča, B.; Jaksch, D. Non-stationarity and dissipative time crystals: Spectral properties and finite-size effects. New J. Phys. 2020, 22, 085007. [Google Scholar] [CrossRef]
- Garbe, L.; Wade, P.; Minganti, F.; Shammah, N.; Felicetti, S.; Nori, F. Dissipation.induced bistability in the two.photon Dicke model. Sci. Rep. 2020, 10, 13408. [Google Scholar] [CrossRef] [PubMed]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 119, 48. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarsahan, E.C. Completely positive semigroups of n-level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Redfield, A. The theory of relaxation processes. In Advances in Magnetic Resonance, Advances in Magnetic and Optical Resonance; Waugh, J.S., Ed.; Academic Press: Cambridge, MA, USA, 1965; Volume 1. [Google Scholar]
- Puri, R.R. Mathematical Methods of Quantum Optics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Milburn, G.J. Intrinsic decoherence in quantum mechanics. Phys. Rev. A 1991, 44, 5401. [Google Scholar] [CrossRef] [Green Version]
- Cahill, K.E.; Glauber, R.J. Density Operators and Quasiprobability Distributions. Phys. Rev. 1969, 117, 1882. [Google Scholar] [CrossRef] [Green Version]
- Wigner, E.P. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 47, 749. [Google Scholar] [CrossRef]
- Hillery, M.; Ò’Connell, R.F.; Scully, M.O.; Wigner, E.P. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121. [Google Scholar] [CrossRef]
- Mohamed, A.-B.; Eleuch, H. Quasi-probability information in a coupled two.qubit system interacting non.linearly with a coherent cavity under intrinsic decoherence. Sci. Rep. 2020, 10, 13240. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, M.; Faghihi, M.J.; Safari, H. Wigner function and entanglement dynamics of a two-atom two-mode nonlinear Jaynes-Cummings model. J. Opt. Soc. Am. B 2017, 34, 1884. [Google Scholar] [CrossRef]
- Ren, G.; Zhang, W. Nonclassicality of superposition of photon-added two-mode coherent states. Optik 2019, 181, 191. [Google Scholar] [CrossRef]
- Harder, G.; Silberhorn, C.; Rehacek, J.; Hradil, Z.; Motka, L.; Stoklasa, B.; Sánchez-Soto, L.L. Local sampling of the Wigner function at telecom wavelength with loss-tolerant detection of photon statistics. Phys. Rev. Lett. 2016, 116, 133601. [Google Scholar] [CrossRef] [Green Version]
- Weiher, K.; Agudelo, E.; Bohmann, M. Conditional nonclassical field generation in cavity QED. Phys. Rev. A 2019, 100, 043812. [Google Scholar] [CrossRef] [Green Version]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, P. Separability criterion and inseparable mixed states with positive partial transposition. Phys. Lett. A 1997, 232, 333. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef] [Green Version]
- Banerji, A.; Singh, R.P.; Bandyopadhyay, A. Entanglement measure using Wigner function: Case of generalized vortex state formed by multiphoton subtraction. Optics Commun. 2014, 330, 85–90. [Google Scholar] [CrossRef] [Green Version]
- Arkhipov, I.I.; Barasiński, A.; Svozilík, J. Negativity volume of the generalized Wigner function as an entanglement witness for hybrid bipartite states. Sci. Rep. 2018, 8, 16955. [Google Scholar] [CrossRef] [Green Version]
- Albarelli, F.; Genoni, M.G.; Paris, M.G.A. Resource theory of quantum non-Gaussianity and Wigner negativity. Phys. Rev. A 2018, 98, 052350. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Cai, Y.; Zheng, Z.; Barral, D.; Zhang, Y.g.; Xiao, M.; Bencheikh, K. Non-Gaussian nature and entanglement of spontaneous parametric nondegenerate triple-photon generation. Phys. Rev. A 2021, 103, 013704. [Google Scholar] [CrossRef]
- Walschaers, M.; Fabre, C.; Parigi, V.; Treps, N. Entanglement and Wigner Function Negativity of Multimode Non-Gaussian States. PRL 2017, 119, 183601. [Google Scholar] [CrossRef] [Green Version]
- Douce, T.; Eckstein, A.; Walborn, S.P.; Khoury, A.Z.; Ducci, S.; Keller, A.; Coudreau1, T.; Milman, P. Direct measurement of the biphoton Wigner function through two-photon interference. Sci. Rep. 2013, 3, 3530. [Google Scholar] [CrossRef] [Green Version]
- You, J.Q.; Nori, F. Superconducting Circuits and Quantum Information. Phys. Today 2005, 58, 42. [Google Scholar] [CrossRef] [Green Version]
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A.; Homid, A.H. Efficient protocol of N-bit discrete quantum Fourier transform via transmon qubits coupled to a resonator. Quantum Inf. Process. 2014, 13, 475. [Google Scholar] [CrossRef]
- Abovyan, G.A.; Kryuchkyan, Y.G. Quasienergies and dynamics of a superconducting qubit in a time-modulated field. Phys. Rev. A 2013, 88, 033811. [Google Scholar] [CrossRef] [Green Version]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.-X.; Wei, L.F.; Nori, F. Generation of nonclassical photon states using a superconducting qubit in a microcavity. Europhys. Lett. 2004, 67, 941. [Google Scholar] [CrossRef] [Green Version]
- Hofheinz, M.; Weig, E.M.; Ansmann, M.; Bialczak, R.C.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Wang, H.; Martinis, J.M.; Cleland, A.N. Generation of Fock states in a superconducting quantum circuit. Nature 2008, 454, 310. [Google Scholar] [CrossRef]
- DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.; Schuster, D.I.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.M.; et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240. [Google Scholar] [CrossRef]
- Vlastakis, B.; Kirchmair, G.; Leghtas, Z.; Nigg, S.E.; Frunzio, L.; Girvin, S.M.; Mirrahimi, M.; Devoret, M.H.; Schoelkopf, R.J. Deterministically Encoding Quantum Information Using 100-Photon Schrödinger Cat States. Science 2013, 342, 607. [Google Scholar] [CrossRef]
- Riste, D.; Dukalski, M.; Watson, C.A.; de Lange, G.; Tiggelman, M.J.; Blanter, Y.M.; Lehnert, K.W.; Schouten, R.N.; DiCarlo, L. Deterministic entanglement of superconducting qubits by parity measurement and feedback. Nature 2013, 502, 350. [Google Scholar] [CrossRef] [Green Version]
- Teh, R.Y.; Sun, F.-X.; Polkinghorne, R.E.S.; He, Q.Y.; Gong, Q.; Drummond, P.D.; Reid, M.D. Dynamics of transient cat states in degenerate parametric oscillation with and without nonlinear Kerr interactions. Phys. Rev. A 2020, 101, 043807. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.-G.; Goan, H.-S.; Wang, J.-S.; Zhang, R. Nonclassical thermal-state superpositions: Analytical evolution law and decoherence behavior. Opt. Commun. 2018, 411, 15. [Google Scholar] [CrossRef]
- Mohamed, A.-B.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar]
- Mohamed, A.-B.A.; Eleuch, H.; Obada, A.-S.F. Obada: Influence of the Coupling between Two Qubits in an Open Coherent Cavity: Nonclassical Information via Quasi-Probability Distributions. Entropy 2019, 21, 1137. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.-B.A. Long-time death of nonclassicality of a cavity field interacting with a charge qubit and its own reservoir. Phys. Lett. A 2010, 374, 4115. [Google Scholar]
- Liu, Y.-X.; Wei, L.F.; Nori, F. Preparation of macroscopic quantum superposition states of a cavity field via coupling to a superconducting charge qubit. Phys. Lett. A 2005, 71, 063820. [Google Scholar] [CrossRef] [Green Version]
- Pashkin, Y.A.; Yamamoto, T.; Astafiev, O.; Nakamura, Y.; Averin, D.V.; Tsai, J.S. Quantum oscillations in two coupled charge qubits. Nature 2003, 421, 823. [Google Scholar]
- Abdalla, M.S.; Khalil, E.M.; Obada, A.-S.F. Obada: Exact treatment of the Jaynes-Cummings model under the action of an external classical field. Ann. Phys. 2011, 326, 2486. [Google Scholar] [CrossRef]
- Barnett, S.M.; Knight, P.L. Dissipation in a fundamental model of quantum optical resonance. Phys. Rev. A 1986, 33, 2444. [Google Scholar] [CrossRef]
- Puri, R.R.; Agarwal, G.S. Finite-Q cavity electrodynamics: Dynamical and statistical aspects. Phys. Rev. A 1987, 35, 3433. [Google Scholar]
- Moya-Cessa, H.; Knight, P.L. Series representation of quantum-field quasiprobabilities. Phys. Rev. A 1993, 48, 2479. [Google Scholar] [CrossRef]
- Hessian, H.A.; Mohamed, A.-B.A. Quasi-Probability Distribution Functions for a Single Trapped Ion Interacting with a Mixed Laser Field. Laser Phys. 2008, 18, 1217. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.-B.A.; Khalil, E.M.; AL-Rezami, A.Y.; Eleuch, H. Wigner Function Non-Classicality Induced in a Charge Qubit Interacting with a Dissipative Field Cavity. Symmetry 2021, 13, 802. https://doi.org/10.3390/sym13050802
Mohamed A-BA, Khalil EM, AL-Rezami AY, Eleuch H. Wigner Function Non-Classicality Induced in a Charge Qubit Interacting with a Dissipative Field Cavity. Symmetry. 2021; 13(5):802. https://doi.org/10.3390/sym13050802
Chicago/Turabian StyleMohamed, Abdel-Baset A., Eied M. Khalil, Afrah Y. AL-Rezami, and Hichem Eleuch. 2021. "Wigner Function Non-Classicality Induced in a Charge Qubit Interacting with a Dissipative Field Cavity" Symmetry 13, no. 5: 802. https://doi.org/10.3390/sym13050802
APA StyleMohamed, A.-B. A., Khalil, E. M., AL-Rezami, A. Y., & Eleuch, H. (2021). Wigner Function Non-Classicality Induced in a Charge Qubit Interacting with a Dissipative Field Cavity. Symmetry, 13(5), 802. https://doi.org/10.3390/sym13050802





