Quantum Information in Neural Systems
Abstract
1. Introduction
2. Basic Postulates of Quantum Mechanics
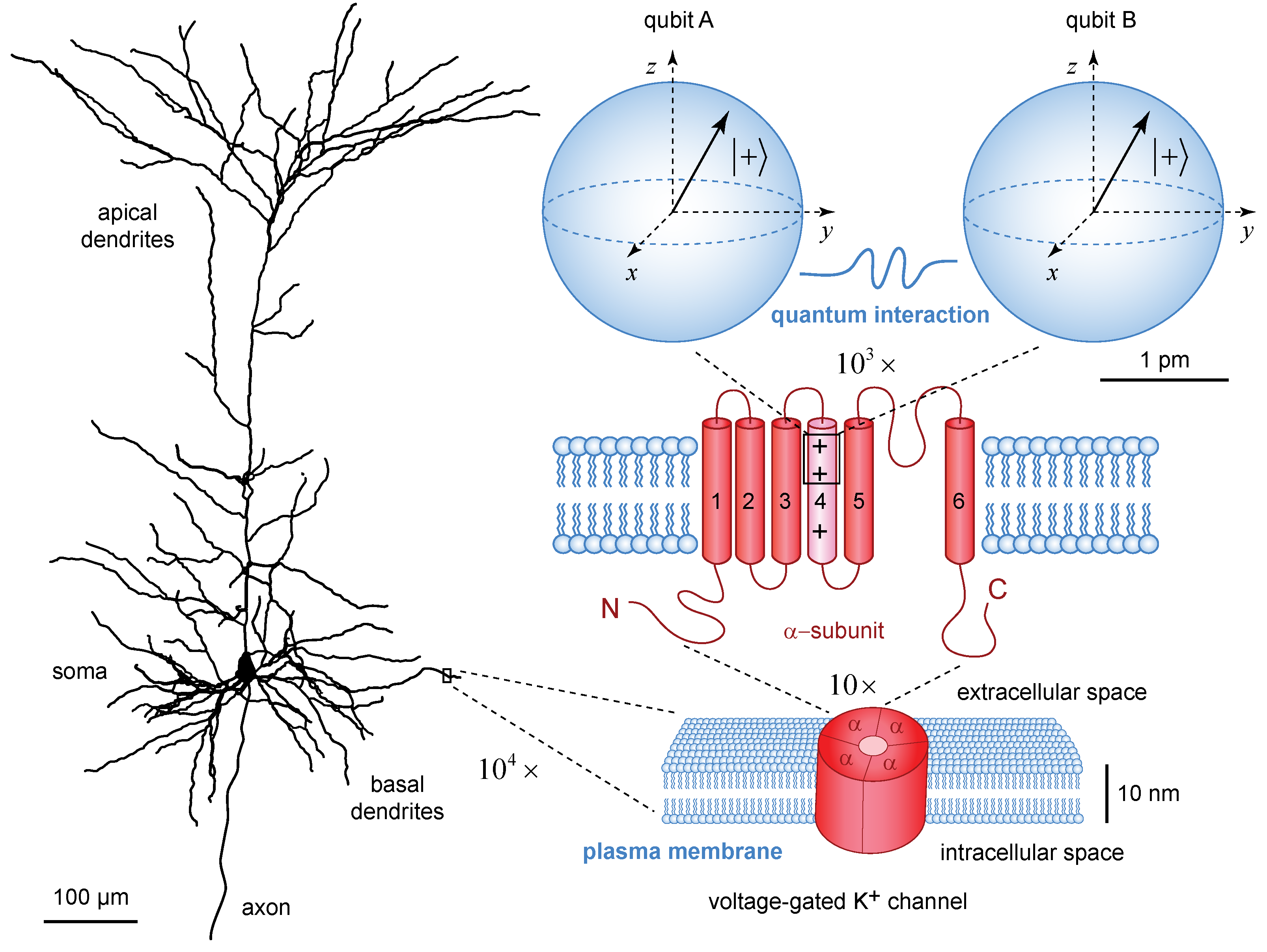
3. Minimal Quantum Toy Model
3.1. Hamiltonian of the Toy Model
3.2. Energy Eigenstates and Eigenvalues of the Toy Model
3.3. Quantum Dynamics of the State Vector
4. Quantum Dynamic Timescale
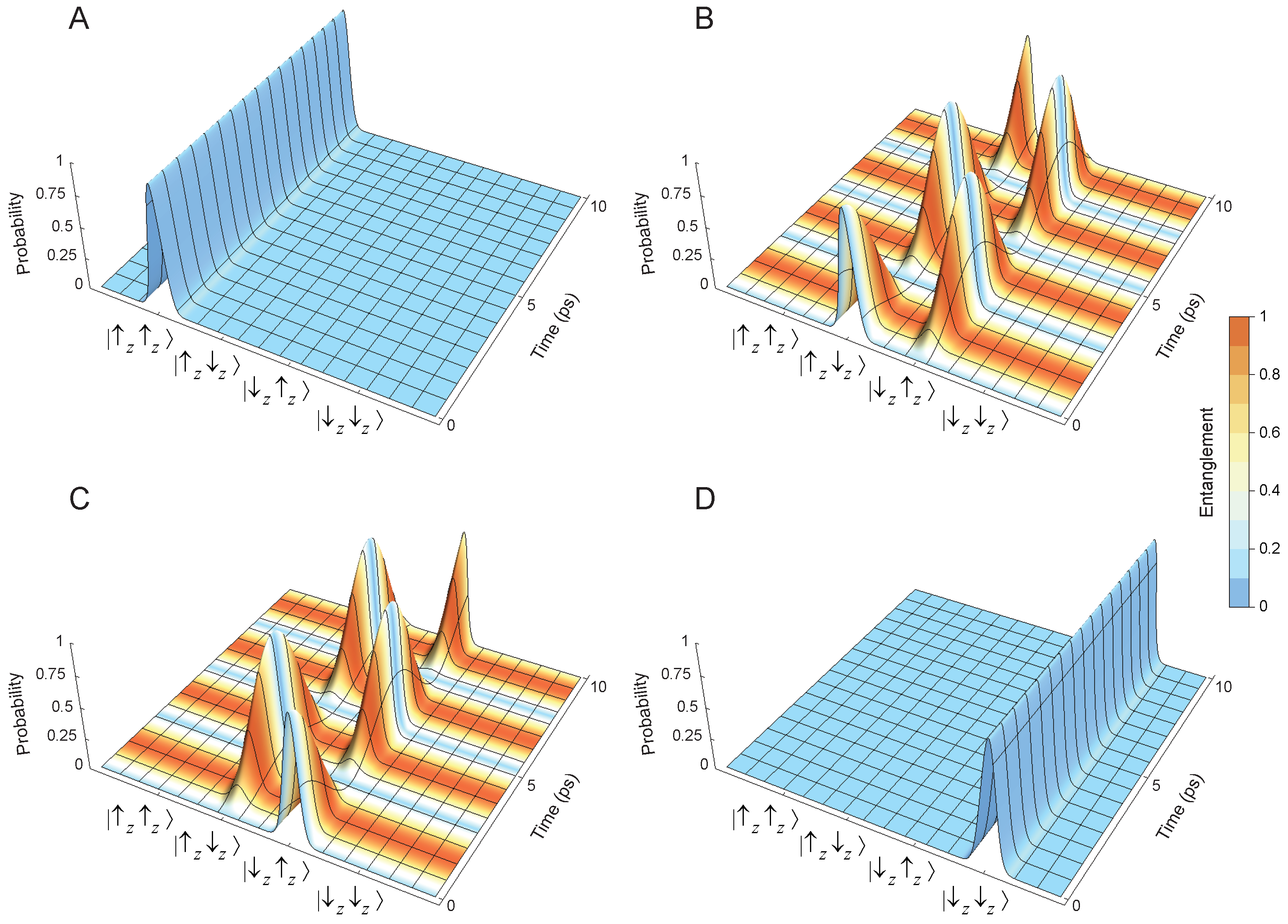
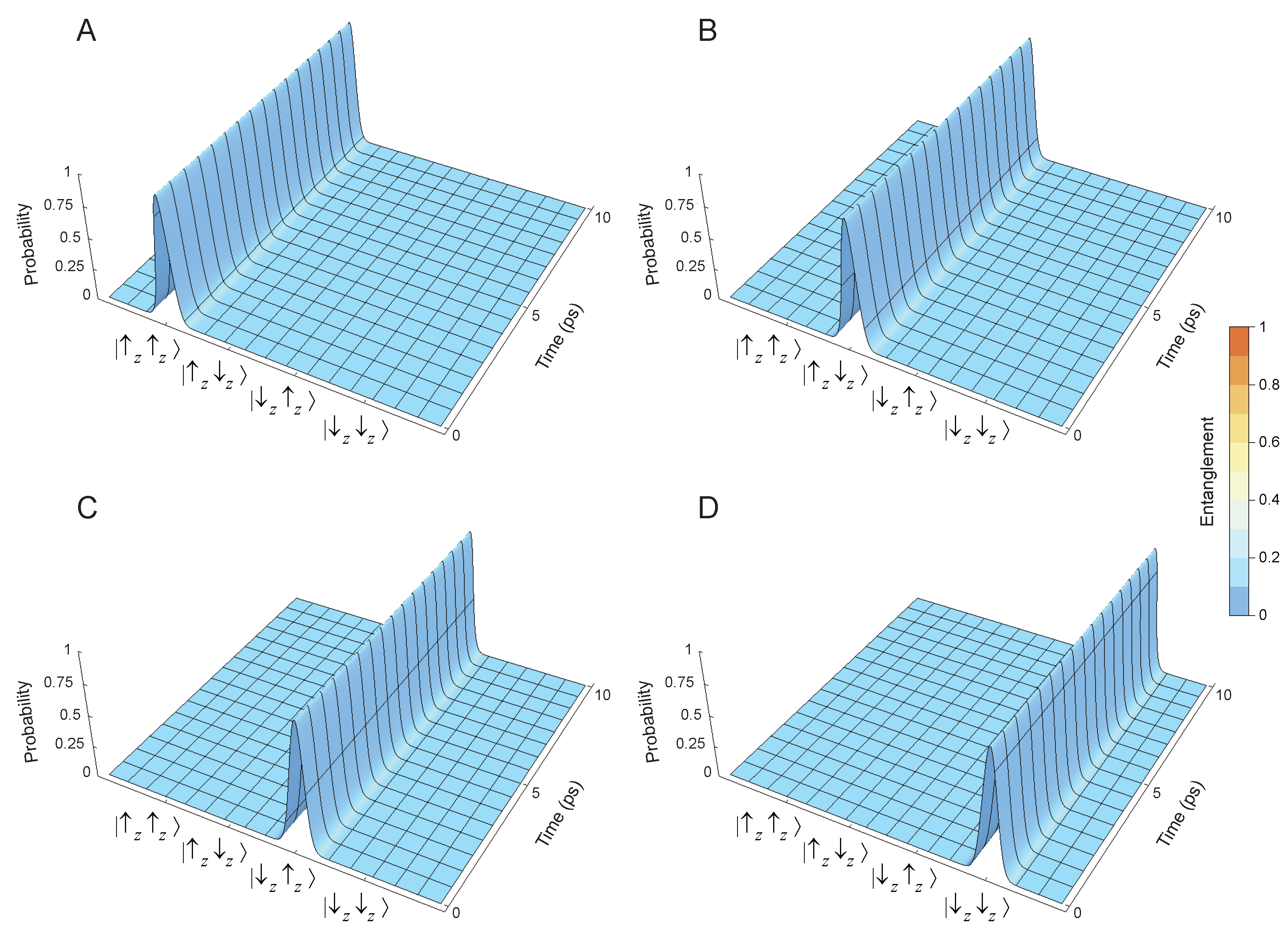
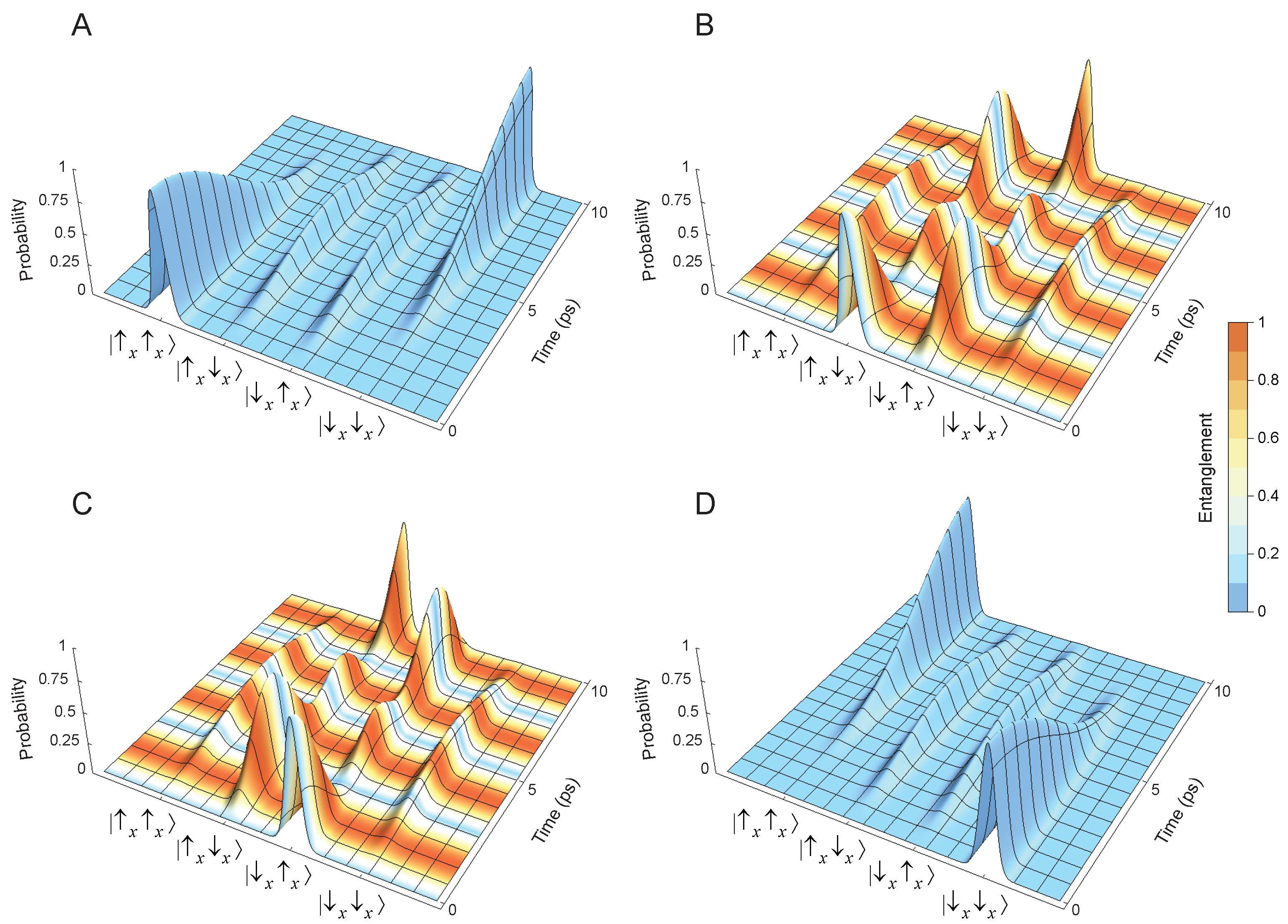
5. Quantum Entanglement
6. Quantum Coherence
7. Measurement of Quantum Observables
7.1. Quantum Observables in Spin Basis
7.2. Complementary Observables in Spin Basis
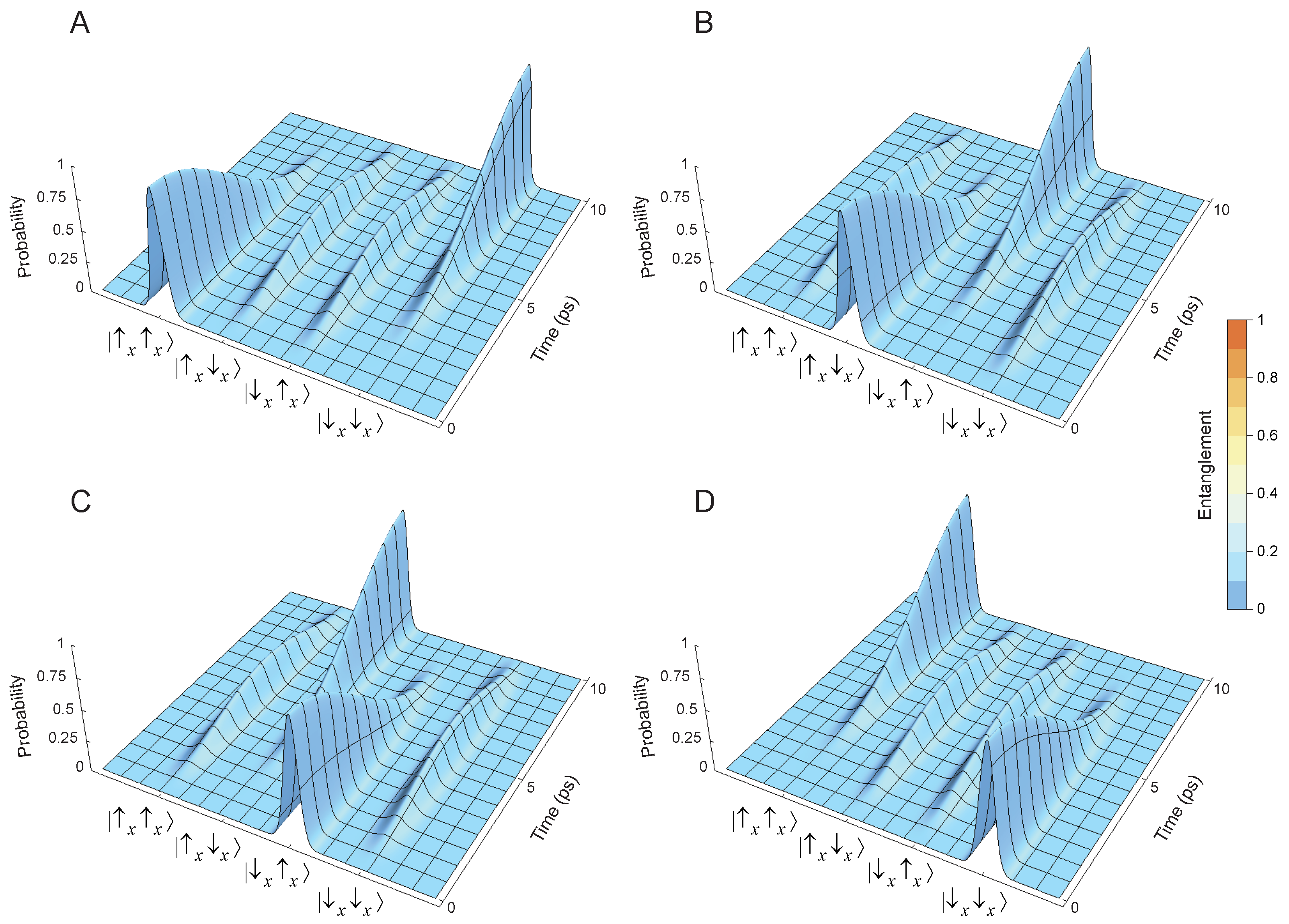
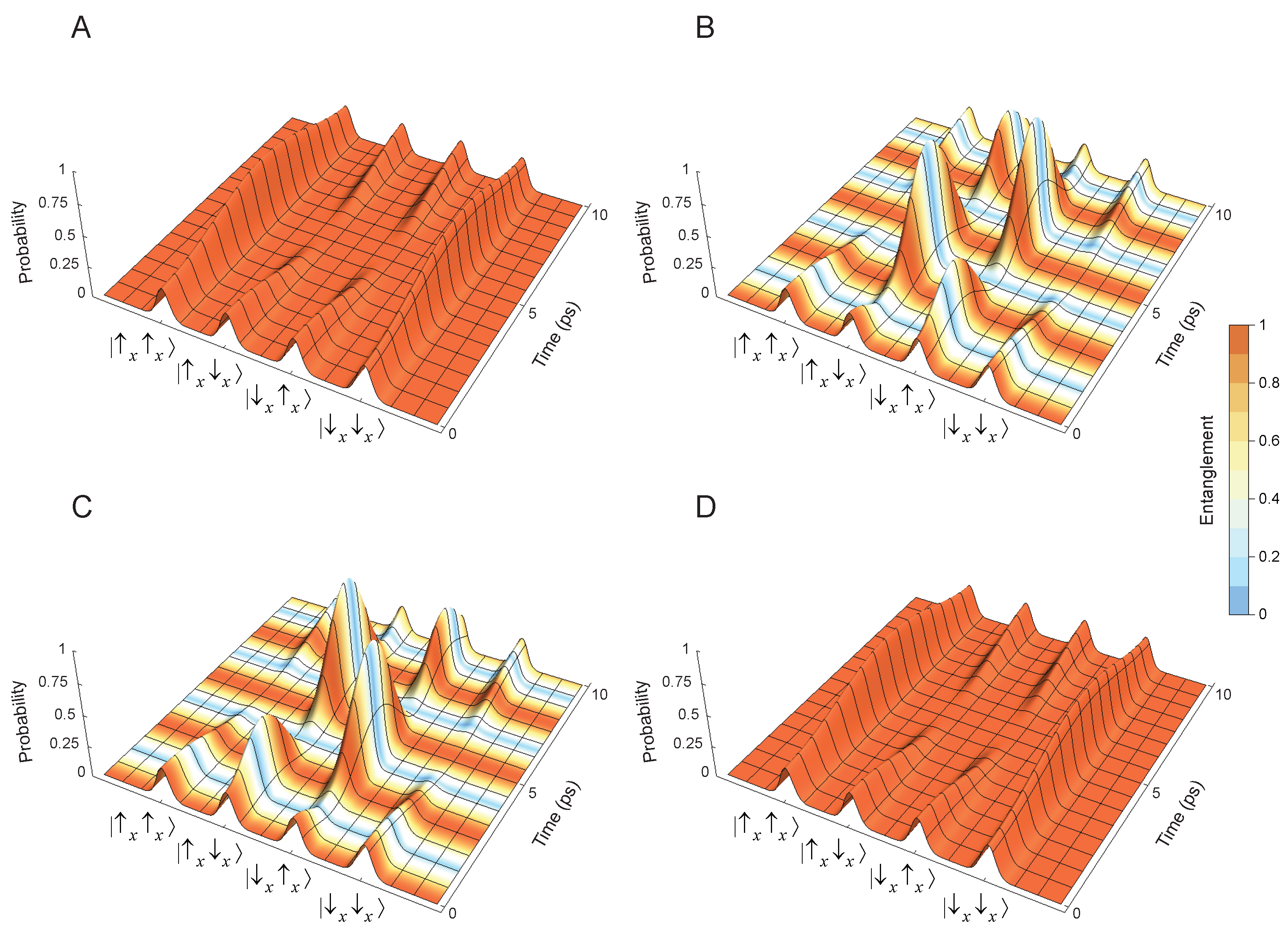
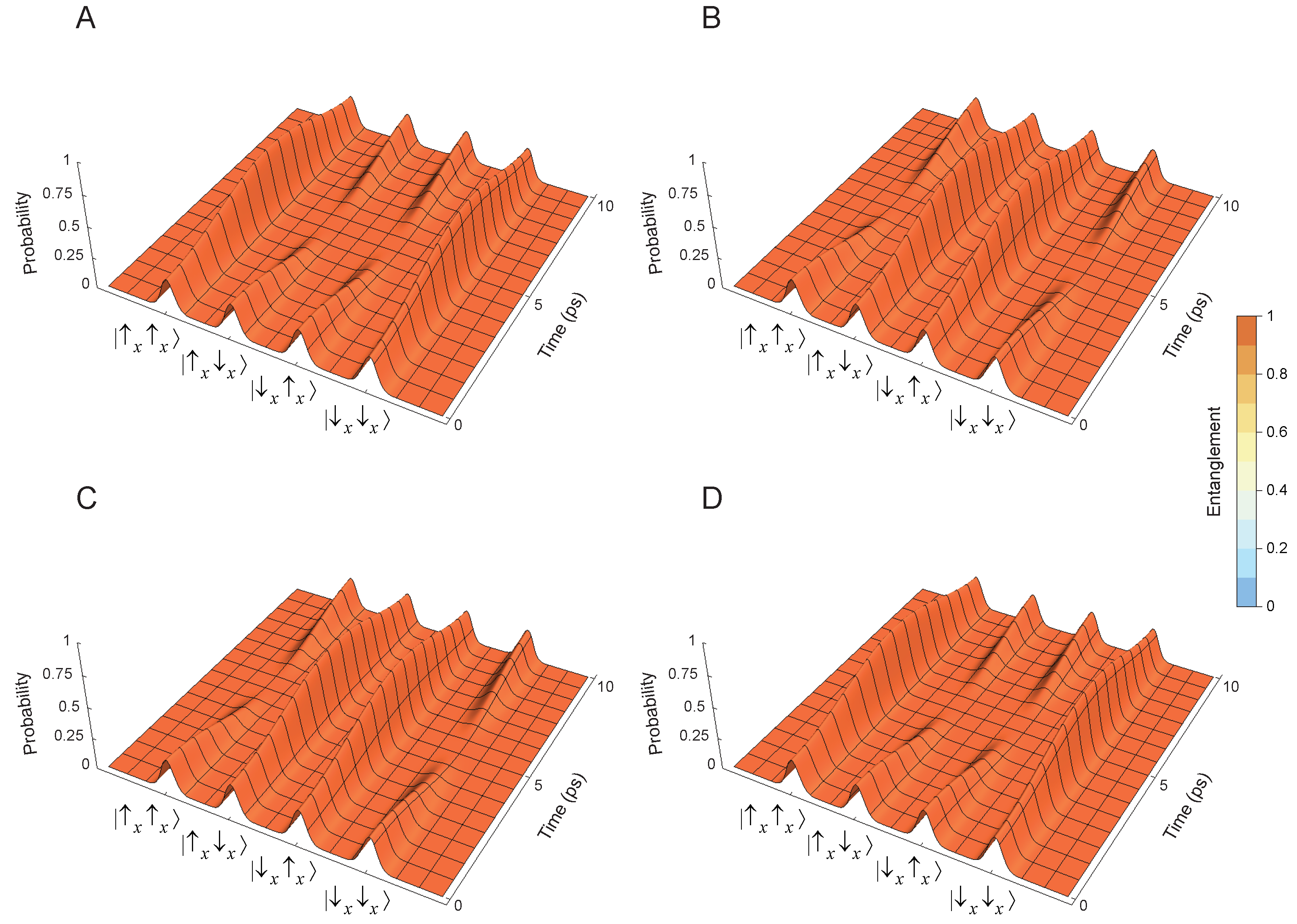
8. Quantum Dynamics of Initial Quantum Entangled States
9. Quantum Coherence Cannot Bind Conscious Experiences
10. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duhem, P.M.M. The Aim and Structure of Physical Theory; Princeton University Press: Princeton, NJ, USA, 1954. [Google Scholar]
- Susskind, L.; Hrabovsky, G. The Theoretical Minimum: What You Need to Know to Start Doing Physics; Basic Books: New York, NY, USA, 2013. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Mechanics: Volume 1, 2nd ed.; Course of Theoretical Physics; Pergamon: Oxford, UK, 1960. [Google Scholar]
- Kibble, T.W.B.; Berkshire, F.H. Classical Mechanics, 5th ed.; Imperial College Press: London, UK, 2004. [Google Scholar] [CrossRef]
- Morin, D. Introduction to Classical Mechanics: With Problems and Solutions; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Strauch, D. Classical Mechanics: An Introduction; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Georgiev, D.D. Quantum no-go theorems and consciousness. Axiomathes 2013, 23, 683–695. [Google Scholar] [CrossRef]
- Georgiev, D.D. Quantum Information and Consciousness: A Gentle Introduction; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Georgiev, D.D. Chalmers’ principle of organizational invariance makes consciousness fundamental but meaningless spectator of its own drama. Act. Nerv. Super. 2019, 61, 159–164. [Google Scholar] [CrossRef]
- Darwin, C. From So Simple a Beginning: The Four Great Books of Charles Darwin (The Voyage of the Beagle, On the Origin of Species, the Descent of Man, the Expression of the Emotions in Man and Animals); W. W. Norton & Company: New York, NY, USA, 2006. [Google Scholar]
- Dawkins, R. The Ancestor’s Tale: A Pilgrimage to the Dawn of Life; Weidenfeld & Nicolson: London, UK, 2004. [Google Scholar]
- Hodge, R. Evolution: The History of Life on Earth; Genetics & Evolution, Facts on File: New York, NY, USA, 2009. [Google Scholar]
- James, W. Are we automata? Mind 1879, 4, 1–22. [Google Scholar] [CrossRef]
- James, W. The Principles of Psychology; Henry Holt and Company: New York, NY, USA, 1890; Volume 1. [Google Scholar]
- Popper, K.R.; Eccles, J.C. The Self and its Brain: An Argument for Interactionism; Routledge & Kegan Paul: London, UK, 1983. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef]
- Feynman, R.P. QED: The Strange Theory of Light and Matter; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M.L. The Feynman Lectures on Physics. Volume III. Quantum Mechanics; California Institute of Technology: Pasadena, CA, USA, 2013. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; Oxford University Press: Oxford, UK, 1967. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Susskind, L.; Friedman, A. Quantum Mechanics: The Theoretical Minimum. What You Need to Know to Start Doing Physics; Basic Books: New York, NY, USA, 2014. [Google Scholar]
- Mermin, N.D. Is the moon there when nobody looks? Reality and the quantum theory. Phys. Today 1985, 38, 38–47. [Google Scholar] [CrossRef]
- Georgiev, D.D. Inner privacy of conscious experiences and quantum information. BioSystems 2020, 187, 104051. [Google Scholar] [CrossRef]
- Georgiev, D.D. Quantum information theoretic approach to the mind–brain problem. Prog. Biophys. Mol. Biol. 2020, 158, 16–32. [Google Scholar] [CrossRef]
- Tegmark, M. Importance of quantum decoherence in brain processes. Phys. Rev. E 2000, 61, 4194–4206. [Google Scholar] [CrossRef] [PubMed]
- Everett, H., III. “Relative state” formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Albert, D.Z. Quantum Mechanics and Experience; Harvard University Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Lockwood, M. ‘Many minds’ interpretations of quantum mechanics. Br. J. Philos. Sci. 1996, 47, 159–188. [Google Scholar] [CrossRef]
- Hemmo, M.; Pitowsky, I. Probability and nonlocality in many minds interpretations of quantum mechanics. Br. J. Philos. Sci. 2003, 54, 225–243. [Google Scholar] [CrossRef][Green Version]
- Wigner, E.P. Remarks on the mind-body question. In The Collected Works of Eugene Paul Wigner. Volume 6B: Philosophical Reflections and Syntheses; Mehra, J., Ed.; Springer: Berlin, Germany, 1995; pp. 247–260. [Google Scholar] [CrossRef]
- Squires, E. Conscious Mind in the Physical World; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar] [CrossRef]
- Barrett, J.A. The single-mind and many-minds versions of quantum mechanics. Erkenntnis 1995, 42, 89–105. [Google Scholar] [CrossRef]
- Whitaker, A. Many worlds, many minds, many views. Rev. Int. Philos. 2000, 54, 369–391. [Google Scholar]
- Fuchs, C.A.; Schack, R. Quantum-Bayesian coherence. Rev. Mod. Phys. 2013, 85, 1693–1715. [Google Scholar] [CrossRef]
- Frauchiger, D.; Renner, R. Quantum theory cannot consistently describe the use of itself. Nat. Commun. 2018, 9, 3711. [Google Scholar] [CrossRef]
- Pusey, M.F. An inconsistent friend. Nat. Phys. 2018, 14, 977–978. [Google Scholar] [CrossRef]
- Bhaumik, M.L. Is the quantum state real in the Hilbert space formulation? Quanta 2020, 9, 37–46. [Google Scholar] [CrossRef]
- Bellman, R. Introduction to Matrix Analysis. In Classics in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1987; Volume 19. [Google Scholar]
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 1926, 28, 1049–1070. [Google Scholar] [CrossRef]
- Schrödinger, E. Collected Papers on Wave Mechanics; Blackie & Son: London, UK, 1928. [Google Scholar]
- Berezin, F.A.; Shubin, M.A. The Schrödinger Equation; Mathematics and its Applications; Kluwer: Dordrecht, The Netherlands, 1991. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Akhiezer, N.I.; Glazman, I.M. Theory of Linear Operators in Hilbert Space; Dover Publications: New York, NY, USA, 1993. [Google Scholar]
- Birman, M.S.; Solomjak, M.Z. Spectral Theory of Self-Adjoint Operators in Hilbert Space; Mathematics and Its Applications; D. Reidel: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Dirac, P.A.M. The quantum theory of the electron. Proc. R. Soc. Lond. Ser. A 1928, 117, 610–624. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the electron. Part II. Proc. R. Soc. Lond. Ser. A 1928, 118, 351–361. [Google Scholar] [CrossRef]
- Thaller, B. The Dirac Equation; Texts and Monographs in Physics; Springer: Berlin, Germany, 1992. [Google Scholar] [CrossRef]
- Hayashi, M.; Ishizaka, S.; Kawachi, A.; Kimura, G.; Ogawa, T. Introduction to Quantum Information Science; Graduate Texts in Physics; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Busch, P. Is the quantum state (an) observable? In Potentiality, Entanglement and Passion-at-a-Distance: Quantum Mechanical Studies for Abner Shimony; Boston Studies in the Philosophy of Science; Cohen, R.S., Horne, M., Stachel, J., Eds.; Kluwer: Dordrecht, The Netherlands, 1997; Volume 2, pp. 61–70. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Levitin, L.B. Energy cost of information transmission (along the path to understanding). Phys. D Nonlinear Phenom. 1998, 120, 162–167. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Kolev, S.K.; Cohen, E.; Glazebrook, J.F. Computational capacity of pyramidal neurons in the cerebral cortex. Brain Res. 2020, 1748, 147069. [Google Scholar] [CrossRef] [PubMed]
- Georgiev, D.D.; Glazebrook, J.F. On the quantum dynamics of Davydov solitons in protein α-helices. Phys. A Stat. Mech. Appl. 2019, 517, 257–269. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Glazebrook, J.F. Quantum tunneling of Davydov solitons through massive barriers. Chaos Sol. Fractals 2019, 123, 275–293. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Glazebrook, J.F. Quantum transport and utilization of free energy in protein α-helices. Adv. Quantum Chem. 2020, 82, 253–300. [Google Scholar] [CrossRef]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. I. J. Chem. Phys. 1956, 24, 966–978. [Google Scholar] [CrossRef]
- Vos, M.H.; Rappaport, F.; Lambry, J.C.; Breton, J.; Martin, J.L. Visualization of coherent nuclear motion in a membrane protein by femtosecond spectroscopy. Nature 1993, 363, 320–325. [Google Scholar] [CrossRef]
- Beck, F.; Eccles, J.C. Quantum aspects of brain activity and the role of consciousness. Proc. Natl. Acad. Sci. USA 1992, 89, 11357–11361. [Google Scholar] [CrossRef] [PubMed]
- Beck, F. Can quantum processes control synaptic emission? Int. J. Neural Syst. 1996, 7, 343–353. [Google Scholar] [CrossRef]
- Beck, F.; Eccles, J.C. Quantum processes in the brain: A scientific basis of consciousness. Cogn. Stud. Bull. Jpn. Cogn. Sci. Soc. 1998, 5, 95–109. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of probability relations between separated systems. Math. Proc. Camb. Philos. Soc. 1935, 31, 555–563. [Google Scholar] [CrossRef]
- Gudder, S.P. A theory of entanglement. Quanta 2020, 9, 7–15. [Google Scholar] [CrossRef]
- Miszczak, J.A. Singular value decomposition and matrix reorderings in quantum information theory. Int. J. Mod. Phys. C 2011, 22, 897–918. [Google Scholar] [CrossRef]
- Gudder, S.P. Quantum entanglement: Spooky action at a distance. Quanta 2020, 9, 1–6. [Google Scholar] [CrossRef]
- Tegmark, M. Consciousness as a state of matter. Chaos Sol. Fractals 2015, 76, 238–270. [Google Scholar] [CrossRef]
- Qureshi, T. Coherence, interference and visibility. Quanta 2019, 8, 24–35. [Google Scholar] [CrossRef]
- Qureshi, T. Interference visibility and wave-particle duality in multipath interference. Phys. Rev. A 2019, 100, 042105. [Google Scholar] [CrossRef]
- Bera, M.N.; Qureshi, T.; Siddiqui, M.A.; Pati, A.K. Duality of quantum coherence and path distinguishability. Phys. Rev. A 2015, 92, 012118. [Google Scholar] [CrossRef]
- Streltsov, A.; Kampermann, H.; Wölk, S.; Gessner, M.; Bruß, D. Maximal coherence and the resource theory of purity. New J. Phys. 2018, 20, 053058. [Google Scholar] [CrossRef]
- Finkelstein, J. Definition of decoherence. Phys. Rev. D 1993, 47, 5430–5433. [Google Scholar] [CrossRef] [PubMed]
- Zeh, H.D. What is achieved by decoherence? In New Developments on Fundamental Problems in Quantum Physics; Ferrero, M., van der Merwe, A., Eds.; Springer: Dordrecht, The Netherlands, 1997; pp. 441–451. [Google Scholar] [CrossRef]
- Zeh, H.D. The meaning of decoherence. In Decoherence: Theoretical, Experimental, and Conceptual Problems; Blanchard, P., Joos, E., Giulini, D., Kiefer, C., Stamatescu, I.O., Eds.; Springer: Berlin, Germany, 2000; pp. 19–42. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Born, M. Statistical interpretation of quantum mechanics. Science 1955, 122, 675–679. [Google Scholar] [CrossRef]
- Campbell, J.E. On a law of combination of operators (second paper). Proc. Lond. Math. Soc. 1897, 29, 14–32. [Google Scholar] [CrossRef]
- Baker, H.F. Alternants and continuous groups. Proc. Lond. Math. Soc. 1905, 3, 24–47. [Google Scholar] [CrossRef]
- Strichartz, R.S. The Campbell–Baker–Hausdorff–Dynkin formula and solutions of differential equations. J. Funct. Anal. 1987, 72, 320–345. [Google Scholar] [CrossRef]
- Nishimura, H. The Baker–Campbell–Hausdorff formula and the Zassenhaus formula in synthetic differential geometry. Math. Appl. 2013, 2, 61–91. [Google Scholar] [CrossRef]
- Yang, C.H.; Leon, R.C.C.; Hwang, J.C.C.; Saraiva, A.; Tanttu, T.; Huang, W.; Camirand Lemyre, J.; Chan, K.W.; Tan, K.Y.; Hudson, F.E.; et al. Operation of a silicon quantum processor unit cell above one kelvin. Nature 2020, 580, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Roth, E.F.; Lunde, I.; Boysen, G.; Genefke, I.K. Torture and its treatment. Am. J. Public Health 1987, 77, 1404–1406. [Google Scholar] [CrossRef]
- Rasmussen, O.V.; Lunde, I. The treatment and rehabilitation of victims of torture. Int. J. Ment. Health 1989, 18, 122–130. [Google Scholar] [CrossRef]
- Reyes, H. The worst scars are in the mind: Psychological torture. Int. Rev. Red Cross 2007, 89, 591–617. [Google Scholar] [CrossRef]
- Raz, M. Alone again: John Zubek and the troubled history of sensory deprivation research. J. Hist. Behav. Sci. 2013, 49, 379–395. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Int. J. Comput. Math. 1968, 2, 157–168. [Google Scholar] [CrossRef]
- Shen, A.; Uspensky, V.A.; Vereshchagin, N.K. Kolmogorov Complexity and Algorithmic Randomness; American Mathematical Society: Providence, RI, USA, 2017. [Google Scholar]
- Marshall, I.N. Consciousness and Bose–Einstein condensates. New Ideas Psychol. 1989, 7, 73–83. [Google Scholar] [CrossRef]
- Susskind, L. Three Lectures on Complexity and Black Holes; Springer Briefs in Physics; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Lowe, J.P.; Peterson, K. Quantum Chemistry, 3rd ed.; Academic Press: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Rieke, F.; Warland, D.; de Ruyter van Steveninck, R.; Bialek, W. Spikes: Exploring the Neural Code; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Zhang, W.; Linden, D.J. The other side of the engram: Experience-driven changes in neuronal intrinsic excitability. Nat. Rev. Neurosci. 2003, 4, 885–900. [Google Scholar] [CrossRef]
- Citri, A.; Malenka, R.C. Synaptic plasticity: Multiple forms, functions, and mechanisms. Neuropsychopharmacology 2007, 33, 18–41. [Google Scholar] [CrossRef]
- Chklovskii, D.B. Synaptic connectivity and neuronal morphology: Two sides of the same coin. Neuron 2004, 43, 609–617. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, D.D. Quantum Information in Neural Systems. Symmetry 2021, 13, 773. https://doi.org/10.3390/sym13050773
Georgiev DD. Quantum Information in Neural Systems. Symmetry. 2021; 13(5):773. https://doi.org/10.3390/sym13050773
Chicago/Turabian StyleGeorgiev, Danko D. 2021. "Quantum Information in Neural Systems" Symmetry 13, no. 5: 773. https://doi.org/10.3390/sym13050773
APA StyleGeorgiev, D. D. (2021). Quantum Information in Neural Systems. Symmetry, 13(5), 773. https://doi.org/10.3390/sym13050773





