Abstract
High blood pressure (BP) may lead to further health complications if not monitored and controlled, especially for critically ill patients. Particularly, there are two types of blood pressure monitoring, invasive measurement, whereby a central line is inserted into the patient’s body, which is associated with infection risks. The second measurement is cuff-based that monitors BP by detecting the blood volume change at the skin surface using a pulse oximeter or wearable devices such as a smartwatch. This paper aims to estimate the blood pressure using machine learning from photoplethysmogram (PPG) signals, which is obtained from cuff-based monitoring. To avoid the issues associated with machine learning such as improperly choosing the classifiers and/or not selecting the best features, this paper utilized the tree-based pipeline optimization tool (TPOT) to automate the machine learning pipeline to select the best regression models for estimating both systolic BP (SBP) and diastolic BP (DBP) separately. As a pre-processing stage, notch filter, band-pass filter, and zero phase filtering were applied by TPOT to eliminate any potential noise inherent in the signal. Then, the automated feature selection was performed to select the best features to estimate the BP, including SBP and DBP features, which are extracted using random forest (RF) and k-nearest neighbors (KNN), respectively. To train and test the model, the PhysioNet global dataset was used, which contains 32.061 million samples for 1000 subjects. Finally, the proposed approach was evaluated and validated using the mean absolute error (MAE). The results obtained were 6.52 mmHg for SBS and 4.19 mmHg for DBP, which show the superiority of the proposed model over the related works.
1. Introduction
High blood pressure (BP) is one of the acute health concerns that may lead to hazardous health complications such as atherosclerosis, clots, heart attack, stroke, kidney diseases, and dementia [1]. Therefore, monitoring the blood pressure is one of the critical health practices that should be monitored to avoid further complications [2,3]. Such monitoring becomes necessary for critically ill patients admitted to intensive care units (ICUs). For critically ill patients, there are two types of blood pressure monitoring. The first one is aneroid blood pressure, whereby the doctors use a cuff, stethoscope or squeeze bulb. This blood pressure monitor is used to monitor the blood pressure within predefined time intervals (i.e., twice a day, every hour or every 15 min) depending on the severity of the case [1]. The second type is called invasive arterial BP measurement procedure, whereby the blood pressure is monitored dynamically with no delay to produce a continuous reading [4,5]. One of the techniques used in invasive BP measurement is the central venous catheter, also known as the central line [6,7]. Such a central line is an intravascular access device or catheter that is inserted through one of the major vessels to be placed at or near the heart [8]. It can be inserted either centrally or peripherally. A central line can be placed at the pulmonary artery, inferior vena cava, superior vena cava, internal jugular veins, brachiocephalic veins, subclavian veins, common iliac veins, external iliac veins or femoral veins [9]. However, this technique is associated with infection risk, such as the central line associated-bloodstream infection (CLABSI) [4]. CLABSI occurs when bacteria or other pathogens enter a patient’s central line and cause an infection associated with increased morbidity, mortality, and healthcare costs. An increase in the number of line accesses is associated with a higher probability of CLABSI [5]. Moreover, the arterial pressure waveform, produced by the central line, is a complex wave that reflects the sum of a series of mechanical pressure signals of different frequencies.
With all the aforementioned issues of invasive arterial measurement, monitoring the BP without harming the patient health is highly required. Therefore, a non-invasive, cuff-less, continuous BP monitoring through wearable devices become an iterating topic for researchers and doctors [10]. Wearable blood pressure monitors allow frequent blood pressure measurements (ideally continuous beat-by-beat monitoring of blood pressure) with minimal stress on the patient [10]. Moreover, there are many initiatives to use signal processing and machine learning algorithms to capture essential human vital signs using wearable sensors with the advent of automated sensors [11,12]. Out of this vital health, signs are the BP estimation using PPG signals, which has become more realistic [13,14,15,16]. A PPG waveform is a simple and inexpensive optical technique that detects changes in blood volume in the microvascular bed of tissue. It is also used noninvasively to determine the measurements at the surface of the skin [11]. Usually, the pulse oximeter is placed on the index finger of the patient to measure mean blood oxygen saturation levels in ICU [17]. This PPG signal is a time-variant signal originating from Aoyagi [18] and Yoshiya [19]. The PPG signal measures blood volume changes by calculating the light absorption changes on the skin when the skin is illuminated. The PPG signal from any position on the skin can be divided into the oscillating (AC) and steady-state (DC) components and their amplitudes depend on the structure and flow of the vascular bed [11]. The AC component is divided by the DC component to normalize the signal and then scale the waveform within a specific range [20].
Several works have been discussed in the literature to measure the BP from PPG signals [21,22,23,24,25]. These works span from calculating the normalized BP waveforms for the PPG [20,26] using Fast Fourier Transform to the use of linear and neural network system identification techniques to correlate BP and PPG [12]. The authors in [12] relied on auto-regression to extract waveform features and provided the justification for this paper’s machine learning approach as it confirmed the link between BP and PPG waveforms. Other techniques have relied on multiple signal inputs, namely integrating the ECG and PPG waveform data to produce a reliably accurate derivation of BP [20].
Moreover, another direction in measuring BP from PPG is to extract the influential features of PPG through signal processing to produce a vector of features, then apply machine learning to infer the function in terms of the blood pressure variables: Systolic blood pressure (SBP) and diastolic blood pressure (DBP) [27]. Many works in the literature used the conventional machine-learning algorithms to measure BP from PPG [28,29,30,31]. However, conventional machine learning techniques suffer from different issues. For instance, no algorithm can achieve good performance on all possible issues [32]. Thus, this paper employed a tree-based pipeline optimization tool (TPOT) approach that automatically designs and optimizes machine learning pipelines for a given problem domain without any need for human intervention [33] or calibration. This approach automates the whole process of BP estimation, starting from choosing the best ML classifier and ending by automating the feature selection and construction process, which results in better accuracy, as presented in Section 4. Hence, this approach can be implemented in medical wearable devices where there is a need for developing an alternative to conventional BP monitoring using cuff-less, easy-to-use, fast, and cost-effective devices for controlling and lowering the physical harm of cardiovascular diseases (CVDs) to the human body [34]. On the other hand, designing an effective machine learning pipeline is often a time-consuming effort, which generally requires considerable experience with machine learning algorithms, professional knowledge of the problem domain, and brute force search [35,36,37]. In response to the aforementioned issues, the need to automate the feature extraction steps and select the suitable machine learning algorithm is based on the dataset fulfilled by employing TPOT. Aside from that, automated machine learning can enhance the accuracy and save time and effort by optimizing a series of feature extractors, preprocessors, and ML models to maximize the classification/regression accuracy for cuffless blood pressure estimation.
Therefore, this paper aims to build an automated machine learning model using TPOT to estimate the blood pressure from the photoplethysmography signals. TPOT maintains a balance between high performance and low model complexity [29]. As a result, the pipelines learned by TPOT consist of a relatively small number of operators (e.g., in the single digits) that can still meet or exceed the performance of competing state-of-the-art ML approaches. Hence, this study’s experimental results demonstrate the potential for high accuracy BP estimation that can be acquired at a low-cost, continuous, and noninvasively from the patient beyond their ICU stay. Significantly, the results achieved were evaluated and approved based on BHS and AAMI standards.
The rest of this paper is structured as follows: Section 2 discusses the background and related works, and Section 3 describes the dataset and the proposed approach used in this study. The results and analysis are discussed in Section 4. Finally, Section 5 includes the conclusion and the future work of the study.
2. Background and Related Works
Several methods were proposed in the literature to estimate BP from PPG. Over the different studies, PPG, when calibrated, expresses great opportunities to monitor BP variations utilizing the various bio features, which in turn brings incredible health and economic benefits. Some algorithms [38,39] integrate the waveform analysis and PPG biometrics, which have been evaluated in subjects of various ages, heights, and weights to estimate BP without calibration in certain populations. When calibrated, it shows great potential to serially monitor BP fluctuation, bringing tremendous economic and health benefits. Another study [40] suggested a bio-inspired and precise mathematical model estimating the systolic BP (SBP) and the diastolic BP (DBP) from the PPG physiological signal sampling time-series. The authors developed a smart method for measuring BP through careful neural and mathematical analysis of PPG signals. In addition, some studies estimate SBP and DBP levels utilizing the pulse transit time (PTT) [41,42], as well as a combination of heart rate and paroxysmal atrial tachycardia (PAT) [43]. The combination presented an enhancement over PTT alone. In [12], the authors measured the BP by implementing a beat-to-beat optical BP using only PPG from the fingertips. Many other studies have examined different PPG signal characteristics for various applications [44,45,46]. Various groups utilized these features for SBP and DBP measurements, therefore, there is still plenty of space for enhancement since many previous attempts rely on wearable sensors and conventional ML. Meanwhile, it has been proven that automated machine learning (AutoML) is more effective and provides better performance. Another direction in this field is estimating BP from PPG through an artificial neural network (ANN) [20,29], whereby the key features such as amplitudes and cardiac component phases have been extracted using a fast Fourier transformation (FFT). Subsequently, these extracted features were used to train the ANN model. The ANN model was trained with more than 170,000 waveforms from 69 patients to improve the fitting accuracy of BP. Furthermore, due to the recent advancement in deep learning, estimating BP from PPG using deep learning became feasible by enhancing the estimation accuracy. Therefore, the authors in [47] addressed the issue of reducing accuracy due to the necessity of regular calibration in current models for BP estimation from PPG. In their model [47], a deep recurrent neural network (DRNN) with long short-term memory (LSTM) is utilized to construct a model for the time-series BP data, whereby PPG and electrocardiogram (ECG) have been taken as inputs, and PTT with some other characteristics were utilized as predictors to estimate BP. According to the authors in [47], this approach demonstrated enhancements in BP prediction compared to other existing approaches where it achieved the root mean square error (RMSE) of 3.90 and 2.66 mmHg for SBP and DBP, respectively. The findings indicate that modeling the BP dynamics’ temporal dependencies increases the long-term BP prediction accuracy dramatically [47]. In addition, the authors in [48] investigated, with fair results, the likelihood of utilizing raw PPG data to detect arrhythmias using wearable devices in real-time, demonstrating the possibility of using the raw PPG signal as inputs for deep learners (RNN-LSTM). Their approach achieved a receiver operator characteristic (ROC) curve of 0.9999, with false positive and false negative rates both below 2 × 10−3. This approach achieved a sufficient result, however, it is time-consuming and required an expert to understand the raw PPG data of the subjects. Likewise, the authors have developed a novel Spectro temporal deep neural network [STDNN] in [39], whereby the PPG signal and its first and second derivatives were taken as inputs. Authors in [39] have attempted to extract the PPG signal from BP using a deep neural network (DLN) and based on the MIMIC III database belonging to 510 subjects. Therefore, the study employed MAE to conduct cross-validation experiments, achieving 9.43 mmHg for SBP and 6.88 mmHg for DBP. Comparatively, the support vector machine (SVM) method for continuous blood pressure estimation from a PPG signal presented better precision in [49] than the linear regression [50,51] and ANN methods. The results in [49] show that the mean error was 11.6415 ± 8.2022 mmHg for systolic BP and 7.617 ± 6.7837 mmHg for diastolic BP based on a large sample data, while the results achieved using ANN were 11.8984 ± 10.180 mmHg for SBP and 13.94 ± 11.24 for DBP. In [51], the 2-Element Windkessel model was used to approximate the overall peripheral resistance and arterial compliance of an individual using PPG functions, followed by linear regression to simulate the arterial blood pressure. The experimental findings on a regular hospital dataset yielded absolute errors of 0.78 ± 13.01 and 0.59 ± 10.23 mmHg for systolic and diastolic blood pressure values, respectively. A similar approach was suggested in [50], where the findings of the experiments show that the average error in measuring BP is less than 10% of the currently available optical BP tracking system.
A time-consuming approach was suggested in [52] for estimating SBP and DBP based on back-propagation error neural networks. Several techniques were implemented to reduce feature redundancy, optimize the BP estimation, and determine the initial weights and threshold of the network. Such a system needs an expert and is not easy-to-use, which draws a limitation even though the achieved results were promising in terms of BP estimation. Authors in [53] proposed a non-contact approach based on laser Doppler vibrometry for BP measurement that aimed to demonstrate the possibility to assess arterial blood pressure without the need to put any element in physical contact with the subject (except for the signal calibration). Authors in [54] conducted a pilot study to determine the standard characteristics to evaluate the accuracy of wearable devices. However, the results of [54] concluded that there is a lack of a standard test protocol and meteorological parameters such as uncertainty of error to be taken into consideration for the validation of a wearable device. In addition, authors in [55] proposed a study to compare between the PPG methods based and standard cuff-based manometry devices. The authors highlighted that the Biobeat’s cuffless blood pressure monitor is a PPG-based wearable health device that provides non-invasive, cuffless, wireless, and repeated measurement of blood pressure and heart rate. This device transmits data in real-time to a user app and to a medical management system. Meanwhile, authors in [50] have suggested a technique to estimate BP based on thousands of subjects using PPG and ECG. In [50], several regression models are implemented and evaluated using 10-fold cross-validation testing, and the best performance was obtained utilizing adaptive boosting (AdaBoost), precisely their approach obtained 11.17 and 5.35 mmHg for SBP and DBP, respectively by the mean absolute error (MAE). However, the same evaluation metrics were used in our study.
The massive rise in deep learning, which has been proved to perform exceptionally well in a wide variety of fields, is also reflected in this area of study [56]. Authors in [57] have proposed a work in which they highlighted the accuracy decay issue over long periods of existing models to estimate BP from PPG signals. This issue implies that it requires periodic calibration. To model temporal dependencies in BP, a deep RNN with LSTM has been utilized. PPG and ECG have been utilized as inputs, and PTT was used to predict BP alongside some other characteristics. Compared to the existing approaches, they demonstrated long-term gains in BP prediction accuracy, while maintaining a real-time prediction accuracy at a level comparable to the related work. Authors in [58] proposed a deep learning model called Res-LSTM for continuous BP measurement that contains a 50-layer ResNet and LSTM model. The results achieved using MAE were 7.10 mmHg for SBP and 4.61 mmHg for DBP with the calibration method involved. One of the highly cited papers dealing with the PPG BP estimate using a neural network was presented in [58]. First, 21 features were computed that define the shape of the individual PPG cycle in a more informative way, where they utilized a small subset of data from the MIMIC II database, and the reported MAE results were 3.80 ± 3.46 mmHg for SBP and 2.21 ± 2.09 mmHg for DBP. Therefore, cuff-less blood pressure prediction methods in the literature such as [41,42], suffer from various drawbacks such as requiring calibration for each subject. While this study provides a continuous cuff-less blood pressure, the measurement method is estimated by extracting several features from the PPG signal and then applying signal processing and AutoML algorithm. To conclude, numerous automated ML techniques have been evaluated and reported for different research domains. However, to the best of our knowledge, no recent study has proposed a cuff-less systolic and diastolic blood pressure estimation method for estimating BP from PPG using TPOT. Therefore, AutoML is a recent and challenging area [13] that automates the time-consuming process of identifying effective machine learning (ML) pipelines. Thus, AutoML solutions blossomed across research communities to smartly find ML pipelines with good performance.
3. Methods
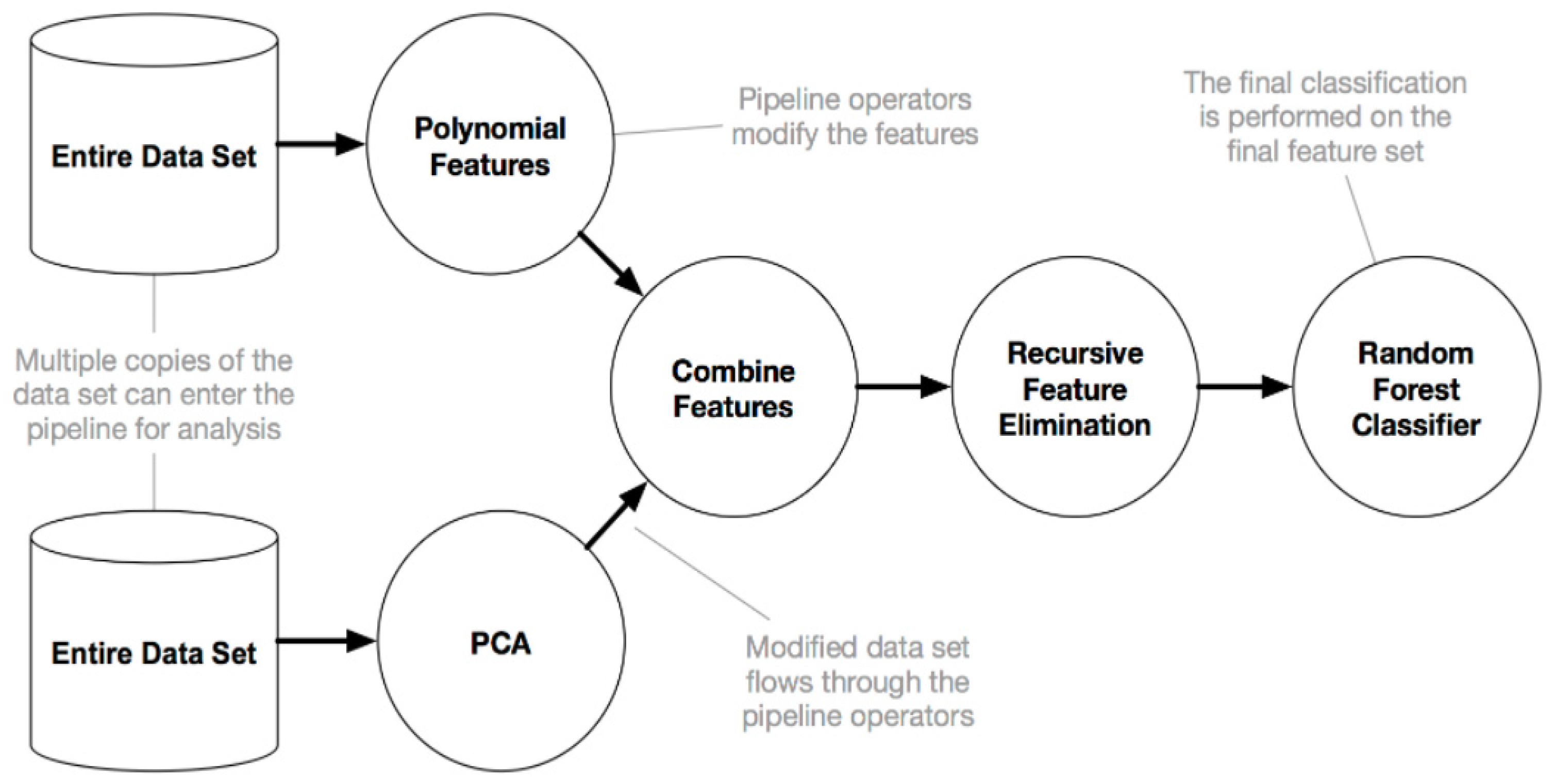
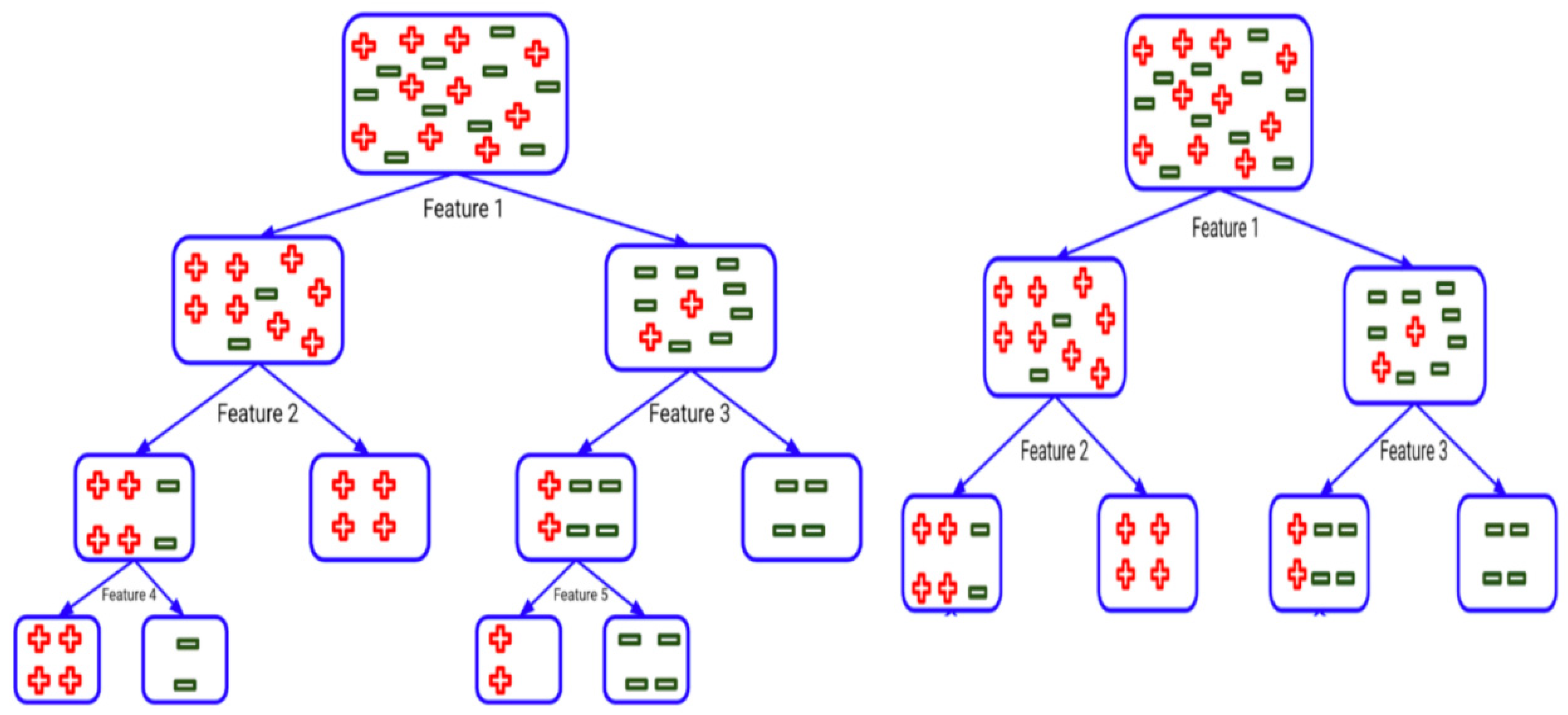
The biomedical signal analysis of BP and PPG requires several steps, including data pre-processing to prepare the data, selecting appropriate features using feature extraction and engineering, model selection and validation, and tuning of hyperparameters. All these steps aim to effectively produce an accurate machine learning model to estimate BP from PPG. To achieve this goal, a tree-based pipeline optimization tool (TPOT) is used in this paper to estimate the blood pressure from PPG. To simplify, TPOT uses genetic programming from the Python package DEAP [59] to pick a series of pre-processing data functions and ML classification or regression algorithms to optimize the model’s performance for a dataset of interest. In addition to the ML algorithm, the TPOT model pipeline, as presented in the example illustrated in Figure 1, includes a variety of data transformers implemented in the Scikit-learn Python library, such as various pre-processors (Min-Max Scaler, Standard Scaler, Max Abs Scaler, Normalizer, polynomial features expansion) and feature selectors (Select Percentile, Variance Threshold, recursive feature elimination). In some instances, designing a new feature set may help extract valuable information (e.g., when a selected method analyses one feature simultaneously while complex feature interactions are present in the dataset). TPOT also provides several custom function constructor implementations: Zero counts (count of zero/non-zeros per sample), stacking estimator (SE) (generates predictions and class probabilities with a classifier of choice as new features), one hot encoder (converts categorical features to binary features), and a range of sklearn transformer implementations: PCA, independent component analysis, and a selection of sklearn transformer implementations (Nystroem, RBF Sampler). The complete TPOT configuration includes 11 classification algorithms, 14 feature transformers, and five feature selectors (for the full list, please refer to http://epistasislab.github.io/tpot/using/) (accessed on 18 January 2021). TPOT uses a tree-based structure to incorporate all these operators (Figure 1). Any pipeline begins at the root of the tree structure with one or more copies of the entire dataset and continues with the feature transformation/selection operators mentioned above or with the ML algorithm. The original dataset is then modified and moved down the tree to the next operator or if there are several copies of the dataset, they can be merged into a single set using a combination operator.
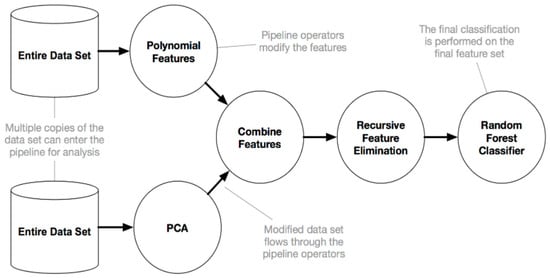
Figure 1.
Example of the tree-based pipeline optimization tool (TPOT) pipeline.
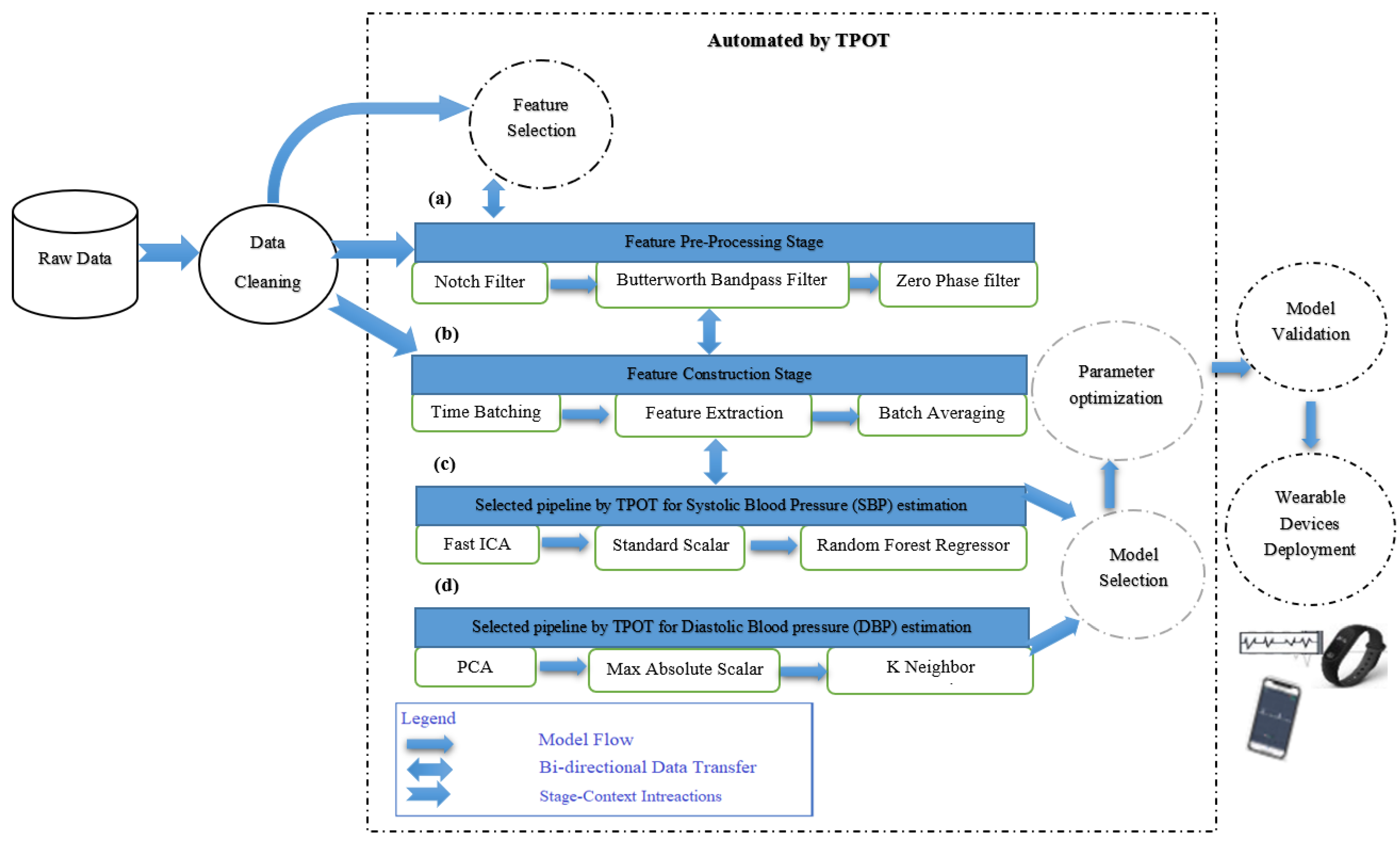
A conceptual framework for the proposed study is presented in Figure 2. We have employed TPOT to select the best model with the best parameters to avoid the time-consuming and complex problems of the traditional machine learning algorithms. In addition, the proposed approach will come out with the best regression model to predict the expected blood pressure that can be acquired at a low-cost, continuously, and noninvasively from the patient beyond their ICU stay. However, the deployment of the wearable devices will be one of the future directions, whereby the regression model selected by TPOT will be integrated with real-time BP wearable devices to predict the situation of the patient in a particular timeframe.
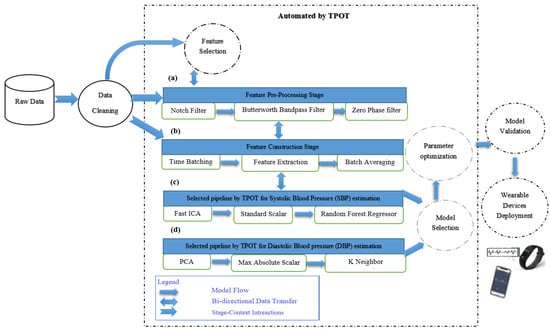
Figure 2.
Automated search of machine learning (ML) model using the tree-based pipeline optimization tool. A machine learning operator corresponds to each circle, and the arrows indicate the direction of the flow of data: (a) Feature preprocessing pipeline; (b) feature construction pipeline; (c) the best pipeline chosen by TPOT for systolic blood pressure (SBP), and (d) the best pipeline chosen by TPOT for diastolic blood pressure (DBP). The following subsections will discuss the steps in detail.
Additionally, TPOT designs a generic algorithm for searching a wide range of supervised classification algorithms that adopt the Python Scitkit learning library, including preprocessors, transformers, feature selection techniques, estimators, and their hyperparameters, without any domain knowledge or human data inputs. As demonstrated in the correlation matrix heatmap for the dataset of this study, the stronger correlation on both ends of the spectrum presented in a darker color and weaker correlation has been presented in a lighter shade color. Thus, the feature extraction pipeline must precisely map the PPG diastolic peak to the foot (signal minimum) of the BP signal. In the following sub-sections, the details of TPOT phases will be elaborated.
3.1. Dataset
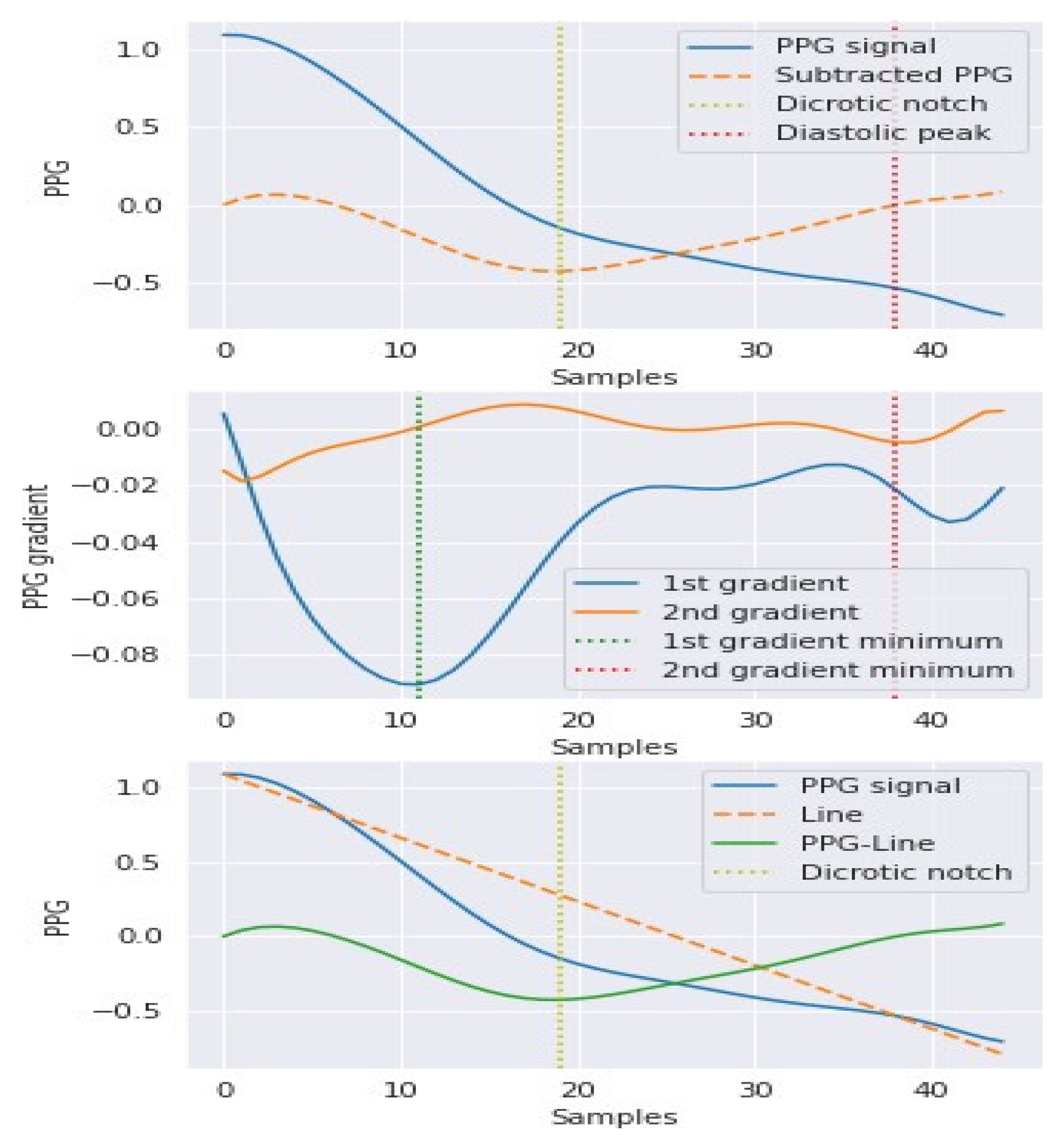
To conduct the experiment of estimating the BP from PPG, a global dataset, called PhysioNet dataset, which contains 32.061 million samples for 1000 individuals, were used. This dataset is obtained from Kaggle and also freely available for researchers (https://physionet.org/, accessed on 15 January 2021), whereby a blood pressure signal is obtained from the invasive arterial blood pressure (in mmHg), and a photoplethysmography is extracted from the fingertip and an electrocardiograph from channel II [42]. Notably, all the samples were produced using a sampling frequency of 125 Hz to increase the detection accuracy of the key points, as presented in Figure 4. The key points of each pulse should be detected before extracting the features of the PPG signals. The key features of the PPG pulse are presented in Figures 4 and 6. Since PPG signals have different morphologies, point detection methods should have limited sensitivity to different morphologies. Figure 3 shows the BP, PPG, and ECG signals obtained from the collected PhysioNet dataset in this study. As depicted in Figure 4, the feature extraction technique is used to divide the waveform into ascending and descending components, in which the descending component is isolated. In addition, the first and second derivatives are computed and plotted to determine the features required in this study. The first derivative waveform is mainly used to determine the maximum slope point and diastolic peak, and the second derivative waveform is used to determine the dicrotic notch [60].
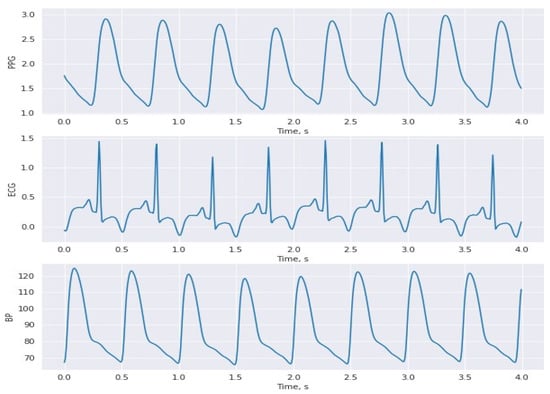
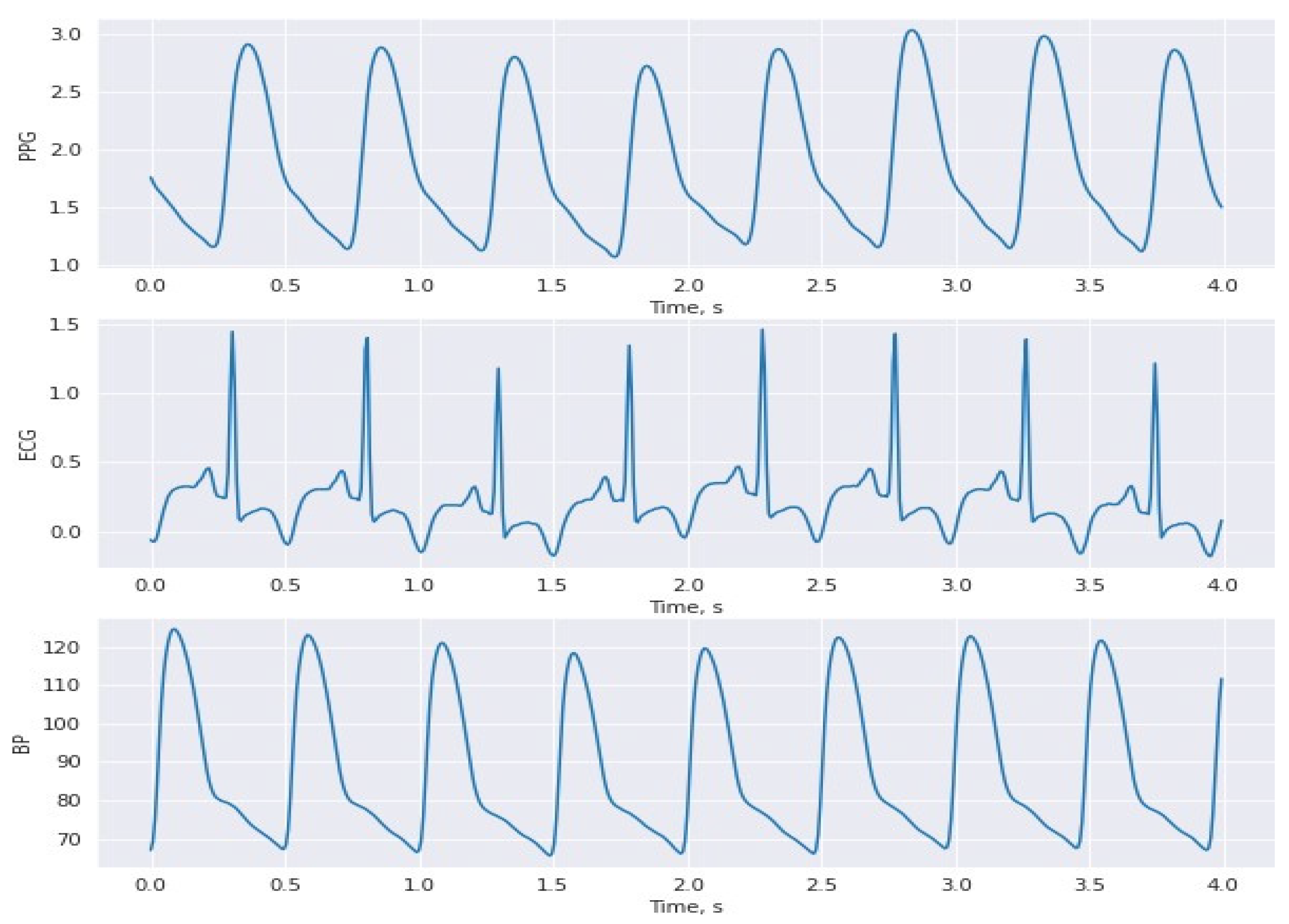
Figure 3.
BP, photoplethysmogram (PPG), and electrocardiogram (ECG) signal plots from the collected PhysioNet dataset in this study.
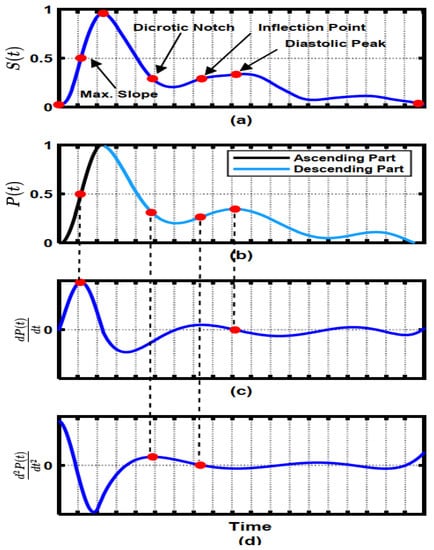
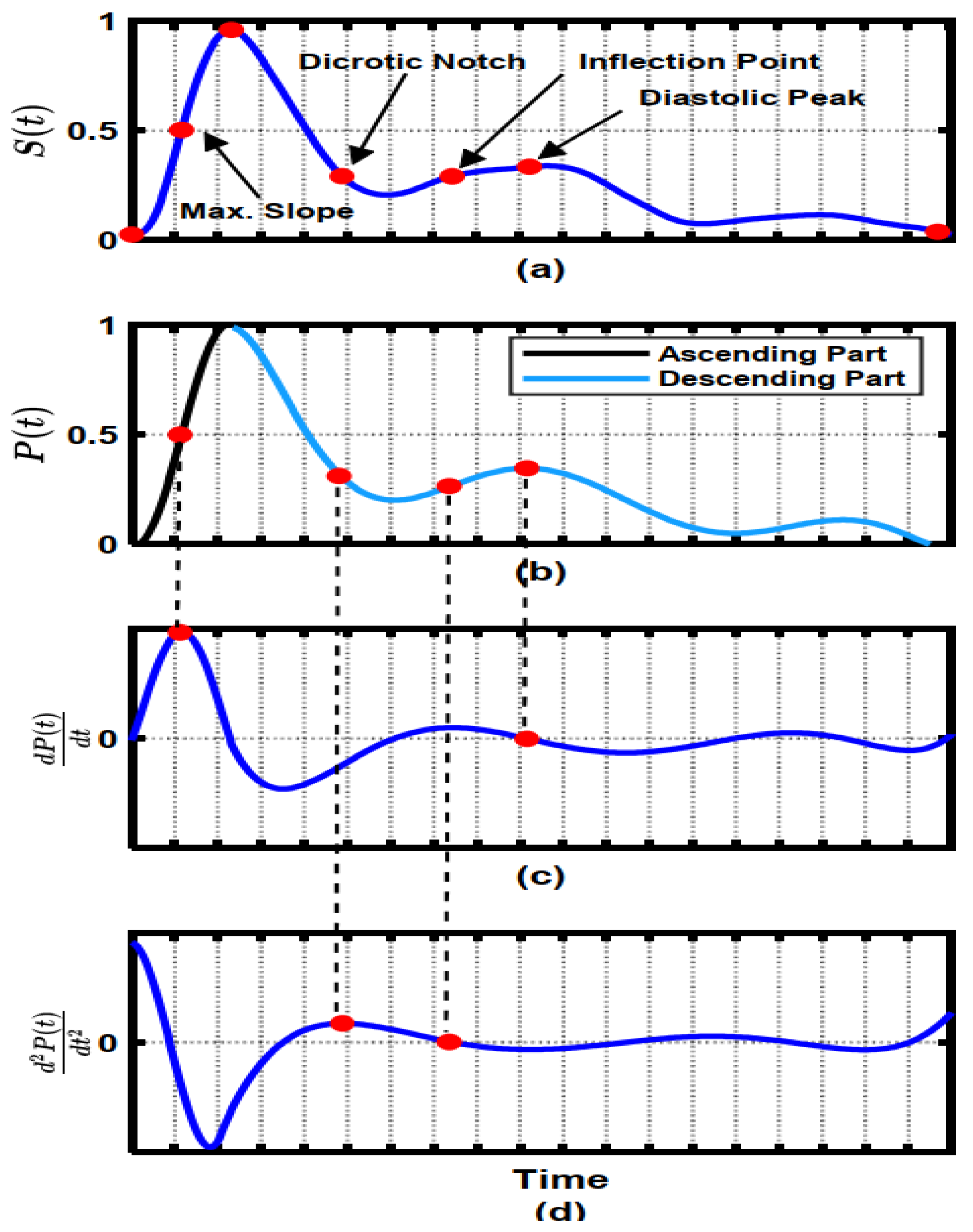
Figure 4.
Key points of PPG pulse; (a) The location of the key points; (b) division of PPG into ascending and descending components; (c) first derivative waveform; (d) second derivative waveform [60].
3.2. Hybrid Pre-Processing Stage
For better usage of any dataset, pre-processing is an essential step. Thus, in this study, the signals imported from the dataset should undergo pre-processing to eliminate any potential noise inherent in the signal. As the used dataset contains different signals (i.e., ECG, PPG, BP), a hybrid pre-processing stage was conducted to deal with any noise in the three signals used in this study (Figure 2a). The hybrid pre-processing stage comprises three filters, notch filter (band-stop filter), a band-pass Butterworth filter, and zero-phase filtering. The following lines will be dedicated to explaining these three techniques.
The first pre-processing technique used to limit the potential noise of the signal is a notch filter. Notch filters have a wide variety of uses in signal processing, particularly when there is a specific frequency component that needs to be removed from a signal [61]. One of the vital notch filter applications to the pre-processing of the signals used in this project is the notch filter’s ability to reject 60 Hz AC interference in biomedical signals [61]. This 60 Hz AC interference is seen in various signals due to the frequency of the power lines in North America and should be removed from the signals in the dataset before feature extraction. An IIR notch filter in this stage was configured with a cutoff frequency of 60 Hz to achieve this goal.
After removing the 60 Hz AC interference, the band-pass Butterworth filter was used to allow a specific range of frequencies to be selected out of the signal, and any frequencies outside of the given range would be suppressed. Such a selection of a range of signals limits any motion artefacts in the dataset and prevents high-frequency noise in the signal [62]. The crucial criterion in designing this filter is to know the proper band-pass frequency range that is needed.
In this study’s context, PPG signals are typically found within the frequency range of 0.5 to 4 Hz [62]. Therefore, the band-pass filter was tuned within the frequency range of 0.5 to 8 Hz. According to [39], anything below 0.5 Hz can be attributed to baseline wandering, while anything above 8 Hz is high-frequency noise. All the shorter-length recordings were removed since we needed waveforms that were long enough to include at least some SBP and DBP changes. The PPG signal was then normalized to zero mean unit variance and filtered, with 0.5 and 8 Hz cutoff frequencies, with a 4th order Butterworth band-pass filter.
The third pre-processing step used in this study is the zero-phase filter, which is built using the fitful function in Python library, called SciPy. A zero-phase filter’s importance is to minimize any distortion in the waveform of the original signal, which minimizes the delay in the signal processing [63,64]. Figure 2 depicts the sequence of the three filters used in this study to isolate PPG-derived BP signals from the dataset, which were then compared to the arterial BP features.
3.3. Features Selection Methods
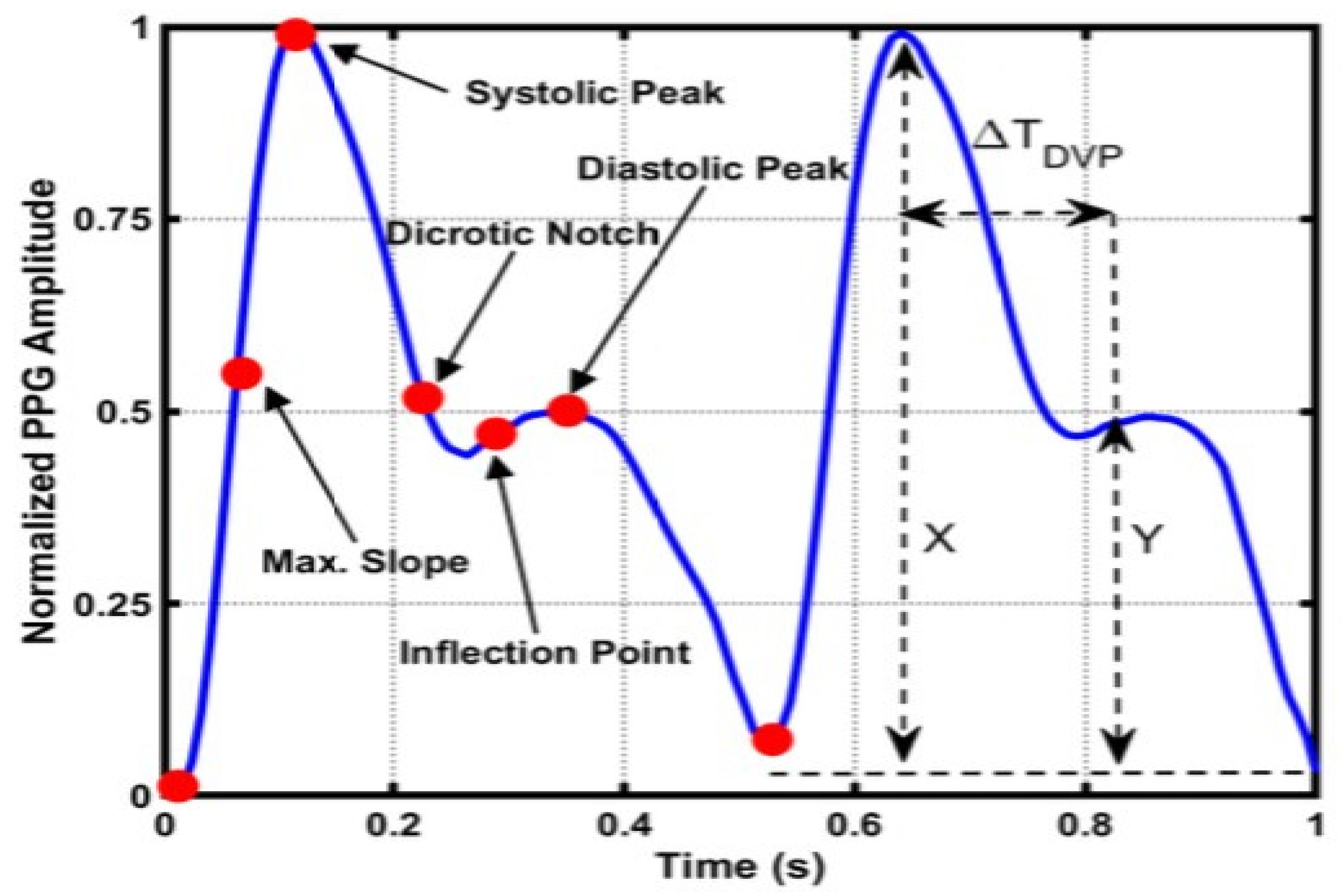
The blood pressure waveform characterized by four points: The systolic peak (maximum pressure point), the anacrotic notch (reversal of the inflection point or slope corresponding to the arrival of the reflected wave), the dicrotic notch (minimum local pressure corresponding to the closure of the aortic valve), and the diastolic foot, respectively (the point of lowest pressure). These points represent the key features that should be extracted for the purpose of this study, and Figure 5 depicts these four key features in the BP waveform.
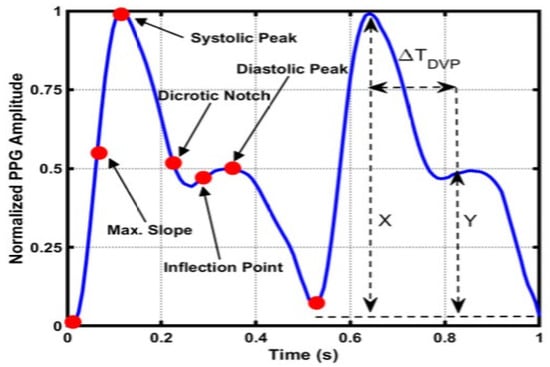
Figure 5.
PPG key features, where X and Y are the amplitudes of systolic peak and inflection points, respectively, and ∆TDVP is the interval of time between the two [60].
The dicrotic notch distinguishes the end of systole and the beginning of diastole in the central arteries pressure waveform, being more prominent in the BP waveform than the PPG waveform [60]. When the blood pressure propagates towards the fingertips from the left ventricle, the systolic peak results, the diastolic peak, another key feature, is produced when the reflected blood pressure from small blood vessels of the lower body propagates towards the aorta and fingertips [60]. In addition to the four BP waveform’s features, the PPG signal was isolated into ascending and descending components to create labels, as shown in Figure 6.
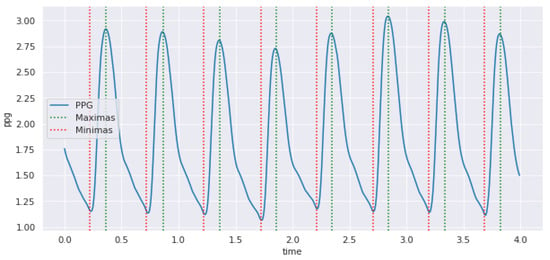
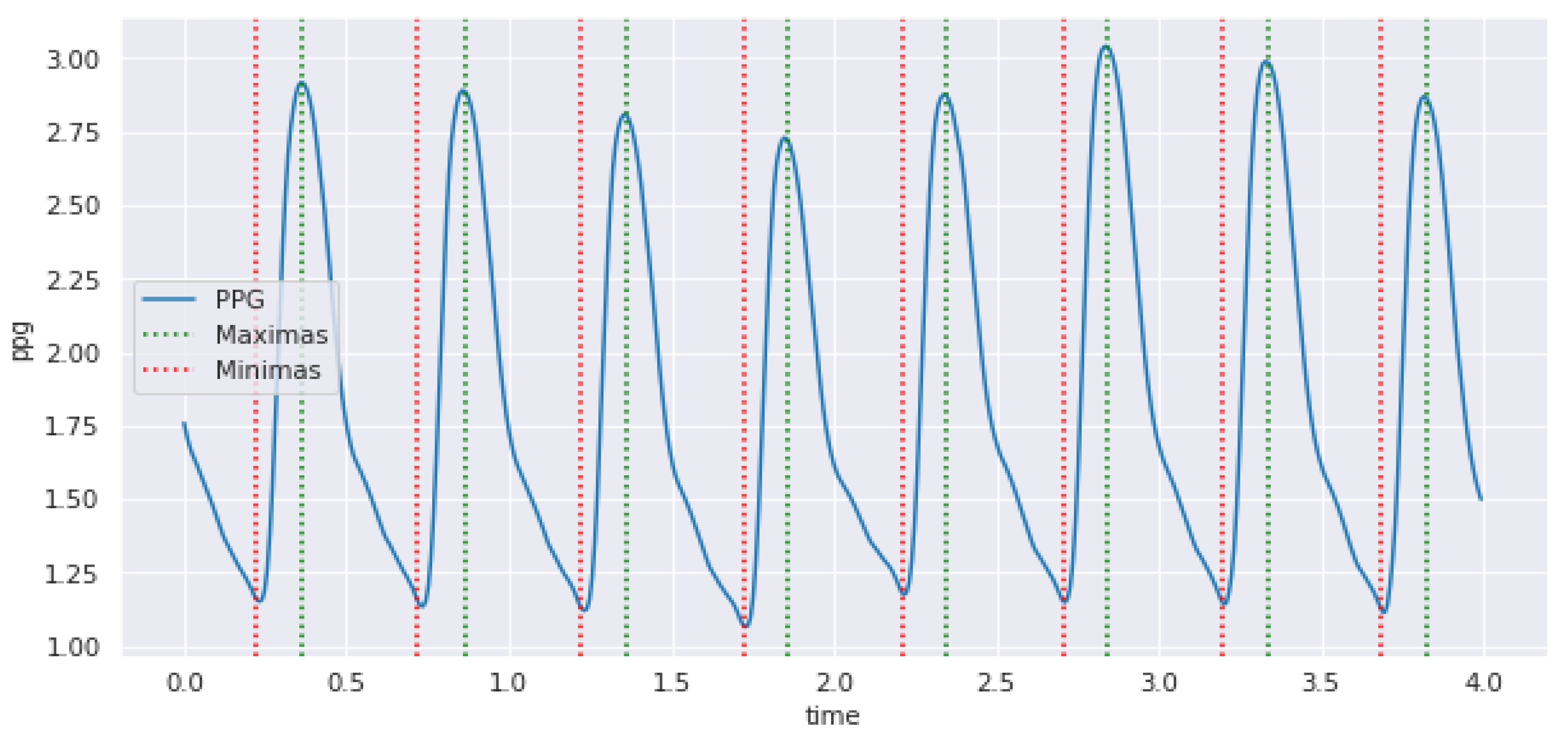
Figure 6.
PPG signal with labeled maximum and minimum points.
For an interval length of 4 s of PPG signal, the descending portion of the BP or PPG signal is then normalized to the amplitude of 1, considering the systolic peak to the end. The first derivative is computed to find the maximum slope point using polyfit. Since the diastolic peak is not easily detectable, the second derivative is computed, and a polynomial is fitted again. Through experimentation, the diastolic peak was isolated as the last local minimum in the descending interval selected. Furthermore, the dicrotic notch was isolated from the PPG signal as it is defined as the point where the second derivative of the PPG is a local maximum [60]. The dicrotic notch occurs before the diastolic peak, as presented in Figure 7.
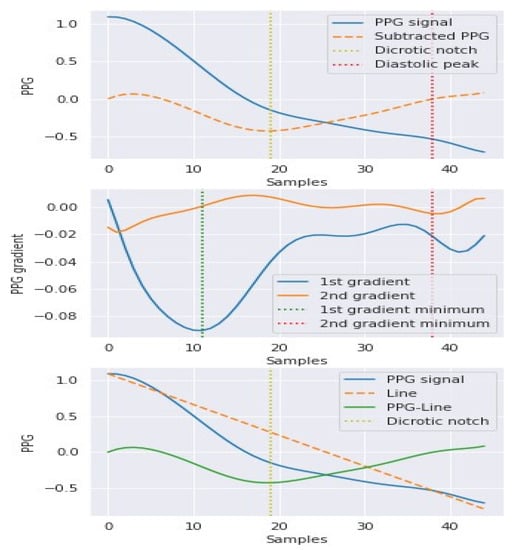
Figure 7.
The 4 s interval sample data of PPG obtained in this study.
Additionally, seven features were extracted using the feature construction stage depicted in Figure 2. Exploratory data analysis (EDA) is a method of analyzing datasets to summarize their key characteristics, often using statistical graphics and other data visualization methods. In this study, we have presented our dataset key characteristics in Table 1 where EDA is an essential step for feature selection in ML. The statistical data analysis performed in this study explores the data from two different angles (descriptive and correlative). Each type introduces information on the predictive power of the features and enables an informed decision based on the analysis outcome. However, the EDA shows that TPOT has selected seven main features based on the given dataset. These features are PPG systolic pressure, PPG diastolic pressure, PPG foot pressure, PPG notch pressure, and BP systolic pressure, BP diastolic pressure, and BP notch pressure. These seven key features and their statistical analysis are presented in Table 1. In addition, correlation matrices are a necessary tool for exploratory data analysis. Correlation heatmaps present the same data in a more visually appealing way. Furthermore, they show us at a glance if the variables are correlated, to what extent, and in which direction, and potential multicollinearity issues. The correlation heatmaps for these features are presented in Figure 9.

Table 1.
Feature correlations with the statistical analysis.
3.4. Automated Machine Learning
AutoML is the approach used to automate the means of applying machine learning to problems in the real world [33]. AutoML covers the entire pipeline from the raw dataset to the deployable machine learning model. AutoML is an artificial intelligence approach to the machine learning’s ever-increasing problem [27]. TPOT has been used in this study, and it is one of the promising AutoML in several research domains [65]. It is a python automated machine learning platform that utilizes genetic programming to optimize machine learning pipelines. By intelligently testing thousands of potential pipelines to find the right one for the data used, TPOT can simplify the most tedious part of ML as presented in Figure 2 (at the beginning of Section 3). In addition, TPOT uses genetic algorithms inspired by Darwinian natural selection to optimize and generate solutions [33]. Genetic algorithms have three components:
- Selection: At every generation, each solution is evaluated.
- Crossover: The most fit solution is selected, and crossover occurs to create a new population.
- Mutation: The children from the new population are mutated randomly, and the process is repeated once more to obtain the best solution.
The automating optimization process using genetic programming begins with the random generation of a fixed number of tree-based pipelines, which are then subjected to the evolutionary algorithm through rounds (generations) of mutation, recombination of pipeline components, and selection. The fitness of the pipeline is measured using a Pareto multi-objective function that seeks to optimize the output metrics of choice for the ML algorithm, (in our case, MAE and MSE were utilized) while minimizing the pipeline’s complexity (i.e., the number of data transformers/selectors in the pipeline). The crossover and mutation are two sources of variation that alter a TPOT pipeline structure and make it easier to pick the best match for a given dataset. Second, a user-specified percentage of pipelines were subjected to a one-point crossover, in which two randomly chosen pipelines separated at a random point in the tree, and their contents were exchanged. Following that, the mutation is implemented at a fixed user-defined frequency, with adjustments in the type of pipeline operator addition, elimination or substitution. After the improvements are applied, and their fitness impact is measured, the TPOT pipeline with the highest fitness from the current generation is chosen to replace 10% of the next generation population. A three-way tournament of two-way parsimony chooses the remaining 90% of the population: Three pipelines are chosen for the tournament, with the lowest fitness one eliminated first and the least complex of the remaining two chosen to be replicated in the next generation. However, we have set the population size of 20 and 10 generations were used, which indicates the number of iterations to run during the pipeline optimization process, with a 60:40 training-validation split. The population size indicates the number of individuals that are retained in programming the new population at every generation. The 10-fold cross-validation method was used to evaluate the pipelines. The random state indicates the seed of the pseudo-random number generator used (the same results are generated for that seed). Early stop denotes stopping before 10 generations are reached if the pipeline is optimized earlier with no improvement in the optimization process to speed up the model selection. For 10 generations of population size 20, TPOT evaluated 200 pipeline configurations, which is akin to 200 hyperparameter combinations of an ML algorithm. The best pipeline was determined, and upon completion, the test error was computed for validation purposes, using well-known evaluation matrices, namely MAE and MSE as described in Section 3.5. BP is measured using two main items. TPOT-generated ML pipelines with selected ML classifiers, optimized with a grid search approach, applied for both SBP and DBP. Figure 2c,d shows the best-automated pipeline for SBP and DBP produced by TPOT automatically based on our dataset.
The best pipeline for the determination of systolic BP was a combination of the FastICA, Standard Scaler, and Random Forest Regressor as shown in Figure 2c. The algorithm of Fast Independent Component Analysis (FastICA) [66], a fast-converging algorithm based on non-Gaussian maximization and implementation utilized an approximate Newton optimization method, has become a norm for both sub-Gaussian and super-Gaussian sources to be segregated. The algorithm has been shown to exhibit cubic convergence in the symmetric orthogonalization method when in the deflationary mode (utilizing the cost function of kurtosis) and local quadratic convergence [67]. To allow for the separation of the complex, the FastICA algorithm has been subsequently expanded. The use of FastICA algorithm in our study was chosen by TPOT and can be described as follows.
The iterative algorithm finds the direction for w ∈RN, ∈the weight vector that maximizes a measure of wT X non-Gaussianity of the projection, with X ∈R(N+M) representing a pre-whitened data matrix as discussed in [68]. Note that w is a column vector. FastICA relies on a nonquadratic nonlinear function f(u), its first derivative g(u), and its second derivative g(u), to calculate non-Gaussianity. The steps taken in FastICA to extract the weight vector w for the SBP portion are as follows.
- ⯀
- Whiten data.
- ⯀
- Randomize the initial weight vector w.
- ⯀
- Select a non-quadratic function, for example:
Since tanh is an odd function, its series expansion is of the form tanh(a1u). According to loops continually iterate until their convergence. The absolute value of E(xg(WTx)) would get smaller and smaller. Descendent Newton can be used to boost the stability and uniformity of the convergence. Furthermore, standard scalar standardizes data set characteristics by scaling to unit variance and eliminating the mean utilizing column summary statistics on the samples in the training set (optionally). This process is a pre-processing phase that is very popular. During the optimization process, standardization enhances the convergence rate. During model training, it also prevents characteristics with large variances from exerting a tremendous effect.
Finally, a random forest is a meta estimator that fits several decision trees on different data set sub-samples [69] and uses averaging to improve the predictive accuracy and over-fitting control [70]. If bootstrap = True (default), the sub-sample size is managed with a max sample parameter. Otherwise, the entire dataset will be used to construct each tree. The default value of the minimum sample split is assigned to 2 in our case. This implies that, as shown in Figure 8, if any terminal node has more than two observations and is not a pure node, we can further break it into sub-nodes. Having a default value of 2 raises the problem that a tree sometimes breaks until the nodes are entirely pure. Consequently, the tree increases in size and overfits the data as a result.
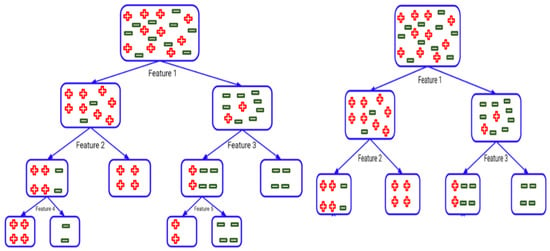
Figure 8.
Random forest estimator hyperparameter tuning.
As explained in the previous section, DBP measures the human arteries pressure when their heart rests between beats [71]. Firstly, the principal component analysis (PCA) minimizes dimensionality which is utilized to decrease the dimensionality of large datasets by converting a large set of variables into a smaller one that still retains much of the large set of information [72]. This phase was automatically carried out with TPOT since our dataset contained 32.06 million samples for 1000 individuals. According to [73], PCA can be solved using two methods: Covariance matrix and singular value decomposition (SVD).
The SVD-based approach to address the issue of PCA is discussed as follows. Let X be an arbitrary n m matrix, and XT X be a rank r, square, symmetric m m matrix. {} is an orthonormal set of m l eigenvectors with associated eigenvalues for {λ1, λ2, λ3, ……… λr} the symmetric matrix XT X.
where are positive true and called the singular values {} which is the set of n 1 vectors described by:
= Eigenvectors are orthonormal.
The singular value decomposition of a matrix is:
where the σi are ordered such that σi ≥ σi+1 and X multiplied by an eigenvector of XT X is equal to a scalar time, another vector. The set of eigenvectors {} and the set of vectors are {} both orthonormal sets and bases in r dimensional space. Hence, the constructed accompanying orthogonal matrices are:
Therefore, the SVD matrix version can be computed as:
where ∑ is the symmetric m m matrix. If the decomposition’s scalar version is performed by each column of V and U since V is orthogonal, we can multiply both sides by V1 = T to arrive at the decomposition’s final form.
where is the coefficient for reconstructing the samples. The second technique chosen by TPOT to scale each function by its maximum absolute value is the max absolute scalar. This estimator scales and independently translates each function such that the overall absolute value of each function in the training set will be 1.0. It does not alter/center the data and thus does not remove any sparsity. Finally, the regression selected by TPOT to detect the DBP signal is KNN regression. KNN regression is one of the simplest supervised machine learning algorithms and is primarily utilized for classification or regression problems [74,75]. It estimates a data point on the basis of how its neighbours are categorized. It is fundamentally based on the principle that objects close to each other have similar characteristics. The closest neighbour rule is the simplest form of KNN when K = 1. In this case, each sample should be graded in the same way as the neighbour sample. Therefore, if the sample’s regression is not known, consideration can be given to the regression of the nearest neighbour sample. Therefore, unidentified samples can be categorized based on this regression of the nearest neighbors [76]. KNN makes predictions, as described above, based on the outcome of the K-neighbors closest to that point. Therefore, we need to define a metric for calculating the distance between the request point and cases from the example sample to make predictions with KNN. One of the most widely used metrics in evaluating the distance between two points is known as the Euclidean distance. It is possible to define the Euclidean distance by:
XV = U∑
3.5. Evaluation Metrics
To analyze and evaluate the performance of AutoML (TPOT) approach for estimating BP, three evaluation metrics were employed in this study, namely the mean absolute error (MAE), mean squared error (MSE), and correlation coefficient. Hence, the forecast data is Xp, while the ground truth data is X and the number of samples is N:
- Mean absolute error (MAE): Absolute error is the sum of error expected. The mean absolute error is the mean for all absolute errors.
- Mean squared error (MSE): MSE measures the squared number of errors. MSE is a risk function that corresponds to the estimated value of the squared error loss. MSE includes both the variance and bias of the estimator.
- Correlation coefficient (R): A statistical technique that calculates how closely connected two variables are (predictors and the predictions). It also informs us how close the prediction is to the trend line.
In these equations, Xp is the actual value, is the predicted value, and N is the number of observations. The optimum value is 0 for MAE and MSE. R takes value –∞ and 1. Negative values are indicated as worse prediction. When utilizing the AutoML (TPOT) approach in python, the above criteria are automatically calculated by python, and these values were utilized to evaluate the performance of the algorithms that TPOT has chosen.
4. Results and Analysis
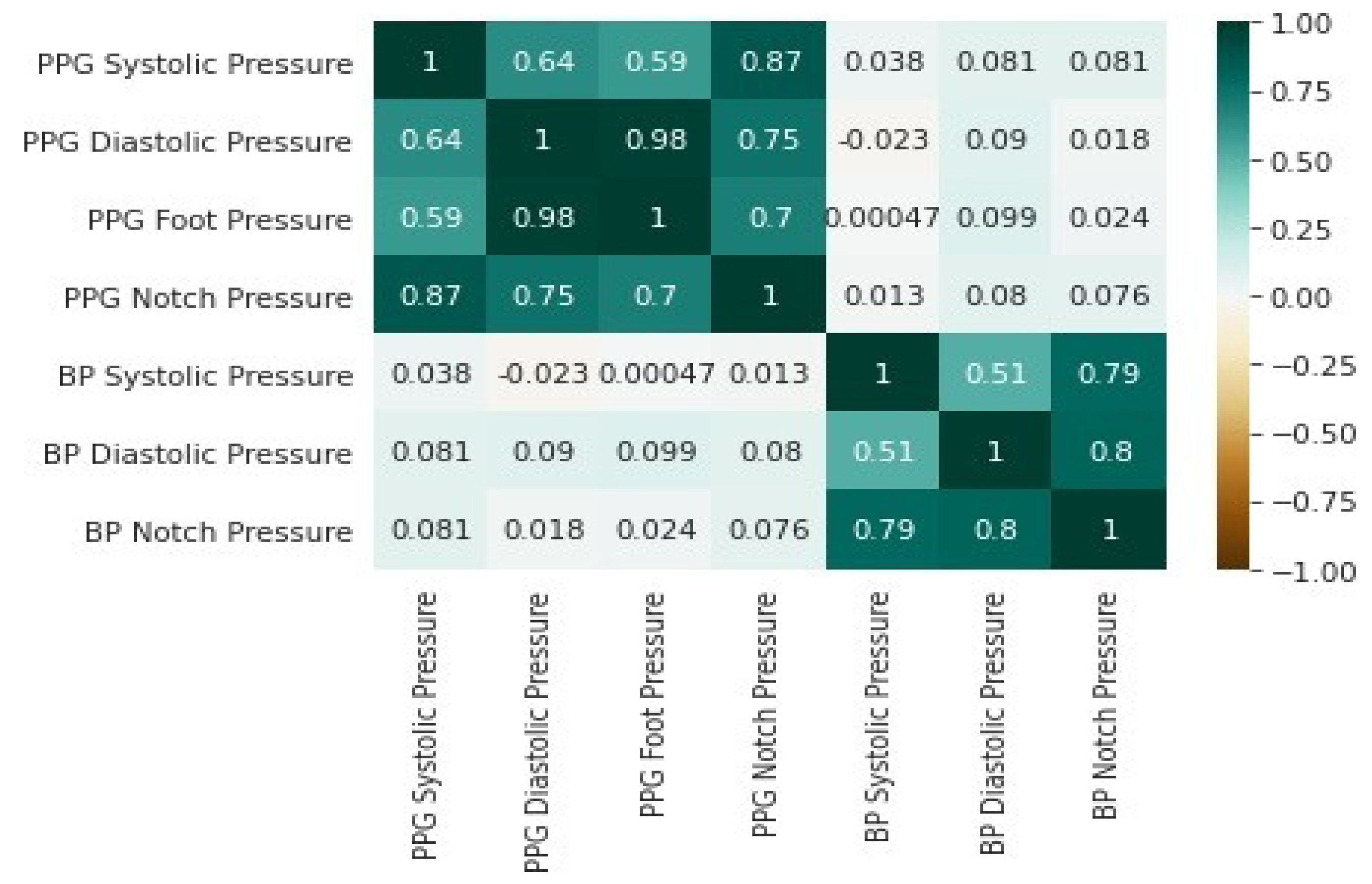
A heatmap is a graphical representation of data in which individual values in a matrix are expressed as colors. Then, by coding numerical values of various data types into colors, heatmaps offer a simple representation of quantitative variations in expression levels. Furthermore, thanks to the PCA analysis, a heatmap will outline and display the association and relationship between variables. We used the heatmap in particular to reflect the degree of expression of several BP or characteristics across a range of comparable samples. Indeed, this graphical representation allows for an instant visual description of the information and the identification of relationships between data values that would be far more difficult to grasp if viewed numerically as presented in Table 1. The heat map visualization technique in Figure 9 shows the correlation values of the seven features that were selected by the TPOT model proposed in this study. There is a high correlation between PPG features, as indicated by the darker green. Hence, a stronger correlation on both ends of the spectrum pops out in darker colors and a weaker correlation in lighter shades.
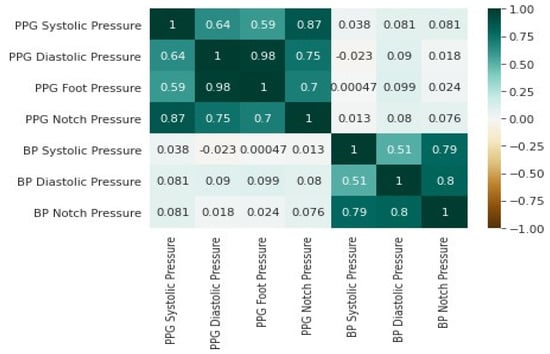
Figure 9.
The heatmap of the seven features selected automatically by the TPOT approach shows how these features are correlated.
The biomedical signal analysis of BP and PPG requires several steps, including pre-processing and preparing the data, selecting appropriate features, feature extraction and engineering, model selection and validation, and tuning of hyperparameters to effectively produce an accurate machine learning model for feature prediction of BP from PPG. As demonstrated in a heat map in Figure 9, BP and PPG signals are not correlated. Thus, the feature extraction pipeline must precisely map the PPG diastolic peak to the foot (signal minimum) of the BP signal.
Therefore, the PPG waveform does not have as a prominent a peak for diastolic pressure, and thus the second derivative was computed to extract this feature from the dataset. The auto-machine learning TPOT was used to train the derivation of BP from PPG features using genetic programming. Out of the 64,121 total number of samples, six values were dropped. Sixty-four thousand and one hundred fifteen samples were used with a 60:40 train-validate split: 38,469 samples for training and 25,646 samples for validation. BP features were successfully derived from the PPG signal, with a mean square error of 395.493 for SBP validation and 218.386 for DBP validation, as presented in Table 2. The mean absolute error was applied, and the results obtained were 6.52 and 4.29 mmHg for SBP and DBP, respectively.

Table 2.
Evaluation of the best performing algorithm for SBP and DBP.
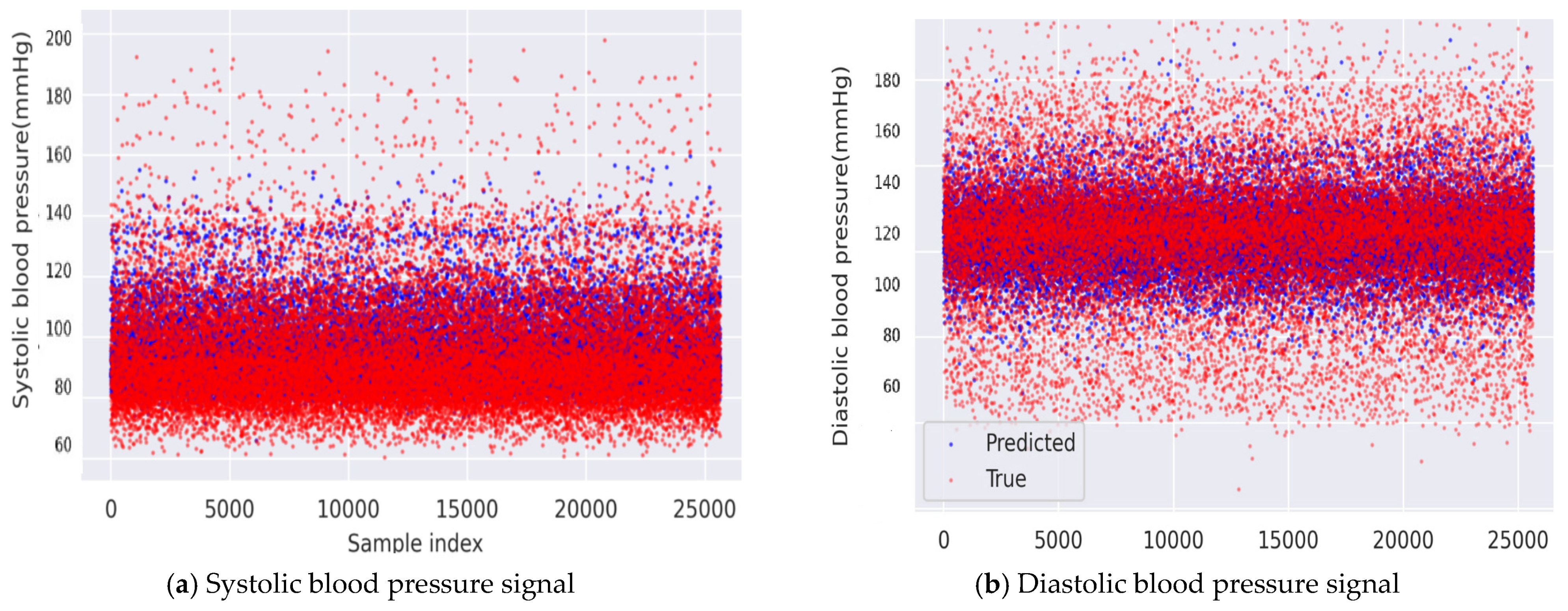
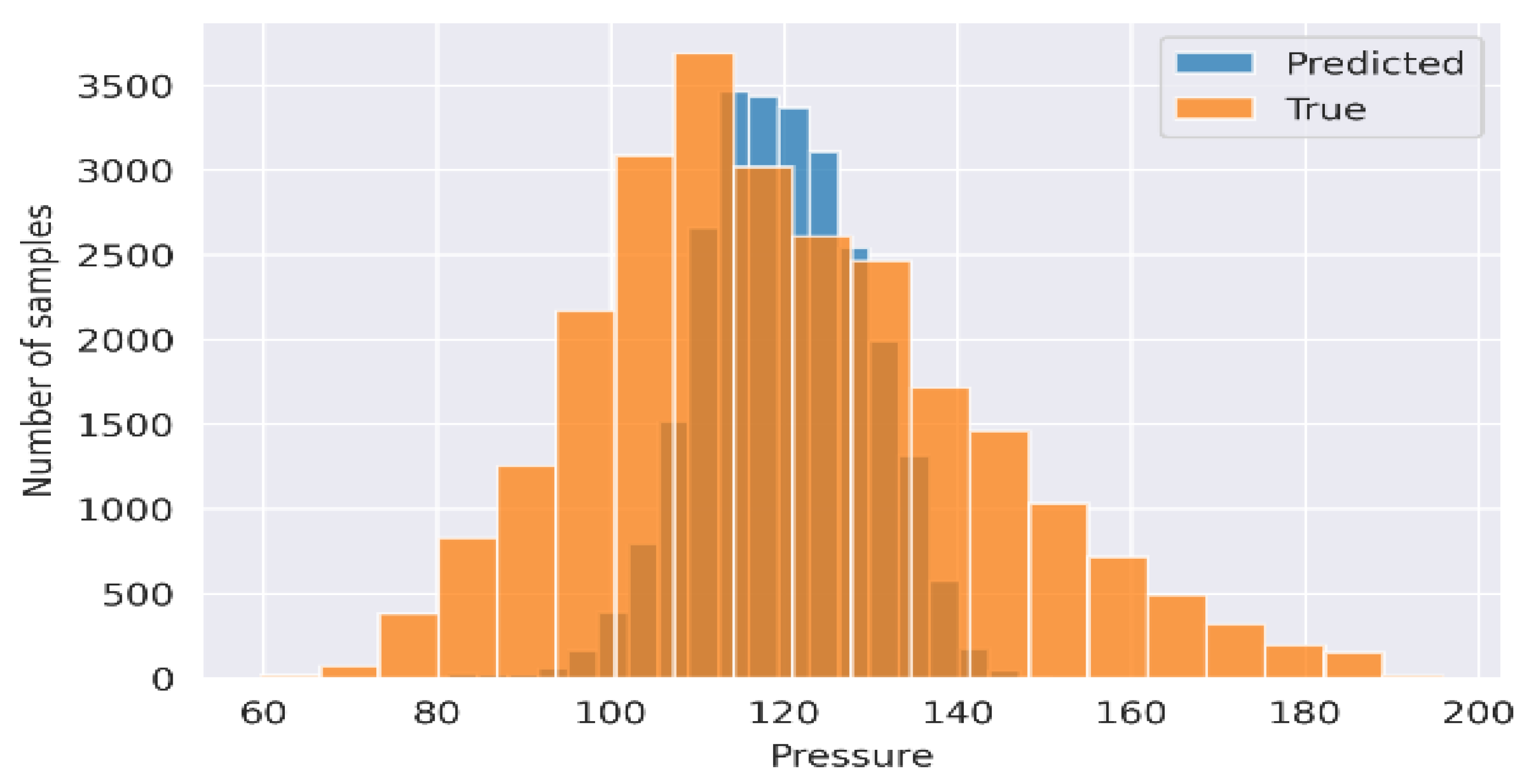
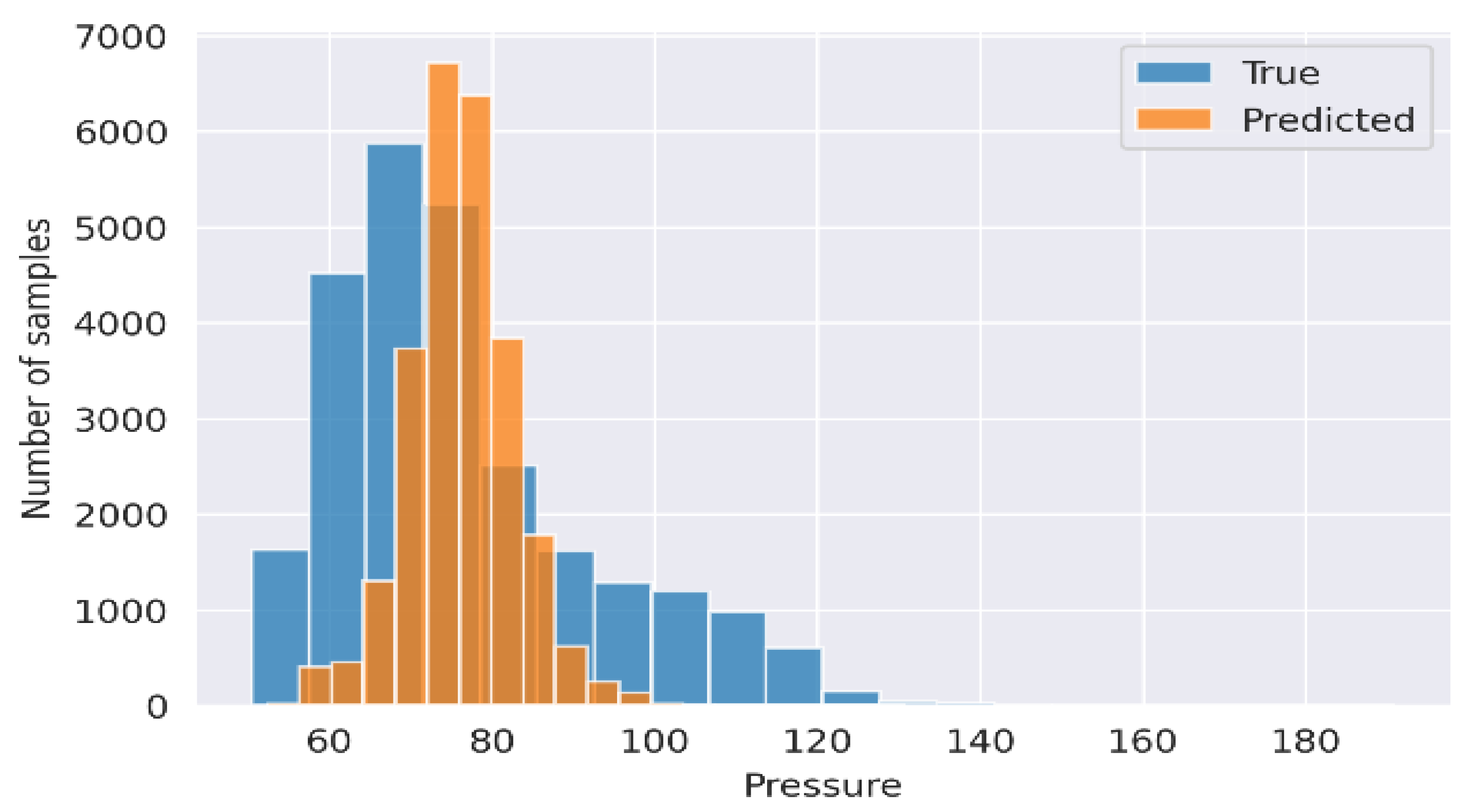
In examining systolic and diastolic plots (Figure 10), the red points had a greater range of distribution, while the blue points are more centrally distributed. The pressure range of the predicted BP was narrower than the true BP. Thus, it is apparent that the model is optimized for Gaussian distribution, and feature extraction does not indicate the variation in pressure seen in the BP. A shortcoming of the approach is that the ML algorithm does not successfully predict BP values far from the median systolic. This is further evidenced by the left skew of the distribution with a right tail that is not accounted for similarly, for diastolic, the prediction is skewed to the right. Figure 11 presents the SBP estimation using RF as the best regression method selected by TPOT and Figure 12 presents the DBP estimation using k-NN as the best regression method selected by TPOT.
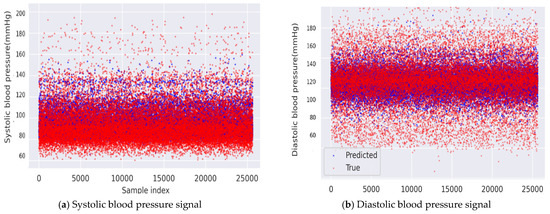
Figure 10.
Results of (a) systolic pressure signal produced using the random forest (RF) regression. Blue—predicted values; red—true values and (b) diastolic pressure signal produced using the k-nearest neighbor (k-NN) regression. Blue—predicted values; red—true value.
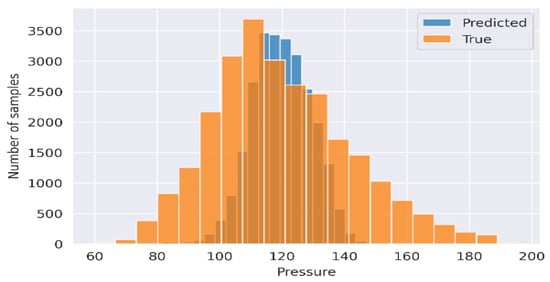
Figure 11.
Results of SBP signal produced using the RF regression. Blue means the predicted values, and orange presented the true values.
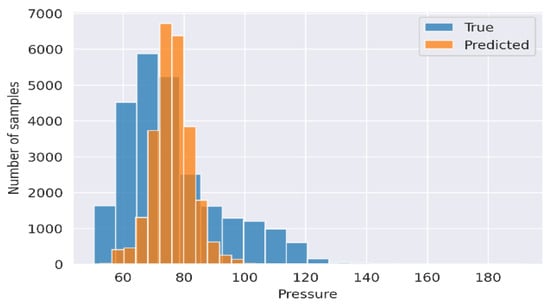
Figure 12.
Diastolic pressure signal produced through the use of k-NN regression. Blue presented the predicted values and orange the true values.
Table 2 presents the accuracy of the proposed model that has been tested using the BHS standards. According to BHS [77], our suggested TPOT approach is grade A in the estimation of DBP and grade B in the estimation of SBP. The results for DBP and SBP are acceptable and approved by a substantial margin, according to the AAMI [78]. Additionally, the performance evaluation in Table 2 shows that the results obtained for SBP and DBP are 6.52 and 4.19 mmHg, respectively. In addition, the MSE results achieved were 7.48 mmHg for SBS and 5.13 mmHg for DBP.
Comparison with Literature
Table 3 presents the comparison results obtained in this study and the literature in terms of SBP and DBP. The MAE is used as the main evaluation measure in this study. The MAE is a linear score which means that all the individual differences are weighted equally in the average. The MAE values obtained in this study are lesser than the values obtained in [39,55,58] since TPOT is an effective and powerful tool. As presented in Table 3, TPOT demonstrates an improvement compared to the Res-LSTM approach suggested by [58], Adaboosting algorithm proposed by [50], and the deep neural networks (DNN) approach proposed by [39] since TPOT optimizes a series of feature selectors, preprocessors, and ML models to maximize the estimation accuracy, where the MAE results achieved in this work were collaboration-free. Moreover, the feature selectors technique has selected the most useful and informative features to be used in the model training to further improve the accuracy of BP estimation, which brings great significance in mobile wearable devices.

Table 3.
Comparison between the results obtained in this study and the literature in terms of SBP and DBP.
Authors in [55] achieved a better result compared to this study. However, TPOT is still beneficial since it maintains a balance between high performance and low model complexity compared to the approach proposed in [55]. As a result, the pipelines learned by TPOT consist of a relatively small number of operators (e.g., in the single digits) that can still meet or exceed the performance of competing for state-of-the-art ML approaches [29].
A derived BP signal is successfully produced from the PPG features using Auto-ML techniques. Thus, cuff-less BP monitoring can be implemented using a PPG device that is both non-invasive and allows for continuous patient monitoring without the use of an invasive line. While invasive lines such as the central venous line and arterial line (used as the BP waveform in this data) remain the gold standard for cardio-vascular monitoring of cardiac critical care unit patients, the results of this paper present the possibility of accurate, lower cost, and less invasive means of detection beyond a patient’s ICU stay. A PPG sensor can acquire a waveform through the low-cost implementation of a LED light from their smartphone. As a result, this method can be applied in medical wearable devices where there is a need for developing an alternative to traditional BP monitoring using cuff-less, easy-to-use, fast, and cost-effective devices for maintaining and lowering the physical harm of CVDs to the human body [79].
5. Conclusions
This paper focused on the extraction of PPG signals to derive key features of invasive arterial BP. The proposed approach in this study was evaluated based on MAE and MSE where the results achieved for MAE were 6.52 and 4.19 mmHg for SBP and DBP, respectively. In addition, the MSE results obtained were 7.48 mmHg for SBS and 5.13 mmHg for DBP. The low difference in MAE and MSE between the training and validation sets implemented in this study demonstrates the potential for high accuracy BP data that can be acquired at a low-cost, continuously, and noninvasively from the patient beyond their ICU stay. Significantly, the results achieved were evaluated and approved based on BHS and AAMI standards. However, one of the future directions of this work is to deploy the proposed model in wearable devices or a portable smartphone that noninvasively captures PPG signals to derive the BP signal and other physiological feature data from the subject. In addition, further work can be conducted to explore critical care unit artifacts, such as line access interruptions in the BP waveform, to assess infection risk due to CLABSI in both pediatric and adult ICU settings. The signal processing and model training on ICU-specific patient data is the next step in validating the techniques used in this paper to assess different morphological features of medicated patients or those with abnormal conditions that may cause alterations in the model’s ability to detect BP from PPG. Furthermore, additional features can be extracted, and TPOT generations can be increased to test more hyperparameters and improve the derived BP features’ quality. Through the development of a machine learning-based model for artifact detection, real-time patient health risk assessments can be developed to inform clinical staff better and provide timely and precise health-based care to the patient.
Author Contributions
Conceptualization, A.M., N.A.A., and S.M.F.; methodology, S.M.F., and A.M.; software, A.M. and N.A.A.; validation, N.A.A., A.M., and S.M.T.; formal analysis, N.A.A., S.M.F., and A.M.; investigation, A.M.; data curation, A.M, and N.A.A.; writing—original draft preparation, N.A.A. and A.M.; writing—review and editing, S.M.F. and S.M.T.; visualization, A.M., S.M.F., and S.M.T.; supervision, S.M.F. and S.M.T.; project administration, A.M.; funding S.M.F. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges (APC) of this publication.
Data Availability Statement
The proposed model source code in this study is available upon request from the authors. We expect researchers to add new ideas to take this model in interesting directions. The dataset used in this study is available on https://www.kaggle.com/mkachuee/BloodPressureDataset (accessed on 18 January 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chowdhury, M.H.; Shuzan, M.N.I.; Chowdhury, M.E.; Mahbub, Z.B.; Uddin, M.M.; Khandakar, A.; Reaz, M.B.I. Estimating Blood Pressure from the Photoplethysmogram Signal and Demographic Features Using Machine Learning Techniques. Sensors 2020, 20, 3127. [Google Scholar] [CrossRef]
- Muneer, A.; Fati, S.M.; Fuddah, S. Smart health monitoring system using IoT based smart fitness mirror. Telkomnika 2020, 18, 317–331. [Google Scholar] [CrossRef]
- Muneer, A.; Fati, S.M. Automated Health Monitoring System Using Advanced Technology. J. Inf. Technol. Res. 2019, 12, 104–132. [Google Scholar] [CrossRef]
- Haddadin, Y.; Annamaraju, P.; Regunath, H. Central line associated blood stream infections (CLABSI). StatPearls [Internet] 2020. Available online: https://www.ncbi.nlm.nih.gov/books/NBK430891/ (accessed on 18 January 2021).
- Ling, M.L.; Apisarnthanarak, A.; Jaggi, N.; Harrington, G.; Morikane, K.; Thu, L.T.A.; Ching, P.; Villanueva, V.; Zong, Z.; Jeong, J.S.; et al. APSIC guide for prevention of Central Line Associated Bloodstream Infections (CLABSI). Antimicrob. Resist. Infect. Control 2016, 5, 16. [Google Scholar] [CrossRef]
- Meidert, A.S.; Saugel, B. Techniques for Non-Invasive Monitoring of Arterial Blood Pressure. Front. Med. 2018, 4, 231. [Google Scholar] [CrossRef]
- Ribezzo, S.; Spina, E.; Di Bartolomeo, S.; Sanson, G. Noninvasive Techniques for Blood Pressure Measurement Are Not a Reliable Alternative to Direct Measurement: A Randomized Crossover Trial in ICU. Sci. World J. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Patel, A.R.; Patel, A.R.; Singh, S.; Singh, S.; Khawaja, I. Central Line Catheters and Associated Complications: A Review. Cureus 2019, 11, e4717. [Google Scholar] [CrossRef]
- O’Brien, E.; Waeber, B.; Parati, G.; Staessen, J.; Myers, M.G. Blood pressure measuring devices: Recommendations of the European Society of Hypertension. BMJ 2001, 322, 531–536. [Google Scholar] [CrossRef] [PubMed]
- Kario, K. Management of Hypertension in the Digital Era: Small Wearable Monitoring Devices for Remote Blood Pressure Monitoring. Hypertension 2020, 76, 640–650. [Google Scholar] [CrossRef] [PubMed]
- Subasi, A. Practical Guide for Biomedical Signals Analysis Using Machine Learning Techniques: A Matlab Based Approach; Academic Press: New York, NY, USA, 2019. [Google Scholar]
- Allen, J.; Murray, A. Modelling the relationship between peripheral blood pressure and blood volume pulses using linear and neural network system identification techniques. Physiol. Meas. 1999, 20, 287. [Google Scholar] [CrossRef]
- Guyon, I.; Bennett, K.; Cawley, G.; Escalante, H.J.; Escalera, S.; Ho, T.K.; Macia, N.; Ray, B.; Saeed, M.; Statnikov, A.; et al. Design of the 2015 chalearn automl challenge. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–8. [Google Scholar]
- Datta, S.; Banerjee, R.; Choudhury, A.D.; Sinha, A.; Pal, A. Blood pressure estimation from photoplethysmogram using latent parameters. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–7. [Google Scholar]
- Choudhury, A.D.; Banerjee, R.; Sinha, A.; Kundu, S. Estimating blood pressure using Windkessel model on photoplethysmogram. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 4567–4570. [Google Scholar]
- Fujita, D.; Suzuki, A.; Ryu, K. PPG-Based Systolic Blood Pressure Estimation Method Using PLS and Level-Crossing Feature. Appl. Sci. 2019, 9, 304. [Google Scholar] [CrossRef]
- Frey, B.; Waldvogel, K.; Balmer, C. Clinical applications of photoplethysmography in paediatric intensive care. Intensiv. Care Med. 2007, 34, 578–582. [Google Scholar] [CrossRef][Green Version]
- Aoyagi, T. Pulse oximetry: Its invention, theory, and future. J. Anesth. 2003, 17, 259–266. [Google Scholar] [CrossRef]
- Yoshiya, I.; Shimada, Y.; Tanaka, K. Spectrophotometric monitoring of arterial oxygen saturation in the fingertip. Med. Biol. Eng. Comput. 1980, 18, 27–32. [Google Scholar] [CrossRef]
- Xing, X.; Sun, M. Optical blood pressure estimation with photoplethysmography and FFT-based neural networks. Biomed. Opt. Express 2016, 7, 3007–3020. [Google Scholar]
- Lee, H.; Kim, E.; Lee, Y.; Kim, H.; Lee, J.; Kim, M.; Yoo, H.Y.; Yoo, S. Toward all-day wearable health monitoring: An ultralow-power, reflective organic pulse oximetry sensing patch. Sci. Adv. 2018, 4, eaas9530. [Google Scholar]
- Chandrasekhar, A.; Kim, C.-S.; Naji, M.; Natarajan, K.; Hahn, J.-O.; Mukkamala, R. Smartphone-based blood pressure monitoring via the oscillometric finger-pressing method. Sci. Transl. Med. 2018, 10, eaap8674. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Chen, Z.; Ward, R.; Elgendi, M. Hypertension assessment using photoplethysmography: A risk stratification approach. J. Clin. Med. 2019, 8, 12. [Google Scholar]
- Liang, Y.; Chen, Z.; Ward, R.; Elgendi, M. Photoplethysmography and Deep Learning: Enhancing Hypertension Risk Stratification. Biosensors 2018, 8, 101. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Fletcher, R.; Liang, Y.; Howard, N.; Lovell, N.H.; Abbott, D.; Lim, K.; Ward, R. The use of photoplethysmography for assessing hypertension. NPJ Digit. Med. 2019, 2, 1–11. [Google Scholar]
- Millasseau, S.C.; Guigui, F.G.; Kelly, R.P.; Prasad, K.; Cockcroft, J.R.; Ritter, J.M.; Chowienczyk, P.J. Noninvasive assessment of the digital volume pulse: Comparison with the peripheral pressure pulse. Hypertension 2000, 36, 952–956. [Google Scholar] [CrossRef] [PubMed]
- Kavsaoğlu, A.R.; Polat, K.; Hariharan, M. Non-invasive prediction of hemoglobin level using machine learning techniques with the PPG signal’s characteristics features. Appl. Soft Comput. 2015, 37, 983–991. [Google Scholar] [CrossRef]
- Kılıçkaya, S.; Güner, A.; Dal, B. Comparison of Different Machine Learning Techniques for the Cuffless Estimation of Blood Pressure using PPG Signals. In Proceedings of the 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Turkey, Ankara, 26–27 June 2020; pp. 1–6. [Google Scholar]
- Romano, J.D.; Le, T.T.; Fu, W.; Moore, J.H. TPOT-NN: Augmenting tree-based automated machine learning with neural network estimators. Genet. Program. Evolv. Mach. 2021, 1–21, 8. [Google Scholar]
- Xie, Q.; Wang, G.; Peng, Z.; Lian, Y. Machine learning methods for real-time blood pressure measurement based on photoplethysmography. In Proceedings of the 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 19–21 November 2018; pp. 1–5. [Google Scholar]
- Yang, S.; Zaki, W.S.; Morgan, S.P.; Cho, S.Y.; Correia, R.; Wen, L.; Zhang, Y. Blood Pressure Estimation from Photoplethysmogram and Electrocardiogram Signals Using Machine Learning; IET: Washington, DC, USA, 2018; pp. 1–5. [Google Scholar]
- Waring, J.; Lindvall, C.; Umeton, R. Automated machine learning: Review of the state-of-the-art and opportunities for healthcare. Artif. Intell. Med. 2020, 104, 101822. [Google Scholar] [CrossRef] [PubMed]
- Olson, R.S.; Moore, J.H. TPOT: A Tree-Based Pipeline Optimization Tool for Automating Machine Learning. In Automated Machine Learning; Springer: Cham, Switzerland, 2019; pp. 151–160. [Google Scholar]
- Rajkomar, A.; Dean, J.; Kohane, I. Machine Learning in Medicine. N. Engl. J. Med. 2019, 380, 1347–1358. [Google Scholar] [CrossRef] [PubMed]
- Beam, A.L.; Kohane, I.S. Big Data and Machine Learning in Health Care. JAMA 2018, 319, 1317–1318. [Google Scholar] [CrossRef]
- Auffray, C.; Balling, R.; Barroso, I.; Bencze, L.; Benson, M.; Bergeron, J.; Bernal-Delgado, E.; Blomberg, N.; Bock, C.; Conesa, A.; et al. Making sense of big data in health research: Towards an EU action plan. Genome Med. 2016, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Xing, X.; Ma, Z.; Zhang, M.; Zhou, Y.; Dong, W.; Song, M. An Unobtrusive and Calibration-free Blood pressure estimation Method using photoplethysmography and Biometrics. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef]
- Rundo, F.; Ortis, A.; Battiato, S.; Conoci, S. Advanced bio-inspired system for noninvasive cuff-less blood pressure estimation from physiological signal analysis. Computation 2018, 6, 46. [Google Scholar] [CrossRef]
- Slapničar, G.; Mlakar, N.; Luštrek, M. Blood Pressure Estimation from Photoplethysmogram Using a Spectro-Temporal Deep Neural Network. Sensors 2019, 19, 3420. [Google Scholar] [CrossRef]
- Kim, J.Y.; Cho, B.H.; Im, S.M.; Jeon, M.J.; Kim, I.Y.; Kim, S.I. Comparative study on artificial neural network with multiple regressions for continuous estimation of blood pressure. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 6942–6945. [Google Scholar]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuff-less high-accuracy calibration-free blood pressure estimation using pulse transit time. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 1006–1009. [Google Scholar]
- Cattivelli, F.S.; Garudadri, H. Noninvasive cuffless estimation of blood pressure from pulse arrival time and heart rate with adaptive calibration. In Proceedings of the 2009 Sixth International Workshop on Wearable and Implantable Body Sensor Networks, Berkeley, CA, USA, 3–5 June 2009; pp. 114–119. [Google Scholar]
- Elgendi, M. On the analysis of fingertip photoplethysmogram signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Kavsaoğlu, A.R.; Polat, K.; Bozkurt, M.R. A novel feature ranking algorithm for biometric recognition with PPG signals. Comput. Biol. Med. 2014, 49, 1–14. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Y.; Cho, S.-Y.; Morgan, S.P.; Correia, R.; Wen, L. Cuff-less blood pressure measurement using fingertip photoplethysmogram signals and physiological characteristics. In Proceedings of the Optics in Health Care and Biomedical Optics VIII, Beijing, China, 23 October 2018; p. 1082036. [Google Scholar]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 847–855. [Google Scholar]
- Gotlibovych, I.; Crawford, S.; Goyal, D.; Liu, J.; Kerem, Y.; Benaron, D.; Yilmaz, D.; Marcus, G.; Li, Y. End-to-end deep learning from raw sensor data: Atrial fibrillation detection using wearables. arXiv 2018, arXiv:1807.10707. [Google Scholar]
- Zhang, Y.; Feng, Z. A SVM method for continuous blood pressure estimation from a PPG signal. In Proceedings of the 9th International Conference on Machine Learning and Computing, Singapore, 24–26 February 2017; pp. 128–132. [Google Scholar]
- Su, P.; Ding, X.R.; Zhang, Y.T.; Liu, J.; Miao, F.; Zhao, N. Long-term blood pressure prediction with deep recurrent neural networks. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 323–328. [Google Scholar]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuffless blood pressure estimation algorithms for continuous healthcare monitoring. IEEE Trans. Biomed. Eng. 2017, 64, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Cosoli, G.; Spinsante, S.; Scalise, L. Wrist-worn and chest-strap wearable devices: Systematic review on accuracy and metrological characteristics. Measurement 2020, 159, 107789. [Google Scholar] [CrossRef]
- Nachman, D.; Gepner, Y.; Goldstein, N.; Kabakov, E.; Ishay, A.B.; Littman, R.; Azmon, Y.; Jaffe, E.; Eisenkraft, A. Comparing blood pressure measurements between a photoplethysmography-based and a standard cuff-based manometry device. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Scalise, L.; Cosoli, G.; Casacanditella, L.; Casaccia, S.; Rohrbaugh, J.W. The measurement of blood pressure without contact: An LDV-based technique. In Proceedings of the 2017 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rochester, MN, USA, 7–10 May 2017; pp. 245–250. [Google Scholar]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef]
- Kurylyak, Y.; Lamonaca, F.; Grimaldi, D. A Neural Network-based method for continuous blood pressure estimation from a PPG signal. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; pp. 280–283. [Google Scholar]
- Aguirre, N.; Grall-Maës, E.; Cymberknop, L.J.; Armentano, R.L. Blood Pressure Morphology Assessment from Photoplethysmogram and Demographic Information Using Deep Learning with Attention Mechanism. Sensors 2021, 21, 2167. [Google Scholar] [CrossRef]
- Fortin, F.A.; De Rainville, F.M.; Gardner, M.A.G.; Parizeau, M.; Gagné, C. DEAP: Evolutionary algorithms made easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Miao, F.; Wen, B.; Hu, Z.; Fortino, G.; Li, Y. Continuous Blood Pressure Measurement from One-Channel Electrocardiogram Signal Using Deep-Learning Techniques. Artif. Intell. Med. 2020, 108, 101919. [Google Scholar] [CrossRef]
- Hasanzadeh, N.; Ahmadi, M.M.; Mohammadzade, H. Blood Pressure Estimation Using Photoplethysmogram Signal and Its Morphological Features. IEEE Sens. J. 2019, 20, 4300–4310. [Google Scholar] [CrossRef]
- Piskorowski, J. Suppressing harmonic powerline interference using multiple-notch filtering methods with improved transient behavior. Measurement 2012, 45, 1350–1361. [Google Scholar] [CrossRef]
- Moraes, J.L.; Rocha, M.X.; Vasconcelos, G.G.; Vasconcelos Filho, J.E.; De Albuquerque, V.H.C.; Alexandria, A.R. Advances in Photopletysmography Signal Analysis for Biomedical Applications. Sensors 2018, 18, 1894. [Google Scholar] [CrossRef]
- De-Cheveigné, A.; Nelken, I. Filters: When, why, and how (not) to use them. Neuron 2019, 102, 280–293. [Google Scholar] [CrossRef] [PubMed]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef]
- Oja, E.; Yuan, Z. The FastICA Algorithm Revisited: Convergence Analysis. IEEE Trans. Neural Netw. 2006, 17, 1370–1381. [Google Scholar] [CrossRef]
- Haider, A.W.; Larson, M.G.; Franklin, S.S.; Levy, D. Systolic Blood Pressure, Diastolic Blood Pressure, and Pulse Pressure as Predictors of Risk for Congestive Heart Failure in the Framingham Heart Study. Ann. Intern. Med. 2003, 138, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Madhav, K.V.; Ram, M.R.; Krishna, E.H.; Reddy, K.N.; Reddy, K.A. Estimation of respiratory rate from principal components of photoplethysmographic signals. In Proceedings of the 2010 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 30 November–2 December 2010; pp. 311–314. [Google Scholar]
- Muneer, A.; Fati, S.M. A Comparative Analysis of Machine Learning Techniques for Cyberbullying Detection on Twitter. Future Internet 2020, 12, 187. [Google Scholar] [CrossRef]
- Akbar, N.A.; Sunyoto, A.; Rudyanto Arief, M.; Caesarendra, W. Improvement of decision tree classifier accuracy for healthcare insurance fraud prediction by using Extreme Gradient Boosting algorithm. In Proceedings of the 2020 International Conference on Informatics, Multimedia, Cyber and Information System (ICIMCIS), Multimedia, Cyber, 19–20 November 2020. [Google Scholar] [CrossRef]
- Imandoust, S.B.; Bolandraftar, M. Application of k-nearest neighbor (knn) approach for predicting economic events: Theoretical background. Int. J. Eng. Res. Appl. 2013, 3, 605–610. [Google Scholar]
- Čisar, P.; Čisar, S.M. Skewness and kurtosis in function of selection of network traffic distribution. Acta Polytech. Hung. 2010, 7, 95–106. [Google Scholar]
- Tjahjadi, H.; Ramli, K. Non-invasive blood pressure classification based on Photoplethysmography using K-Nearest Neighbors algorithm: A feasibility study. Information 2020, 11, 93. [Google Scholar] [CrossRef]
- Wall, M.E.; Rechtsteiner, A.; Rocha, L.M. Singular value decomposition and principal component analysis. In A Practical Approach to Microarray Data Analysis; Springer: Boston, MA, USA, 2003; pp. 91–109. [Google Scholar]
- Al-Ghobari, M.; Muneer, A.; Fati, S.M. Location-Aware Personalized Traveler Recommender System (LAPTA) Using Collaborative Filtering KNN. Comput. Mater. Continu. 2021, 68. [Google Scholar]
- Alsharif, M.H.; Kelechi, A.H.; Yahya, K.; Chaudhry, S.A. Machine learning algorithms for smart data analysis in internet of things environment: Taxonomies and research trends. Symmetry 2020, 12, 88. [Google Scholar] [CrossRef]
- Wu, H.; Ji, Z.; Li, M. Non-Invasive Continuous Blood-Pressure Monitoring Models Based on Photoplethysmography and Electrocardiography. Sensors 2019, 19, 5543. [Google Scholar] [CrossRef] [PubMed]
- Atkins, N. The British Hypertension Society protocol for the evaluation of automated and semi-automated blood pressure measuring devices with special reference to ambulatory systems. J. Hypertens. 1990, 8, 607–619. [Google Scholar]
- Association for the Advancement Instrumentation. American National Standard for Electronic or Automated Sphygmomanometers; ANSI/AAMI SP 10 2002; AAMI: Arlington, VA, USA, 2002. [Google Scholar]
- Rastegar, S.; GholamHosseini, H.; Lowe, A. Non-invasive continuous blood pressure monitoring systems: Current and proposed technology issues and challenges. Phys. Eng. Sci. Med. 2020, 43, 11–28. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).