Parallelization of Finding the Current Coordinates of the Lidar Based on the Genetic Algorithm and OpenMP Technology
Abstract
1. Introduction
- Processes the value of the parameters of the task itself, and their encoded form;
- Searches a solution to leave not from a single point, but with their some population;
- Uses only target function, not its derivatives or other additional information;
- Applies probabilistic rather than deterministic selection rules.
- We have proposed a simple yet accurate and computationally efficient approach to finding the lidar position based on a genetic algorithm and the OpenMP parallel computing technology. It provides the possibility of significant optimization of the computing process by its parallelization; the ability to solving the task for the case of an extensive data processing;
- We have developed the algorithmic implementation of the proposed method. It is especially relevant in the development of the multi-core architecture of modern computers.
- We have demonstrated the reduction in computational complexity using the proposed method; we have received an acceleration that goes to the number of cores of the appropriate computing system (we have achieved the parallel efficiency of about 1 in this case).
2. Analysis of Literary Sources
3. Materials and Methods
- Scans space around itself with a particular error.
- Moves on some vector also with a particular error.
- Creating an initial population.
- Calculation of bumping function for populations (evaluation).
- Repeat to perform the algorithm stop criterion:
- Choosing Individuals from current population (selection);
- Crossing or/and mutation;
- Calculation of bumping function for all persons;
- Formation of a new generation.
3.1. Modeling Sequential Algorithm Support
- Creating an initial population
- The initial point is known.
- The initial point is not specified.
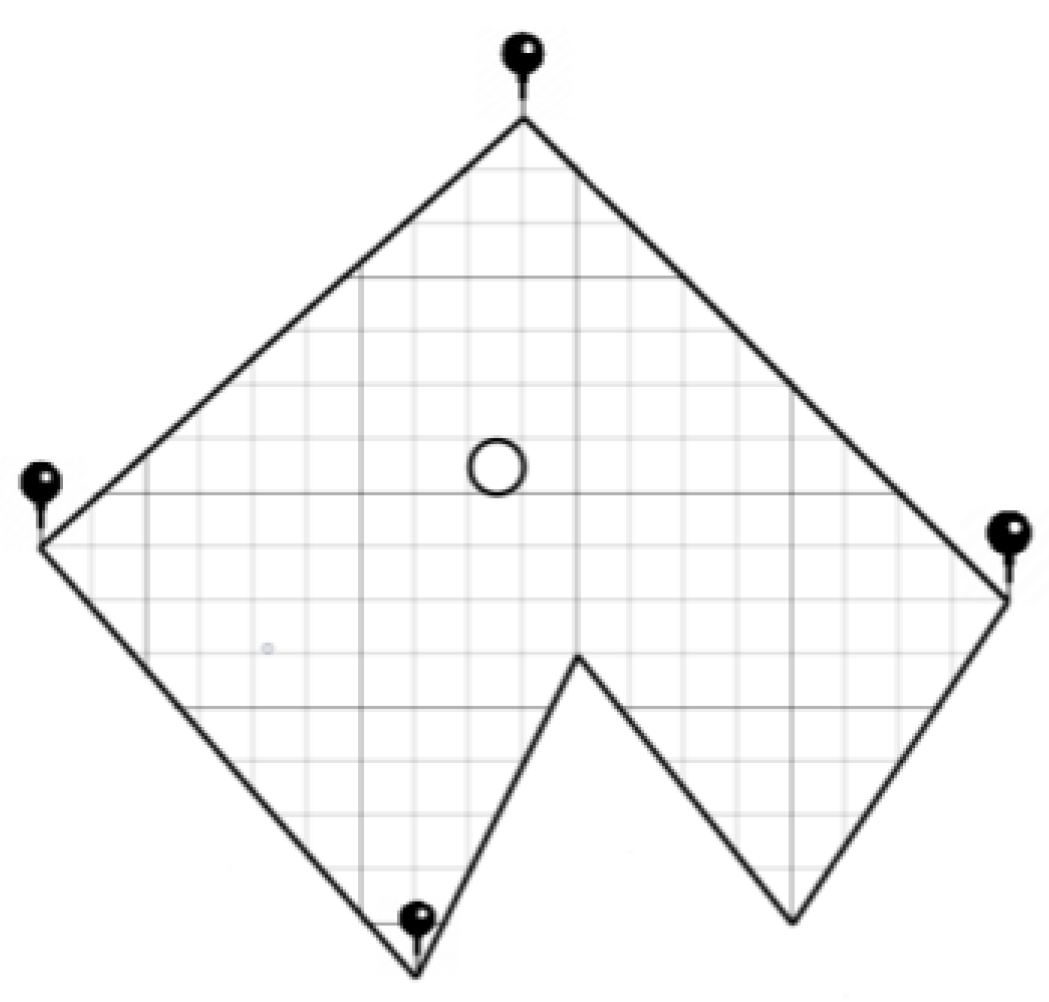
- Lidar’s Space Scanning Process
- Data analysis received from lidar after scanning
- Save all lidar measurements.
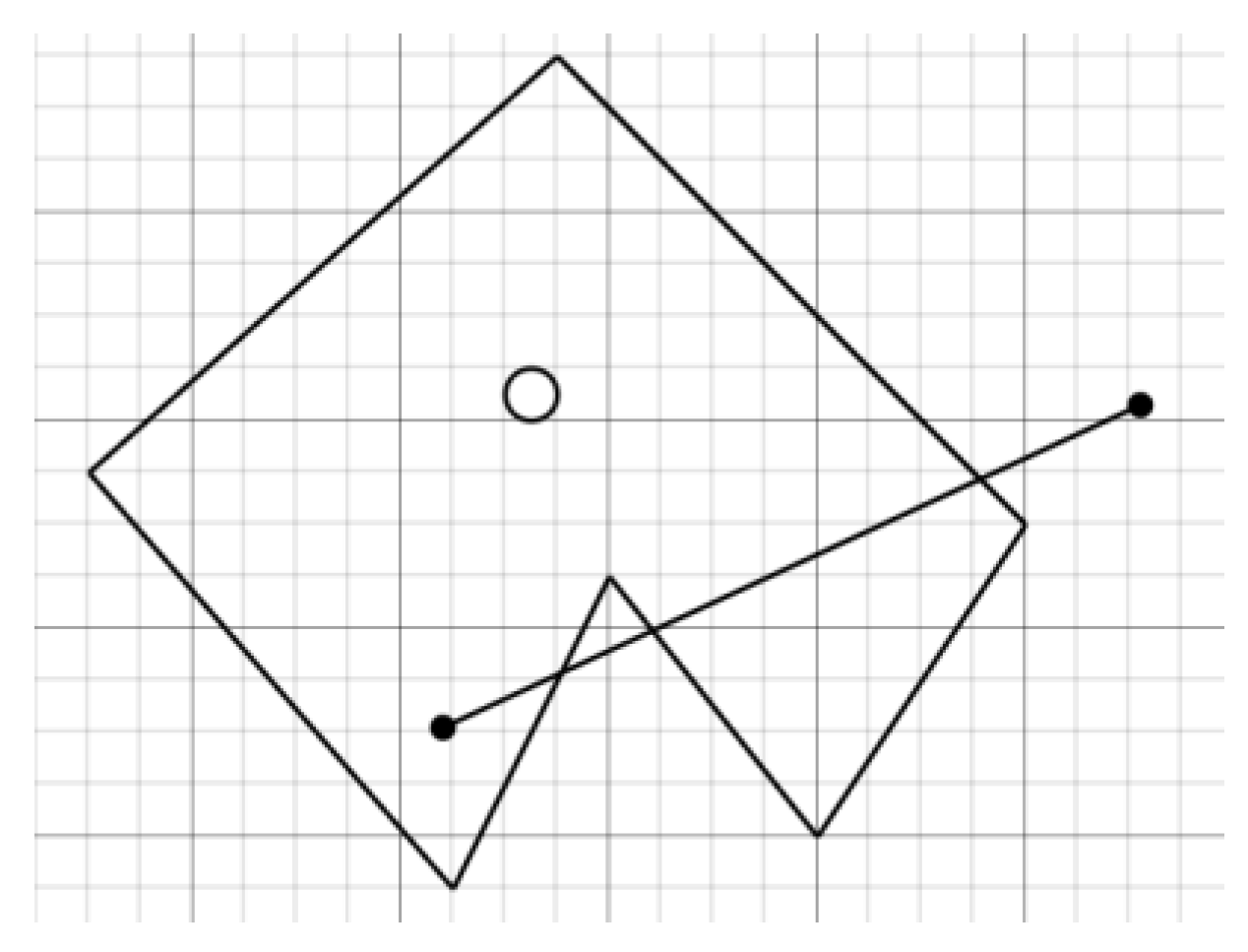
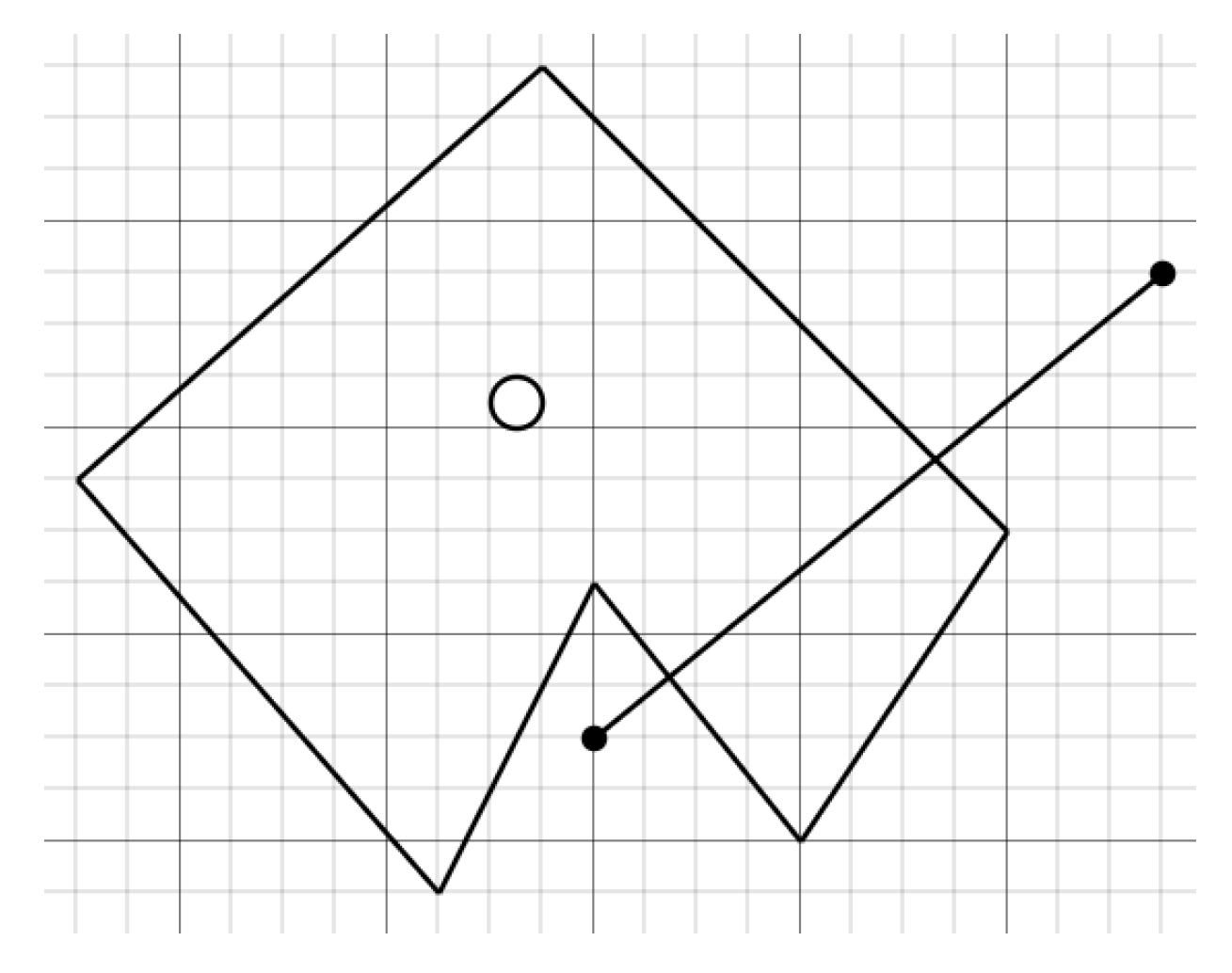
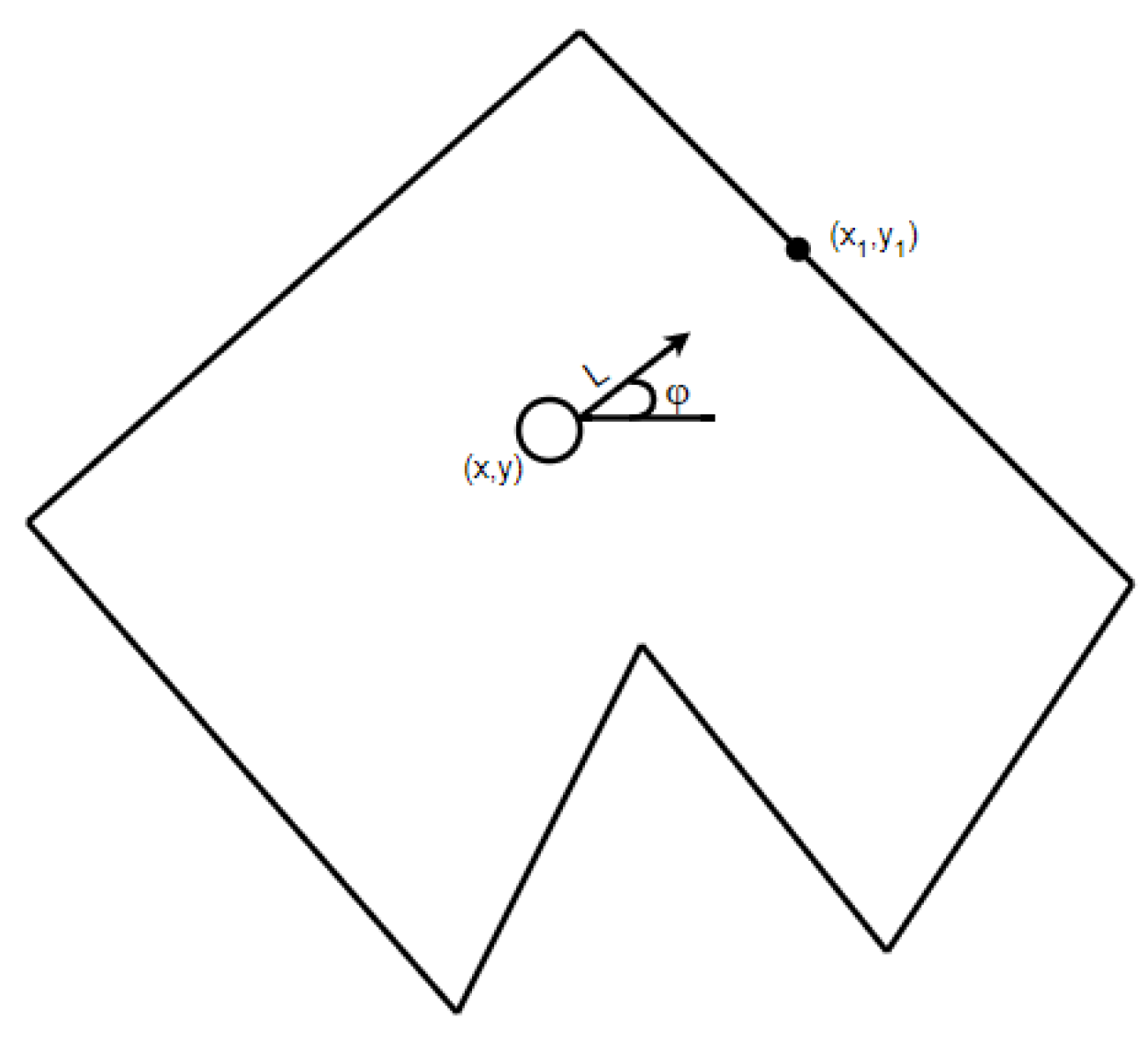
- By approaching the states of the placement represented by a certain point, for each of them, we find a possible point of collision with an obstacle. Since we know on which angle of the laser sends a laser, and the distance it has passed we can find a point of collision (see Figure 7):
- For each such point we find its deviation—a minimum among the distances to all sides of the polygon. We argue that the closest wall and will be able to go to the lidar laser, so we can estimate the deviation of this state as the amount of deviations of all measurements of the lidar:where is the minimum among the distances to the walls of our polygon.
- Transfer an estimate of deviation in a probability using a function of normal distributionwhere, mathematical expectation and standard deviation are given by the lidar parameter.
- The process of evolution and development of states
- We find the probability of each state.
- Normalize their likelihood so that the amount is equal to 1.
- Convert a set of probabilities into an interval amount. For example:
- Generate arbitrary numbers with a normal distribution of the gap . Then, if the generated number lies on the interval corresponding to the state with the number, we add this state into a set of newly formed ones.
3.2. Parallel Algorithm
- —the number of iterations of our lidar,
- —the number of measurements of lidar on each iteration,
- —number of vertices in our room,
- —number of generated initial states.
- Analysis of data from lidar;
- Evolutionary process.
4. Research Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abbasi, M.; Rafiee, M.; Khosravi, M.R.; Jolfaei, A.; Menon, V.G.; Koushyar, J.M. An efficient parallel genetic algorithm solution for vehicle routing problem in cloud implementation of the intelligent transportation systems. J. Cloud Comp. 2020, 9, 6. [Google Scholar] [CrossRef]
- Goldberg, D.E. (Ed.) The Design of Innovation: Lessons from and for Competent Genetic Algorithms; Springer-Science+Business Media, B.V.: Berlin/Heidelberg, Germany; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2002; Volume 7. [Google Scholar]
- Calaiselvy, C.; Yong, F.T.; Ping, L.W. A Genetic Algorithm for Robot Navigation. In Parallel and Distributed Computing: Applications and Technologies; Liew, K.M., Shen, H., See, S., Cai, W., Fan, P., Horiguchi, S., Eds.; PDCAT 2004. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3320. [Google Scholar] [CrossRef]
- Christophe, S. Genetic Algorithms with Deep Learning for Robot Navigation; 2016; 80p, Available online: https://www.doc.ic.ac.uk (accessed on 13 March 2021).
- López-González, A.; Meda Campaña, J.; Martínez, E.G.; Contro, P. Multi robot distance based formation using Parallel Genetic Algorithm. Appl. Soft Comput. 2019, 86, 105929. [Google Scholar] [CrossRef]
- Rutkovskaya, D.; Pilignan, M.; Rutkovsky, L. Neural Networks, Genetic Algorithms and Fuzzy Systems; Translation Polish, I.D., Rudinsky, M., Eds.; Hotline. Telecom; Goryachaya Liniya-Telecom Publ: Moscow, Russia, 2007; 452p. [Google Scholar]
- Keco, D.; Subasi, A. Parallelization of genetic algorithms using Hadoop Map/Reduce. S. Eur. J. Soft Comput. 2012, 1. [Google Scholar] [CrossRef]
- Azevedo, F.; Shinde, P.; Santos, L.; Mendes, J.; Santos, F.N.; Mendonça, H. Parallelization of a vine trunk detection algorithm for a real time robot localization system. In Proceedings of the 2019 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Gondomar, Portugal, 24–26 April 2019; pp. 1–6. [Google Scholar]
- Li, Z.; Hodgson, M.E.; Li, W. A general-purpose framework for parallel processing of large-scale LiDAR data. Int. J. Digit. Earth 2018, 11, 26–47. [Google Scholar] [CrossRef]
- Elhoseny, M.; Tharwat, A.; Hassanien, A.E. Bezier curve based path planning in a dynamic field using modified genetic algorithm. J. Comput. Sci. 2018, 25, 339–350. [Google Scholar] [CrossRef]
- Jan, B.; Montrucchio, B.; Ragusa, C.; Khan, F.G.; Khan, O. Fast parallel sorting algorithms on GPUS. Int. J. Distrib. Parallel Syst. IJDPS 2012, 3, 107–118. [Google Scholar] [CrossRef]
- Koguciuk, D. Parallel RANSAC for Point Cloud Registration. Found. Comput. Decis. Sci. 2017, 42, 15. [Google Scholar] [CrossRef]
- Amor, N.B.; Baklouti, M.; Barhoumi, K.; Jallouli, M. Efficient embedded software implementation of a low cost robot localization system. In Proceedings of the 2019 IEEE International Conference on Design & Test of Integrated Micro & Nano-Systems (DTS), Gammarth, Tunisia, 28 April–1 May 2019; pp. 1–5. [Google Scholar]
- Mochurad, L.; Solomiia, A. Optimizing the Computational Modeling of Modern Electronic Optical Systems. In Lecture Notes in Computational Intelligence and Decision Making; Lytvynenko, V., Babichev, S., Wójcik, W., Vynokurova, O., Vyshemyrskaya, S., Radetskaya, S., Eds.; ISDMCI 2019; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1020, pp. 597–608. [Google Scholar] [CrossRef]
- Mochurad, L.I.; Boyko, N.I. Technologies of Distributed Systems and Parallel Computation: Monograph; Publishing House “Bona”: Lviv, Ukraine, 2020; 261p, ISBN 978-617-7815-25-8. [Google Scholar]
- Mochurad, L.; Shchur, G. Parallelization of Cryptographic Algorithm Based on Different Parallel Computing Technologies. In Proceedings of the Symposium on Information Technologies & Applied Sciences (IT&AS 2021), Bratislava, Slovak Republic, 5 March 2021; Volume 2824, pp. 20–29, ISSN 1613-0073. [Google Scholar]
- Agarwal, R.C.; Gustavson, F.; Zubair, M. A high-performance matrix multiplication algorithm on a distributed memory parallel computer using overlapped communication. IBM J. Res. Dev. 1994, 38, 673–682. [Google Scholar] [CrossRef][Green Version]
- Andrés, R.; Masegosa, A.M.; Martínez, D.R.-L.; Rafael Cabañas, A.; Salmerón, H.; Langseth, T.D.; Nielsen, A.L.M. AMIDST: A Java toolbox for scalable probabilistic machine learning. Knowl. Based Syst. 2019, 163, 595–597. [Google Scholar]
- Lorenzo, O.G.; Martínez, J.; Vilariño, D.L.; Pena, T.F.; Cabaleiro, J.C.; Rivera, F.F. Landing sites detection using LiDAR data on manycore systems. J. Supercomput. 2017, 73, 557–575. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R.; Vitynskyi, P.; Zub, K.; Tkachenko, P.; Dronyuk, I. Stacking-based GRNN-SGTM Ensemble Model for Prediction Tasks. In Proceedings of the 2020 International Conference on Decision Aid Sciences and Application (DASA), Sakheer, Bahrain, 8–9 November 2020; pp. 326–330. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R.; Dronyuk, I.; Tkachenko, P.; Gregus, M.; Rashkevych, M. Predictive modeling based on small data in clinical medicine: RBF-based additive input-doubling method. Math. Biosci. Eng. 2021, 18, 2599–2613. [Google Scholar] [CrossRef]
- Lonely, V.; Dzelandzyk, U. Using genetic algorithms for approximation of function real numbers. In Computer Science and Information Technologies: Bulletin of the National University “Lviv Polytechnic”; No 694; Published by Lviv Polytechnic National University: Lviv Oblast, Ukraine, 2011; pp. 313–318. [Google Scholar]
- Kanungo, P.; Nanda, P.K.; Ghosh, A. Detection of earth surface cracks using parallel genetic algorithm based thresholding. In Proceedings of the Accepted for the International conference on Advances in Computing, Control and Telecommunication Technology, ACT-2009, Kerala, India, 28–29 December 2009; pp. 4–11. [Google Scholar]
- Kanungo, P.; Nanda, P.K.; Ghosh, A.; Samal, U.C. Classification of objects and background using Parallel Genetic Algorithm based Clustering. In Proceedings of the IEEEInternational Conference on Signal and Image Processing, BCET, Hubli, India, 7–9 December 2006; pp. 42–53. [Google Scholar]
- Fivos, P. Spatial Complexity: Theory, Mathematical Methods and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2020; 319p, ISBN 10 3030596702. [Google Scholar]





| 4-Core Processor | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 Threads | 4 Threads | 8 Threads | ||||||||
| 100 | 375 | 337 | 1.3274 | 0.2781 | 290 | 1.3923 | 0.3232 | 370 | 1.4082 | 0.25325 |
| 200 | 703 | 562 | 1.4761 | 0.3252 | 504 | 1.5312 | 0.37022 | 478 | 1.7361 | 0.418 |
| 500 | 1325 | 974 | 1.694 | 0.3314 | 793 | 1.7837 | 0.38308 | 713 | 2.0863 | 0.43312 |
| 1000 | 2172 | 1873 | 1.8431 | 0.3908 | 1418 | 1.9658 | 0.4238 | 1256 | 2.3595 | 0.5259 |
| 8-Core Processor | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 Threads | 4 Threads | 8 Threads | ||||||||
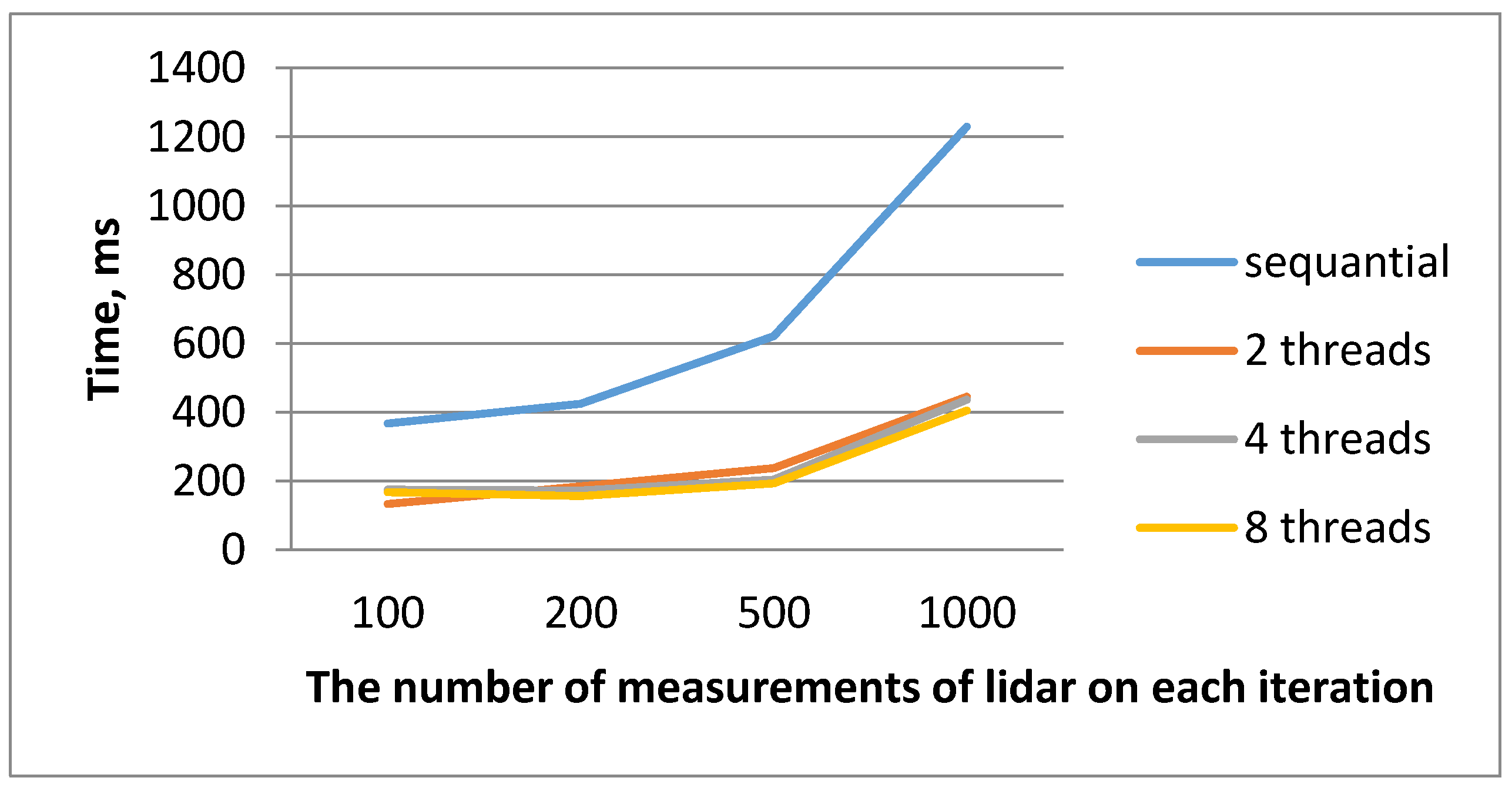
| 100 | 367 | 133 | 1.6738 | 0.34492 | 175 | 1.9857 | 0.262 | 167 | 1.223 | 0.1529 |
| 200 | 424 | 184 | 1.9741 | 0.345 | 172 | 2.3463 | 0.3641 | 156 | 3.426 | 0.42825 |
| 500 | 621 | 237 | 2.7459 | 0.3389 | 204 | 2.9746 | 0.3655 | 193 | 3.774 | 0.4717 |
| 1000 | 1230 | 445 | 3.0735 | 0.34112 | 436 | 3.8735 | 0.37512 | 405 | 4.103 | 0.53662 |
| 8-Core Processor | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 4 Threads | 8 Threads | 16 Threads | ||||||||
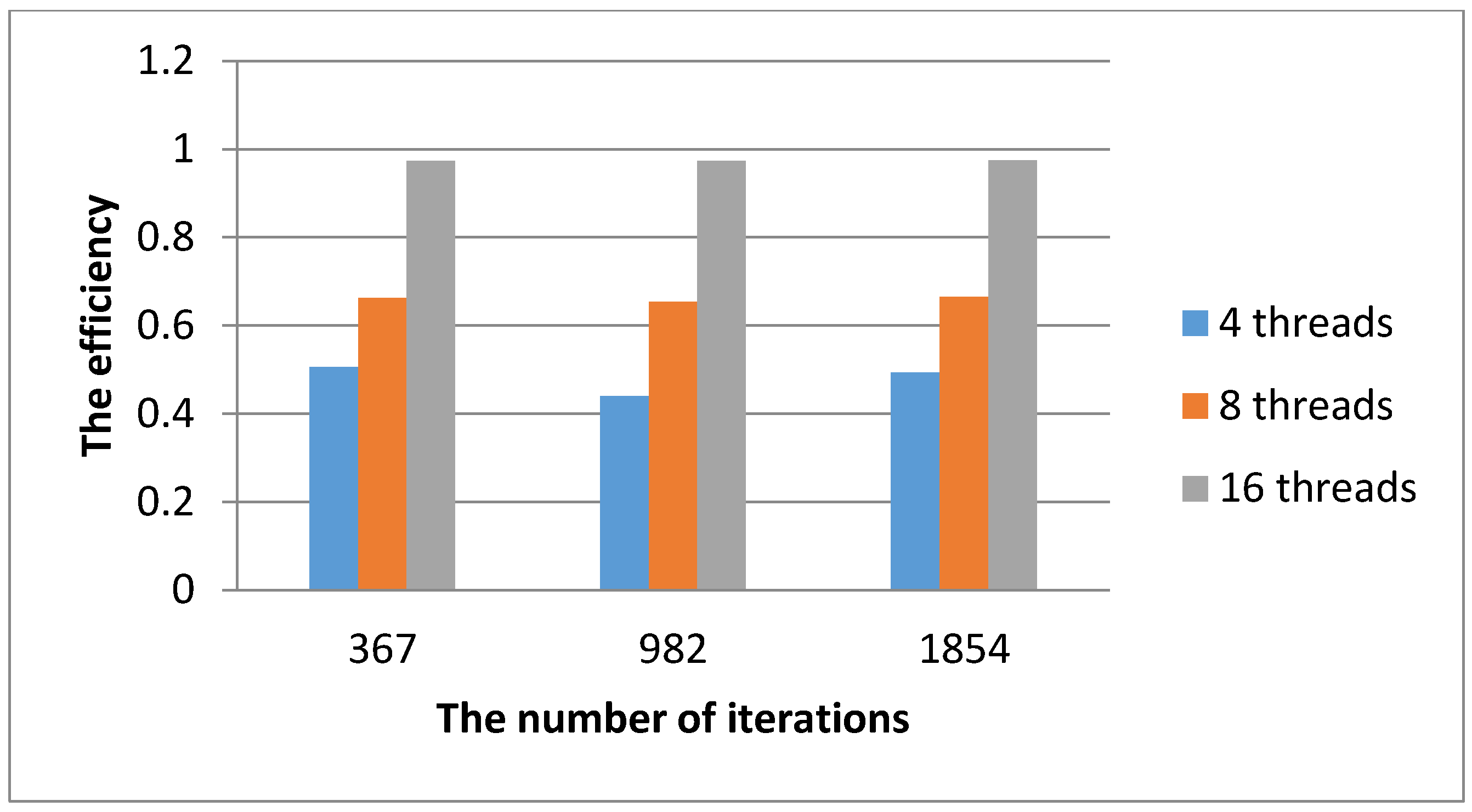
| 367 | 109.807 | 26.151 | 4.0445 | 0.506 | 20.738 | 5.297 | 0.6621 | 14.107 | 7.7883 | 0.97354 |
| 982 | 214.007 | 60.913 | 3.513 | 0.4391 | 40.888 | 5.234 | 0.65424 | 27.468 | 7.791 | 0.973875 |
| 1854 | 335.25 | 84.8734 | 3.95 | 0.49375 | 62.986 | 5.323 | 0.6653 | 42.9917 | 7.798 | 0.97475 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mochurad, L.; Kryvinska, N. Parallelization of Finding the Current Coordinates of the Lidar Based on the Genetic Algorithm and OpenMP Technology. Symmetry 2021, 13, 666. https://doi.org/10.3390/sym13040666
Mochurad L, Kryvinska N. Parallelization of Finding the Current Coordinates of the Lidar Based on the Genetic Algorithm and OpenMP Technology. Symmetry. 2021; 13(4):666. https://doi.org/10.3390/sym13040666
Chicago/Turabian StyleMochurad, Lesia, and Natalia Kryvinska. 2021. "Parallelization of Finding the Current Coordinates of the Lidar Based on the Genetic Algorithm and OpenMP Technology" Symmetry 13, no. 4: 666. https://doi.org/10.3390/sym13040666
APA StyleMochurad, L., & Kryvinska, N. (2021). Parallelization of Finding the Current Coordinates of the Lidar Based on the Genetic Algorithm and OpenMP Technology. Symmetry, 13(4), 666. https://doi.org/10.3390/sym13040666






