The Cosmological OTOC: A New Proposal for Quantifying Auto-Correlated Random Non-Chaotic Primordial Fluctuations †
Abstract
| Contents | ||
| 1 | Introduction | 4 |
| 2 | Formulation of Non-Chaotic Auto-Correlated OTO Functions in Primordial Cosmology | 9 |
| 2.1 Non-Chaotic Auto-Correlated OTO Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 9 | |
| 2.2 Eigenstate Representation of Non-Chaotic OTOC in Quantum Statistical Mechanics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 12 | |
| 2.3 Constructing Non-Chaotic OTOC in Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 21 | |
| 2.3.1 For Massless Scalar Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 22 | |
| 2.3.2 For Partially Massless Scalar Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 24 | |
| 2.3.3 For Partially Massless Scalar Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 25 | |
| 3 | Quantum Non-Chaotic Auto-Correlated OTO Amplitudes and OTOC in Primordial Cosmology | 26 |
| 3.1 Computational Strategy for Non-Chaotic Auto-Correlated OTO Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 27 | |
| 3.2 Classical Mode Functions to Compute Non-Chaotic Auto-Correlated OTO Functions in Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 29 | |
| 3.3 Quantum Mode Function to Compute Non-Chaotic Auto-Correlated OTO Functions in Primordial Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 32 | |
| 3.4 Quantum Operators for Non-Chaotic Auto-Correlated OTO Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 32 | |
| 3.5 Cosmological Two-Point and Four-Point “In-In” Non-Chaotic OTO Amplitudes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 33 | |
| 3.5.1 Non-Chaotic Auto-Correlators in Primordial Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 33 | |
| 3.5.2 Fourier Space Representation of the Commutator Bracket: Application to Two-Point Non-Chaotic Auto-Correlated OTO Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 36 | |
| 3.5.3 Fourier Space Representation of Square of the Commutator Bracket: Application to Four-Point Non-Chaotic Auto-Correlated OTO Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 38 | |
| 3.6 Thermal Partition Function in Primordial Cosmology: Quantum Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 40 | |
| 3.6.1 Initial Quantum State in Primordial Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 40 | |
| 3.6.2 Quantum Partition Function in Terms of Rescaled Perturbation Field Variable in Primordial Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 42 | |
| 3.6.3 Quantum Partition Function in Terms of the Cosmological Scalar Curvature Perturbation Field Variable in Primordial Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 42 | |
| 3.7 Trace of Two-Point “In-In” Non-Chaotic Extension of OTO Amplitudes for Primordial Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 43 | |
| 3.8 New OTOCS from Regularised Two-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Rescaled Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 44 | |
| 3.9 New OTOCS from Regularised Two-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Curvature Perturbation Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 46 | |
| 3.10 Trace of Four-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitude for Primordial Cosmology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 50 | |
| 3.11 New OTOCs from Regularised Four-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Rescaled Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 51 | |
| 3.11.1 Without Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 51 | |
| 3.11.2 With Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 52 | |
| 3.12 New OTOCS from Regularised Four-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Curvature Perturbation Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 55 | |
| 3.12.1 Without Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 55 | |
| 3.12.2 With Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 55 | |
| 4 | Numerical Analysis I: Interpretation of Two-Point Non-Chaotic Auto-Correlated OTO Functions | 55 |
| 5 | Numerical Analysis II: Interpretation of Four-Point Non-Chaotic Auto-Correlated OTO Functions | 58 |
| 6 | Classical Limit of Non-Chaotic Auto-Correlated OTO Amplitudes and OTOC in Primordial Cosmology | 70 |
| 6.1 Computational Strategy for Non-Chaotic Auto-Correlated OTO Functions in the Classical Limit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 70 | |
| 6.2 Classical Limit of Cosmological Two-Point “In-In” Non-Chaotic OTO Amplitudes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 71 | |
| 6.3 Classical Limit of Cosmological Four-Point “In-In” Non-Chaotic OTO Amplitudes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 72 | |
| 6.4 Cosmological Partition Function: Classical Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 74 | |
| 6.4.1 Classical Partition Function in Terms of Rescaled Field Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 74 | |
| 6.4.2 Classical Partition Function in Terms of Curvature Perturbation Field Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 74 | |
| 6.5 Classical Limit of Cosmological Two-Point Non-Chaotic OTOC: Rescaled Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 75 | |
| 6.6 Classical Limit of Cosmological Two-Point Non-Chaotic OTOC: Curvature Perturbation Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 77 | |
| 6.7 Classical Limit of Cosmological Four-Point Non-Chaotic OTOC: Rescaled Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 77 | |
| 6.7.1 Without Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 77 | |
| 6.7.2 With Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 80 | |
| 6.8 Classical Limit of Cosmological Four-Point Non-Chaotic OTOC: Curvature Perturbation Field Version . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 81 | |
| 6.8.1 Without Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 81 | |
| 6.8.2 With Normalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 81 | |
| 7 | Summary and Outlook | 82 |
| A | Asymptotic Features of the Scalar Mode Functions in Cosmological Perturbation Theory | 84 |
| B | Quantum Two-Point OTO Amplitudes for Cosmology | 86 |
| B.1 Definition of OTO Amplitude . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 86 | |
| B.2 Definition of OTO Amplitude . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 86 | |
| C | Quantum Four-Point OTO Amplitudes for Cosmology | 87 |
| C.1 Definition of OTO Amplitude and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 87 | |
| C.2 Definition of OTO Amplitude and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 89 | |
| C.3 Definition of OTO Amplitude and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 91 | |
| C.4 Definition of OTO Amplitude and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 92 | |
| D | Computation of Classical Limit of Four-Point “In-In” OTO Amplitudes for Cosmology | 94 |
| E | Computation of the Trace of the Two-Point Amplitude in OTOC | 98 |
| F | Computation of the Trace of the Four-Point Amplitude in OTOC | 100 |
| G | Computation of the Trace of the Four-Point Amplitude in OTOC | 103 |
| H | Time-Dependent Four-Point Amplitudes in OTOC | 105 |
| H.1 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 106 | |
| H.2 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 109 | |
| H.3 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 109 | |
| H.4 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 110 | |
| H.5 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 110 | |
| H.6 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 111 | |
| H.7 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 112 | |
| H.8 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 112 | |
| H.9 Computation of and . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 113 | |
| I | Computation of the Normalisation Factor in Four-Point OTOC | 114 |
| I.1 Normalisation Factor of Four-Point OTOC Computed from Rescaled Field Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 114 | |
| I.2 Normalisation Factor of Four-Point OTOC Computed from Curvature Perturbation Field Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 117 | |
| J | Computation of the Normalisation Factor in Classical Limit of Four-Point OTOC | 119 |
| J.1 Normalisation Factor of the Classical Version of Four-Point OTOC Computed from Rescaled Field Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 119 | |
| J.2 Normalisation Factor of the Classical Version of Four-Point OTOC Computed from Curvature Perturbation Field Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 120 | |
| References | 122 | |
1. Introduction
- First possibility:The first possibility is to include future observational aspects to verify various theoretical proposals in cosmology. These theoretical proposals are appended below:
- Second possibility:The second possibility is probing of new physics by including significant features in primordial cosmology. This can be done by incorporating the concept of out-of-equilibrium in primordial cosmological quantum correlation functions. Before this work and previous work done by us in Reference [53], it was not at all mentioned in the corresponding literature how to compute and finally quantify the cosmological correlators at out-of-equilibrium. It is also not even clear to what exact quantity one needs to compute to give an estimation of these mentioned new correlators. After this work, we are hopeful that at least technically we have provided some correct estimations of these non-equilibrium quantum correlators within the framework of primordial cosmology. Now to connect with the real cosmological scenario, let us mention some aspects appearing in the timeline of our universe where one can implement the presented methodology:
- Highlight I:The computation method presented in this paper helps us to quantify the quantum auto-correlations within the framework of primordial cosmology with random fluctuations. In this article, we have computed the expressions for the two-point and four-point auto-correlated cosmological OTO functions in the quantum regime. These computed expressions are completely new and the detailed discussions will be helpful to understand the underlying physical problem that we have studied in this paper.
- Highlight II:We have additionally studied the classical limits of the two-point and four-point auto-correlated cosmological OTO functions in terms of the phase-space thermal weighted average of classical Poisson brackets. Most importantly, this computation will provide the non-standard random behaviour, which is perfectly consistent with the expectations from the present scenario. Last but not the least, this particular computation will be very helpful to understand the super-horizon classical limiting behaviour of the computed auto-correlated OTO functions.
- Highlight III:The late time behaviour of the four-point auto-correlated OTO functions helps us to study the equilibrium feature of the quantum correlations which we have computed from the scalar cosmological perturbations. Obviously the scalar cosmological perturbation and its related stuffs upto quantizing the Hamiltonian is very well known, but the rest of the computations in this context are completely new. For better understanding purposes, we have provided a small portion of the cosmological perturbation with scalar modes before starting the computation of two- and four-point auto-correlated OTO functions.
- Highlight IV:We have provided the detailed computation of the normalised version of the four-point auto-correlated cosmological OTO functions which we found that are completely independent of the choice of the time-dependent perturbation variable appearing in the cosmological perturbation theory. To justify this statement, we have used co-moving gauge for simplicity.
- In Section 2, we discuss the formalism of computing the auto-correlated OTO functions in the context of primordial cosmology. This formalism is new, which we have highlighted in this paper.
- In Section 3, we provide the detailed derivation of quantum two-point and four-point auto-correlated OTO amplitudes and the related OTO function within the framework of primordial cosmology. This is the new calculation that we have provided in this paper.
- In Section 4 and Section 5, we present the numerical results from the quantum two-point and four-point auto-correlated OTO functions and also discuss about its physical interpretation. It is important to note that the numerical predictions obtained from the mentioned computations are also new and provide a new direction in the framework of primordial cosmology.
- In Section 6, we discuss the classical limit of the two-point and four-point OTO amplitudes and the related implications in cosmology. This is another new result we have provided in this paper which gives us a better understanding of the super-horizon classical limiting behaviour of the system under consideration.
- In Appendix A, Appendix B, Appendix C, Appendix D, Appendix E, Appendix F, Appendix G, Appendix H, Appendix I and Appendix J, we provide the details of the computations used in various sections of the paper. We believe this will help the general readers to understand the underlying physical problem that we have addressed in this paper.
2. Formulation of Non-Chaotic Auto-Correlated OTO Functions in Primordial Cosmology
2.1. Non-Chaotic Auto-Correlated OTO Functions
2.2. Eigenstate Representation of Non-Chaotic OTOC in Quantum Statistical Mechanics
- First family of quantum systems:The first family of quantum mechanical systems deals with only the micro-canonical part of the OTOCs. After taking the sum over all possible contributions from the eigenstates, one can find out that for these classes of quantum systems the cumulative contribution actually gives the expression for the thermal partition function for the class of quantum systems which will further cancel with the expression for the thermal partition function which is appearing in the denominator of these OTOCs to make the consistency with the definition of thermal average of any quantum mechanical operator at finite temperature over all possible eigenstates of the Hamiltonian of the system. This makes the final expression for OTOCs completely dependent on the micro-canonical part of the OTOCs after taking the sum over all eigenstate contributions. One of the well-known examples of these classes of models is the quantum harmonic oscillator (QHO) which can be solely represented by the contributions from the micro-canonical part after summing over all possible eigenstates of the Hamiltonian of the QHO. In this connection here, it is important to note that, at the perturbation level, cosmology with a free massive scalar field theory in an FLRW space-time can be represented as a quantum parametric oscillator with a time-dependent frequency in the Fourier space, but instead of having a harmonic oscillator type of representation within the framework of quantum mechanical framework of cosmology, we do not have any eigenstates (We all know that our universe evolved with respect to the time scale once. Therefore, if we want to explain the background framework of primordial cosmology in the quantum regime then the Euclidean vacuum state or the Bunch–Davies vacuum state or the more generalized De Sitter isommetric -vacua cannot be treated as the eigenstate of the quantum Hamiltonian of parametric harmonic oscillator in the Fourier space representation as we cannot repeat the evolution of our universe. Therefore, that time-dependent Fourier mode integrated continuous function of energy cannot be treated as the eigen energy spectrum as appearing in the present context, where eigenstates of the Hamiltonian play a significant role to determine the expression for OTOCs). Instead of having a eigenstate in the context of cosmology one can define wave function of the universe and instead of having a discrete eigen energy spectrum in the context of cosmology we can find a continuous time-dependent momentum integrated spectrum over all Fourier modes.
- Second family of quantum systems:The second family of the quantum systems are those in which these defined OTOCs are quantified by the Boltzmann part as well as the micro-canonical part. In addition, after summing over all possible quantum states and implementing the definition of the thermal average of a quantum operator one can find out the final result is dependent on the inverse of the temperature, which can take care of the behaviour of the OTOCs when it reaches the thermodynamic equilibrium after waiting for large enough time in the late time scale and particularly this feature is completely absent in the context of the first family of the quantum mechanical systems. One of the simplest examples of this class of models is a particle in one dimensional potential. Like the previous class, here also at the perturbation level cosmology with a self interacting scalar field or considering the interaction between different scalar fields in a FLRW background, one can represent the total theory by a perturbation in the single quantum parametric oscillator with a time-dependent frequency in the Fourier space for the self interacting case. Instead of having a very simple perturbation theory of harmonic oscillator within the framework of quantum mechanical framework of cosmology, we have a very complicated version because of the absence of eigenstates. By applying the general perturbation technique, one can actually compute the correction in the energy eigen spectrum if the Hamiltonian of the quantum system has the eigenstate representation. In this connection, one needs to cite the example of simple harmonic oscillator again where one can analytically compute these corrections very easily and most of us have studied this from all quantum mechanics books exist in the literature. On the other hand, in the self interacting picture or for the case of the interaction between many scalar fields in the spatially flat FLRW cosmological background, computation of the quantum correction factors are extremely complicated.
2.3. Constructing Non-Chaotic OTOC in Cosmology
2.3.1. For Massless Scalar Field
2.3.2. For Partially Massless Scalar Field
2.3.3. For Massive Scalar Field
3. Quantum Non-Chaotic Auto-Correlated OTO Amplitudes and OTOC in Primordial Cosmology
- Motivation 1:The first physical motivation of this work is to explicitly provide the result of quantum mechanical correlation function in the context of primordial cosmology when the system under consideration goes to out-of-equilibrium regime in the early time scale of the evolution history of our universe. We all know this particular regime in quantum statistical field theory is extremely complicated to probe through usual understandings of cosmological correlators defined in the same late time slice. On the other hand, in the spatially flat FLRW curved background explaining such phenomena is even more harder. Our prime objective is to probe this extremely complicated physics through some basic and very simple concepts of quantum field theory prescription. This methodology is applicable to explain particularly the quantum mechanical correlation functions in the epoch of reheating and during the the stochastic particle production procedure during inflation which was not explored in this literature earlier. We are very hopeful that our computation and the derived results can perfectly capture the phenomena of quantum randomness and in this way one can treat the OTOCs to be the significant theoretical probe through which one can explain the out-of-equilibrium features very easily.
- Motivation 2:The second physical motivation of this work is to explicitly provide and understand the equilibrium behaviour of the quantum mechanical correlation functions in the context of primordial cosmology which we have a plan to derive in terms of the previously mentioned OTOCs. When we give an initial response to a quantum system in the context of cosmology, it goes to the out-of-equilibrium regime. Now, if we wait for a long time and consider the late time regime in the evolutionary scale of cosmology, then it is expected from the basic understanding that the quantum mechanical system under consideration has to reach the state of thermodynamic equilibrium which can be understood in terms of the saturation of the desired set of OTOCs at the late time scale. Our expectation is to understand this phenomena within the framework of cosmological perturbation theory in the early universe, which will be also helpful to estimate the thermodynamic temperature of the equilibrium state from the saturation value of the desired OTOCs in the present context. We are very hopeful to provide the details of the equilibrium behaviour of the quantum OTOCs from cosmology at the late time scale which will be helpful to give a physically consistent interpretation and estimation of the reheating temperature in terms of the equilibrium temperature of the quantum mechanical system under consideration. Apart from this, one can further give a physical interpretation and estimation of the equilibrium temperature at the end of the stochastic particle production procedure during the epoch of inflation. Therefore, using the late time behaviour of the cosmological desired OTOCs, one can give the estimation of reheating temperature as well the temperature of the universe at the end of inflation by following a proper physically consistent theoretical framework, which will be further helpful to determine the energy scales of that specific epoch appearing in the evolutionary time scale of our universe.
- Motivation 3:The third and the last physical motivation of this work is to explicitly provide and understand the intermediate behaviour of the quantum mechanical correlation functions in the context of primordial cosmology which we have a plan to derive in terms of the previously mentioned OTOCs. Our expectation is the present structure of OTOCs not only to provide the physical understanding of the early time out-of-equilibrium and late time equilibrium phenomena in the context of primordial cosmological perturbation theory, but also to provide the correct and physically justifiable explanation of the intermediate behaviour of the quantum correlation functions which will able to explain the phase transition from the out-of-equilibrium regime to the equilibrium regime. As far as the previous literatures in the present context are concerned, people have not addressed this issue clearly; that is, the earlier computations implementation of this phase transition phenomena was extremely complicated. From the present computation, one of the great expectations is to address the intermediate behaviour of the cosmological quantum correlation functions through the desired expressions for OTOCs which can further give physical interpretation during the phase transition from the out-of-equilibrium regime to the equilibrium regime and the quantum randomness behaviour in the vicinity of the transition region within the framework of primordial cosmological perturbation theory.
3.1. Computational Strategy for Non-Chaotic Auto-Correlated OTO Functions
- To compute these OTOCs, at first we need to find out the analytical classical solution of the equation of motion of the massless, partially massless and heavy scalar fields which can describe the super-horizon, sub-horizon limit and horizon crossing phenomena in the spatially flat FLRW cosmological background.
- After obtaining the classical solution which can describe the physical phenomena in the asymptotic region, super-horizon and sub-horizon scale in a specific gauge of cosmological perturbation theory of early universe, we further have to find out the canonically conjugate momentum of the perturbation field variable. Further, using both of these classical solutions, our job is to promote them in the quantum regime by writing them in terms of the creation and annihilation operators. Once this job is done, then using that quantum extended operators, our job is to compute the square of the quantum mechanical commutator brackets appearing in the expressions for the two desired OTOCs on which we are interested in this paper. It is important to note that such square of the commutator brackets are of course the fundamental components which will play a significant role in quantifying the desired OTOCs.
- Once we know the full solution in the quantum regime, which can describe super-horizon and sub-horizon, the asymptotic limiting solutions in the presence of a preferred choice of quantum mechanical vacuum state, which fix the initial condition for the quantum random fluctuations in the context of early universe cosmology. Then using that we have to explicitly compute the expression for the thermal average value of the square of the commutator bracket of the field and its canonically conjugate momenta, which can be obtained as a by-product of cosmological perturbation theory in a preferred choice of gauge. Such combinations physically signify the four-point quantum correlation function in the out-of-time ordered sense.
- Further, we have to derive the expression for another fundamental quantity, which is the partition function of the quantum mechanical system under consideration for the cosmological perturbation theoretical setup. This can be done by determining the quantum mechanical Hamiltonian which actually represents a quantum oscillator with conformal time-dependent frequency. Once this is done, then we need to compute the expression for the thermal trace of the thermodynamic Boltzmann factor. Here, it is important to note that, in the context of quantum field theory, the equivalent representation of the thermal trace operation can be presented in terms of path integral operation which can be performed in the presence of a wave function of the universe defined for a preferred choice of quantum mechanical vacuum state.
- Before computing the mentioned OTOCs, which are related to the connected part of the four-point correlation functions, we need derive the expression for the thermal two-point OTOCs from the perturbation variable appearing in the preferred choice of gauge in cosmological perturbation theory of early universe (Here, it is important to note that for the four-point OTOCs we have observed that at very large dissipation time scale one can factorize them into connected and disconnected parts. Obviously the connected part carries the physical information, but the disconnected part is actually written in terms of the product of two two-point functions defined at two different time scales which are separated in time scale. Now these two-point functions help us to normalise these two OTOCs which further is very significant to analyse the amplitude of the connected part of the desired four-point functions in the present context. In addition, the thermal expectation value of the commutator bracket of two cosmologically relevant operators in the context of cosmological perturbation theory can be considered to be the relative difference between the thermal expectation value of two different two-point functions which are appearing in the normalisation of the disconnected part of the four-point functions as mentioned earlier.). These two-point functions further have been used to normalise the four-point desired OTOCs in the present paper and for this reason can be treated as the fundamental building blocks in the present computational purpose.
- The quantum operators appearing as a by-product of cosmological perturbation theory are the fundamental objects of this computation and we are going to use them to define the desired expressions for the OTOCs in this paper. We first use the coordinate system basis. To make the further simplification, we transform both of the quantum operators defined in two different time scales into Fourier space where we write both of them in the momentum basis. We particularly use this simple trick because in the context of cosmology, momentum space description is simpler and easily understandable compared to the expressions obtained in the context of coordinate space basis. The prime physical reason behind this approach is that the quantum correlation functions in the context of primordial cosmological perturbation theory preserve the overall mathematical structure under the application of conformal transformations (Here represents the De Sitter isommetry group which is preserved under conformal transformations.). In the context of quasi De Sitter space, this symmetry is slightly broken in the momentum basis after doing Fourier transformation from the coordinate basis and the amount of symmetry breaking is proportional to the slowly varying time-dependent slow-roll parameters, which we have explicitly taken into account to get the correct physical interpretation of the final results of the desired OTOCs in our computations in this paper.
- Another important ingredient of the present computation of the desired two OTOCs is deep rooted in the cosmological perturbation theory setup used for early universe quantum mechanical setup that we are using for the present computation. In this context, the preferred choice of gauge used for the perturbation setup plays a very significant role to finally quantifying the mathematical structure of the OTOCs studied in this paper. For this purpose, unitary gauge, Newtonian gauge, comoving gauge choices are very relevant and most commonly used. Out of them, for the present computational purpose, we use the comoving gauge, which makes the final mathematical structure and the detailed computation of the desired OTOCs very simple compared to performing the derivation in terms of the field and its canonically conjugate momentum , which appear directly from the ungauged version of the cosmological action in spatially flat FLRW background.
3.2. Classical Mode Functions to Compute Non-Chaotic Auto-Correlated OTO Functions in Cosmology
3.3. Quantum Mode Function to Compute Non-Chaotic Auto-Correlated OTO Functions in Primordial Cosmology
3.4. Quantum Operators for Non-Chaotic Auto-Correlated OTO Functions
3.5. Cosmological Two-Point and Four-Point “In-In” Non-Chaotic OTO Amplitudes
3.5.1. Non-Chaotic Auto-Correlators in Primordial Cosmology
- Information I:First of all, one needs to start with the quantum mechanical operators in which we are interested in the context of cosmology, those are the perturbed time-dependent field and the associated canonically conjugate momenta written in Fourier transformed momentum space. This can easily be done using the obtained asymptotically viable total conformal time-dependent solution of the perturbed field from the classical Mukhanov–Sasaki equation which we are going to write in the quantum regime as an operator by including the creation and annihilation operators of the quantum initial vacuum state. In the framework of cosmological perturbation theory, one can construct the conformal time-dependent Hamiltonian density operator in Fourier space which can be made up of two important components, the kinetic operator and the potential operator, where both of them can be expressed in terms of the previously mentioned perturbed field operator and its canonically conjugate momentum operator in the quantum regime of field space. After constructing the time-dependent Hamiltonian density operator in the Fourier space, our next job is to integrate over all possible momenta spanned over a physically acceptable range to derive the total time-dependent Hamiltonian operator frequently used for the present computation. Additionally, it is important to note that in this paper we will consider the canonical technique for the quantization purpose which we will follow throughout the paper.
- Information II:In the next step, one needs to explicitly compute the expression for the commutator and square of the commutator bracket between the two perturbed field variable quantum operators and the two canonically conjugate momentum variable quantum operators defined at two different conformal time scales in the classical geometrical background of spatially flat FLRW space-time specifically in coordinate space representation. These are the crucial parts which form the building blocks of the desired OTOCs in the context of cosmological perturbation theory of the early universe. In this section of the paper, we explicitly derive the commutator and square of the commutator or these two operators in terms of two and four parts respectively where each of the components mimics the role of scattering amplitudes in Fourier space. In the present context, commutator and the square of the commutator bracket in the Fourier space involved two momenta and four momenta, respectively, and in both the cases two different conformal time scales appear which will finally fix the structure of the desired OTOCs which we want to study in the context of cosmological perturbation theory. If we look into the structure of these commutator and square of the commutator quantum mechanical operators very closely, then one can observe that these two different momenta and four different momenta are appearing in OTOCs as we are dealing with the product of two and quantum mechanical operators, respectively, in this computation. Though the OTOC computed from the square of the commutator bracket looks like scattering amplitude in the Fourier space, technically these are actually representing the unequal time, out-of-time-ordered four-point quantum correlation function in the context of cosmology. In the quantum field theory version of the trace operation, one needs to consider the same quantum initial vacuum state, which implies the initial and final state are exactly same, and identified to be “in” quantum state in the context of cosmology. This further implies that within the framework of primordial cosmology, we deal with in-in amplitude rather than using the usual “in-out” amplitude in the S-matrix formalism, which is actually a Schwinger Dyson series. Instead of calling this quantity which we want to explicitly determine in this section as “in-in” amplitude, we call these quantities as “in-in” quantum mechanical correlation functions within the framework of primordial cosmological perturbation theory.
- Information III:Another important issue is to fix the proper definition of the trace operation within the framework of quantum field theory written in classical spatially flat FLRW curved cosmological background. In the context of quantum field theory of curved space-time, particularly in the context of cosmology, we have to define the quantum wave function of our universe which will help us to set up the equivalent representation of the thermal trace operation in terms of the quantum mechanical path integral formulation. To construct the wave function of the universe as an initial condition, one chooses the standard definition of Euclidean false vacuum state, which is commonly known as the Bunch–Davies vacuum state and it basically represents a thermal ground state in the context of primordial cosmological perturbation theory. In the quantum field theory of curved space-time literature, sometimes this is identified to be the Hartle–Hawking or Cherenkov vacuum state. In this computation, the most generalized choice is the vacua, which is commonly known as the Motta–Allen (MA) vacua in the context of quantum field theory of De Sitter space-time, which are invariant under all the conformal group isometries and commonly known as the -vacua which is CPT violating. Here, is a real parameter which forms a real parameter family of continuous numbers and particularly is appearing in the phases. This phase factor is actually the culprit for which the quantum state CPT symmetry is getting violated. Once we switch off the contribution from this phase factor by fixing , the one can get back the CPT symmetry preserving quantum vacua states. Sometimes the vacua is characterized as the squeezed quantum vacuum state. Bunch–Davies vacuum state is a very special case of the generalized vacua state which can be obtained by fixing in the definition of the quantum vacuum state, which perfectly satisfies the Hadamard condition in the Green’s functions. Using Bogoliubov transformation, one can express the vacua in terms of the Bunch Davies state.
- Information IV:Once we fix the definition of the quantum field theory version of the trace operation in terms of path integral formalism in the Euclidean formalism, we can then further compute the expression for the desired two sets of OTOCs on which we are interested in this paper. Another important component which will fix the definition of the OTOC is the thermal partition function for the scalar mode fluctuations obtained from the primordial cosmological perturbation where the same trick has to be applied to define the trace operation as mentioned earlier. In this context, instead of performing a complete quantum calculation, we use the semi-classical approximations for the computations. The primordial perturbations in the spatially flat classical FLRW background can be written in terms of scalar, vector and tensor modes in Fourier space using the SVT decomposition from which the quantum fluctuations are generated. For this reason, we will do a semi-classical (not purely quantum or classical) computation for the computation of OTOC in the framework of primordial cosmology.
- Information V:Last but not least, we have to fix the normalisation factor of all the desired new OTOCs that we have introduced in this paper. In this connection, it is important to remind ourself again that normalisation factors of these desired OTOCs are actually made up of a product of two disconnected thermal two-point functions in the dissipation time scale , where T is the equilibrium temperature of the quantum cosmological system under study in the present context. Whatever results we have obtained for the un-normalised OTOCs, we use them and divide them into the mentioned disconnected part of the correlator. This helps to treat the overall amplitude of four-point OTOCs in a dimensionless fashion. Not only that trick in normalisation but in OTOC also helps us to know about the exact time dependence in the quantum correlator of which we are interested in. More precisely, this can be done by making use of the previously mentioned equivalent operation of thermal trace operation in the presence of vacua or Bunch–Davies quantum vacuum state in the context of primordial cosmological perturbation theory. We have explicitly demonstrated the detailed computation of these normalisation factors in the Appendix of this paper. Please look into the technical details in the Appendix for more details on this issue.
3.5.2. Fourier Space Representation of the Commutator Bracket: Application to Two-Point Non-Chaotic Auto-Correlated OTO Functions
3.5.3. Fourier Space Representation of Square of the Commutator Bracket: Application to Four-Point Non-Chaotic Auto-Correlated OTO Functions
3.6. Thermal Partition Function in Primordial Cosmology: Quantum Version
3.6.1. Initial Quantum State in Primordial Cosmology
3.6.2. Quantum Partition Function in Terms of Rescaled Perturbation Field Variable in Primordial Cosmology
3.6.3. Quantum Partition Function in Terms of the Cosmological Scalar Curvature Perturbation Field Variable in Primordial Cosmology
3.7. Trace of Two-Point “In-In” Non-Chaotic Extension of OTO Amplitudes for Primordial Cosmology
3.8. New OTOCS from Regularised Two-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Rescaled Field Version
3.9. New OTOCS from Regularised Two-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Curvature Perturbation Field Version
- The results obtained for two-point OTOCs for different types of initial choice of the quantum vacuum states are the same. No specific information of the initial condition in terms of the chosen quantum vacuum will be propagated in the overall factor of the final result of the two-point OTOCs. The information of the initial quantum vacuum will be there in the momentum integrated function and within a finite length cut-off L as it captures the effect of the full asymptotic solution of the scalar modes and its associated momentum, and both of them are dependent on the factors and which carry the required information. In this computation, both the quantum and the classical contributions have been taken care of. If we only concentrate on the quantum fluctuation part then the most interesting information is coming from the sub-Hubble or sub-horizon limiting region. By a very careful observation one can explicitly see that in the sub-Hubble region the final result of the two-point OTOCs obtained from different types of the initial quantum states will give approximately the same answer and can solely be described by the well-known Euclidean Bunch–Davies initial condition. This is quite an interesting fact appearing in the context of two-point OTOC computation, because if we recap the similar computation of time ordered or anti time ordered correlators or any equal time two-point correlators within the framework of cosmological perturbation theory, then we find that the final result, which we call in cosmologist’s language power spectrum in the Fourier transformed space, always captures the explicit information regarding the initial quantum vacuum state even in the super-Hubble region where the quantum effects dominate over the classical super-Hubble contribution.
- In the presence of a very heavy mass particle, which is within the framework of cosmology and identified by the limiting situation, , where H is the characteristic Hubble scale, one needs to take the analytical continuation of the mass parameter to the imaginary axis such that, . As a consequence of this we get a exponential Boltzmann suppression by a factor of , which can be treated as a correction term in the final expressions for the two-point OTOCs. Now, if the magnitude of the mass parameter is extremely large then one can simply drop this exponential Boltzmann factor in the final expression for the two-point OTOCs and can be written as:where we define new functions and , which are given by:Here, it is important to note that to define this function we have used the following expansion:where we have considered the fact that, and to get the leading and the sub-leading or the next to leading order contribution, which is used for the further simplification of the obtained result for the two-point OTOC in the large limit. We also have introduced the following symbolic representation for the sake of simplicity and clarity:On the other hand, if the magnitude of the mass parameter is small then one can expand the exponential Boltzmann factor in the Taylor series and keep up to the linear order term in in the expansion. This will give rise to an overall contribution, which is given by and the corresponding two-point OTOCs can be approximately written as:where we define new functions and , which are given by:Here, it is important to note that to define this function we have used the following expansion:where we have considered the fact that and to get the leading and the sub-leading or the next to leading order contribution, which is used for the further simplification of the obtained result for the two-point OTOC in the small limit.We also have introduced the following symbolic representation for the sake of simplicity and clarity:
- One can also consider various important cases, described by the mass parameter values , and . Here represents the massless field limiting situation and representing the conformally coupled case, where we have . On the other hand, represents the situation where we have . Here, one can treat both and in the partially massless field category.
- We have explicitly shown that the two-point OTOCs defined in this work are completely independent of the choice of the coordinate system and at the end only depend on the time scale on which the cosmologically relevant operators in perturbation theory are separated in time scale. To define properly, we define these operators in terms of a specific space coordinate point but at different time scales and found that the final answer of the two-point OTOCs are only dependent on time scale.
- From the present computation we found that the final expression for the two-point OTOCs are completely independent on temperature even though we start with a thermal canonical statistical ensemble in the trace formula of the two-point OTOCs. It implies that we will get ultimately the description in terms of statistical ensembles following the present description within the framework of cosmological perturbation theory, which is obviously a quite interesting observation to point out in the present context of computation.
- Now if we fix the conformal time coordinate of the two operators, and , that means if both the cosmologically relevant operators are defined at the same time coordinate (time separation vanishes) then two-point OTOCs show divergence. On the other hand, if we compare the obtained result with the expression for any two-point equal time cosmological correlators of the perturbation field variables then the amplitude of such correlators, which we commonly identified to be the power spectrum within the framework of cosmology, are found to be finite. Therefore, this observation implies that just by converting OTOC to ETOC one cannot get a correct and finite answer. This is because of the fact that OTOC deals with completely out-of-equilibrium phenomena and ETOC deals with completely equal phenomena. It is expected that after taking a very large late time limit, it is possible to achieve equilibrium in any one of the time coordinates involved in the cosmological operators, but to get a complete equilibrium description in ETOC one needs to follow a completely different approach starting from the definition.
- After doing simple computation, one can explicitly show that, in the present context, the one-point and three-point functions are explicitly zero and can be written as:Here, we have used the well-known Kubo Martin Schwinger condition, which basically deals with the time translational symmetry at finite temperature and using this fact one can explicitly show that the above two combinations of the three point function for the cosmological perturbation theory explicitly vanishes in the present context. Not only these combinations, but also the other possible cross correlated three-point function will become similarly zero. If we do the computation for the primordial cosmological scalar perturbations explicitly in zero temperature then one can explicitly find non-zero but small answers for all the possible three-point correlators using the concept of OTOC. Using the Kubo–Martin–Schwinger condition, one can further show that for any odd N-point function at finite temperature the corresponding contribution vanishes due to the time translational symmetry. For these mentioned reasons OTOCs are not defined in terms of any odd N-point function within the framework of out-of-equilibrium quantum field theory. All even N-point OTOCs are normalised with appropriate factors which actually appear from the expansion in the large time dissipation time scale , which is basically proportional to the equilibrium temperature of the quantum system under consideration at very late time limit. On the other hand, since one cannot decompose the odd N-point thermal correlators in symmetric combinations and each correlator is trivially zero there is no normalisation possible to express these correlators. Therefore, the only physical information is appearing from all even N-point correlators. For we get the two-point OTOCs which we do not need to normalise because in this computation these are treated as the smallest building block for the computation. Any other even -point correlators can be normalised in terms of the combinations of the point disconnected part of the OTOCs which are basically appearing in the large time dissipation time scale as previously we have mentioned. In our previous paper [53], we have provided the detailed computation of a specific type of two-point and four-point OTOC out of which one is able to extract various unknown physical information within the framework of cosmological perturbation theory described in the out-of-equilibrium regime of quantum field theory. In this paper we actually go beyond this understanding of the OTOC and can provide two new sets of two-point and four-point OTOCs which we believe can give other information regarding the quantum system under study within the framework of cosmological perturbation theory in the out of equilibrium regime of the quantum field theory. In the next subsections, we are going to provide the detailed computations of the “in-in” OTO amplitudes and the related four-point OTOCs from the primordial scalar perturbations.
3.10. Trace of Four-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitude for Primordial Cosmology
3.11. New OTOCs from Regularised Four-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Rescaled Field Version
3.11.1. Without Normalisation
3.11.2. With Normalisation
3.12. New OTOCS from Regularised Four-Point “In-In” Non-Chaotic Auto-Correlated OTO Amplitudes: Curvature Perturbation Field Version
3.12.1. Without Normalisation
3.12.2. With Normalisation
4. Numerical Analysis I: Interpretation of Two-Point Non-Chaotic Auto-Correlated OTO Functions
- In Figure 6 and Figure 7, conformal time dependent behaviour of the two-point auto-correlated field and momentum OTO functions with respect to the two time scales is explicitly shown. From these plots, it is clearly observed that with respect to both the time scales the two-point auto-correlated field and momentum OTO functions show random fluctuating behaviour.
- For both the cases, it is observed that we get the significant distinguishable features in the time-dependent two-point auto-correlated field and momentum OTO functions for partially massless or heavy scalar fields. In Figure 8, if we change the quantum initial conditions by changing the vacuum state by introducing the non-standard Mota–Allen vacua, then a clear distinctive feature can be observed by changing the vacuum parameters and , respectively. The behaviour of the two-point auto-correlated field and momentum OTO functions is explicitly depicted in Figure 9 and Figure 10. From these plots, one can clearly see that for the results obtained using Bunch–Davies vacuum, vacua and Mota–Allen vacua state initial conditions, the two-point auto-correlated field and momentum OTO functions significantly decay very fast in a non-standard fashion with respect to the magnitude of the mass parameter for partially massless and heavy scalar fields in primordial cosmology. We have explicitly shown the behaviour of the two-point auto-correlated field and momentum OTO functions for , where it is clearly observed that the correlation decays very rapidly with the increase in the magnitude of the mass parameter .
- In addition, we have observed from the plots that the random fluctuations with respect to the conformal time scale show decaying time-dependent behaviour at the very late time scale. First of all, all of them show a saturating behaviour and then it increases at a particular value in the time scale and then these plots show decaying features. This large peak value of the two-point auto-correlated spectra is obtained at the scale when the two time scales of the theory becomes comparable. Physically, this is a very crucial fact as it shows at this particular time scale we are actually getting zero information from the two-point auto-correlations. Only the preferred information can be extracted from the very early time scale as well as at the very late time scale after the peak.
5. Numerical Analysis II: Interpretation of Four-Point Non-Chaotic Auto-Correlated OTO Functions
- Before normalising the four-point auto-correlated field and momentum OTO functions, the results computed from rescaled field and momentum and the curvature perturbation field variable and its conjugate momenta, the sides are not at all the same and are connected via a time-dependent Mukhanov–Sasaki variable dependent conformal factor in the final results.
- After normalising the four-point auto-correlated field and momentum OTO functions, the results computed from rescaled field and momentum and the curvature perturbation field variable and its conjugate momenta, the sides are not at all the same. In this case, particularly for the computational purpose, it is the best one as we really do not care about the origin of the quantum operators in the cosmological perturbation theory.
- In our computed four-point auto-correlated field and momentum OTO functions, two time scales are involved. During the study of the behaviour of the four-point auto-correlated field and momentum OTO functions, we have actually fixed one time scale and have studied the time-dependent dynamical behaviour with respect to the other time scale. We have found the behaviour with respect to both and , using Bunch–Davies, and the generalised Mota–Allen vacua as the initial choice of quantum vacuum state. See Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 for more information about the detailed conformal time-dependent feature of the normalised four-point auto-correlated field and momentum OTO functions. In the conformal time scale, all of these plots vary from (Big Bang) to 0 (present day universe), and show significant distinctive features in the time scale.
- If we fix the time scale, , and study the behaviour of the four-point auto-correlated field and momentum OTO functions with respect to the scale , then we find that as we approach from the very early universe to the late time scale the normalised correlators show random non-standard non-chaotic behaviour.
- Additionally, we have found that we can get the desired features from the obtained results which can be visible only when the mass parameter, , can be analytically continued to . Therefore, massless De Sitter possibility () is not allowed. Consequently, we have the following options:
- Partially massless De Sitter case is one of the possibilities where we can estimate the following parameter from the present understanding:which implies the following bound on the mass parameter:This is consistent with the plots obtained for the following values of the mass parameter:
- Massive De Sitter case is one of the possibilities where we can estimate the following parameter:Since we have studied the case for , we get the following bound on the mass of the heavy field:
- Reheating case is the last possibility, where we can estimate:
- All the momentum-dependent integrals are divergent at ∞, for which we have introduced a UV regulator at (large value). This makes the final results of four-point auto-correlated field and momentum OTO functions numerically convergent.
- Further, we define a relative change in normalised four-point auto-correlated field and momentum OTO functions where the relativeness is defined with respect to the definition of quantum mechanical vacuum state, given by:In Figure 28, Figure 29, Figure 30, Figure 31, Figure 32, Figure 33, Figure 34, Figure 35, Figure 36, Figure 37 and Figure 38, we have explicitly shown the behaviour of the relative change in normalised four-point auto-correlated field and momentum OTO functions with respect to the two time scales. Here is the relative change we have studied for , and with respect to for all previously allowed values of the mass parameters for partially massless and heavy scalar fields. From this relative change, one can also study the large or small deviation from the Bunch–Davies result compared to the other results obtained from all non-standard quantum vacuum states.
- In addition, we have to mention here that the computed four-point auto-correlated field and momentum OTO functions are independent of any specific choice of the coordinate system. Finally, we get a momentum integrated cut-off regulated result for the four-point auto-correlated field and momentum OTO functions which only depend on the two dynamical conformal time scales on which we have defined the rescaled perturbation variable and its canonically conjugate momenta. This is quite a good outcome. In the generalised prescriptions, when one introduces the quantum operators in a specific time and coordinate system, it always appears that in the final result it captures the effect of inhomogeneity in the space-time coordinate. In the context of spatially flat FLRW cosmology, we have found that the final result of the four-point auto-correlated field and momentum OTO functions captures the effect of inhomogeneity. This is because in cosmology we are actually interested in the time evolution of the quantum operators which are separated in time scale, which is one of the crucial constraints in the definition of any general four-point auto-correlated field and momentum OTO function. Such four-point auto-correlated field and momentum OTO functions do not capture the inhomogeneity.
- The final result of the four-point auto-correlated field and momentum OTO functions are not explicitly dependent on the factor which is appearing in the expression for the thermal partition function. This further implies that the final results are also independent of the thermal partition function computed for primordial cosmology.
6. Classical Limit of Non-Chaotic Auto-Correlated OTO Amplitudes and OTOC in Primordial Cosmology
6.1. Computational Strategy for Non-Chaotic Auto-Correlated OTO Functions in the Classical Limit
- First of all, we have to take the quantum to classical map. For this purpose, we consider the classical mode function and its canonically conjugate momentum which we have derived in an earlier section of this paper.
- Next, in the classical limit, we use the Poisson brackets of the classical mode function and its canonically conjugate momentum variables in cosmological perturbation theory.
- In the classical limit, the definition of quantum trace will be replaced by phase-space volume measure, , which mimics the role of path integral measure, , in the classical limit.
- In addition, during this computation, we have to include an additional thermal Boltzmann factor which is serving the purpose of thermal weight factor taking the phase-space average over the classical micro-canonical statistical ensemble.
- Next, we compute the expression for the classical thermal partition function for cosmological perturbations which is consistent with the quantum result computed from completely different formalism. To compute the classical partition function one need to compute the expression by following the principles of classical statistical mechanics very carefully. We will show that the final expressions for the classical limit of auto-correlated OTOs are independent of the partition function for the cosmological scenario in which we are interested in.
- Last but not least, we compute the expression for the normalisation factor for the classical limiting version of the auto-correlated OTO functions by following the above-mentioned general formalism.
6.2. Classical Limit of Cosmological Two-Point “In-In” Non-Chaotic OTO Amplitudes
6.3. Classical Limit of Cosmological Four-Point “In-In” Non-Chaotic OTO Amplitudes
- For white noise, two-point classical auto-correlation functions are time translation invariant, which is kind of expected from this analysis.
- Random white noise also has the following properties:andwhere and are the conformal time-dependent white noise field variable and its canonically conjugate momentum variable. In addition, and , are the amplitudes of the spectra of any and even-point classical auto-correlation functions. Here, all even-point amplitudes are non-zero and all odd-point amplitudes become zero for Gaussian white noise contributions, which are again sourced from random fluctuations.
- Here time-dependent noise kernels describe the randomness of quantum mechanical fluctuations at the classical limit.
- If we compare the obtained result in the classical limit with the quantum version of the four-point auto-correlated results then it is clearly observed that for both the cases we get the same twelve contributions in the classical limit. In the quantum case, we have different individual contributions for these mentioned twelve terms in the auto correlations.
- Additionally, in both classical and quantum results, momentum conservation is established via momentum-dependent three dimensional Dirac Delta function contributions.
6.4. Cosmological Partition Function: Classical Version
6.4.1. Classical Partition Function in Terms of Rescaled Field Variable
6.4.2. Classical Partition Function in Terms of Curvature Perturbation Field Variable
6.5. Classical Limit of Cosmological Two-Point Non-Chaotic OTOC: Rescaled Field Version
6.6. Classical Limit of Cosmological Two-Point Non-Chaotic OTOC: Curvature Perturbation Field Version
6.7. Classical Limit of Cosmological Four-Point Non-Chaotic OTOC: Rescaled Field Version
6.7.1. Without Normalisation
6.7.2. With Normalisation
6.8. Classical Limit of Cosmological Four-Point Non-Chaotic OTOC: Curvature Perturbation Field Version
6.8.1. Without Normalisation
6.8.2. With Normalisation
7. Summary and Outlook
- First of all, in this paper we have provided a computation using which it is now possible to derive the expressions for the two specific types of OTOCs made up of cosmological scalar perturbation field variables and its associated canonically conjugate momentum variable auto-correlations to study the feature of randomness without having chaotic behaviour in a primordial cosmology setup. It is expected that our presented computation and findings for the two new types of cosmological OTOCs in this paper will surely be helpful to understand the quantum field theoretic features of random non-chaotic cosmological events in detail. Apart from using the presented methodology in the present context of discussion, we believe that these results will also be used in other contexts of cosmological phenomena to study similar types of random non-chaotic events appearing in the timeline of the universe.
- The computation is presented by making use of the well-known Euclidean vacuum, i.e., Bunch–Davies vacuum, CPT invariant vacua and CPT violating Motta–Allen vacua as a choice of initial quantum mechanical vacuum state. In each case we get very distinctive features in the auto-correlated two types of OTO functions studied in this paper. We have studied this issue analytically as well as numerically in detail in this paper, which completely physically justify our prescription proposed.
- In general, the construction of OTOCs demands to have two quantum mechanical operators defined at two different time scales, which are the same operators for auto-correlations and different operators for cross-correlations. In this paper, we follow the exact same strategy to define auto-correlated two different types of OTO functions within the framework of primordial cosmological perturbation theory for scalar mode fluctuations in the quantum regime. To construct these crucial auto-correlated OTO functions, we use the scalar mode field variable and its associated canonically conjugate momenta, which according to the mathematical construction are defined in two different conformal time scales. To study the behaviour of the two types of the auto-correlated OTO functions, we freeze one of the conformal time scales between the two and study the dynamical feature with respect to the other conformal time. By doing this analysis, we have found that the dynamical features with respect to both the time scales for the two different types of auto-correlated OTO functions are significantly different and all of them describe distinctive randomness at out-of-equilibrium without having any specific chaoticity. For both the cases, we have explicitly studied the long time behaviour of these two types of auto-correlated OTO functions. We found that the obtained behaviour from the numerical plots are perfectly consistent with the expectation from the present setup within the framework of primordial cosmology. The most interesting part of this finding is that, using the present methodology, it is now possible to probe various cosmological aspects at out-of-equilibrium using quantum field theory calculations in terms of quantum mechanical correlation functions. In addition, we are very hopeful regarding the fact that these results can be verifiable in near-future cosmological observational probes.
- By doing this analysis, we have found that at a very early epoch of our universe during random cosmological events, quantum fluctuations generated from the scalar perturbations go to the out-of-equilibrium phase. Then, the auto-correlators decay in a non-standard fashion with respect to the conformal time scale up to the very late time scale of the universe. After that, the system reaches equilibrium and one can perform all the possible computations in the quantum regime. This computation can be applicable to describe the particle production phenomena during the reheating epoch.
- In addition, we have found that the derived cosmological OTOCs at finite temperature are dependent on two time scales and are independent of any preferred choice of the coordinate system. The derived expressions for the cosmological OTOCs are homogeneous in nature with respect to the space coordinate, or its Fourier transformed momentum coordinate. We also have found that the final results obtained for the two different types of cosmological OTOCs are independent of the partition function, which we have computed for primordial cosmological perturbations for scalar fluctuation. It is important to note that the obtained features in these auto-correlations are exact mimics of the features obtained for OTOCs computed from an inverted harmonic oscillator having a conformal time-independent frequency. Here, one can exactly map the stochastic particle production problem in cosmology in terms of findings from the inverted harmonic oscillator with time-dependent frequency because both setups describe the same underlying physics.
- In addition, we have found that the presented analysis is valid for partially massless () or massive () spin-0 scalar particle production in the primordial universe.
- Further, we have studied the classical limiting behaviours of the two-point and four-point two types of auto-correlated OTO functions in terms of the phase-space averaged Poisson brackets and the square of the Poisson brackets to check the consistency with the late time behaviour in the super-horizon region of cosmological perturbations, which supports classical behaviour.
- Finally, in this paper we have shown that the normalised auto-correlated OTO functions are completely independent of the choice of cosmological perturbation field variable and the associated canonically conjugate momentum in a specific gauge.
- We are very hopeful that our obtained results for the two different types of auto-correlators can be probed by future observations with significant statistical accuracy and can be treated as a benchmark for which one can study the out-of-equilibrium features in primordial cosmological perturbation theory. To know about the implications of our derived results, one can further extend the present methodology for various cosmological events as well where random quantum fluctuations play a significant role in the timeline of our universe. To date, this is not a very well studied fact and for this reason it will be interesting to study these mentioned aspects in detail.
- The presented methodology can also be extended to derive the auto-corrected OTO functions in the context of bouncing cosmology. It is expected to get different random features in the context of the bouncing paradigm. It is not clear to date how exactly and in which respect it will be different due to having a lack of understanding about the present formalism in a broader perspective. For this reason, it will be very interesting to study out-of-equilibrium features in the quantum regime from the bouncing cosmology framework and compare the results obtained from the presented analysis in this paper.
- The explicit role of quantum entanglement in the present framework is also not yet studied. To date, the explicit role of the quantum entanglement phenomena [149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176] has been studied within the framework of cosmological perturbation theory finding the quantum correlation function in the equilibrium regime; but, it is not studied in the out-of-equilibrium regime in the presence of quantum entanglement. Therefore, it will be interesting to investigate such possibilities in detail. Most importantly, the role of cosmological Bell’s inequality violation [177,178,179,180,181,182] can also be tested to know about the long range effect in the cosmological correlation functions.
- It is also very important to verify the connecting relationship between the quantum circuit complexity [183,184,185,186,187,188,189,190,191,192,193,194,195] and OTO correlators [53,196] within the framework of the primordial cosmology setup. To date, work has been done on both sides separately in the cosmological framework; but, no effort has been made to connect this two theoretical ideas.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Asymptotic Features of the Scalar Mode Functions in Cosmological Perturbation Theory
Appendix B. Quantum Two-Point OTO Amplitudes for Cosmology
Appendix B.1. Definition of OTO Amplitude
Appendix B.2. Definition of OTO Amplitude
Appendix C. Quantum Four-Point OTO Amplitudes for Cosmology
Appendix C.1. Definition of OTO Amplitude and
Appendix C.2. Definition of OTO Amplitude and
Appendix C.3. Definition of OTO Amplitude and
Appendix C.4. Definition of OTO Amplitude and
Appendix D. Computation of Classical Limit of Four-Point “In-In” OTO Amplitudes for Cosmology
- The time-dependent part is very complicated as it contains the information regarding the classical version of random stochastic quantum fluctuations in the primordial universe. In the present context, it is hypothesised by random functions and which incorporate the two conformal time scales in the results.
- In addition, it is important to note that and are homogeneous and isotropic functions, which captures the dynamical effect of the spatially flat FLRW background. For this reason, the random functions, and , are completely i and j momentum index independent. This is actually the outcome of the stochastic randomness in the present context. Due to this fact, these random functions, and , are non-zero in the present computation. This is a non-trivial result and, as in the usual classical field theory, these two correlators give vanishing contribution without having any random fluctuations in the theory.
- Moreover, it is interesting to point out here that one can explicitly separately write down the contribution of the inhomogeneity and time dynamics in Fourier space after computing the classical Poisson brackets.
- Finally, the appearance of the three dimensional Dirac Delta function confirms the momentum conservation in the Fourier space in the classical two-point OTO micro-canonical amplitudes.
Appendix E. Computation of the Trace of the Two-Point Amplitude in OTOC
Appendix F. Computation of the Trace of the Four-Point Amplitude in OTOC
Appendix G. Time-Dependent Two-Point Amplitude in OTOC
Appendix H. Time-Dependent Four-Point Amplitudes in OTOC
Appendix H.1. Computation of and
Appendix H.2. Computation of and
Appendix H.3. Computation of and
Appendix H.4. Computation of and
Appendix H.5. Computation of and
Appendix H.6. Computation of and
Appendix H.7. Computation of and
Appendix H.8. Computation of and
Appendix H.9. Computation of and
Appendix I. Computation of the Normalisation Factor in Four-Point OTOC
Appendix I.1. Normalisation Factor of Four-Point OTOC Computed from Rescaled Field Variable
Appendix I.2. Normalisation Factor of Four-Point OTOC Computed from Curvature Perturbation Field Variable
Appendix J. Computation of the Normalisation Factor in Classical Limit of Four-Point OTOC
Appendix J.1. Normalisation Factor of the Classical Version of Four-Point OTOC Computed from Rescaled Field Variable
Appendix J.2. Normalisation Factor of the Classical Version of Four-Point OTOC Computed from Curvature Perturbation Field Variable
References
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. JHEP 2016, 8, 106. [Google Scholar] [CrossRef]
- Hashimoto, K.; Murata, K.; Yoshii, R. Out-of-time-order correlators in quantum mechanics. JHEP 2017, 10, 138. [Google Scholar] [CrossRef]
- Chakrabarty, B.; Chaudhuri, S.; Loganayagam, R. Out of Time Ordered Quantum Dissipation. JHEP 2019, 7, 102. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Chowdhury, C.; Loganayagam, R. Spectral Representation of Thermal OTO Correlators. JHEP 2019, 2, 18. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Loganayagam, R. Probing Out-of-Time-Order Correlators. JHEP 2019, 7, 6. [Google Scholar] [CrossRef]
- Haehl, F.M.; Loganayagam, R.; Narayan, P.; Nizami, A.A.; Rangamani, M. Thermal out-of-time-order correlators, KMS relations, and spectral functions. JHEP 2017, 12, 154. [Google Scholar] [CrossRef]
- Akutagawa, T.; Hashimoto, K.; Sasaki, T.; Watanabe, R. Out-of-time-order correlator in coupled harmonic oscillators. JHEP 2020, 8, 13. [Google Scholar] [CrossRef]
- Bhagat, K.Y.; Bose, B.; Choudhury, S.; Chowdhury, S.; Das, R.N.; Dastider, S.G.; Gupta, N.; Maji, A.; Pasquino, G.D.; Paul, S. The Generalized OTOC from Supersymmetric Quantum Mechanics—Study of Random Fluctuations from Eigenstate Representation of Correlation Functions. Symmetry 2020, 13, 44. [Google Scholar] [CrossRef]
- Romero-Bermúdez, A.; Schalm, K.; Scopelliti, V. Regularization dependence of the OTOC. Which Lyapunov spectrum is the physical one? JHEP 2019, 7, 107. [Google Scholar] [CrossRef]
- Larkin, A.; Ovchinnikov, N.Y. Quasiclassical Method in the Theory of Superconductivity. Sov. Phys. JETP 1969, 28, 1200–1205. [Google Scholar]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rept. 2000, 323, 183–386. [Google Scholar] [CrossRef]
- Shenker, S.H.; Stanford, D. Black holes and the butterfly effect. JHEP 2014, 3, 67. [Google Scholar] [CrossRef]
- Roberts, D.A.; Stanford, D.; Susskind, L. Localized shocks. JHEP 2015, 3, 51. [Google Scholar] [CrossRef]
- Shenker, S.H.; Stanford, D. Multiple Shocks. JHEP 2014, 12, 46. [Google Scholar] [CrossRef]
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black Holes and Random Matrices. JHEP 2017, 5, 118. [Google Scholar] [CrossRef]
- Stanford, D.; Susskind, L. Complexity and Shock Wave Geometries. Phys. Rev. D 2014, 90, 126007. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Tarnopolsky, G. Uncolored random tensors, melon diagrams, and the Sachdev-Ye-Kitaev models. Phys. Rev. D 2017, 95, 046004. [Google Scholar] [CrossRef]
- Maldacena, J.; Stanford, D. Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D 2016, 94, 106002. [Google Scholar] [CrossRef]
- Choudhury, S.; Dey, A.; Halder, I.; Janagal, L.; Minwalla, S.; Poojary, R. Notes on melonic O(N)q-1 tensor models. JHEP 2018, 6, 94. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Popov, F.; Tarnopolsky, G. TASI Lectures on Large N Tensor Models. arXiv 2018, arXiv:1808.09434. [Google Scholar] [CrossRef]
- Bulycheva, K.; Klebanov, I.R.; Milekhin, A.; Tarnopolsky, G. Spectra of Operators in Large N Tensor Models. Phys. Rev. D 2018, 97, 026016. [Google Scholar] [CrossRef]
- Kim, J.; Klebanov, I.R.; Tarnopolsky, G.; Zhao, W. Symmetry Breaking in Coupled SYK or Tensor Models. Phys. Rev. X 2019, 9, 021043. [Google Scholar] [CrossRef]
- Gurau, R. A review of the 1/N expansion in random tensor models. In Proceedings of the 17th International Congress on Mathematical Physics, Aalborg, Demark, 6–11 August 2012. [Google Scholar]
- Gurau, R. A review of the large N limit of tensor models. Symmetries Groups Contemp. Phys. 2012, 109–120. [Google Scholar]
- Gurau, R. The 1/N expansion of tensor models with two symmetric tensors. Commun. Math. Phys. 2018, 360, 985–1007. [Google Scholar] [CrossRef]
- Gurau, R. Notes on Tensor Models and Tensor Field Theories. arXiv 2019, arXiv:1907.03531. [Google Scholar]
- Benedetti, D.; Gurau, R. Symmetry breaking in tensor models. Phys. Rev. D 2015, 92, 104041. [Google Scholar] [CrossRef]
- Fu, W.; Gaiotto, D.; Maldacena, J.; Sachdev, S. Supersymmetric Sachdev-Ye-Kitaev models. Phys. Rev. D 2017, 95, 026009. [Google Scholar] [CrossRef]
- Witten, E. An SYK-Like Model Without Disorder. J. Phys. A 2019, 52, 474002. [Google Scholar] [CrossRef]
- Li, T.; Liu, J.; Xin, Y.; Zhou, Y. Supersymmetric SYK model and random matrix theory. JHEP 2017, 6, 111. [Google Scholar] [CrossRef]
- Turiaci, G.; Verlinde, H. Towards a 2d QFT Analog of the SYK Model. JHEP 2017, 10, 167. [Google Scholar] [CrossRef]
- Rosenhaus, V. An introduction to the SYK model. J. Phys. A 2019, 52, 323001. [Google Scholar] [CrossRef]
- Gross, D.J.; Rosenhaus, V. All point correlation functions in SYK. JHEP 2017, 12, 148. [Google Scholar] [CrossRef]
- Gross, D.J.; Rosenhaus, V. The Bulk Dual of SYK: Cubic Couplings. JHEP 2017, 5, 92. [Google Scholar] [CrossRef]
- Gross, D.J.; Rosenhaus, V. A line of CFTs: From generalized free fields to SYK. JHEP 2017, 7, 86. [Google Scholar] [CrossRef]
- Polchinski, J.; Rosenhaus, V. The Spectrum in the Sachdev-Ye-Kitaev Model. JHEP 2016, 4, 1. [Google Scholar] [CrossRef]
- Dhar, A.; Gaikwad, A.; Joshi, L.K.; Mandal, G.; Wadia, S.R. Gravitational collapse in SYK models and Choptuik-like phenomenon. JHEP 2019, 11, 67. [Google Scholar] [CrossRef]
- Mandal, G.; Nayak, P.; Wadia, S.R. Coadjoint orbit action of Virasoro group and two-dimensional quantum gravity dual to SYK/tensor models. JHEP 2017, 11, 046. [Google Scholar] [CrossRef]
- Gaikwad, A.; Joshi, L.K.; Mandal, G.; Wadia, S.R. Holographic dual to charged SYK from 3D Gravity and Chern-Simons. JHEP 2020, 2, 33. [Google Scholar] [CrossRef]
- Krishnan, C.; Sanyal, S.; Bala Subramanian, P.N. Quantum Chaos and Holographic Tensor Models. JHEP 2017, 3, 56. [Google Scholar] [CrossRef]
- Krishnan, C.; Pavan Kumar, K.V.; Rosa, D. Contrasting SYK-like Models. JHEP 2018, 1, 64. [Google Scholar] [CrossRef]
- Krishnan, C.; Kumar, K.V.P.; Sanyal, S. Random Matrices and Holographic Tensor Models. JHEP 2017, 6, 36. [Google Scholar] [CrossRef]
- Sorokhaibam, N. Phase transition and chaos in charged SYK model. JHEP 2020, 7, 55. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Chakrabarti, S.; Jatkar, D.P.; Kundu, A. SYK Model, Chaos and Conserved Charge. JHEP 2017, 11, 180. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Jatkar, D.P.; Sorokhaibam, N. Quantum Quenches and Thermalization in SYK models. JHEP 2019, 7, 66. [Google Scholar] [CrossRef]
- Samui, T.; Sorokhaibam, N. Thermalization in different phases of charged SYK model. arXiv 2020, arXiv:2004.14376. [Google Scholar]
- Das, S.R.; Ghosh, A.; Jevicki, A.; Suzuki, K. Near Conformal Perturbation Theory in SYK Type Models. arXiv 2020, arXiv:2006.13149. [Google Scholar]
- Das, S.R.; Ghosh, A.; Jevicki, A.; Suzuki, K. Space-Time in the SYK Model. JHEP 2018, 7, 184. [Google Scholar] [CrossRef]
- Das, S.R.; Ghosh, A.; Jevicki, A.; Suzuki, K. Three Dimensional View of Arbitrary q SYK models. JHEP 2018, 2, 162. [Google Scholar] [CrossRef]
- Das, S.R.; Ghosh, A.; Jevicki, A.; Suzuki, K. Duality in the Sachdev-Ye-Kitaev Model. Springer Proc. Math. Stat. 2017, 255, 43–61. [Google Scholar] [CrossRef]
- Das, S.R.; Jevicki, A.; Suzuki, K. Three Dimensional View of the SYK/AdS Duality. JHEP 2017, 9, 17. [Google Scholar] [CrossRef]
- Choudhury, S. The Cosmological OTOC: Formulating new cosmological micro-canonical correlation functions for random chaotic fluctuations in Out-of-Equilibrium Quantum Statistical Field Theory. Symmetry 2020, 12, 1527. [Google Scholar] [CrossRef]
- Maldacena, J.M. Non-Gaussian features of primordial fluctuations in single field inflationary models. JHEP 2003, 5, 13. [Google Scholar] [CrossRef]
- Maldacena, J.M.; Pimentel, G.L. On graviton non-Gaussianities during inflation. JHEP 2011, 9, 45. [Google Scholar] [CrossRef]
- Senatore, L.; Smith, K.M.; Zaldarriaga, M. Non-Gaussianities in Single Field Inflation and their Optimal Limits from the WMAP 5-year Data. JCAP 2010, 1, 28. [Google Scholar] [CrossRef]
- Senatore, L.; Tassev, S.; Zaldarriaga, M. Non-Gaussianities from Perturbing Recombination. JCAP 2009, 9, 38. [Google Scholar] [CrossRef]
- Baumann, D.; Duaso Pueyo, C.; Joyce, A.; Lee, H.; Pimentel, G.L. The cosmological bootstrap: Weight-shifting operators and scalar seeds. JHEP 2020, 12, 204. [Google Scholar] [CrossRef]
- Baumann, D.; Duaso Pueyo, C.; Joyce, A.; Lee, H.; Pimentel, G.L. The Cosmological Bootstrap: Spinning Correlators from Symmetries and Factorization. arXiv 2020, arXiv:2005.04234. [Google Scholar]
- Baumann, D.; Duaso Pueyo, C.; Joyce, A. Bootstrapping Cosmological Correlations. AAPPS Bull. 2020, 30, 2–9. [Google Scholar] [CrossRef]
- Baumann, D. Inflation. In Theoretical Advanced Study Institute in Elementary Particle Physics: Physics of the Large and the Small, Boulder, Colorado, USA, 1–26 June 2009; World Scientific Publishing Co Pte Ltd: Singapore, 2011; pp. 523–686. [Google Scholar] [CrossRef]
- Baumann, D. Primordial Cosmology. arXiv 2018, arXiv:1807.03098. [Google Scholar]
- Meerburg, P.D.; Green, D.; Abidi, M. Primordial Non-Gaussianity. arXiv 2019, arXiv:1903.04409. [Google Scholar]
- Senatore, L. Lectures on Inflation. In Theoretical Advanced Study Institute in Elementary Particle Physics: New Frontiers in Fields and Strings; World Scientific Publishing Co Pte Ltd: Singapore, 2017; pp. 447–543. [Google Scholar] [CrossRef]
- Creminelli, P.; Nicolis, A.; Senatore, L.; Tegmark, M.; Zaldarriaga, M. Limits on non-gaussianities from wmap data. JCAP 2006, 5, 4. [Google Scholar] [CrossRef]
- Creminelli, P.; Senatore, L.; Zaldarriaga, M.; Tegmark, M. Limits on f_NL parameters from WMAP 3yr data. JCAP 2007, 3, 5. [Google Scholar] [CrossRef]
- Smith, K.M.; Senatore, L.; Zaldarriaga, M. Optimal limits on f_{NL}⌃{local} from WMAP 5-year data. JCAP 2009, 9, 6. [Google Scholar] [CrossRef]
- Senatore, L. TASI 2012 Lectures on Inflation. In Theoretical Advanced Study Institute in Elementary Particle Physics: Searching for New Physics at Small and Large Scales; World Scientific Publishing Co Pte Ltd: Singapore, 2013; pp. 221–302. [Google Scholar] [CrossRef]
- Green, D.; Lewandowski, M.; Senatore, L.; Silverstein, E.; Zaldarriaga, M. Anomalous Dimensions and Non-Gaussianity. JHEP 2013, 10, 171. [Google Scholar] [CrossRef][Green Version]
- Smith, K.M.; Senatore, L.; Zaldarriaga, M. Optimal analysis of the CMB trispectrum. arXiv 2015, arXiv:1502.00635. [Google Scholar]
- Flauger, R.; Mirbabayi, M.; Senatore, L.; Silverstein, E. Productive Interactions: Heavy particles and non-Gaussianity. JCAP 2017, 10, 58. [Google Scholar] [CrossRef]
- Creminelli, P. On non-Gaussianities in single-field inflation. JCAP 2003, 10, 3. [Google Scholar] [CrossRef]
- Creminelli, P.; Zaldarriaga, M. Single field consistency relation for the 3-point function. JCAP 2004, 10, 6. [Google Scholar] [CrossRef]
- Creminelli, P.; D’Amico, G.; Musso, M.; Norena, J.; Trincherini, E. Galilean symmetry in the effective theory of inflation: New shapes of non-Gaussianity. JCAP 2011, 2, 6. [Google Scholar] [CrossRef]
- Assassi, V.; Baumann, D.; Green, D. On Soft Limits of Inflationary Correlation Functions. JCAP 2012, 11, 47. [Google Scholar] [CrossRef]
- Behbahani, S.R.; Green, D. Collective Symmetry Breaking and Resonant Non-Gaussianity. JCAP 2012, 11, 56. [Google Scholar] [CrossRef][Green Version]
- Green, D.; Porto, R.A. Signals of a Quantum Universe. Phys. Rev. Lett. 2020, 124, 251302. [Google Scholar] [CrossRef] [PubMed]
- Creminelli, P.; Senatore, L.; Zaldarriaga, M. Estimators for local non-Gaussianities. JCAP 2007, 3, 19. [Google Scholar] [CrossRef][Green Version]
- Choudhury, S.; Pal, S. Primordial non-Gaussian features from DBI Galileon inflation. Eur. Phys. J. C 2015, 75, 241. [Google Scholar] [CrossRef]
- Bordin, L.; Creminelli, P.; Mirbabayi, M.; Noreña, J. Tensor Squeezed Limits and the Higuchi Bound. JCAP 2016, 9, 41. [Google Scholar] [CrossRef]
- Mirbabayi, M.; Zaldarriaga, M. Double Soft Limits of Cosmological Correlations. JCAP 2015, 3, 25. [Google Scholar] [CrossRef]
- Baumann, D.; Lee, H.; Pimentel, G.L. High-Scale Inflation and the Tensor Tilt. JHEP 2016, 1, 101. [Google Scholar] [CrossRef]
- Baumann, D.; McAllister, L. Inflation and String Theory; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Baumann, D.; Zaldarriaga, M. Causality and Primordial Tensor Modes. JCAP 2009, 6, 13. [Google Scholar] [CrossRef][Green Version]
- Choudhury, S.; Mazumdar, A. An accurate bound on tensor-to-scalar ratio and the scale of inflation. Nucl. Phys. B 2014, 882, 386–396. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A.; Pal, S. Low & High scale MSSM inflation, gravitational waves and constraints from Planck. JCAP 2013, 7, 41. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A. Reconstructing inflationary potential from BICEP2 and running of tensor modes. arXiv 2014, arXiv:1403.5549. [Google Scholar]
- Choudhury, S.; Mazumdar, A. Sub-Planckian inflation—& large tensor to scalar ratio with r≥0.1. arXiv 2014, arXiv:1404.3398. [Google Scholar]
- Choudhury, S. Can Effective Field Theory of inflation generate large tensor-to-scalar ratio within Randall–Sundrum single braneworld? Nucl. Phys. B 2015, 894, 29–55. [Google Scholar] [CrossRef]
- Choudhury, S. Reconstructing inflationary paradigm within Effective Field Theory framework. Phys. Dark Univ. 2016, 11, 16–48. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S. COSMOS-e’-GTachyon from string theory. Eur. Phys. J. C 2016, 76, 278. [Google Scholar] [CrossRef]
- Choudhury, S. CMB from EFT. Universe 2019, 5, 155. [Google Scholar] [CrossRef]
- Choudhury, S. COSMOS-e′- soft Higgsotic attractors. Eur. Phys. J. C 2017, 77, 469. [Google Scholar] [CrossRef]
- Creminelli, P.; Dubovsky, S.; López Nacir, D.; Simonović, M.; Trevisan, G.; Villadoro, G.; Zaldarriaga, M. Implications of the scalar tilt for the tensor-to-scalar ratio. Phys. Rev. D 2015, 92, 123528. [Google Scholar] [CrossRef]
- Creminelli, P.; Gleyzes, J.; Noreña, J.; Vernizzi, F. Resilience of the standard predictions for primordial tensor modes. Phys. Rev. Lett. 2014, 113, 231301. [Google Scholar] [CrossRef]
- Cheung, C.; Creminelli, P.; Fitzpatrick, A.L.; Kaplan, J.; Senatore, L. The Effective Field Theory of Inflation. JHEP 2008, 3, 14. [Google Scholar] [CrossRef]
- Choudhury, S.; Pal, S. DBI Galileon inflation in background SUGRA. Nucl. Phys. B 2013, 874, 85–114. [Google Scholar] [CrossRef]
- Choudhury, D.; Ghoshal, D.; Jatkar, D.P.; Panda, S. Hybrid inflation and brane—Anti-brane system. JCAP 2003, 7, 9. [Google Scholar] [CrossRef][Green Version]
- Choudhury, S.; Pal, S. Fourth level MSSM inflation from new flat directions. JCAP 2012, 4, 18. [Google Scholar] [CrossRef]
- Choudhury, S.; Pal, S. Brane inflation in background supergravity. Phys. Rev. D 2012, 85, 043529. [Google Scholar] [CrossRef]
- Choudhury, S.; Pal, S. Brane inflation: A field theory approach in background supergravity. J. Phys. Conf. Ser. 2012, 405, 012009. [Google Scholar] [CrossRef]
- Choudhury, S.; Chakraborty, T.; Pal, S. Higgs inflation from new Kähler potential. Nucl. Phys. B 2014, 880, 155–174. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A.; Pukartas, E. Constraining N=1 supergravity inflationary framework with non-minimal Kähler operators. JHEP 2014, 4, 77. [Google Scholar] [CrossRef]
- Mazumdar, A.; Panda, S.; Perez-Lorenzana, A. Assisted inflation via tachyon condensation. Nucl. Phys. B 2001, 614, 101–116. [Google Scholar] [CrossRef]
- Panda, S.; Sami, M.; Tsujikawa, S. Prospects of inflation in delicate D-brane cosmology. Phys. Rev. D 2007, 76, 103512. [Google Scholar] [CrossRef]
- Ali, A.; Deshamukhya, A.; Panda, S.; Sami, M. Inflation with improved D3-brane potential and the fine tunings associated with the model. Eur. Phys. J. C 2011, 71, 1672. [Google Scholar] [CrossRef][Green Version]
- Ali, A.; Chingangbam, R.; Panda, S.; Sami, M. Prospects of inflation with perturbed throat geometry. Phys. Lett. B 2009, 674, 131–136. [Google Scholar] [CrossRef][Green Version]
- Panda, S.; Sami, M.; Tsujikawa, S.; Ward, J. Inflation from D3-brane motion in the background of D5-branes. Phys. Rev. D 2006, 73, 083512. [Google Scholar] [CrossRef]
- Panda, S.; Sami, M.; Tsujikawa, S. Inflation and dark energy arising from geometrical tachyons. Phys. Rev. D 2006, 73, 023515. [Google Scholar] [CrossRef]
- Chingangbam, P.; Panda, S.; Deshamukhya, A. Non-minimally coupled tachyonic inflation in warped string background. JHEP 2005, 2, 52. [Google Scholar] [CrossRef]
- Panda, S.; Sami, M.; Ward, J. Bounds on Tensor wave and Twisted Inflation. Phys. Rev. D 2010, 82, 103511. [Google Scholar] [CrossRef]
- Vargas Moniz, P.; Panda, S.; Ward, J. Higher order corrections to Heterotic M-theory inflation. Class. Quant. Grav. 2009, 26, 245003. [Google Scholar] [CrossRef]
- Lidsey, J.E.; Tavakol, R. Running of the scalar spectral index and observational signatures of inflation. Phys. Lett. B 2003, 575, 157–164. [Google Scholar] [CrossRef]
- Zarei, M. On the running of the spectral index to all orders: A new model dependent approach to constrain inflationary models. Class. Quant. Grav. 2016, 33, 115008. [Google Scholar] [CrossRef]
- Li, J.; Huang, Q.G. Measuring the spectral running from cosmic microwave background and primordial black holes. Eur. Phys. J. C 2018, 78, 980. [Google Scholar] [CrossRef]
- Gruzinov, A. Consistency relation for single scalar inflation. Phys. Rev. D 2005, 71, 027301. [Google Scholar] [CrossRef]
- Gong, J.O.; Seo, M.S. Consistency relations in multi-field inflation. JCAP 2018, 2, 8. [Google Scholar] [CrossRef]
- Hui, L.; Joyce, A.; Wong, S.S.C. Inflationary soft theorems revisited: A generalized consistency relation. JCAP 2019, 2, 60. [Google Scholar] [CrossRef]
- Choudhury, S.; Mukherjee, A.; Chauhan, P.; Bhattacherjee, S. Quantum Out-of-Equilibrium Cosmology. Eur. Phys. J. C 2019, 79, 320. [Google Scholar] [CrossRef]
- Choudhury, S.; Mukherjee, A. Quantum randomness in the Sky. Eur. Phys. J. C 2019, 79, 554. [Google Scholar] [CrossRef]
- Amin, M.A.; Baumann, D. From Wires to Cosmology. JCAP 2016, 2, 45. [Google Scholar] [CrossRef]
- Garcia, M.A.G.; Amin, M.A.; Green, D. Curvature Perturbations From Stochastic Particle Production During Inflation. JCAP 2020, 6, 39. [Google Scholar] [CrossRef]
- Garcia, M.A.G.; Amin, M.A.; Carlsten, S.G.; Green, D. Stochastic Particle Production in a de Sitter Background. JCAP 2019, 5, 12. [Google Scholar] [CrossRef]
- Deshamukhya, A.; Panda, S. Warm tachyonic inflation in warped background. Int. J. Mod. Phys. D 2009, 18, 2093–2106. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef]
- Berera, A. The warm inflationary universe. Contemp. Phys. 2006, 47, 33–49. [Google Scholar] [CrossRef]
- Özsoy, O.; Giblin, J.T.; Nesbit, E.; Şengör, G.; Watson, S. Toward an Effective Field Theory Approach to Reheating. Phys. Rev. D 2017, 96, 123524. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Towards the theory of reheating after inflation. Phys. Rev. D 1997, 56, 3258–3295. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Reheating after inflation. Phys. Rev. Lett. 1994, 73, 3195–3198. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, S.; Pal, S. Reheating and leptogenesis in a SUGRA inspired brane inflation. Nucl. Phys. B 2012, 857, 85–100. [Google Scholar] [CrossRef]
- Panda, S.; Sami, M.; Thongkool, I. Reheating the D-brane universe via instant preheating. Phys. Rev. D 2010, 81, 103506. [Google Scholar] [CrossRef]
- Matacz, A. A New theory of stochastic inflation. Phys. Rev. D 1997, 55, 1860–1874. [Google Scholar] [CrossRef]
- Pattison, C.; Vennin, V.; Assadullahi, H.; Wands, D. Stochastic inflation beyond slow roll. JCAP 2019, 7, 31. [Google Scholar] [CrossRef]
- Ando, K.; Vennin, V. Power spectrum in stochastic inflation. arXiv 2020, arXiv:2012.02031. [Google Scholar]
- Vennin, V. Stochastic Inflation and Primordial Black Holes. arXiv 2020, arXiv:2009.08715. [Google Scholar]
- Noorbala, M.; Vennin, V.; Assadullahi, H.; Firouzjahi, H.; Wands, D. Tunneling in Stochastic Inflation. JCAP 2018, 09, 32. [Google Scholar] [CrossRef]
- Mandal, G.; Paranjape, S.; Sorokhaibam, N. Thermalization in 2D critical quench and UV/IR mixing. JHEP 2018, 1, 27. [Google Scholar] [CrossRef]
- Kulkarni, M.; Mandal, G.; Morita, T. Quantum quench and thermalization of one-dimensional Fermi gas via phase space hydrodynamics. Phys. Rev. A 2018, 98, 043610. [Google Scholar] [CrossRef]
- Mandal, G.; Morita, T. Quantum quench in matrix models: Dynamical phase transitions, Selective equilibration and the Generalized Gibbs Ensemble. JHEP 2013, 10, 197. [Google Scholar] [CrossRef]
- Banerjee, P.; Gaikwad, A.; Kaushal, A.; Mandal, G. Quantum quench and thermalization to GGE in arbitrary dimensions and the odd-even effect. JHEP 2020, 9, 27. [Google Scholar] [CrossRef]
- Das, S.R.; Hampton, S.; Liu, S. Quantum quench in c=1 matrix model and emergent space-times. JHEP 2020, 4, 107. [Google Scholar] [CrossRef]
- Das, S.R.; Hampton, S.; Liu, S. Quantum Quench in Non-relativistic Fermionic Field Theory: Harmonic traps and 2d String Theory. JHEP 2019, 8, 176. [Google Scholar] [CrossRef]
- Caputa, P.; Das, S.R.; Nozaki, M.; Tomiya, A. Quantum Quench and Scaling of Entanglement Entropy. Phys. Lett. B 2017, 772, 53–57. [Google Scholar] [CrossRef]
- Das, S.R.; Galante, D.A.; Myers, R.C. Quantum Quenches in Free Field Theory: Universal Scaling at Any Rate. JHEP 2016, 5, 164. [Google Scholar] [CrossRef]
- Das, S.R.; Galante, D.A.; Myers, R.C. Smooth and fast versus instantaneous quenches in quantum field theory. JHEP 2015, 8, 73. [Google Scholar] [CrossRef]
- Das, S.R.; Galante, D.A.; Myers, R.C. Universality in fast quantum quenches. JHEP 2015, 2, 167. [Google Scholar] [CrossRef]
- Das, S.R.; Galante, D.A.; Myers, R.C. Universal scaling in fast quantum quenches in conformal field theories. Phys. Rev. Lett. 2014, 112, 171601. [Google Scholar] [CrossRef]
- Basu, P.; Das, D.; Das, S.R.; Sengupta, K. Quantum Quench and Double Trace Couplings. JHEP 2013, 12, 70. [Google Scholar] [CrossRef][Green Version]
- Choudhury, S.; Panda, S. Entangled de Sitter from stringy axionic Bell pair I: An analysis using Bunch–Davies vacuum. Eur. Phys. J. C 2018, 78, 52. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S. Quantum entanglement in de Sitter space from stringy axion: An analysis using α vacua. Nucl. Phys. B 2019, 943, 114606. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S. Cosmological Spectrum of Two-Point Correlation Function from Vacuum Fluctuation of Stringy Axion Field in De Sitter Space: A Study of the Role of Quantum Entanglement. Universe 2020, 6, 79. [Google Scholar] [CrossRef]
- Akhtar, S.; Choudhury, S.; Chowdhury, S.; Goswami, D.; Panda, S.; Swain, A. Open Quantum Entanglement: A study of two atomic system in static patch of de Sitter space. Eur. Phys. J. C 2020, 80, 748. [Google Scholar] [CrossRef]
- Banerjee, S.; Choudhury, S.; Chowdhury, S.; Das, R.N.; Gupta, N.; Panda, S.; Swain, A. Indirect detection of Cosmological Constant from large N entangled open quantum system. arXiv 2020, arXiv:2004.13058. [Google Scholar]
- Bohra, H.; Choudhury, S.; Chauhan, P.; Narayan, P.; Panda, S.; Swain, A. Relating the curvature of De Sitter Universe to Open Quantum Lamb Shift Spectroscopy. arXiv 2019, arXiv:1905.07403. [Google Scholar]
- Narayan, K. De Sitter space and extremal surfaces for spheres. Phys. Lett. B 2016, 753, 308–314. [Google Scholar] [CrossRef]
- Narayan, K. Extremal surfaces in de Sitter spacetime. Phys. Rev. D 2015, 91, 126011. [Google Scholar] [CrossRef]
- Narayan, K. On dS4 extremal surfaces and entanglement entropy in some ghost CFTs. Phys. Rev. D 2016, 94, 046001. [Google Scholar] [CrossRef]
- Narayan, K. On extremal surfaces and de Sitter entropy. Phys. Lett. B 2018, 779, 214–222. [Google Scholar] [CrossRef]
- Narayan, K. De Sitter entropy as entanglement. Int. J. Mod. Phys. D 2019, 28, 1944019. [Google Scholar] [CrossRef]
- Narayan, K. De Sitter future-past extremal surfaces and the entanglement wedge. Phys. Rev. D 2020, 101, 086014. [Google Scholar] [CrossRef]
- Manu, A.; Narayan, K.; Paul, P. Cosmological singularities, entanglement and quantum extremal surfaces. arXiv 2020, arXiv:2012.07351. [Google Scholar]
- Fernandes, K.; Kolekar, K.S.; Narayan, K.; Roy, S. Schwarzschild de Sitter and extremal surfaces. Eur. Phys. J. C 2020, 80, 866. [Google Scholar] [CrossRef]
- Maldacena, J.; Pimentel, G.L. Entanglement entropy in de Sitter space. JHEP 2013, 2, 38. [Google Scholar] [CrossRef]
- Albrecht, A.; Kanno, S.; Sasaki, M. Quantum entanglement in de Sitter space with a wall, and the decoherence of bubble universes. Phys. Rev. D 2018, 97, 083520. [Google Scholar] [CrossRef]
- Arias, C.; Diaz, F.; Sundell, P. De Sitter Space and Entanglement. Class. Quant. Grav. 2020, 37, 015009. [Google Scholar] [CrossRef]
- Huang, Z.; Tian, Z. Dynamics of quantum entanglement in de Sitter spacetime and thermal Minkowski spacetime. Nucl. Phys. B 2017, 923, 458–474. [Google Scholar] [CrossRef]
- Van Raamsdonk, M. Lectures on Gravity and Entanglement. In Theoretical Advanced Study Institute in Elementary Particle Physics: New Frontiers in Fields and Strings; World Scientific Publishing Co Pte Ltd: Singapore, 2017; pp. 297–351. [Google Scholar] [CrossRef]
- Kanno, S. Quantum Entanglement in the Multiverse. Universe 2017, 3, 28. [Google Scholar] [CrossRef]
- Soda, J.; Kanno, S.; Shock, J.P. Quantum Correlations in de Sitter Space. Universe 2017, 3, 2. [Google Scholar] [CrossRef]
- Kanno, S.; Sasaki, M.; Tanaka, T. Vacuum State of the Dirac Field in de Sitter Space and Entanglement Entropy. JHEP 2017, 3, 68. [Google Scholar] [CrossRef]
- Kanno, S.; Shock, J.P.; Soda, J. Quantum discord in de Sitter space. Phys. Rev. D 2016, 94, 125014. [Google Scholar] [CrossRef]
- Kanno, S. A note on initial state entanglement in inflationary cosmology. EPL 2015, 111, 60007. [Google Scholar] [CrossRef]
- Kanno, S. Cosmological implications of quantum entanglement in the multiverse. Phys. Lett. B 2015, 751, 316–320. [Google Scholar] [CrossRef]
- Kanno, S.; Shock, J.P.; Soda, J. Entanglement negativity in the multiverse. JCAP 2015, 3, 15. [Google Scholar] [CrossRef]
- Kanno, S. Impact of quantum entanglement on spectrum of cosmological fluctuations. JCAP 2014, 7, 29. [Google Scholar] [CrossRef]
- Kanno, S.; Murugan, J.; Shock, J.P.; Soda, J. Entanglement entropy of α-vacua in de Sitter space. JHEP 2014, 7, 72. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S.; Singh, R. Bell violation in the Sky. Eur. Phys. J. C 2017, 77, 60. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S.; Singh, R. Bell violation in primordial cosmology. Universe 2017, 3, 13. [Google Scholar] [CrossRef]
- Martin, J.; Vennin, V. Obstructions to Bell CMB Experiments. Phys. Rev. D 2017, 96, 063501. [Google Scholar] [CrossRef]
- Maldacena, J. A model with cosmological Bell inequalities. Fortsch. Phys. 2016, 64, 10–23. [Google Scholar] [CrossRef]
- Kanno, S.; Soda, J. Bell Inequality and Its Application to Cosmology. Galaxies 2017, 5, 99. [Google Scholar] [CrossRef]
- Kanno, S.; Soda, J. Infinite violation of Bell inequalities in inflation. Phys. Rev. D 2017, 96, 083501. [Google Scholar] [CrossRef]
- Jefferson, R.; Myers, R.C. Circuit complexity in quantum field theory. JHEP 2017, 10, 107. [Google Scholar] [CrossRef]
- Guo, M.; Hernandez, J.; Myers, R.C.; Ruan, S.M. Circuit Complexity for Coherent States. JHEP 2018, 10, 11. [Google Scholar] [CrossRef]
- Chapman, S.; Marrochio, H.; Myers, R.C. Complexity of Formation in Holography. JHEP 2017, 1, 62. [Google Scholar] [CrossRef]
- Caceres, E.; Chapman, S.; Couch, J.D.; Hernandez, J.P.; Myers, R.C.; Ruan, S.M. Complexity of Mixed States in QFT and Holography. JHEP 2020, 3, 12. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Shekar, A.; Sinha, A. Circuit complexity in interacting QFTs and RG flows. JHEP 2018, 10, 140. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Nandy, P.; Sinha, A. Renormalized Circuit Complexity. Phys. Rev. Lett. 2020, 124, 101602. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Das, S.; Haque, S.S.; Underwood, B. Rise of cosmological complexity: Saturation of growth and chaos. Phys. Rev. Res. 2020, 2, 033273. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Das, S.; Shajidul Haque, S.; Underwood, B. Cosmological Complexity. Phys. Rev. D 2020, 101, 106020. [Google Scholar] [CrossRef]
- Choudhury, S.; Selvam, S.P.; Shirish, K. Circuit Complexity From Supersymmetric Quantum Field Theory With Morse Function. arXiv 2021, arXiv:2101.12582. [Google Scholar]
- Choudhury, S.; Dutta, A.; Ray, D. Chaos and Complexity from Quantum Neural Network: A study with Diffusion Metric in Machine Learning. arXiv 2020, arXiv:2011.07145. [Google Scholar]
- Choudhury, S.; Chowdhury, S.; Gupta, N.; Mishara, A.; Selvam, S.P.; Panda, S.; Pasquino, G.D.; Singha, C.; Swain, A. Magical Chaotic Cosmological Islands: Generating Page Curve to solve Black Hole Information loss problem from Cosmological Chaos—Complexity connection. arXiv 2020, arXiv:2012.10234. [Google Scholar]
- Bhargava, P.; Choudhury, S.; Chowdhury, S.; Mishara, A.; Selvam, S.P.; Panda, S.; Pasquino, G.D. Quantum aspects of chaos and complexity from bouncing cosmology: A study with two-mode single field squeezed state formalism. arXiv 2020, arXiv:2009.03893. [Google Scholar]
- Khan, R.; Krishnan, C.; Sharma, S. Circuit Complexity in Fermionic Field Theory. Phys. Rev. D 2018, 98, 126001. [Google Scholar] [CrossRef]
- Haque, S.S.; Underwood, B. Squeezed out-of-time-order correlator and cosmology. Phys. Rev. D 2021, 103, 023533. [Google Scholar] [CrossRef]
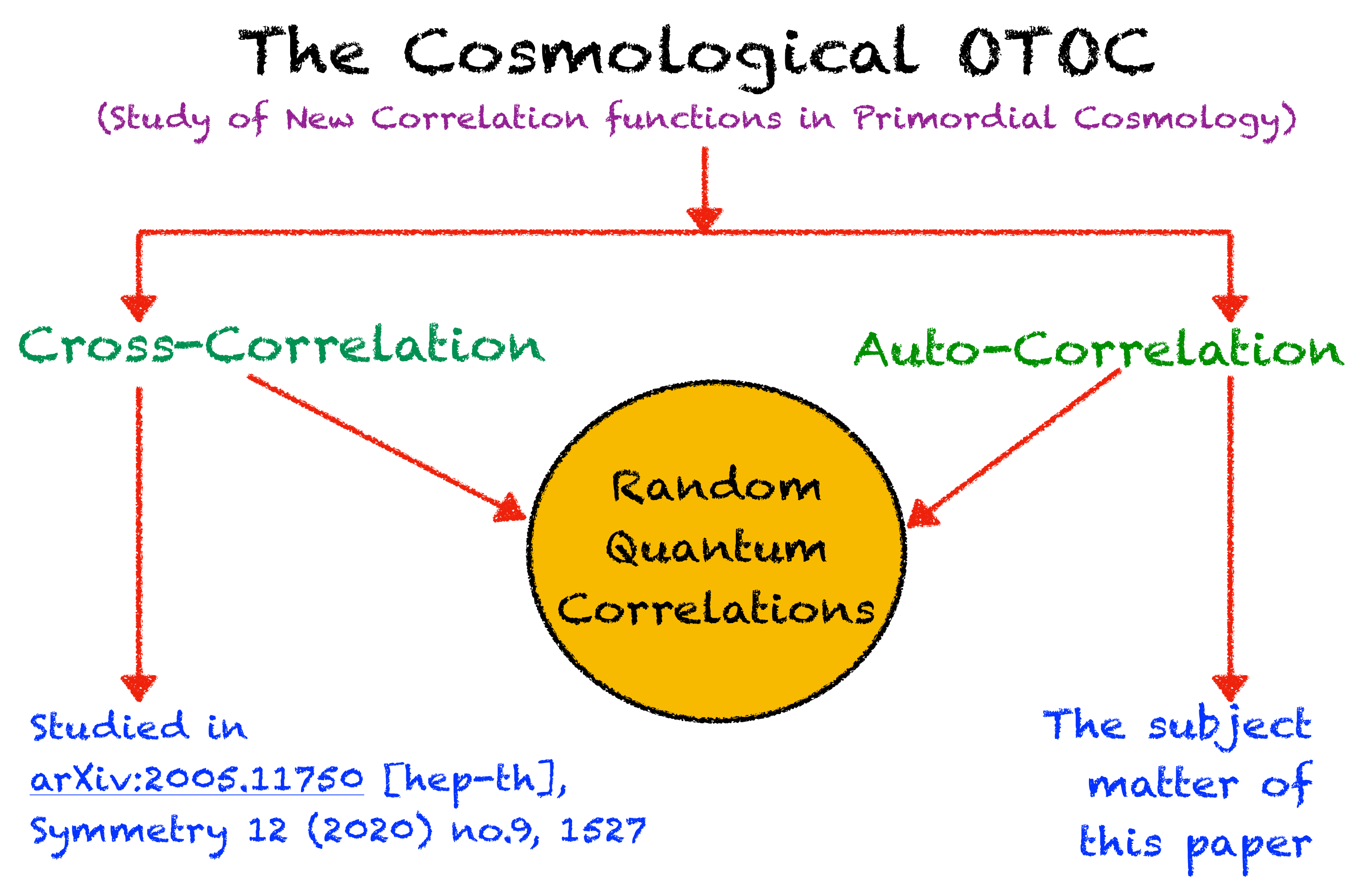
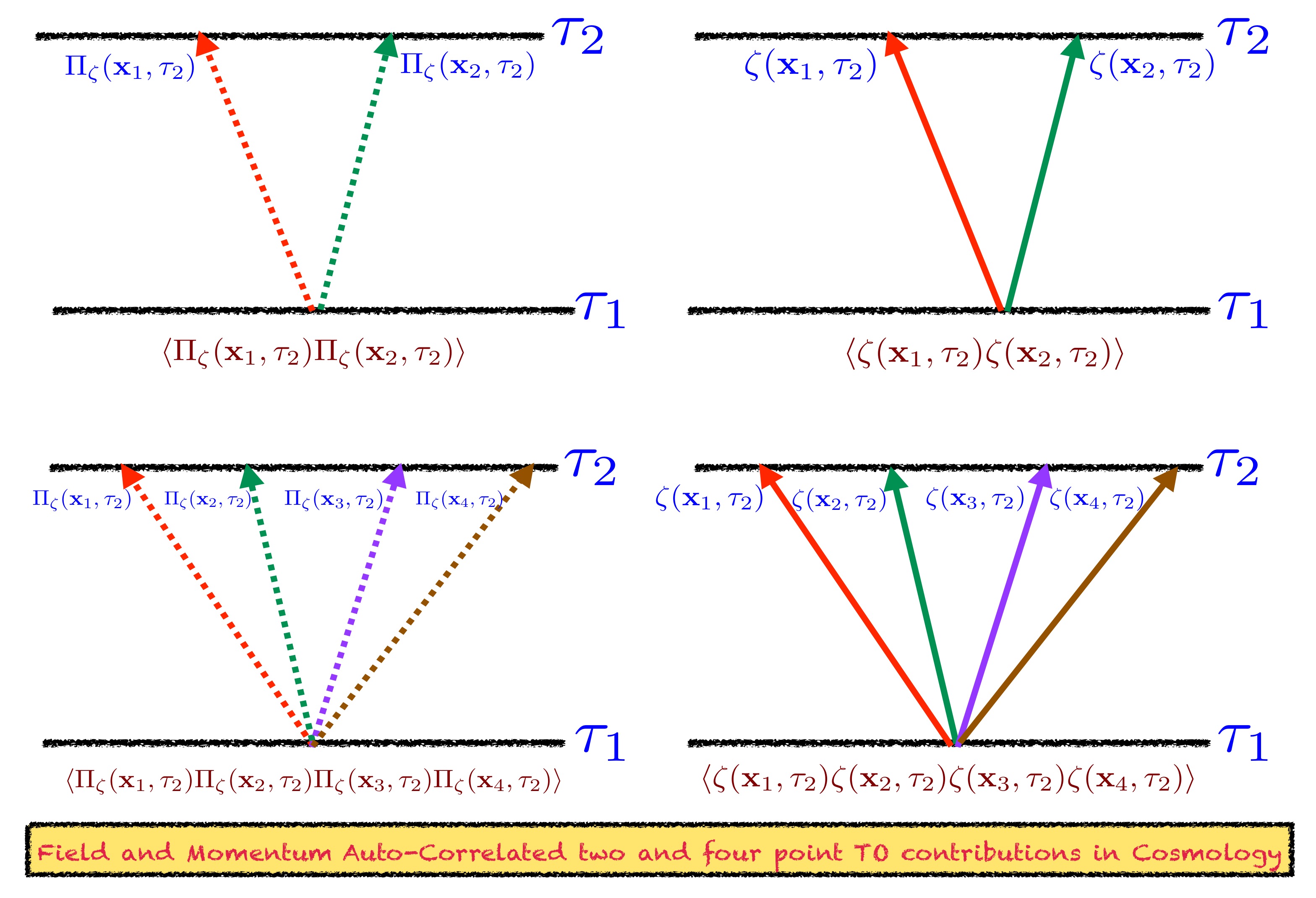

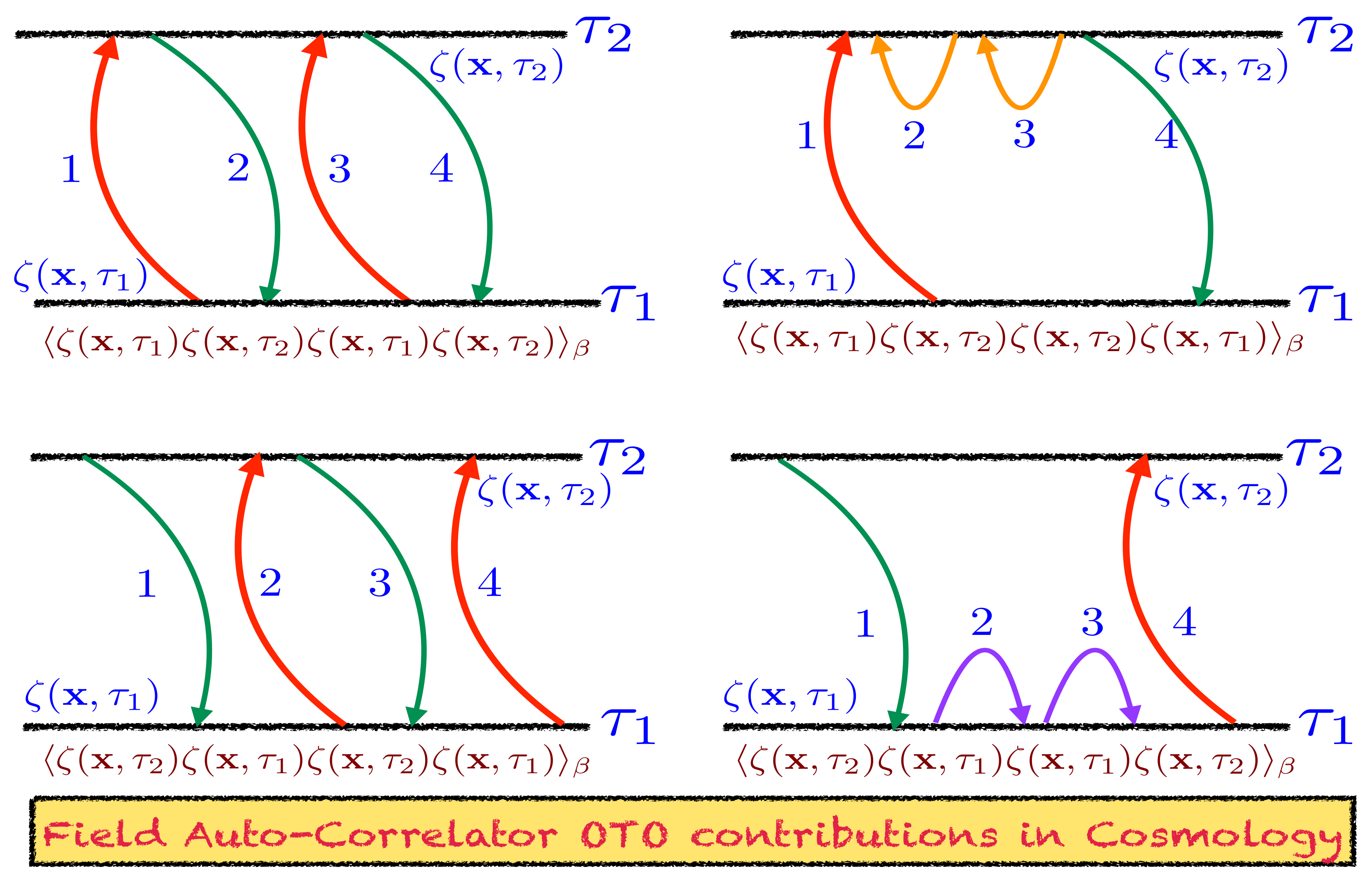
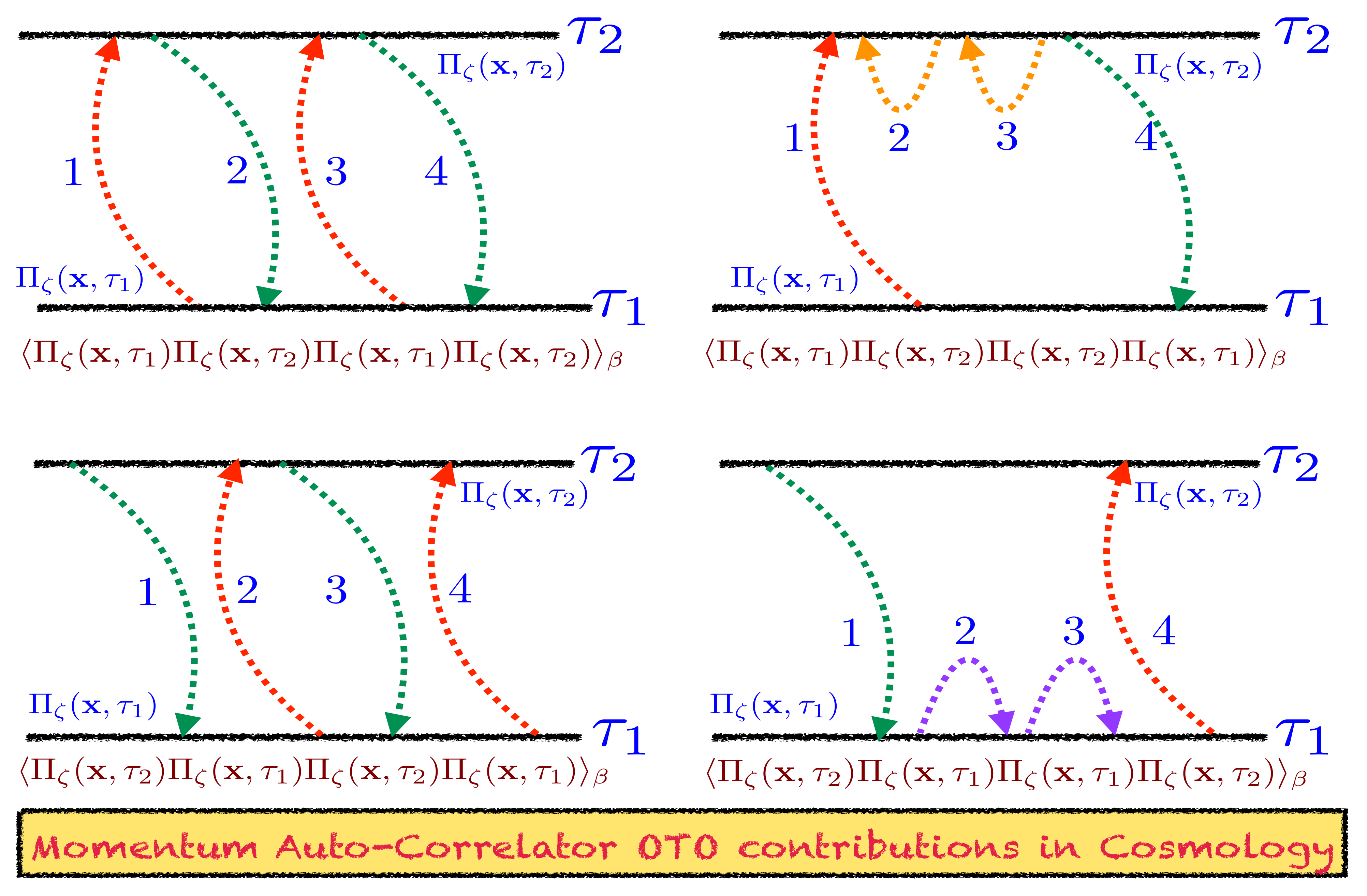
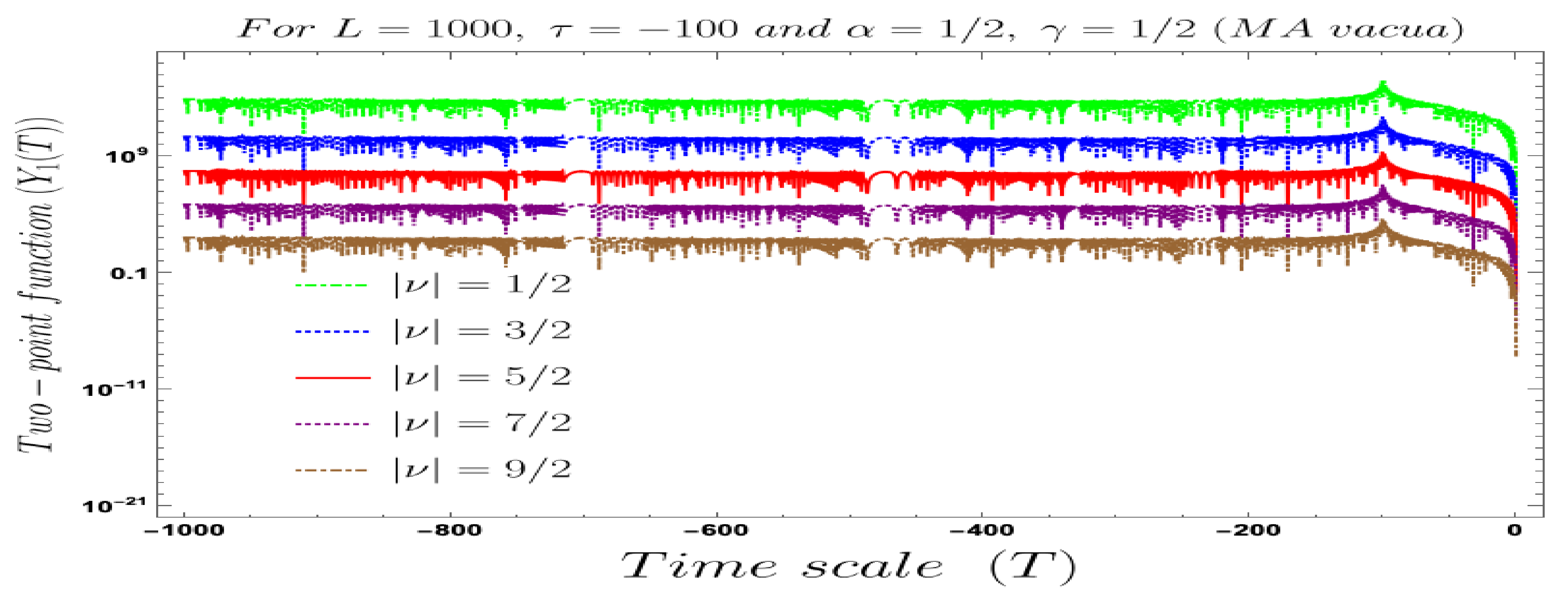
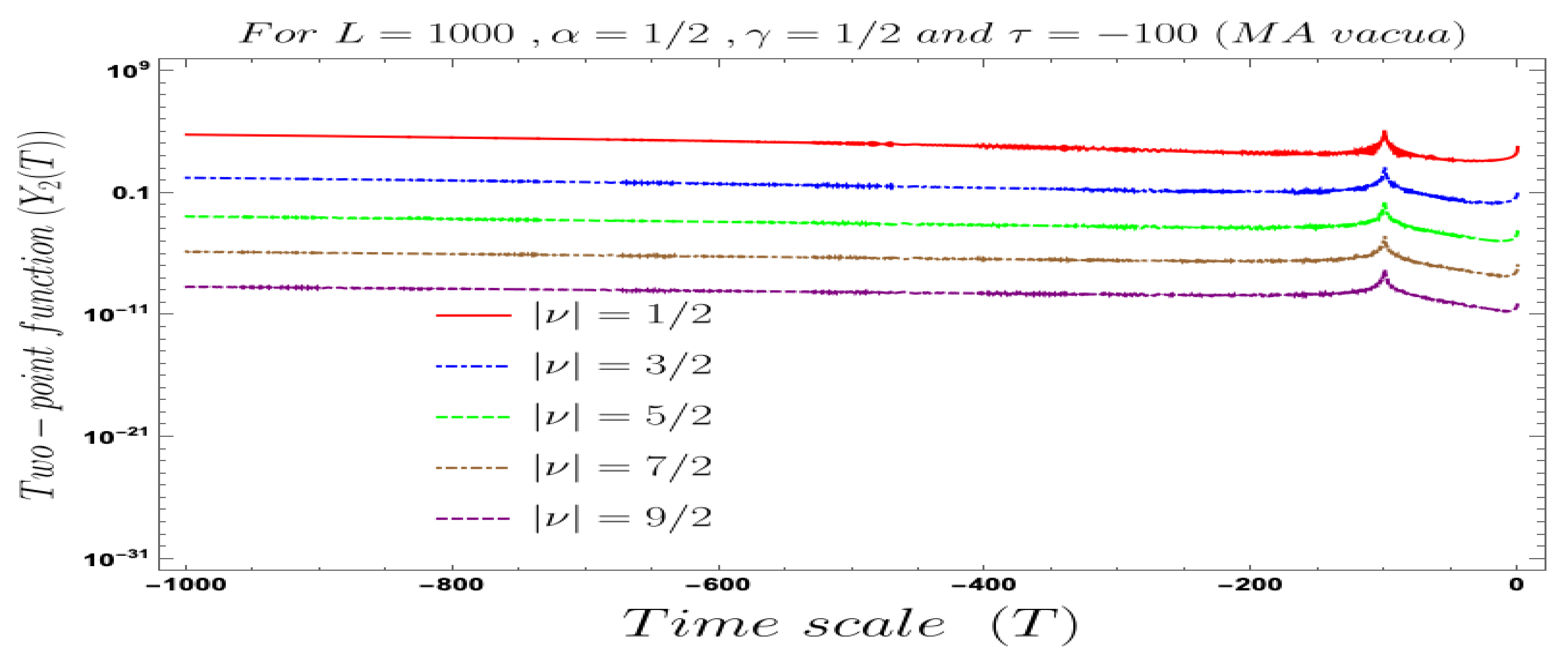
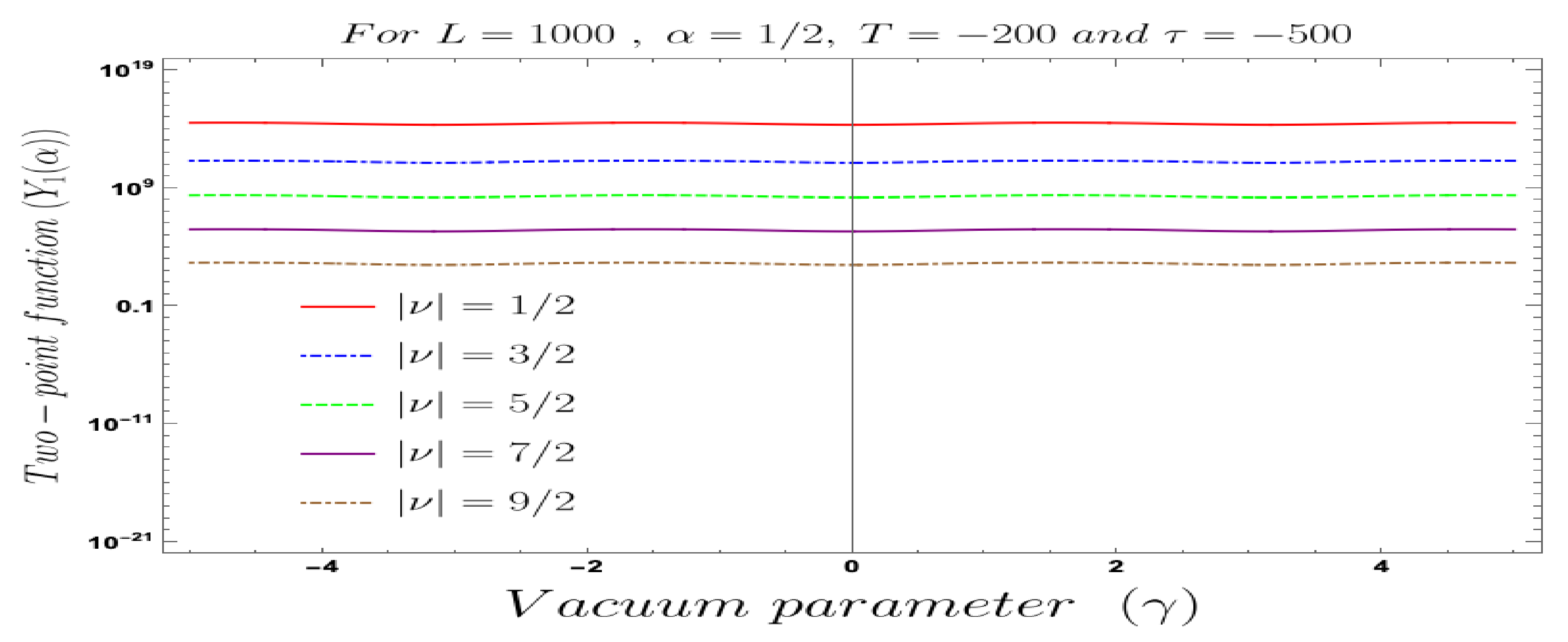
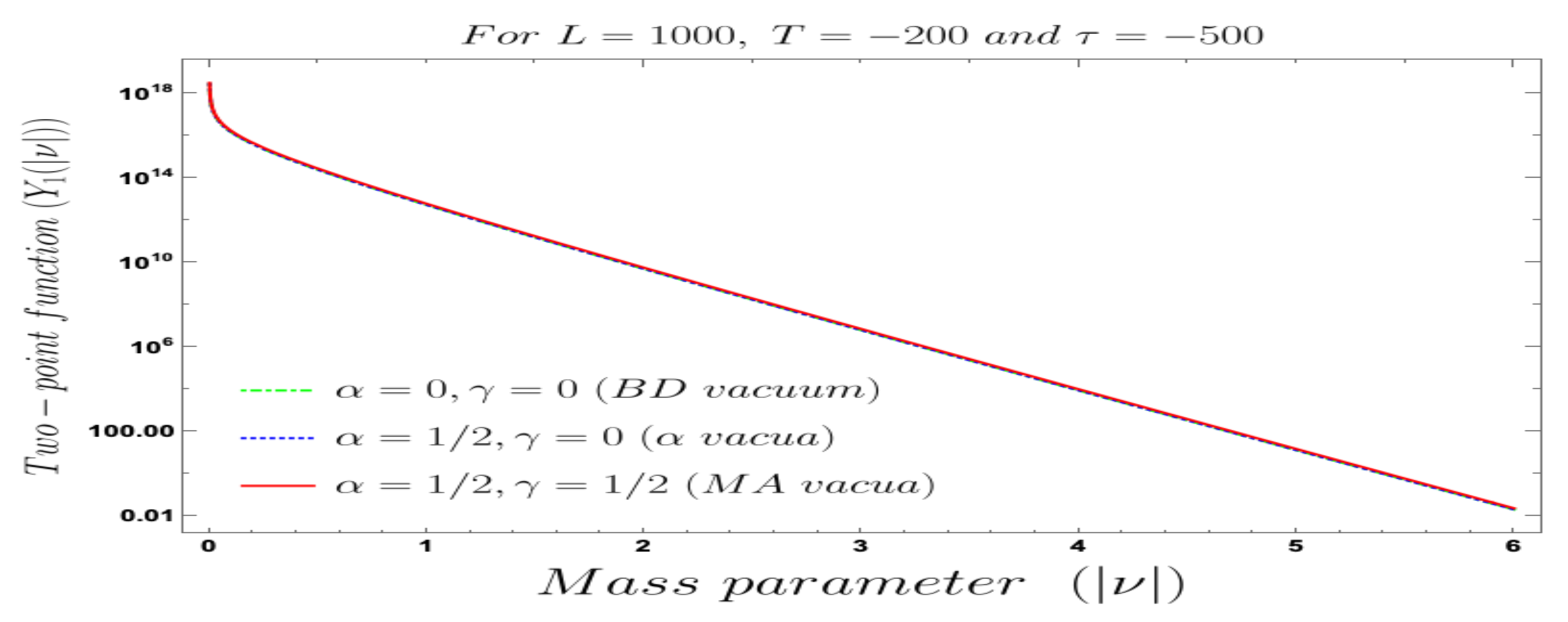
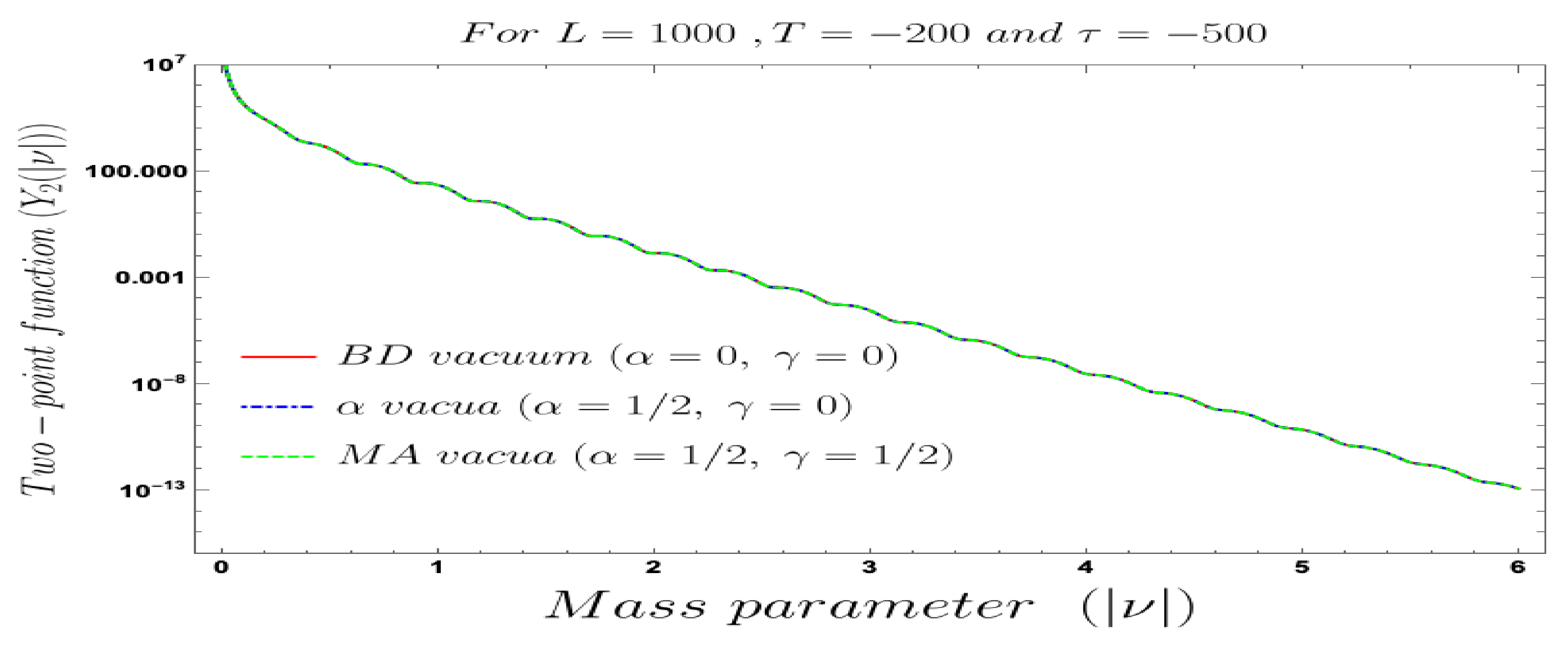
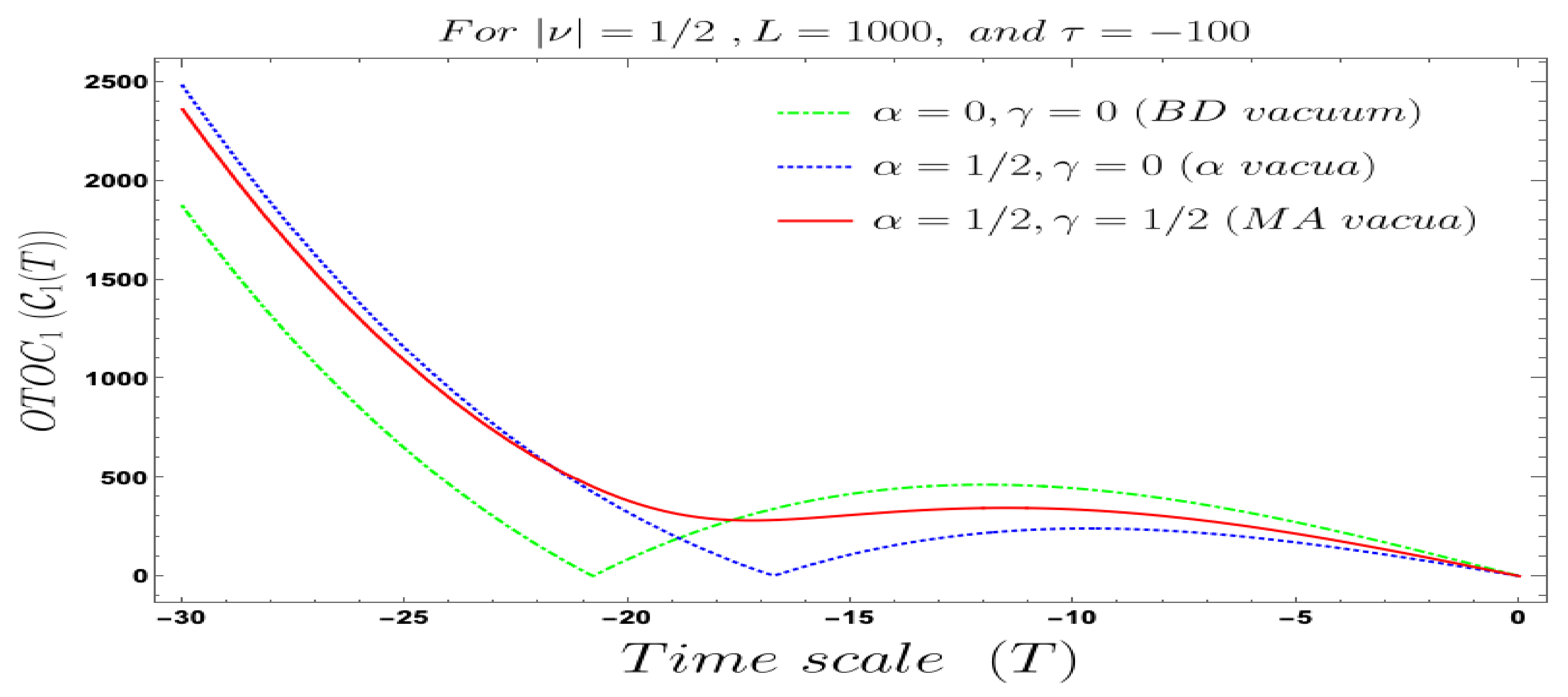
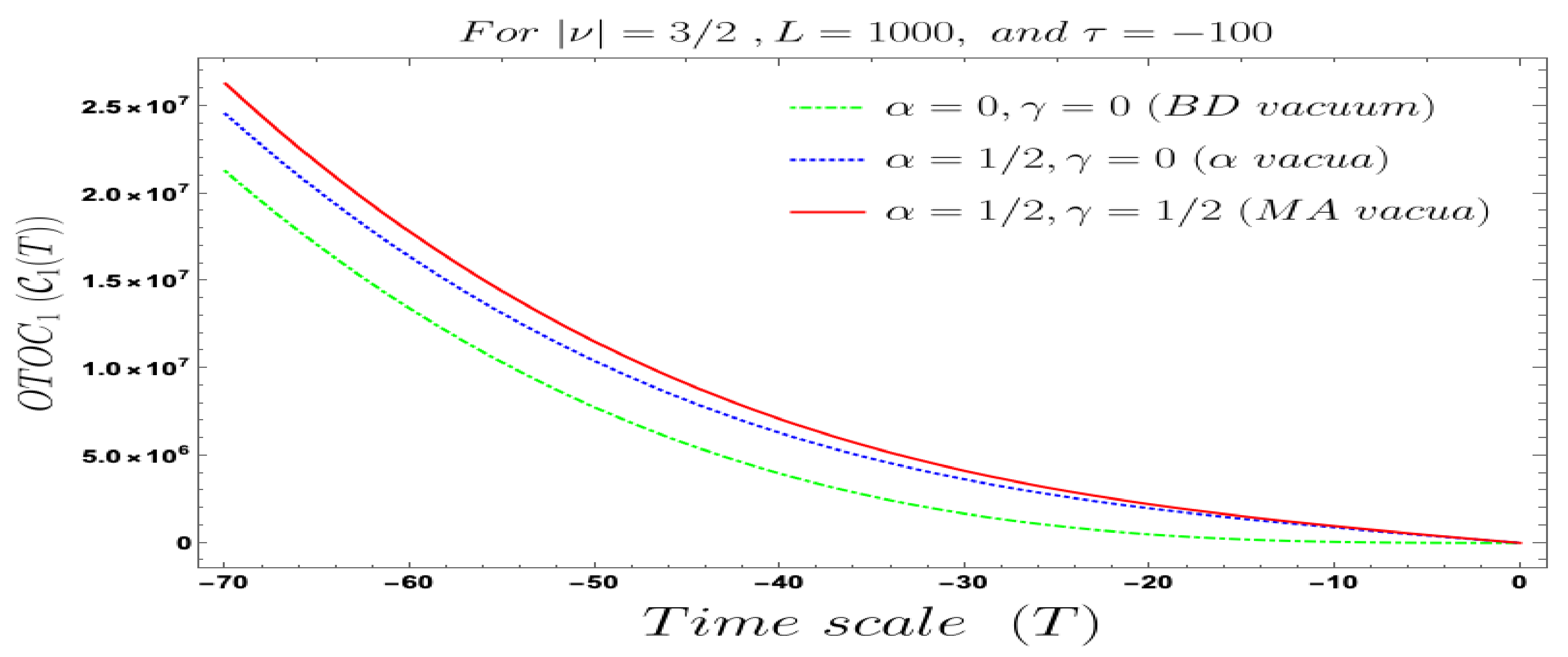
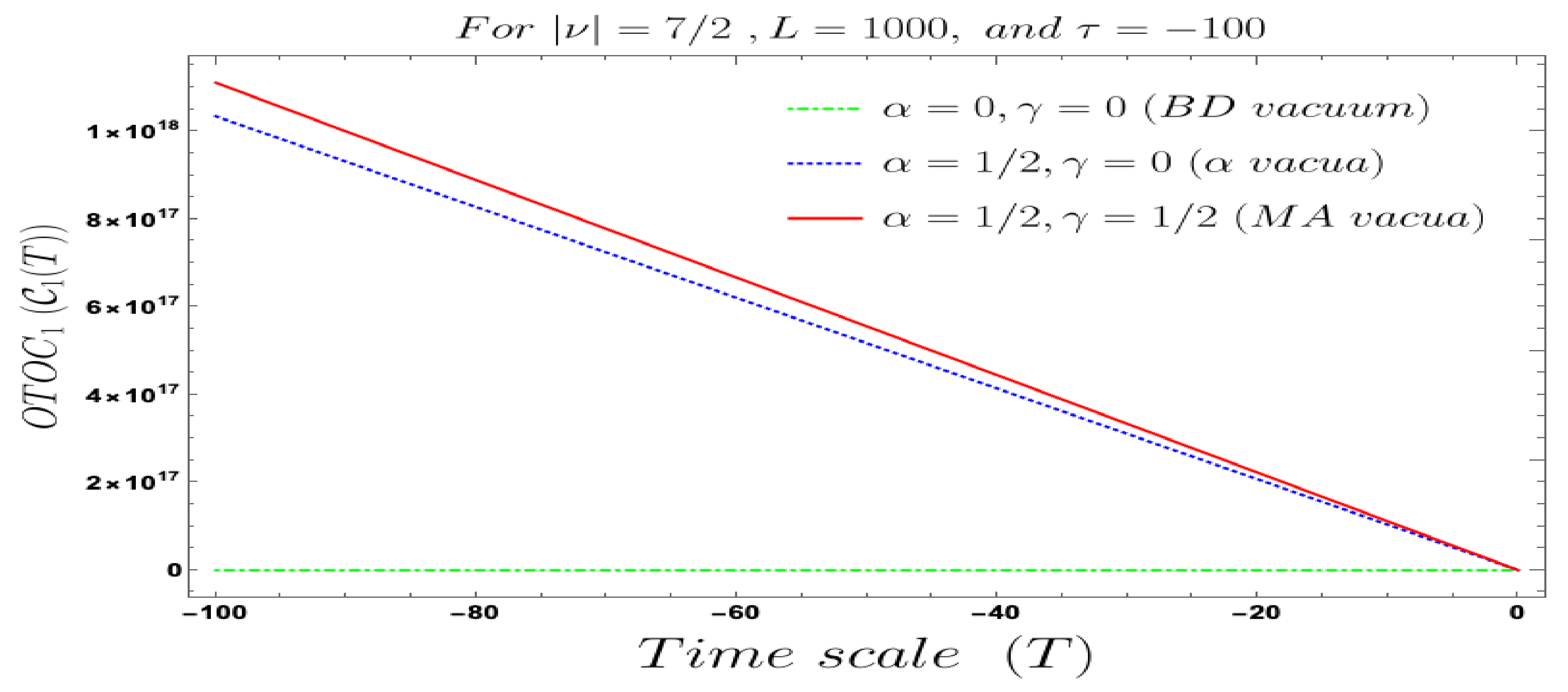
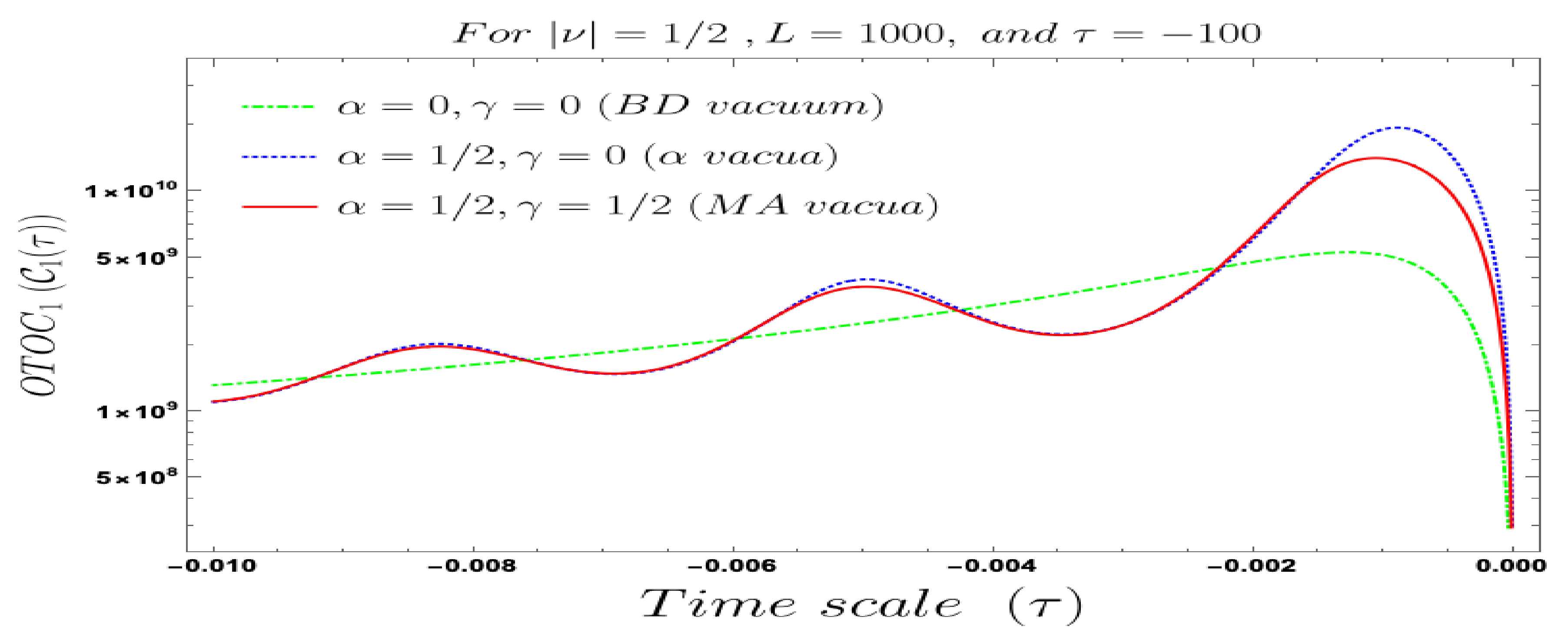
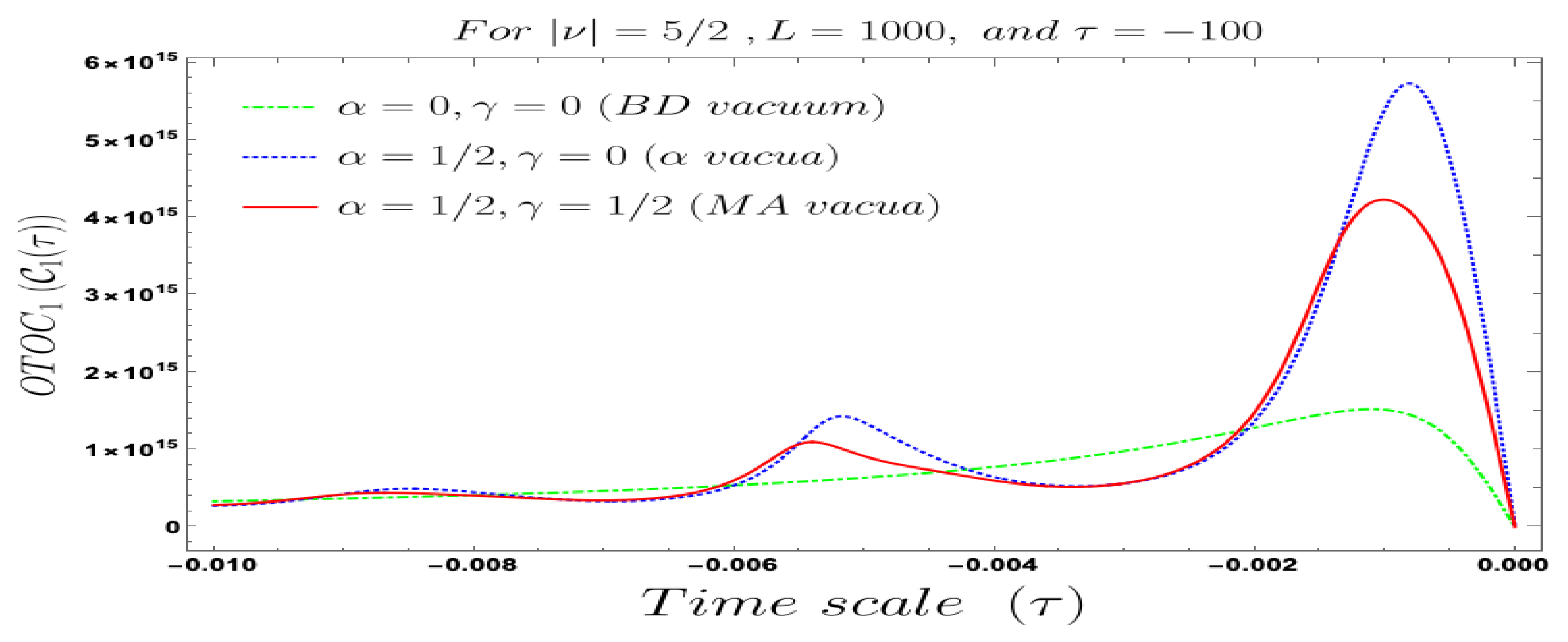
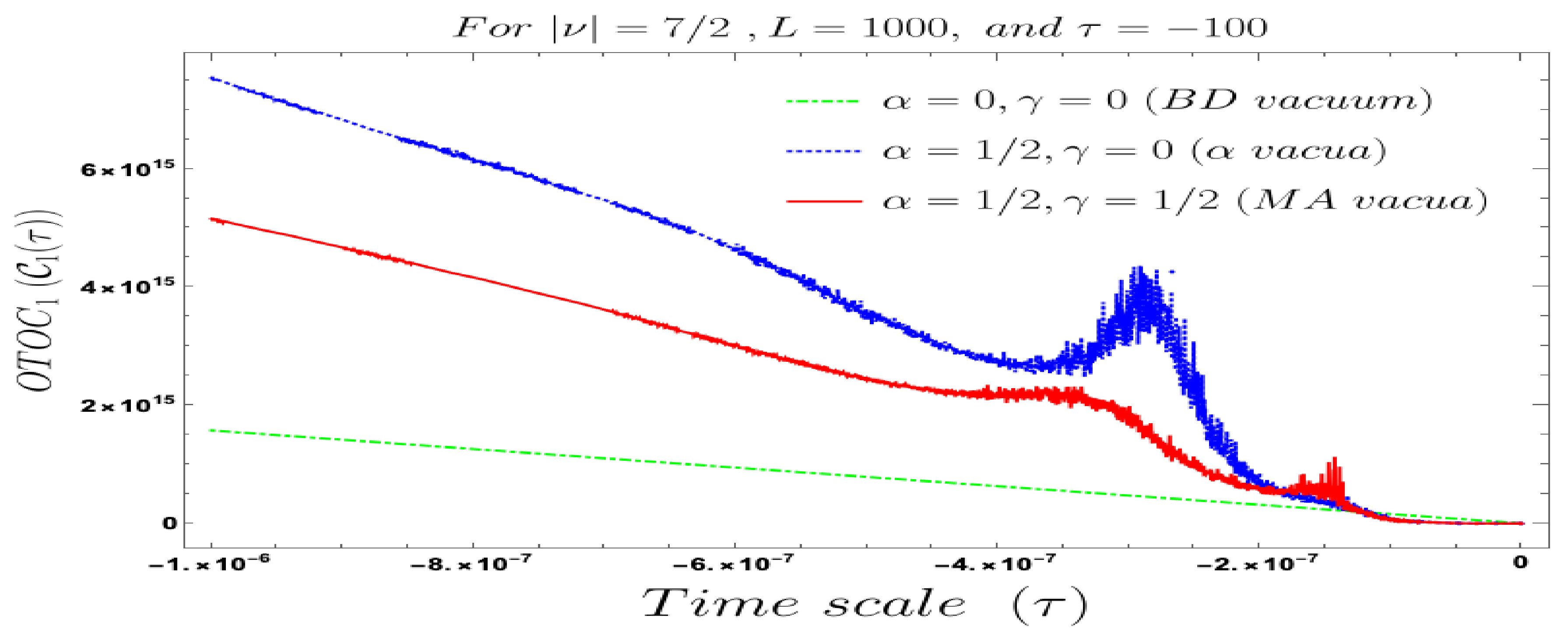
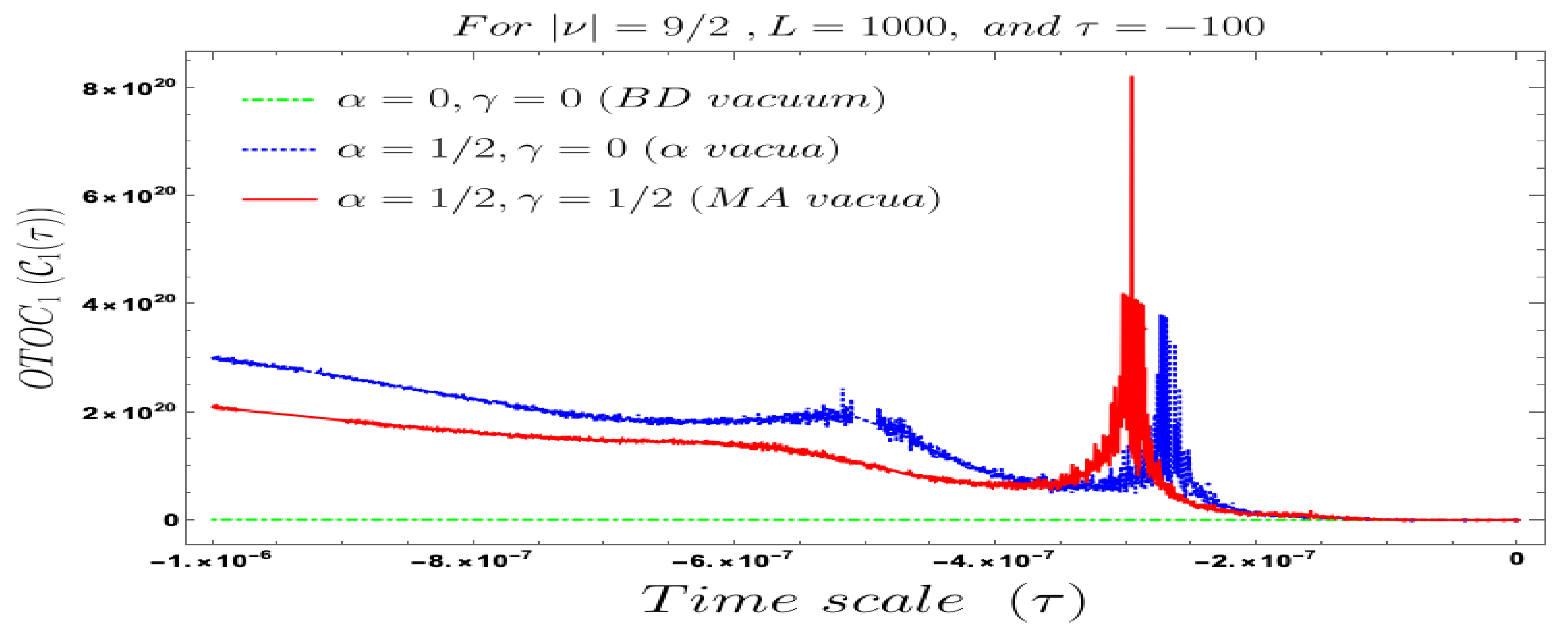

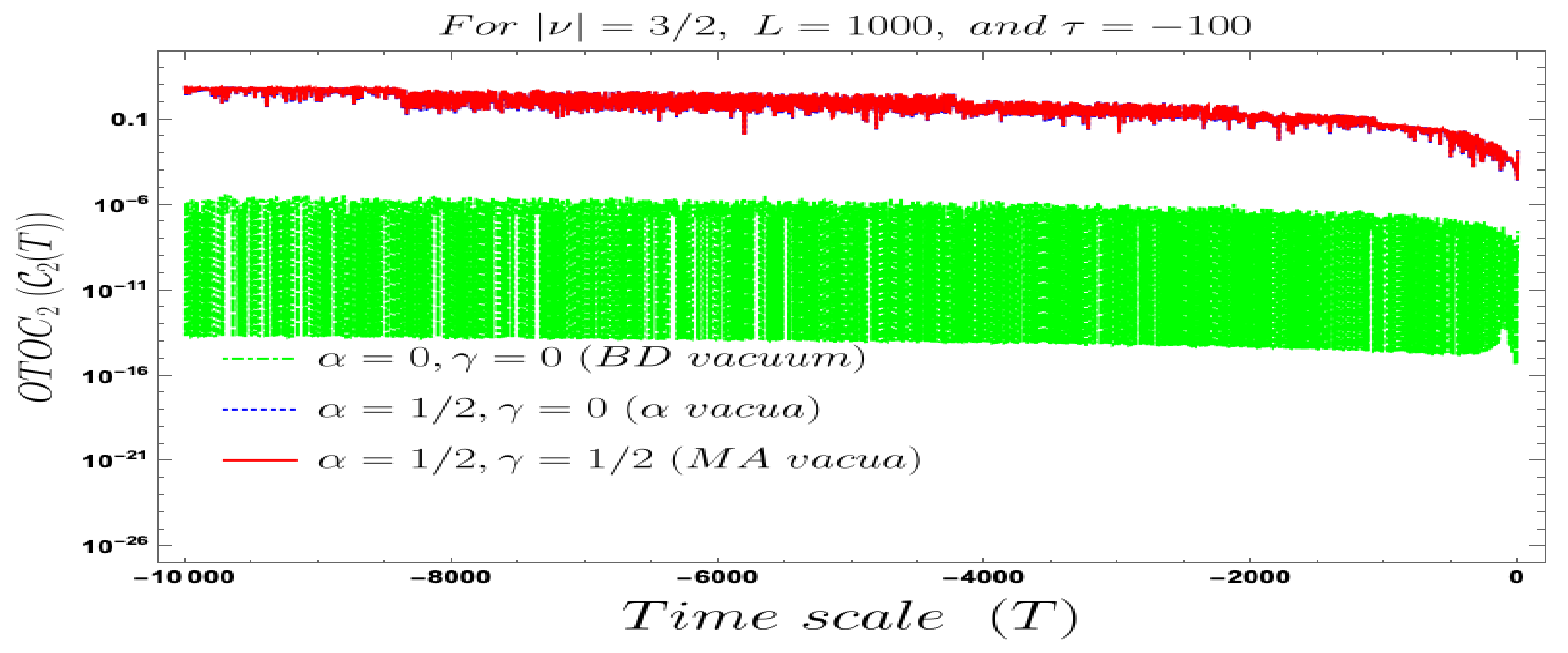
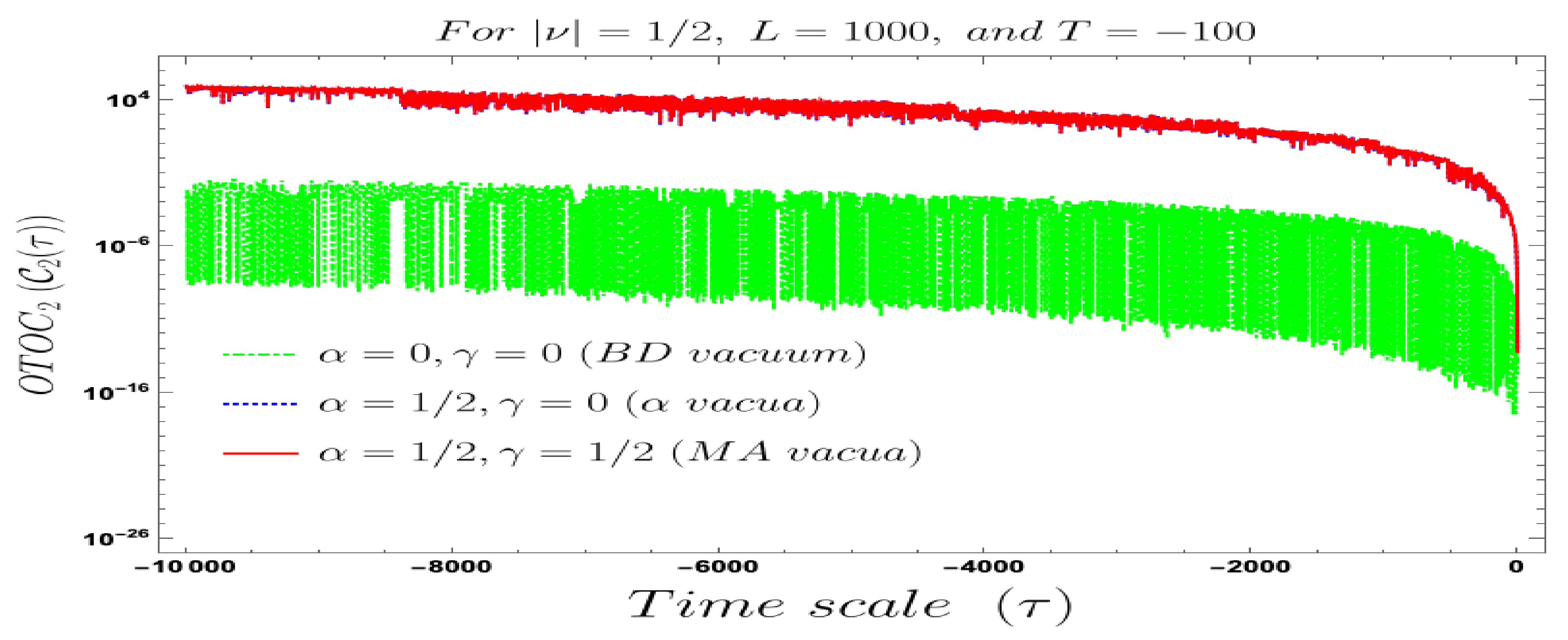
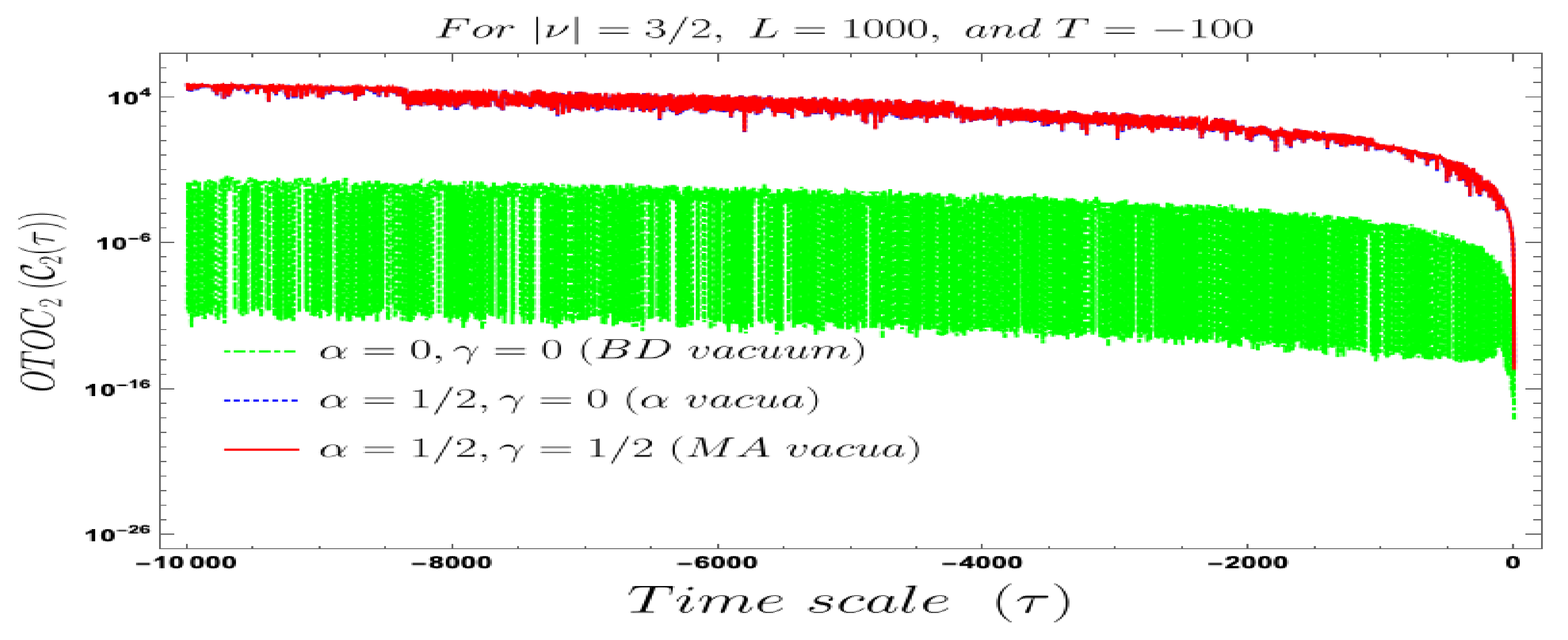
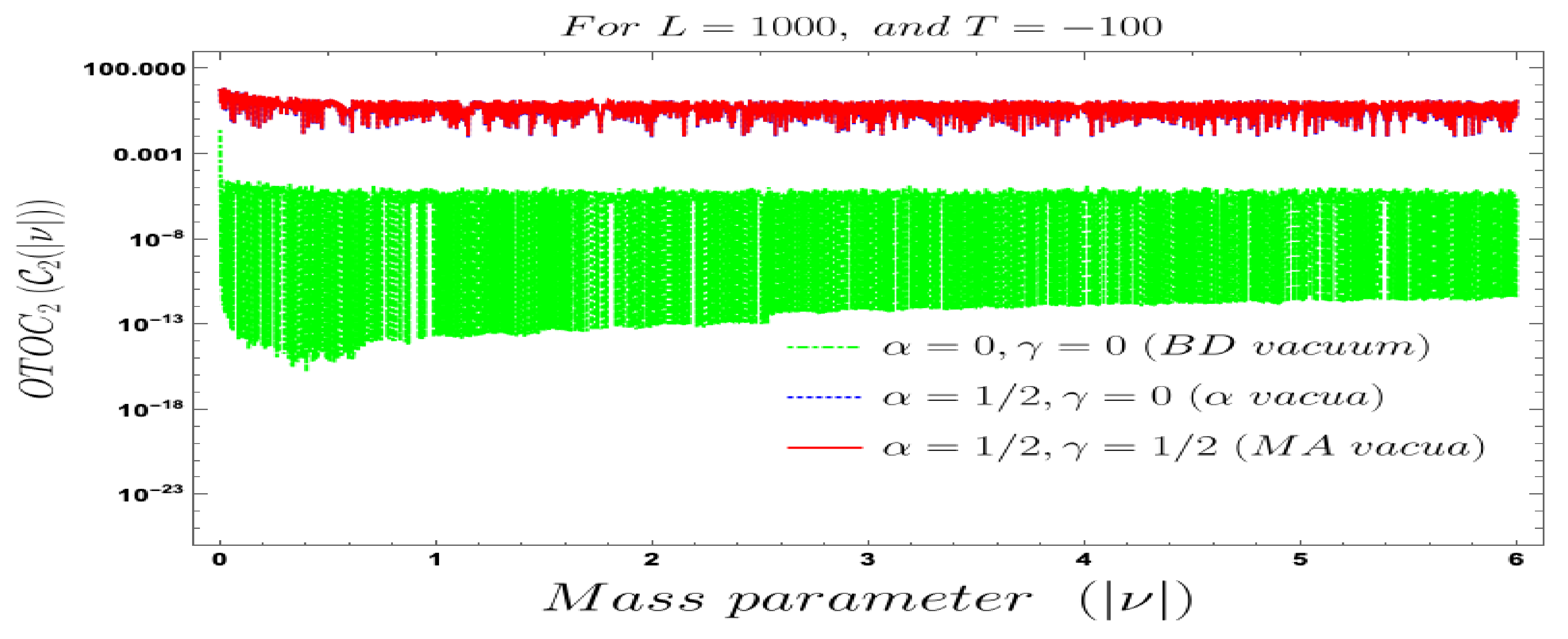
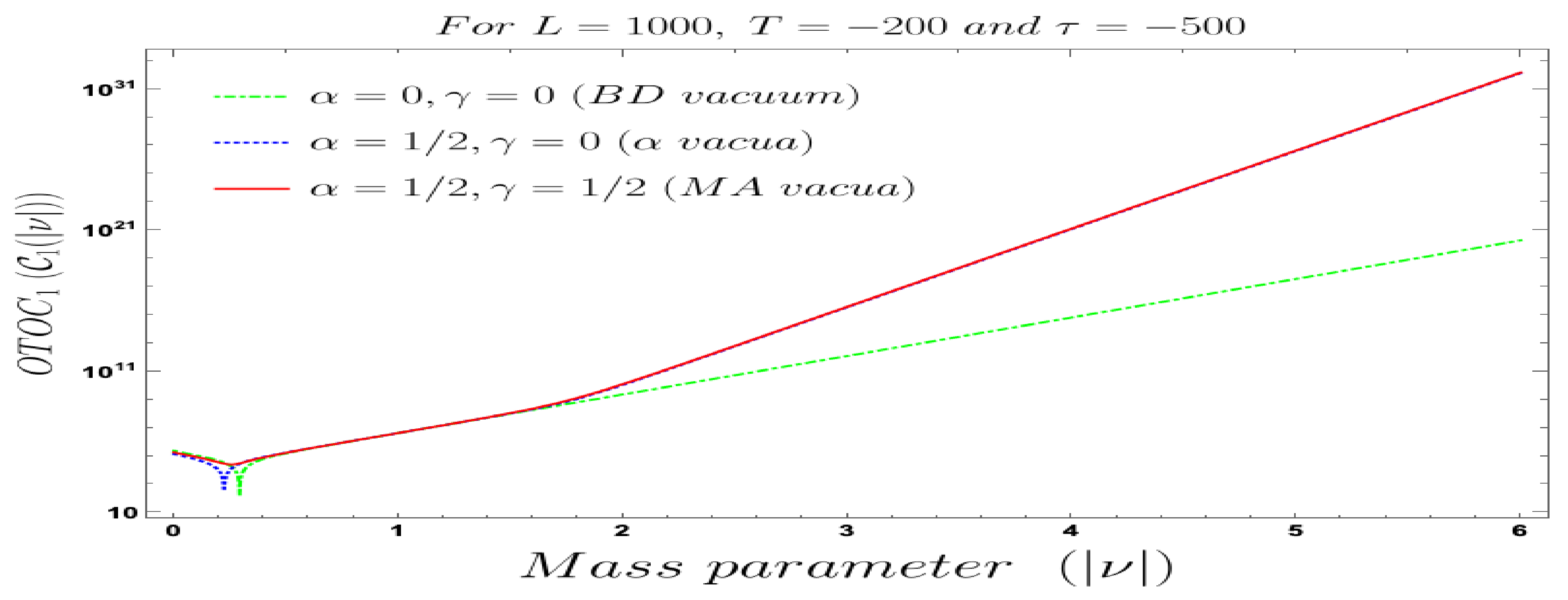
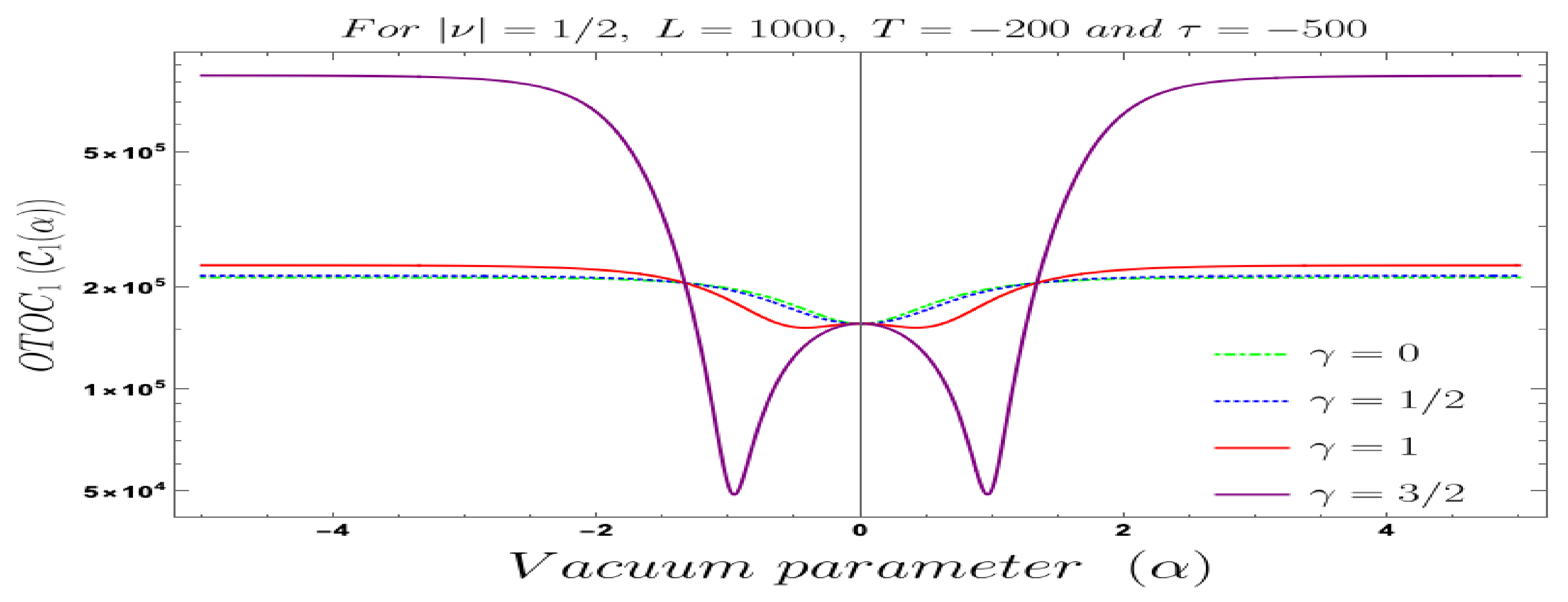
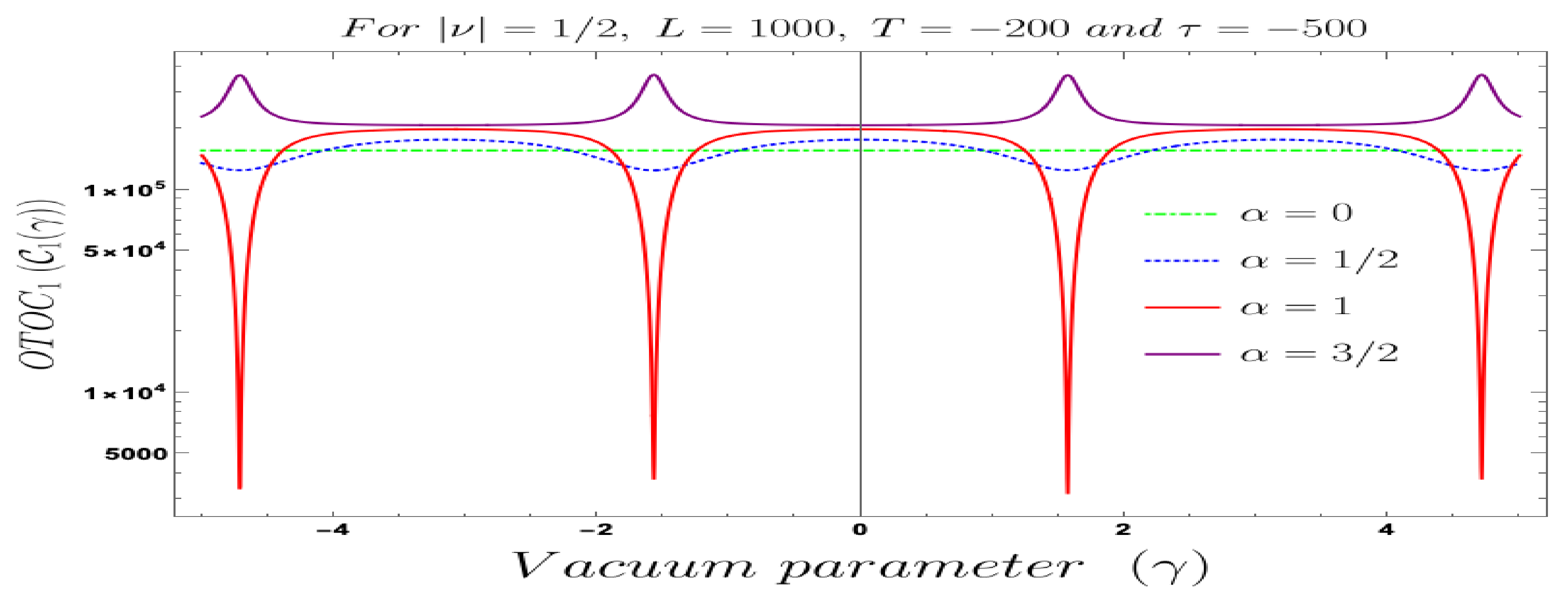
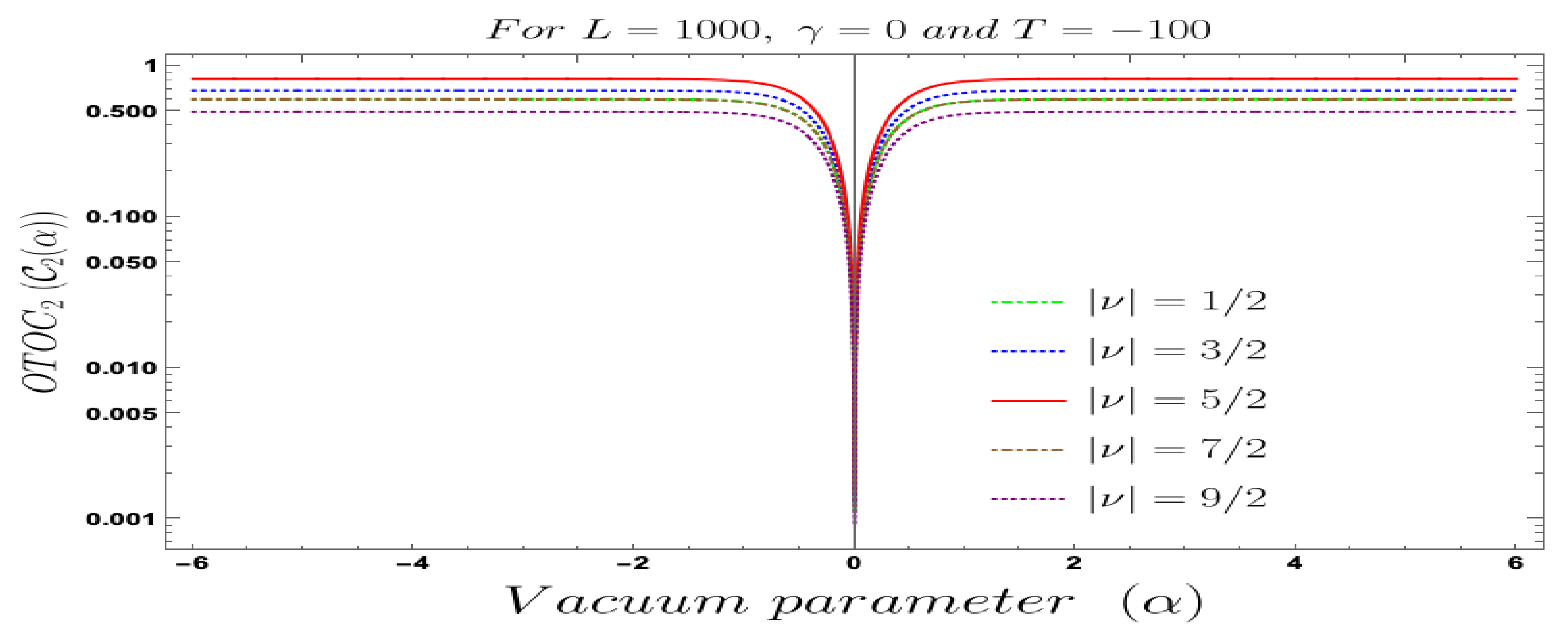
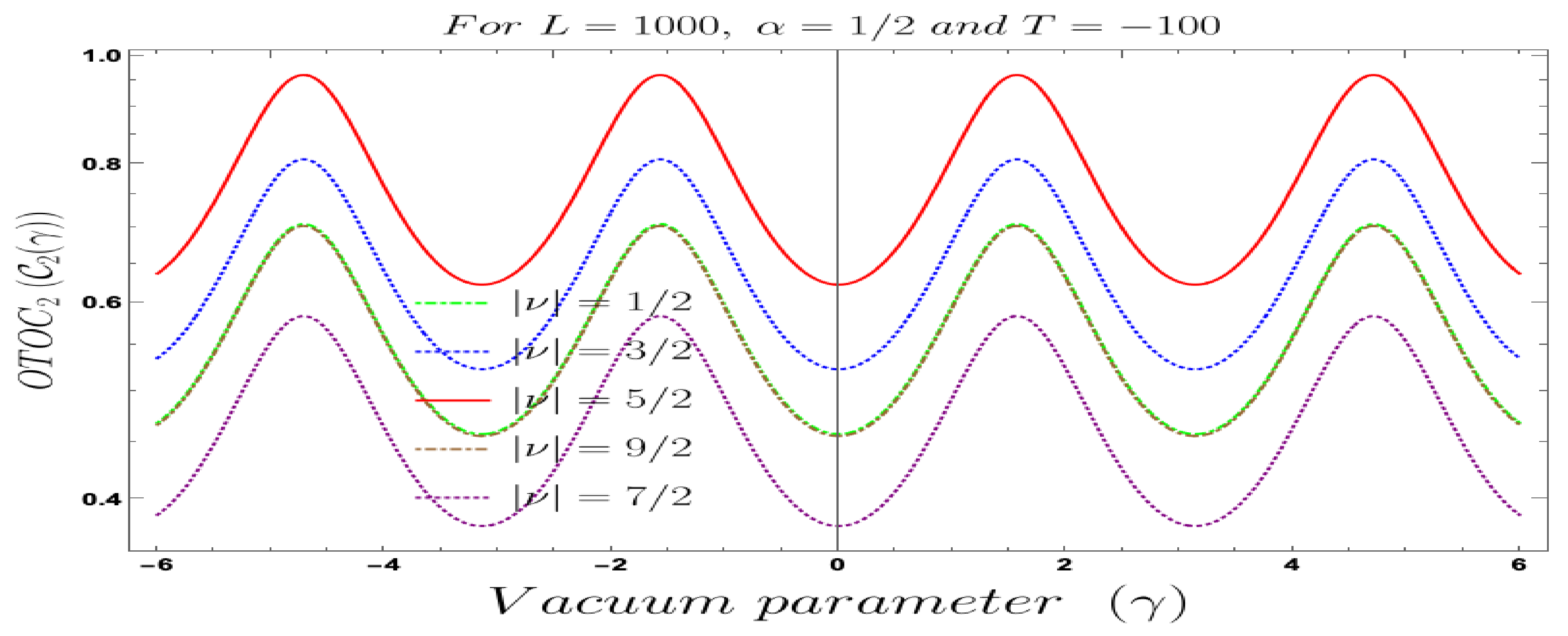
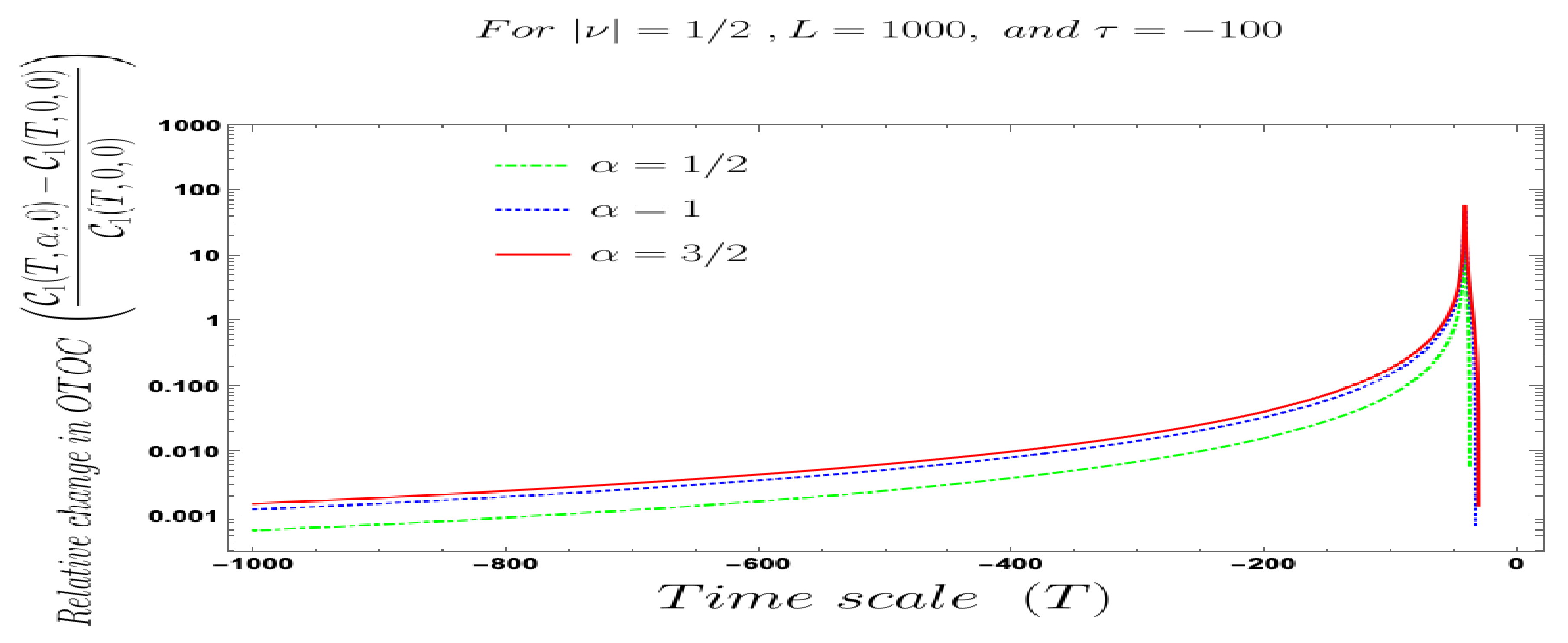

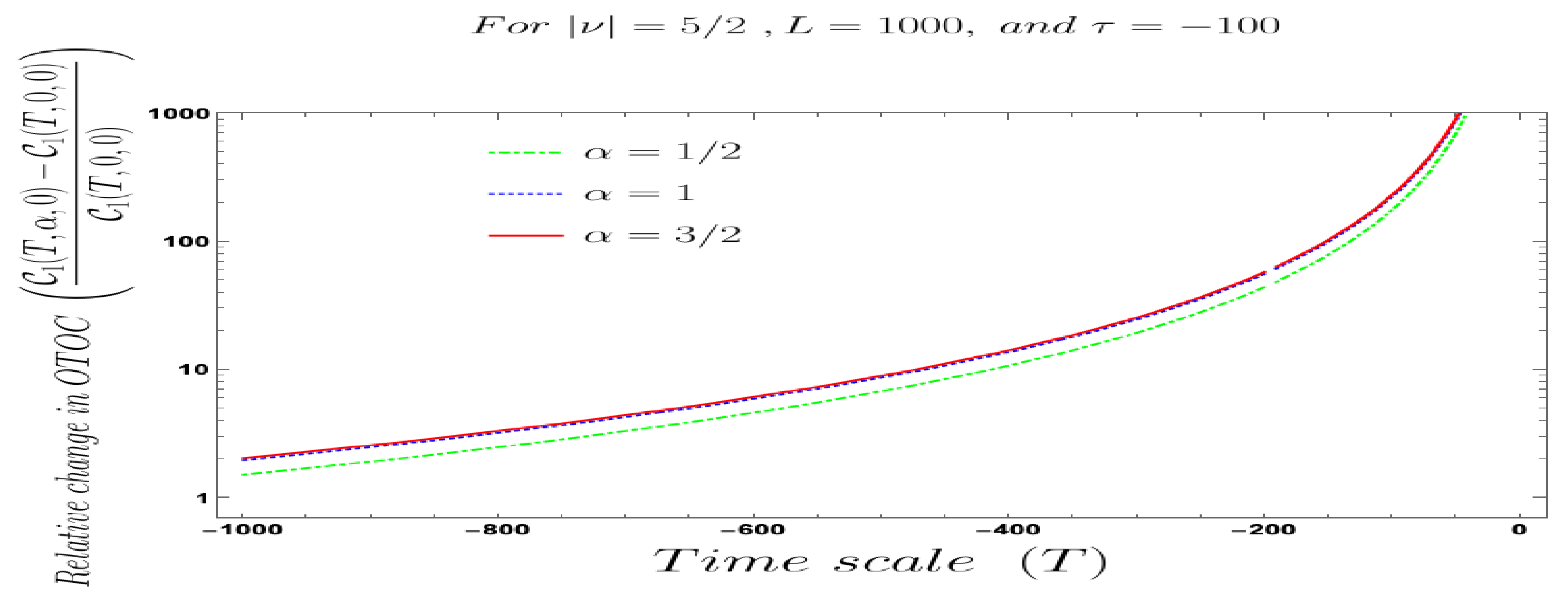
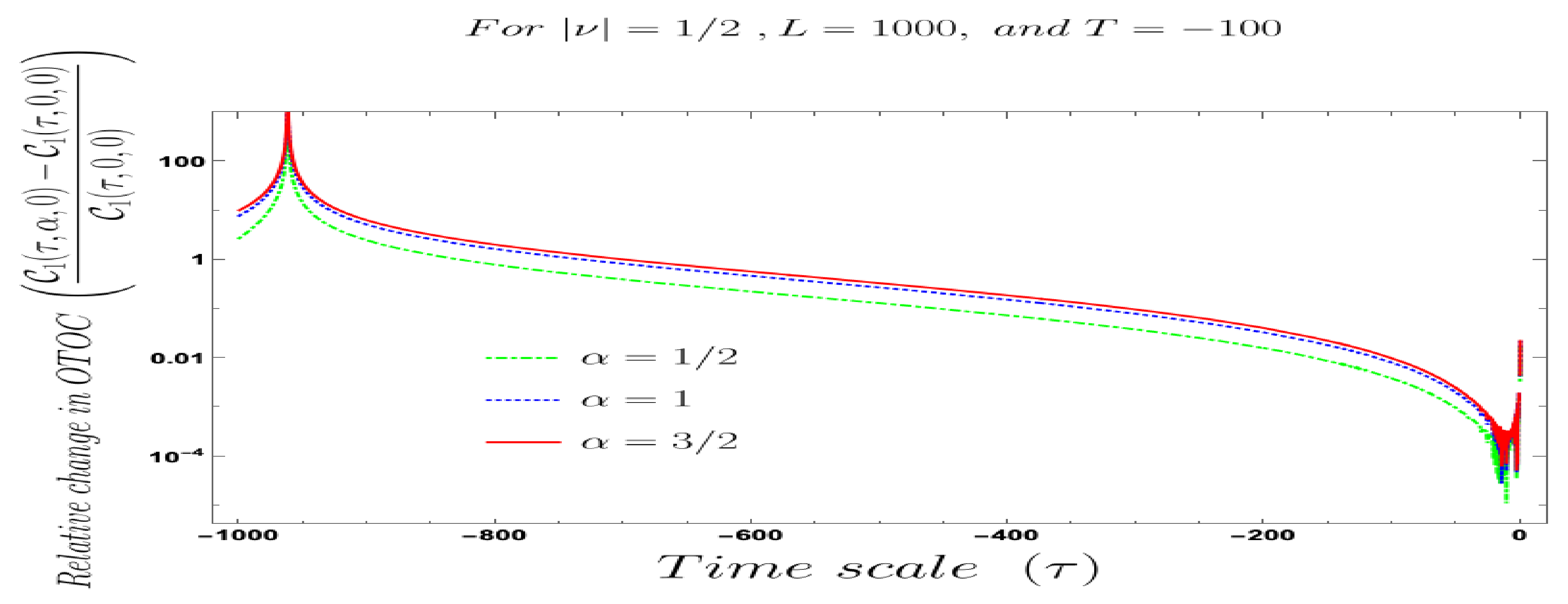
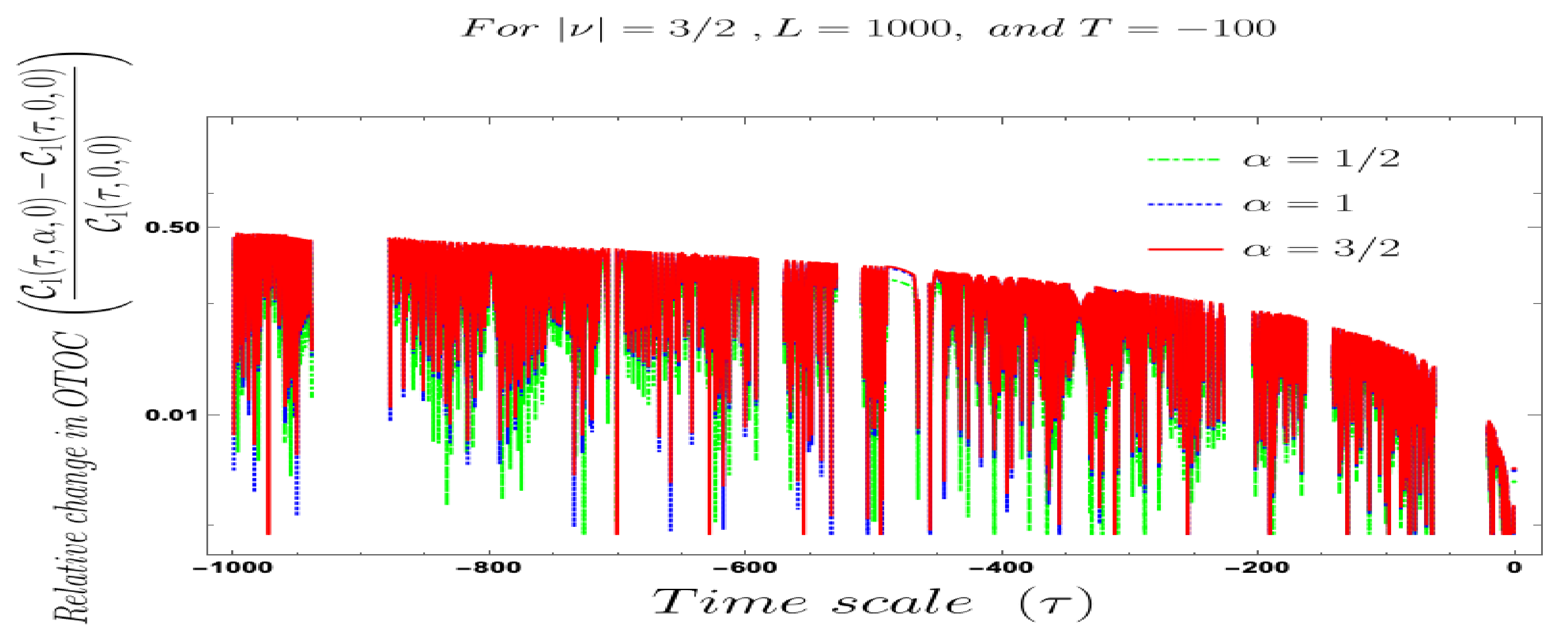
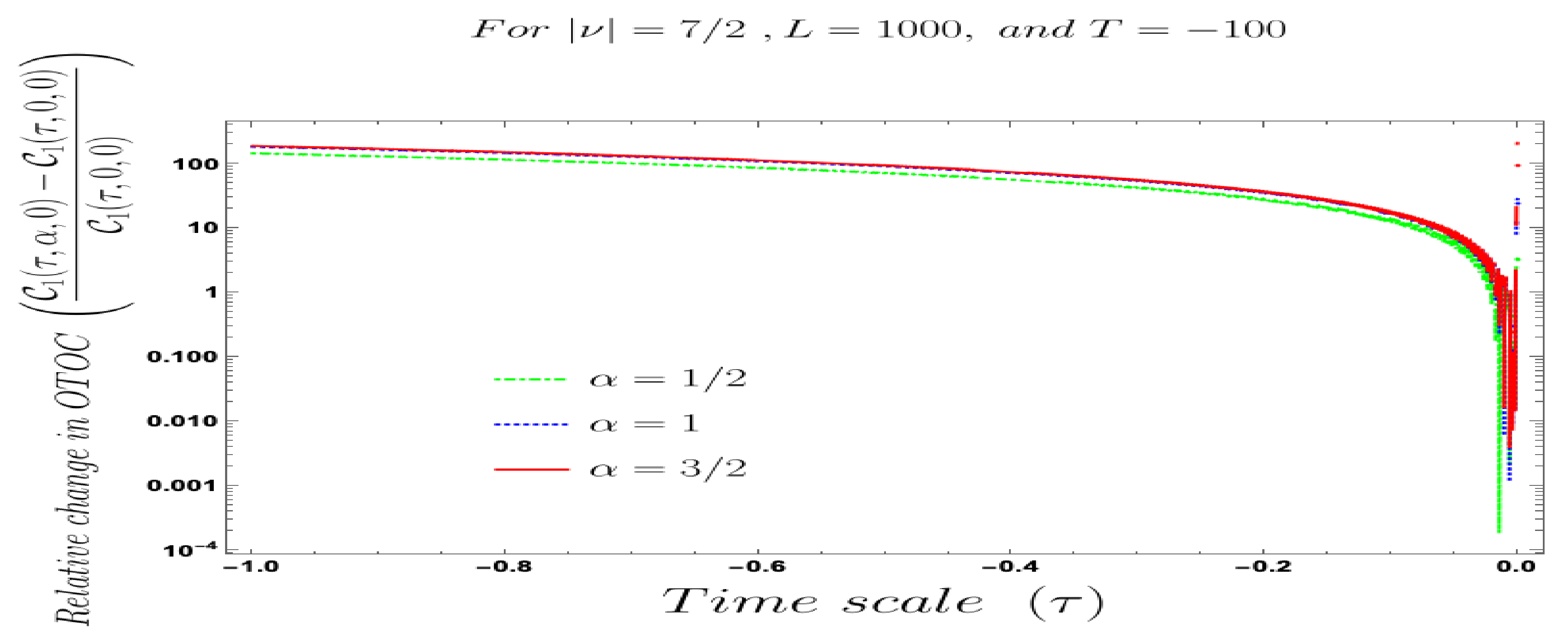
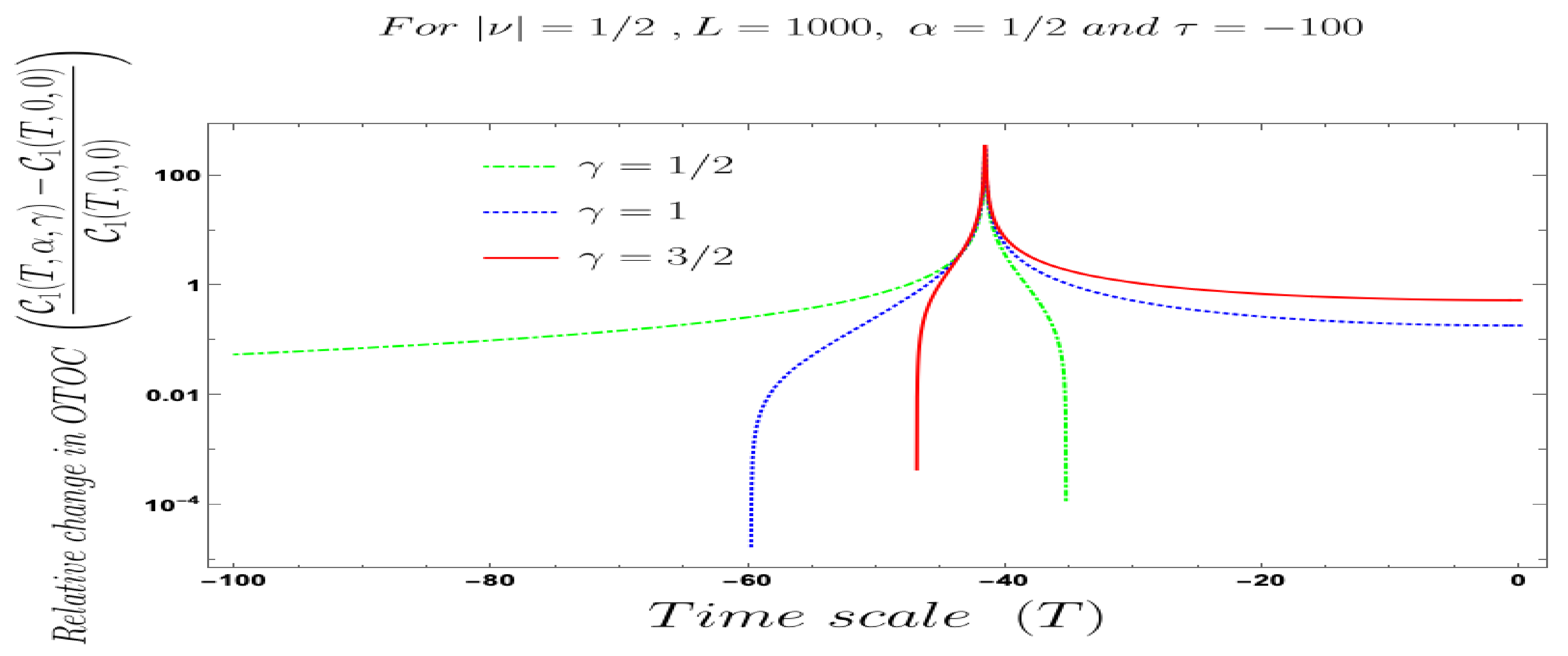
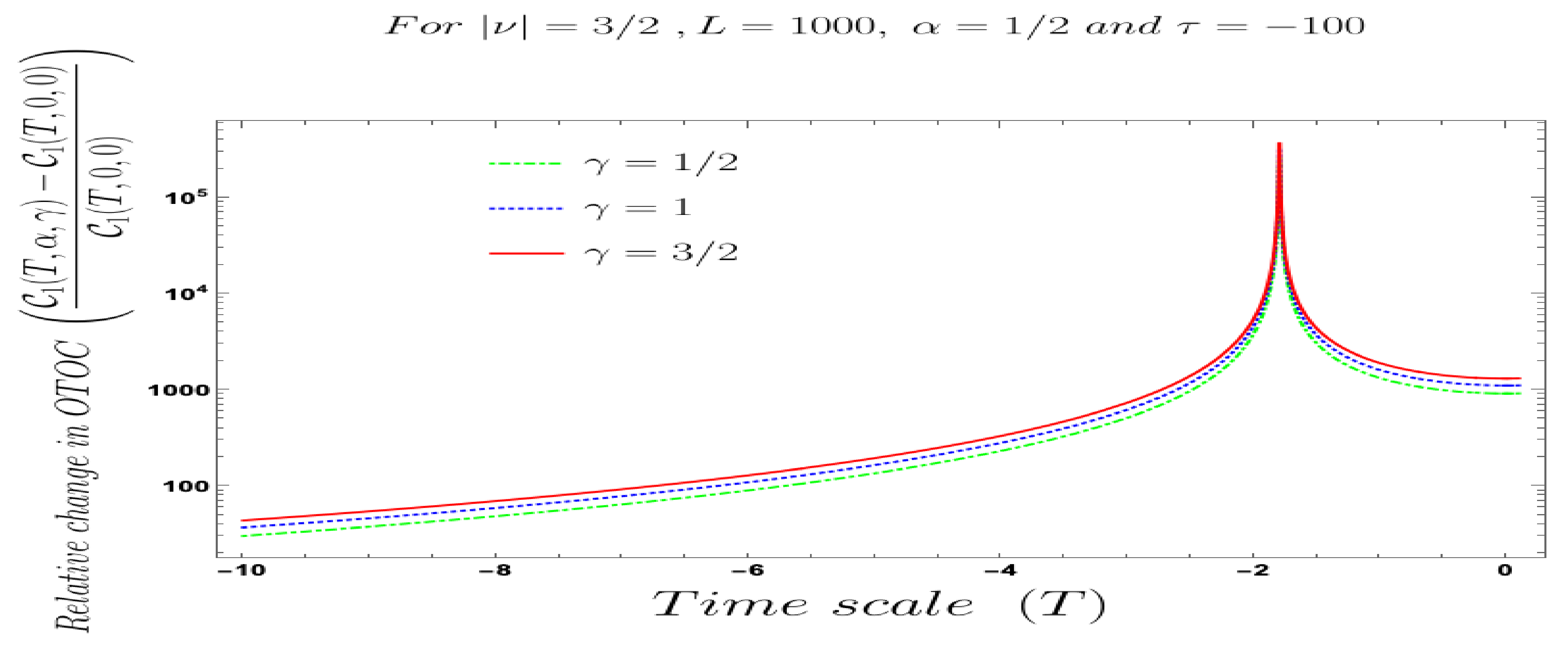

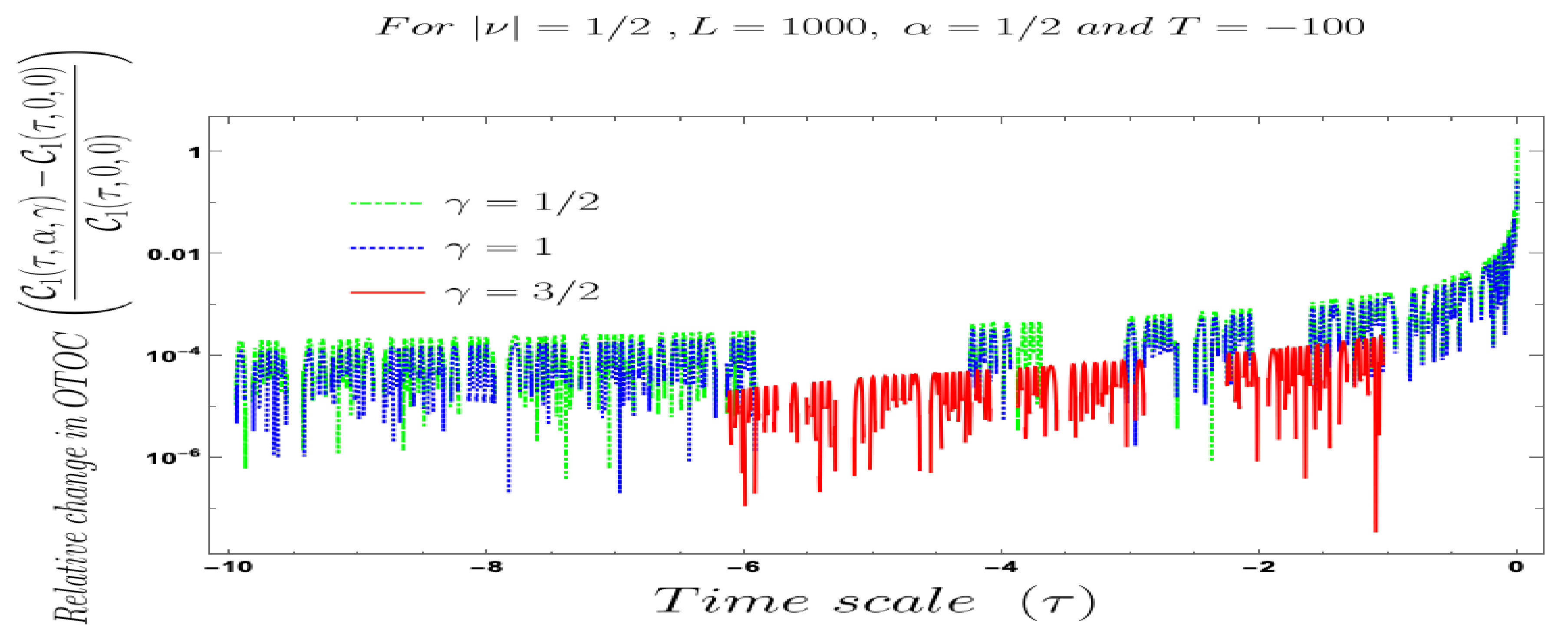
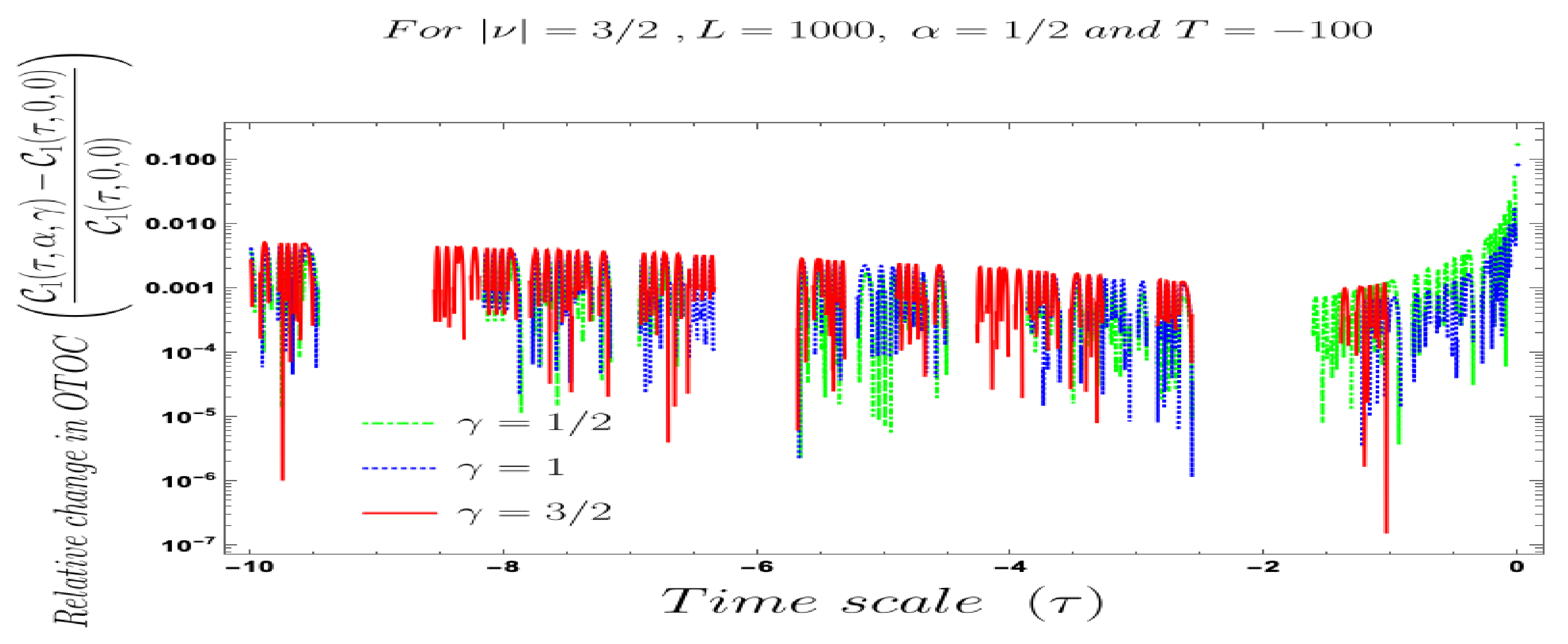
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhury, S. The Cosmological OTOC: A New Proposal for Quantifying Auto-Correlated Random Non-Chaotic Primordial Fluctuations. Symmetry 2021, 13, 599. https://doi.org/10.3390/sym13040599
Choudhury S. The Cosmological OTOC: A New Proposal for Quantifying Auto-Correlated Random Non-Chaotic Primordial Fluctuations. Symmetry. 2021; 13(4):599. https://doi.org/10.3390/sym13040599
Chicago/Turabian StyleChoudhury, Sayantan. 2021. "The Cosmological OTOC: A New Proposal for Quantifying Auto-Correlated Random Non-Chaotic Primordial Fluctuations" Symmetry 13, no. 4: 599. https://doi.org/10.3390/sym13040599
APA StyleChoudhury, S. (2021). The Cosmological OTOC: A New Proposal for Quantifying Auto-Correlated Random Non-Chaotic Primordial Fluctuations. Symmetry, 13(4), 599. https://doi.org/10.3390/sym13040599





