A Time-Variant Reliability Analysis Method Based on the Stochastic Process Discretization under Random and Interval Variables
Abstract
1. Introduction
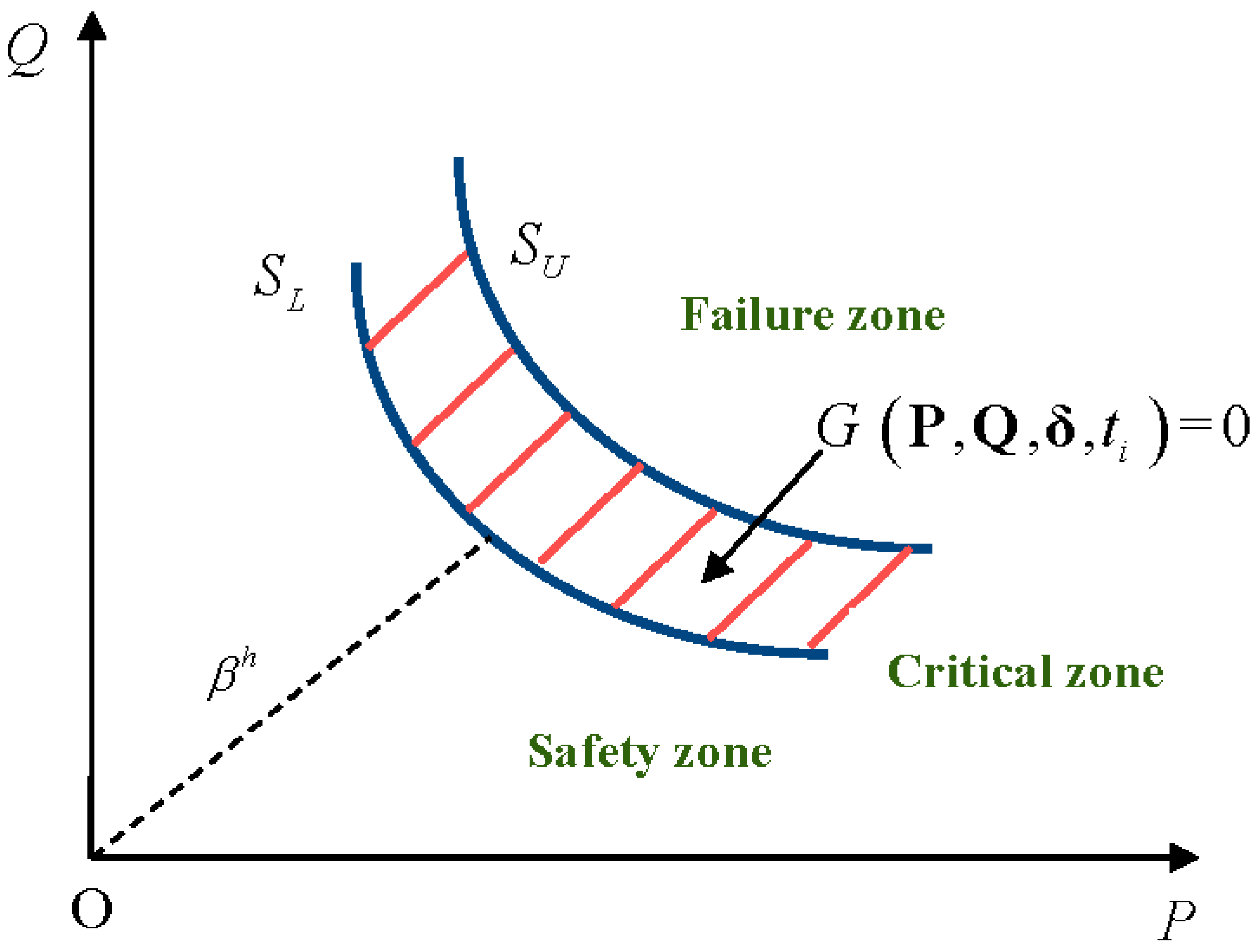
2. Problem of General Time-Variant Reliability Model
3. Problem of General Time-Variant Reliability Model with Random and Interval Variables
3.1. Normalization of Random Variables
3.2. Normalization of Interval Variables
3.3. Solution of Time-Invariant Reliability Problem
- (1)
- Input initial start points , and ; set the number of initial iterations k = 0.
- (2)
- Probability analysis is applied, then MPP points and are searched by FORM method, and interval variables are set to constant values.
- (3)
- Interval analysis is carried out and the MUP can be obtained through the optimization problem of Equation (20). The value of the random variable is achieved from the above probability analysis.
- (4)
- Examine convergence. If and ( and are small positive numbers) go to step 5, otherwise, k = k + 1 go to step (2)
- (5)
- Achieve the MPP and MUP .
4. Numerical Examples
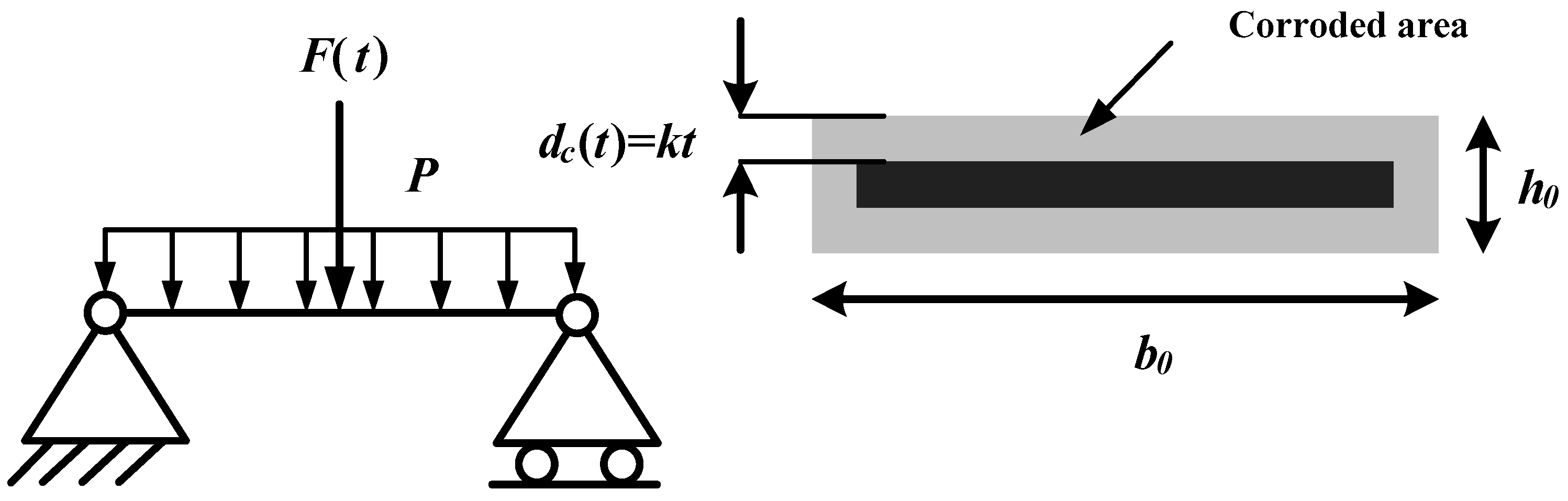
4.1. Steel Beam
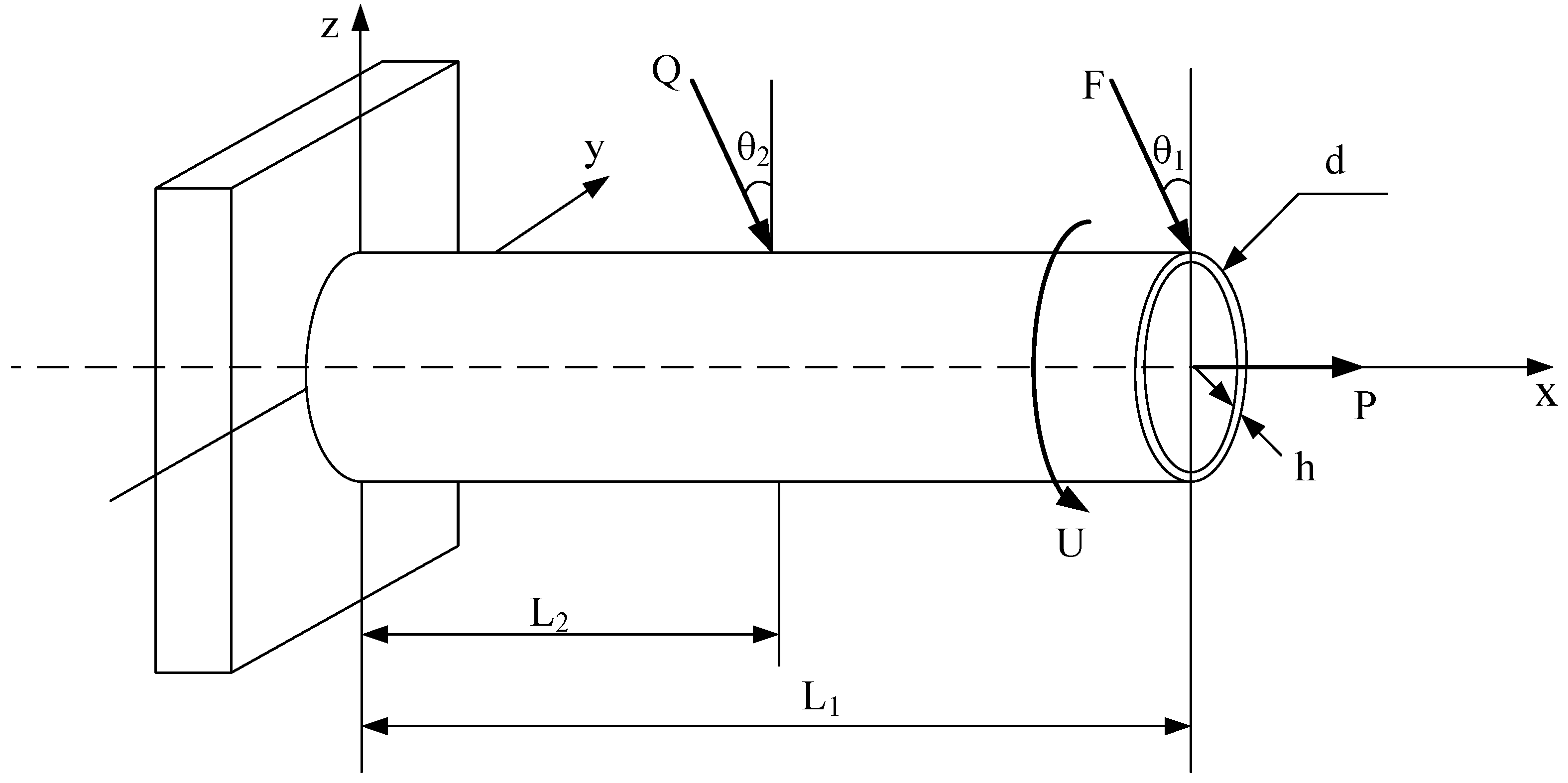
4.2. A Cantilever Tube Structure
4.3. A Vehicle Frame
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, F.; Liu, J.; Wen, G.; Rong, J. Extending SORA method for reliability-based design optimization using probability and convex set mixed models. Struct. Multidiscip. Optim. 2019, 59, 1163–1179. [Google Scholar] [CrossRef]
- Li, F.; Liu, J.; Yan, Y.; Rong, J.; Yi, J.; Wen, G. A time-variant reliability analysis method for non-linear limit-state functions with the mixture of random and interval variables. Eng. Struct. 2020, 213, 110588. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, D.; Liu, J.; Jia, X.; Han, X. A computational framework of kinematic accuracy reliability analysis for industrial robots. Appl. Math. Model. 2020, 82, 189–216. [Google Scholar] [CrossRef]
- Liu, J.; Chen, T.; Zhang, Y.; Wen, G.; Qing, Q.; Wang, H.; Sedaghati, R.; Xie, Y. On sound insulation of pyramidal lattice sandwich structure. Compos. Struct. 2019, 208, 385–394. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Wen, G. An efficient evolutionary structural optimization method for multi-resolution designs. Struct. Multidiscip. Optim. 2020, 62, 787–803. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Yang, J. Analysis of stochastic process to model safety risk in construction industry. J. Civ. Eng. Manag. 2021, 27, 87–99. [Google Scholar] [CrossRef]
- Rice, S.O. Mathematical analysis of random noise. Bell Syst. Tech. J. 1945, 24, 46–156. [Google Scholar] [CrossRef]
- Andrieu-Renaud, C.; Sudret, B.; Lemaire, M. The PHI2 method: A way to compute time-variant reliability. Reliab. Eng. Syst. Saf. 2004, 84, 75–86. [Google Scholar] [CrossRef]
- Sudret, B. Analytical derivation of the outcrossing rate in time-variant reliability problems. Struct. Infrastruct. Eng. 2008, 4, 353–362. [Google Scholar] [CrossRef]
- Hu, Z.; Du, X. Time-dependent reliability analysis with joint upcrossing rates. Struct. Multidiscip. Optim. 2013, 48, 893–907. [Google Scholar] [CrossRef]
- Madsen, P.H.; Krenk, S. An integral equation method for the first-passage problem in random vibration. J. Appl. Mech. 1984, 51, 674–679. [Google Scholar] [CrossRef]
- Jiang, C.; Wei, X.; Huang, Z.; Liu, J. An outcrossing rate model and its efficient calculation for time-dependent system reliability analysis. J. Mech. Des. 2017, 139, 41402. [Google Scholar] [CrossRef]
- Wei, P.; Song, J.; Lu, Z.; Yue, Z. Time-dependent reliability sensitivity analysis of motion mechanisms. Reliab. Eng. Syst. Saf. 2016, 149, 107–120. [Google Scholar] [CrossRef]
- Wang, J.; Gao, X.; Cao, R.; Sun, Z. A multilevel Monte Carlo method for performing time-variant reliability analysis. IEEE Access 2021, 9, 31773–31781. [Google Scholar] [CrossRef]
- Mori, Y.; Ellingwood, B.R. Time-dependent system reliability analysis by adaptive importance sampling. Struct. Saf. 1993, 12, 59–73. [Google Scholar] [CrossRef]
- Wang, J.; Cao, R.; Sun, Z. Importance sampling for time-variant reliability analysis. IEEE Access 2021, 9, 20933–20941. [Google Scholar] [CrossRef]
- Wang, Z.; Mourelatos, Z.P.; Li, J.; Baseski, I.; Singh, A. Time-dependent reliability of dynamic systems using subset simulation with splitting over a series of correlated time intervals. J. Mech. Des. 2014, 136, 61008. [Google Scholar] [CrossRef]
- Li, H.-S.; Wang, T.; Yuan, J.-Y.; Zhang, H. A sampling-based method for high-dimensional time-variant reliability analysis. Mech. Syst. Signal Process. 2019, 126, 505–520. [Google Scholar] [CrossRef]
- Du, W.; Luo, Y.; Wang, Y. Time-variant reliability analysis using the parallel subset simulation. Reliab. Eng. Syst. Saf. 2019, 182, 250–257. [Google Scholar] [CrossRef]
- Hu, Z.; Du, X. Mixed efficient global optimization for time-dependent reliability analysis. J. Mech. Des. 2015, 137, 51401. [Google Scholar] [CrossRef]
- Jiang, C.; Qiu, H.; Gao, L.; Wang, D.; Chen, L. Real-time estimation error-guided active learning Kriging method for time-dependent reliability analysis. Appl. Math. Model. 2020, 77, 82–98. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, W. Time-variant reliability assessment through equivalent stochastic process transformation. Reliab. Eng. Syst. Saf. 2016, 152, 166–175. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X.; Jiang, C.; Liu, J.; Li, Q. Time-dependent reliability analysis through response surface method. J. Mech. Des. 2017, 139, 41404. [Google Scholar] [CrossRef]
- Jiang, C.; Huang, X.; Han, X.; Zhang, D. A time-variant reliability analysis method based on stochastic process discretization. J. Mech. Des. 2014, 136, 91009. [Google Scholar] [CrossRef]
- Du, X. Time-dependent mechanism reliability analysis with envelope functions and first-order approximation. J. Mech. Des. 2014, 136, 81010. [Google Scholar] [CrossRef]
- Gong, J.X.; Zhao, G.F. Reliability analysis for deteriortation structures. J. Build. Struct. 1998, 19, 43–51. (in Chinese). [Google Scholar]
- Jiang, C.; Huang, X.P.; Wei, X.P.; Liu, N.Y. A time-variant reliability analysis method for structural systems based on stochastic process discretization. Int. J. Mech. Mater. Des. 2017, 13, 173–193. [Google Scholar] [CrossRef]
- Jiang, C.; Wei, X.P.; Wu, B.; Huang, Z.L. An improved TRPD method for time-variant reliability analysis. Struct. Multidiscip. Optim. 2018, 58, 1935–1946. [Google Scholar] [CrossRef]
- Cazuguel, M.; Renaud, C.; Cognard, J.Y. Time-variant reliability of nonlinear structures: Application to a representative part of a plate floor. Qual. Reliab. Eng. Int. 2006, 22, 101–118. [Google Scholar] [CrossRef]
- Gong, C.; Frangopol, D.M. An efficient time-dependent reliability method. Struct. Saf. 2019, 81, 101864. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, X.; Wang, L.; Ren, Q. Non-probabilistic interval model-based system reliability assessment for composite laminates. Comput. Mech. 2019, 64, 829–845. [Google Scholar] [CrossRef]
- Qiu, Z.; Huang, R.; Wang, X.; Qi, W. Structural reliability analysis and reliability-based design optimization: Recent advances. Sci. China Phys. Mech. Astron. 2013, 56, 1611–1618. [Google Scholar] [CrossRef]
- Xia, H.; Wang, L.; Liu, Y. Uncertainty-oriented topology optimization of interval parametric structures with local stress and displacement reliability constraints. Comput. Methods Appl. Mech. Eng. 2020, 358, 112644. [Google Scholar] [CrossRef]
- Liu, J.; Wen, G.; Xie, Y.M. Layout optimization of continuum structures considering the probabilistic and fuzzy directional uncertainty of applied loads based on the cloud model. Struct. Multidiscip. Optim. 2016, 53, 81–100. [Google Scholar] [CrossRef]
- Huang, L.; Yin, L.; Liu, B.; Yang, Y. Design and error evaluation of planar 2DOF remote center of motion mechanisms with cable transmissions. J. Mech. Des. 2020, 143, 13301. [Google Scholar] [CrossRef]
- Shi, Y.; Lu, Z. Dynamic reliability analysis model for structure with both random and interval uncertainties. Int. J. Mech. Mater. Des. 2018, 15, 521–537. [Google Scholar] [CrossRef]
- Liu, P.-L.; der Kiureghian, A. Multivariate distribution models with prescribed marginals and covariances. Probab. Eng. Mech. 1986, 1, 105–112. [Google Scholar] [CrossRef]
- Li, C.C.; der Kiureghian, A. Optimal discretization of random fields. J. Eng. Mech. 1993, 119, 1136–1154. [Google Scholar] [CrossRef]
- Ling, C.; Lu, Z. Adaptive kriging coupled with importance sampling strategies for time-variant hybrid reliability analysis. Appl. Math. Model. 2020, 77, 1820–1841. [Google Scholar] [CrossRef]

| Parameters | Distribution Type | Mean Value | Coefficient of Variation | Autocorrelation Coefficient |
|---|---|---|---|---|
| Yield stress (MPa) | Lognormal | 160 | 10 | NA |
| (m) | Lognormal | 0.2 | 5 | NA |
| (m) | Lognormal | 0.04 | 10 | NA |
| (N) | Gauss process | 3500 | 20 |
| Parameters | Nominal Value | Lower Bound | Upper Bound |
|---|---|---|---|
| Beam length (m) | 5 | 4.5 | 5.5 |
| (N/m3) | 78,500 | 74,575 | 82,425 |
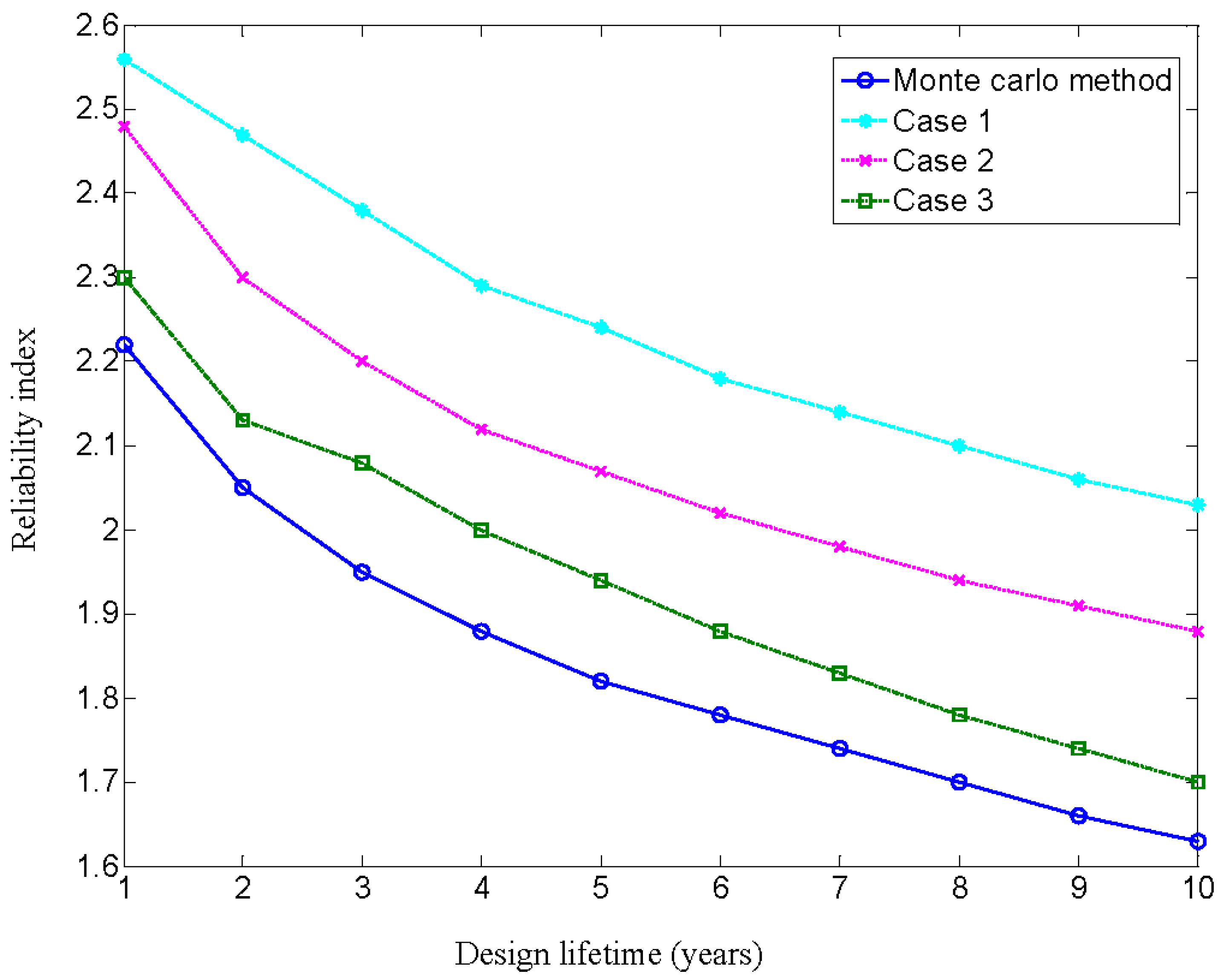
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Monte carlo method | 2.22 | 2.05 | 1.95 | 1.88 | 1.82 | 1.78 | 1.74 | 1.70 | 1.66 | 1.63 |
| Case1 | 2.56 | 2.47 | 2.38 | 2.29 | 2.24 | 2.18 | 2.14 | 2.10 | 2.06 | 2.03 |
| Deviation (%) | 15.3 | 20.4 | 22.1 | 21.8 | 23.1 | 22.5 | 23.0 | 23.5 | 24.1 | 24.5 |
| Case2 | 2.48 | 2.30 | 2.20 | 2.12 | 2.07 | 2.02 | 1.98 | 1.94 | 1.91 | 1.88 |
| Deviation (%) | 11.7 | 12.2 | 12.8 | 12.8 | 13.7 | 13.5 | 13.8 | 14.1 | 15.6 | 15.3 |
| Case3 | 2.30 | 2.13 | 2.08 | 2.00 | 1.94 | 1.88 | 1.83 | 1.78 | 1.74 | 1.70 |
| Deviation (%) | 3.60 | 3.90 | 6.67 | 6.38 | 6.59 | 5.62 | 5.17 | 4.71 | 4.82 | 4.29 |
| Parameter | Mean | Standard Deviation | Type of Distribution | Autocorrelation Coefficient Function |
|---|---|---|---|---|
| R0 (Mpa) | 550 | 55 | Normal | NA |
| Q(t) (N) | 1800 | 180 | Gaussian process | sin(0.3τ)/0.3τ |
| U(t) (Nm) | 1900 | 190 | Gaussian process | exp(−0.1τ) |
| F (N) | 1800 | 180 | Normal | NA |
| P (N) | 1000 | 100 | Type I extreme value | NA |
| d (mm) | 42 | 0.5 | Normal | NA |
| h (mm) | 5 | 0.1 | Normal | NA |
| Parameter | Interval |
|---|---|
| L1 | [0.11, 0.13] m |
| L2 | [0.05, 0.07] m |
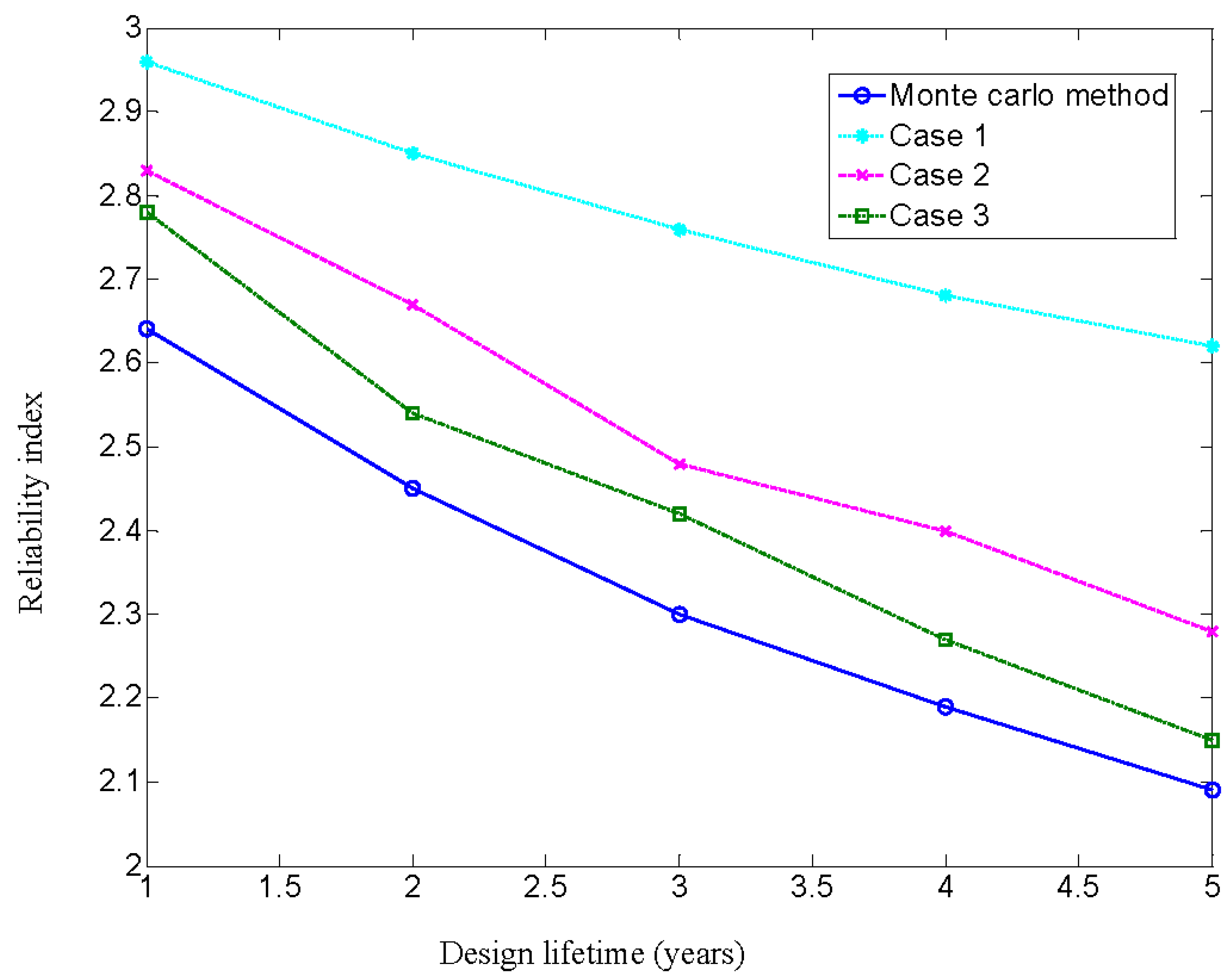
| Time/Year | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Monte Carlo method | 2.64 | 2.45 | 2.30 | 2.19 | 2.09 |
| Case1 | 2.96 | 2.85 | 2.76 | 2.68 | 2.62 |
| Deviation (%) | 12.1 | 16.3 | 20.0 | 22.4 | 25.4 |
| Case2 | 2.83 | 2.67 | 2.48 | 2.40 | 2.28 |
| Deviation (%) | 7.2 | 9.0 | 7.8 | 9.6 | 9.1 |
| Case3 | 2.78 | 2.54 | 2.42 | 2.27 | 2.15 |
| Deviation (%) | 5.3 | 3.7 | 5.2 | 3.7 | 2.9 |
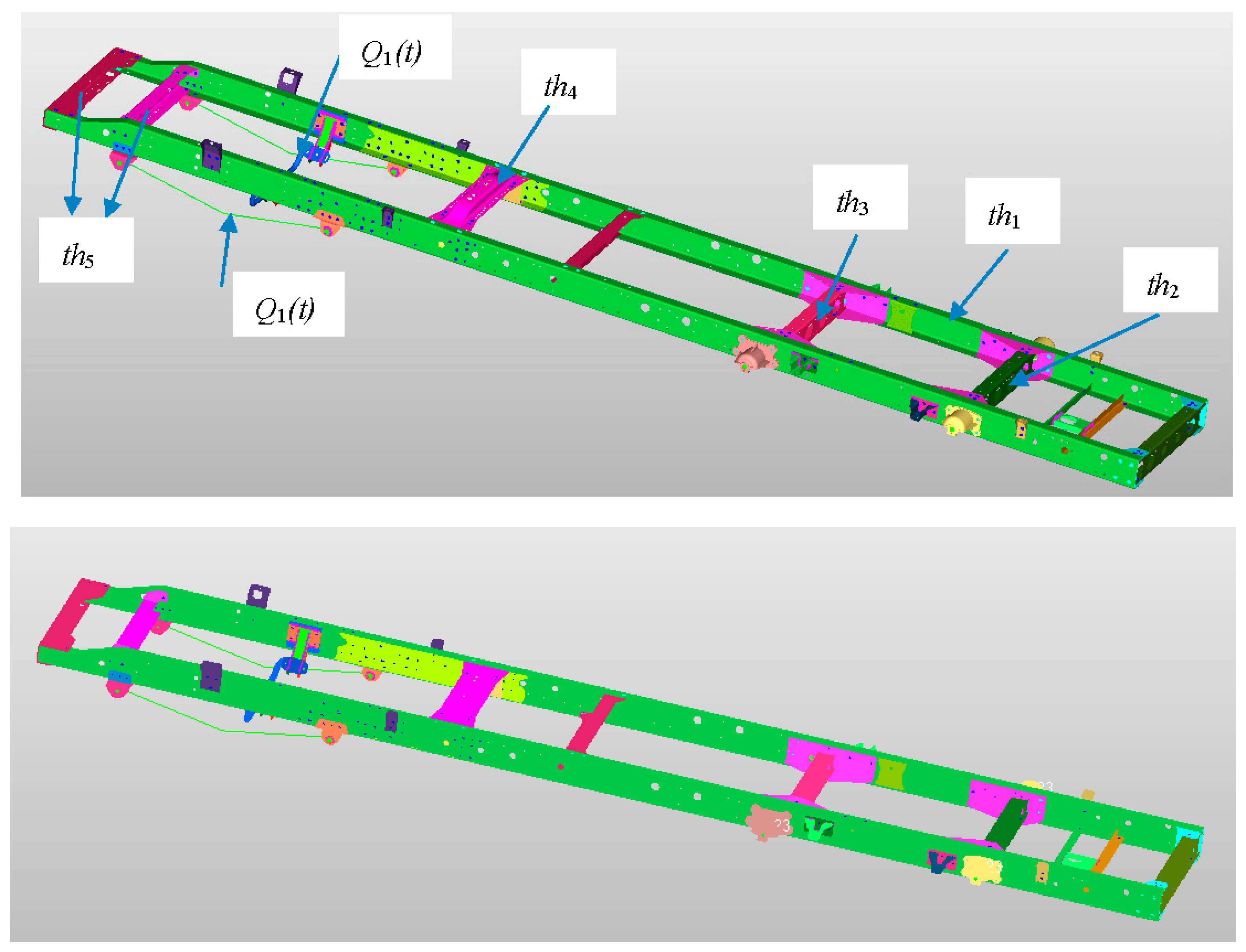
| Parameter | Type of Distribution | Mean | Coefficient of Variation (%) | Autocorrelation Coefficient Function |
|---|---|---|---|---|
| D0/mm | Type I extreme | 3.2 | 10 | NA |
| th1/mm | Normal | 5 | 10 | NA |
| th2/mm | Normal | 5 | 10 | NA |
| th3/mm | Normal | 5 | 10 | NA |
| th4/mm | Normal | 5 | 10 | NA |
| th5/mm | Normal | 5 | 10 | NA |
| Q1(t)/N | Gaussian process | 2000 | 10 | exp[−(2.5τ)2] |
| Parameter | Interval |
|---|---|
| E1/GPa | [189,231] |
| ρ/kg × m−3 | [7.41 × 103, 8.19 × 103] |
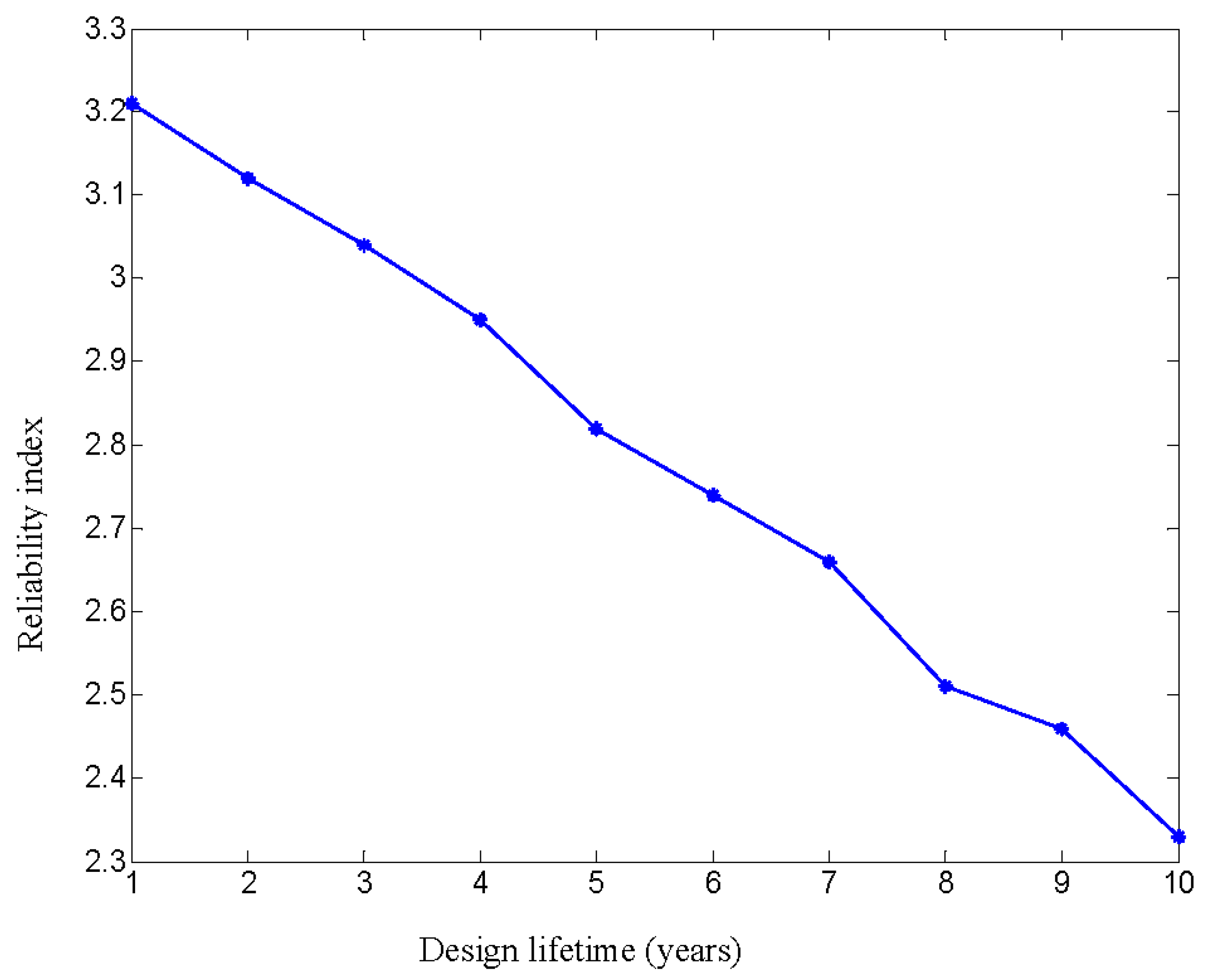
| Time/Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Propose method | 3.21 | 3.12 | 3.04 | 2.95 | 2.82 | 2.74 | 2.66 | 2.51 | 2.46 | 2.33 |
| Failure probability(10−3) | 66 | 90 | 118 | 159 | 240 | 307 | 391 | 604 | 695 | 990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Liu, J.; Yan, Y.; Rong, J.; Yi, J. A Time-Variant Reliability Analysis Method Based on the Stochastic Process Discretization under Random and Interval Variables. Symmetry 2021, 13, 568. https://doi.org/10.3390/sym13040568
Li F, Liu J, Yan Y, Rong J, Yi J. A Time-Variant Reliability Analysis Method Based on the Stochastic Process Discretization under Random and Interval Variables. Symmetry. 2021; 13(4):568. https://doi.org/10.3390/sym13040568
Chicago/Turabian StyleLi, Fangyi, Jie Liu, Yufei Yan, Jianhua Rong, and Jijun Yi. 2021. "A Time-Variant Reliability Analysis Method Based on the Stochastic Process Discretization under Random and Interval Variables" Symmetry 13, no. 4: 568. https://doi.org/10.3390/sym13040568
APA StyleLi, F., Liu, J., Yan, Y., Rong, J., & Yi, J. (2021). A Time-Variant Reliability Analysis Method Based on the Stochastic Process Discretization under Random and Interval Variables. Symmetry, 13(4), 568. https://doi.org/10.3390/sym13040568