An Intelligent Fusion Algorithm and Its Application Based on Subgroup Migration and Adaptive Boosting

Abstract

Imbalanced data and feature redundancies are common problems in many fields, especially in software defect prediction, data mining, machine learning, and industrial big data application. To resolve these problems, we propose an intelligent fusion algorithm, SMPSO-HS-AdaBoost, which combines particle swarm optimization based on subgroup migration and adaptive boosting based on hybrid-sampling. In this paper, we apply the proposed intelligent fusion algorithm to software defect prediction to improve the prediction efficiency and accuracy by solving the issues caused by imbalanced data and feature redundancies. The results show that the proposed algorithm resolves the coexisting problems of imbalanced data and feature redundancies, and ensures the efficiency and accuracy of software defect prediction.

1. Introduction

In machine learning applications, the class imbalance problem refers to the large difference in the number of different datasets, namely, one class has more samples than the other. Classic classification algorithms such as decision tree, Bayesian algorithms, Support Vector Machine (SVM) and neural networks are widely used in software defect prediction. Traditional algorithms assume that a data set is balanced and a focus on achieving the best overall classification accuracy. However, in an imbalanced data set, the number of samples in a class can be significantly larger than those in other classes. When a traditional classification algorithm is applied to an imbalanced data set, it can misclassify a large number of minority class samples into the majority class. As a result, the classification results favor the majority class, reducing the classification accuracy of the minority classes [1]. Because the classification accuracy of high-risk modules is more critical than the overall classification accuracy, the minority class can be more important than the majority class.

With the development of information technology, high-dimensional data has spread throughout the fields of machine learning, data processing, and pattern recognition. The data contain a large number of irrelevant and redundant features, which greatly reduces the classification performance and causes a “dimension disaster”. The number of features in a software module has significantly increased as software complexity increases. However, these features have different weights in the module. Some of them are irrelevant, which can obscure the essential classification features, affecting the performance of the learning algorithm and reducing the effectiveness of prediction models [2]. Research shows that the number of training samples exponentially increases as the redundancy feature attributes increase [3]. Hence, deleting can reduce computation, improve classification accuracy, and optimize the classification algorithm model.

Software defect prediction, which is a typical unbalanced classification problem, is an essential tool used in software quality assurance. The efficiency and accuracy of the prediction algorithm can significantly affect the quality of a software system. The key to software defect prediction is to identify the high-risk modules, which are far fewer than the low-risk modules, and identify the defects in the high-risk modules.

In this paper, we propose an intelligent fusion algorithm, SMPSO-HS-AdaBoost, which is a combination of sampling, feature selection, and classification methods. The proposed algorithm (1) solves the imbalance problem using AdaBoost classification based on hybrid-sampling, and (2) solves the feature redundancy problem using particle swarm optimization based on subgroup migration feature selection.

2. Related Work

2.1. Research on Imbalanced Data

Software defect prediction models use the code metrics of modular structures (such as lines of code and class inheritance depth) as the input and output. Software defect prediction performance is affected by various methods used in the prediction, including data preprocessing, model building, optimization, and evaluation [4]. In addition, the distribution characteristics of the data set also affect the performance of software defect prediction models. The research of imbalanced data focuses on improving the algorithms to increase classification accuracy and balancing the data set to achieve good results.

2.1.1. Sampling Techniques

In a software system, the ratio of high-risk modules is relatively small and the data sets are typically imbalanced, causing the prediction accuracy of traditional software defect prediction models to be relatively low. Data sampling techniques were introduced to balance the data set, improving the accuracy of the prediction [5].

Data sampling techniques include under-sampling and over-sampling techniques. The under-sampling algorithms reduce the number of negative class samples by deleting negative samples, and hence they are likely to lose some important information during the deletion process. Oversampling algorithms increase the number of positive classes, but they can introduce overfitting. Some sampling algorithms simply copy or delete samples, and they cause classifier overfitting and generate poor classification results.

Wang et al. [6] proposed an entropy and confidence-based under-sampling boosting framework to solve imbalanced problems. Hou et al. [7] initially used the synthetic minority over-sampling technique to balance a training set before generating a candidate classifier pool. Chawla et al. [8] proposed the Synthetic Minority Over-sampling Technique (SMOTE). The experiments show that SMOTE can ease over-fitting and improve the classification accuracy of the minority class and maintain overall accuracy. Verbiest et al. [9] used SMOTE enhanced with fuzzy rough prototype selection to process noisy imbalanced data sets and achieve good results. In practical applications, using data sampling combined with ensemble learning algorithms to process imbalanced data can generate good results. Chawlet al. [10] proposed SMOTEBoost, which uses SMOTE to generate new minority classes in each iteration, and the results show that SMOTEBoost can improve the classification accuracy of the minority class. Liu et al. [11] proposed a software defect prediction method based on integrated sampling and ensemble learning. These algorithms combine data sampling with ensemble approaches and have relatively good classification accuracy. However, software defect prediction requires both high classification accuracy and efficiency.

2.1.2. Ensemble Methods

Ensemble learning algorithms are effective methods to address the class imbalance problem [12,13,14,15]. General classification algorithms assume that misclassifying the different classes will lead to the same loss. However, in the imbalanced data sets, misclassifying different classes can have different costs. Ensemble algorithms make the classifier focus more on the misclassified samples by changing the weight of training samples, which can improve classification performance. In recent years, ensemble algorithms have been increasingly used in software defect prediction. Wang et al. [16] proposed a multiple kernel ensemble learning (MKEL) approach for software defect classification and prediction, which integrates the advantages of ensemble learning and multiple kernel learning. Rathore et al. [17] proposed ensemble methods to predict the number of faults in software modules, demonstrating the effectiveness of software fault prediction based on ensemble methods. Malhotra et al. [18] proposed four ensemble learning strategies to predict change-prone classes of software. As a boosting learning algorithm, the AdaBoost algorithm has a wide range of applications in dealing with imbalanced data.

2.2. Feature Selection

The software modules face not only the problem of imbalanced data but also the problem of redundant features. Feature selection has been widely used in pattern recognition and machine learning applications in recent decades to reduce redundant features and keep the remaining features consistent with the original features. A subset with useful features is selected and irrelevant and redundant features are removed [19,20]. There are two types feature selection methods: wrapper and filter. In wrapper methods, a pre-determined classifier is required to evaluate the performance of the chosen features, whereas the filter methods are independent of any classifier in the feature subset evaluation process [21]. Although the filter method runs quickly, it makes the results of subsequent operations significantly deviate, and it is easy to delete some feature combinations that should be retained. The wrapper method runs slowly, but it can select the optimal feature subset according to the evaluation criteria such as classification accuracy and feature number. Assuming that there are n-dimensional features in the data set, the feature selection for this data set will be an NP-hard problem [22]. Therefore, performing exhaustive searches for the optimal feature subset is both resourcing-demanding and time-consuming, and is not suitable for feature selection in high-dimensional data sets.

In contrast, heuristic search algorithms can obtain a set of solutions in one run, allowing them to find the ideal solution set with less time and resources. In recent years, many feature selection methods based on heuristic algorithms, such as genetic (GA), ant colony (ACO), artificial bee colony (ABC), and particle swarm optimization (PSO) algorithms, have been proposed and achieved good results. Among these, PSO has attracted many researchers’ attention due to its low complexity, fast convergence speed, and requirement of fewer parameters. Lu et al. [23] proposed improved PSO models based on both functional constriction factors and functional inertia weights for text feature selection. The experimental results show that the proposed model is both effective and stable. Gu et al. [24] used the competitive swarm optimizer (CSO), a recent PSO variant to solve high-dimensional feature selection problems. Tran et al. [25] proposed a variable-length PSO that defines a smaller search space by making the particles have different and shorter lengths, and then a smaller search space is defined. This method can obtain smaller feature subsets in a shorter time and significantly improve the classification performance.

3. SMPSO-HS-AdaBoost Algorithm

3.1. Hybrid-Sampling (HS)

It is commonly assumed that various types of data samples are balanced in numbers. However, in practice, data classes are typically imbalanced, and classifiers can be overwhelmed by the majority class, so they ignore the minority class. Data imbalance can lead to the loss of key attributes in high-risk modules during software attribute reduction and reduce the classification accuracy. When processing imbalanced data, traditional learning algorithms tend to produce high prediction accuracy for the majority class but produce poor prediction accuracy for the minority class that is more interesting to the researchers. The reason is that traditional classifiers are designed to process balanced data sets and generate predictions for the whole data set. They are not suitable to perform learning tasks on imbalanced data sets because they tend to assign all instances to the majority class, which is usually less important. Because of the high cost of misclassifying minority class data [26], in this paper, we propose a hybrid-sampling (HS) method to handle imbalanced data.

SMOTE is an oversampling technique that generates synthetic samples from the minority class using the available information in the data. It is a typical data synthesis algorithm, and its main goal is to synthesize new samples by interpolation rather than randomly copy samples from the original data. First, for each sample in the minority class, SMOTE finds the k nearest neighbors from the original samples. Then, artificial minority instances are added between the minority instances and their k nearest neighbors, until the data set is balanced. The new synthetic sample S was defined as:

$$S=x+u·\left(y-x\right)$$

(1)

where u is a random number between (0, 1), y is one of k nearest neighbors.

Random under-sampling is an under-sampling technique that reduces the number of samples in the majority class by randomly removing the majority samples. The under-sampling algorithm is likely to cause loss of significant information of the majority class due to the loss of majority samples.

Definition 1.

Hybrid-sampling (HS). If S is the training sample data set, M is the over-sampling rate, and N is the under-sampling rate, then the hybrid-sampling can be defined as:

Dataset_new = under − sampling(SMOTE (Dataset_old, M), N)

(2)

First, SMOTE over-sampling is used to add the instances of the minority class with an over-sampling rate of M, and then random under-sampling is used to process the over-sampled data set with an under-sampling rate of N.

3.2. Feature Selection Method Based SMPSO

3.2.1. Standard Particle Swarm Optimization

PSO is a global random search algorithm based on swarm intelligence, and it simulates the migration and clustering behavior of birds in the process of foraging [27]. PSO treats each particle in the population as a standalone solution and assigns each particle with a fitness value representing the quality of the solution. Each particle has two attributes, position and velocity. The position vector represents the solution of the corresponding particle. The velocity vector is used to adjust the particle’s next flight to update the position and search for a new solution set. Based on the global optimal solution and the optimal solution found by the particle itself, the particle can adjust its moving direction and speed and gradually approach the optimal particle.

The basic principles of PSO summarized below [28].

Assuming that m particles search for the optimal solution in an N-dimensional target space, vectors $x_i$ and $v_i$ represent the position and flight speed of particle i, respectively.

$$x_i=\left(x_{i1},x_{i2},\dots ,x_{iN}\right)$$

(3)

$$v_i=\left(v_{i1},v_{i2},\dots ,v_{iN}\right)$$

(4)

$p_i$ represents the optimal location discovered by particle i.

$$p_i=\left(p_{i1},p_{i2},\dots ,p_{iN}\right)$$

(5)

$p_{gbest}$ represents the optimal location discovered by all particles.

$$p_{gbest}=\left(p_{g1},p_{g2},\dots ,p_{gN}\right)$$

(6)

The position and velocity of particle i are updated as follows.

$$v_{in}^{k+1}=w·v_{in}^k+c_1·rand()·\left(p_{in}-x_{in}^k\right)+c_2·rand()·\left(p_{gn}-x_{in}^k\right)$$

(7)

$$x_{in}^{k+1}=x_{in}^k+v_{in}^{k+1}$$

(8)

where w is inertia weight, c₁, c₂ are two positive constants representing the acceleration factors, $v_{in}^{k+1}$ represents the nth-dimensional velocity component generated by the (k+1)th iteration of the ith particle, and $x_{in}^{k+1}$ represents the nth-dimensional position component generated by the (k+1)th iteration of the ith particle.

3.2.2. SMPSO

PSO features fast convergence speed and simple implementation, but it often falls into a local optimum. To solve this issue, we propose a Particle Swarm Optimization algorithm based on Subgroup Migration (SMPSO), which improves the evolutionary strategy of PSO. SMPSO uses the knowledge of other particles in the population and expands the search space as much as possible to guide the particle to avoid the local optimum.

During the evolutionary process, the population is defined into three subgroups, A, B and C, based on the fitness values. Subgroup A consists of particles with large fitness values, indicating that the convergence degree is high and making it easy to fall into the local optimum. In this case, the particle adjusts its speed and direction based on the position of the nearest particle and performs a more detailed search near the extreme value point to find a better position than the previous position’s fitness. Equations (9) and (10) demonstrate how a particle in subgroup A updates its speed and position. The updating strategy enhances the local search using its inertia speed, the optimal value calculated by itself, and the location of its nearest particle. Subgroup B consists of particles with moderate fitness values, and the speed and location of these particles are updated using the standard PSO. Subgroup C consists of particles with poor fitness values, and the speed and location of these particles are updated based on Equations (11) and (12). The updating strategy covers all possible solutions and enhances the global search ability using its inertia speed, its optimal value, and the positions of the random particles. Subgroups A, B, and C evolve separately based on their updating strategies. The particles migrate to the corresponding subgroup according to new fitness values after every iteration until the termination condition is satisfied.

$$v_{in}^{k+1}=w·v_{in}^k+c_1·rand()·\left(p_{in}-x_{in}^k\right)+c_2·rand()·\left(l_n^k-x_{in}^k\right)$$

(9)

$$x_{in}^{k+1}=x_{in}^k+v_{in}^{k+1}$$

(10)

$$v_{in}^{k+1}=w·v_{in}^k+c_1·rand()·\left(p_{in}-x_{in}^k\right)+c_2·rand()·\left(x_{randomn}^k-x_{in}^k\right)$$

(11)

$$x_{in}^{k+1}=x_{in}^k+v_{in}^{k+1}$$

(12)

where $v_{in}^{k+1}$ represents the nth-dimensional velocity component generated by the (k+1)th iteration of the ith particle, $x_{in}^{k+1}$ represents the nth-dimensional position component generated by the (k+1)th iteration of the ith particle, $l_n^k$ represents the nth-dimensional position component generated by the kth iteration of the ith particle’s nearest particle, and $x_{randomn}^k$ represents the nth-dimensional position component of the random particle, random $\in \left\{1,2,\dots \mathrm{N}\right\}$.

3.2.3. SMPSO for Feature Selection

In a continuous SMPSO, each particle can change its position to any point in space. If SMPSO is used for feature selection, the value of each dimension for the particle’s position is represented by 0 or 1, where 0 means that none of the features corresponding to the position is selected and 1 means that the features corresponding to the position are selected. Below, Equations (13) and (14) summarize SMPSO’s updating strategy for feature selection and Figure 1 demonstrates the SMPSO workflow.

$$x_{in}^{k+1}=\{\begin{array}{cc}1\hfill & \hfill \mathrm{if} \mathrm{sigmoid}\left(x_{in}^{k+1}\right)\ge 0.5\\ 0\hfill & \hfill \mathrm{otherwise}\end{array}$$

(13)

$$\mathrm{sigmoid}\left(a\right)=\frac{1}{1+e^{-10\left(a-5\right)}}$$

(14)

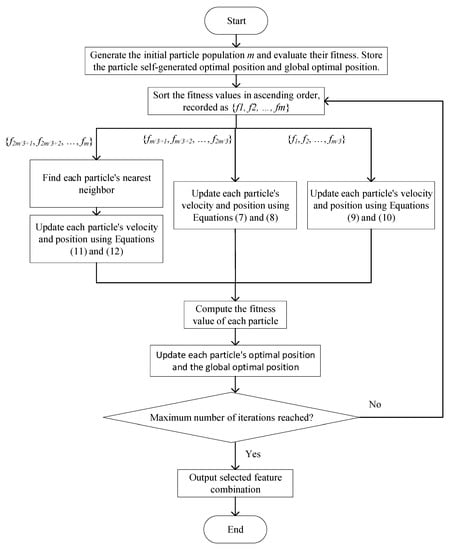
Figure 1. SMPSO Workflow.

3.3. SMPSO-HS-AdaBoost

Adaptive boosting (AdaBoost) is an adaptive enhancement technique. It is a typical ensemble algorithm that improves classification performance by combining multiple weak classifiers into one strong classifier. Firstly, AdaBoost gives each training sample the same weight and obtains a learning machine by training the samples. Secondly, it evaluates the learning results and improves the weights of samples with poor learning effect. Samples with poor learning results are more likely to appear in the next training set, thus enhancing the learning dynamics and iteratively improving the learning results, especially for the samples with poor learning results. By repeating the above process, an optimal learning machine will eventually be built. The training procedure of AdaBoost is shown in Algorithm 1.

Algorithm 1. The AdaBoost algorithm.

Input:

Sample distribution D;

Base learning algorithm C;

Number of learning iterations T;

Process:

1. D1 = D.                   % Initialize distribution

2. for t = 1, …, T:

3. ht = C(Dt);                  % Train a weak learner from distribution Dt

4. ${\epsilon }_t=P_{x~D_t}\left(h_t\left(x\right)\ne f\left(x\right)\right)$         % Evaluate the error of ht

5. Dt+1 = Adjust_Distribution(Dt, ${\epsilon }_t$)

6. end

Output:

H(x) = Combine_Outputs({ht(x)})

Although AdaBoost reduces the variance and the bias in the final ensemble, it may not be effective for data sets with skewed class distributions. The standard boosting procedure gives equal weights to all misclassified examples. Because the boosting algorithm samples from a pool that predominantly consists of the majority class samples, subsequent training set samplings may still be skewed towards the majority class.

This paper proposes SMPSO-HS-AdaBoost, an algorithm that combines the data sampling method (HS), feature selection method (SMPSO), and classification algorithm (AdaBoost). Firstly, it processes the data using HS and SMPSO. Secondly, it uses the processed data to train the weak classifiers and update weight values based on the sample classification results. After finite iterations, it generates the final output through the voting results generated by of weak classifiers. The training procedure of SMPSO-HS-AdaBoost is shown in Algorithm 2.

Algorithm 2. The proposed SMPSO-HS-AdaBoost algorithm.

Training sets $S=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots \left(x_m,y_m\right)\right\}$,

Feature vector $x_i\in X^d$ is $d$ dimension,

Class tag $y_i\in \left\{1,-1\right\}$, 1 is the Positive class, −1 is the Negative class.

Input:

Training sets $S$;

Base classifiers $G$;

Over-sampling rate $M$;

Under-sampling rate $N$;

Process:    Step1  Initialize the weight of samples in data set $D_1=\left(w_{11},\cdots ,w_{1i},\cdots ,w_{1m}\right),w_{1i}=\frac{1}{m},i=1,2,\cdots ,m$    Step2  Use SMOTE over-sampling to add the instances of the minority class with an over-sampling rate of M, and use random under-sampling to process the over-sampled data set with an under-sampling rate of N. Then perform feature selection using SMPSO to generate the training data set $S_t^{\prime }$ with weight distribution $D_t^{\prime }$.    Step3  for t = 1 to T

(1) Compute $G_t\left(x\right)=\left\{-1,+1\right\}$ based on $S_t^{\prime }$, weight distribution $D_t^{\prime }$, and weak classifier $G$. (2) Compute the classification loss of $G_t$.

$e_t=P\left(G_t\left(x\right)\ne y_i\right)={{\displaystyle \sum }}_{i=1}^m{w}_{ti}I\left(G_t\left(x\right)\ne y_i\right)$

(3) Calculate the coefficient of $G_t\left(x\right):{\alpha }_t=\frac{1}{2}log\frac{1-e_t}{e_t}$

(4) Update the weight distribution.

$D_{m+1}=\left(w_{m+1,1},\cdots ,w_{m+1,i},\cdots ,w_{m+1,N}\right)$

(5) Normalize the results.

$w_{m+1,i}=\frac{w_{mi}\exp \left(-{\alpha }_m{y}_i{G}_m\left(x_i\right)\right)}{{{\displaystyle \sum }}_{i=1}^N{w}_{mi}\exp \left(-{\alpha }_m{y}_i{G}_m\left(x_i\right)\right)}$

Step4 Generate the classification model.

$H\left(X\right)=\mathrm{sign}({\displaystyle \sum _{t=1}^T}{\alpha }_t{G}_t\left(x\right))$

Output:

Classification model $H\left(x\right)$

4. Results and Analysis

4.1. Performance Metric

Evaluation criterion plays an important role in classification performance evaluation. Evaluation criteria, such as the ROC curve, AUC, and confusion matrix-based measures including recall, precision, F-measure, and G-mean, are commonly used to evaluate imbalanced data classification performance. As shown in Table 1, the classification results can be represented by a confusion matrix with two rows and two columns reporting true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN). In binary classification, the minority class with a high recognition is considered a positive class and the majority class is considered a negative class.

Table 1. Confusion Matrix.

Title	Predicted Positive Class	Predicted Negative Class
Actual positive class	True Positive (TP)	False Negative (FN)
Actual negative class	False Positive (FP)	True Negative (TN)

Based on the confusion matrix, precision and recall can be defined as:

$$Recall=\frac{TP}{TP+FN}$$

(15)

$$\mathit{Precision}=\frac{TP}{TP+FP}$$

(16)

Precision and recall are essential measures to evaluate the classification performance of the positive class. In this paper, F-value [29], G-mean [30], and AUC [31] are used to evaluate the performance of the classifier.

Equation (17) shows how the F-value is obtained.

$$F-value=\frac{\left(1+{\beta }^2\right)\times Recall\times Precision}{{\beta }^2\times Recall+Precision}$$

(17)

β indicates the relative importance between recall and precision. Usually β = 1, and F-value is written as F1. Recall equals true positive divided by the sum of true positive and false positive. Precision equals true positive divided by the sum of true positive and false negative.

Recall that precision, and F-value are used as the evaluation criteria of the positive class (minority class). F-value is the harmonic mean of recall rate and precision rate and is typically used to evaluate imbalanced data classification performance. Because its value is close to the smaller of the recall and precision rates, a large F-value value indicates that the recall and precision rates are large.

G-mean is typically used to evaluate the overall classification performance of imbalanced data. Equation (18) shows how G-mean is obtained.

$$G-mean=\sqrt{\frac{TP}{TP+FN}·\frac{TN}{TN+FP}}$$

(18)

Curve ROC [32] describes the performance of classifiers in different discrimination threshold values, but in practice, the AUC value (the area between the ROC curve and the axis), not the ROC curve, is used to evaluate the classifier performance.

4.2. Experimental Results

To evaluate SMPSO-HS-AdaBoost, seven data sets from aerospace software systems, CM1, KC1, KC3, PC1, PC3, PC4, and PC5 (publicly available NASA MDP software defect data sets), were selected. The class label of these data sets is {Y, N}, where Y (high-risk module) is the minority class, and N (low-risk module) is the majority class. The basic information of the data sets is summarized in Table 2.

Table 2. Data sets used in evaluation.

Data Set	Total Samples	Majority Class Samples	Minority Class Samples	Minority Class Sample (%)
CM1	505	457	48	9.3
KC1	1183	869	314	26.5
KC3	194	158	36	18.5
PC1	705	644	61	9.4
PC3	1077	943	134	12.4
PC4	1287	1110	177	13.7
PC5	1711	1240	471	27.5

We evaluated the performance of SMPSO and SMPSO-HS-AdaBoost using Pycharm. The neighborhood k value in SMOTE was set to 5. After SMOTE over-sampling and random under-sampling, the ratio of minority class instances to majority class instances was 1:2.

To increase the evaluation accuracy, all experimental results were obtained using five-fold cross-validation (CV). The samples were divided into five groups. In each iteration, four groups were randomly selected to train the model, and the remaining group was used to test the model. Five trials were performed, and the cross-validation results were obtained by averaging the results of the five trials.

4.3. Results and Analysis of SMPSO

The classical KNN single classifier and classical AdaBoost combination classifier were used as benchmark classifiers to evaluate the performance of SMPSO in comparison with PSO (wrapper method), ANOVA (filter method), and no feature selection method, labeled as NFS. Again, five-fold CV was used, and the evaluation results, including accuracy, F1, AUC, and G-mean values, are summarized in Table 3. Results show that regardless of using AdaBoost or KNN as the base classifier, SMPSO achieves the best accuracy, F1, AUC, and G-mean, compared to the other approaches. Thus, SMPSO can effectively improve the performance of software defect prediction.

Table 3. SMPSO performance comparison.

Data Set	Metrics	AdaBoost				KNN
		SMPSO	PSO	ANOVA	NFS	SMPSO	PSO	ANOVA	NFS
CM1	Accuracy	0.936	0.928	0.881	0.887	0.93	0.928	0.879	0.887
	F1	0.576	0.505	0.218	0.156	0.513	0.459	0.061	0.114
	AUC	0.722	0.689	0.578	0.545	0.69	0.66	0.504	0.526
	G-mean	0.667	0.616	0.374	0.261	0.618	0.568	0.128	0.215
KC1	Accuracy	0.782	0.777	0.742	0.753	0.782	0.772	0.711	0.742
	F1	0.435	0.411	0.267	0.325	0.5	0.471	0.291	0.367
	AUC	0.633	0.622	0.562	0.584	0.663	0.647	0.555	0.595
	G-mean	0.548	0.528	0.408	0.459	0.593	0.589	0.445	0.505
KC3	Accuracy	0.933	0.902	0.794	0.814	0.896	0.871	0.789	0.799
	F1	0.783	0.709	0.313	0.406	0.639	0.484	0.181	0.152
	AUC	0.829	0.8	0.593	0.635	0.743	0.662	0.539	0.534
	G-mean	0.811	0.783	0.443	0.555	0.7	0.571	0.278	0.208
PC1	Accuracy	0.945	0.924	0.899	0.883	0.944	0.931	0.906	0.912
	F1	0.575	0.488	0.258	0.212	0.57	0.455	0.125	0.56
	AUC	0.714	0.691	0.581	0.566	0.711	0.658	0.532	0.581
	G-mean	0.658	0.628	0.434	0.407	0.639	0.567	0.215	0.413
PC3	Accuracy	0.893	0.889	0.861	0.85	0.893	0.889	0.858	0.857
	F1	0.476	0.429	0.202	0.216	0.473	0.428	0.2	0.21
	AUC	0.676	0.652	0.553	0.558	0.672	0.654	0.551	0.557
	G-mean	0.610	0.569	0.367	0.382	0.598	0.564	0.368	0.381
PC4	Accuracy	0.926	0.912	0.902	0.882	0.919	0.902	0.853	0.87
	F1	0.702	0.654	0.584	0.509	0.668	0.592	0.266	0.39
	AUC	0.802	0.781	0.734	0.697	0.782	0.739	0.577	0.632
	G-mean	0.784	0.759	0.695	0.648	0.757	0.703	0.427	0.537
PC5	Accuracy	0.782	0.779	0.744	0.749	0.798	0.773	0.742	0.735
	F1	0.533	0.504	0.378	0.433	0.594	0.552	0.469	0.458
	AUC	0.68	0.665	0.601	0.624	0.717	0.691	0.64	0.634
	G-mean	0.64	0.613	0.509	0.559	0.673	0.666	0.598	0.591

G-mean is a robust evaluation index of an imbalanced data classification method that can evaluate the comprehensive performance of a learning algorithm, thus, we compare the G-mean values of SMPSO+AdaBoost with the G-mean values of SMPSO+KNN. Figure 2 shows that the G-mean value of SMPSO+AdaBoost is significantly higher than that of SMPSO+KNN on the five data sets of CM1, PC1, PC3, PC4, and KC3, which are seriously unbalanced. The comparison results show that the proposed SMPSO can generate better feature selection results when combined with AdaBoost, especially for data sets with high degrees of imbalance. Therefore, the proposed SMPSO-HS-AdaBoost was used as the final classification algorithm in our approach.

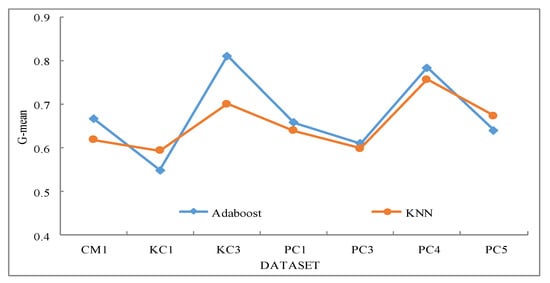
Figure 2. Comparison of G-mean values generated by AdaBoost and KNN.

4.4. Results and Analysis of SMPSO-HS-AdaBoost

In this section, we evaluate the performance of SMPSO-HS-AdaBoost according to accuracy, precision, recall, F1, AUC, and G-mean, in comparison with PSO-HS-AdaBoost, SMPSO-AdaBoost, HS-AdaBoost, SMOTE-AdaBoost, and Random-AdaBoost. Seven data sets were used, and the results are summarized in Table 4. The results show that SMPSO-AdaBoost and Random-AdaBoost generate poor F1, AUC, and G-mean values on imbalanced data, indicating that classification suffers performance loss if only under-sampling is used or data set balancing is not performed. HS-AdaBoost performs better than SMOTE-AdaBoost except on CM1, which indicates that hybrid-sampling performs better than over-sampling. The proposed SMPSO-HS-AdaBoost approach is based on hybrid-sampling, and it improves feature selection and AdaBoost classification to enhance the performance. The results show that it achieves better performance in accuracy, precision, recall, F1, AUC, and G-mean on all data sets.

Table 4. SMPSO-HS-AdaBoost performance comparison.

Data Set	Algorithm	Accuracy	Precision	Recall	F1	AUC	G-Mean
CM1	SMPSO-HS-AdaBoost	0.921	0.907	0.858	0.875	0.905	0.911
	PSO-HS-AdaBoost	0.890	0.810	0.870	0.838	0.885	0.883
	SMPSO-AdaBoost	0.936	0.824	0.457	0.576	0.722	0.667
	HS-AdaBoost	0.827	0.747	0.747	0.728	0.807	0.792
	SMOTE-AdaBoost	0.882	0.793	0.752	0.768	0.841	0.832
	Random-AdaBoost	0.716	0.585	0.475	0.519	0.652	0.624
KC1	SMPSO-HS-AdaBoost	0.745	0.708	0.414	0.519	0.719	0.660
	PSO-HS-AdaBoost	0.741	0.692	0.409	0.512	0685	0.608
	SMPSO-AdaBoost	0.781	0.695	0.318	0.435	0.633	0.548
	HS-AdaBoost	0.713	0.639	0.323	0.429	0.616	0.542
	SMOTE-AdaBoost	0.716	0.637	0.302	0.409	0.609	0.525
	Random-AdaBoost	0.695	0.578	0.280	0.371	0.587	0.497
KC3	SMPSO-HS-AdaBoost	0.917	0.888	0.861	0.872	0.903	0.901
	PSO-HS-AdaBoost	0.897	0.853	0.846	0.844	0.884	0.880
	SMPSO-AdaBoost	0.933	0.96	0.664	0.783	0.829	0.811
	HS-AdaBoost	0.774	0.664	0.676	0.661	0.750	0.739
	SMOTE-AdaBoost	0.767	0.595	0.538	0.538	0.699	0.652
	Random-AdaBoost	0.628	0.418	0.385	0.387	0.561	0.519
PC1	SMPSO-HS-AdaBoost	0.935	0.894	0.908	0.898	0.928	0.936
	PSO-HS-AdaBoost	0.917	0.851	0.904	0.876	0.913	0.913
	SMPSO-AdaBoost	0.939	0.779	0.443	0.555	0.714	0.658
	HS-AdaBoost	0.865	0.779	0.8	0.782	0.848	0.838
	SMOTE-AdaBoost	0.873	0.770	0.769	0.751	0.839	0.828
	Random-AdaBoost	0.730	0.534	0.526	0.528	0.670	0.652
PC3	SMPSO-HS-AdaBoost	0.877	0.801	0.833	0.813	0.866	0.862
	PSO-HS-AdaBoost	0.861	0.774	0.811	0.790	0.848	0.844
	SMPSO-AdaBoost	0.893	0.623	0.387	0.476	0.676	0.610
	HS-AdaBoost	0.820	0.714	0.730	0.712	0.797	0.783
	SMOTE-AdaBoost	0.845	0.727	0.683	0.685	0.795	0.771
	Random-AdaBoost	0.700	0.512	0.484	0.495	0.640	0.617
PC4	SMPSO-HS-AdaBoost	0.928	0.882	0.909	0.892	0.923	0.922
	PSO-HS-AdaBoost	0.923	0.882	0.890	0.882	0.915	0.912
	SMPSO-AdaBoost	0.926	0.790	0.633	0.702	0.802	0.784
	HS-AdaBoost	0.896	0.832	0.865	0.843	0.888	0.884
	SMOTE-AdaBoost	0.901	0.809	0.837	0.818	0.881	0.876
	Random-AdaBoost	0.838	0.756	0.769	0.761	0.821	0.819
PC5	SMPSO-HS-AdaBoost	0.764	0.694	0.533	0.601	0.706	0.684
	PSO-HS-AdaBoost	0.756	0.682	0.507	0.581	0.694	0.668
	SMPSO-AdaBoost	0.782	0.652	0.454	0.533	0.680	0.640
	HS-AdaBoost	0.717	0.614	0.419	0.497	0.643	0.602
	SMOTE-AdaBoost	0.724	0.588	0.392	0.469	0.633	0.584
	Random-AdaBoost	0.710	0.627	0.483	0.544	0.660	0.635

Next, we evaluate the effectiveness and stability of SMPSO-HS-AdaBoost using two data sets with the minority class sample ratio less than 10%, CM1, and PC1. Again, five-fold CV was performed, and the G-mean values of each trial are shown in Figure 3 and Figure 4. In Figure 3, we can see that the G-mean value of SMPSO-HS-AdaBoost is the best on each trial, and the overall G-mean values of SMPSO-AdaBoost and Random-AdaBoost are the worst. In Figure 4, we can see that the G-mean value of SMPSO-HS-AdaBoost is still the best on each trial, and the overall G-mean values of SMPSO-AdaBoost and Random-AdaBoost are still the worst. Results show that the proposed SMPSO-HS-AdaBoost outperforms the others in each trial, demonstrating its performance and stability.

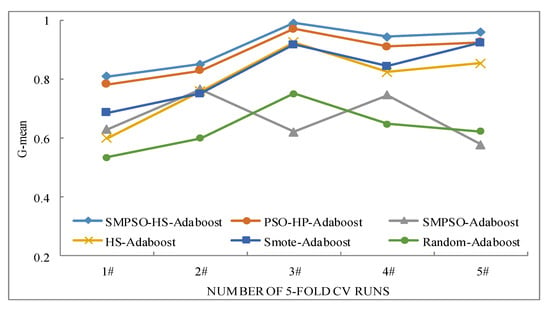
Figure 3. Comparison of G-mean values generated by AdaBoost and KNN.

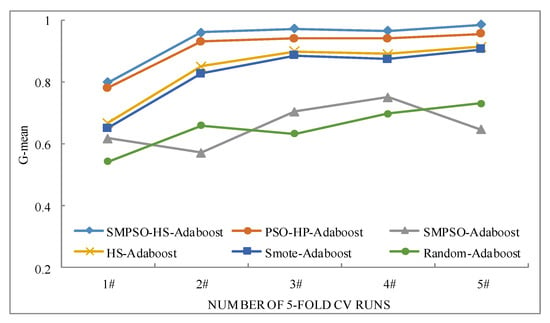
Figure 4. G-mean value comparison on PC1.

5. Conclusions

It is critical to identify the high-risk modules in a software system to assure its quality. There are two key problems in software defect prediction, imbalanced data and feature redundancies. In this paper, we propose an intelligent fusion algorithm, SMPSO-HS-AdaBoost, which can be used to build software defect prediction models. SMPSO-HS-AdaBoost focuses on solving the imbalanced data issue to ensure the efficiency and accuracy of software defect prediction. Firstly, it uses SMOTE and under-sampling to balance the data set. Then, it extracts the significant features using the proposed SMPSO. Finally, AdaBoost is used to perform classification on the new data set. Experimental results show that the proposed SMPSO-HS-AdaBoost improves the efficiency and accuracy of the software defect prediction model by resolving the coexisting problems of imbalanced data and feature redundancies.