Optical-Cavity-Induced Current
Abstract
1. Introduction
2. Materials and Methods
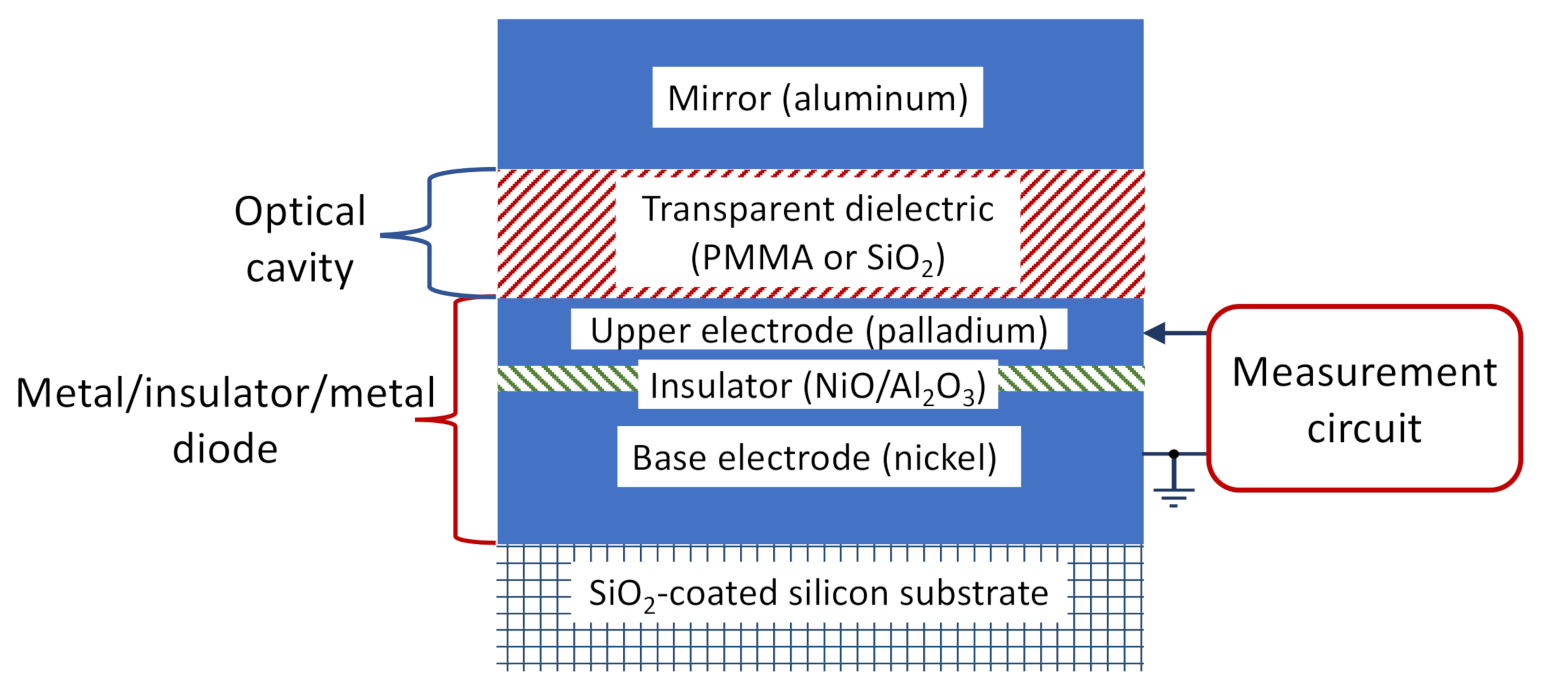
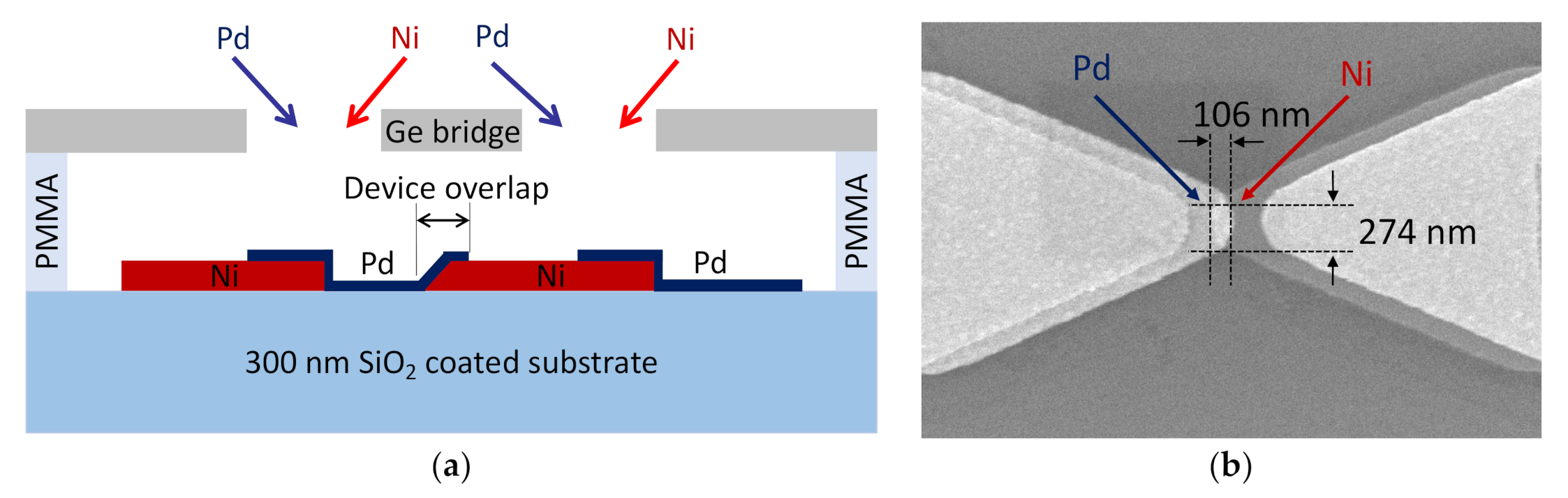
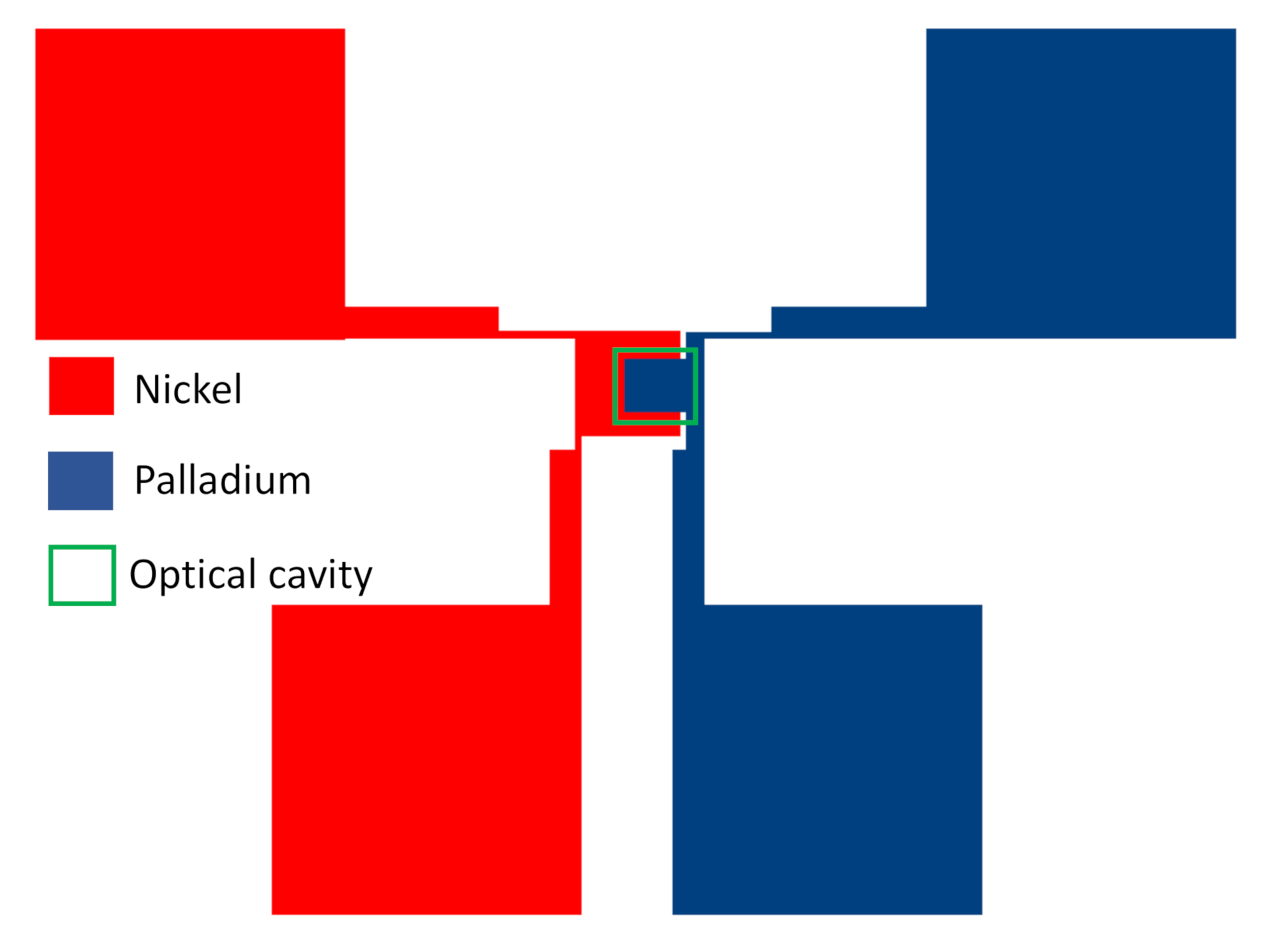
2.1. Device Fabrication
2.2. Device Measurement
3. Results
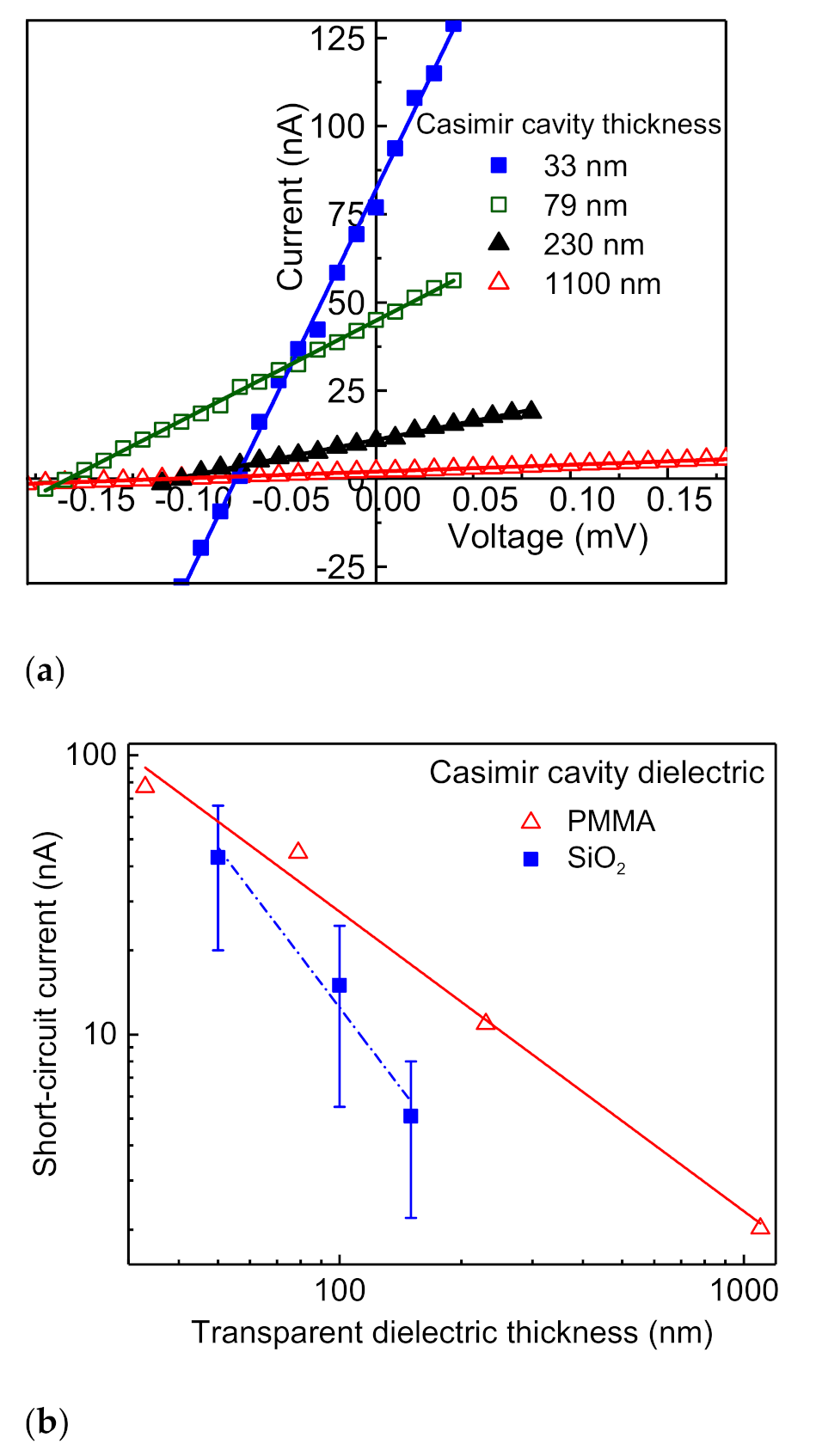
3.1. Electrical Response Measurements
3.2. Testing for Experimental Artifacts
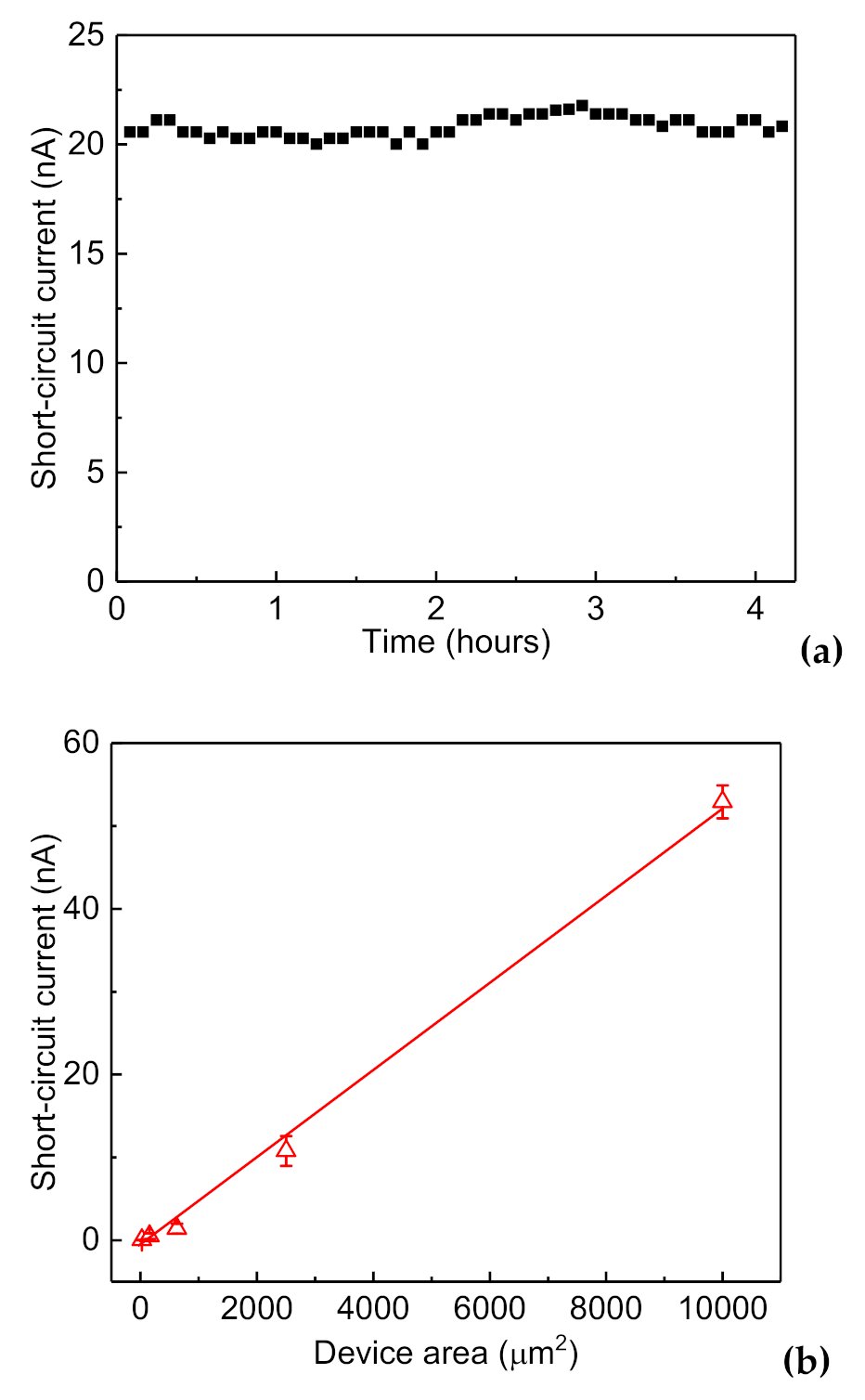
3.2.1. Stability over Time
3.2.2. Area Dependence
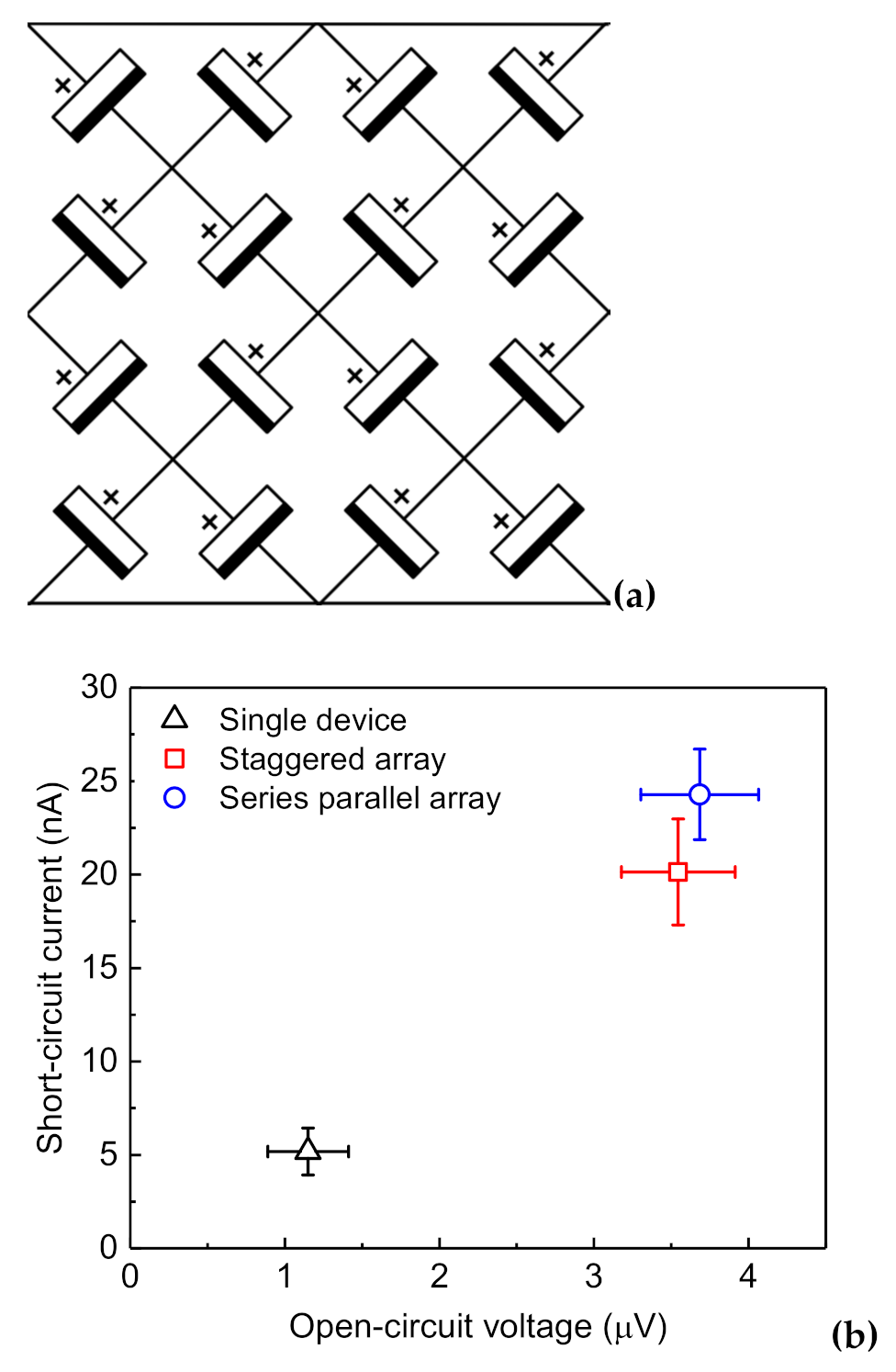
3.2.3. Array Dependence
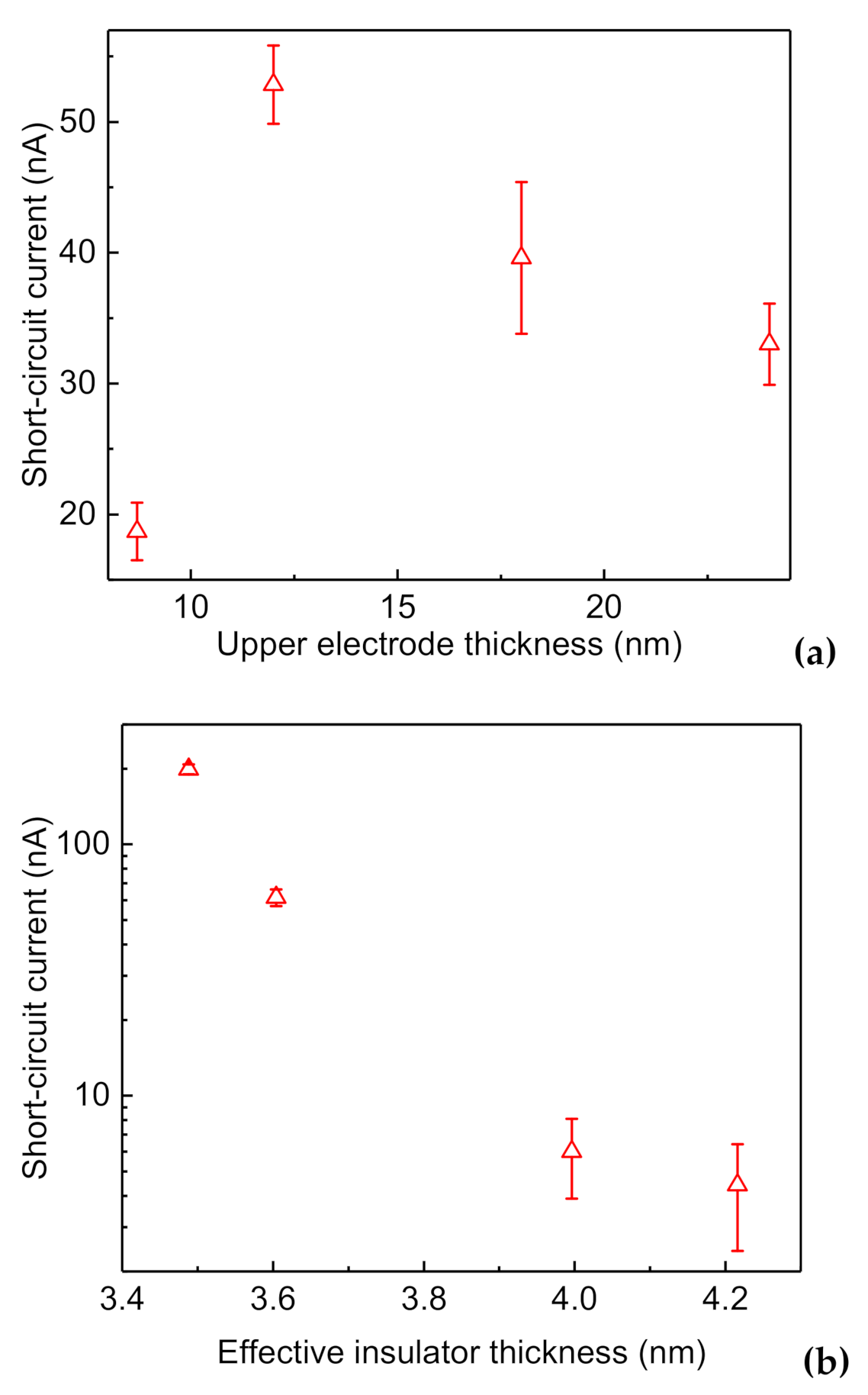
3.2.4. Processing Dependence
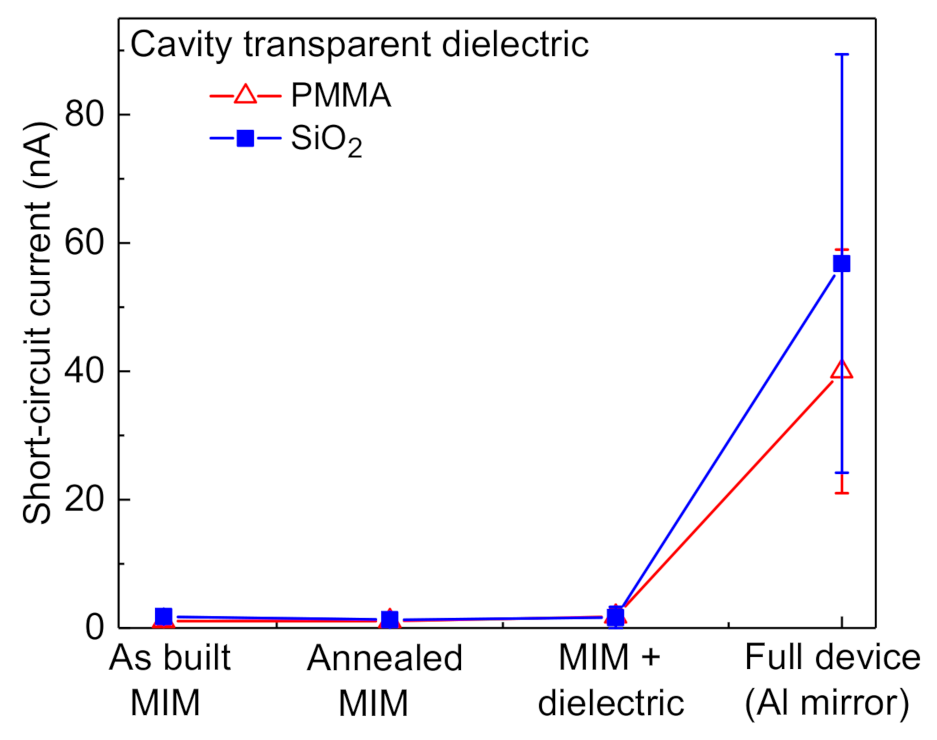
3.2.5. Current Leakage through the Cavity
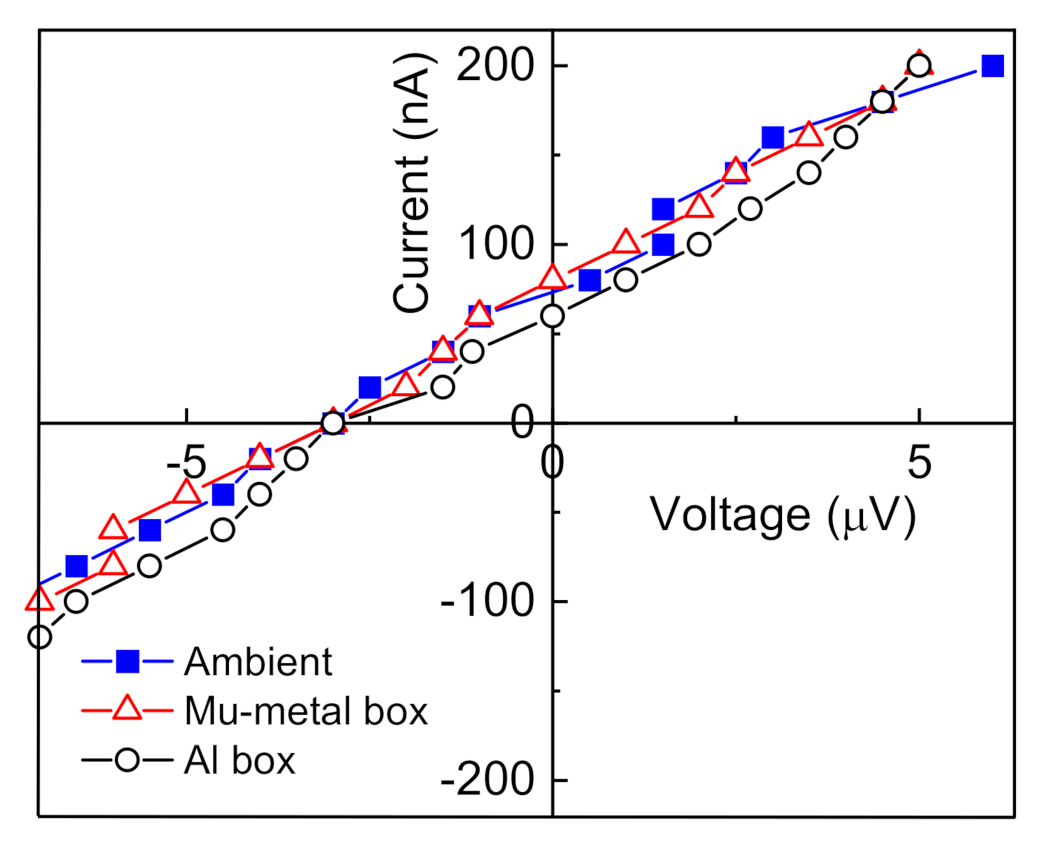
3.2.6. Electromagnetic Pickup
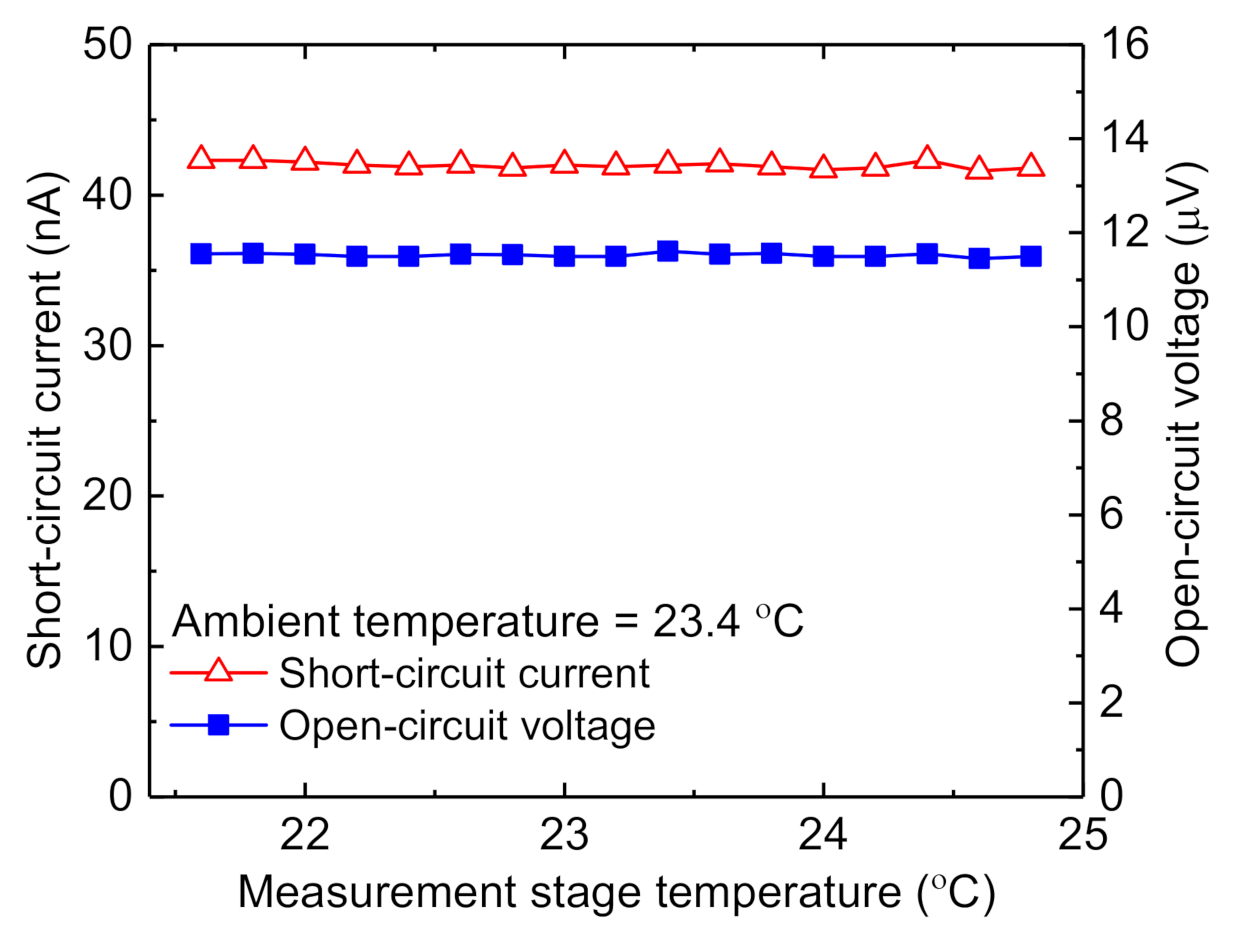
3.2.7. Thermoelectric Effects on Electrodes
3.2.8. Thermoelectric Effects on Devices
4. Discussion
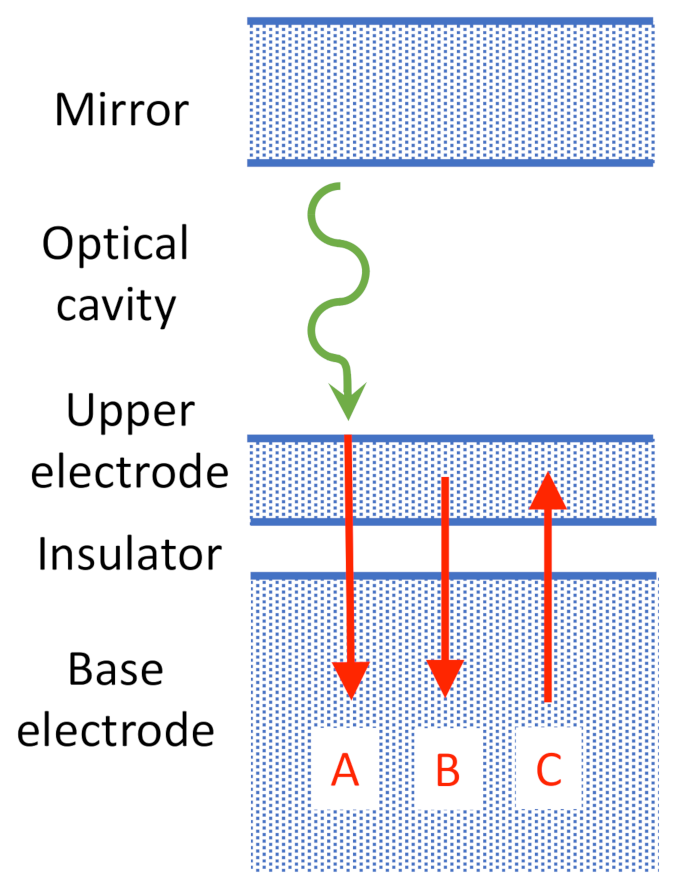
- We consider first the MIM device in the absence of the optical cavity and the mirror. Component A is produced by free-space ambient optical modes impinging on the upper electrode, where they excite hot electrons. These hot electrons are injected into the insulator and then are absorbed in the base electrode. Component B is due to electrons excited within the upper electrode, e.g., from plasmonic zero-point fluctuations [28]. The electrons are injected into the insulator and then absorbed in the base electrode. Component C, in the opposite direction, is due to electrons that are excited by fluctuations within the base electrode, injected into the insulator, and then absorbed in the upper electrode. There is no optically excited current component of electrons from the base electrode to the upper electrode because the base electrode is thicker than the electron mean-free path length, and so any electrons excited at the outer (lower) surface of the electrode are scattered before reaching the insulator. In equilibrium, the net current is zero, and component C is balanced by the sum of components A and B.
- We now consider the MIM device in the presence of an adjoining optical cavity and the mirror. The addition of the adjoining structure upsets the balance in current components. Because the cavity reduces the density of the optical modes impinging on the upper electrode, component A is reduced while components B and C remain unchanged. This results in a net electron current from the base electrode to the upper electrode, which is consistent with our observations.
- In examining the balance of current components when the MIM device is not perturbed by the presence of the optical cavity and mirror, we consider first the device in the absence of the cavity structure. To maintain the zero net current, this increase in photoinjection yield with changing layer thickness must be balanced by a decrease in the internally generated component B or an increase in the internally generated component C. These changes in components B and C result from the thickness changes and are independent of whether there is an adjoining optical cavity or not.
- We once again consider the MIM device in the presence of an adjoining optical cavity and mirror. With the reintroduction of this adjoining structure, the enhanced photoinjection yield represented by component A now leads to a greater suppression of component A. Because of the greater reduction in component A, the net electron current from the base electrode to the upper electrode is enhanced. Thus, increasing the photoinjection yield leads to an enhanced current that is induced by the presence of an adjoining optical cavity, in the direction opposite to the photoinjection current.
- Additional components result from the fact that the insulator itself forms a very thin optical cavity. This cavity is symmetric with respect to the MIM structure itself, as opposed to the optical cavity shown in the figure, which is to one side of the MIM structure. Because there is no longer a cavity having a reduced density of vacuum modes on one side of the tunneling region, the current components in each direction balance each other out, resulting in no net current. This is consistent with the observation that MIM structures without the adjoining optical cavity do not produce a current, as shown in Figure 8.
- Another component results from the upper electrode being slightly transparent. As a result, a small fraction of the optical radiation from the optical cavity impinges on the lower electrode and produces hot carriers. Because the optical transmission through the upper electrode is small, this produces only negligible effects.
- Additional effects, such as those from the surface plasmon modes in the cavity [29], cannot be ruled out.
5. Conclusions
Author Contributions
Funding
Institutional Review
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sanchez, A.; Davis, C.F., Jr.; Liu, K.C.; Javan, A. The MOM Tunneling Diode: Theoretical Estimate of Its Performance at Microwave and Infrared Frequencies. J. Appl. Phys. 1978, 49, 5270–5277. [Google Scholar] [CrossRef]
- Fumeaux, C.; Herrmann, W.; Kneubuhl, F.K.; Rothuizen, H. Nanometer Thin-Film Ni-NiO-Ni Diodes for Detection and Mixing of 30 THz Radiation. Infrared Phys. Technol. 1998, 39, 123–183. [Google Scholar] [CrossRef]
- Grover, S.; Moddel, G. Engineering the Current-Voltage Characteristics of Metal-Insulator-Metal Diodes Using Double-Insulator Tunnel Barriers. Solid-State Electron. 2012, 67, 94–99. [Google Scholar] [CrossRef]
- Kadlec, J.; Gundlach, K.H. Results and Problems of Internal Photoemission in Sandwich Structures. Phys. Status Solidi (A) 1976, 37, 11–28. [Google Scholar] [CrossRef]
- Kovacs, D.A.; Winter, J.; Meyer, S.; Wucher, A.; Diesing, D. Photo and Particle Induced Transport of Excited Carriers in Thin Film Tunnel Junctions. Phys. Rev. B—Condens. Matter Mater. Phys. 2007, 76. [Google Scholar] [CrossRef]
- Simmons, J.G. Potential Barriers and Emission-limited Current Flow between Closely Spaced Parallel Metal Electrodes. J. Appl. Phys. 1964, 35, 2472–2481. [Google Scholar] [CrossRef]
- Moddel, G.; Weerakkody, A.; Doroski, D.; Bartusiak, D. Optical-Cavity-Induced Conductance Change. 2021. Unpublished work. [Google Scholar]
- Lambrecht, A.; Jaekel, M.-T.; Reynaud, S. The Casimir Force for Passive Mirrors. Phys. Lett. A 1997, 225, 188–194. [Google Scholar] [CrossRef][Green Version]
- Pelz, B.; Moddel, G. Demonstration of Distributed Capacitance Compensation in a Metal-Insulator-Metal Infrared Rectenna Incorporating a Traveling-Wave Diode. J. Appl. Phys. 2019, 125. [Google Scholar] [CrossRef]
- Hobbs, P.C.D.; Laibowitz, R.B.; Libsch, F.R. Ni–NiO–Ni Tunnel Junctions for Terahertz and Infrared Detection. Appl. Opt. 2005, 44, 6813–6822. [Google Scholar] [CrossRef]
- Weerakkody, A.; Belkadi, A.; Moddel, G. Nonstoichiometric Nanolayered Ni/NiO/Al2O3/CrAu Metal–Insulator–Metal Infrared Rectenna. ACS Appl. Nano Mater. 2021. [Google Scholar] [CrossRef]
- Keithley. Low Level Measurements Handbook Precision DC Current, Voltage, and Resistance Measurements Low Level Measurements Handbook, 7th ed.; Keithley Instruments Inc.: Cleveland, OH, USA, 2013. [Google Scholar]
- Herner, S.B.; Belkadi, A.; Weerakkody, A.; Pelz, B.; Moddel, G. Responsivity-Resistance Relationship in MIIM Diodes. IEEE J. Photovolt. 2018, 8, 499–504. [Google Scholar] [CrossRef]
- Gall, D. Electron Mean Free Path in Elemental Metals. J. Appl. Phys. 2016, 119. [Google Scholar] [CrossRef]
- Borghesi, A.; Guizzetti, G. Palladium. In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic: New York, NY, USA, 1991; Volume II. [Google Scholar]
- Nelson, O.L.; Anderson, D.E. Hot-Electron Transfer through Thin-Film Al–Al2O3 Triodes. J. Appl. Phys. 1966, 37, 66–76. [Google Scholar] [CrossRef]
- Simmons, J.G. Generalized Formula for the Electric Tunnel Effect between Similar Electrodes Separated by a Thin Insulating Film. J. Appl. Phys. 1963, 34, 1793–1803. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On the Attraction between Two Perfectly Conducting Plates. In Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, 29 May 1948; Volume 51, p. 793. [Google Scholar]
- Lamoreaux, S.K. Demonstration of the Casimir Force in the 0.6 to 6 μ m Range. Phys. Rev. Lett. 1997, 78, 5. [Google Scholar] [CrossRef]
- Woods, L.M.; Krüger, M.; Dodonov, V. Perspective on Some Recent and Future Developments in Casimir Interactions. Appl. Sci. 2021, 11, 293. [Google Scholar] [CrossRef]
- Woods, L.M.; Dalvit, D.A.R.; Tkatchenko, A.; Rodriguez-Lopez, P.; Rodriguez, A.W.; Podgornik, R. Materials Perspective on Casimir and van Der Waals Interactions. Rev. Mod. Phys. 2016, 88. [Google Scholar] [CrossRef]
- Lamb, W.E., Jr.; Retherford, R.C. Fine Structure of the Hydrogen Atom by a Microwave Method. Phys. Rev. 1947, 72, 241. [Google Scholar] [CrossRef]
- Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics; Academic press: Boston, MA, USA, 1994; ISBN 0080571492. [Google Scholar]
- Cole, D.C.; Puthoff, H.E. Extracting Energy and Heat from the Vacuum. Phys. Rev. E 1993, 48, 1562–1565. [Google Scholar] [CrossRef]
- Chalabi, H.; Schoen, D.; Brongersma, M.L. Hot-Electron Photodetection with a Plasmonic Nanostripe Antenna. Nano Lett. 2014, 14, 1374–1380. [Google Scholar] [CrossRef]
- Tagliabue, G.; Jermyn, A.S.; Sundararaman, R.; Welch, A.J.; DuChene, J.S.; Pala, R.; Davoyan, A.R.; Narang, P.; Atwater, H.A. Quantifying the Role of Surface Plasmon Excitation and Hot Carrier Transport in Plasmonic Devices. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Ludeke, R.; Bauer, A.; Cartier, E. Hot Electron Transport through Metal–Oxide–Semiconductor Structures Studied by Ballistic Electron Emission Spectroscopy. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1995, 13, 1830–1840. [Google Scholar] [CrossRef]
- Rivera, N.; Wong, L.J.; Joannopoulos, J.D.; Soljačić, M.; Kaminer, I. Light Emission Based on Nanophotonic Vacuum Forces. Nat. Phys. 2019, 15, 1284–1289. [Google Scholar] [CrossRef]
- Intravaia, F.; Henkel, C.; Lambrecht, A. Role of Surface Plasmons in the Casimir Effect. Phys. Rev. A At. Mol. Opt. Phys. 2007, 76, 1–11. [Google Scholar] [CrossRef]
- Knoesel, E.; Hotzel, A.; Wolf, M. Ultrafast Dynamics of Hot Electrons and Holes in Copper: Excitation, Energy Relaxation, and Transport Effects. Phys. Rev. B 1998, 57, 12812. [Google Scholar] [CrossRef]
- Williams, R. Injection by Internal Photoemission. In Williams, Richard. “Injection by Internal Photoemission.” Semiconductors and Semimetals; Academic Press: Amsterdam, The Netherlands, 1970; pp. 97–139. [Google Scholar]
- Heiblum, M.; Fischetti, M. Ballistic Hot-Electron Transistors. IBM J. Res. Dev. 1990, 34, 530–549. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Cutler, P.H.; Feuchtwang, T.E.; Huang, Z.-H.; Kuk, Y.; Silverman, P.J.; Lucas, A.A.; Sullivan, T.E. Mechanisms of Current Rectification in an STM Tunnel Junction and the Measurement of an Operational Tunneling Time. IEEE Trans. Electron Devices 1989, 36, 2671–2678. [Google Scholar] [CrossRef]
- Ford, L.H. Constraints on Negative-Energy Fluxes. Phys. Rev. D 1991, 43, 3972. [Google Scholar] [CrossRef]
- Davies, P.C.W.; Ottewill, A.C. Detection of Negative Energy: 4-Dimensional Examples. Phys. Rev. D 2002, 65. [Google Scholar] [CrossRef]
- Huang, H.; Ford, L.H. Quantum Electric Field Fluctuations and Potential Scattering. Phys. Rev. D Part. Fieldsgravitation Cosmol. 2015, 91, 1–8. [Google Scholar] [CrossRef]
- Maclay, G.J.; Davis, E.W. Testing a Quantum Inequality with a Meta-Analysis of Data for Squeezed Light. Found. Phys. 2019, 49, 797–815. [Google Scholar] [CrossRef]

| Figure | Area | NiOx | Al2O3 | Pd Upper Electrode | Transparent Dielectric | |
|---|---|---|---|---|---|---|
| (µm2) | (nm) | (nm) | (nm) | Values (nm) | Material | |
| 4 (a) | 0.02 | 1.3 | 8.3 | 33–1100 | PMMA | |
| 4 (b) | 0.02 | 1 | 0.9 | 8.3 | 33–1100 | PMMA or SiO2 |
| 5 (a) 1 | 10,000 | 2.3 + 0.4 resist | 2.3 | 8.7–24 | 11 | SiO2 |
| 5 (b) 1 | 625 | 2.3 + 0.4 resist | 0.7–1.5 | 15 | 11 | SiO2 |
| 6 (a) | 0.02 | 1 | 0.7 | 8.3 | 35 | PMMA |
| 6 (b) | 25–10,000 | 2.3 + 0.4 resist | 2.3 | 12 | 11 | SiO2 |
| 7 (b) | 0.02 × 16 | 1 | 0.9 | 15.6 | 107 | PMMA |
| 8 | 0.02 | 1 | 0.9 0.7 | 8.3 | 36 50 | PMMA SiO2 |
| 9 | 0.02 | 1 | 0.7 | 8.7 | – | PMMA |
| 10 | 0.02 | 1 | 05 | 8.7 | 33 | PMMA |
| 11 | 0.02 | 1 | 0.7 | 8.7 | 35 | PMMA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moddel, G.; Weerakkody, A.; Doroski, D.; Bartusiak, D. Optical-Cavity-Induced Current. Symmetry 2021, 13, 517. https://doi.org/10.3390/sym13030517
Moddel G, Weerakkody A, Doroski D, Bartusiak D. Optical-Cavity-Induced Current. Symmetry. 2021; 13(3):517. https://doi.org/10.3390/sym13030517
Chicago/Turabian StyleModdel, Garret, Ayendra Weerakkody, David Doroski, and Dylan Bartusiak. 2021. "Optical-Cavity-Induced Current" Symmetry 13, no. 3: 517. https://doi.org/10.3390/sym13030517
APA StyleModdel, G., Weerakkody, A., Doroski, D., & Bartusiak, D. (2021). Optical-Cavity-Induced Current. Symmetry, 13(3), 517. https://doi.org/10.3390/sym13030517






