Abstract
In this work, we outline a general method for calculating Auger spectra in molecules, which accounts for the underlying symmetry of the system. This theory starts from Fano’s formulation of the interaction between discrete and continuum states, and it generalizes this formalism to deal with the simultaneous presence of several intermediate quasi-bound states and several non-interacting decay channels. Our theoretical description is specifically tailored to resonant autoionization and Auger processes, and it explicitly includes the incoming wave boundary conditions for the continuum states and an accurate treatment of the Coulomb repulsion. This approach is implemented and applied to the calculation of the Auger and autoionization spectra of ozone, which is a symmetric molecule, whose importance in our atmosphere to filter out radiation has been widely confirmed. We also show the effect that the molecular point group and, in particular, the localization of the core-hole in the oxygen atoms related by symmetry operations, has on the electronic structure of the Auger states and on the spectral lineshape by comparing our results with the experimental data.
1. Introduction
Ozone has attracted enormous interest in recent years, due, in particular, to its paramount role that is played in atmospheric chemistry. On the one hand, a dramatic decrease in ozone concentration within the Earth’s upper atmosphere has shown a major negative impact on the effective shielding of our planet from ultraviolet sunlight, whose absence would be fatal to life [1]. On the other hand, ozone is known to act as greenhouse gas [2,3], thus increasing global warming, as well as to be a harmful pollutant in metropolitan areas being produced by exhaust gases of combustion processes with a considerable human health hazard potential.
These reports on the importance of ozone in the chemical dynamics of the atmosphere, as well as in the absorption of virtually all the ultraviolet light that passes into the stratosphere, fuelled ozone research. However, while several studies focused on the ground state electronic and vibrational properties of ozone [4,5,6], little to no theoretical and experimental information regarding electronic excited state dynamics can be found [7,8,9]. This investigation turns out to be crucial, e.g., to identify the molecular species that filter out the highest energy light, such as , X, and UV-rays, and to determine the amount of radiation reaching the surface of our Earth.
Moreover, the analysis of the excited states is also interesting in view of the fact that all of the ozone bands are dissociative [10,11], which means that the molecule falls apart to upon photon absorption. This dissociative mechanism drives further helpful or harmful reactions, depending on where in the Earth’s atmosphere they occur [12]. In these photo-excited processes, the system often goes through intermediate quasi-bound states, which have long lifetimes if compared with the collision times. Afterwards, the excited system undergoes a dissociative path into final channels that are characterized by the presence of a few asymptotically non-interacting fragments, the observation of which provides useful information on the properties of the system under examination. In general, these decay processes are due to the fact that the resonant excited state that is produced by the initial collision with the high-energy photon is embedded in the continua of the final fragments.
Auger spectroscopy, in particular, is a type of electron spectroscopy that is based on scattering processes in which the initial state consists of a projectile, typically X-ray or UV photons or electrons, which collides with an atomic, molecular, or solid state target, and the final states feature electrons, photons, or heavy particles according to the type of experiment. The analysis of the energies and intensity distribution of these secondary electrons represents the central problem of Auger spectroscopy. Indeed, Auger electrons are emitted with system-dependent probabilities in several open channels, characterized by different kinetic energies and identified by different quantum numbers. Of course, the Auger spectral lineshape reflects the symmetry of the perturbed system.
From the standpoint of computation, one notes the existence of an ample body of techniques developed for atomic systems, whereas, for molecules, the number is much more limited [13,14]. This is mainly due to the difficulties that are created by the reduced symmetry of molecular systems, which hinders the use of numerical techniques for representing the electron as it moves outward through the field of the ionized molecule. Furthermore, another relevant difficulty of molecules is represented by the inclusion of the nuclear motion and its coupling with the electronic degrees of freedom. For example, in ozone, fast excited dissociation may occur at once with the Auger emission [10], generating an interplay between the vibrational and electronic degrees of freedom beyond the Born–Oppenheimer approximation [15,16,17], which affects the kinetic energy of the emitted Auger electrons.
In this work, we first present a general theoretical and computational method for interpreting core-electron spectroscopies on molecules, such as autoionization and Auger, which allows for one to accurately reproduce the experimental results, by including, in principle, the vibrational details as well as the combined effects on the spectral lineshapes due to the intrinsic features of the transition, the characteristics of the incident radiation and those of the electron spectrometer. In particular, we discuss the central feature of our approach, which is the ability to calculate accurate wave functions for continuum states of polycentric symmetric (or asymmetric) systems at a computational effort that is similar to that of standard bound-state calculations. This method is used for calculating the resonant photoemission and the Auger spectra of the ozone molecule. The accuracy of the results is progressively increased by using different levels of theory, from mean field Hartree–Fock (HF) to correlated method, such as Configuration Interaction (CI), measuring the relative importance of the different contributions of the electron-electron correlation to the experimental spectrum. Furthermore, the effect on the Auger lineshape of the presence of core-hole localized in the orbitals of symmetry-related oxygen atoms, rather than in a delocalized molecular orbital, is discussed.
2. Theoretical and Computational Methods
2.1. Autoionization and Auger Decay as Resonant Multichannel Processes
Auger states are excited, quasi-bound states created by inner-shell excitation or ionization that are embedded in the continuum of the next higher charge state of the system. They can decay by either electron emission (radiationless transition) or by radiation emission. The radiationless decay is called autoionization or Auger transition, depending on whether the system initially undergoes a neutral excitation by promoting an electron to an empty orbital or is ionized by the impinging photons. The primary excitation process is often accompanied by the simultaneous ionization (shake-off) or excitation (shake-up) of a valence electron. The resulting peaks in the spectrum are called satellite lines. Shake-up and shake-off processes typically account for 10% of the total spectral intensity and they will be neglected in our analysis.
We rely on the time-independent approach developed by Fano [18] to evaluate the autoionization (or Auger) cross section. This approach interprets the decay process as due to the interaction between a quasi-bound state, produced by the primary excitation (ionization), and the continuum states of the single (double) ionized target.
Let us describe this method in the case of an autoionization process, in which one electron is excited to a discrete (resonant) state that is degenerate with several continua of the ionized target [19]. We notice that the label is a notation standing for "good quantum numbers” (angular momentum, spin, etc...) in spherically symmetric systems, such as atoms, and symmetric molecules. The total Hamiltonian of the problem, assuming the validity of the Born–Oppenheimer approximation, is , where is the many-body Hamiltonian of the isolated system, is the electromagnetic radiation Hamiltonian, where is the wavenumber of a wave that is confined within a box of volume , is the polarization direction and , and, finally, the interaction operator , where is the component of the dipolar operator in the polarization direction .
The continuum wave function of the system is characterized by the incoming wave boundary condition (−), which means that asymptotically represents one electron released, with energy , into a channel that is specified by the state of the ionized target at the energy . In Fano’s approach, the scattering eigenstate of the Hamiltonian of the isolated system is represented by the following linear combination of discrete and continuum states:
with the normalization condition:
The states , which appear in Equation (1), are continuum states that are obtained through the diagonalization of the many-electron Hamiltonian matrix of the system that is constructed using a set of interacting continuum states , as follows:
A solution of this set of equations is characterized by the following asymptotic behavior:
where are symmetry-adapted wave functions that describe the possible states of the ionized target and also containing the angular coordinates and the spin state of the outgoing electron. The radial phases depend on the nature of the long-range interaction inside each channel and is the scattering amplitude into channel . The coefficients of Equation (1) are obtained by solving the following equations
which explicitly read:
where
By moving into the complex plane to avoid singularities that appear in the coefficients of Equations (6) and (7), one obtains the following expression
with and defined as follows
Finally, knowing the stationary states for each possible combination of the quantum numbers and , one can obtain the cross section for the autoionization process, in which the photon absorption of appropriate energy promotes an electron to a discrete resonant state , and, afterward, the ionized target decays non-radiatively into channel . Indeed, according to the general theory of scattering [20,21], the autoionization cross section is proportional to the square element of the transition matrix. Using Equations (8)–(11), one obtains:
connecting the initial state , which is the tensorial product of the ground state of the system and of the state of the radiation with N -frequency photons, to the final state , which is the tensorial product of the continuum state, of the system and of a state of the radiation in which one photon of frequency has been absorbed. In Equation (12), the following definition has been used:
By neglecting the first term in the right hand side of Equation (12), which represents the contribution to the cross section of direct photoemission, the cross section of the resonant autoionization process can be approximated, as follows:
where is the cross section of the excitation process . One can observe that, as long as , which represents the decay rate into channel and , which represents the total decay rate, are slowly energy dependent in the range of interest, the cross section per unit energy that is defined by Equation (14) has a Lorentzian profile. The energy shift , as defined in Equation (11), usually represents a small correction to , so it can typically be neglected.
We notice that similar results can also be obtained for the Auger decay, where, at odds with the resonant autoionzation process, the intermediate state is constituted by a quasi-bound state of the ionized target plus one electron emitted upon the initial photoionization, while the final state is characterized by the presence of two electrons in the continuum. In our model, which explicitly includes the incoming wave boundary conditions for the continuum states, the Auger decay is described as a two-step process in which no interaction occurs between the primary photo-emitted and Auger electrons. This approximation is typically acceptable when the projectile’s kinetic energy is much higher than the ionization energy of the inner-shell electrons.
Therefore, the matrix of the process can be written, as follows:
where and are the energies of the outgoing electrons that are related to the other characteristic energies of the problem by the following relationship: ( is the ground state energy of the system). The intermediate state is a continuum state that, as long as , can be approximated by an antisymmetrized product, , where represents the state of the primary electron. In a similar way, the final state can be represented by , where is the state of the primary electron.
When neglecting the first terms in the right-hand side of Equation (15), which represents the probability amplitude of the double direct ionization process, one obtains
where is the photoionization cross section of the primary process. This result, again, displays a Lorentzian behaviour and indicates that is the rate of the non-radiative decay process from the ion intermediate state into the channel , and is the total Auger decay rate.
The cross sections (14), (16) represent the starting point for constructing the “theoretical” spectrum that is to be compared with the experimental one. They give the contributions to the spectrum due to the intrinsic features of the target, while the finite resolution of the electron spectrometer, the specific characteristics of the incident photon beam, and the broadening of the Auger lineshapes due to vibrational modes can be taken into account by performing a convolution with a Gaussian function [14].
2.2. The Projected Potential Approach and the Many-Body Hamiltonian
Basically, in order to assess the cross sections (14) and (16), we are left with the problems of calculating the intermediate resonant state and the continuum wavefunction. In particular, the problem of finding the eigensolutions of the Hamiltonian is separated with respect to finding the bound and continuum orbitals. This means neglecting the effects that the continuum orbital has on the bound orbitals. The latter are obtained separately, thus, without taking the presence of the outgoing electron into account. This is the so-called “Static Exchange Approximation”. In general, the interacting decay channels are represented by the tensor product
between a set of functions that describes the spin-orbital of the unbound electron and that is the determinant representing the bound state of the remaining system ( for Auger processes), and is the antisymmetrizer that also includes the normalization constant.
On the one hand, since both the intermediate and the final ionic states are bound states of the molecule, one can calculate their energies while using the standard quantum mechanical techniques proposed for bound-state calculations, such as the single Slater determinant HF, or many configuration wave functions methods, such as CI or MC-SCF, or Green’s function based techniques [14]. In particular, the solutions of the secular problem for the -electron system ( for Auger processes) are obtained inside the space spanned by the orbitals that were taken from a set of n bound orbitals . The HF single-determinant wavefunction and the CI treatment of symmetry-adapted orbitals will both be used to obtain the bound state eigenfunctions in Equation (17) as:
This solution is searched within the Hilbert space spanned by a basis set that we use to expand the orbital wavefunctions. Our basis set is typically built with Hermite Gaussian functions (HGF)
where gives the position where g is centered, is a coefficient determining the HGF width, the order of derivation () determines the symmetry type, and N is a normalization factor
Using a mixed basis set of HGFs of every order and centrature, we evaluate the mono and bi-electronic integrals of the many-body Hamiltonian (18).
On the other hand, to construct the continuum orbital of Equation (17) in the effective field of the bound orbitals, we developed a method that is capable to also include the interchannel coupling among various and, furthermore, the interaction among continuum and discrete states. We use the projected potential approach in order to include these effects. Within the projected potential framework, a model Hamiltonian is defined, in which the monoelectronic and the bielectronic part of the potential are both represented in terms of -functions. The use of this model Hamiltonian allows for us to also include the interchannel coupling and directly obtain the correct, non-interacting decay channels defined in the previous section (see Equation (4)).
To present this approach, we consider the case of a N-electron system with one electron in the continuum. We define a projector into a m-dimensional space of functions, spanned by the orthonormal set . We project both the electron-nuclei attraction potential , and the electron-electron Coulomb repulsion operators, obtaining the following model electronic Hamiltonian
By only projecting out the potential terms of the Hamiltonian, we come up with the solution to the issues of (i) accurately representing the orbital inside the scattering region, which is the important volume where the matrix elements that couple bound and continuum states (see Equation (8)) have to be appropriately calculated; and, (ii) recovering the continuum part of the spectrum by means of the unprojected kinetic term. The region where the potential is projected can, of course, be incremented by including, e.g., more diffuse HGFs so as to more accurately approximate the Coulomb potential tail. Outside this region, where only the long-range part of the potential survives, one can represent the continuum orbital as a linear combination of eigenfunctions of the long-range potential, which are typically known analytically (e.g., Coulomb wave functions).
In order to construct the product (17) and find the continuum eigenfunctions of the Hamiltonian (19) with positive eigenvalues, we notice that the Hamiltonian matrix diagonalization within the entire functional space is equivalent to solve the following projected Lippmann–Schwinger (LS) equation, which also includes the appropriate boundary condition:
where is the free-particle Green’s function and is the transition operator that is defined by the equation:
In Equation (23) is the approximate representation of the Coulomb operator (see Equations (20) and (21)), including both electron–electron and electron–nuclei interactions, projected using a finite set of functions. The elements of this basis set are chosen to minimize the difference inside the scattering volume. We notice that, in Equation (22), the correction to the free-wave state to obtain the scattering wavefunction is represented by a linear combination of functions of the type .
By using the previous definitions, one gets the following expression for the matrix element that couples two interacting channels:
where
and is the operator that interchanges the variables.
If, now, we assume that the bound-state problem has been solved, i.e., the eigenvectors of ( for the Auger process) have been found inside the space of the Slater determinants built up using the orbitals, we can look at the matrix elements that are defined in Equation (24) as the representation of an effective one-particle Hamiltonian over a set of basis vectors . Indeed, this Hamiltonian is that of a particle, with internal degrees of freedom, which moves in an effective potential, depending on the internal states of the particle itself. We notice that the basis vectors are labelled by two indices, one continuous and one discrete , and that they shall satisfy orthonormality constraints, both with respect to and to . Finally, the bound orbitals and continuum wavefunctions can be made mutually orthogonal.
3. Results and Discussion
3.1. The Ozone Molecular Geometry and Its Electronic Structure
The ozone ground state has a trigonal planar bent molecular geometry belonging to the symmetry group (similar to the water molecule), whereby the central oxygen atom is in a -hybridized configuration. In order to optimize the ozone atomic coordinates, we started from experimental oxygen positions and accommodated the molecule in a cell with side of 10 Å. The ozone geometry was relaxed below Ry/Å for the interatomic forces via first-principles density functional theory (DFT) calculations, as implemented in the Quantum Espresso code suite [22], using a PBE-GGA functional [23]. We have used the Troullier–Martins (TM) norm-conserving pseudopotentials that were tabulated in the Quantum Espresso web page. Including the point only to sample the Brillouin zone and using a kinetic energy cut-off of 130 Ry, the self-consistent DFT convergence is reached within the energy error of . Upon optimization, the O–O bond length turns out to be 1.273 Å, while the O–O–O angle is 117.16, which compares well with the experimental data [24] (1.272 Å and 116.78, respectively). Figure 1 shows the ozone ground state geometry. The molecular bonds in ozone can be represented as a resonance between two contributing structures, each with a single bond on one side and double bond on the other, where the terminal O atoms are more electron rich than the central O atom. The three hybrid orbitals form a net of 2 O–O bonds and five lone pairs (two on each terminal O and one on the central O). The remaining four valence electrons are distributed among the three unhybridized orbitals on each oxygen atom, forming one lowest energy bond, one highest energy antibonding, and one intermediate energy nonbonding orbitals, respectively.
Figure 1.
Ozone geometry in the ground state.
3.2. The Auger Spectrum of Ozone
Electronic structure calculations have been initially carried out at mean-field HF level for the ground state, a set of highly-excited core-hole intermediate states and the double-ionized molecule. In this respect, several studies pointed out the bi-radical character of the electronic ground state [5,25]. We remind that the HF method is based on a set of non-linear equations, minimized to deliver the best variational wavefuntions and energy. Thus, they are sensitive to the kick-off orbitals. In this regard, below we will show the effect of localizing the inner hole on atomic or molecular symmetry orbitals.
The ground state of the ozone molecule is described by the following configuration .
The intermediate quasi-bound states that are populated by the primary ionization are the following:
- ;
- ;
- .
The final states of the doubly ionized target are characterized by two holes distributed in all possible ways among the 3,4,5,6, 2,3,4, 1, and 1 orbitals, which results in 81 different possible final channels. We will limit the discussion to the electronic spectrum, using only the electronic Hamiltonian and taking the effects of the nuclear motion into account in a simplified manner by adding a broadening of the Auger lines only at the end, in order to compare the theoretical and experimental spectra. A further line broadening will be included to take the finite resolution of the spectrometer used in electron spectroscopy measurements into account. Furthermore, the two-step and static exchange approximations are used and only the decay process from the intermediate quasi-bound state is analyzed. In the case of the Auger decay, we further assume that the primary electron is fast enough to avoid any appreciable interaction with the ionized ozone molecule.
The basis functions that were used in the expansion of bound and continuum orbitals is taken from the aug–cc–pVQZ basis set with HGF contracted to centered on each oxygen nucleus. In order to increase the accuracy and rely on a larger number of diffuse functions to represent the continuum orbital, in our simulations we completely decontracted the aug–cc–pVQZ HGF basis set to HGF without the g-symmetry Gaussian to limit the computational cost. Indeed, this decontraction procedure will significantly add to the computational cost of the calculation of the Auger spectra. The HGF basis set has been decontracted in order to have eigenvectors of an average HF operator at energies near to those of the Auger electron in the various decay channels. Using this HGF basis set, we calculated the total and orbital energies of the neutral ground state of ozone by numerical solution of the HF equations with and without the inclusion of relativistic effects [26], where, in the latter simulation, the electronic repulsion also takes the Gaunt term into account [27]. These results are reported in Table 1 in a.u. Analyzing these values we conclude that relativistic effects are negligible and a non-relativistic approximation can be adopted to simulate the Auger lineshape of ozone.

Table 1.
Relativistic (rel.) vs. non relativistic (non rel.) Hartree–Fock (HF) total () and orbital energies (), calculated for the ozone ground state. The values are reported in a.u.
The final decay states are represented by the wave functions of Equation (17), where is the wave function for the state , representing the final single and double ionized target for autoionization and Auger processes, respectively, while is the spin-orbital describing the Auger electron. We remind that the use of instead of the well behaving wave function that diagonalizes the Hamiltonian (3) is equivalent to disregard the coupling among the decay channels. This approximation is, in general, too drastic [13,14] and will be abandoned in our calculations. The following linear combinations of Slater determinants represent the intermediate and final bound states of the single and double ionized molecule:
The coefficients and are variationally determined by solving the secular problem with respect to the standard electronic Hamiltonian. The bound orbitals and are obtained by solving separate HF equations for the various states of interest and, therefore, the resulting orbitals for a given state are not orthogonal to those of a different state of charge.
The matrix elements (8) that couple the intermediate and final states are calculated between Slater determinants built up in terms of orbitals that belong to mutually non-orthogonal sets, as follows:
where is the following overlap matrix
and is the determinant of the minor that is obtained by taking away row l and column m and that of the minor obtained by taking away rows and columns . In order to calculate these matrix elements, which give the relative decay rates onto the various channels, one has to evaluate integrals between -functions, used to represent both the bound and continuum orbitals. Analytical expressions of these integrals using HGF of any order and centre as basis functions for the bound orbitals can be derived [14], which decrease the computational cost.
We stress that, besides a truncated multi-configuration expansion, the only approximation in our bound state calculations is represented by the decoupling of the electronic and nuclear motion, without including the effects of the latter from the first-principles. Therefore, both the intermediate and the final states are purely electronic states obtained at the equilibrium geometry of the molecule.
In Table 2, we report the HF energy , which was calculated by assuming a single determinant wavefunction with a core-hole in the Auger states , , and , respectively. Moreover, in Table 2, we also report the energies calculated using CIS from the reference configuration for an active space of 27 and 63 orbitals, labelled and , respectively. and were both calculated preserving the molecular symmetry, whereby the hole is not localized on a particular oxygen atom, rather “delocalized” on a molecular symmetry orbital. Furthermore, in Table 2, we also report the ionization energies (IE) that are necessary to extract inner electrons. We notice that IEs from and orbitals are almost identical, with these molecular orbitals being almost localized on the two C symmetry-related oxygen atoms. While HF orbital optimization was achieved, starting from a hole initially delocalized on the inner shells, a partial relocalization of the holes is reached by adding dynamic correlation via CIS. In our simulations of the Auger spectral profiles by CIS, we mean to include single excitations from all of the possible states that can be formed with the presence of one or two holes in a given subspace of orbitals and, thus, not only single excitations with respect to the excited state of reference. For example, our CIS procedure concerning the intermediate state includes all single excitations, starting from all the HF determinants of the single ionized state that are characterized by one hole in all possible configurations within the system. Basically, in our CI expansion, we do include all of the single excitations from multi-reference states, where the hole is positioned in all system’s occupied orbitals. Within this approach, we actually include more terms in the CI expansion than meant in the standard CIS procedure of quantum chemistry. Moreover, in the final state, we perform single electron excitations, starting from all the configurations with two holes in all possible orbital positions, thus including in the CI expansion determinants e.g., with three holes and one electron excited in the virtual orbital within the active space. Therefore, in the final decay states, by our CIS procedure, we include more determinants than only considering single excitations from the reference state. The inclusion of double excitations beyond this modified CIS typically does not increase the accuracy of the Auger spectra simulations, while significantly increasing the computational cost.

Table 2.
Auger state energies in a.u. for different core-hole configurations. is the single-configuration HF energy; is calculated by using single-excitation Configuration Interaction (CIS) with an active space up to the 27th excited state with respect to the relevant configuration. In active space was increased to include up to 63 molecular orbitals. Ionization energies (in eV) at the same level of theory are also reported in parenthesis for each Auger state.
However, the most difficult part is the treatment of the continuum wavefunction. Experience tells us that a major source of error is due to the poor representation of the continuum orbital, which is typically expanded using plane-waves. Our approach overcome this problem by the use of the model Hamiltonian with projected potential defined in Equation (19). The construction of its scattering stationary states inside the space spanned by the orthonormal wave functions , as defined in Equation (17), is obtained by the numerical solution of the LS Equation (22). The analytic expressions of the elements of the matrix representative of the transition operator (23) while using HGF can be obtained from the knowledge of those relative to and . In order to improve the theoretical reproduction of the experimental Auger spectra, we finally diagonalize the interchannel Hamiltonian (24), which includes the coupling among the various decay channels, each one being described by a wave function that takes into account, at CIS level of theory, the intrachannel correlation effects. The diagonalization of the interchannel coupling between interacting channels redistributes the decay probability among independent channels.
In Figure 2, Figure 3 and Figure 4, we plot the Auger spectra of ozone that was calculated with the decoupled channel approach, in which the intermediate states are characterized by single inner-shell vacancies in the molecular orbitals and the final states by two vacancies in all possible valence orbitals. In particular, the green line represents 80 principal decay channels using HF level of theory, while the black, red, and blue lines represent simulations with 20, 70, and 140 final states, respectively, using CIS level of theory. In these calculations, the active space consists of 27 molecular orbitals, which means that, at the CIS level, the hole can be created in any of the occupied orbitals, and while the electrons can populate up to the 27-th virtual molecular orbital. In Table 3, we report the total Auger decay rates from the core-hole intermediate states as a function of the number of final states included in the calculations. The calculated transition energies, partial and total decay rates of the Auger processes are reported in Table A1 (), Table A2 (), and Table A3 () of the Appendix A, respectively, along with the final state orbital occupations for the 20 brightest final states. We notice that the Auger transition spectra in Figure 3 and Figure 4 are almost identical, and the total Auger probability does not differ significantly, being 2.9127 a.u. and 2.9485 a.u. (see Table 3, third column), respectively. This result is obtained, despite the symmetry of the intermediate state is different, as the initial hole created upon photoionization belongs to different irriducible representation of the symmetry group. This is interpreted as the effect of the inclusion of the single excitations from the reference states in the description of the orbital wavefunctions, which results in the quasi-relocalization of the core-hole into one of the two symmetry-equivalent oxygen atoms, despite the HF orbitals being optimized starting from a hole “delocalized” in each of the molecular orbitals. By analyzing Table 2, we conclude that the gain in energy to relocalize the core-hole in one of the oxygen atoms due to the interaction among all the configurations (≈900) appearing in the CIS expansion, is about 17 eV (see the difference in a.u. between the energy of the states in column , which is the Hartree–Fock value, and the value in column , which is the energy value after CIS with 63 orbitals in the active space).
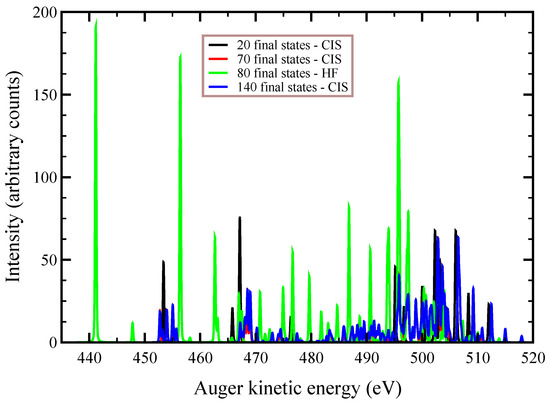
Figure 2.
Auger spectrum of ozone, where . Green line: HF level of theory with 80 independent final states, obtained by diagonalization of the multichannel Hamiltonian (24). The black, red, and blue lines represent the spectral lineshape obtained with an active space of 27 molecular orbitals and a number of 20, 70, 140 independent final channels, respectively.
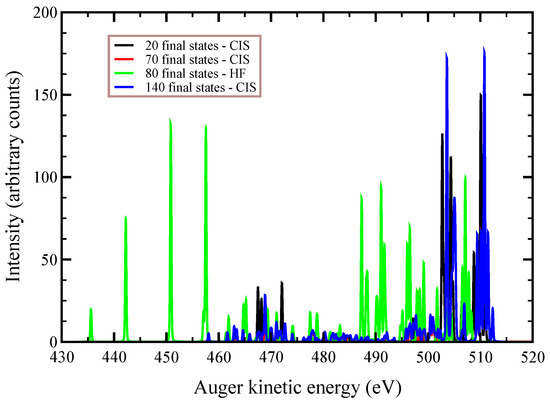
Figure 3.
Auger spectrum of ozone, where . Green line: HF level of theory with 80 independent final states, obtained by diagonalization of the multichannel Hamiltonian (24). Black, red, and blue lines represent the spectral lineshape obtained with an active space of 27 molecular orbitals and a number of 20, 70, and 140 independent final channels, respectively.
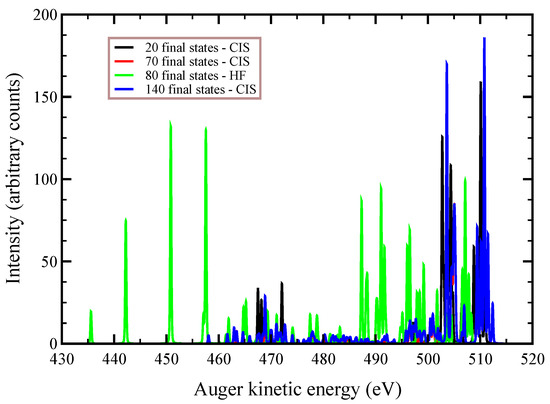
Figure 4.
Auger spectrum of ozone, where . Green line: HF level of theory with 80 independent final states, obtained by diagonalization of the multichannel Hamiltonian (24). Black, red, and blue lines represent the spectral lineshape obtained with an active space of 27 molecular orbitals and a number of 20, 70, and 140 independent final channels, respectively.

Table 3.
Total Auger decay rates of the three different intermediate states using CIS with an active space that includes up to 27 molecular orbitals for 20, 70, and 140 final channels. The data are reported in a.u.
At variance, the total Auger probability for an initial hole in the deepest molecular orbital is lower independent of the number of final channels used (see Table 3). We notice that the use of CIS to treat the orbital wavefunctions has large impact on the accuracy of the Auger decay rate and peak position, showing a large blueshift with respect to the HF values in excess of 10 (see Figure 2) to 20 eV (see Figure 3 and Figure 4).
The Auger lines, peaked at the transition energies calculated as by Equation (10), were broadened by Lorentzian functions, whose widths were obtained from Equation (10). Finally, we convolved the theoretical lineshape with a Gaussian having full width at half maximum (FWHM) of eV in order to take the finite resolution of the experimental set-up and the vibrational broadening into account.
We observe that, by increasing the number of non interacting final channels, from 20 (black lines) to 70 (red lines) and 140 (blue lines), the partial probability of Auger decay of course redistributes among different channels, and also the total probability changes significatively, moving, e.g., from 1.4321 a.u. to 2.6241 a.u. for the Auger state (see Table 3).
Finally, in Figure 5, we compare our ab-initio calculations with the experimental data of Ref. [10] that were recorded at a photon energy of 536.7 eV, finding an overall good agreement. We stress that the experimental data refer to a spectator transition , which is a process similar (not exactly the same) to that one we considered here. Auger lineshapes were broadened by a convolution with a 0.8 eV Gaussian function. These large observed linewidths have been attributed to both the dissociative character of the final states and nuclear vibrations.
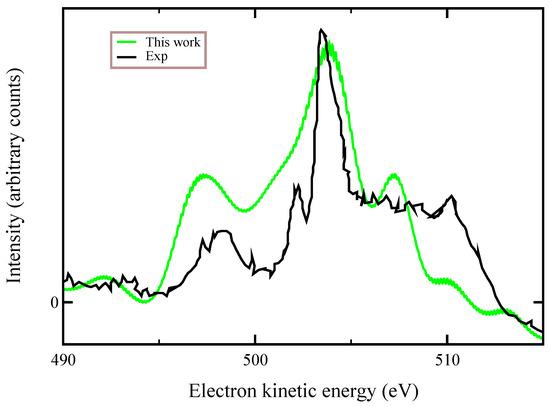
Figure 5.
A comparison between the () Auger experimental spectrum of ozone (black line) [10] and our first-principles simulation (green line) obtained with an active space of 27 molecular orbitals and 140 independent final channels. Our lineshapes were convolved via 0.8 eV Gaussian function to achieve the experimental broadening.
3.3. The Autoionization Spectrum of Ozone
In this section, we deal with the resonant autoionization spectrum of ozone following the photo-electronic excitation . These results have been obtained at the ground state geometry, disregarding the nuclear motion.
The transition energy of this process is 538.39 eV for the two atoms related by symmetry operations and 543.73 eV if the excitation involves the central oxygen atom . Indeed, while molecular orbitals were obtained by carrying out CI on HF optimized symmetry orbitals, which are thus delocalized all over ozone, the core-hole almost relocalizes in and upon CI.
In Figure 6, we plot the behavior of both the resonant and direct contributions to the spectrum as a function of the autoionized electron kinetic energy. The plotted lineshapes have been obtained after convolution with Lorentzian functions, whose width is provided by our ab-initio calculations (see Equation (10)), and by a further convolution with 1 eV FWHM Gaussian profile to take into account the nuclear broadening and the dissociative nature of the excited states of ozone. In particular, the red and blue lines represent CIS calculations of the resonant autoionization spectra of ozone, in which a core-hole is created upon excitation from the molecular symmetry orbital that is almost localized in one of the two oxygen atoms () related by symmetry operations. In green we plot the spectral lineshape for a core-hole created in the symmetry orbital almost localized in the central oxygen atom (), whose atomic orbital of character (corresponding to the molecular symmetry orbital) is lower in energy than the other two oxygen orbitals (). In these simulations, 140 final states have been included.
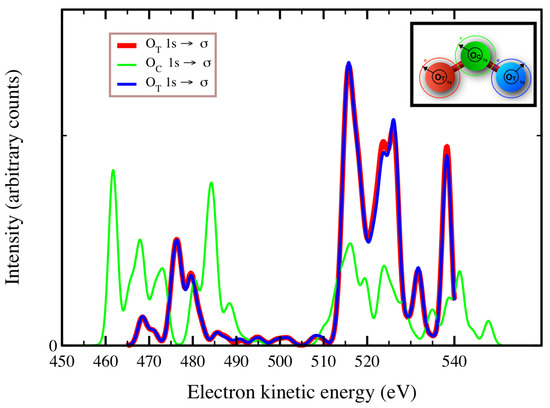
Figure 6.
autoionization spectrum of ozone. Red, blue lines: CIS lineshapes with 140 final states obtained upon diagonalization of the multichannel Hamiltonian (24). The core-hole belongs to molecular symmetry orbitals, which are optimized using HF and extend all over the ozone molecule. However, upon CI the hole relocalizes in one of the two oxygen atoms () related by symmetry operations (see inset). Green line: the spectral lineshape for a core-hole relocalized after the CIS procedure in the central oxygen atom .
3.4. Core-Hole Orbital Symmetry and Localization
In Auger experiments, core-electrons are extracted from a localized inner orbital of one particular oxygen. In our previous calculations, core-hole localization was obtained by including single excitations starting from HF molecular symmetry orbitals. This means that, at HF level, molecular orbitals were optimized by assuming that the core-hole is “delocalized” over the ozone molecule. Core-hole localization was basically achieved by adding part of the dynamical correlation neglected by HF via CIS procedure.
However, it is interesting (and actually more representative of what actually happens in experiments) to show the Auger spectrum that was obtained by optimizing the molecular orbitals starting from an atomic core-hole completely localized in one of the two s, equivalent by symmetry operation (thus using atomic orbitals to kick-off the self-consistent HF optimization, breaking the orbital symmetry). Indeed the holes, which are created upon primary ionization in localized atomic sites, favor intra-atomic more than inter-atomic transitions. This difference in the HF kick-off orbitals reflects into the final spectrum plotted in Figure 7 (black line), obtained at the same level of theory as in previous calculations (red line) with initial core holes delocalized in the molecular symmetry orbitals. In particular, the spectral intensity of the highest energy peaks is quite modified by core-hole localization.
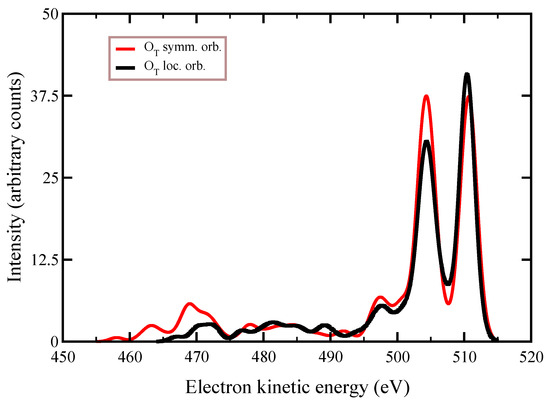
Figure 7.
Auger spectrum of ozone obtained from CIS calculations after convolution with both Lorentzian functions having the theoretical widths and with 1 eV full width at half maximum (FWHM) Gaussian functions to reproduce the combined effect of the finite resolution of the spectrometer and of the nuclear vibrations. Black line: HF orbitals optimized starting from an atomic core-hole localized in one of the two oxygen centers. Red line: HF orbitals are optimized with the initial core-hole “delocalized” in the molecular symmetry orbitals. Calculations were carried out with an active space of 27 molecular orbitals and 140 independent final channels, including the interchannel coupling (24).
4. Conclusions
In this work, a first-principles method for the calculation and interpretation of core-electron spectra of ozone has been described. This method is based on Fano’s theory of decay, due to the interaction between discrete and continuum states. We discussed this theoretical framework in the general case of several continua interacting with several quasi-bound states, explicitly including the boundary conditions that are appropriate to the study of Auger emission.
Our approach uses a model Hamiltonian with a projected potential represented in terms of -functions in order to achieve a relevant reduction in the computational effort required by the application of the theory. The spectral properties of this projected Hamiltonian are such that the subspace of the scattering eigenstates significant for the physical problem is finite and isomorphous to the subspace of the functions that were used for representing the potential energy operator. Furthermore, the many-body problem can be reduced to an effective single-particle problem, in which the scattering states can be obtained from the solution of a projected Lippmann–Schwinger equation with the proper boundary condition.
The wave functions of the bound and continuum orbitals have been expanded onto a Gaussian basis set, which includes decontracted diffuse functions, therefore reducing the Schrödinger equation to a matrix equation. The calculation of mono and bielectronic integrals (and of the transition matrix elements between discrete and continuum states with non-orthonormal orbitals) is carried out numerically on the basis of analytical expressions. Furthermore, we introduced the effects of interactions among final decay states along with the many-body interaction within the remaining ionic system in order to accurately assess the partial decay rates into different channels.
Finally, the analytic expression of the autoionization and Auger cross sections has been applied to predict the ozone radiationless decay lineshape as functions of the kinetic energy of the emitted electron. These Auger lineshapes have been broadened with a Lorentzian profile, whose width is a direct result of our ab-initio calculations. We also included “a posteriori” the specific features of the incident radiation, of the electron spectrometer, and of the effects of nuclear motion in the framework of the Born-Oppenheimer approximation by convolution with a Gaussian profile, finding a good agreement with available experimental data.
The effect of electronic correlation and the influence of core-hole localization on the Auger peak energy positions and intensities have been also analyzed, finding different spectral properties when the HF molecular orbitals are optimized, starting from a core-hole localized in a specific oxygen atom that favors intra-atomic transitions. While localization breaks the symmetry of the molecular orbitals, which is afterwards recovered by multi-configuration expansion of the wavefunctions, intensity and energy peak both differ from those obtained by delocalizing the inner-hole on the two symmetry-equivalent oxygen centers.
Our method is applicable to molecular systems, owing to the polycentric nature of the basis functions and to the fact that all of the integrals that are involved in the calculation of the Auger matrix elements are analytical, cost-effective, and easily programmable. Moreover, it is possible to take into account the effects of interaction among the final channels without resorting to numerical integration on the energy, as foreseen by Fano’s formulae. Finally, the possibility of obtaining continuum wave functions also makes the method useful for studying other scattering problems, such as photoionization, internal conversion, electron–atom and electron–molecule scattering, and so on.
Author Contributions
Conceptualization, S.T. and S.S.; methodology, S.S. and S.T.; software, S.S.; calculations and validation, S.S. and S.T.; investigation, S.T. and S.S.; resources, S.T. and S.S.; data curation, S.T. and S.S.; writing—original draft preparation, S.T.; writing—review and editing, S.T.; funding acquisition, S.S. and S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the INFN experiment PANDORA.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
S.T. and S.S. acknowledge the National Institute of Nuclear Physics for unlimited access to their computing facilities.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DFT | Density Functional Theory |
| HF | Hartree–Fock |
| CI | Configuration Interaction |
| CIS | Configuration Interaction Single |
| HGF | Hermite Gaussian Function |
| FWHM | Full width at half maximum |
| HGF | Hermite Gaussian Function |
| PBE-GGA | Perdew–Burke–Ernzerhof generalized gradient approximation |
Appendix A. The Auger Spectrum of Ozone

Table A1.
Auger spectrum of ozone with a primary hole localized in the molecular orbital. First column: double occupancy of the final transition states. Second: Auger transition energy (, eV). Third column: partial Auger probabilities (, units: a.u. ) according to Equation (10). The theory used is CIS with an active space of 27 orbitals.
Table A1.
Auger spectrum of ozone with a primary hole localized in the molecular orbital. First column: double occupancy of the final transition states. Second: Auger transition energy (, eV). Third column: partial Auger probabilities (, units: a.u. ) according to Equation (10). The theory used is CIS with an active space of 27 orbitals.
| Trans. State Occ. | Trans. En. | Trans. Prob. |
|---|---|---|
| 2.00 | 2.00 | 1.97 | 1.59 | 1.42 | 1.64 | 0.09 | 1.71 | 495.17 | 0.1100 |
| 0.39 | 2.00 | 1.94 | 1.65 | 1.60 | 0.13 | 1.86 | ||
| 2.00 | 2.00 | 1.58 | 1.63 | 1.77 | 1.86 | 0.37 | 1.69 | 467.14 | 0.1818 |
| 0.15 | 2.00 | 1.58 | 1.67 | 1.84 | 0.25 | 1.61 | ||
| 2.00 | 2.00 | 2.00 | 1.95 | 1.63 | 1.53 | 0.19 | 1.38 | 502.3 | 0.0879 |
| 0.34 | 2.00 | 1.99 | 1.89 | 1.59 | 0.17 | 1.34 | ||
| 2.00 | 2.00 | 2.00 | 1.96 | 1.70 | 1.62 | 0.14 | 1.39 | 506.25 | 0.0767 |
| 0.54 | 2.00 | 1.99 | 1.90 | 1.68 | 0.05 | 1.01 | ||
| 2.00 | 2.00 | 1.99 | 1.94 | 1.80 | 1.53 | 0.34 | 1.21 | 500.02 | 0.0804 |
| 0.21 | 2.00 | 1.99 | 1.89 | 1.46 | 0.24 | 1.40 | ||
| 2.00 | 2.00 | 2.00 | 1.96 | 1.94 | 1.78 | 0.06 | 1.50 | 506.065 | 0.0697 |
| 0.55 | 2.00 | 1.98 | 1.31 | 1.91 | 0.03 | 0.98 | ||
| 2.00 | 2.00 | 1.99 | 1.93 | 1.74 | 1.54 | 0.14 | 1.44 | 506.03 | 0.0761 |
| 0.53 | 2.00 | 1.99 | 1.88 | 1.65 | 0.06 | 1.12 | ||
| 2.00 | 2.00 | 2.00 | 1.88 | 1.67 | 1.49 | 0.21 | 1.90 | 503.195 | 0.0596 |
| 0.18 | 2.00 | 1.98 | 1.33 | 1.70 | 0.12 | 1.55 | ||
| 2.00 | 2.00 | 1.69 | 1.67 | 1.45 | 1.83 | 0.19 | 1.79 | 476.33 | 0.0352 |
| 0.44 | 2.00 | 1.61 | 1.77 | 1.73 | 0.15 | 1.67 | ||
| 2.00 | 2.00 | 1.99 | 1.90 | 1.47 | 1.35 | 0.17 | 1.81 | 502.25 | 0.0693 |
| 0.26 | 2.00 | 1.97 | 1.73 | 1.50 | 0.27 | 1.58 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.36 | 1.22 | 0.03 | 1.95 | 508.36 | 0.0705 |
| 0.30 | 2.00 | 1.99 | 1.82 | 1.59 | 0.03 | 1.74 | ||
| 2.00 | 2.00 | 2.00 | 1.96 | 1.46 | 1.52 | 0.10 | 1.97 | 504.16 | 0.0518 |
| 0.54 | 2.00 | 1.99 | 1.67 | 1.21 | 0.11 | 1.47 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.94 | 1.13 | 0.02 | 1.54 | 512.03 | 0.0553 |
| 0.59 | 2.00 | 2.00 | 1.98 | 1.93 | 0.01 | 0.89 | ||
| 2.00 | 2.00 | 1.34 | 1.59 | 1.78 | 1.86 | 0.30 | 1.87 | 453.39 | 0.1166 |
| 0.29 | 2.00 | 1.41 | 1.76 | 1.72 | 0.27 | 1.81 | ||
| 2.00 | 2.00 | 1.99 | 1.73 | 1.67 | 1.59 | 0.09 | 1.77 | 503.62 | 0.0466 |
| 0.44 | 2.00 | 1.97 | 1.68 | 1.25 | 0.05 | 1.77 | ||
| 2.00 | 2.00 | 1.99 | 1.87 | 1.80 | 1.67 | 0.28 | 1.42 | 496.73 | 0.0512 |
| 0.28 | 2.00 | 1.99 | 1.63 | 1.50 | 0.26 | 1.31 | ||
| 2.00 | 2.00 | 2.00 | 1.95 | 1.95 | 1.49 | 0.49 | 1.83 | 502.45 | 0.0416 |
| 0.16 | 2.00 | 1.99 | 1.35 | 1.84 | 0.06 | 0.90 | ||
| 2.00 | 2.00 | 1.99 | 1.82 | 1.81 | 1.67 | 0.21 | 1.61 | 500.80 | 0.0432 |
| 0.23 | 2.00 | 1.99 | 1.60 | 1.59 | 0.27 | 1.21 | ||
| Total Transition Probability () | A.U. |

Table A2.
Auger spectrum of ozone with a primary hole localized in the molecular orbital. First column: double occupancy of the final transition states. Second: Auger transition energy (, eV). Third column: partial Auger probabilities (, units: a.u. ) according to Equation (10). The theory used is CIS with an active space of 27 orbitals.
Table A2.
Auger spectrum of ozone with a primary hole localized in the molecular orbital. First column: double occupancy of the final transition states. Second: Auger transition energy (, eV). Third column: partial Auger probabilities (, units: a.u. ) according to Equation (10). The theory used is CIS with an active space of 27 orbitals.
| Trans. State Occ. | Trans. En. | Trans. Prob. |
|---|---|---|
| 2.00 | 2.00 | 2.00 | 1.99 | 1.98 | 1.92 | 0.04 | 1.93 | 510.751 | 0.2255 |
| 0.03 | 2.00 | 1.99 | 1.98 | 1.87 | 0.03 | 0.24 | ||
| 2.00 | 2.00 | 2.00 | 2.00 | 1.97 | 1.90 | 0.03 | 1.86 | 510.17 | 0.1713 |
| 0.08 | 2.00 | 1.99 | 1.98 | 1.10 | 0.02 | 1.07 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.46 | 1.58 | 0.05 | 1.89 | 502.71 | 0.1755 |
| 0.38 | 2.00 | 1.98 | 1.80 | 1.19 | 0.03 | 1.67 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.36 | 1.22 | 0.03 | 1.95 | 502.79 | 0.1453 |
| 0.30 | 2.00 | 1.99 | 1.82 | 1.59 | 0.03 | 1.74 | ||
| 2.00 | 2.00 | 2.00 | 1.97 | 1.49 | 1.94 | 0.03 | 1.78 | 504.44 | 0.1286 |
| 0.33 | 2.00 | 1.99 | 1.98 | 1.56 | 0.02 | 0.90 | ||
| 2.00 | 2.00 | 2.00 | 1.99 | 1.97 | 1.09 | 0.02 | 1.90 | 510.93 | 0.1439 |
| 0.07 | 2.00 | 2.00 | 1.98 | 1.94 | 0.02 | 1.03 | ||
| 2.00 | 2.00 | 2.00 | 1.97 | 1.84 | 1.29 | 0.02 | 1.95 | 508.79 | 0.1289 |
| 0.18 | 2.00 | 1.99 | 1.96 | 1.09 | 0.02 | 1.69 | ||
| 2.00 | 2.00 | 2.00 | 1.97 | 1.84 | 1.03 | 0.02 | 1.98 | 509.47 | 0.1359 |
| 0.19 | 2.00 | 2.00 | 1.97 | 1.16 | 0.01 | 1.82 | ||
| 2.00 | 2.00 | 2.00 | 1.99 | 1.98 | 1.81 | 0.04 | 1.10 | 504.35 | 0.1162 |
| 0.17 | 2.00 | 1.99 | 1.88 | 1.93 | 0.04 | 1.09 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.91 | 1.67 | 0.07 | 1.62 | 503.07 | 0.0798 |
| 0.33 | 2.00 | 1.99 | 1.52 | 1.82 | 0.03 | 1.07 | ||
| 2.00 | 2.00 | 2.00 | 1.92 | 1.87 | 1.69 | 0.02 | 1.92 | 503.99 | 0.0706 |
| 0.25 | 2.00 | 1.98 | 1.32 | 1.20 | 0.01 | 1.83 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.94 | 1.67 | 0.02 | 1.68 | 504.29 | 0.0608 |
| 0.29 | 2.00 | 1.98 | 1.52 | 1.86 | 0.01 | 1.06 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.94 | 1.13 | 0.02 | 1.54 | 506.46 | 0.0554 |
| 0.59 | 2.00 | 2.00 | 1.98 | 1.93 | 0.01 | 0.89 | ||
| 2.00 | 2.00 | 2.00 | 1.94 | 1.79 | 1.10 | 0.01 | 1.81 | 504.77 | 0.0777 |
| 0.47 | 2.00 | 1.99 | 1.59 | 1.65 | 0.01 | 1.64 | ||
| 2.00 | 2.00 | 1.91 | 1.62 | 1.55 | 1.65 | 0.29 | 1.83 | 472.09 | 0.0856 |
| 0.32 | 2.00 | 1.65 | 1.50 | 1.65 | 0.22 | 1.80 | ||
| 2.00 | 2.00 | 1.99 | 1.84 | 1.77 | 1.16 | 0.42 | 1.95 | 497.19 | 0.0339 |
| 0.28 | 2.00 | 1.96 | 1.59 | 1.23 | 0.04 | 1.76 | ||
| 2.00 | 2.00 | 1.73 | 1.70 | 1.70 | 1.57 | 0.34 | 1.91 | 467.51 | 0.0790 |
| 0.15 | 2.00 | 1.62 | 1.44 | 1.62 | 0.30 | 1.90 | ||
| 2.00 | 2.00 | 1.99 | 1.60 1.88 | 1.54 | 0.25 | 1.67 | 499.45 | 0.0032 |
| 0.18 | 2.00 | 1.99 | 1.83 | 1.87 | 0.05 | 1.15 | ||
| 2.00 | 2.00 | 1.68 | 1.70 | 1.68 | 1.68 | 0.19 | 1.68 | 468.17 | 0.0622 |
| 0.51 | 2.00 | 1.70 | 1.70 | 1.53 | 0.18 | 1.78 | ||
| 2.00 | 2.00 | 1.99 | 1.88 | 1.86 | 1.81 | 0.22 | 1.54 | 491.23 | 0.0032 |
| 0.37 | 2.00 | 1.73 | 1.62 | 1.74 | 0.14 | 1.09 | ||
| Total Transition Probability () | A.U. |

Table A3.
Auger spectrum of ozone with a primary hole localized in the molecular orbital. First column: double occupancy of the final transition states. Second: Auger transition energy (, eV). Third column: partial Auger probabilities (, units: a.u. ) according to Equation (10). Last row: total decay rate. The theory used is CIS with an active space of 27 orbitals.
Table A3.
Auger spectrum of ozone with a primary hole localized in the molecular orbital. First column: double occupancy of the final transition states. Second: Auger transition energy (, eV). Third column: partial Auger probabilities (, units: a.u. ) according to Equation (10). Last row: total decay rate. The theory used is CIS with an active space of 27 orbitals.
| Trans. State Occ. | Trans. En. | Trans. Prob. |
|---|---|---|
| 2.00 | 2.00 | 2.00 | 1.99 | 1.98 | 1.92 | 0.04 | 1.93 | 510.07 | 0.2515 |
| 0.03 | 2.00 | 1.99 | 1.98 | 1.87 | 0.03 | 0.24 | ||
| 2.00 | 2.00 | 2.00 | 2.00 | 1.97 | 1.90 | 0.03 | 1.86 | 510.17 | 0.1693 |
| | 0.08 | 2.00 | 1.99 | 1.98 | 1.10 | 0.02 | 1.07 | ||
| 2.00 | 2.00 2.00 | 1.98 | 1.46 | 1.58 | 0.05 | 1.89 | 502.71 | 0.1708 |
| 0.38 | 2.00 | 1.98 | 1.80 | 1.19 | 0.03 | 1.67 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.36 | 1.22 | 0.03 | 1.95 | 502.79 | 0.1478 |
| 0.30 | 2.00 | 1.99 | 1.82 | 1.59 | 0.03 | 1.74 | ||
| 2.00 | 2.00 | 2.00 | 1.97 | 1.49 | 1.94 | 0.03 | 1.78 | 504.44 | 0.1290 |
| 0.33 | 2.00 | 1.99 | 1.98 | 1.56 | 0.02 | 0.90 | ||
| 2.00 | 2.00 | 2.00 | 1.97 | 1.84 | 1.29 | 0.02 | 1.95 | 508.79 | 0.1401 |
| 0.18 | 2.00 | 1.99 | 1.96 | 1.09 | 0.02 | 1.69 | ||
| 2.00 | 2.00 2.00 | 1.99 | 1.97 | 1.09 | 0.02 | 1.90 | 510.92 | 0.1443 |
| 0.07 | 2.00 | 2.00 | 1.98 | 1.94 | 0.02 | 1.03 | ||
| 2.00 | 2.00 2.00 | 1.97 | 1.84 | 1.03 | 0.02 | 1.98 | 509.46 | 0.1225 |
| 0.19 | 2.00 | 2.00 | 1.97 | 1.16 | 0.01 | 1.82 | ||
| 2.00 | 2.00 | 2.00 | 1.99 | 1.98 | 1.81 | 0.04 | 1.10 | 504.35 | 0.1091 |
| 0.17 | 2.00 | 1.99 | 1.88 | 1.93 | 0.04 | 1.09 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.91 | 1.67 | 0.07 | 1.62 | 503.06 | 0.0797 |
| 0.33 | 2.00 | 1.99 | 1.52 | 1.82 | 0.03 | 1.07 | ||
| 2.00 | 2.00 | 2.00 | 1.92 | 1.87 | 1.69 | 0.02 | 1.92 | 503.99 | 0.0808 |
| 0.25 2.00 | 1.98 | 1.32 | 1.20 | 0.01 | 1.83 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.94 | 1.13 | 0.02 | 1.54 | 506.45 | 0.0552 |
| 0.59 | 2.00 | 2.00 | 1.98 | 1.93 | 0.01 | 0.89 | ||
| 2.00 | 2.00 | 2.00 | 1.98 | 1.94 | 1.67 | 0.02 | 1.68 | 504.28 | 0.0610 |
| 0.29 | 2.00 | 1.98 | 1.52 | 1.86 | 0.01 | 1.06 | ||
| 2.00 | 2.00 | 2.00 | 1.94 | 1.79 | 1.10 | 0.01 | 1.81 | 504.77 | 0.0663 |
| 0.47 | 2.00 | 1.99 | 1.59 | 1.65 | 0.01 | 1.64 | ||
| 2.00 | 2.00 | 1.91 | 1.62 | 1.55 | 1.65 | 0.29 | 1.83 | 472.09 | 0.0878 |
| 0.32 | 2.00 | 1.65 | 1.50 | 1.65 | 0.22 | 1.80 | ||
| 2.00 | 2.00 | 1.99 | 1.84 | 1.77 | 1.16 | 0.42 | 1.95 | 497.19 | 0.030 |
| 0.28 | 2.00 | 1.96 | 1.59 | 1.23 | 0.04 | 1.76 | ||
| 2.00 | 2.00 | 1.99 | 1.60 | 1.88 | 1.54 | 0.25 | 1.67 | 499.45 | 0.0033 |
| 0.18 | 2.00 | 1.99 | 1.83 | 1.87 | 0.05 | 1.15 | ||
| 2.00 | 2.00 | 1.73 | 1.70 | 1.70 | 1.57 | 0.34 | 1.91 | 467.51 | 0.0799 |
| 0.15 | 2.00 | 1.62 | 1.44 | 1.62 | 0.30 | 1.90 | ||
| 2.00 | 2.00 | 1.68 | 1.70 | 1.68 | 1.68 | 0.19 | 1.68 | 468.17 | 0.0637 |
| 0.51 | 2.00 | 1.70 | 1.70 | 1.53 | 0.18 | 1.78 | ||
| 2.00 | 2.00 | 1.99 | 1.88 | 1.86 | 1.81 | 0.22 | 1.54 | 491.23 | 0.0032 |
| 0.37 | 2.00 | 1.73 | 1.62 | 1.74 | 0.14 | 1.09 | ||
| Total Transition Probability () | A.U. |
References
- McElroy, C.; Fogal, P. Ozone: From discovery to protection. Atmos. Ocean 2008, 46, 1–13. [Google Scholar] [CrossRef]
- Shindell, D.T.; Faluvegi, G.; Bell, N.; Schmidt, G.A. An emissions-based view of climate forcing by methane and tropospheric ozone. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Fuglestvedt, J.S.; Berntsen, T.K.; Isaksen, I.S.; Mao, H.; Liang, X.Z.; Wang, W.C. Climatic forcing of nitrogen oxides through changes in tropospheric ozone and methane; global 3D model studies. Atmos. Environ. 1999, 33, 961–977. [Google Scholar] [CrossRef]
- Shao, J.-X.; Zhu, Z.-H.; Huang, D.-H.; Wang, J.; Cheng, X.-L.; Yang, X.-D. Potential energy surfaces of ozone in the ground state. Chin. Phys. 2007, 16, 2650–2655. [Google Scholar]
- Banichevich, A.; Peyerimhoff, S.D.; Grein, F. Potential energy surfaces of ozone in its ground state and in the lowest-lying eight excited states. Chem. Phys. 1993, 178, 155–188. [Google Scholar] [CrossRef]
- Tyuterev, V.G.; Kochanov, R.V.; Tashkun, S.A.; Holka, F.; Szalay, P.G. New analytical model for the ozone electronic ground state potential surface and accurate ab initio vibrational predictions at high energy range. J. Chem. Phys. 2013, 139, 134307. [Google Scholar] [CrossRef] [PubMed]
- Lopaev, D.V.; Malykhin, E.M.; Namiot, V.A. UV absorption of vibrationally excited ozone. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 085104. [Google Scholar] [CrossRef]
- Allan, M.; Mason, N.J.; Davies, J.A. Study of electronically excited states of ozone by electron-energy-loss spectroscopy. J. Chem. Phys. 1996, 105, 5665–5671. [Google Scholar] [CrossRef]
- Chien, A.D.; Holmes, A.A.; Otten, M.; Umrigar, C.J.; Sharma, S.; Zimmerman, P.M. Excited States of Methylene, Polyenes, and Ozone from Heat-Bath Configuration Interaction. J. Phys. Chem. A 2018, 122, 2714–2722. [Google Scholar] [CrossRef]
- Rosenqvist, L.; Wiesner, K.; Naves de Brito, A.; Bässler, M.; Feifel, R.; Hjelte, I.; Miron, C.; Wang, H.; Piancastelli, M.N.; Svensson, S.; et al. Femtosecond dissociation of ozone studied by the Auger Doppler effect. J. Chem. Phys. 2001, 115, 3614–3620. [Google Scholar] [CrossRef]
- Ndengué, S.; Dawes, R.; Wang, X.G.; Carrington, T.; Sun, Z.; Guo, H. Calculated vibrational states of ozone up to dissociation. J. Chem. Phys. 2016, 144, 074302. [Google Scholar] [CrossRef] [PubMed]
- McConnell, J.C.; Jin, J.J. Stratospheric ozone chemistry. Atmos. Ocean 2008, 46, 69–92. [Google Scholar] [CrossRef]
- Taioli, S.; Simonucci, S.; Dapor, M. SURPRISES: When ab initio meets statistics in extended systems. Comput. Sci. Discov. 2009, 2, 015002. [Google Scholar] [CrossRef]
- Taioli, S.; Simonucci, S.; Calliari, L.; Dapor, M. Electron spectroscopies and inelastic processes in nanoclusters and solids: Theory and experiment. Phys. Rep. 2010, 493, 237–319. [Google Scholar] [CrossRef]
- Verucchi, R.; Aversa, L.; Nardi, M.V.; Taioli, S.; a Beccara, S.; Alfè, D.; Nasi, L.; Rossi, F.; Salviati, G.; Iannotta, S. Epitaxy of nanocrystalline silicon carbide on Si (111) at room temperature. J. Am. Chem. Soc. 2012, 134, 17400–17403. [Google Scholar] [CrossRef] [PubMed]
- Tatti, R.; Aversa, L.; Verucchi, R.; Cavaliere, E.; Garberoglio, G.; Pugno, N.M.; Speranza, G.; Taioli, S. Synthesis of single layer graphene on Cu (111) by C 60 supersonic molecular beam epitaxy. RSC Adv. 2016, 6, 37982–37993. [Google Scholar] [CrossRef]
- Segatta, F.; Cupellini, L.; Jurinovich, S.; Mukamel, S.; Dapor, M.; Taioli, S.; Garavelli, M.; Mennucci, B. A quantum chemical interpretation of two-dimensional electronic spectroscopy of Light-Harvesting complexes. J. Am. Chem. Soc. 2017, 139, 7558. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Åberg, T.; Howat, G. Theory of the Auger Effect. Handbuch der Physik 1982, 6, 469–619. [Google Scholar]
- Newton, R.G. Scattering Theory of Waves and Particles; Springer: New York, NY, USA, 1982. [Google Scholar]
- Taylor, J.R. Scattering Theory; Dover Publications, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Morino, Y. Coriolis interaction and anharmonic potential function of ozone from the microwave spectra in the excited vibrational states. J. Mol. Spectrosc. 1970, 33, 538–551. [Google Scholar] [CrossRef]
- Kalemos, A.; Mavridis, A. Electronic structure and bonding of ozone. J. Chem. Phys. 2008, 129, 054312. [Google Scholar] [CrossRef] [PubMed]
- Morresi, T.; Taioli, S.; Simonucci, S. Nuclear Beta Decay: Relativistic Theory and Ab Initio Simulations of Electroweak Decay Spectra in Medium-Heavy Nuclei and of Atomic and Molecular Electronic Structure (Adv. Theory Simul. 11/2018). Adv. Theory Simul. 2018, 1, 1870030. [Google Scholar] [CrossRef]
- Reiher, M.; Wolf, A. Relativistic Quantum Chemistry: The Fundamental Theory of Molecular Science; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).