3.2. The Auger Spectrum of Ozone
Electronic structure calculations have been initially carried out at mean-field HF level for the ground state, a set of highly-excited core-hole intermediate states and the double-ionized molecule. In this respect, several studies pointed out the bi-radical character of the electronic ground state [
5,
25]. We remind that the HF method is based on a set of non-linear equations, minimized to deliver the best variational wavefuntions and energy. Thus, they are sensitive to the kick-off orbitals. In this regard, below we will show the effect of localizing the inner hole on atomic or molecular symmetry orbitals.
The ground state of the ozone molecule is described by the following configuration .
The intermediate quasi-bound states that are populated by the primary ionization are the following:
;
;
.
The final states of the doubly ionized target are characterized by two holes distributed in all possible ways among the 3,4,5,6, 2,3,4, 1, and 1 orbitals, which results in 81 different possible final channels. We will limit the discussion to the electronic spectrum, using only the electronic Hamiltonian and taking the effects of the nuclear motion into account in a simplified manner by adding a broadening of the Auger lines only at the end, in order to compare the theoretical and experimental spectra. A further line broadening will be included to take the finite resolution of the spectrometer used in electron spectroscopy measurements into account. Furthermore, the two-step and static exchange approximations are used and only the decay process from the intermediate quasi-bound state is analyzed. In the case of the Auger decay, we further assume that the primary electron is fast enough to avoid any appreciable interaction with the ionized ozone molecule.
The basis functions that were used in the expansion of bound and continuum orbitals is taken from the aug–cc–pVQZ basis set with
HGF contracted to
centered on each oxygen nucleus. In order to increase the accuracy and rely on a larger number of diffuse functions to represent the continuum orbital, in our simulations we completely decontracted the aug–cc–pVQZ HGF basis set to
HGF without the
g-symmetry Gaussian to limit the computational cost. Indeed, this decontraction procedure will significantly add to the computational cost of the calculation of the Auger spectra. The HGF basis set has been decontracted in order to have eigenvectors of an average HF operator at energies near to those of the Auger electron in the various decay channels. Using this HGF basis set, we calculated the total and orbital energies of the neutral ground state of ozone by numerical solution of the HF equations with and without the inclusion of relativistic effects [
26], where, in the latter simulation, the electronic repulsion also takes the Gaunt term into account [
27]. These results are reported in
Table 1 in a.u. Analyzing these values we conclude that relativistic effects are negligible and a non-relativistic approximation can be adopted to simulate the Auger lineshape of ozone.
The final decay states are represented by the wave functions of Equation (
17), where
is the wave function for the state
, representing the final single and double ionized target for autoionization and Auger processes, respectively, while
is the spin-orbital describing the Auger electron. We remind that the use of
instead of the well behaving wave function
that diagonalizes the Hamiltonian (
3) is equivalent to disregard the coupling among the decay channels. This approximation is, in general, too drastic [
13,
14] and will be abandoned in our calculations. The following linear combinations of Slater determinants represent the intermediate and final bound states of the single and double ionized molecule:
The coefficients
and
are variationally determined by solving the secular problem with respect to the standard electronic Hamiltonian. The bound orbitals
and
are obtained by solving separate HF equations for the various states of interest and, therefore, the resulting orbitals for a given state are not orthogonal to those of a different state of charge.
The matrix elements (
8) that couple the intermediate and final states are calculated between Slater determinants built up in terms of orbitals that belong to mutually non-orthogonal sets, as follows:
where
is the following overlap matrix
and
is the determinant of the minor that is obtained by taking away row
l and column
m and
that of the minor obtained by taking away rows
and columns
. In order to calculate these matrix elements, which give the relative decay rates onto the various channels, one has to evaluate integrals between
-functions, used to represent both the bound and continuum orbitals. Analytical expressions of these integrals using HGF of any order and centre as basis functions for the bound orbitals can be derived [
14], which decrease the computational cost.
We stress that, besides a truncated multi-configuration expansion, the only approximation in our bound state calculations is represented by the decoupling of the electronic and nuclear motion, without including the effects of the latter from the first-principles. Therefore, both the intermediate and the final states are purely electronic states obtained at the equilibrium geometry of the molecule.
In
Table 2, we report the HF energy
, which was calculated by assuming a single determinant wavefunction with a core-hole in the Auger states
,
, and
, respectively. Moreover, in
Table 2, we also report the energies calculated using CIS from the reference configuration for an active space of 27 and 63 orbitals, labelled
and
, respectively.
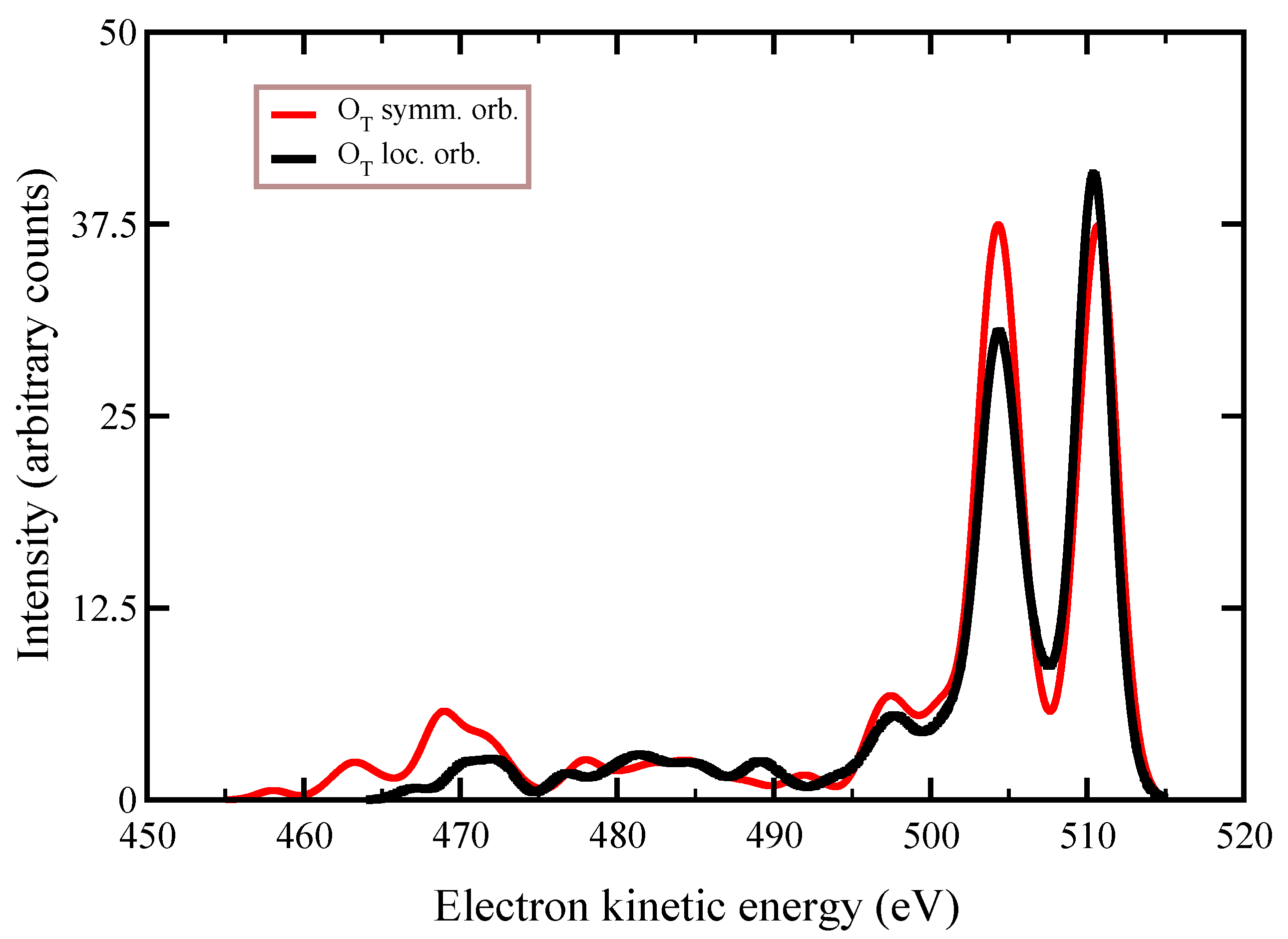
and
were both calculated preserving the molecular symmetry, whereby the hole is not localized on a particular oxygen atom, rather “delocalized” on a molecular symmetry orbital. Furthermore, in
Table 2, we also report the ionization energies (IE) that are necessary to extract inner electrons. We notice that IEs from
and
orbitals are almost identical, with these molecular orbitals being almost localized on the two C
symmetry-related oxygen atoms. While HF orbital optimization was achieved, starting from a hole initially delocalized on the
inner shells, a partial relocalization of the holes is reached by adding dynamic correlation via CIS. In our simulations of the Auger spectral profiles by CIS, we mean to include single excitations from all of the possible states that can be formed with the presence of one or two holes in a given subspace of orbitals and, thus, not only single excitations with respect to the excited state of reference. For example, our CIS procedure concerning the intermediate state includes all single excitations, starting from all the HF determinants of the single ionized state that are characterized by one hole in all possible configurations within the system. Basically, in our CI expansion, we do include all of the single excitations from multi-reference states, where the hole is positioned in all system’s occupied orbitals. Within this approach, we actually include more terms in the CI expansion than meant in the standard CIS procedure of quantum chemistry. Moreover, in the final state, we perform single electron excitations, starting from all the configurations with two holes in all possible orbital positions, thus including in the CI expansion determinants e.g., with three holes and one electron excited in the virtual orbital within the active space. Therefore, in the final decay states, by our CIS procedure, we include more determinants than only considering single excitations from the reference state. The inclusion of double excitations beyond this modified CIS typically does not increase the accuracy of the Auger spectra simulations, while significantly increasing the computational cost.
However, the most difficult part is the treatment of the continuum wavefunction. Experience tells us that a major source of error is due to the poor representation of the continuum orbital, which is typically expanded using plane-waves. Our approach overcome this problem by the use of the model Hamiltonian with projected potential defined in Equation (
19). The construction of its scattering stationary states inside the space spanned by the orthonormal wave functions
, as defined in Equation (
17), is obtained by the numerical solution of the LS Equation (
22). The analytic expressions of the elements of the matrix representative of the transition operator (
23) while using HGF can be obtained from the knowledge of those relative to
and
. In order to improve the theoretical reproduction of the experimental Auger spectra, we finally diagonalize the interchannel Hamiltonian (
24), which includes the coupling among the various decay channels, each one being described by a wave function that takes into account, at CIS level of theory, the intrachannel correlation effects. The diagonalization of the interchannel coupling between interacting channels redistributes the decay probability among independent channels.
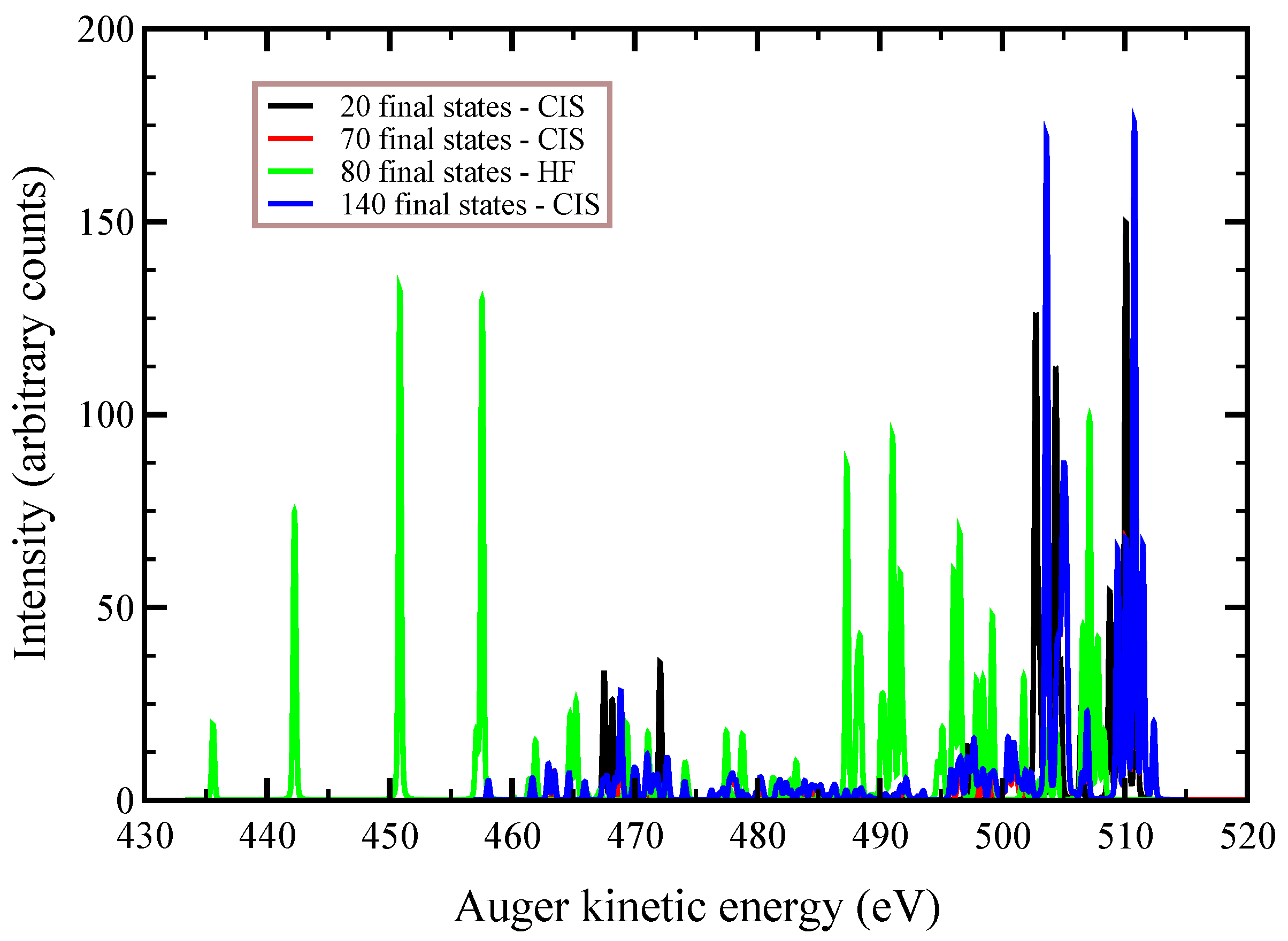
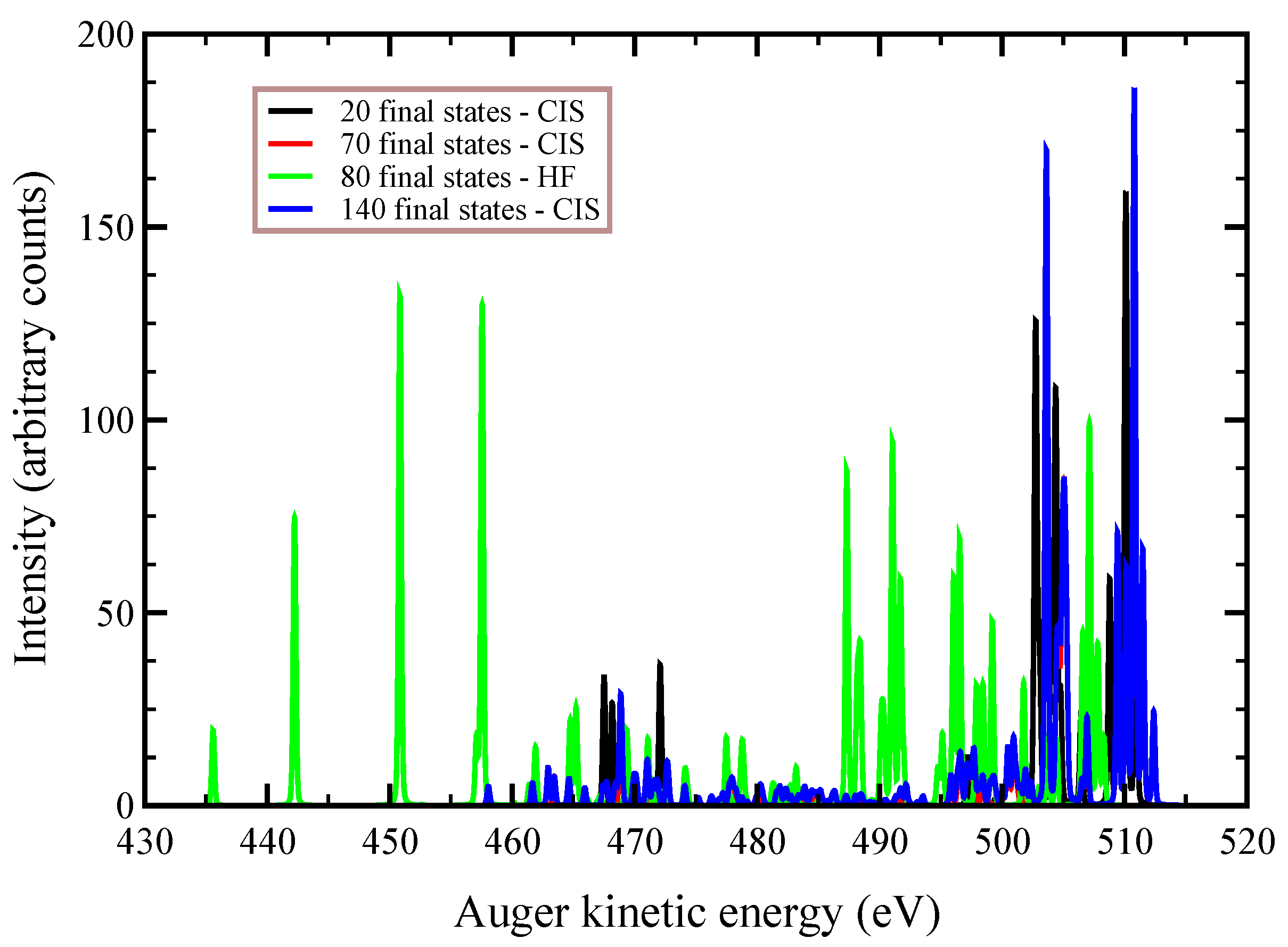
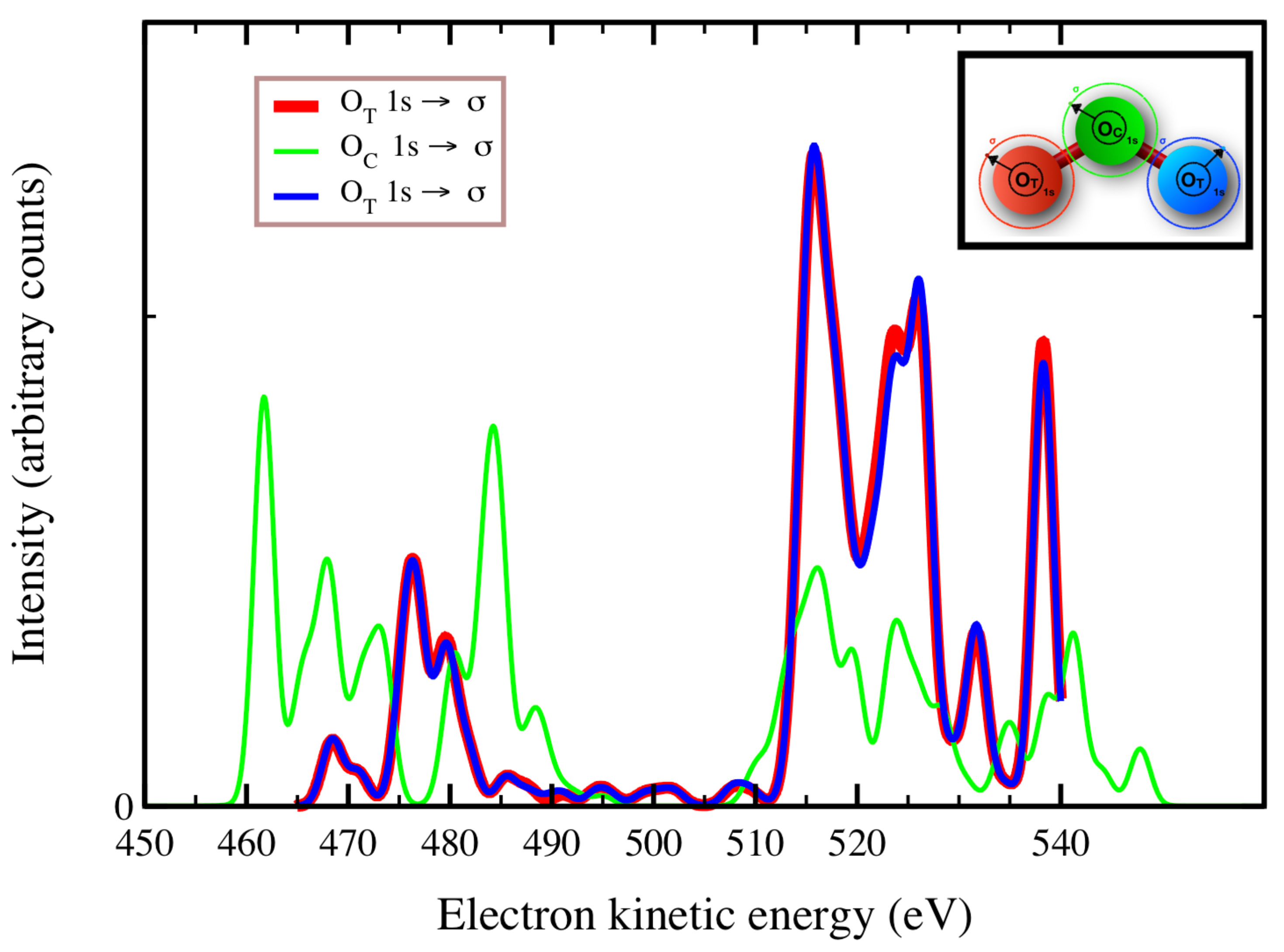
In
Figure 2,
Figure 3 and
Figure 4, we plot the
Auger spectra of ozone that was calculated with the decoupled channel approach, in which the intermediate states are characterized by single inner-shell vacancies in the
molecular orbitals and the final states by two vacancies in all possible valence orbitals. In particular, the green line represents 80 principal decay channels using HF level of theory, while the black, red, and blue lines represent simulations with 20, 70, and 140 final states, respectively, using CIS level of theory. In these calculations, the active space consists of 27 molecular orbitals, which means that, at the CIS level, the hole can be created in any of the occupied orbitals, and while the electrons can populate up to the 27-th virtual molecular orbital. In
Table 3, we report the total
Auger decay rates from the
core-hole intermediate states as a function of the number of final states included in the calculations. The calculated transition energies, partial and total decay rates of the
Auger processes are reported in
Table A1 (
),
Table A2 (
), and
Table A3 (
) of the
Appendix A, respectively, along with the final state orbital occupations for the 20 brightest final states. We notice that the
Auger transition spectra in
Figure 3 and
Figure 4 are almost identical, and the total Auger probability does not differ significantly, being 2.9127
a.u. and 2.9485
a.u. (see
Table 3, third column), respectively. This result is obtained, despite the symmetry of the intermediate state is different, as the initial hole created upon photoionization belongs to different irriducible representation of the
symmetry group. This is interpreted as the effect of the inclusion of the single excitations from the reference states in the description of the orbital wavefunctions, which results in the quasi-relocalization of the core-hole into one of the two symmetry-equivalent oxygen atoms, despite the HF orbitals being optimized starting from a hole “delocalized” in each of the molecular orbitals. By analyzing
Table 2, we conclude that the gain in energy to relocalize the core-hole in one of the oxygen atoms due to the interaction among all the configurations (≈900) appearing in the CIS expansion, is about 17 eV (see the difference in a.u. between the energy of the states in column
, which is the Hartree–Fock value, and the value in column
, which is the energy value after CIS with 63 orbitals in the active space).
At variance, the total
Auger probability for an initial hole in the deepest
molecular orbital is lower independent of the number of final channels used (see
Table 3). We notice that the use of CIS to treat the orbital wavefunctions has large impact on the accuracy of the Auger decay rate and peak position, showing a large blueshift with respect to the HF values in excess of 10 (see
Figure 2) to 20 eV (see
Figure 3 and
Figure 4).
The Auger lines, peaked at the transition energies calculated as by Equation (
10), were broadened by Lorentzian functions, whose widths were obtained from Equation (
10). Finally, we convolved the theoretical lineshape with a Gaussian having full width at half maximum (FWHM) of
eV in order to take the finite resolution of the experimental set-up and the vibrational broadening into account.
We observe that, by increasing the number of non interacting final channels, from 20 (black lines) to 70 (red lines) and 140 (blue lines), the partial probability of Auger decay of course redistributes among different channels, and also the total probability changes significatively, moving, e.g., from 1.4321
a.u. to 2.6241
a.u. for the
Auger state (see
Table 3).
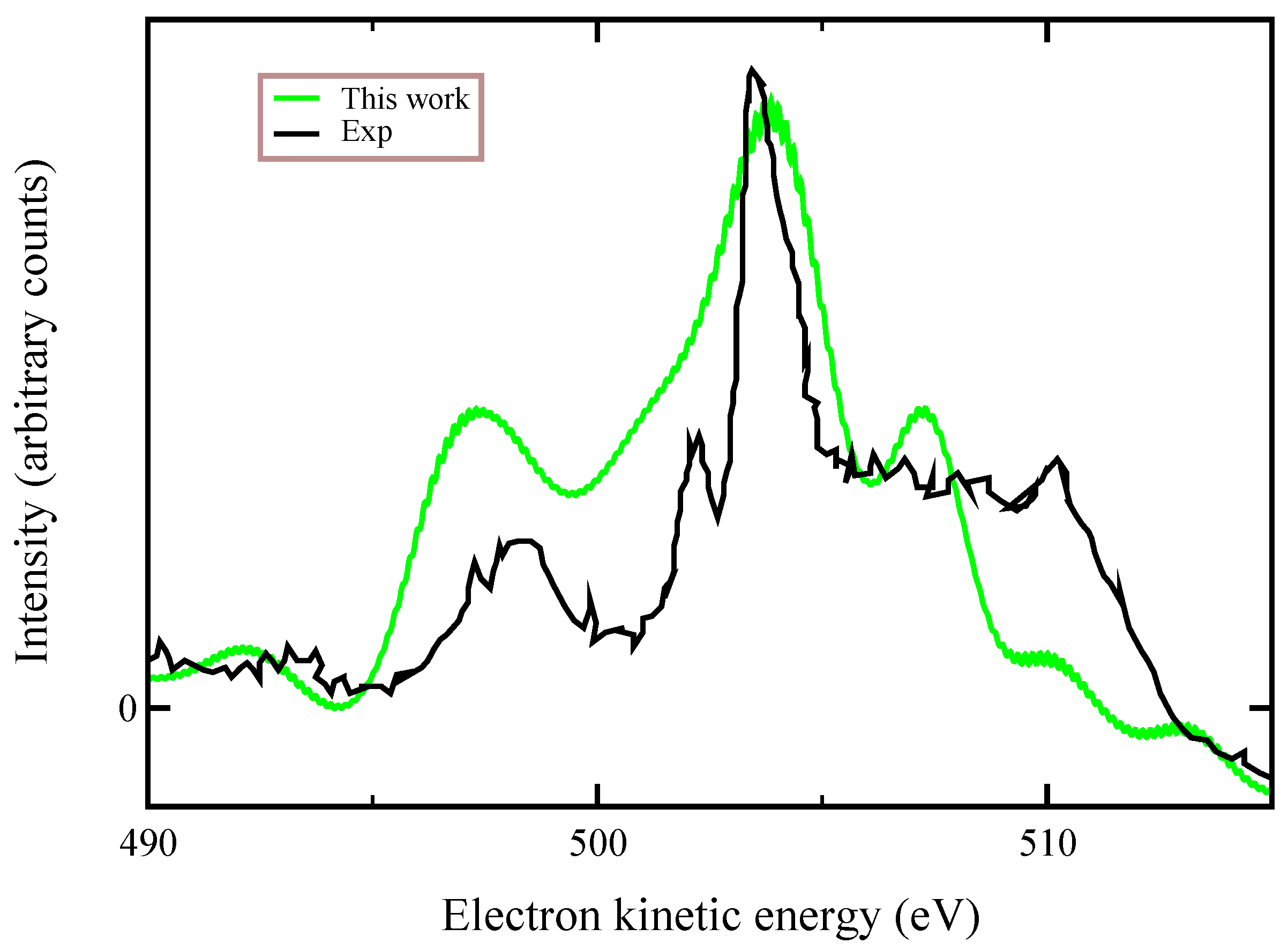
Finally, in
Figure 5, we compare our ab-initio calculations with the experimental data of Ref. [
10] that were recorded at a photon energy of 536.7 eV, finding an overall good agreement. We stress that the experimental data refer to a spectator transition
, which is a process similar (not exactly the same) to that one we considered here. Auger lineshapes were broadened by a convolution with a 0.8 eV Gaussian function. These large observed linewidths have been attributed to both the dissociative character of the final states and nuclear vibrations.