1. Introduction
We only consider simple and loopless graph
with order
and size
. If
, we say that
v is a neighbor of
u. The degree of a vertex
v in a graph
G is the number of neighbors of
v in
G, denoted as
. The minimum degree (and maximum degree) of
G is the minimum (and maximum) degree among the vertices of
G, denoted as
(and
). A vertex of degree 0 is called an isolated vertex and a vertex of degree 1 is called a pendant vertex; its incident edge is called a pendant edge. The set of all neighbors of
u is denoted as
. For
, let
be the set of all neighbors of the vertices in
S. We shall drop the subscript
G if there is no ambiguity. For
, the set of integers from
a to
b is denoted as
. For notations not defined in this paper, we refer to [
1].
The magic square [
2] is one of the oldest problems on symmetry [
3]. It was later extended to the idea of magic graphs [
4], super magic graphs [
5], and super edge-magic graphs [
6]. The notion of the strength of a graph
G was then introduced by Ichishima et al. [
7] as a generalization of super magic strength [
8], which is effectively defined only for super edge-magic graphs (also called strong vertex-graceful [
9] and strongly indexable [
10]), to any nonempty graphs as follows.
A bijection is called a numbering of the graph G of order p.
Definition 1. The strength of a numbering of G is defined by and the strength of a graph G itself is A numbering f is called a strength labeling of G if .
The super magic strength,
, of a graph
G is defined as the minimum of all magic constants over all super edge-magic labelings of
G. A necessary and sufficient condition for a graph to be super edge-magic [
11] then gives rise to the concept of the consecutive strength labeling of a graph, which is equivalent to super edge-magic labeling. In [
7] (Section 4), Ichishima et al. showed that a graph
G of order
p has
. Several new lower bounds of
in terms of other graph parameters were also obtained. Moreover, all of the bounds are sharp. Thus, one may use the strength of graphs to establish the super magic strength of the corresponding graphs.
Several lower and upper bounds for
were obtained in [
7]. The following two are needed in what follows.
Lemma 1. If H is a subgraph of a graph G, then Lemma 2. For every graph G of order p with , Let be the disjoint union of G and H with and . The disjoint union of m copies of G is denoted as . We first extend Lemma 2 to graphs with isolated vertices.
Lemma 3. Let G be a graph with . If , then Proof. Let f be a strength labeling of the graph G. We extend f to a numbering of by assigning all m isolated vertices by labels in . Clearly, . Hence . Combining with Lemma 1, we have the lemma. □
Thus, from now on, we only consider graphs without isolated vertices. In [
7,
12], the authors showed that
if
G is a path, cycle, complete graph, complete bipartite graph, ladder graph, prism graph, Möbius ladder, book graph, or
, each of which has order
p. Moreover, if
for a graph
G of order
p with
, then
, where
is the corona product of
G and
H. The following problems are posed.
Problem 1. Find sufficient conditions for a graph G of order p with to ensure .
Problem 2. Find good bounds for the strength of a graph.
Problem 3. For every lobster T, determine the exact value of .
Problem 4. For every integer , determine the strength of , the n-dimensional hypercube.
In this paper, we obtained a sufficient condition for a graph to have . Moreover, we showed that every graph G either has or is a proper subgraph of a graph H that has with . Further, new good lower bounds of are obtained. Consequently, Problems 1 to 3 are solved. Moreover, we completely determine the strength of 2-regular graphs and give a partial solution to Problem 4.
2. Sufficient Condition
Let be a graph of order p with . Suppose that , , is not for nor with for some . We may denote by , where and . Let be a graph obtained from by deleting the isolated vertices that exist in , and a vertex of degree together with all its neighbors in . Continue the procedure until is either with or with for some . This sequence of subgraphs is called a -sequence of G. When , we let by convention. Let for .
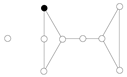
Example 1. The following are two examples to illustrate the above construction. The black vertex is the chosen vertex that will be deleted at each stage.
| 1. | | | | | | | | |
![Symmetry 13 00513 i001 Symmetry 13 00513 i001]() | → | ![Symmetry 13 00513 i002 Symmetry 13 00513 i002]() | → | ![Symmetry 13 00513 i003 Symmetry 13 00513 i003]() | → | ![Symmetry 13 00513 i004 Symmetry 13 00513 i004]() | → | ![Symmetry 13 00513 i005 Symmetry 13 00513 i005]() |
| | | | | | | | |
| | | | | | | | |
Now, . So, this δ-sequence of the graph does not satisfy the condition of (1) mentioned below. | 2. | | | | | | |
![Symmetry 13 00513 i006 Symmetry 13 00513 i006]() | → | ![Symmetry 13 00513 i007 Symmetry 13 00513 i007]() | → | ![Symmetry 13 00513 i008 Symmetry 13 00513 i008]() | → | ![Symmetry 13 00513 i009 Symmetry 13 00513 i009]() |
| | | | | | |
| | | | | | |
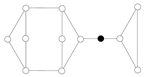
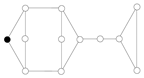
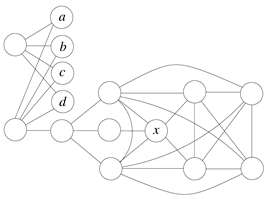
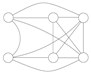
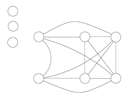
This δ-sequence of the graph satisfies the condition of (1). Example 2. Consider the following graph G:
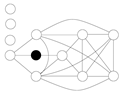
![Symmetry 13 00513 i010 Symmetry 13 00513 i010]() (1). Suppose that we choose a as the first vertex (similarly, we can choose b, c, or d). So, we have
(1). Suppose that we choose a as the first vertex (similarly, we can choose b, c, or d). So, we have![Symmetry 13 00513 i011 Symmetry 13 00513 i011]() | → | ![Symmetry 13 00513 i012 Symmetry 13 00513 i012]() | → | ![Symmetry 13 00513 i013 Symmetry 13 00513 i013]() | | K1 |
| | | | | | |
| | | | | | |
Now, .
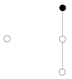
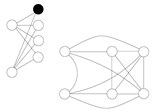
(2). Suppose that we choose x as the first vertex. So, we have
![Symmetry 13 00513 i014 Symmetry 13 00513 i014]() | → | ![Symmetry 13 00513 i015 Symmetry 13 00513 i015]() | → | ![Symmetry 13 00513 i016 Symmetry 13 00513 i016]() | | K1 |
| | | | | | |
| | | | | | |
Now, .
So, every δ-sequence of G does not satisfy condition (1). The following theorem gives a sufficient condition for a graph to have minimal strength.
Theorem 1. For a graph G of order p with , if there is a δ-sequence of G such thatthen . Note that a sum with an empty term is treated as zero, as usual. If there is no ambiguity, we will write as and as .
Proof. Let
be a
-sequence of
G satisfying condition (
1). Let
be a vertex in
of degree
, which is deleted from
to obtain
,
. Now,
. We shall construct a numbering
f of
G such that
.
Label by p and all its neighbors by 1 to in arbitrary order. This guarantees that the largest induced edge label is at this stage.
Suppose that we have labeled vertices in by using the labels in , where . Moreover, the neighbors of are labeled with labels in , and all induced edge labels are at most , up to now. Note that a sum with an empty term is treated as zero.
Now, we consider the graph .
(a) Suppose that . We label the isolated vertices of with labels in , respectively (if , then this process does not exist), and by and its neighbors with labels in , respectively.
Now, the vertices of are labeled by using the labels in .
Since each isolated vertex of
is only adjacent to some neighbors of
, and
may be adjacent with some neighbors of
, the largest new induced edge label related to these vertices is
The largest new induced edge label related to
and its neighbors in
is
Repeat this process until .
(b) Suppose that . Now, with or for some and . In this case, the set of unused labels is . That is, or .
When , the process is the same as in the above case. Hence, we have a numbering for G with the strength .
When
, where
, we label the
isolated vertices of
with labels in
, respectively (if
, then this process is not performed). Finally, label the vertices of
with labels in
, respectively. Then, the largest new induced edge labels related to the neighbors of
are
The largest new induced edge labels in
are
Hence, we have a numbering f such that . Therefore, . By Lemma 2, . □
Example 3. Consider the graph described in Example 1. Using the second δ-sequence of and following the construction in the proof of Theorem 1, we have the following strength labeling f of such that .
![Symmetry 13 00513 i017 Symmetry 13 00513 i017]()
From Example 2,
G does not satisfy the hypothesis of Theorem 1, but there is a strength labeling
f for it with
as follows.
![Symmetry 13 00513 i018 Symmetry 13 00513 i018]()
So, the converse of Theorem 1 is not true.
Thus, Theorem 1 provides a solution to Problem 1. Note that every tree T has the property that and for each . We immediately have and the following corollary that answers more than what Problem 3 asks.
Corollary 2. If G is a forest without an isolated vertex, then .
Corollary 3. The one-point union of cycles G of order p has .
Proof. Remove a degree 2 vertex that is adjacent to the maximum degree vertex of
G and its neighbors to obtain a subgraph
, which is a disjoint union of path(s). So,
G admits a
-sequence that satisfies (
1). □
Corollary 4. If G is a wheel or fan graph of order p, then .
In constructing a -sequence of G, if we change the choice of choosing a vertex of degree to a vertex of degree , then we get another sequence of subgraphs of G. This sequence is called a d-sequence of G. Let , and denote as . By the same argument as that when proving Theorem 1, we have:
Theorem 5. For a graph G of order p with , if there is a d-sequence of G such that then . The equality holds if . Example 4. Consider the graph G in Example 2. The following is a d-sequence of G.
![Symmetry 13 00513 i019 Symmetry 13 00513 i019]() | → | ![Symmetry 13 00513 i020 Symmetry 13 00513 i020]() | → | ![Symmetry 13 00513 i021 Symmetry 13 00513 i021]() | → | ![Symmetry 13 00513 i022 Symmetry 13 00513 i022]() |
| | | | | | |
| | | | | | |
Now, , , and . By Theorem 5, , as shown in Example 3.
Lemma 4. Let T be a forest without an isolated vertex of an order at of least 3, and let be the set of pendant vertices that are adjacent to a vertex of a degree of at least 2. There is a δ-sequence of T of length s such that , where is defined in (1). Moreover, all satisfy (1). Proof. Obviously, the lemma holds when T is of order 3. Suppose that the lemma holds when the order of T is k or less, where .
Now, consider a forest T of order . Choose a vertex . Let v be the vertex adjacent to u with degree d. We shall consider the forest .
Suppose that , which is a star; then, and is a -sequence of T. Note that and . Clearly, .
Now, we assume that T is not a star. Let , where and is a forest without an isolated vertex.
Suppose that the order of is 2; then, and is a -sequence of T, where . Now, . If , then and . We get . If T is a tree, then and . So, we still get .
Suppose that the order of is greater than 2. By the induction assumption, there is a -sequence of , say , such that for some .
Now, consider of T. Note that . Let a be the number of vertices of degree 2 in T, but degree 1 in ; then, , where . Let . Therefore, (some vertices in may not be in ).
If a vertex w in T of degree 2 becomes of degree 1 in , then w may be in and may have at most one neighbor in that is not in . So, .
By induction, the lemma holds for any forest T of an order greater than 2. □
Remark 1. In the proof of Lemma 4, we can see that if T is a star.
Theorem 6. Keep all notations defined in Theorem 1 and Lemma 4. Let H be a graph with . Suppose that is a d-sequence of H. Suppose that is not positive. Suppose that T is a graph with a d-sequence satisfying (2). Let . If ; then, . Proof. Since is either for some or for some , we have the following two cases.
For the first case, and is a d-sequence of G. Then,
, ;
;
.
For the last case, is a d-sequence of G. We will get that
, ;
;
, .
By Theorem 5, . The lower bound follows from Lemma 2. □
Remark 2. In Theorem 6, suppose that H and T are connected. Let be chosen to construct , let be a neighbor of x, and let , which is not chosen to construct . We add an edge to the graph . All of the values of this connected graph are the same as those of .
Theorem 7. Keep all notations defined in Theorem 1 and Lemma 4. Let H be a graph with . Suppose that is a d-sequence of H. Suppose Let , where T is a forest without an isolated vertex of an order of at least 3. If ; then, .
Proof. By Lemma 4, there is a
-sequence
of
T such that
and all
satisfy (
1). Since this
-sequence is a particular
d-sequence of
T, it satisfies the condition of Theorem 6. Since
now, by Theorem 6, we have
. Hence, we have the theorem, since
. □
Corollary 8. Let H be a graph with . Suppose that is a d-sequence of H.
Let . If , then .
Let
for
. It is proven in [
7] (Theorem 3.5) that
. So, we have the following.
Corollary 9. There exists a graph G with for each .
Suppose that
H is a graph with
. So, there is a
d-sequence of
H with
such that
Z is non-positive, where
Z is defined in (
3). Let
. Since
is a
d-sequence of
T,
. Suppose that
and
. Since
,
. By Theorem 6, we have
. So, together with Remark 2, we have the following theorem.
Theorem 10. For every graph H, either or H is a proper subgraph of a graph G such that with .
Example 5. It is easy to obtain a δ-sequence of with Thus, . Let . By the construction before Theorem 10, we have . A required labeling can be obtained by similarly following the proof of Theorem 1. Moreover, adding an edge joining a vertex of degree 5 of and a vertex of gives a connected graph G that contains as a proper subgraph with , as required.
Example 6. For 2-regular graphs with exactly odd cycles, we have . Let . By the construction before Theorem 10, we have .
3. New Lower Bounds
Theorem 11. Suppose that G is a graph of order p with an independent number α; then, .
Proof. For any numbering of G, by the pigeonhole principle, at least two integers in are assigned to two adjacent vertices. So, the induced edge label is at least . This completes the proof. □
Corollary 12. Suppose that G is a graph of order p with minimum degree δ. Suppose that ; then, , where α is the independence number of G.
Proof. From Theorem 11, we have . □
Let
G be a graph of order
p. Let
Theorem 13. Let G be a graph of order p; then, .
Proof. Let
for some
i. Let
f be a strength labeling of
G. Consider the labels in
. Let
; then,
. Now,
. Let
a be the largest label in
. There is a vertex
such that
. Moreover,
u is adjacent to
. Thus,
□
Thus, we provided two good bounds for the strength of a graph, as raised in Problem 2. Note that Lemma 2 is a corollary of Theorem 13 when for .
Theorem 14. If , where , , and , then .
Proof. Note that if , then the first summand does not appear, similarly for the second summand. Now, . By Theorem 11, we have .
Let and . Let such that when .
We shall construct a numbering f on G. If , we first label H with integers in as follows.
Label with in the natural order. In general, for , we label the vertices of even cycle with , , , ⋯, , in the natural order. Continue this process until . Hence, the maximum induced edge label is .
If , then we label the vertices of odd cycle by in the natural order. Up to now, the maximum induced edge label is still .
Now, we label the vertices of odd cycle with , , , ⋯, , in the natural order. Note that . So, the current maximum induced edge label is .
In general, for , we label the vertices of odd cycle with , , , ⋯, , in the natural order. Note that . So, the current maximum induced edge label is .
Continue this process until . Hence, we have . □
Example 7. Consider . Now, and .
We label the vertices of
with integers in (max. induced edge label is 29);
with integers in (max. induced edge label is 29);
with integers in ; (max. induced edge label is 29);
with integers in (max. induced edge label is 30);
with integers in (max. induced edge label is 31).
So, .
Let be the Cartesian product of graphs G and H.
Lemma 5. Let G be a bipartite graph with bipartition such that . Suppose that there is a numbering f of G such that ; then, there is a numbering F of such that , where is a bipartition of . Moreover, .
Note that the following proof is modified from the proof of Theorem 3.10 in [
7].
Proof. Note that, from the hypotheses, . Let u and v be vertices of . Then,
and .
Define
by
Clearly, .
Now, and . Suppose that and are adjacent in . By definition, . Similarly, if and are adjacent in , then . Thus, . □
Let be a hypercube of dimension n, . Since there is a strength numbering f of satisfying the hypotheses of Lemma 5, by applying this lemma repeatedly, we get the following.
Theorem 15. For , .
This is a known result in [
7] (Theorem 3.10).
We shall improve the lower bound of the strength of . The vertices of often used the elements of the vector space over . Two vertices u and v are adjacent if and only if , where is the standard basis of . Note that for any vector . In the proofs of the following lemmas, all algebra involving vectors is over .
For any vertex v, we let , the closed neighborhood of v. Hence, for any subset of vertices S, . We shall omit the subscript G when there is no ambiguity.
Lemma 6. If u and v are two distinct vertices of , , then is either 0 or 2.
Proof. Suppose that u and v are adjacent. Clearly, . Suppose that u and v are not adjacent. If , then the distance between u and v is two. Hence, , and (equivalently, ), where . Since , for some . So, or . Thus, . Hence, . □
Lemma 7. For any three distinct vertices u, v, and w of , , Proof. If one of , and is 0, then . Otherwise, Lemma 6 implies that .
- (1).
Suppose that only one pair of u, v, and w are adjacent—say, is an edge—then, the distances from w to u and to v are 2. This creates a five-cycle, which is impossible.
- (2).
Suppose that two pairs of u, v, and w are adjacent—say, and are edges. Note that v and w cannot be adjacent. Then, and . Hence, . This implies that .
- (3).
Suppose that none of u, v, and w are adjacent. By the proof of Lemma 6, we have and for some , , and . This implies that . Since the distance of u and w is 2, . Without loss of generality, we may assume that . Now, , , and . Here, . Hence, . Since , .
This completes the proof. □
Theorem 16. For the hypercube , , we have ; ; ; and for .
Proof. Keeping the notations defined in Theorem 13, we want to compute and . Clearly, .
Suppose that
with
.
So, . Actually, when , . Thus, .
Suppose that , where are distinct.
- (1).
If all
,
and
are not zero, then by Lemma 7,
. Thus,
Actually, .
- (2).
If all , and are zero, then .
- (3).
If at least one of
,
, and
is not zero and at least one of them is zero, then
Thus, .
Let us consider
, where
are distinct. Then,
- (1).
If only one of , then by Lemma 7, the third summand is 1 and the fourth summand is 0. Then, .
Actually, .
- (2).
If more than one of , then the third and fourth summands are 0. Thus, .
- (3).
If all of
, then
Therefore, .
Hence, by Theorem 13, we have when ; when ; when ; and when . Thus, we have ; ; ; and when . □
From the proof of Theorem 16, we have , , , and for .
Suppose that
for some subset of vertices
S with
. Let
with
.
So, . Since , by induction, we will get , where .
Let ; then, . So, is increasing when .
Suppose that , ; then, . So, . We have .
Suppose that , ; then, . So, . We have .
Combining with Theorem 16, we have the following.
Theorem 17. For ,
- 1.
; ; ;
- 2.
for ;
- 3.
for .
- 4.
for .
Corollary 18. , , , and .
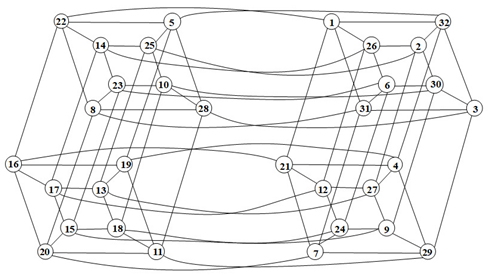
Proof. Combining with Theorems 15 and 16, we have , , and . By considering the following labeling of , we have . □
| | | 000 | 100 | 110 | 010 | 001 | 101 | 111 | 011 | |
| |
|
00 |
00000 |
10000 |
11000 |
01000 |
00100 |
10100 |
11100 |
01100 | |
|
1 |
32 |
3 |
31 |
26 |
2 |
30 |
6 |
37 |
|
10 |
00010 |
10010 |
11010 |
01010 |
00110 |
10110 |
11110 |
01110 | |
|
21 |
4 |
29 |
7 |
12 |
27 |
9 |
24 |
39 |
|
11 |
10011 |
10011 |
11011 |
01011 |
00111 |
10111 |
11111 |
01111 | |
|
16 |
19 |
11 |
20 |
17 |
13 |
18 |
15 |
36 |
|
01 |
00001 |
10001 |
11001 |
01001 |
00101 |
10101 |
11101 |
01101 | |
|
22 |
5 |
28 |
8 |
14 |
25 |
10 |
23 |
39 |
| |
38 |
37 |
40 |
39 |
40 |
40 |
40 |
39 |
max. induced edge label |
Note that
. The first row and the first column are vertices of
and
, respectively. The following is the corresponding figure.
![Symmetry 13 00513 i023 Symmetry 13 00513 i023]()
The following is a numbering for
.
| 000 | 100 | 110 | 010 | 001 | 101 | 111 | 011 | |
| 000 | 000000 | 100000 | 110000 | 010000 | 001000 | 101000 | 111000 | 011000 | |
| 1 | 64 | 3 | 63 | 62 | 2 | 52 | 7 | 70 |
| 100 | 000100 | 100100 | 110100 | 010100 | 001100 | 101100 | 111100 | 011100 | |
| 61 | 4 | 45 | 8 | 11 | 57 | 17 | 58 | 75 |
| 110 | 000110 | 100110 | 110110 | 010110 | 001110 | 101110 | 111110 | 011110 | |
| 15 | 49 | 28 | 38 | 56 | 21 | 33 | 19 | 75 |
| 010 | 000010 | 100010 | 110010 | 010010 | 001010 | 101010 | 111010 | 011010 | |
| 60 | 6 | 50 | 10 | 13 | 54 | 25 | 46 | 79 |
| 001 | 000001 | 100001 | 110001 | 010001 | 001001 | 101001 | 111001 | 011001 | |
| 59 | 5 | 37 | 9 | 12 | 53 | 23 | 48 | 76 |
| 101 | 000101 | 100101 | 110101 | 010101 | 001101 | 101101 | 111101 | 011101 | |
| 14 | 44 | 30 | 43 | 55 | 20 | 42 | 18 | 75 |
| 111 | 000111 | 100111 | 110111 | 010111 | 001111 | 101111 | 111111 | 011111 | |
| 39 | 26 | 35 | 31 | 22 | 40 | 32 | 34 | 75 |
| 011 | 000011 | 100011 | 110011 | 010011 | 001011 | 101011 | 111011 | 011011 | |
| 16 | 51 | 27 | 41 | 47 | 24 | 36 | 29 | 78 |
| | 76 | 77 | 78 | 73 | 78 | 78 | 77 | 77 | max. induced edge label |
Thus, .




 (1). Suppose that we choose a as the first vertex (similarly, we can choose b, c, or d). So, we have
(1). Suppose that we choose a as the first vertex (similarly, we can choose b, c, or d). So, we have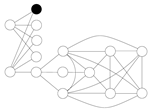

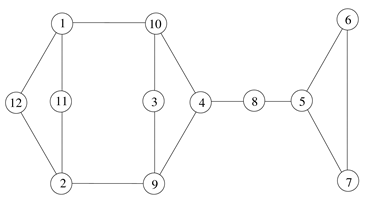 From Example 2, G does not satisfy the hypothesis of Theorem 1, but there is a strength labeling f for it with as follows.
From Example 2, G does not satisfy the hypothesis of Theorem 1, but there is a strength labeling f for it with as follows.