Abstract
In this work, we present a unified approach to the thermodynamics of hadron–quark–gluon matter at finite temperatures on the basis of a quark cluster expansion in the form of a generalized Beth–Uhlenbeck approach with a generic ansatz for the hadronic phase shifts that fulfills the Levinson theorem. The change in the composition of the system from a hadron resonance gas to a quark–gluon plasma takes place in the narrow temperature interval of 150–190 MeV, where the Mott dissociation of hadrons is triggered by the dropping quark mass as a result of the restoration of chiral symmetry. The deconfinement of quark and gluon degrees of freedom is regulated by the Polyakov loop variable that signals the breaking of the center symmetry of the color group of QCD. We suggest a Polyakov-loop quark–gluon plasma model with virial correction and solve the stationarity condition of the thermodynamic potential (gap equation) for the Polyakov loop. The resulting pressure is in excellent agreement with lattice QCD simulations up to high temperatures.
1. Introduction
Recently, continuum extrapolated lattice QCD (LQCD) thermodynamics results for physical quark masses have become available [1,2,3,4]. It has now become a major goal to construct an effective low-energy QCD model that would reproduce these results in the finite temperature and low chemical potential domain to high accuracy. Such a description could form a basis for extrapolations to the region of low temperatures and high baryochemical potentials where the sign problem still prevents LQCD obtaining benchmark solutions.
QCD Dyson–Schwinger equations [5,6] and functional renormalization group (FRG) methods [7,8] are promising tools to investigate the nonperturbative aspects of the QCD phase diagram in the vicinity of the chiral and deconfinement transitions from first principles. However, to date, they do not self-consistently account for the bound state formation. Therefore, despite a satisfactory description of the temperature dependence of the renormalized light chiral condensate [8], a question arises regarding the relationship to the chiral perturbation theory limit, where the onset of chiral condensate melting is solely due to light pseudoscalar meson excitations in the medium [9]. The account for bound states in the FRG approach to low-energy QCD is still under development [10] and not yet applicable to address the role of hadronic bound states for chiral condensate melting.
Complementary to these first-principle approaches is the Polyakov–quark–meson (PQM) model (see, e.g., [11] and references therein), which is suitable to study the interrelation of chiral and deconfinement transitions. Both transitions are closely correlated, but in comparison with LQCD, the chiral restoration temperature result is too high. It could be suspected that the inclusion of further mesonic and baryonic degrees of freedom could improve the situation. Furthermore, the dynamic quark self-energy effects due to dressing by the meson cloud should be taken into account. In the PQM model, mesons are not composites but elementary degrees of freedom.
In order to properly account for the composite nature of mesons and baryons, as well as their Mott dissociation in a hot and dense medium, a Beth–Uhlenbeck approach can be employed [12,13,14,15,16,17,18,19,20,21,22]. This approach has been limited to the application of low-lying mesons only and did not take into account perturbative corrections, meaning that a quantitative description of LQCD thermodynamics has not yet been possible.
To overcome these limitations, the generic behavior of the scattering phase shifts in the hadronic channels has been constructed in the spirit of a cluster expansion model which reproduces the full hadron resonance gas at low temperatures and the quark–gluon plasma (QGP) with virial corrections at high temperatures [21,22]. The model embodied the main consequence of chiral symmetry restoration in the quark sector: the lowering of the thresholds for the two and three-quark scattering state continuous spectrum, which triggers the transformation of hadronic bound states to resonances in the scattering continuum. In the early version of this model, the gap equation for the Polyakov-loop was incomplete, and the model of the phase shifts was a rather complicated one.
We suggest here a Polyakov-loop quark–gluon plasma model with virial correction in order to obtain a satisfactory agreement with lattice QCD simulations up to high temperatures and solve the complete stationarity condition of the thermodynamic potential (gap equation) for the Polyakov loop. The phase shift model employed in this work is simpler than in previous works and universally applicable for all hadronic species. It is in accordance with the Levinson theorem and results in the vanishing of hadronic contributions to the thermodynamics at high temperatures.
2. Cluster Virial Expansion to Quark-Hadron Matter
The main idea behind unifying the description of the quark–gluon plasma (QGP) and the hadron resonance gas (HRG) phase of low-energy QCD matter is the fact that hadrons are strong, nonperturbative correlations of quarks and gluons. In particular, mesons and baryons are bound states (clusters) of quarks and should therefore emerge in a cluster expansion of interacting quark matter as new, collective degrees of freedom.
For the total thermodynamic potential of the model, from which all other equations of state can be derived, we make the following ansatz:
where describes the thermodynamic potential of the quark and gluon degrees of freedom with a perturbative part and a nonperturbative mean field part that can be decomposed into the quark quasiparticle contribution and the gluon contribution that is approximated by a mean field potential . Note that all these contributions to the QGP thermodynamic potential are intertwined by the traced Polyakov loop as the order parameter for confinement. The correlations beyond the mean field approximation which correspond to the hadronic bound states and their scattering state continuum are described by the Mott–HRG pressure . This is an HRG pressure that takes into account the dissociation of hadrons by the Mott effect, when their masses would exceed the mass of the corresponding continuum of unbound quark states. A detailed description and numerical evaluation of these contributions is given below.
2.1. Beth–Uhlenbeck Model for HRG with Mott Dissociation
For the MHRG part of the pressure of the model, we have ,
where the sum extends over all mesonic (M) and baryonic (B) states from the particle data group (PDG), comprising an ideal mixture of hadronic bound and scattering states in the channel i that are described by a Beth–Uhlenbeck formula. Then, the partial pressure of the hadron species i is
where is the degeneracy factor. For the phase shift of the bound states of quarks in the hadron i, we adopt the simple model that is in accordance with the Levinson theorem:
The temperature dependent threshold mass of the two (or three) quark continuum for mesonic (baryonic) bound state channels i is
where is the number of strange quarks in hadron i. The factor originates from quark confinement in the following way. In the confining vacuum, the quarks are not simple plane waves with an arbitrarily long wavelength, but due to the presence of bag-like boundary conditions, their wavelength shall not exceed a certain length scale. Therefore, a minimal quark momentum applies to the quark dispersion relations , which for the choice results in . For details, see [23]. The chiral condensate is defined as
where () is the current-quark mass in the light (strange) quark sector, . It is an order parameter for the dynamical breaking of the chiral symmetry that is reflected in the corresponding temperature dependence of the dynamical quark masses .
In our present model, we do not treat the dynamical quark mass as an order parameter that should follow from the solution of an equation of motion (gap equation) that minimizes the thermodynamic potential, as in the case of the Polyakov-loop variable , but we use the quantity from simulations of 2 + 1 flavor lattice QCD as an input. This quantity has been introduced in [24] with the definition
and was used later on, e.g., in [1,2]. Further, we assume the following for the temperature-dependent light quark mass,
where MeV is the current-quark mass, and for the strange quark mass, we adopt
with MeV. The LQCD result for the temperature dependence of the chiral condensate [1,2] can be fitted by
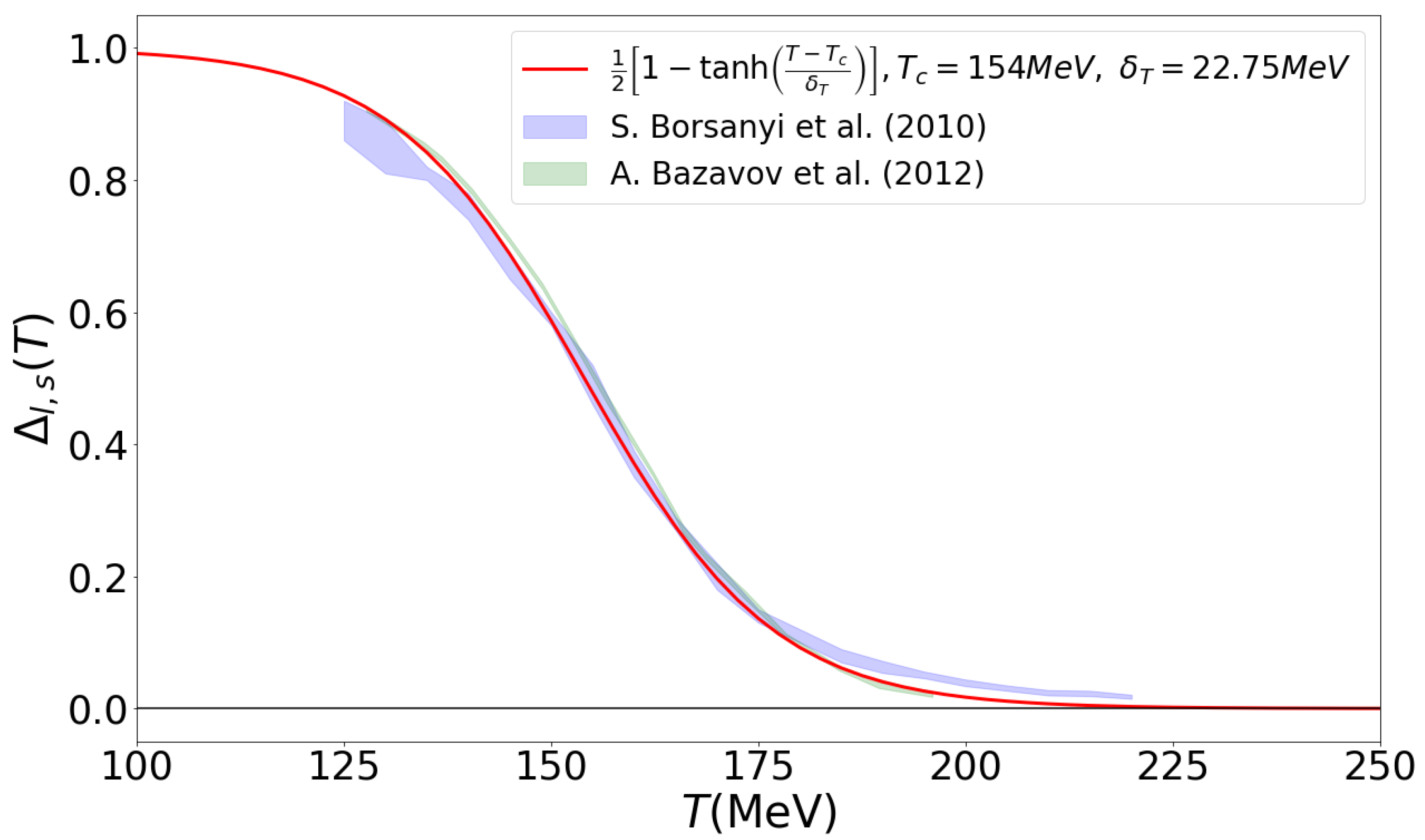
where MeV is the common pseudocritical temperature of the chiral restoration transition of both LQCD Collaborations and MeV is its width for the data from [1], while MeV for those from [2], see Figure 1. For our present applications modeling QCD thermodynamics, we use the fit of the chiral condensate (11), but with the modern value of MeV [25]. We have checked that the results for the total pressure of our model are practically inert against a changing value of within the above range of variation. Inserting (9) and (10) into (6), we get
and using (9) results in
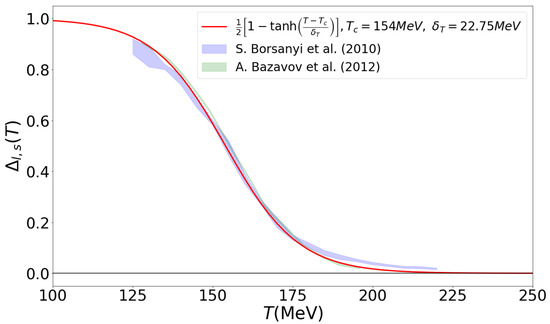
Figure 1.
Comparison of the fit (11) for the temperature dependence of the chiral condensate and the LQCD data for it from the Wuppertal–Budapest Collaboration [1] and the hotQCD Collaboration [2].
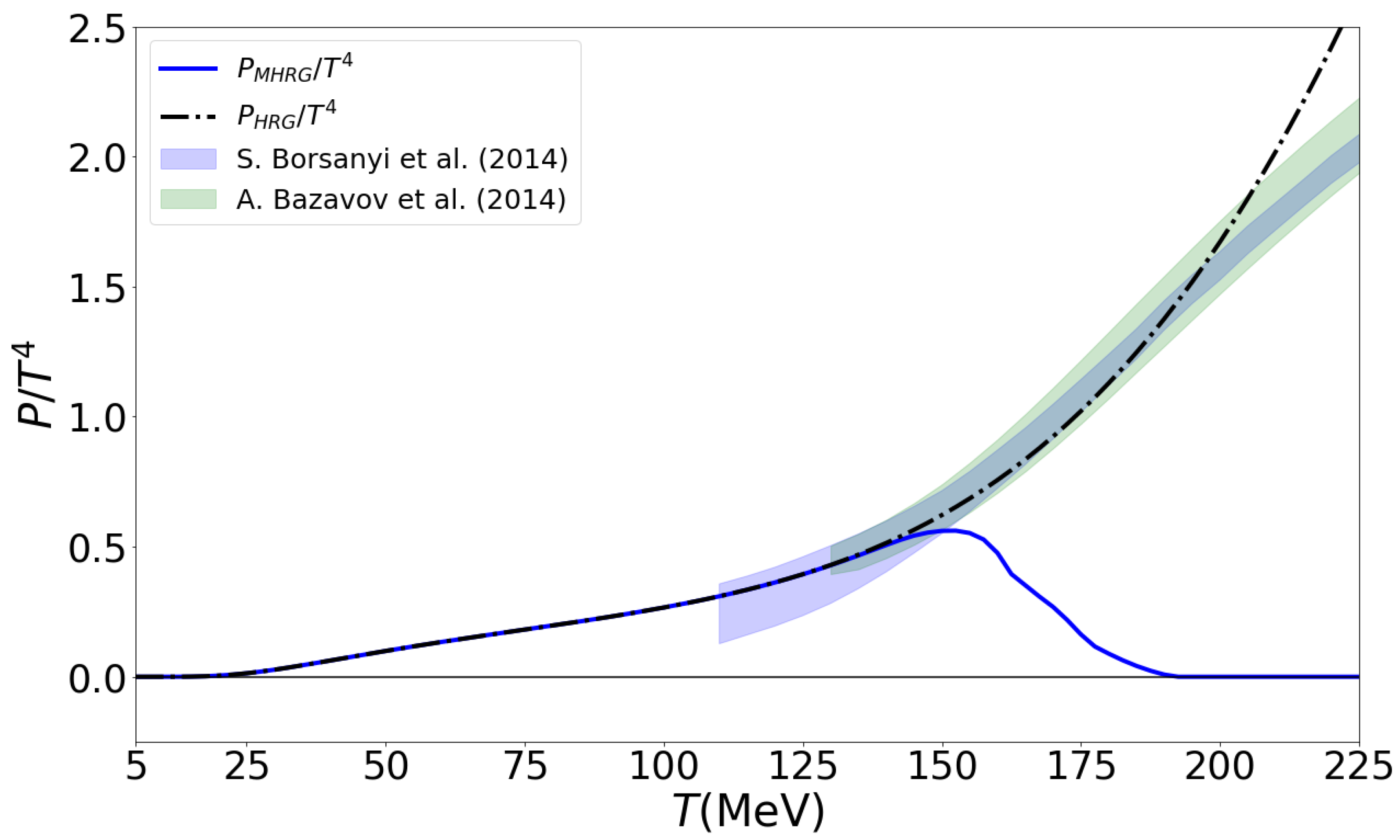
In Figure 2 we show the pressure (2) as a function of temperature for the hadron resonance gas (HRG) model with stable hadrons (red line) and for the HRG with Mott dissociation of hadrons (MHRG) according to the simple phase shift model (4) employed in the present work. These results are compared to the LQCD data from the HotQCD Collaboration [4] (green band) and the Wuppertal–Budapest Collaboration [3] (blue band). We want to point out that due to the Mott dissociation effect hadrons completely vanish from the system at MeV while the pressure of the ideal HRG model is misleadingly still in perfect agreement with LQCD data at this temperature!
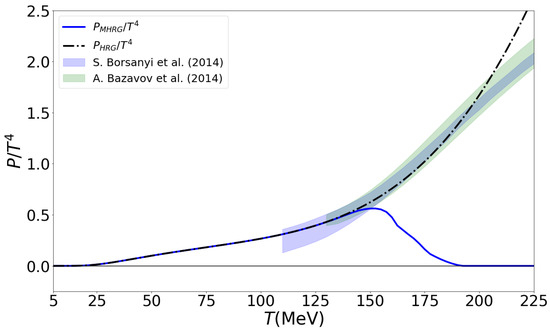
Figure 2.
Pressure as a function of temperature for the HRG model with stable hadrons (red line) and for the MHRG model with Mott dissociation of hadrons according to the simple phase shift model (4) employed in the present work. These results are compared to the LQCD data from the HotQCD Collaboration [4] (green band) and the Wuppertal–Budapest Collaboration [3] (blue band).
2.2. Polyakov-Loop Improved Nambu–Jona-Lasinio (PNJL) Model
The underlying quark and gluon thermodynamics are divided into a perturbative contribution which is treated as virial correction in two-loop order following [26] and a nonperturbative part described within a PNJL model in the form
where the quark quasiparticle contribution is given by
and the Polyakov-loop potential takes into account the nonperturbative gluon background in a meanfield approximation using the polynomial fit of [27]
where the temperature-dependent coefficient is given by
and the coefficients are given in Table 1.

Table 1.
Set of values for the Polyakov-loop potential [27].
2.3. Perturbative Contribution
It is well known that the lattice QCD thermodynamics at high temperatures of GeV follow a Stefan–Boltzmann like behavior , but with a reduction of the effective number of degrees of freedom. It has been observed, e.g., in [26], that this deviation can be described by the virial correction to the pressure due to the quark–gluon scattering at shown in Figure 3. Here, we modify the standard expression [28] of the form
by introducing the modified integral
where the generalized Fermi distribution function of the PNJL model for the case of vanishing quark chemical potential considered here is defined as
and is the momentum range below which nonperturbative physics dominates and is accounted for by the dynamically generated quark mass. Here, we use a temperature-dependent, regularized running coupling [29,30,31]
where , MeV and .
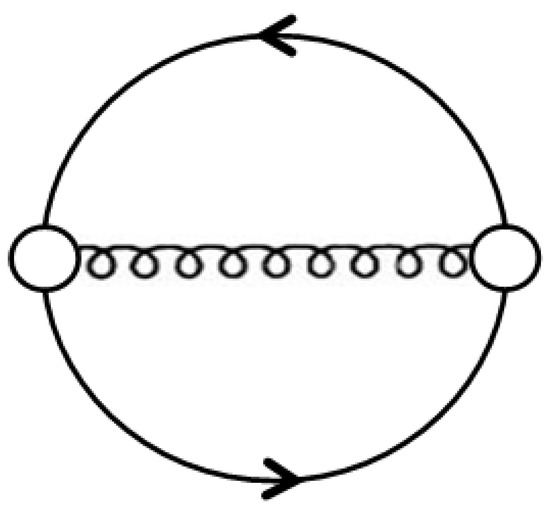
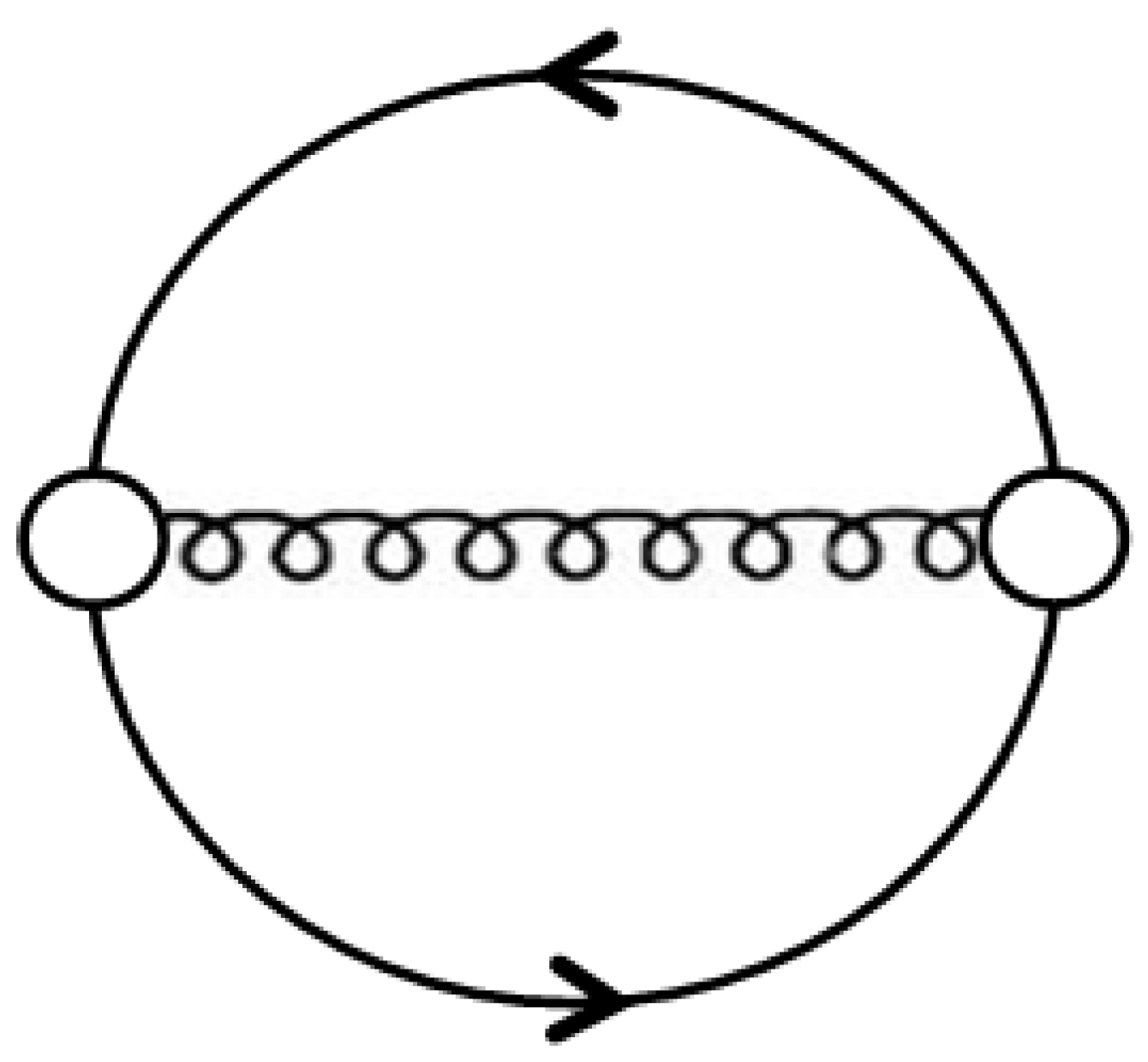
Figure 3.
Two-loop diagram for the contribution of the one-gluon exchange interaction to the thermodynamic potential of quark matter.
3. Stationarity Condition for the Polyakov Loop
The pressure follows from the thermodynamic potential under the condition of stationarity with regard to variations of the order parameters. Since the chiral condensate is fixed by the fit (11) to the numerical result from lattice QCD, the Polyakov loop is the only free-order parameter in the system to be varied; this condition means
This is realized by demanding
where the separate contributions come from the variations of the Polyakov loop potential
and the quark quasiparticle pressure
with , and the quark loop contribution
where
and
The equation resulting from the stationarity condition (23) can be dubbed a “gap equation” for since it has a similar structure to the quark mass gap equation, known from Nambu–Jona-Lasinio models. In previous work [21,22], the contribution to this gap equation from the quark loop diagram was omitted. Since this perturbative contribution is calculated with the Polyakov-loop generalized quark distribution functions , it has to be included to the generalized gap equation for the traced Polyakov loop. This has been done in the present paper for the first time.
Moreover, an infrared cutoff is placed at the loop integrals in the perturbative contribution which is set at the medium-dependent quark mass. Therefore, the full perturbative contribution in accordance with [28] is restored only at high temperatures, where and , while in the vicinity of the chiral and deconfinement transition, the effects of both the quark mass and Polyakov loop are taken into account. The solution of this gap equation gives the temperature dependence of the traced Polyakov loop . This is discussed in the next section.
4. Results
4.1. Polyakov Loop
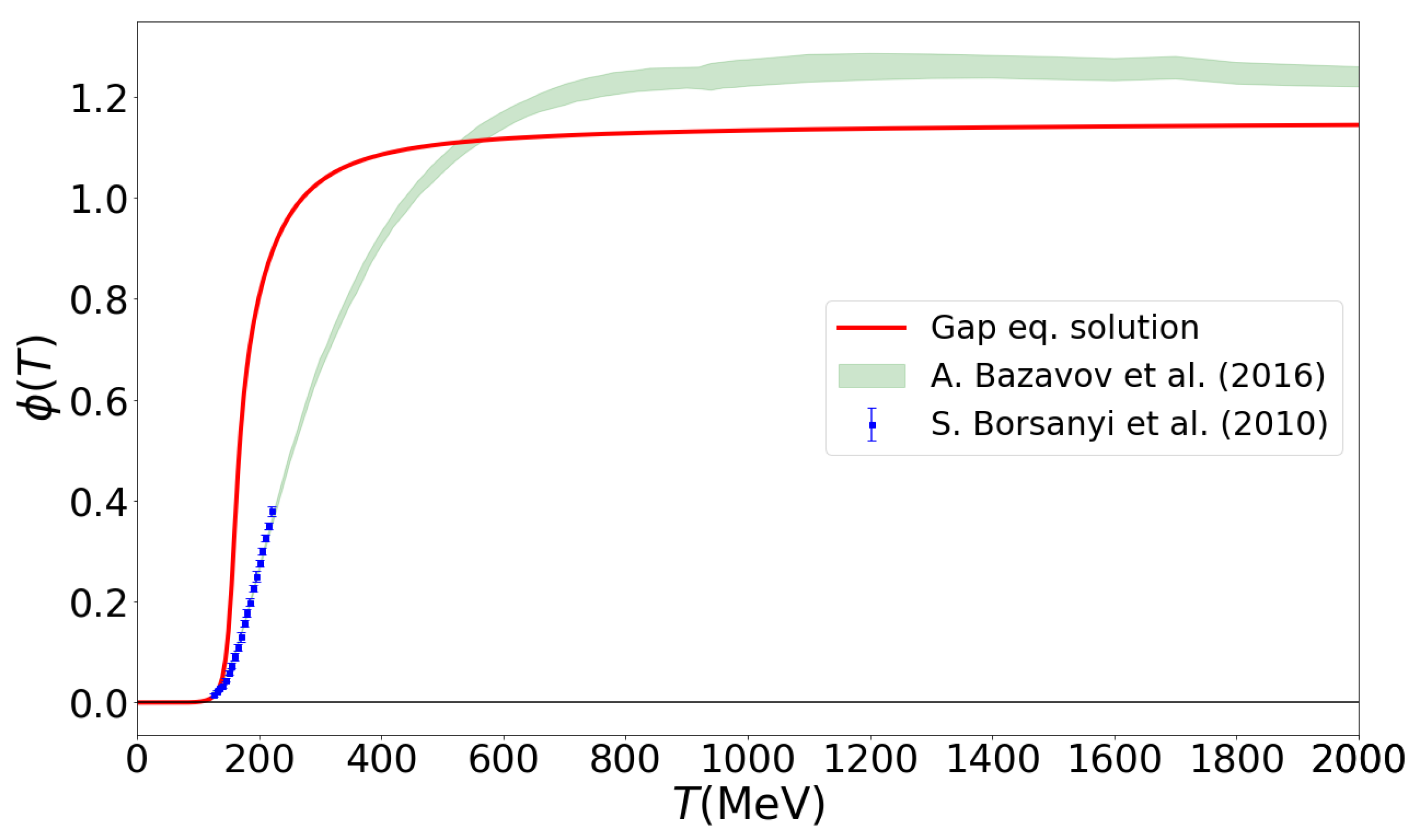
We performed the numerical solution of the gap Equation (23) for the traced Polyakov loop as a function of the temperature which enters via the coefficient of the Polyakov-loop potential (16) and the Boltzmann factors and Y of the distribution functions in the integrals (26) and (27). The result is shown in Figure 4 along with a comparison to the lattice QCD data for the renormalized Polyakov loop from the TUMQCD Collaboration [32] and the Wuppertal–Budapest Collaboration [1].
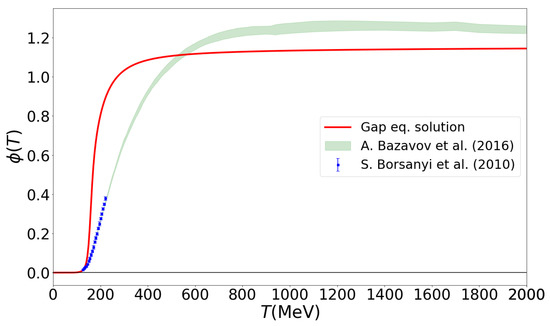
Figure 4.
The traced Polyakov loop from the solution of the stationarity condition (23) on the thermodynamical potential as a function of temperature (magenta solid line) compared with the lattice results for the renormalized Polyakov loop the TU Munich QCD (TUMQCD) Collaboration [32] (green band) and the Wuppertal–Budapest Collaboration [1] (blue symbols).
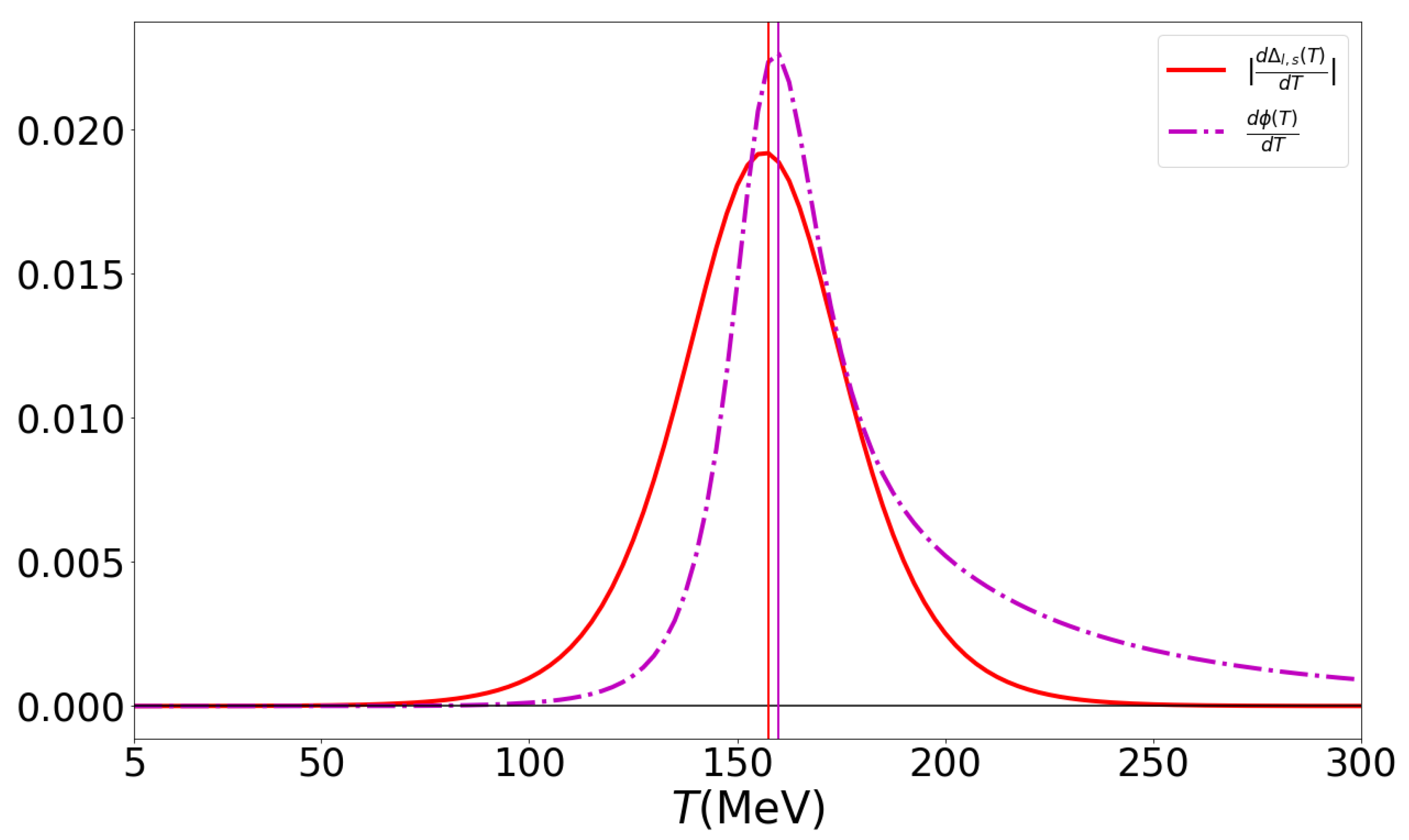
In Figure 5, we compare the Polyakov-loop susceptibility with the chiral susceptibility and obtain a strong synchronization effect of the chiral and Polyakov-loop crossover transitions. This is demonstrated by the almost coincident vertical lines indicating the peak positions of these transitions at MeV and MeV, respectively.
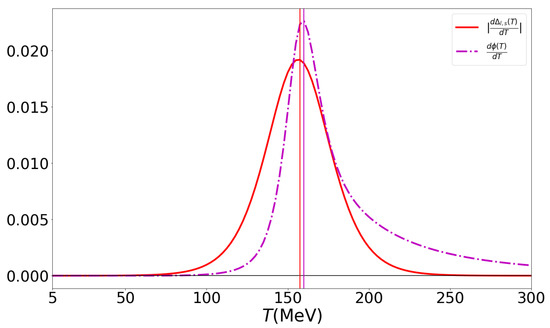
Figure 5.
The temperature derivatives of the chiral condensate (chiral susceptibility , red solid line) and of the Polyakov loop (Polyakov-loop susceptibility , ) as functions of temperature. The vertical lines indicate their almost coincident peak positions at MeV and MeV, respectively.
4.2. Pressure
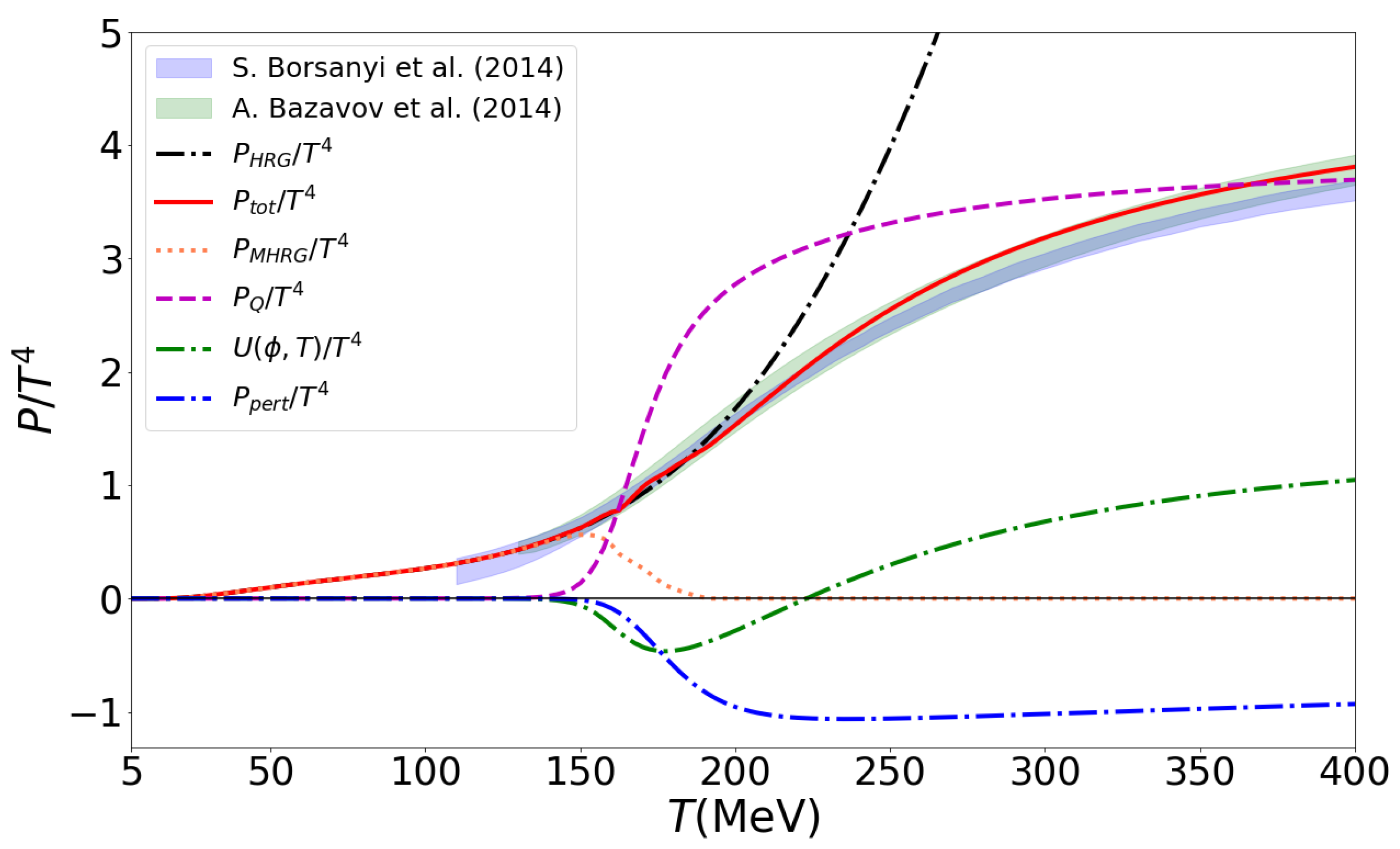
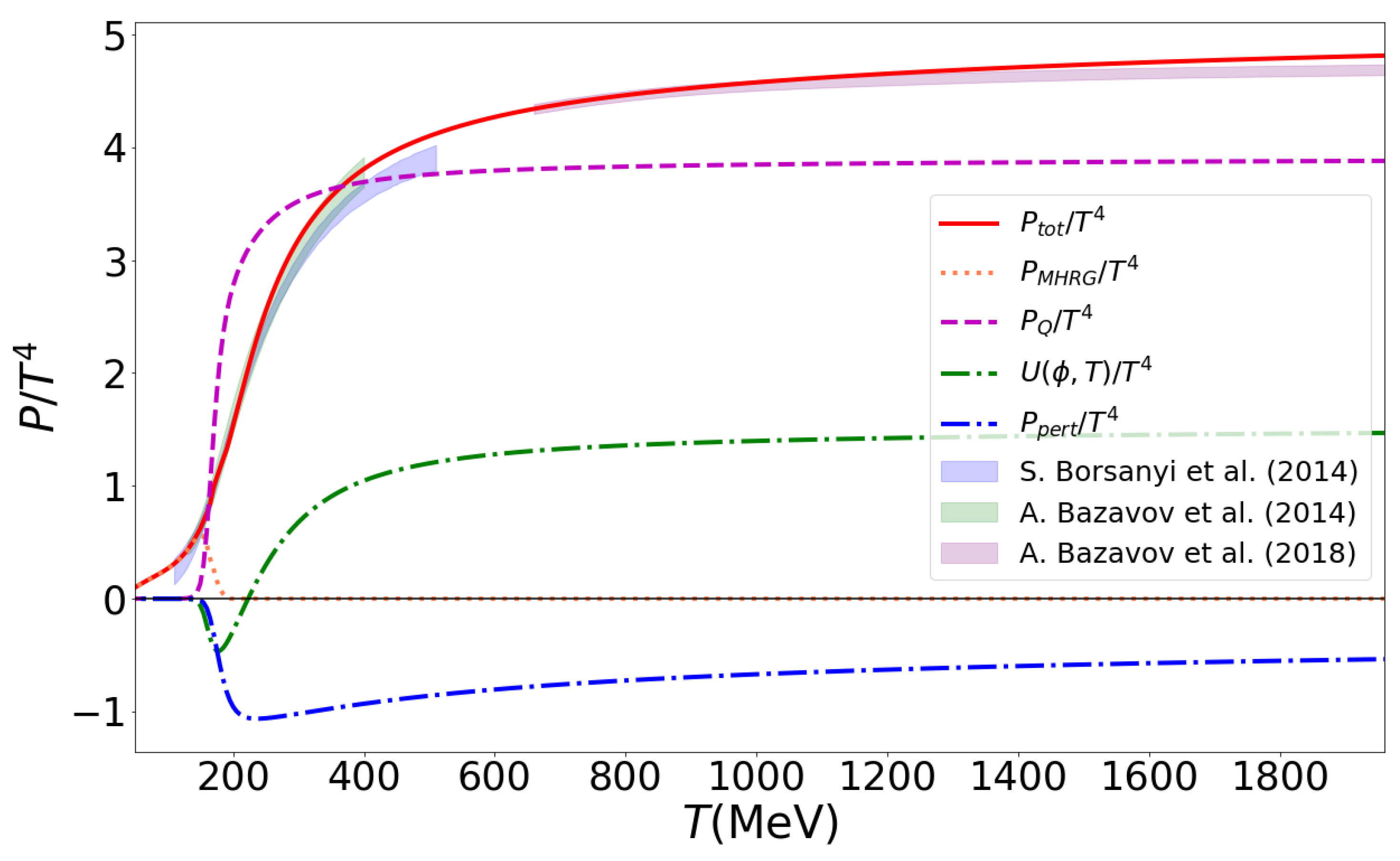
The main result of this work is a unified approach to the pressure of hadron–quark–gluon matter at finite temperatures that is in excellent agreement with lattice QCD thermodynamics (see Figure 6). The nontrivial achievement of the presented approach is that the Mott dissociation of the hadrons described by the MHRG model pressure conspires with the quark–gluon pressure described by the Polyakov-loop quark–gluon model with corrections in such a way that the resulting pressure as a function of temperature yields a smooth crossover behavior. By virtue of the Polyakov-loop-improved perturbative correction, the agreement with the lattice QCD thermodynamics extends to the high temperatures of MeV reported in [33]; see Figure 7.
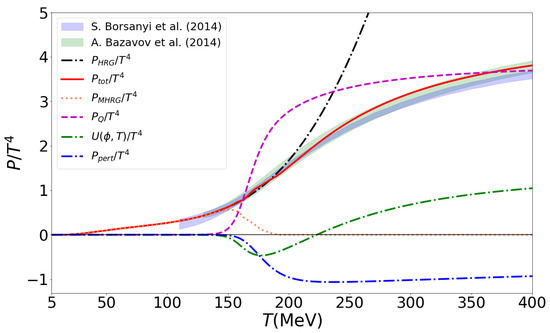
Figure 6.
The temperature dependence of the total scaled pressure (red solid line) and it’s constituents: MHRG (coral dotted line), quark (dashed magenta line), Polyakov-loop potential (dash–dotted green line) and perturbative QCD contribution (dash-dotted blue line) compared to the lattice QCD data: HotQCD Collaboration [4] (green band) and Wuppertal–Budapest Collaboration [3] (blue band).
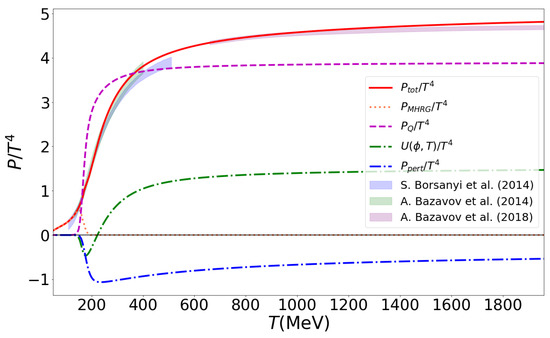
Figure 7.
The temperature dependence of the total scaled pressure (red solid line) and its constituents: MHRG (coral dotted line), quark (dashed magenta line), Polyakov-loop potential (dash-dotted green line) and perturbative QCD contribution (dash-dotted blue line) compared to the lattice QCD data: HotQCD Collaboration [4] (green band) and Wuppertal–Budapest Collaboration [3] (blue band), and the high-temperature result [33] (magenta band).
4.3. Quark Number Susceptibilities
In the present work, we did not consider the generalization of the approach to finite chemical potentials which would then allow us to evaluate the (generalized) susceptibilities as derivatives of pressure with respect to the corresponding chemical potential in appropriate orders. On that basis, ratios of susceptibilities could be formed as they indicate different aspects of the QCD transition between the limiting cases of a HRG and a QGP. Here, we would like to discuss, as an insight into these extensions of the approach, one of the simplest susceptibility ratios, namely the dimensionless ratio of quark number density to quark number susceptibility:
where and . This ratio (29) has two well-known limits. At low temperatures, in the hadron resonance gas phase, it is given by
while in the QGP phase for massless quarks it approaches
An evaluation of (29) for the present model for the QCD pressure would require its extension to a finite , which we will perform in a subsequent work. In the present model, we used our knowledge of the composition as a function of temperature to define a proxy for (29) by interpolating between the two known limits (30) and (31) with the partial pressure of the HRG, , as
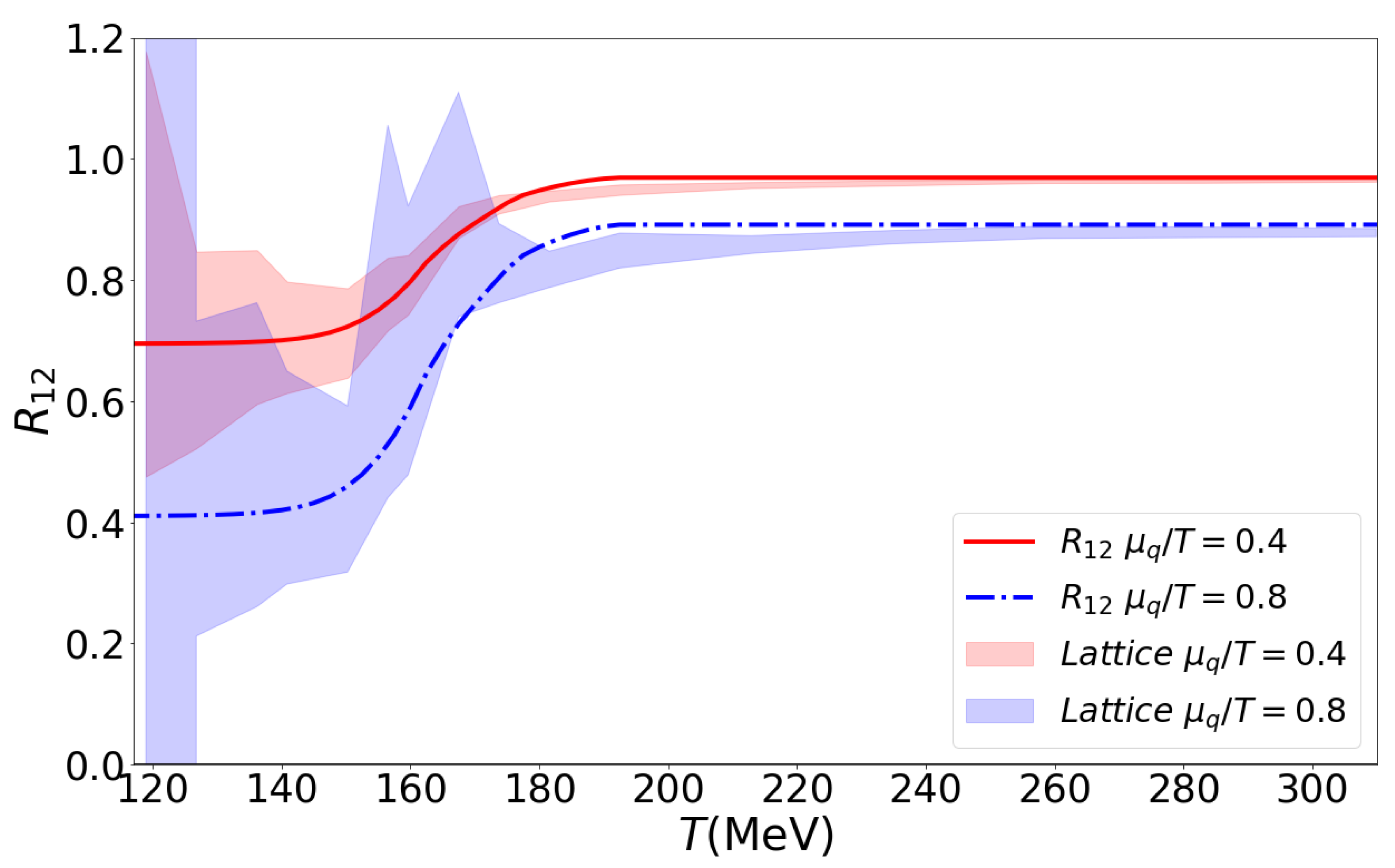
The result is shown in Figure 8 for two values of , for which lattice QCD results in the two-flavor case [34] are shown for a comparison. The fact that the present approach reproduces the transition between HRG and QGP asymptotics well in the narrow range of temperatures is a nontrivial result. In previous effective approaches to describe the finite-temperature lattice QCD thermodynamics results based on a spectral broadening of the HRG states, the transition to the QGP asymptotics occurred at a much higher temperature [35] or never [26,36,37]. In the latter case, the QGP asymptotic behavior is mimicked by an appropriate number of unaffected low-lying hadronic degrees of freedom.
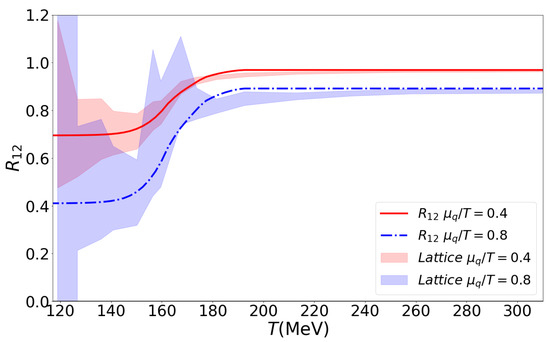
Figure 8.
The dimensionless ratio of quark number density to quark number susceptibility as a function of temperature for (red solid line) and (blue dash-dotted line) compared to the lattice QCD data [34] (red band), (blue band). For details, see text.
5. Discussion and Conclusions
The main result of the present work is a unified approach to the thermodynamic potential of hadron–quark–gluon matter at finite temperatures that is in excellent agreement with lattice QCD thermodynamics on the temperature axis of the QCD phase diagram. The key aspect to this approach is the quark cluster decomposition of the thermodynamic potential within the Beth–Uhlenbeck approach [38], which allowed us to implement the effect of Mott dissociation to the hadron resonance gas phase of low-temperature/low-density QCD. The MHRG model description includes, in principle, the information about the spectral properties of all hadronic channels with their discrete and continuous part of the spectrum, encoded in the hadronic phase shifts. Instead of solving the equations of motion with a coupled hierarchy of Schwinger–Dyson equations in the one, two and many-quark channels self-consistently (a formidable task of finite-temperature quantum field theory), we applied a schematic model for the in-medium phase shifts that was in accordance with the Levinson theorem and sufficiently general to be applicable for all multiquark cluster channels. This phase shift model requires only the knowledge of the vacuum mass spectrum which can come from the particle data group tables or from relativistic quark models and the medium dependence of the multi-quark continuum threshold.
The latter requires the knowledge of the quark mass (i.e., the chiral condensate) with its medium dependence as an order parameter of the chiral symmetry breaking and restoration. Since a quark mean field model of the (P)NJL type is not sufficient as it lacks the back-reaction from the hadron resonance gas on the quark propagator properties, we employ here the chiral condensate measured in continuum-extrapolated, full lattice QCD with physical current quark masses as an input. This procedure restricts the applicability of the present model to small chemical potentials only, where lattice QCD data for the chiral condensate are available. In a further development of the model, a beyond-mean-field derivation of the quark self-energy will be given. Furthermore, at the same level of approximation, the corresponding sunset-type diagrams for the functional of the 2PI approach should be derived and evaluated. This would allow us to calculate the generalized polarization-loop integrals which determine the analytic properties of the multi-quark states. These can be equivalently encoded in the corresponding medium-dependent phase shifts of the generalized Beth–Uhlenbeck approach, as has been demonstrated in particular examples for pions, diquarks [16,39] and nucleons [40] within the Polyakov-loop generalized NJL model.
Another important aspect of the present approach is that it leads to a relativistic density functional theory for QCD matter in the QCD phase diagram, with the known limits of the HRG and pQCD manifestly implemented. Such an approach allows us to predict the existence and location of critical endpoints in the QCD phase diagram, as has been demonstrated, e.g., in [41], where a dependence on a free parameter could have—besides the critical endpoint of the liquid–gas transition in the nuclear matter phase—another endpoint for the deconfinement transition or none. This “crossover all over” case of the QCD phase diagram is impossible to address with two-phase approaches that use a Maxwell construction for the phase transition. Other models that are in use for the analysis of the critical behavior of QCD (see, e.g., [42,43]) impose this by assuming a so-called “switch function” between HRG and QGP phases. They are valuable tools but do not have predictive power.
Author Contributions
Conceptualization, D.B.; Data curation, K.A.D.; Formal analysis, D.B. and K.A.D.; Funding acquisition, D.B.; Investigation, K.A.D.; Software, K.A.D.; Supervision, D.B. and O.K.; Validation, O.K.; Writing original draft, D.B.; Writing review and editing, D.B. and O.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research of D.B. was supported by the Russian Fund for Basic research under grant number 18-02-40137 and from the National Research Nuclear University (MEPhI) in the framework of the Russian Academic Excellence Project under contract number 02.a03.21.0005.
Acknowledgments
D.B. acknowledges discussions with Konstantin Maslov, Krzysztof Redlich and Ludwik Turko about this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Borsányi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabó, K.K.; Wuppertal-Budapest Collaboration. Is there still any Tc mystery in lattice QCD? Results with physical masses in the continuum limit III. J. High Energy Phys. 2010, 1009, 73. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabo, K.K. Full result for the QCD equation of state with 2+1 flavors. Phys. Lett. B 2014, 730, 99. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; HotQCD Collaboration; et al. Equation of state in (2 + 1)-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Dyson-Schwinger equations: Density, temperature and continuum strong QCD. Prog. Part. Nucl. Phys. 2000, 45, S1–S103. [Google Scholar] [CrossRef]
- Fischer, C.S. QCD at finite temperature and chemical potential from Dyson–Schwinger equations. Prog. Part. Nucl. Phys. 2019, 105, 1–60. [Google Scholar] [CrossRef]
- Tripolt, R.A.; Strodthoff, N.; von Smekal, L.; Wambach, J. Spectral Functions for the Quark-Meson Model Phase Diagram from the Functional Renormalization Group. Phys. Rev. D 2014, 89, 034010. [Google Scholar] [CrossRef]
- Gao, F.; Pawlowski, J.M. QCD phase structure from functional methods. Phys. Rev. D 2020, 102, 034027. [Google Scholar] [CrossRef]
- Gerber, P.; Leutwyler, H. Hadrons Below the Chiral Phase Transition. Nucl. Phys. B 1989, 321, 387–429. [Google Scholar] [CrossRef]
- Alkofer, R.; Maas, A.; Mian, W.A.; Mitter, M.; Paris-Lopez, J.; Pawlowski, J.M.; Wink, N. Bound state properties from the functional renormalization group. Phys. Rev. D 2019, 99, 054029. [Google Scholar] [CrossRef]
- Herbst, T.K.; Mitter, M.; Pawlowski, J.M.; Schaefer, B.J.; Stiele, R. Thermodynamics of QCD at vanishing density. Phys. Lett. B 2014, 731, 248–256. [Google Scholar] [CrossRef]
- Hüfner, J.; Klevansky, S.P.; Zhuang, P.; Voss, H. Thermodynamics of a quark plasma beyond the mean field: A generalized Beth-Uhlenbeck approach. Ann. Phys. 1994, 234, 225–244. [Google Scholar] [CrossRef]
- Zhuang, P.; Hüfner, J.; Klevansky, S.P. Thermodynamics of a quark - meson plasma in the Nambu-Jona-Lasinio model. Nucl. Phys. A 1994, 576, 525–552. [Google Scholar] [CrossRef]
- Wergieluk, A.; Blaschke, D.; Kalinovsky, Y.L.; Friesen, A. Pion dissociation and Levinson’s theorem in hot PNJL quark matter. Phys. Part. Nucl. Lett. 2013, 10, 660–668. [Google Scholar] [CrossRef]
- Yamazaki, K.; Matsui, T. Quark-Hadron Phase Transition in the PNJL model for interacting quarks. Nucl. Phys. A 2013, 913, 19–50. [Google Scholar] [CrossRef]
- Blaschke, D.; Buballa, M.; Dubinin, A.; Röpke, G.; Zablocki, D. Generalized Beth–Uhlenbeck approach to mesons and diquarks in hot, dense quark matter. Ann. Phys. 2014, 348, 228. [Google Scholar] [CrossRef]
- Yamazaki, K.; Matsui, T. Quark-hadron phase transition in a three flavor PNJL model for interacting quarks. Nucl. Phys. A 2014, 922, 237–261. [Google Scholar] [CrossRef]
- Torres-Rincon, J.M.; Aichelin, J. Equation of state of a quark-Polyakov loop-meson mixture in the PNJL model at finite temperature. arXiv 2016, arXiv:1601.01706. [Google Scholar]
- Torres-Rincon, J.M.; Aichelin, J. Equation of state of a quark-meson mixture in the improved Polyakov–Nambu–Jona-Lasinio model at finite chemical potential. Phys. Rev. C 2017, 96, 045205. [Google Scholar] [CrossRef]
- Blaschke, D.; Dubinin, A.; Radzhabov, A.; Wergieluk, A. Mott dissociation of pions and kaons in hot, dense quark matter. Phys. Rev. D 2017, 96, 094008. [Google Scholar] [CrossRef]
- Blaschke, D.; Dubinin, A.; Turko, L. Mott-hadron resonance gas and lattice QCD thermodynamics. arXiv 2016, arXiv:1611.09845. [Google Scholar] [CrossRef]
- Blaschke, D.; Dubinin, A.; Turko, L. Generalized Beth-Uhlenbeck approach to the equation of state for quark-hadron matter. Acta Phys. Polon. Supp. 2017, 10, 473–480. [Google Scholar] [CrossRef]
- Dubinin, A.; Blaschke, D.; Kalinovsky, Y.L. Pion and sigma meson dissociation in a modified NJL model at finite temperature. Acta Phys. Polon. Supp. 2014, 7, 215–223. [Google Scholar] [CrossRef]
- Cheng, M.; Christ, N.H.; Datta, S.; Heide, J.V.; Jung, C.; Karsch, F.; Kaczmarek, O.; Laermann, E.; Mawhinney, R.D.; Miao, C.; et al. The QCD equation of state with almost physical quark masses. Phys. Rev. D 2008, 77, 014511. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Karthik, N.; Laermann, E.; Lahiri, A.; Larsen, R.; HotQCD; et al. Chiral crossover in QCD at zero and non-zero chemical potentials. Phys. Lett. B 2019, 795, 15–21. [Google Scholar] [CrossRef]
- Turko, L.; Blaschke, D.; Prorok, D.; Berdermann, J. Mott-Hagedorn Resonance Gas and Lattice QCD Results. Acta Phys. Polon. Supp. 2012, 5, 485. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. D 2006, 73, 014019. [Google Scholar] [CrossRef]
- Kapusta, J.I. Finite Temperature Field Theory; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Peshier, A.; Kämpfer, B.; Soff, G. The QCD equation of state and quark star properties. arXiv 2003, arXiv:hep-ph/0312080. [Google Scholar]
- Shirkov, D.V. On the Fourier transformation of renormalization invariant coupling. Theor. Math. Phys. 2003, 136, 893. [Google Scholar] [CrossRef]
- Blaschke, D.; Kaczmarek, O.; Laermann, E.; Yudichev, V. Heavy quark potential and quarkonia dissociation rates. Eur. Phys. J. C 2005, 43, 81. [Google Scholar] [CrossRef]
- Bazavov, A.; Brambilla, N.; Ding, H.T.; Petreczky, P.; Schadler, H.P.; Vairo, A.; Weber, J.H. Polyakov loop in 2 + 1 flavor QCD from low to high temperatures. Phys. Rev. D 2016, 93, 114502. [Google Scholar] [CrossRef]
- Bazavov, A.; Petreczky, P.; Weber, J.H. Equation of State in 2 + 1 Flavor QCD at High Temperatures. Phys. Rev. D 2018, 97, 014510. [Google Scholar] [CrossRef]
- Allton, C.R.; Döring, M.; Ejiri, S.; Hands, S.J.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Redlich, K. Thermodynamics of two flavor QCD to sixth order in quark chemical potential. Phys. Rev. D 2005, 71, 054508. [Google Scholar] [CrossRef]
- Biro, T.S.; Jakovac, A. QCD above Tc: Hadrons, partons, and the continuum. Phys. Rev. D 2014, 90, 094029. [Google Scholar] [CrossRef]
- Turko, L.; Blaschke, D.; Prorok, D.; Berdermann, J. An effective model of QCD thermodynamics. J. Phys. Conf. Ser. 2013, 455, 012056. [Google Scholar] [CrossRef]
- Turko, L.; Blaschke, D.; Prorok, D.; Berdermann, J. Effective degrees of freedom in QCD thermodynamics. EPJ Web Conf. 2014, 71, 00134. [Google Scholar] [CrossRef]
- Bastian, N.U.F.; Blaschke, D.; Fischer, T.; Röpke, G. Towards a Unified Quark-Hadron Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions. Universe 2018, 4, 67. [Google Scholar] [CrossRef]
- Blaschke, D.; Dubinin, A.; Buballa, M. Polyakov-loop suppression of colored states in a quark-meson-diquark plasma. Phys. Rev. D 2015, 91, 125040. [Google Scholar] [CrossRef]
- Blaschke, D.; Dubinin, A.S.; Zablocki, D. NJL model approach to diquarks and baryons in quark matter. PoS BaldinISHEPPXXII 2015, 083. [Google Scholar] [CrossRef]
- Bastian, N.U.F.; Blaschke, D.B. A unified quark-nuclear matter equation of state from the cluster virial expansion within the generalized Beth–Uhlenbeck approach. Eur. Phys. J. A 2021, 57, 35. [Google Scholar] [CrossRef]
- Plumberg, C.J.; Welle, T.; Kapusta, J.I. QCD matter with a crossover and a first-order phase transition. PoS CORFU2018 2018, 157. [Google Scholar] [CrossRef]
- Parotto, P.; Bluhm, M.; Mroczek, D.; Nahrgang, M.; Noronha-Hostler, J.; Rajagopal, K.; Ratti, C.; Schäfer, T.; Stephanov, M. QCD equation of state matched to lattice data and exhibiting a critical point singularity. Phys. Rev. C 2020, 101, 034901. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).