Application of Wind Tunnel Device for Evaluation of Biokinetic Parameters of Running
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Participants
2.3. The Basic Characteristics of the Wind Tunnel
2.4. Experimental Procedure
- –
- Vertical reaction impulse Jvert, braking impulse Jdec, and accelerator impulse Jacc:
- –
- Contact time:
- –
- Time-averaged contact time:
- –
- Running frequency:
- –
- Time-averaged frequency:
- –
- Stride length
- –
- Time-averaged stride length:
3. Results
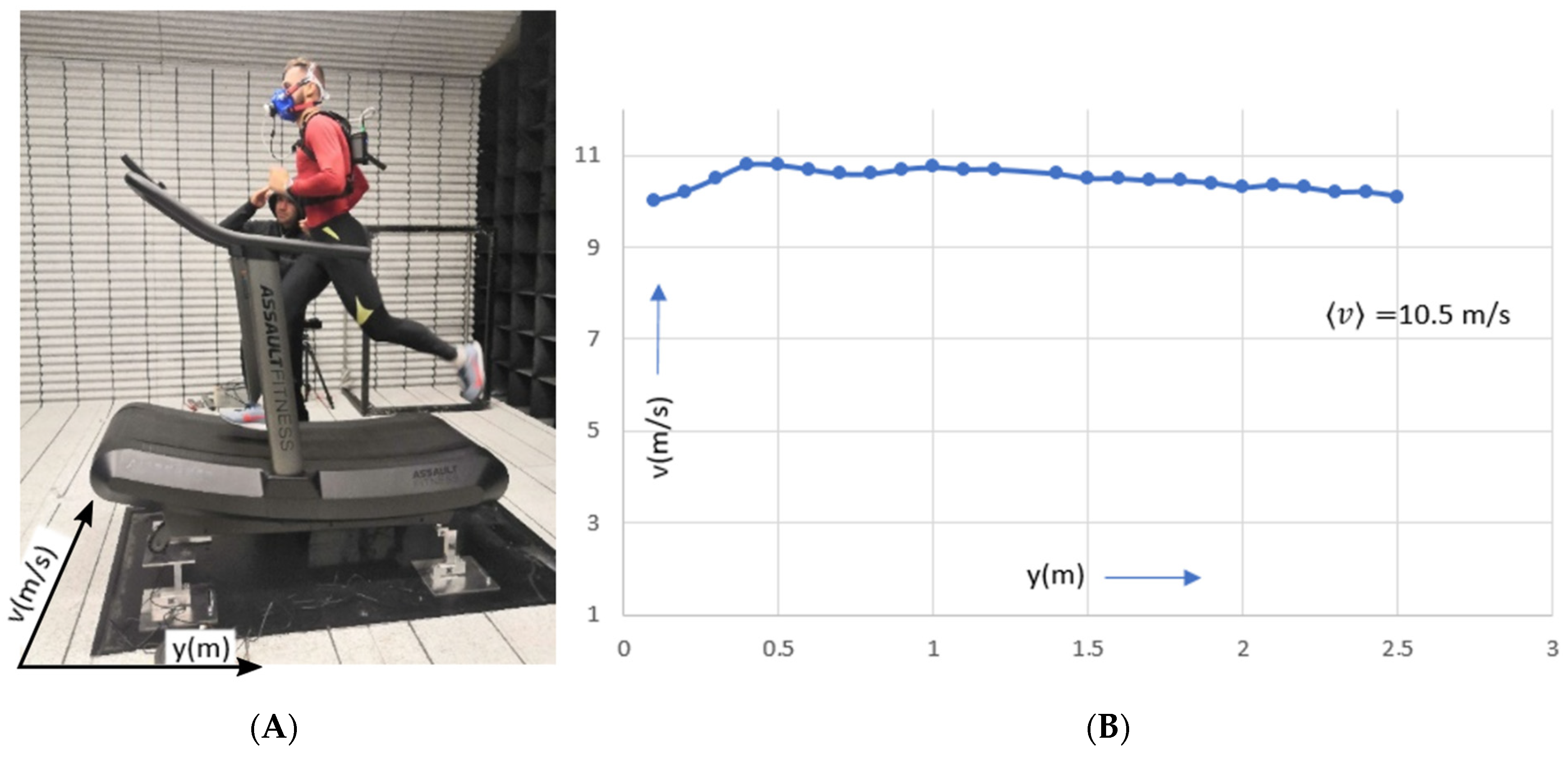
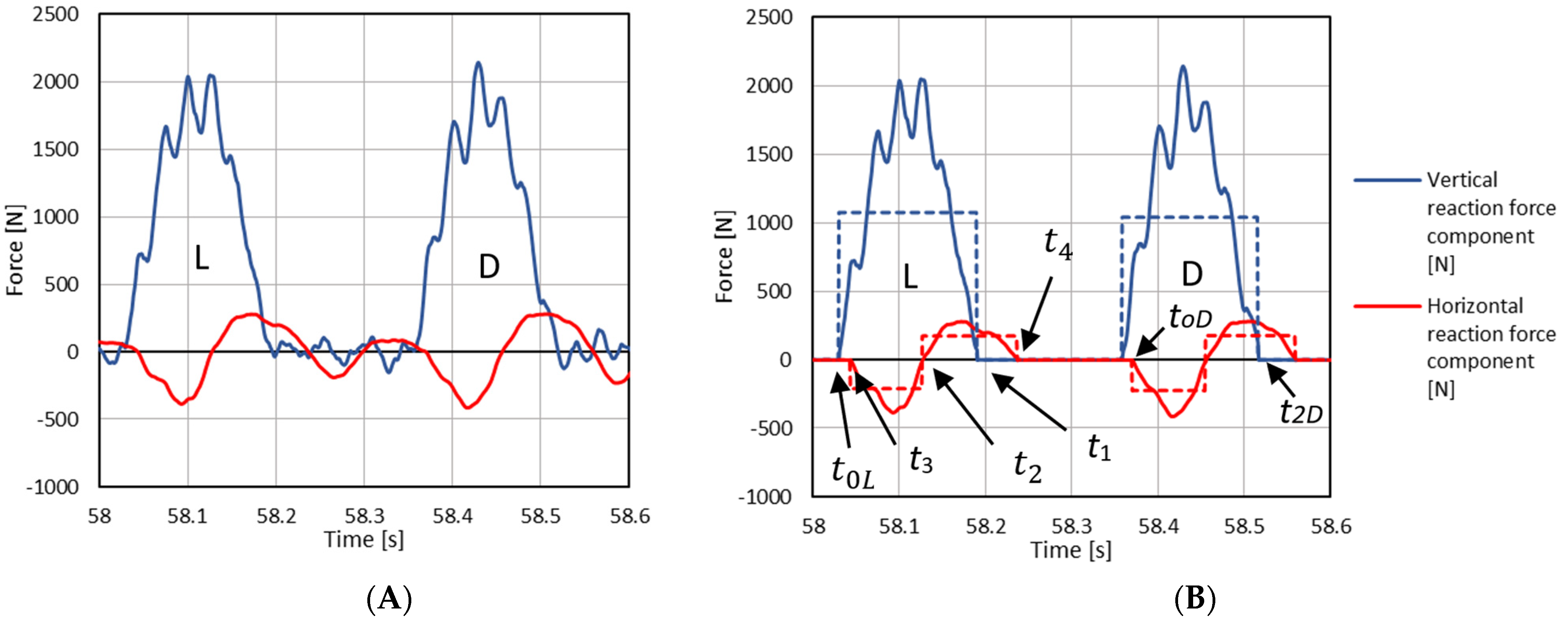
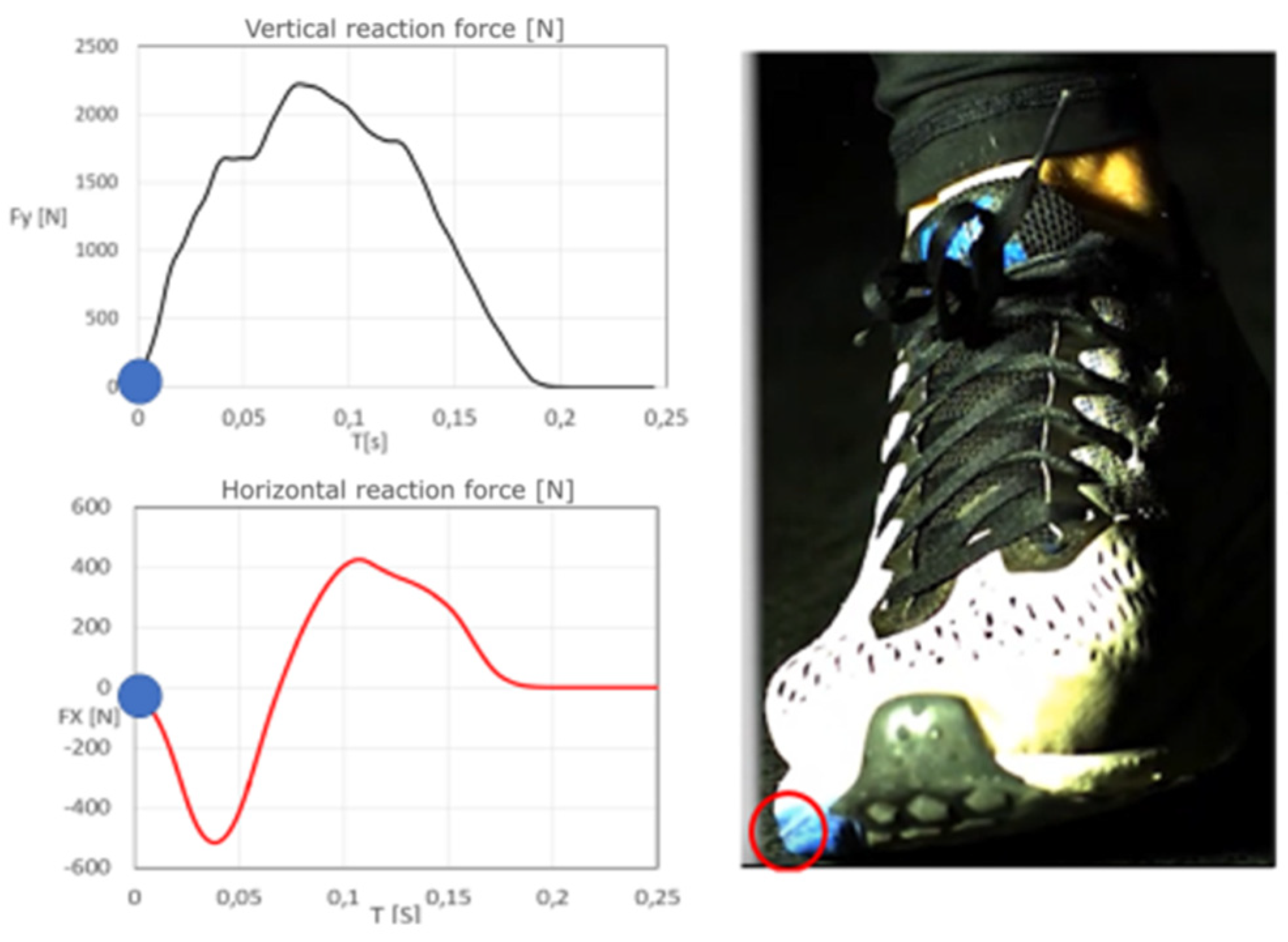
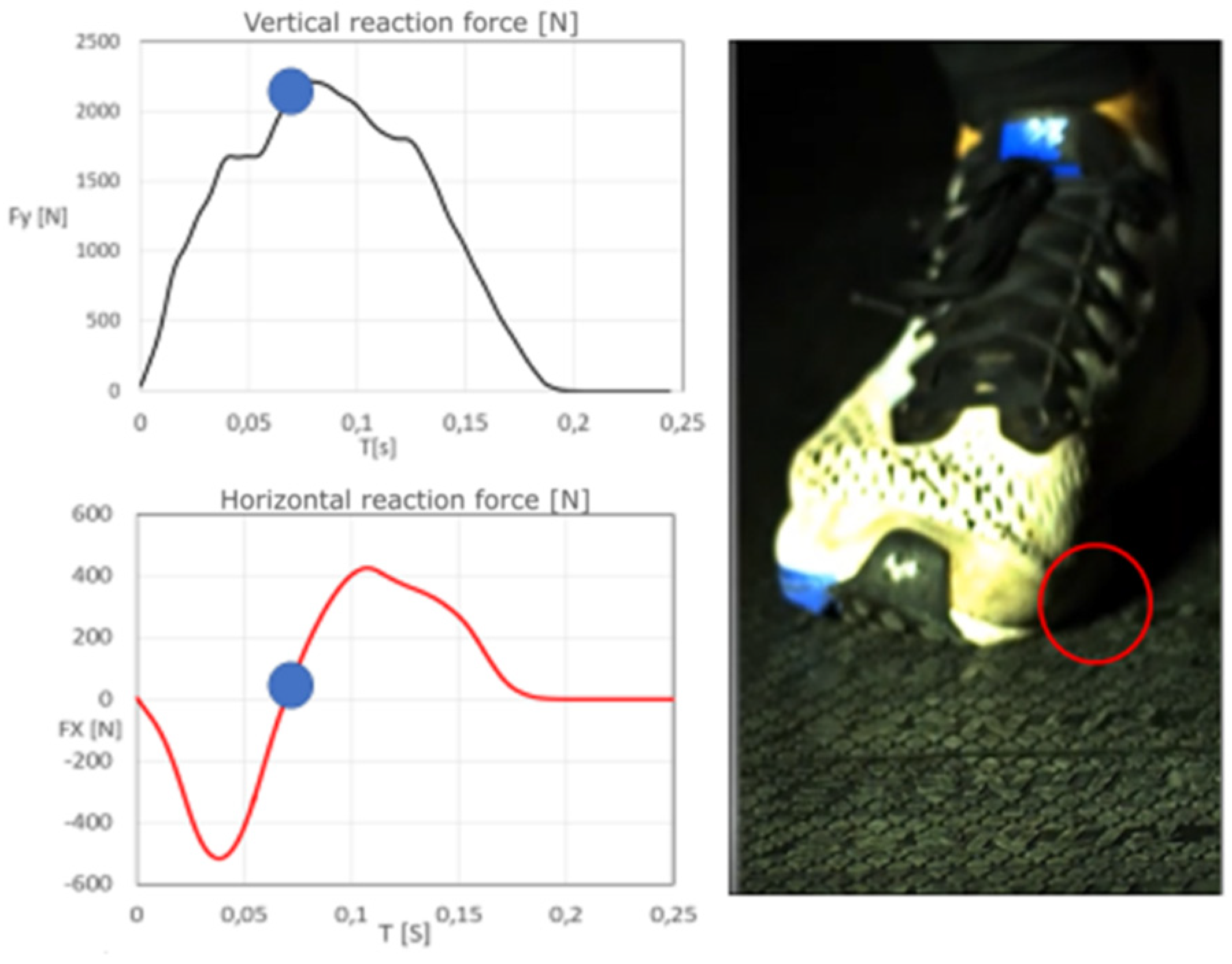
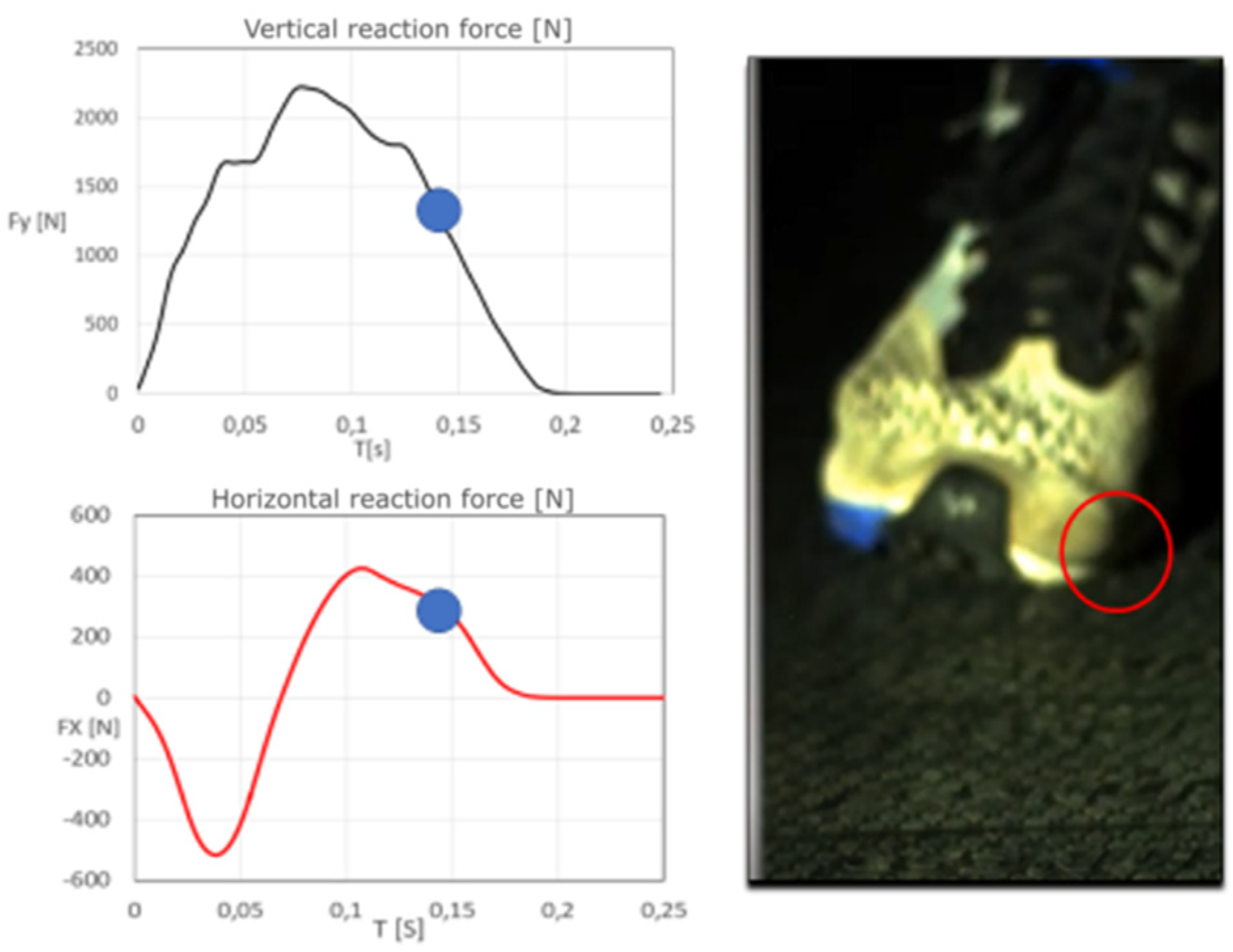
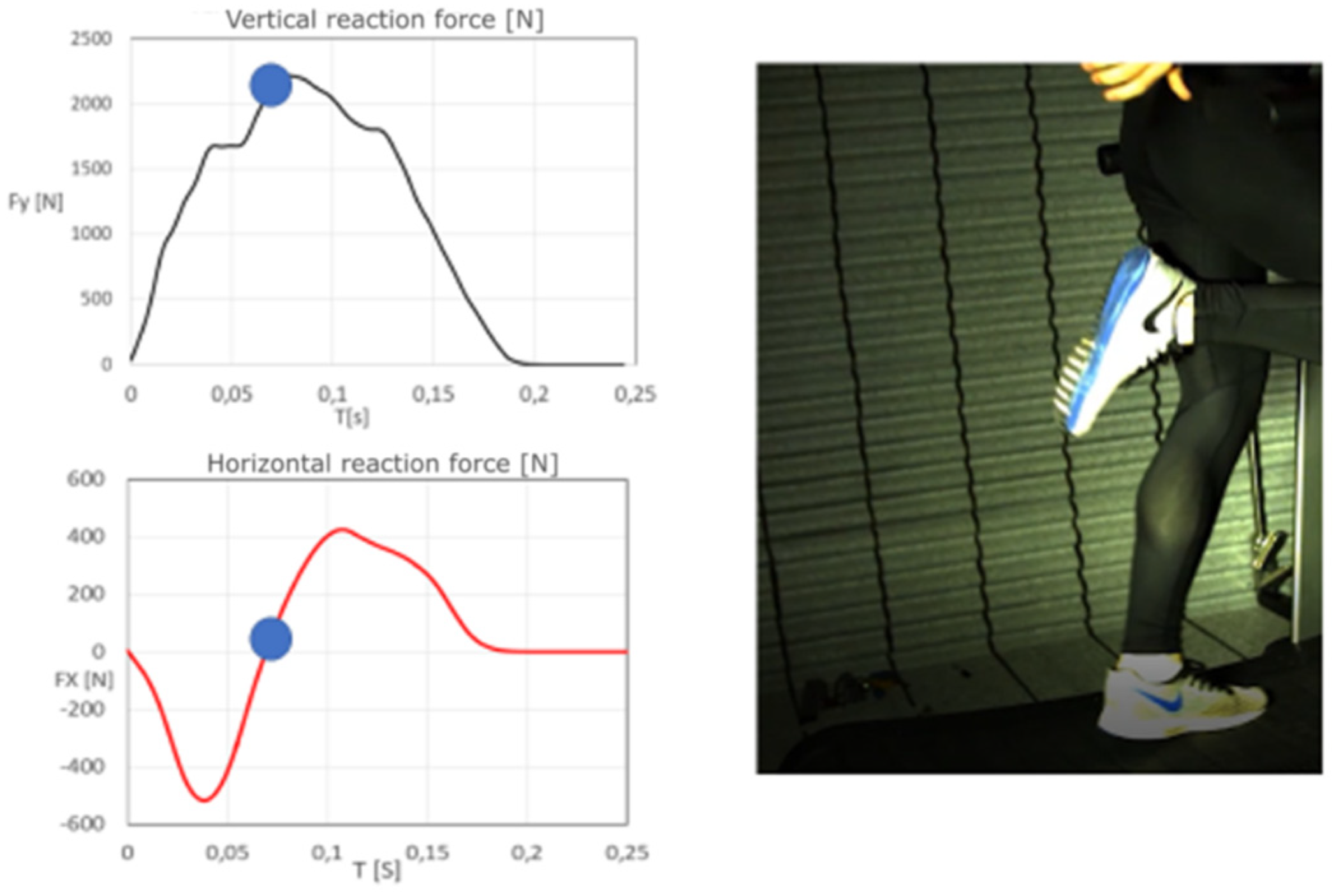
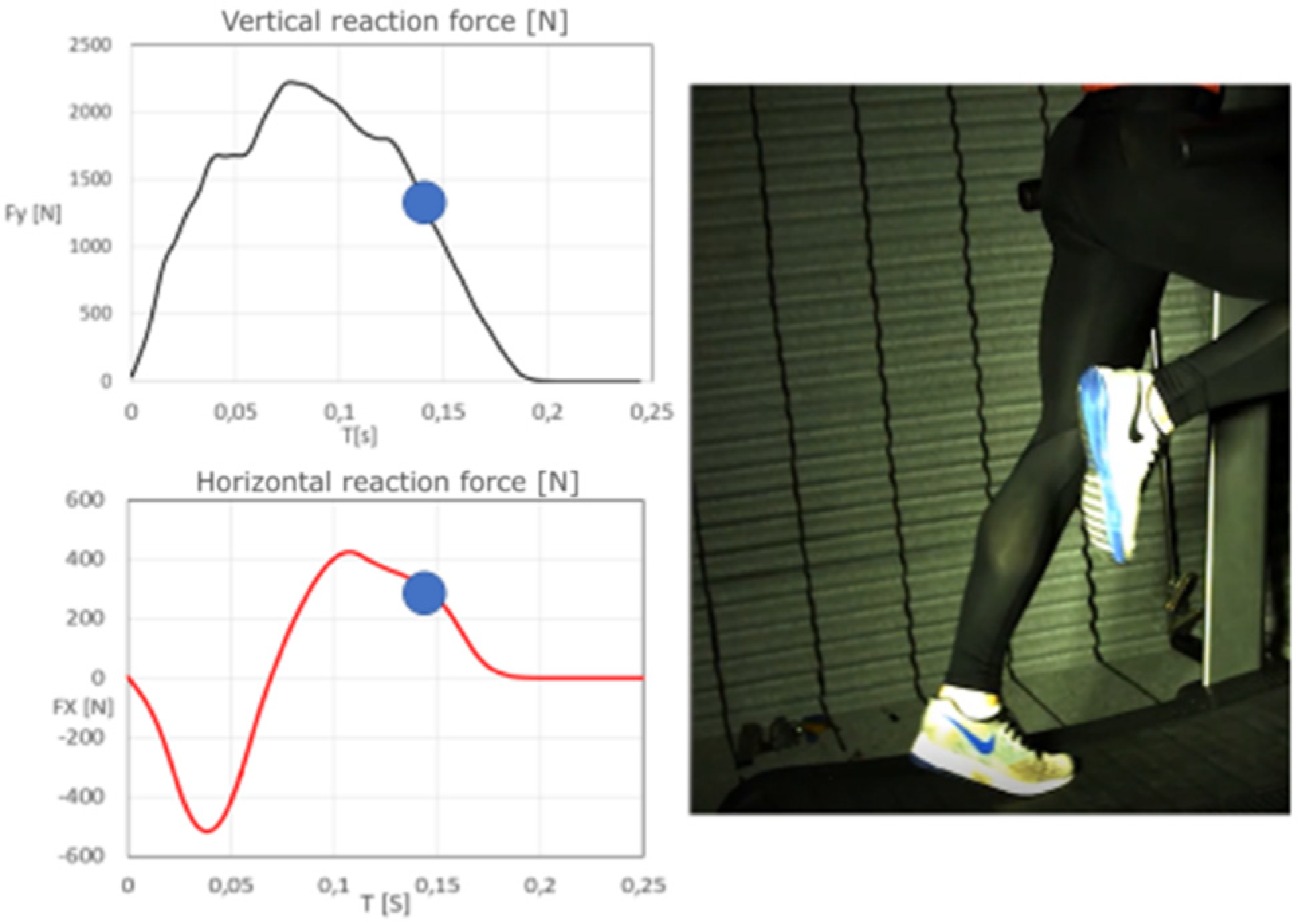
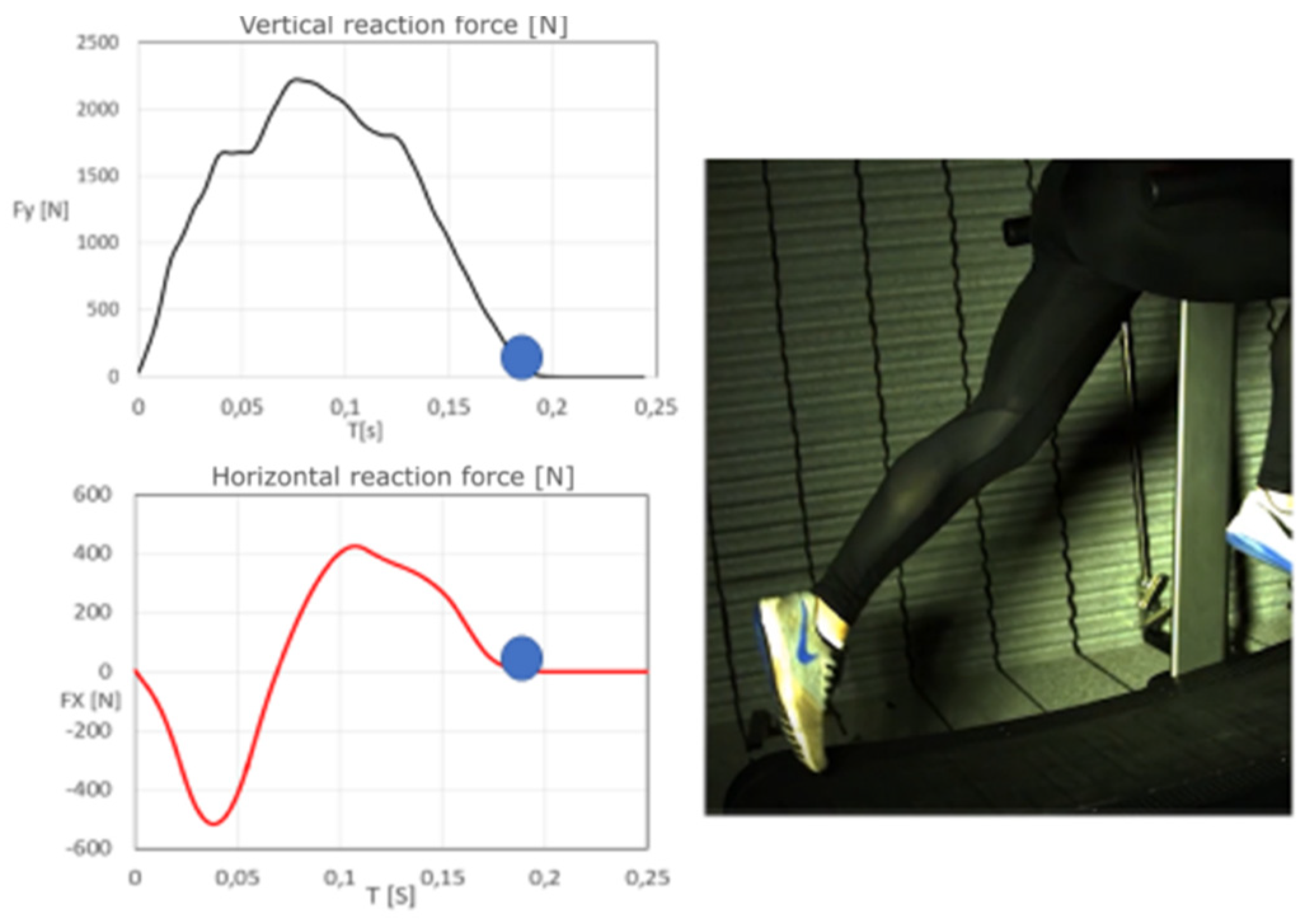
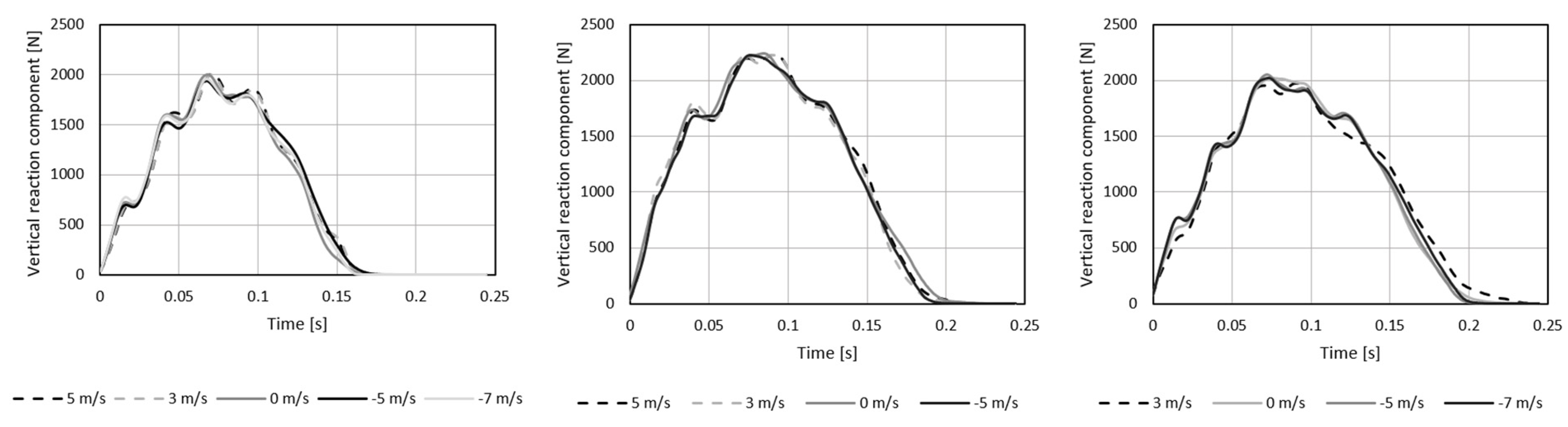
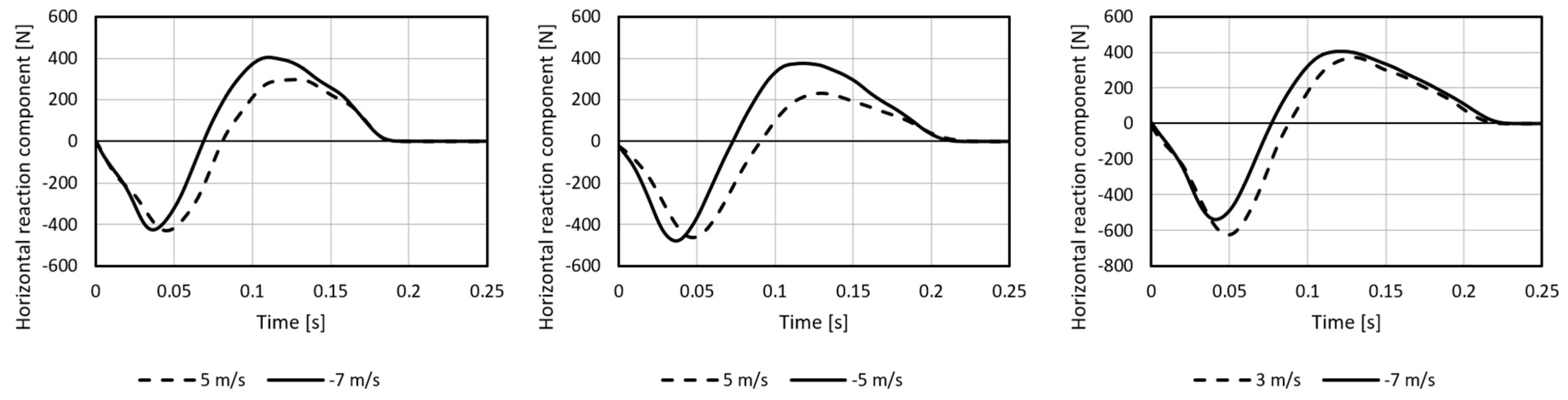
3.1. Simultaneous Analysis of the Running Topology and the Measured Forces of the Athlete on the Running Surface
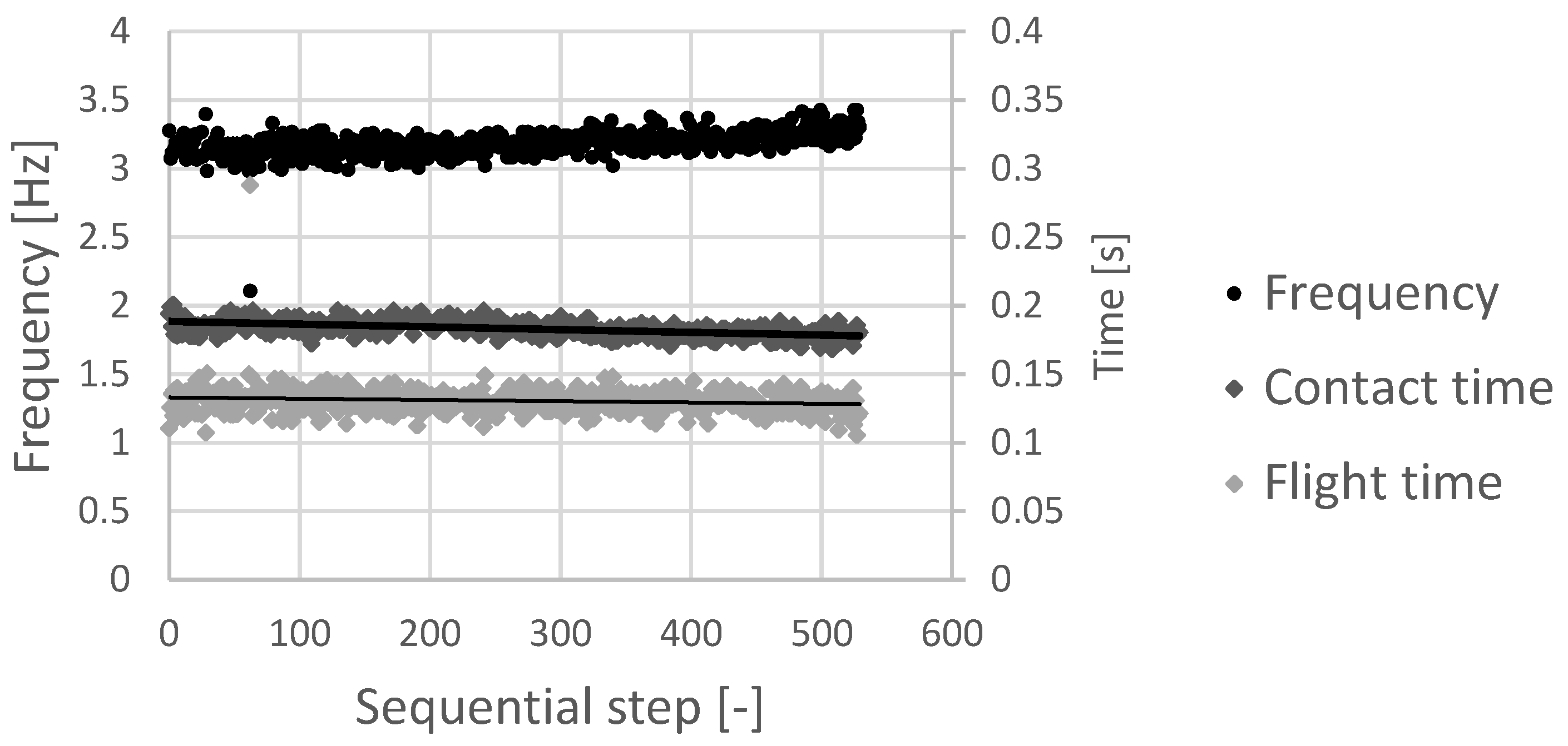
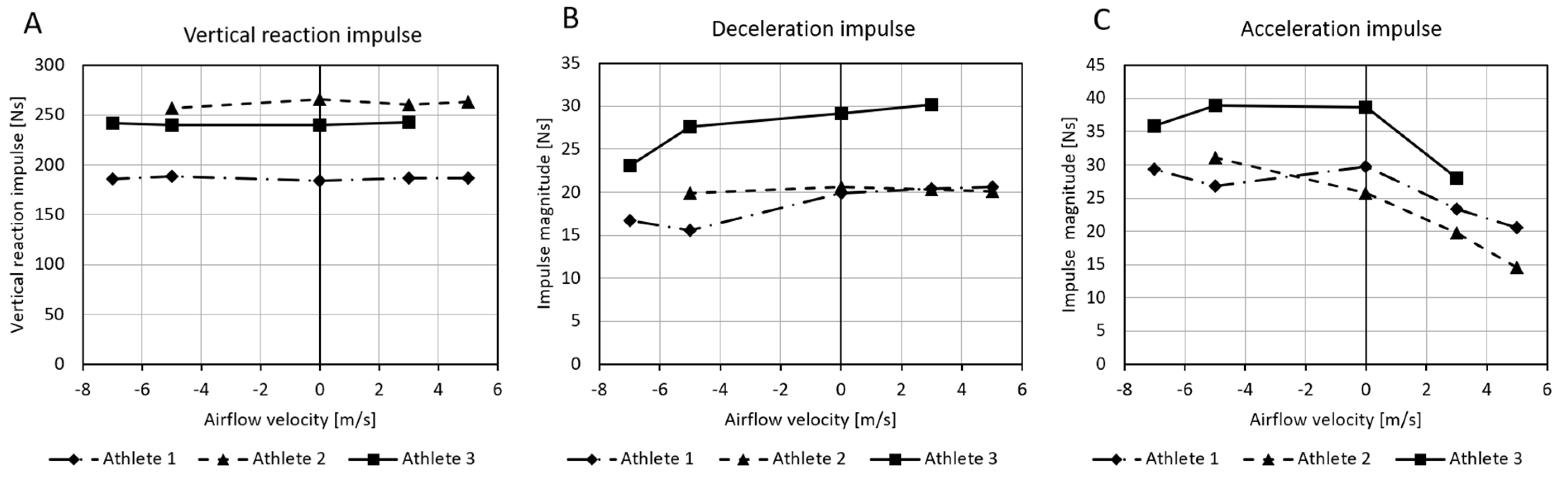
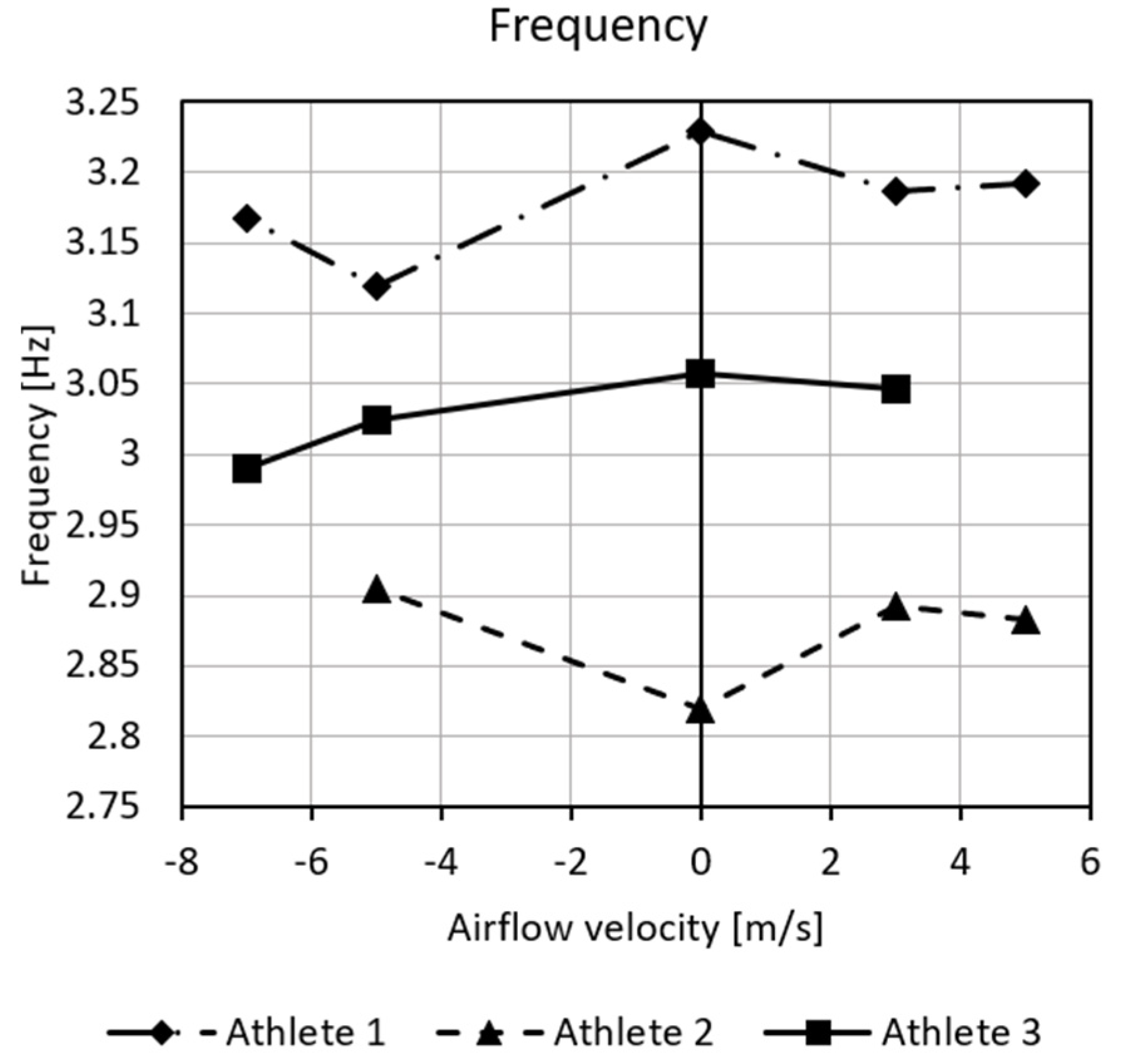
3.2. Integral Analysis of Kinematic and Dynamic Running Characteristics and the Impact of Airflow in the Wind Tunnel
4. Discussion
4.1. The Analysis of the Running Topology and the Forces Measurement on the Treadmill Surface
4.2. The Impact of Airflow on Kinematic and Dynamic Characteristics of Running
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davis, C.T. Effects of wind assistance and resistance on the forward motion of a runner. J. Appl. Physiol. 1980, 48, 702–709. [Google Scholar] [CrossRef]
- Saraslanidis, P. Training for the improvement of maximum speed: Flat running or resistance training? New Stud. Athl. 2000, 15, 45–51. [Google Scholar]
- De Witt, J.K.; Lee, S.M.; Wilson, C.A.; Hagan, R.D. Determinants of time to fatigue during nonmotorized treadmill exercise. J. Strength Cond. Res. 2009, 23, 883–890. [Google Scholar] [CrossRef] [PubMed]
- Fullenkamp, A.M.; Matthew Laurent, C.; Campbell, B.M. Automated gait temporal-spatial assessment fromnon-motorized treadmill belt speed data. Gait Posture 2015, 41, 141–145. [Google Scholar] [CrossRef] [PubMed]
- Stevens, C.J.; Hacene, J.; Wellham, B.; Sculley, D.V.; Callister, R.; Taylor, L.; Dascombe, B.J. The validity of endurance running performance on the Curve 3TM non-motorised treadmill. J. Sports Sci. 2014, 33, 1141–1148. [Google Scholar] [CrossRef]
- Gonzalez, A.M.; Wells, A.J.; Hoffman, J.R.; Stout, J.R.; Fragala, M.S.; Mangine, G.T.; McCormack, W.P.; Townsend, J.R.; Jajtner, A.R.; Emerson, N.S.; et al. Reliability of the Woodway curve non-motorized treadmill for assessing anaerobic performance. J. Sports Sci. Med. 2013, 12, 104–108. [Google Scholar] [PubMed]
- Mangine, G.T.; Hoffman, J.R.; Gonzalez, A.M.; Wells, A.J.; Townsend, J.R.; Jajtner, A.R.; McCormack, W.P.; Robinson, E.H.; Fragala, M.S.; Fukuda, D.H.; et al. Speed, force, and power values produced from nonmotorized treadmill test are related to sprinting performance. J. Strength Cond. Res. 2014, 28, 1812–1819. [Google Scholar] [CrossRef][Green Version]
- Rae, W.H.; Pope, A. Low-Speed Wind Tunnel Testing, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- National Aeronautics and Space Administration. Wind-Tunnel Model Systems Criteria; Langley Research Center: Hampton, VA, USA, 2015. [Google Scholar]
- Placek, R. Errors and problems while conducting research studies in wind tunnel-selected examples. Trans. Inst. Aviat. 2016, 4, 69–177. [Google Scholar]
- Ito, S. Aerodynamic effects by marathon pacemakers on a main runner. Trans. Jpn. Soc. Mech. Eng. Ser. B 2006, 73, 1975–1980. [Google Scholar] [CrossRef]
- Hirata, K.; Okayama, T.; Teraoka, T.; Funaki, J. Precise aerodynamic measurement of track runner using a wind-tunnel moving-belt system. Procedia Eng. 2012, 34, 32–37. [Google Scholar] [CrossRef]
- Tatsuya, I.; Takafumi, O.; Takahiro, T.; Satoshi, M.; Hirata, K. Wind-tunnel experiment on aerodynamic characteristics of a runner using a moving-belt system. Cogent Eng. 2016, 3, 1231–1389. [Google Scholar]
- Mero, A. Force-Time Characteristics and Running Velocity of Male Sprinters during the Acceleration Phase of Sprinting. Res. Q. 1988, 59, 94–98. [Google Scholar] [CrossRef]
- Gambetta, V. Essential consideration for development of teaching model for 100 m sprints. New Stud. Athl. 1991, 1, 36–42. [Google Scholar]
- Donatti, A. The development of stride lenght and frequency in sprinting. New Stud. Athl. 1995, 10, 51–66. [Google Scholar]
- Morin, J.B.; Sève, P. Sprint running performance: Comparison between treadmill and field conditions. Eur. J. Appl. Physiol. 2011, 111, 1695–1703. [Google Scholar] [CrossRef]
- Morin, J.B.; Samozino, P.; Bonnefoy, R.; Edouard, P.; Belli, A. Direct measurement of power during one single sprint on treadmill. J. Biomech. 2010, 43, 1970–1975. [Google Scholar] [CrossRef]
- Novacheck, T. The biomechanics of running. Gait Posture 1998, 7, 77–95. [Google Scholar] [CrossRef]
- Mero, A.; Komi, P.; Gregor, R. Biomechanics of Sprint Running. Sport Med. 1992, 13, 376–392. [Google Scholar] [CrossRef] [PubMed]
- Shanebrook, J.R.; Jaszczak, R.D. Aerodynamic drag analysis of runners. Med. Sci. Sports Exerc. 1976, 8, 43–45. [Google Scholar] [CrossRef]
- Kyle, C. Reduction of wind resistance and power output of racing cyclists and runners travelling in groups. Ergonomics 1979, 22, 387–397. [Google Scholar] [CrossRef]
- Maćkała, K.; Fostiak, M. Acute effects of plyometric intervention—Performance improvement and related changes in sprinting gait variability. J. Strength Cond. Res. 2015, 29, 1956–1965. [Google Scholar] [CrossRef]
- Mann, R.; Sprague, P. A kinetic analysis of the ground leg during sprint running. Res. Q. Exerc. Sport 1980, 51, 334–348. [Google Scholar] [CrossRef]
- Mero, A.; Komi, P. Electromyographic activity in sprinting at speed ranging from sub-maximal to supra-maximal. Med. Sci. Sports Exerc. 1987, 19, 266–274. [Google Scholar] [CrossRef]
- Morin, J.B.; Dalleau, G.; Kyrolainen, H.; Jeannin, T.; Belli, A. A simple method for measuring stiffness during running. J. Appl. Biomech. 2011, 21, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Luhtanen, P.; Komi, P. Force-, power- and elasticity-velocity relationship in walking, running and jumping. Eur. J. Appl. Physiol. 1980, 44, 79–289. [Google Scholar] [CrossRef]
- Morin, J.B. Sprint Running Mechanics New technology, new concepts, new perspectives. Aspetar Sports Med. J. 2020, 2, 326–332. [Google Scholar]
- Young, W. Laboratory strength assessment of athletes. New Stud. Athl. 1995, 10, 89–96. [Google Scholar]
- Bret, C.; Rahmani, A.; Dufour, A.; Messonnier, L.; Lacour, J. Leg strength and stiffness as ability factors in 100 m sprint running. J. Sports Med. Phys. Fit. 2002, 42, 274–281. [Google Scholar]
- Delecluse, C.; Coppenolle, H.; Goris, M. A model for the scientific preparation of high level sprinters. New Stud. Athl. 1992, 7, 57–64. [Google Scholar]
- Prampero, P.; Fusi, S.; Sepulcri, J.; Morin, B.; Belli, A.; Antonutto, G. Sprint running: A new energetic approach. J. Exp. Biol. 2005, 208, 2809–2816. [Google Scholar] [CrossRef]
- Cronin, J.; Hansen, T. Strength and power predictors of sports speed. J. Strength Cond. Res. 2005, 19, 349–357. [Google Scholar] [PubMed]
- Nicol, C.; Avela, J.; Komi, P. The Stretch-Shortening Cycle. Sports Med. 2006, 36, 977–999. [Google Scholar] [CrossRef] [PubMed]
- Hay, J. The Biomechanics of Sports Techniques, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]






| Athlete 1 | Athlete 2 | Athlete 3 | |
| Age (years) | 26 | 22 | 28 |
| Height [cm] | 171 | 186 | 183 |
| Body Mass [kg] | 58 | 72 | 74 |
| 1500 m (PR) * | 03.59, 0 | 03.58, 75 | 03.58, 8 |
| Nominal volume flow rate in the wind tunnel | 510 m3/s |
| Cross-section of the vertical section | Φ 3.6 m |
| Maximum airflow velocity in the vertical section of the wind tunnel | 61 m/s |
| Nominal total pressure differential on installed fans | 4300 Pa |
| Air density range in the wind tunnel | 1.1–1.2 kg/m3 |
| Nominal electrical power of fans | 2.2 MW |
| Nominal volume flow rate in the wind tunnel | 124 m3/s |
| Transverse section of horizontal section A | 10.5 m2 |
| Maximum airflow velocity in the vertical section of the wind tunnel | 45 m/s |
| V1 (m/s) | V2 (m/s) | V3 (m/s) | V4 (m/s) | V5 (m/s) | |
|---|---|---|---|---|---|
| Athlete 1 | 5 | 3 | 0 | −5 | −7 |
| Athlete 2 | 5 | 3 | 0 | −5 | |
| Athlete 3 | 3 | 0 | −5 | −7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Širok, B.; Gostiša, J.; Sečnik, M.; Mackala, K.; Čoh, M. Application of Wind Tunnel Device for Evaluation of Biokinetic Parameters of Running. Symmetry 2021, 13, 505. https://doi.org/10.3390/sym13030505
Širok B, Gostiša J, Sečnik M, Mackala K, Čoh M. Application of Wind Tunnel Device for Evaluation of Biokinetic Parameters of Running. Symmetry. 2021; 13(3):505. https://doi.org/10.3390/sym13030505
Chicago/Turabian StyleŠirok, Brane, Jurij Gostiša, Matej Sečnik, Krzysztof Mackala, and Milan Čoh. 2021. "Application of Wind Tunnel Device for Evaluation of Biokinetic Parameters of Running" Symmetry 13, no. 3: 505. https://doi.org/10.3390/sym13030505
APA StyleŠirok, B., Gostiša, J., Sečnik, M., Mackala, K., & Čoh, M. (2021). Application of Wind Tunnel Device for Evaluation of Biokinetic Parameters of Running. Symmetry, 13(3), 505. https://doi.org/10.3390/sym13030505







