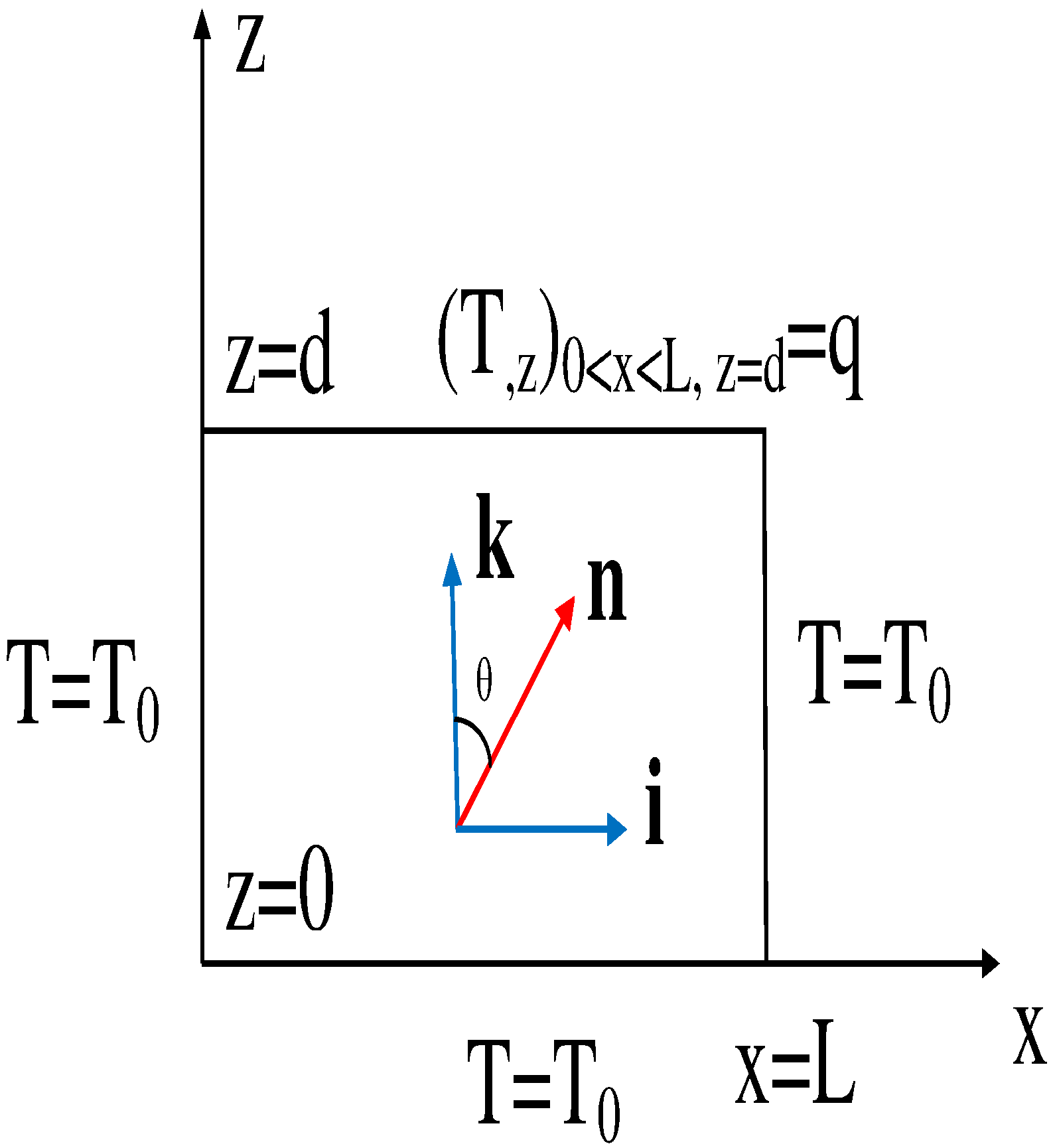In an attempt to better understand the dissipation processes in microfluidic nematic systems confined in the various microsized geometries, under the influences the temperature gradient, we will review a number of numerical studies of these nematic systems. With this aim, a number of theories which include the hydrodynamic equations describing both the director reorientation and flow of nematic fluid, as well as the redistribution of the temperature field, will be described. These equations also will be supplemented by appropriate anchoring conditions for the director field on the bounding surfaces, as well as the no-slip condition for the velocity field. Since the geometry of the microsized nematic channel or capillary affects the nature of the hydrodynamic flow that is formed, two cases will be considered. The first is when dealing with a rectangular channel, and second is the cylindrical capillary.
2.1. Formulation of the Balance of the Momentum and Torque Equations and Conductivity Equation for Nematic Fluids Confined in Rectangular Channel
The aim of this section is to show some useful routes for further examining of the validity of theoretical treatment of the orientational dynamics in the microsized rectangular nematic channel under the effect of externally directed heat flux
across the bounding surface. It will be done in the framework of the extended Ericksen–Leslie theory [
16,
17], supplemented by the thermomechanical correction of shear stress [
7,
15], and the entropy balance equation [
18]. The first part of the section is devoted to the hydrodynamic model, which is the basis for describing the formation of flows in microsized hybrid aligned nematic (HAN) channels and capillaries under the action of the thermomechanical force. This force is the result of interaction of the director
and temperature
T gradients, and it is responsible for the formation of the hydrodynamic flow
in these channels. In our case, the temperature gradient
in the HAN channels is formed by focused laser radiation. In the second part of the section, a numerical analysis of two modes of heating the LC channels is given. These modes are characterized by different laser radiation power and duration: slow and fast heating modes caused by the laser irradiation focused on the lower boundary of the HAN channel.
With this aim we consider the microsized HAN channel delimited by two lower and upper horizontal solid surfaces, located at
and
, respectively, and two lateral solid surfaces at distance
L on scale on the order of micrometers. The coordinate system defined by this task assumes that the director
, where
denotes the polar angle, i.e., the angle between the direction of the director
and the normal
to the horizontal boundary surfaces, is in the
plane. Here,
is the unit vector directed parallel to the horizontal boundaries of the HAN channel, and
(see
Figure 1).
We shall be considering the HAN with the heat flux
across the upper boundary
whereas on the remaining boundaries the temperature is kept constant
Here
is the heat conductivity coefficient perpendicular to the director
. Therefore, the hybrid aligned nematic state, where at the upper boundary of the channel, the nematic phase is anchored homogeneously and the bulk of the nematic sample contains a gradient in
from homeotropic orientation at the lower surface to planar orientation at the upper surface, i.e.,
or
Taking into account that the width of the nematic channel
μm, one can assume that the mass density
across the HAN channel, and one deals with an incompressible fluid. In turn, the incompressibility condition
assumes that
where
and
are the components of the vector
, and
.
The hydrodynamic equations describing the reorientation of the nematic phase in case, when the heat flux across the upper restricted surface exists, whereas the temperature on the rest surfaces is kept constant, can be derived from the balance of elastic, viscous, and thermomechanical torques , the Navier-Stokes equation for the velocity field , excited by the heat flux , and the equation for the heat conduction.
The torque balance equation can be derived from the dimensionless balance of elastic
, viscous
, and thermomechanical
torques [
7,
16,
17], where
is the dimensionless elastic energy,
,
and
are the splay and bend elastic constants of the nematic phase,
is the material derivative of
, whereas
is the viscous, and
is the thermomechanical contributions to the full dimensionless Rayleigh dissipation function [
7,
15,
16,
17], respectively. Here
and
are the symmetric and asymmetric contributions to the rate of strain tensor,
,
is the scalar invariant of the tensor
,
is the transposition of
, and
are the Leslie viscosity coefficients, respectively. We use here the invariant, multiple dot convention:
,
,
, and
, where repeated Cartesian indices are summed.
To be able to observe the formation of the hydrodynamic flow
in the HAN channel, under the effect of the heat flux
, when the heating occurs during some times
, let us consider the dimensionless analog of the torque balance equation [
7,
16,
17,
21]
where
is the dimensionless time,
,
is the heat capacity,
,
and
are the rotational viscosity coefficients,
,
is the dimensionless temperature,
is the nematic-isotropic transition temperature,
,
is the dimensionless distance away from the lower boundary of the HAN channel,
is the dimensionless space variable corresponding to
x-axis, respectively,
is the scaled analog of the stream function
for the velocity field
(see the ref. [
21]),
,
,
,
, and
, respectively. Here,
and
are two parameters of the nematic system, and
is the thermomechanical constant [
7,
15].
The dimensionless Navier–Stokes equation for the velocity field
takes the form [
21]
whereas the dimensionless entropy balance can be written as [
21]
where
is the dimensionless parameter,
is the heat conductivity coefficient parallel to the director. It should be noted that the function
, the coefficients
, the functions
and
are given in the ref. [
21], whereas
(
) is the stress tensor (ST) of the nematic system,
is the hydrostatic pressure in the HAN channel, and
,
, and
are the dimensionless ST components corresponding to the elastic, viscous, and thermomechanical forces, respectively. The set of the rest parameters of the nematic system, corresponding to the case of
, are:
and
, respectively.
In the following we are focused primary on the heat conduction regime in the HAN channel which assumes that across the upper surface the heat flux is set up (see Equation (
1)), whereas on the rest surfaces the temperature is kept constant (see Equation (
2)). Physically, this means that across the LC channel the temperature gradient
, directed from the cooler to the warmer surfaces, excited by the heat flux
across to the upper boundary, may be built up.
Notice that the dimensionless ST can be obtained directly from the elastic contribution to the energy and Rayleigh dissipation function as , , and , for the elastic, viscous, and thermomechanical contributions, respectively.
Straightforward calculations give the following expressions for ST components
,
, and
which are listed in the ref. [
21].
Now the evolution of the director in the HAN channel confined between two horizontal and two vertical solid surfaces, under the influence of viscous, elastic, and thermomechanical forces and taking into account the flow, can be obtained by solving the system of the nonlinear partial differential Equations (
6)–(
8) with the appropriate dimensionless boundary conditions for the director
or the polar angle
velocity field
temperature field
and the initial condition taken in the form
respectively. Here,
, and
is the dimensionless heat flux across the upper restricted surface. The laser-induced heating was used to inject energy
Q across the bounding surface at the microscopic scale [
8,
13]. In that case the nematic channel was heated by a laser beam, focused, for instance, on the upper bounding surface (
), with intensity
, where
is the laser power, and
is the Gaussian spot size. Taking into account that the total absorbed laser power is
, the heat flux across the upper restricted surface can be written as
where
is the absorption coefficient,
,
is the dimensionless heat flux’s coefficient,
is the Heaviside step function, and
is the duration of the energy injection into the nematic sample. Here, and everywhere else in this section,
is equal to
.
For the case of
, at temperature corresponding to nematic phase, the first four parameters
,
,
, and
, that are involved in Equations (
6)–(
8) have the following values [
21]:
,
,
, and
.
Using the fact that
, the Equation (
7) can be considerably simplified and takes the form [
21]
where
and
are functions which have been defined in ref. [
21].
2.2. Orientational Relaxation of the Director, Velocity, and Temperature Fields in Rectangular Microsized Nematic Channels
With the evolution of the director
to its equilibrium orientation
, which is described by the polar angle
from the initial
to the equilibrium
conditions, both the horizontal and vertical components of the velocity field
, and the temperature field
redistribution, can be obtained by solving the system of the nonlinear partial differential Equations (
6), (
8) and (
14), together with the boundary conditions (
9)–(
11), and the initial condition taken in the form of (
12). The calculations have been carried out by using both the relaxation [
24] and the sweep [
25] methods. The initial distribution of the director field
has been obtained from Equation (
6) by means of the relaxation method with
, and with the boundary
,
, and initial
, for
, and
, for
, conditions. Having obtained the initial distribution of the director field
, the initial distribution of the temperature field
, corresponding to the first time step
, has been obtained from Equation (
8), by means of the relaxation method with
and with the boundary and initial conditions in the form of Equations (
9)–(
12). Then the initial distribution of the stream function
, corresponding to the first time step
can be calculated by using the initial distributions of the director
and temperature
fields, as well as the function
, which is involved in Equation (
14). The next time step
for the velocity and temperature fields, as well as for the director’s distribution across the nematic sample is initiated by the sweep method. The stability of the numerical procedure for Equations (
6), (
8) and (
14) was defined by the following conditions [
24]:
where
and
are the space steps in the
x and
z directions, and
and
are the coefficients defined in Equation (
14). In the calculations, the relaxation criterion
was chosen to be equal to
, and the numerical procedure was then carried out until a prescribed accuracy has been achieved. Here,
m is the iteration number and
is the relaxation time of the system.
The evolution of the polar angle
in the middle part of the rectangular HAN channel (
) to its equilibrium distribution
, during the slow heating mode, under the effect of the dimensionless heat flux
(∼
mW/μm
2), caused by the laser irradiation focused on the upper boundary of the HAN channel, at different times, from
μs) [curve (1)] to
[curve (6)], respectively, is shown in
Figure 2a.
Figure 2b shows the same as in
Figure 2a, but at different times, from
[curve (7)] to
[curve (11)], corresponding to the cooling mode. Here, the following times were used
,
, whose values increase from curve (1) to curve (6), and
, and times
,
, whose values increase from curve (7) to curve (11), and
, respectively, whereas the time
denotes the relaxation time of the LC system, and
(∼
ms) is the duration of the energy injection into the HAN channel across the upper boundary by the infrared laser with the power
mW. The distance
z dependence of the polar angle
is characterized by the monotonic increase
from
, on the lower cooler boundary of the HAN channel, to
, on the upper warmer boundary, respectively. The evolution of the polar angle
to its equilibrium distribution
along the width of the HAN channel
in the vicinity of the upper warmer boundary of the channel
, during the slow heating mode at different times, from
μs) [curve (1)] to
[curve (6)], is shown in
Figure 3a, whereas the cooling mode, at different times, from
[curve (7)] to
[curve (11)], is shown in
Figure 3b, respectively. Both the slow heating (see
Figure 3a) and cooling (see
Figure 3b) modes are characterized by nonsymmetric profile of
with respect to the middle part
of the HAN channel, which is caused by nonsymmetric effect of the velocity field components
(see
Figure 4a,b and
Figure 5a,b) and
(see
Figure 6a,b and
Figure 7a,b), respectively.
The maximum of both the absolute magnitudes of the dimensional velocities
and
in the rectangular HAN channel, at the initial stage of the slow heating mode are equal to
mm/s and
mm/s, for the horizontal and vertical components (see
Figure 5a and
Figure 7a), at
9.3
K), respectively.
The distance
z dependence of the temperature field
in the middle part of the dimensionless HAN channel (
), during its evolution to the equilibrium distribution
, under the effect of the dimensionless heat flux
(∼
mW/μm
2), caused by the laser beam, at different times, from
[curve (1)] to
[curve (6)], respectively, is shown in
Figure 8a.
Figure 8b shows the same as in
Figure 8a, but for the cooling mode at different times, from
[curve (7)] to
[curve (11)], respectively. The distance
z dependence of the temperature field
is characterized by the temperature growth on the upper boundary of the HAN channel (
), from
to
, during the slow heating mode (curves, from (1) to (6)) (see
Figure 8a), with the following temperature decrease, from
to
, after switching off the laser power (see
Figure 8b). Here, the value of
is equal to ∼
1.9 ms). The second part of the relaxation process of
(
) is characterized by much faster cooling down of the upper restricted surface than the rest bulk of the nematic sample (see
Figure 8b). The growth of the temperature field
to its equilibrium distribution
along the width of the HAN channel
in the vicinity of the upper warmer boundary
, during the slow heating mode at different times, from
[curve (1)] to
[curve (6)], respectively, is shown in
Figure 9a.
Figure 9b shows the same as in
Figure 9a, but for the cooling mode at different times, from
[curve (7)] to
[curve (11)], respectively. This slow heating mode is characterized by symmetric growth of the profile
with respect to the middle part
of the HAN channel. Such symmetric dependence of the temperature field along the width of the channel can be explained by much faster evolution of
to
, than the evolution both of the director and velocity fields to their equilibrium distributions across the HAN channel, and, as a result, the weak effect of these fields on
[
3].
The equilibrium distributions of the polar angle
, both across the middle part
and in the vicinity of the upper boundary of the HAN channel
, under the effect of the dimensionless heat flux
mW/μm
2) (which is 8 times greater than
Q in the first case A), caused by the laser beam focused on the upper boundary, are shown in
Figure 10a,b, respectively.
Here, the duration
of the energy injection into the HAN channel across the upper boundary is equal to
μs), and during that time the temperature on the upper boundary grows from
to
(see
Figure 10a), with the following cooling down to
. Note that the duration of the laser pulse, at fixed power
mW, is limited by condition that the higher temperature on the upper boundary of the HAN channel
must fall within the nematic stability range. The growth of the temperature field
in the middle part of the dimensionless HAN channel (
) to its equilibrium distribution
, under the effect of the dimensionless heat flux
mW/μm
2), caused by the laser beam at different times, from
μs) [curve (1)] to
[curve (5)], respectively, corresponding to the fast heating mode, is shown in
Figure 11a.
Here,
(∼
μs) is the duration of the energy injection into the HAN channel across the upper boundary by the infrared laser with the power
mW. The sequence of times, from
[curve (6)] to
[curve (12)], corresponding to the cooling mode, is shown in
Figure 11b. The distance
x dependence of the temperature field
during its evolution to the equilibrium distribution
[
21], along the width of the HAN channel
in the vicinity of the upper warmer boundary
, during the fast heating mode at different times, from
[curve (1)] to
[curve (5)], respectively, is shown in
Figure 12a, whereas the cooling mode with the sequence of times, from
[curve (6)] to
[curve (12)], respectively, is shown in
Figure 12b.
The distance
z dependence of the horizontal component
of the velocity field in the middle part of the HAN channel (
), during its evolution to the equilibrium distribution
, under the effect of the dimensionless heat flux
mW/μm
2) at different times, from
μs) [curve (1)] to
μs) [curve (5)], respectively, corresponding to the fast heating mode is shown in
Figure 13a.
Figure 13b shows the evolution of the horizontal component
of the velocity
in the middle part of the HAN channel, during the cooling mode, with the sequence of times, from
[curve (6)] to
[curve (12)], respectively. The distance
z dependence of
(see
Figure 13a) is characterized by strong increase of
, from
to
, within the first part of the fast heating mode (∼
μs), in the vicinity of the upper warmer boundary, with following decrease up to
0, during the rest time term
96 ms), respectively.
The distance
x dependence of the horizontal component
of the velocity
during its evolution to the equilibrium distribution
, along the width of the HAN channel
in the vicinity of the upper warmer restricted surface
[
21], for the fast heating mode at different times, from
[curve (1)] to
[curve (5)], respectively, is shown in
Figure 14a.
Figure 14b shows the same as in
Figure 14a, but the sequence of times, from
[curve (6)] to
[curve (12)], respectively, corresponds to the cooling mode. Both the fast heating (
Figure 14a) and cooling (
Figure 14b) modes are characterized by near symmetric profile of
with respect to the middle part (
) of the HAN channel.
The distance
z dependence of the vertical component
of the velocity
, during its evolution to the equilibrium distribution
across the HAN channel, corresponding to the fast heating mode at different times, from
[curve (1)] to
[curve (5)], respectively, also is characterized by oscillating behavior of
in the vicinity of the upper warmer boundary (see
Figure 15a), with the following velocity decreasing to 0, after switching off the laser power (see
Figure 15b).
In turn, the distance
x dependence of the vertical component
of the velocity
during its evolution to the equilibrium distribution
, along the width of the HAN channel
in the vicinity of the upper warmer boundary
, both during the fast heating and cooling modes, are shown in
Figure 16a,b, respectively.
The fast heating mode is characterized by exciting the vertical component
of the velocity
only in the vicinity of the vertical boundaries of the HAN channel (see
Figure 16a), with the following velocity decreasing to 0, after switching off the laser power (see
Figure 16b), respectively. Note that under the effect of the heat flux across the upper boundary, only approximately 15% of the HAN channel (see
Figure 15a) close to the upper warmer boundary is involved in the moving process, whereas the rest amount of the nematic sample is kept unmoved during the full relaxation term. These numerical studies show that in the hybrid aligned nematic material under the effect of
, in the vicinity of the warmer boundary, the vortical flow may be excited. The maximum for both the absolute magnitudes of the dimensional velocities
and
in the HAN channel, at the initial stage of the fast heating mode, are equal to
mm/s and
mm/s, for horizontal and vertical components (see
Figure 15a and
Figure 16a), at
, respectively.
In summary, we present the review of numerical results describing the evolution of not only the director and velocity fields, but also the redistribution of the temperature field in the hybrid aligned nematic channel to their equilibrium values, under the effect of the heat flux directed normal to the upper bounding surfaces, when the rest bounding surfaces of the HAN channel are kept at constant temperature. In this case, the upper nematic boundary is aligned homogeneously and heated by an infrared laser beam, and the dynamics of heating occurs with two distinct time scales:
- (i)
A fast time scale, with the duration of the dimensional heat flux mW/μm2 over time μs, and the laser power in mW, and
- (ii)
A slow time scale, with the duration of the dimensional heat flux
mW/μm
2 over time
ms, and the laser power in
mW, respectively [
21].
In both these cases, the duration of the laser pulse, at fixed power in mW and mW, is limited by condition that the higher temperature on the upper bounding surface must fall within the nematic stability range. These numerical studies show that in such the hybrid aligned nematic volume under the effect of the heat flux, across the upper boundary, the vortical flow may be excited only in the vicinity of the warmer boundary. After some time more than the relaxation time, for instance, of the director field in the HAN channel, the vortical flow settles down to the rest state regime, where the horizontal u and vertical w components of velocity vector are equal to zero, and the temperature field across the nematic channel is finally falling to the value of temperature on the lower and both lateral bounding surfaces. Note that in the case of the fast heating mode (i) one deals with the heating which is characterized by “shallow” heating of the nematic microvolume in the vicinity of the upper bounding surface up to 40% of the full nematic sample, whereas in the case of the slow heating mode (ii), one deals with the “deeper” heating of the nematic microvolume up to 60% of the nematic sample far from the upper warmer restricted surface.
Thus, it can be concluded that for the formation of a hydrodynamic flow in a microsized HAN channel using laser radiation focused on the channel boundary, such a radiation power is necessary to pump energy into the liquid crystal phase for as long as possible. Another condition for the formation of a more powerful flow in the HAN channel is the planar anchoring condition at the boundary where the laser radiation will focus.
Therefore, a new scenario of the vortical flow formation in the HAN channel under the effect of the focused laser irradiation on the lower homeotropically aligned boundary will be analyzed in the next paragraph.
2.3. Laser Excited Vortical Flow in Microsized Nematic Channels
In the previous paragraph, we analyzed the process of formation and relaxation of the velocity field
in the microsized LC volume under the effect of the heat flux
directed orthogonally to the upper boundary of the HAN channel. The purpose of this paragraph is to show how the direction of the external heat flux
affects the process of formation of the vortex flow in the microsized HAN channel. In this case, the heat flux
directed across the lower bounding surface at an angle
with respect to the unit vector
. Here,
is the unit vector parallel to the horizontal boundaries of the HAN channel, whereas the unit vector
is directed perpendicular to both the horizontal boundaries. This problem will be treated in the framework of the extended Ericksen–Leslie theory [
16,
17], supplemented by the thermomechanical correction for both the shear stress and the Rayleigh dissipation function [
7,
15], as well as the entropy balance equation [
18]. The hydrodynamic model in which the above problem will be considered is the same as in
Section 2.1, and is based on the interaction effect of the director
and temperature
T gradients with the velocity
field. In this case, the magnitude of the hydrodynamic flow
is proportional to
, where
is the tangential component of the thermomechanical stress tensor,
is the viscosity of the nematic phase, and
d is the thickness of the HAN channel. It will be shown below that the tangential component of the thermomechanical stress, the tensor plays a crucial role in the formation of the thermally excited vortical flow in the HAN channel. In our case, the temperature gradient
in the microsized nematic volume is formed by focused laser radiation. At the beginning of the section, we give a detailed description of the boundary conditions for both the director
and temperature
fields, as well as for the velocity field
. The second part of the section presents a numerical analysis of the formation of the thermally excited vortical flow in the HAN channel under the influence of the heat flux
directed across the lower bounding surface at an angle
with respect to the unit vector
.
With this aim, we consider the 2D nematic fluid composed of polar molecules, such as , at density , and delimited by two horizontal and two lateral surfaces at mutual distances and , respectively. We also consider the effect of the orientational defect on the lower bounding surface on the vortex flow excited in the nematic microvolume under the effect of the focused laser beam. This defect is characterized by the continuous change in the orientation of the director’s along the length of the lower restricted surface, from the homeotropic to the planar, and again to the homeotropic orientation.
Therefore, our 2D aligned nematic state with the orientational defect contains a gradient of
on the lower boundary, i.e.,
and the planar orientation on the upper and lateral surfaces, i.e.,
where
,
, and
is the length of the orientational defect on the lower boundary with the director’s orientation changing continuously from the homeotropic to planar, and again to homeotropic orientation, whereas on the rest length of that surface there is the homeotropic director’s orientation (
). Notice that in these calculations the ratio
is equal to 10. Moreover, we will consider dimensionless spatial variables
and
, and in the following equations the overbars will be eliminated.
In order to elucidate the role of both the orientational defect and the heat flux
directed at an angle
across the lower boundary of the HAN channel in formation of the vortical flow we consider the hydrodynamic regime with the heat flux
, where
is the angle between vectors
and
. In the dimensionless form it can be written as [
13,
26]
whereas on the rest boundaries the temperature is kept constant
Here, is the injected energy across the lower boundary, , and is the dimensionless characteristic time needed for reorientation of the director , respectively.
The velocity
on these surfaces has to satisfy the no-slip boundary condition
where
and
are the components of the vector
.
The reorientation of the director in the HAN microvolume confined between two horizontal and two vertical solid surfaces under the effect of the viscous, elastic, and thermomechanical forces and taking into account the flow can be obtained by solving the system of the nonlinear partial differential Equations (
6), (
8) and (
14) with the appropriate dimensionless boundary conditions for the polar angle
(Equations (
15) and (
16)), or for the director field
velocity field
(see Equation (
19)), temperature field
and the initial condition taken in the form
respectively. Here,
is the equilibrium distribution of the director field over the nematic volume obtained from Equation (
6), with
, and with the boundary conditions in the form of Equation (
20), whereas the initial condition is chosen in the form
, at
, and
;
, at
, and
;
, at
, and
, respectively. Notice that the initial distribution of the director field
over the microsized volume has been obtained from Equation (
6) by means of relaxation method [
24]. In calculations, the relaxation criterion
was chosen to be equal to
, and the numerical procedure was then carried out until a prescribed accuracy was achieved. Here,
m is the iteration number.
Figure 17 shows a fragment of initial distribution of the director field
near the orientational defect located at
[
13,
26]. Here,
are the right and left ends of the orientational defect on the lower boundary. According to these calculations the highest value of
is reached in the vicinity of the orientational defect and its effect extends up to
of the thickness of the nematic volume.
The evolution of both the velocity
and the temperature
fields over the nematic microvolume with the orientational defect located on the lower boundary of the HAN channel as the function of the angle
are shown in
Figure 18,
Figure 19,
Figure 20,
Figure 21,
Figure 22 and
Figure 23, respectively. The distribution of the velocity field
in the microscopic nematic volume with the orientational defect located at
, when the laser beam is directed at the values of the angle
equal to 20° and 40° (
Figure 18a,b), 60° and 80° (
Figure 19a,b), 90° (
Figure 20), 100° and 120° (
Figure 21a,b), 140° and 160° (
Figure 22a,b) are shown in
Figure 18,
Figure 19,
Figure 20,
Figure 21 and
Figure 22 [
13,
26,
27], respectively. The heating occurs during the dimensionless time
ms), whereas the value of dimensionless heat flux coefficient
is equal to 0.05.
The distribution of the velocity
in the microscopic HAN channel with the orientational defect located at
, when the heat flux
is directed at two values of the angle
,
and
with respect to the lower bounding surface, is characterized by maintaining of vortices as shown in
Figure 18a,b [
13,
26,
27], respectively. Here, 1 mm of the arrow length is equal to
μm/s. The direction and magnitude of the hydrodynamic flow
is influenced by both the direction of the heat flux
across the lower bounding surface and the character of the orientational defect. According to these calculations of the director field
across the nematic volume, the highest value of
is reached in the vicinity of the orientational defect, and, as a result, the biggest thermally excited velocities occur in the vicinity of the lower hotter surface. In that case, the self-sustaining vortical flow is excited in the negative sense (anti-clockwise) around its center, as the value of the angle
reaches
. Further increase in the angle value of more than 60 degrees leads to the formation of two vortices, one, larger, in the left-hand side of the nematic volume, another, smaller, in the right-side of the HAN channel, as shown in
Figure 19a,b,
Figure 20 and
Figure 21a,b, respectively. With increasing the value of the angle
, the larger vortex begins to decrease in size, while the smaller vortex begins to increase. The size of the smaller vortex reaches its maximum size at the angle
(see
Figure 21b). Notice that the bigger self-sustaining vortical flow in the left-hand side of the HAN channel is thermally excited in the negative sense (anti-clockwise), whereas the smaller vortical flow in the right-hand side of the nematic volume is excited in the positive sense (clockwise) around their centers. With increasing the value of the angle
to more than 120 degrees, the larger vortex disappears and we have only one self-sustaining vortical flow in the positive sense (clockwise) around its center (see
Figure 22a,b).
These results show that the direction of the heat flux across the hotter bounding surface with the orientational defect plays a crucial role in maintaining the thermally excited vortical flow in 2D HAN channel.
The distribution of the temperature field
over the HAN microvolume near the orientational defect located at
, when the dimensional heat flux
is directed at two values of the angle
: 20° (
Figure 23a) and 160° (
Figure 23b), after time term
ms), is shown in
Figure 23 [
13].
The value of dimensionless heat flux coefficient is equal to 0.05 (∼ mW/μm2). In general, under the above conditions, the picture of warming is such that only a small part of the nematic volume is involved in the heating process, while a large part of the volume of the fluid were not heated. It should be noted that in both cases the area of the greatest heating was shifted in the direction in which the heat flux was directed due to laser radiation.
We have reviewed the orientational dynamics in a microsized hybrid aligned nematic channel, where the nematic volume is confined by two horizontal and two lateral surfaces, and under the influence of the temperature gradient , when the nematic material is heated by a laser beam focused on the lower boundary with the orientational defect, whereas the rest bounding surfaces of the LC volume are kept at constant temperature. It has been shown that in the microsized HAN channel, due to interaction between and the gradient of the director field , in the LC volume with the orientational defect on the lower hotter boundary the vortical flow can be excited. The direction and magnitude of the hydrodynamic flow is influenced both by the heat flux across the lower hotter boundary of the HAN channel, directed at the angle with respect to the unit vector , and by the character of the orientational defect. Calculations show that the biggest thermally exited vortical flow occurs in the vicinity of the orientational defect. The analysis showed that at the same power of the laser radiation, with a change in the value of the angle , the picture of the vortex flow in the HAN channel changes. When the heat flux is directed at the angle less than 40 degrees, in the nematic volume one the self-sustaining vortical flow in the negative sense (anti-clockwise) is excited around its center.
The increase in the angle value to more than 60 degrees leads to the formation of two vortices, one, larger, in the left-hand side of the LC volume, another, smaller, in the right-hand side of the LC volume, respectively. With further increasing the value of the angle
up to right angle and more, the larger vortex begins to decrease in size, while the smaller vortex reaches its maximum size at the angle 120 degrees. When the value of the angle
is more than 120 degrees, a single self-sustaining vortex flow is formed in a positive sense (clockwise) around its center [
2].
Based on the analysis of the nature of the thermally excited vortical flow in the microsized HAN volume under the influence of the heat flux directed across the boundary, we can conclude that the formation of the hydrodynamic flow requires such the radiation power that would pump energy into the liquid crystal phase for as long as possible. Another condition for the formation of the more powerful flow in the HAN channel is a planar anchoring condition on the boundary on which the laser radiation would be focused.
It should be noted that the vortical flow in the bulk of the microsized nematic volume is a unique phenomena only exhibited by liquid crystal systems, and expected to be applied for novel opto-thermal tweezers.
Now, in the next paragraph, we turn to the description of the formation of vortex flows in microsized HAN channels with a free upper surface under the effect of focused laser irradiation in the bulk of the nematic phase.
2.4. Laser Excited Motion of Nematics Confined in Microsized Channel with a Free Surface
Despite the fact that certain qualitative and quantitative advances in a hydrodynamic description of the relaxation processes in the microsized nematic volume under the effect of the temperature gradient have been achieved, it is still too early to talk about the development of a theory which would make it possible to describe the dissipation processes in confined nematic channel with a free upper LC/air interface under the influence of the temperature gradient
[
11,
12]. Thus, we are primarily concerned here on describing the set of numerical results which show the way how the temperature gradient caused by the laser radiation focused in the interior of the microsized hybrid aligned nematic (HAN) volume with a free upper LC/air interface can produce the hydrodynamic flow and, as a result, how it can deform the free LC/air interface [
11,
12].
This problem will be treated in the framework of the appropriate nonlinear extension of the Ericksen–Leslie theory [
16,
17], supplemented by the thermomechanical correction of shear stress [
7,
15], and the entropy balance equation [
18]. The hydrodynamic model in which the above problem will be considered is the same as in
Section 2.1, and is based on the interaction effect of the director
and temperature
T gradients with the velocity
field. The magnitude of the hydrodynamic flow
is proportional to
, where
is the tangential component of the thermomechanical stress tensor,
is the viscosity of the nematic phase, and
d is the thickness of the HAN channel. It will be shown below that the tangential component of the thermomechanical stress tensor plays a crucial role in the formation of the thermally excited vortical flow in the HAN channel with the free upper surface. In this case, the temperature gradient
in the microsized HAN volume is formed by a laser beam focused in the interior of the HAN channel. At the beginning of the section, we give a detailed description of the boundary conditions for both the director
and temperature
fields, as well as for the velocity field
. The bounding condition for the velocity on the upper free LC/air interface
can be obtained from the linear momentum balance equation transmitted to the surface
. The temperature regime without the heat flux
across the free LC/air interface
will be analyzed. The second part of the section presents a numerical analysis of two modes of the thermally excited vortical flow in the HAN channel with the free upper surface. These modes are characterized by different laser radiation power and duration: slow and fast heating modes caused by the laser irradiation focused in the interior of the HAN channel with the free upper surface.
With this aim, we consider the HAN channel delimited by one lower horizontal solid surface, located at , one upper free flat LC/air interface, initially located at , and two lateral solid surfaces at distance on scale on the order of micrometers. The coordinate system defined by our task is the same as in the previous paragraph.
Therefore, the hybrid aligned nematic phase contains a gradient of
from planar orientation on the lower and both lateral surfaces to homeotropic orientation on the upper free LC/air interface
, i.e.,
Here,
is the normal to the free LC/air interface
at any time and is directed from the nematic phase into air,
is the height of the LC film on the top of the smooth surface, and
. We consider the temperature regime without the heat flux
across the free LC/air interface
whereas on the rest boundaries the temperature is kept constant
We will assume the no-slip boundary conditions for the nematogenic molecules on these solid bounding surfaces, i.e.,
where
is the velocity vector with the horizontal
and vertical
components. The bounding condition for the velocity on the upper free LC/air interface
can be obtained from the linear momentum balance equation transmitted to the surface
. In our case, that balance leads to the tangential
and normal
force balances, where
is an additional unit tangent vector,
is the LC/air surface tension,
is the curvature of free LC/air interface
at any time, and
is the full stress tensor (ST). Taking into account the microsized HAN volume, one can assume the mass density
to be constant across the sample, and thus one deal with an incompressible fluid. The incompressibility condition
assumes that
The hydrodynamic equations describing the reorientation of the nematic phase in 2D case, when the system is subjected to a temperature gradient
, due to uniform heat flux
, can be derived from the torque balance equation Equation (
6), the linear momentum equation for the velocity field
, which can be written in the form of Equation (
14), and the heat conduction equation [
11,
12]
where
denotes the dimensional heat flux in the HAN channel,
is the dimensional heat source,
is the Heaviside step function,
is the dimensional heat source coefficient,
is the coefficient of absorption,
is the laser beam power,
is the Gaussian spot size, and
is the duration of the energy injection into the HAN channel.
Now the dynamics of the height
of the LC/air interface under the influence of the temperature gradient can be obtained by solving the system of nonlinear partial differential Equations (
6), (
14) and (
30) with the appropriate boundary and initial conditions. Equations (
27) and (
28), together with the torque balance Equation (
6), transmitted to the LC/air interface, can be combined to yield equation for the height
in the form [
11,
12]
where
and
are the horizontal and vertical components of the velocity
on the LC/air interface
, respectively.
Below, the set of dimensionless analog balance Equations (
6), (
14) and (
30) will be considered. The dimensionless entropy balance equation now can be written as [
11,
12]
where the extra one parameter of the LC system is
. Taking into account that the dimensionless temperature
should be in the range of
, the parameter
can be estimated as
. This estimation of
was made taking into account the fact that the value of the dimensional heat flux coefficient is equal to
, whereas the heating occurs during time
μs (slow heating regime).
The evolution of the free LC/air interface under the effect of the temperature gradient
, caused by the laser irradiation focused in the interior of the HAN channel, is governed by Equations (
6), (
14) and (
32), together with the boundary conditions at the solid boundaries [
11,
12]
and at the flexible free LC/air interface
[
1]
respectively, and the initial condition in the form of Equation (
22). Here,
, and both the matrix
and vector
are given in the Appendix, whereas the vector
is obtained from Equation (
6), with
.
Now the dimensionless height
of the nematic–air interface at any time
can be calculated as [
11,
12]
where
and
are the vertical and horizontal components of the velocity vector
on the interface
. Notice that the overbar in the function
H has been (and will be) eliminated in the last, as well as in the following equations.
Thus, when the director
is strongly homogeneously anchored to the lower boundary and planar to the lateral boundaries of the HAN channel, the value of
has to satisfy the boundary conditions (
33) and (
34) and its initial orientation (
22), and then, under the action of the viscous, elastic, and thermomechanical forces, is allowed to relax to its equilibrium value
.
Let us initially consider the case when the hybrid aligned nematic microvolume is heated by the laser beam focused in the interior of the HAN channel with the free upper boundary. In this case the value of the dimensional heat flux coefficient is equal to , whereas the heating occurs during time μs.
Figure 24 shows the distance
x dependence of both the dimensionless height
(
Figure 24a) of the LC/air interface and the dimensionless temperature
(
Figure 24b) on the free LC/air interface
[
11,
12], during the slow heating mode when the laser beam is focused in the interior (
and
) of the HAN channel, at different times
, respectively, whereas
Figure 25 shows the distance
x dependence of both the horizontal
(
Figure 25a) and vertical
(
Figure 25b) components of the vector
on the LC/air interface. According to these calculations [
10,
11], the evolution of the height
of the LC/air interface is characterized by the wavelike profile along the
x-axis (
). At the final stage of the evolution process, for
, the highest value of
is reached in the vicinity of points
, whereas the evolution of the temperature
is characterized by symmetric profile of
with respect to the middle point (
) of the LC/air interface
(see
Figure 24b). In that case, during the heat step (
μs)) the evolution of the temperature profile
is characterized by its strong growth in the vicinity of the middle point
, up to the highest value of 0.987 (∼307 K), whereas the evolution of the dimensionless height
h of the LC/air interface is characterized by two combs with the highest value of
μm), which are directed in the opposite sense with respect to their center
(see
Figure 24a). The thermally excited flow in the case of the slow heating mode, with
and
μs, is characterized by maintaining of two vortices as shown in
Figure 25a,b and
Figure 26 [
11,
12].
According to these calculations, the thermally driven bi-vortical flow is maintained in the left-hand side of the HAN channel, whereas the focuses of both vortices are shifted to the left-hand side of the nematic channel due to strong up to ∼
μm/s) horizontal flow directed in the negative sense (see
Figure 25a), whereas the vertical flow
w (see
Figure 25b) is characterized by very small value ∼
nm/s) directed in the opposite sense ref. [
1].
Now we consider the case when the hybrid aligned nematic microvolume is heated by the laser beam focused in the interior (
and
) of the HAN channel, at different times
1.5 ns) [curve (1)],
6.0 ns) [curve (2)],
10.5 ns) [curve (3)], and
15.0 ns) [curve (4)], respectively. In this case, the value of the dimensional heat flux coefficient is equal to
, whereas the heating occurs during time
ns.
Figure 27 shows how three vortices can be maintained in the HAN channel with a free LC/vacuum interface
, during the fast heating mode, one biggest vortical flow in the vicinity of the heat source and directed in the negative sense (anticlockwise) around their center
,
, and two smallest vortices, which are settled down close to the points
and
[
11], respectively. These calculations also show that the range of distance
z, counted from the lower boundary of the HAN channel, over which the laser beam cannot disturb the nematic phase, is
, i.e., which is approximately 80% of the LC sample (see
Figure 27). Notice that the duration of the energy injection
into the LC sample is restricted only by the nematic phase stability. Further calculations (cooling mode), based on the nonlinear extension of the Ericksen–Leslie theory, show that the nematic material settles down to the rest during the time term
0.5 s), after switching off the laser power, where both the horizontal
u and vertical
w components of the velocity
are equal to zero, and the temperature field
across the HAN channel finally downfalls to the value on the lower and two lateral boundaries.
The results presented in [
11,
12,
13] indicate that with a change in the nature of laser radiation focusing, from the surface of the nematic channel to its volume, leads to a significant change in hydrodynamic flows. The question of how the depth of laser radiation focus affects the nature of hydrodynamic flows in the hybrid aligned nematic channel will be discussed in the next paragraph.
2.5. How the Depth of Laser Radiation Focus Affects the Nature of Hydrodynamic Flows in Nematic Channel
In this paragraph, we will consider the effect of the depth of focus of laser radiation in the microscopic volume of the HAN channel with the free LC/air interface on the nature of formation of the hydrodynamic flow and temperature distribution [
11,
12].
Figure 28 and
Figure 29 show the distribution of the dimensionless temperature
along the
z-axis (
), when the laser beam is focused in the center (
) of the HAN channel, at different depths [
11,
12]:
(see
Figure 28a),
(see
Figure 28b),
(see
Figure 29c), and
(see
Figure 29d), respectively.
The heating mode when the laser beam is focused in the interior of the HAN channel is given at different times
, respectively. It has been shown that as the focus of the laser beam is shifted in the depth of the nematic microvolume, the temperature profiles across the nematic channel do not undergo the crucial change. For instance, in the case when the laser beam is focused on the maximum depth (
), the heating does not reach the LC/air interface (see
Figure 28a [
11,
12]).
In turn, the velocity profiles across the HAN channel undergo the crucial change.
Figure 30,
Figure 31,
Figure 32 and
Figure 33 show the distribution of the horizontal
and vertical
components of the velocity vector
along the
z-axis (
), when the laser beam is focused in the center (
) of the HAN channel, at different depths.
Figure 30a,b [
11,
12] show the distribution of the horizontal
component of the velocity
along the
z-axis (
), when the laser beam is focused in the center (
) of the HAN channel, but at different depths [
11,
12]:
Figure 30a, at
and
Figure 30b, at
, respectively. In turn, the
Figure 31c,d show the distribution of the horizontal
component of the velocity
along the
z-axis (
), at different depths [
11,
12],
Figure 31c, at
,
Figure 31d, at
, respectively.
Figure 32a,b show the distribution of the vertical
component of the velocity field
along the
z-axis (
), when the laser beam is focused in the center (
) of the HAN channel, at different depths:
Figure 32a, at
,
Figure 32b, at
, respectively. In turn,
Figure 33c,d show the distribution of the vertical
component of the velocity
along the
z-axis (
), at different depths,
Figure 33c, at
, and
Figure 33d, at
, respectively.
It has been shown that as the focus of the laser beam is shifted in the depth of the HAN channel in the vicinity of the LC/air interface, the horizontal component of the velocity
changes its direction from negative to positive, approximately at the point
, whereas the vertical component of the velocity
rapidly drops to zero. It should be noted that the greatest value of
, directed in the positive sense in the vicinity of the LC/air interface, is achieved in the case when the laser beam is focused on the maximum depth of penetration (
) in the LC volume, whereas the greatest value of
, directed in the negative sense in the vicinity of the LC/air interface, is achieved in the case when the laser beam is focused on the minimum depth of penetration (
) in the LC volume. In both of these cases, the vertical component of the velocity vector
at the free LC/air interface is almost zero. Therefore, this distribution of components of the velocity field shows that in the area close to the LC/air interface (
), the vortex flow is excited due to the energy pumping by laser radiation, similar to what is shown in
Figure 26. These calculations [
11,
12] also show that with further penetration of the injecting energy to the bulk of the LC phase, from
to
, the thermally excited vortical flow changes the direction from anticlockwise, around the point
, to clockwise, around the point
, approximately at the point
.
Based on the numerical results describing the formation of hydrodynamic flows in microsized HAN channels with free surfaces under the effect of laser radiation focused in the volume of the LC phase, the following conclusion can be made. First, the calculations, based on the appropriate nonlinear extension of the classical Ericksen–Leslie theory, show that due to the interaction between and the gradient of the director field , in the nematic volume the thermally excited three-vortical fluid flow is maintained. Second, the direction and magnitude of the hydrodynamic flow at a fixed time of pumping energy and the laser output power are affected by the depth of the laser injection. The above calculations also show that the range of distances measured from the lower solid boundary at which the laser beam cannot disturb the nematic phase is approximately 80% of the nematic sample.
It should be noted that the vortical flow in homeotropically oriented LC film doped by chiral molecules, using the circular polarization techniques, recently has been observed [
10]. It has been shown that at the beginning of laser irradiation, the thermocapillary radial flow is transformed into a circular flow around the position of the laser spot on the free LC interface. The formation of the circular flow on the top of the LC film has been ascribed to thermocapillary convection in the LC sample.
In turn, in the above-mentioned cases [
11,
12], the vortical flow occurred in the vicinity of the free LC/air interface and penetrated to the bulk of the LC sample. The mechanism responsible for the occurrence of the vortical flow near the LC/air interface is based on the coupling between the director and the temperature gradients initiated by the laser beam radiation. Thus, this vortical flow is a unique phenomenon that is exhibited only by liquid crystal systems, and is expected to be applied to new optical-thermal tweezers [
1].