An Improved Estimation Method of Mutual Inductance Angle for a Two-Dimensional Wireless Power Transfer System

Abstract

The improvement of power transmission efficiency (PTE) is an important issue in the design of a wireless power transfer (WPT) system. The WPT system with multiple transmitting (Tx) or receiving (Rx) coils is a way to improve the PTE. This paper deals with the estimation of the mutual inductance angle for a two-dimensional (2D) WPT system with two Tx coils and one Rx coil. The mutual inductance angle is one of the most important parameters to determine the PTE in the 2D WPT system. The condition for the maximum PTE is investigated and the mutual inductance angle is defined for the 2D WPT system. An improved estimation method of the mutual inductance angle is proposed based on the phase-locked loop (PLL) technique using the voltages and currents of the Tx coils. The simulation and experimental results are provided to validate the effectiveness of the proposed method.

1. Introduction

The wireless power transfer (WPT) technique using inductive coupling is widely used for the chargers of mobile electronics. However, its application area is still limited because the power transmission efficiency (PTE) is very sensitive to the location of the transmitting (Tx) and receiving (Rx) coils. It is known that the coupling coefficient is the most important parameter to determine the PTE, which depends on the shape, distance, and alignment of the Tx and Rx coils.

Multi-dimensional WPT systems with additional Tx coils can be considered to overcome this problem [1,2,3,4,5,6,7,8,9,10,11,12], where the magnetic field synthesized using the multiple Tx coils can improve the PTE even under the variation of the distance and alignment. The current control method for the two and three dimensional (2D and 3D) WPT systems was presented in [1]. The flux vector control methods with two or three Tx coils were proposed in [2,4,8], where the modeling and numerical analysis for the 2D WPT system were provided. The mathematical analysis of the WPT systems with two and three orthogonal Tx coils can be found in [5,6], where the power and efficiency of 2D and 3D WPT systems were calculated based on the mathematical model, respectively. The concept of the mutual inductance angle in the 2D WPT system is introduced and a simple estimation method is presented in [7]. Research related to the control issue to maximize the PTE in the 2D WPT system was presented in [9], where the control method in the d-q axis based on the mutual inductance angle was proposed. More recently, the omnidirectional WPT system for movable devices was studied in [10].

In order to obtain the maximum PTE in the WPT system, it is very important to know the key relationship between the Tx and Rx coils such as the coupling coefficient. Most previous studies on the multi-dimensional WPT systems dealt with the characteristic analysis and current or magnetic flux control. However, rare studies on the sensing or estimation of the key parameters were provided. The concept of the mutual inductance angle, a key parameter for the maximum PTE, and its estimation and control application were studied in [7,9]. However, there are some practical issues in the estimation owing to a direct calculation using the high frequency voltages and currents.

This paper presents an improved estimation method of the mutual inductance angle based on the phase-locked loop (PLL) technique. The modeling and analysis for the 2D WPT system including the definition of the mutual inductance angle are first presented, and the improved estimation method based on the PLL using the voltages and currents of the Tx coils is proposed. The concept and design of the proposed method are discussed. The simulation and experimental works are carried out for the actual 2D WPT system and the results verify the effectiveness of the proposed estimation method.

2. 2D WPT System

2.1. Structure of Coils

Figure 1 shows the structure of the Tx and Rx coils for the 2D WPT system considered in this paper. It has two Tx coils and one Rx coils with a circular shape, where two Tx coils are orthogonal and generate the magnetic fields on the α- and β-axis, respectively. It is assumed that the Rx coil is placed on the tangential line of the circle made by two Tx coils, as shown in this figure, and thus the centers of all Tx and Rx coils are aligned to the origin O. The angle φ denotes the physical angle between the center of the Rx coil and direction of the magnetic field generated from the α-axis Tx coil.

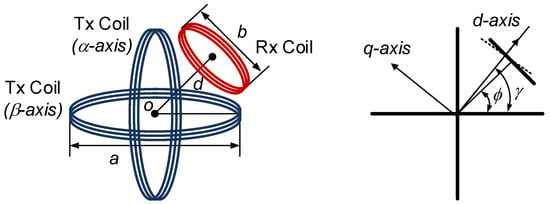
Figure 1. Structure of Tx and Rx coils for 2D wireless power transfer (WPT) system.

2.2. Coupled Circuit Model

The equivalent circuit of the inductive 2D WPT system with the resonant capacitors can be represented as shown in Figure 2 [2,5,7,9], where the inductive coupling between two Tx coils is neglected under the assumption that two coils are orthogonal.

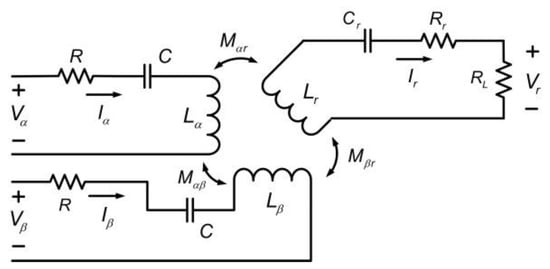
Figure 2. Equivalent circuit for inductive 2D WPT system with resonant capacitors.

The voltage equation of the 2D WPT system referred to the input terminals of the Tx coils in α- and β-axis is given as follows [9]:

$$V_{\alpha \beta }=Z_s{I}_{\alpha \beta }+j{X}_s{I}_r$$

(1)

where

$$V_{\alpha \beta }=\left(\begin{array}{c}{V}_{\alpha }\\ V_{\beta }\end{array}\right),I_{\alpha \beta }=\left(\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right),Z_s=\left(\begin{array}{cc}R+jX& 0\\ 0& R+jX\end{array}\right),X_s=\left(\begin{array}{c}{X}_{M\alpha r}\\ X_{M\beta r}\end{array}\right)=\omega M_s=\omega \left(\begin{array}{c}{M}_{\alpha r}\\ M_{\beta r}\end{array}\right)$$

The self-inductances and reactance of the Tx circuits are defined as L_α = L_β = L and $X=\omega L-1/\omega C$, respectively, where ω denotes the frequency of the input voltages. The mutual inductances between in Tx and Rx coils are represented as $M_{\alpha r}$ and $M_{\beta r}$ for the α- and β-axis, respectively. The mutual inductance between the α- and β-axis is assumed as zero because two Tx coils are orthogonal, as mentioned.

2.3. Power Transmission Efficiency (PTE) and Mutual Inductance Angle

The voltage equation in the Rx coil is represented using the superposition principle of the induced voltage from the Tx coils as

$$I_r\left(R_r+R_L+j{X}_r\right)=j{X}_s^T\cdot I_{\alpha \beta }$$

(2)

and the current of the Rx coil can be calculated as

$$I_r=\frac{1}{R_r+R_L+j{X}_r}\cdot j{X}_s^T\cdot I_{\alpha \beta }$$

(3)

where $X_r=\omega L_r-1/\omega C_r$. If the input currents applied to the Tx terminals are sinusoidal as

$$I_{\alpha \beta }=\left(\begin{array}{c}{I}_{\alpha m}\\ I_{\beta m}\end{array}\right)\cdot \cos \omega t$$

(4)

where the magnitude of currents in the α- and β-axes, I_αm and I_βm, are defined as

$$\left(\begin{array}{c}{I}_{\alpha m}\\ I_{\beta m}\end{array}\right)=I\cdot \left(\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right)$$

(5)

The symbols I and θ denote the magnitude and angle of the current vector synthesized by two Tx coils, respectively, as shown in Figure 3.

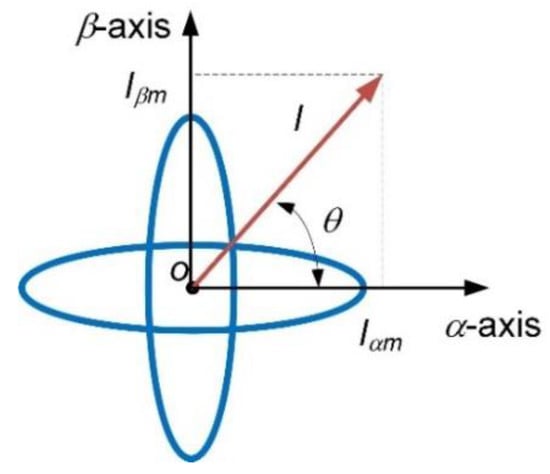
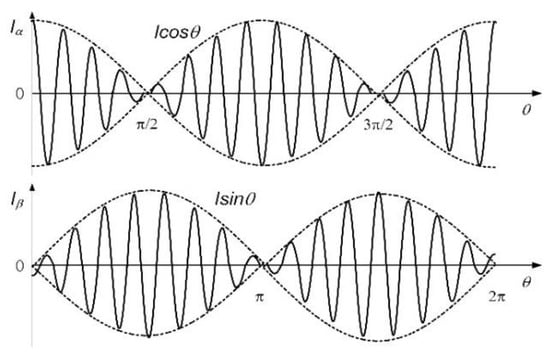
Figure 3. Current vector and α- and β-axes’ waveforms synthesized by Tx and Rx coils.

The PTE can calculated with the sinusoidal currents as [9]

$$\eta =\frac{P_{out}}{P_{in}}=\frac{P_{out}}{P_{\alpha }+P_{\beta }+P_r+P_{out}}=\frac{1}{1+\frac{R_r}{R_L}+\frac{R}{R_L}\left(\frac{1}{k{\cos }^2\left(\theta -\gamma \right)}\right)}$$

(6)

where $P_{\alpha }=I_{\alpha ,rms}^{2}R$, $P_{\beta }=I_{\beta ,rms}^{2}R$, $P_r=I_{r,rms}^2{R}_r$, $P_{out}=I_{r,rms}^2{R}_L$, and

$$k=\frac{{\omega }^2{M}^2}{{\left(R_r+R_L\right)}^2+X_r^2}$$

(7)

$$M=\sqrt{M_{\alpha r}^2+M_{\beta r}^2},\gamma ={\tan }^{-1}\left(\frac{M_{\beta r}}{M_{\alpha r}}\right)$$

(8)

It is shown in (6) that the PTE is at a maximum at $\theta =\gamma$. The angle γ is defined as the mutual inductance angle and the PTE depends on this angle. Figure 4 shows the vector diagram between the Tx and Rx coils in the 2D WPT system [7,9]. If the magnetic field generated from the Tx coils is concentrated to the center of each coil, the mutual inductance angle γ is the same as the physical angle φ. However, the magnetic fields of the Tx coils are distributed over the whole area of the inside of the coil. Thus, the mutual inductance angle is not identical to the physical angle because of the edge effect of the coils.

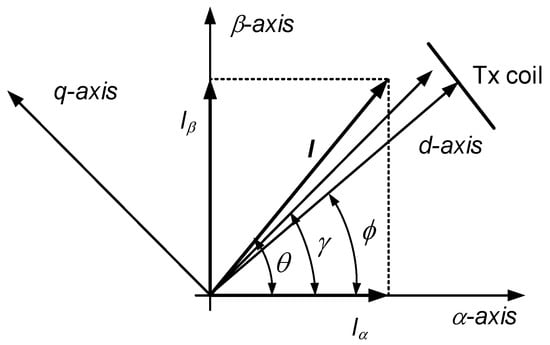
Figure 4. Vector diagram between Tx and Rx coils in the 2D WPT system.

The d-q coordinates are also defined in this figure for the control of the current vector, where the d axis is aligned to the vector with the mutual inductance angle γ and the q axis is advanced 90° degrees from the d-axis. The mutual inductance in the d-q coordinates can be represented as

$$\left(\begin{array}{c}{M}_{dr}\\ M_{qr}\end{array}\right)=T\left(\gamma \right)\left(\begin{array}{c}{M}_{\alpha r}\\ M_{\beta r}\end{array}\right)=T\left(\gamma \right)\left(\begin{array}{c}{M}_{dr}\cos \gamma \\ M_{dr}\sin \gamma \end{array}\right)$$

(9)

where

$$T\left(\gamma \right)=\left(\begin{array}{cc}\cos \gamma & \sin \gamma \\ -\sin \gamma & \cos \gamma \end{array}\right)$$

(10)

3. Estimation of Mutual Inductance Angle

3.1. Structure Od Proposed Estimator

The purpose of this work is to estimate the mutual inductance angle using the information of the voltages and currents in the Tx coils. The mutual inductance angle can be obtained from the direct calculation using (1). It is, however, very difficult to obtain the accurate value using the direct calculation from the high frequency voltages and currents. In order to overcome this problem, the improved estimation method with a closed-loop based on the PLL technique is proposed in this paper. Figure 5 shows the structure of the proposed mutual inductance estimator, which consists of the demodulator, phase detector, loop filter, and voltage controlled oscillator (VCO) [13,14,15].

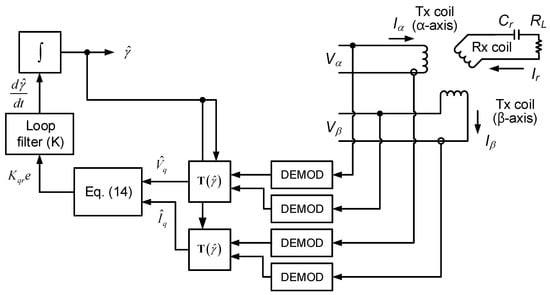
Figure 5. Structure of estimator for mutual inductance angle in the 2D WPT system.

The first step of the proposed estimation method is a demodulation of the measured voltage and current signals for the Tx coils because these signals are modulated by a high frequency carrier of cosωt as shown in Figure 3. The envelop of the modulated signals has the information of the angle between the Tx and Rx coils.

It is known in [13,14] that the d-q transform of the two orthogonal signals with the phase difference of 90° can be used as a phase detector. The voltage equation shown in (1) can be transformed into the d-q coordinates using the mutual inductance angle γ as

$$V_{dq}=Z_e{I}_{dq}+j{X}_e{I}_r$$

(11)

where

$$\begin{gathered} V_{dq}=\left(\begin{array}{c}{V}_d\\ V_q\end{array}\right)=T\left(\gamma \right)V_{\alpha \beta },I_{dq}=\left(\begin{array}{c}{I}_d\\ I_q\end{array}\right)=T\left(\gamma \right)I_{\alpha \beta }, \\ {Z}_e=T\left(\gamma \right)Z_{\alpha \beta }{T}^{-1}\left(\gamma \right)=Z_s\mathrm{and}{X}_e=T\left(\gamma \right)X_s=\omega \left(\begin{array}{c}{M}_{dr}\\ 0\end{array}\right) \end{gathered}$$

At the resonant frequency, ω = ω_r, X = 0, thus the q-axis voltage equation can be simply rewritten as

$$V_q=R{I}_q\mathrm{or}{V}_q-R{I}_q=0.$$

(12)

If the coordinate transform is performed using the transformation matrix with the estimated mutual inductance angle $\widehat{\gamma }$ given as

$$T\left(\widehat{\gamma }\right)=\left(\begin{array}{cc}\cos \widehat{\gamma }& \sin \widehat{\gamma }\\ -\sin \widehat{\gamma }& \cos \widehat{\gamma }\end{array}\right)$$

(13)

then the q-axis voltage equation is modified with respect to the estimation error $e=\widehat{\gamma }-\gamma$ as

$${\widehat{V}}_q-R{\widehat{I}}_q=K_{qr}\sin \left(\widehat{\gamma }-\gamma \right)$$

(14)

where ${\widehat{V}}_q=-V_{\alpha }\sin \widehat{\gamma }+V_{\beta }\cos \widehat{\gamma }$, ${\widehat{I}}_q=-I_{\alpha }\sin \widehat{\gamma }+I_{\beta }\cos \widehat{\gamma }$, and $K_{qr}=V_q-R{I}_q$.

For a small error, Equation (14) can be approximated as $K_{qr}\sin \left(\widehat{\gamma }-\gamma \right)\approx K_{qr}\cdot e$. It is noted in this equation that the mutual inductance angle can be estimated if the tracking control loop causes the error to be zero. Figure 6 shows the concept of the estimation for the mutual inductance angle using the proposed method. It is known in this figure that the estimated angle is aligned to the actual value as $e=\widehat{\gamma }-\gamma =0$ when ${\widehat{V}}_q-R{\widehat{I}}_q=0$.

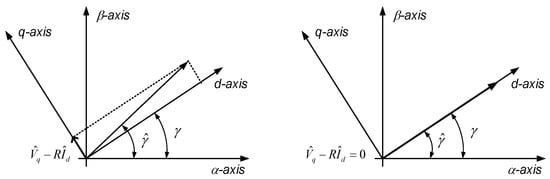
Figure 6. The concept of the proposed estimation method for the mutual inductance angle.

The loop filter and VCO for making the tracking control loop can be given as

$$\frac{d\widehat{\gamma }}{dt}=K\cdot K_{qr}e$$

(15)

The loop filter K is a proportional-integral (PI) type function given as

$$K=K_p\left(\frac{Ts+1}{Ts}\right)$$

(16)

where K_p and T denote the proportional gain and time constant, respectively.

3.2. Design of Proposed Estimator

In order to verify the operation of the proposed estimator, the design example is provided. The parameters of the coils and circuits used in the design are given in Table 1. The diameters of Tx and Rx coils are a = 10 cm and b = 4 cm, respectively. The measured coil parameters including the resistance and inductance are shown in Table 1. As the 2D WPT system considered in this paper is designed to be operated at a frequency range of 500 kHz, the value of the series capacitor C of each Tx circuit is chosen as 10 nF. Thus, the resonant frequency of the Tx circuit is 530 kHz. The series capacitor C_r of the Rx circuit is selected as 20 nF for matching to the resonant frequency.

Table 1. Parameters of the 2D WPT system used in the design example.

Item	Value	Item	Value
a	10 cm	b	4 cm
R	0.42 Ω	Rr	0.26 Ω
L	9 uH	Lr	4.4 uH
C	10 nF	Cr	20 nF
f	530 kHz	RL	10 Ω

Figure 7 shows the block diagram of the demodulator, where f_m means the measured signals of the voltage and current modulated with cosωt. The carrier frequency is given as 530 kHz, which is the same as the frequency of the input voltage and current. The second-order low-pass filter with a cut-off frequency of 10 kHz is used to extract the envelope of the voltages and currents of the Tx coils, which is a trade-off between the filtering performance and control loop dynamics.

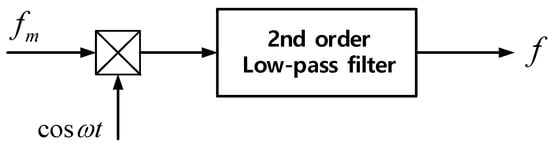
Figure 7. Structure of the demodulator.

The next design step is to determine the closed-loop dynamics through the design of the loop filter. The linearized model of the tracking control loop to estimate the mutual inductance angle is described as shown in Figure 8. The closed-loop system has the second-order dynamics with the PI type loop filter given in (17) and can be generally represented as

$$\frac{\widehat{\mathsf{\Gamma }}(s)}{\mathsf{\Gamma }(s)}=\frac{2\varsigma {\omega }_{n}s+{\omega }_n^2}{s^2+2\varsigma {\omega }_{n}s+{\omega }_n^2}$$

(17)

where

$${\omega }_n=\sqrt{\frac{K_{qr}{K}_p}{T}},\varsigma =\sqrt{\frac{T\cdot K_{dr}{K}_p}{2}}$$

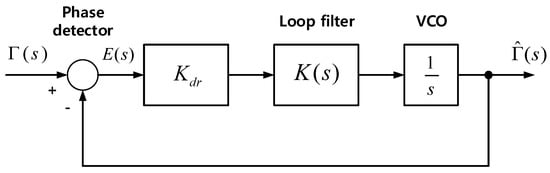
Figure 8. Linearized model of proposed estimator for mutual inductance angle.

4. Simulation and Experiments

The simulation and experimental works are carried out for the actual 2D WPT system with the parameters given in Table 1. The photograph of the experimental setup is shown in Figure 9. The mutual inductances and γ are measured for this system and the values for various physical angle φ are given in Table 2. The mutual inductances M_αr and M_βr can be measured using the open and short circuit test of the Tx and Rx as shown in Figure 10, and the mutual inductance angles are calculated using (8).

Figure 9. Experimental setup for the 2D WPT system.

Table 2. Mutual inductance M_αr and M_βr for various physical angles ϕ.

φ (deg)	d = 0 cm			d = 2 cm
	Mαr (uH)	Mβr (uH)	γ (deg)	Mαr (uH)	Mβr (uH)	γ (deg)
0	1.777	0.003	0.09	1.085	0.004	0.21
15	1.602	0.327	11.54	1.179	0.517	23.68
30	1.308	0.655	26.60	1.267	0.925	36.13
45	1.008	1.008	45	1.407	1.407	45
60	0.655	1.308	63.40	0.925	1.267	53.87
75	0.327	1.602	78.46	0.517	1.179	66.32
90	0.003	1.777	89.90	0.004	1.085	89.79

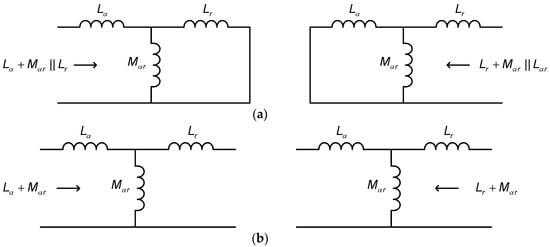
Figure 10. The short and open circuit test for the mutual inductance measurement between the α-axis and RX coils. (a) Short circuit test and (b) open circuit test.

The simulation results for the transient response of the proposed estimator are shown in Figure 11, where the gains of the loop filter are given as K_p = 1.0 and T = 0.002, respectively. It is shown in this figure that the settling time is 1.2 ms for the given gain.

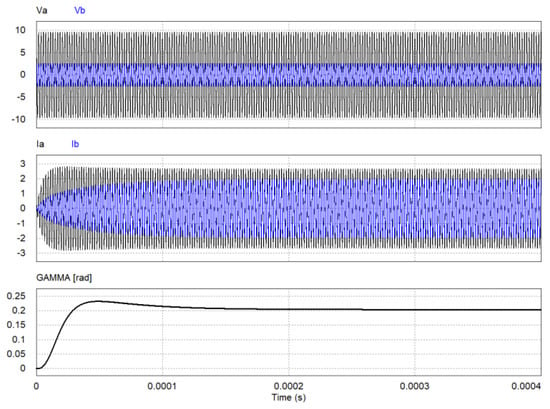
Figure 11. Transient response of the proposed estimator (d = 0 cm, Φ = 15°).

Figure 12 and Figure 13 show the simulation results for the steady-state response of the proposed estimator for the physical angles Φ of 15°, 30°, and 45° when d = 0 and 2 cm, where the voltages, currents of the Tx coils, estimated mutual inductance angle, and estimation error are shown, respectively. The estimated mutual inductance angles $\widehat{\gamma }$ are shown as 11.64°, 26.79°, and 45.21° (0.203, 0.468, and 0.789 radians) for d = 0 cm, and 23.59° and 36.49°, and 45.19° (0.412, 0.637, and 0.789 radians) for d = 2 cm, respectively. It is known in these results and Table 2 that the mutual inductance angle can be estimated using the voltages and currents of the Tx coils in the proposed estimator.

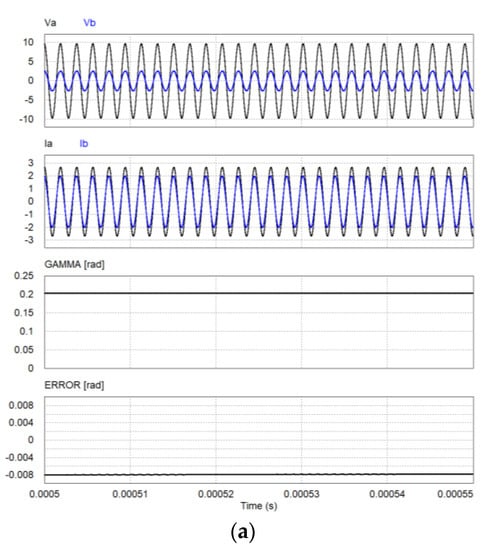
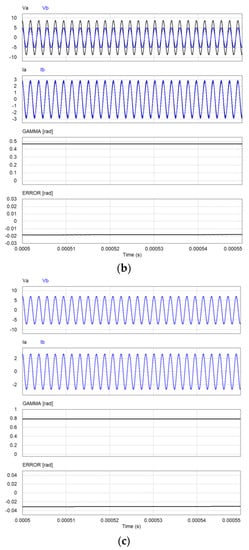
Figure 12. Steady-state response of proposed estimator (d = 0 cm). (a) Φ = 15°, (b) Φ = 30°, (c) Φ = 45°.

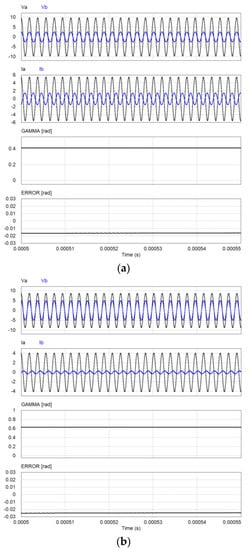
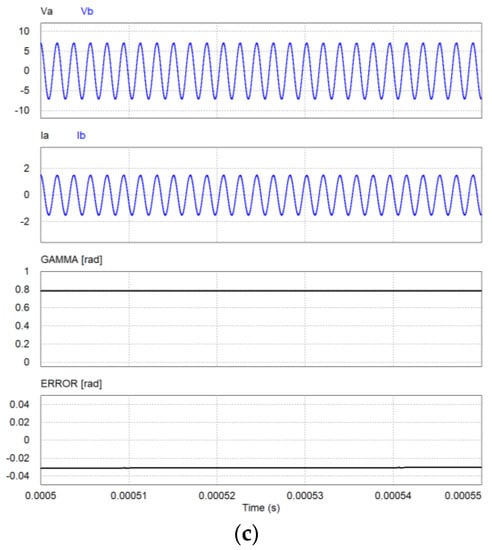
Figure 13. Steady-state response of proposed estimator (d = 2 cm). (a) Φ = 15°, (b) Φ = 30°, (c) Φ = 45°.

Figure 14 shows the experimental results for the proposed estimator for various physical angles. Figure 13a shows the measured and estimated mutual inductance angles and Figure 13b shows the estimation error, where the measured values are from Table 2. The maximum error is 0.97° at Φ = 30° and d = 2 cm. It is known in the experimental results that the mutual inductance angle can be estimated with an error of less than 1° using the proposed estimator in the experimental WPT system.

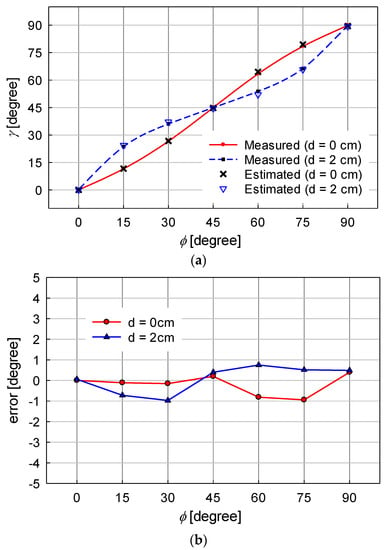
Figure 14. Experimental results for proposed estimator. (a) Measured and estimated mutual inductance, (b) estimation error.

In order to verify the effectiveness of using the estimated mutual inductance angle $\widehat{\gamma }$ instead of the physical angle ϕ, the proposed estimation method is applied to the actual 2D WPT system. The applied currents I_α and I_β for the input terminals in the α- and β-axis are calculated using the estimated mutual inductance angle $\theta$ as

$$I_{\alpha \beta }=\left(\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right)=T{\left(\theta \right)}^{-1}{I}_{dq}$$

(18)

where the reference voltages are given as I_d = 3 A and I_q = 0 for the experiment. The load resistance is given as R_L = 10 Ω. Figure 15 shows the experimental results for the 2D WPT system when the physical angle is Φ = 30° and d = 0 cm between the Tx and Rx coils. Figure 14a,b show the input and output currents when $\theta =\varphi =30°$ and $\theta =\widehat{\gamma }=26.79°$, respectively. The output powers of both cases are calculated as 8.56 W and 9.32 W, respectively, where the PTEs are 80.2% and 81.4%, respectively. Figure 16 shows the results for Φ = 30° and d = 2 cm. The output powers and PTEs are 11.2 W and 12.4 W, and 83.7% and 84.9% for $\theta =\varphi =30°$ and $\theta =\widehat{\gamma }=36.49°$, respectively. The output power and PTE of the 2D WPT system for various physical angles are shown in Figure 17. It is noted in these results that the power transferred to the Rx coil and PTE is improved when the estimated mutual inductance angle is applied instead of the physical angle.

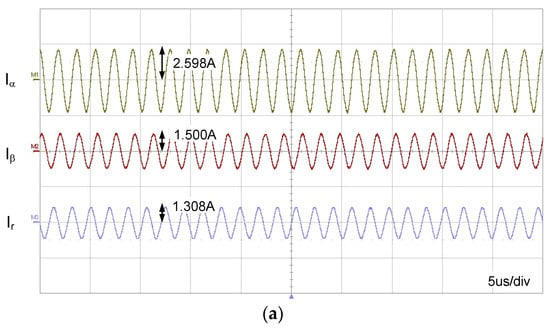
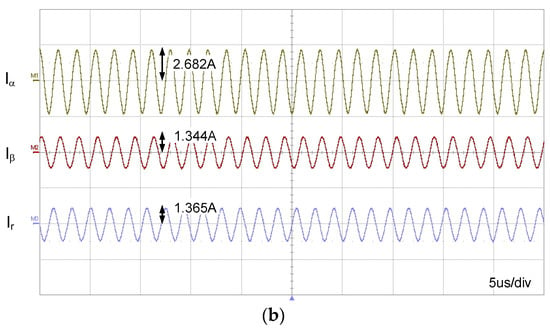
Figure 15. Experimental results for the 2D WPT system using the proposed estimator (d = 0 cm). (a) Input and output currents for $\theta =\varphi =30°$. (b) Input and output currents for $\theta =\widehat{\gamma }=26.79°$.

Figure 16. Experimental results for the 2D WPT system using the proposed estimator (d = 2 cm). (a) Input and output currents for $\theta =\varphi =30°$. (b) Input and output currents for $\theta =\widehat{\gamma }=36.49°$.

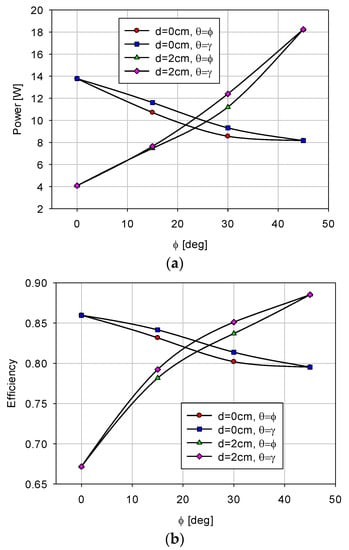
Figure 17. Output power and power transmission efficiency (PTE) of the 2D WPT system for various physical angles. (a) Output power (b) Power transmission efficiency.

5. Conclusions

This paper described the estimation of the mutual inductance angle between the Tx and Rx coils in the 2D WPT system, which is regarded as the most important parameter to determine the PTE. The improved estimator for the mutual inductance angle using the PLL technique was proposed, and the simulation and experimental works were carried out for the actual 2D WPT system. The results showed that the mutual inductance angle can be estimated using the proposed estimator with an error of less than 1° in the given experimental 2D WPT system. It is also shown in the results that the transferred output power and PTE are improved using the proposed estimator.