Abstract
In a previous paper, we have shown that Newton’s third law cannot strictly hold in a distributed system of which the different parts are at a finite distance from each other. This is due to the finite speed of signal propagation which cannot exceed the speed of light in vacuum, which in turn means that when summing the total force in the system the force does not add up to zero. This was demonstrated in a specific example of two current loops with time dependent currents, the above analysis led to suggestion of a relativistic engine. Since the system is effected by a total force for a finite period of time this means that the system acquires mechanical momentum and energy, the question then arises how can we accommodate the law of momentum and energy conservation. The subject of momentum conservation was discussed in a pervious paper, while preliminary results regarding energy conservation where discussed in some additional papers. Here we give a complete analysis of the exchange of energy between the mechanical part of the relativistic engine and the field part, the energy radiated from the relativistic engine is also discussed. We show that the relativistic engine effect on the energy is 4th-order in and no lower order relativistic engine effect on the energy exists.
1. Introduction
Special relativity is a theory of the structure of space-time. It dictates that the equations of any physical theory should be invariant under the Lorentz group of coordinate transformations. The theory was first introduced in Einstein’s famous 1905 paper: “On the Electrodynamics of Moving Bodies” [1]. This theory was a consequence of empiric observations and the laws of electromagnetism which were formulated in the middle of the nineteenth century by Maxwell in their famous four partial differential equations [2,3,4] which owe their current form to Oliver Heaviside [5]. One of the consequences of these equations is that an electromagnetic signal travels at the speed of light c, which led people to believe that light is an electromagnetic wave. This was later used by Albert Einstein [1,3,4] to formulate their special theory of relativity which postulates that the speed of light in vacuum c is the maximal allowed velocity in nature. According to the theory of relativity no object, message, signal (even if not electromagnetic) or field can travel faster than the speed of light in vacuum. Hence retardation, if someone at a distance R from me changes something I may not know about it for at least a retardation time of . This means that action and its reaction cannot be generated at the same time because of the signal finite propagation speed.
Newton’s laws of motion are three physical laws that, together, laid the foundation for classical mechanics. They describe the relationship between a body and the forces acting upon it, and its motion in response to those forces. The three laws of motion were first compiled by Isaac Newton in their Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), first published in 1687 [6,7]. We will only be interested in this paper in the third law which states: When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
According to the third law, the total force in a system not affected by external forces is thus zero. This law has numerous experimental verifications and seems to be one of the corner stones of physics. However, in light of the previous discussion it is obvious that action and its reaction cannot be generated at the same time because of the finite speed of signal propagation, hence the third law is false in an exact sense although it can be true for most practical application due to the high speed of signal propagation. Thus, the total force cannot be null at a given time.
Most modern locomotive systems are based on two material parts each obtaining momentum, which is equal and opposite to the momentum gained by the second part. A typical example of this type of system is a rocket which sheds exhaust gas to propel itself. However, the above relativistic considerations suggest’s a new type of motor in which the system is not composed of two material bodies but of a material body and field. Ignoring the field a naive observer will see the material body gaining momentum created out of nothing, however, a knowledgeable observer will understand that the opposite amount of momentum is obtained by the field as was shown in [8]. Indeed Noether’s theorem dictates that any system possessing translational symmetry will conserve momentum and the total physical system containing matter and field is indeed symmetrical under translations, while every sub-system (either matter or field) is not. This was already noticed by Feynman [4]. Feynman describes two orthogonally moving charges, apparently violating Newton’s third law as the forces that the charges induce on each other do not cancel (last part of 26-2), this paradox is resolved in (27-6) in which it is shown that the momentum gained by the two charge system is balanced by the field momentum.
We will define a relativistic engine as a physical system in which its center of mass is in motion due to the interaction of its material parts. Those parts may be free to move with respect to each other or more practically held in a rigid frame. This is of no consequence as we will only be interested in the motion of the center of mass in this paper. We stress that a relativistic motor allows 3-axis motion (including vertical), it has no moving parts, it has zero fuel consumption (and thus zero carbon emission) and needs only electromagnetic energy as explained in the current paper which may be provided by solar panels. The relativistic engine is an ideal solution for space travel in which currently much of the space vehicle mass is devoted to fuel.
It should be noted that there is no Lorentz covariant definition for the relativistic center of mass, as pointed out by Pryce [9]. Indeed, the center of mass mentioned in our work is not Lorentz covariant, it is defined with respect to a specific frame of reference in which the relativistic engine is at rest (the laboratory frame of reference). Even after the engine is set into motion its velocity is small compared to the speed of light, and thus the Newtonian definition of the center of mass still holds approximately in that specific frame. One should not confuse the retardation speed of the electromagnetic field (which is equal to speed of light in vacuum) with the speed of the engine itself that may be quite modest. The device is denoted a relativistic engine because it takes advantage of the relativistic retardation effect not because it can reach relativistic speeds, in fact one can think of reasons why a macroscopic relativistic engine will not reach relativistic speed due to the high energy required. However, if one still would like to consider an engine moving at relativistic speeds then perhaps the center of mass concept should be replaced by something else, perhaps a relativistic center of momentum, however, this option is beyond the scope of the current paper.
To be sure, other systems can introduce retardation such as for two objects that are connected by a long spring, in which conservation of momentum and energy do not apply if one ignores the momentum and energy of the spring. This case along with other interesting cases are discussed in an excellent book “Dynamics of Particles and the Electromagnetic Field” [10], where more problems, and solutions, were treated than in the current paper, this includes the problem of initial conditions. This work is not about retardation in long springs but about retardation caused by the relativistic effect of a finite speed of signal propagation. Only in this later case, momentum and energy is transferred between field and material allowing the relativistic engine effect. This is quite different than transfer of momentum and energy between two material bodies such as two objects and a connecting long spring. Momentum and energy transfer between material bodies is well known and the center of mass of the two objects and the connecting long spring viewed as one system cannot move, if not initially in motion. However, this is rather different from the current case in which momentum and energy are transferred from the electromagnetic field to a material body. In the later example momentum and energy are transferred from one material body (the two objects) to another material body (the long spring) this is well known and perhaps of less interest than the transfer of momentum and energy from a material body to a field which is involved in the motion of the center of mass of the material body. The latter case suggests a new form of motor which is the relativistic engine.
In what follows, we will assume that the magnetization and polarization of the medium are small and therefore we neglect corrections to the Lorentz force suggested in [11]. In a paper by Griffiths and Heald [12], it was pointed out that strictly Coulomb’s law and the Biot-Savart law determine the electric and magnetic fields for static sources only. Time-dependent generalizations of these two laws introduced by Jefimenko [13] were used to explore the applicability of Coulomb and Biot-Savart outside the static domain.
In a previous paper, we used Jefimenko’s [3,13] equation to discuss the force between two current carrying coils [14]. This was later expanded to include the interaction between a current carrying loop and a permanent magnet [15,16], see Figure 1.
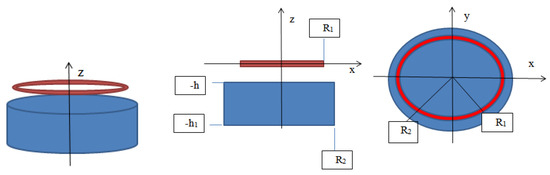
Figure 1.
A cylindrical magnet (blue) and a current loop (red) above it. (three different sections).
Since the system is affected by a total force for a finite period of time this means that the system acquires mechanical momentum and energy, the question then arises if we need to abandon the law of momentum and energy conservation. The subject of momentum conversation was discussed in [8]. In [17,18,19], some preliminary aspects of the exchange of energy between the mechanical part of the relativistic engine and the electromagnetic field were discussed. In particular it was shown that the electric energy expenditure is twice the kinetic energy gained by the relativistic motor. It was also shown how some energy may be radiated from the relativistic engine device if the coils are not configure properly. In this paper, we develop a methodology to deal with all aspects of the energy transformation in a relativistic engine.
The plan of this paper is as follows: First, we introduce the conservation of energy and momentum in a general electromagnetic system. Then we discuss the particular case of a simple relativistic engine made of two current loops of arbitrary geometry, in which we shall consider the mechanical momentum and energy gained by the engine. This will be followed by a general analysis of the energy transformations between the field and mechanical components in a relativistic engine. Which will be followed by a specific analysis of a relativistic engine taking into account the various energy contributions expanded in powers of , in which c is the speed of light in vacuum. We show that the relativistic engine effect on the energy is 4th-order in and no lower order relativistic engine effect on the energy exists.
2. Energy and Momentum Conservation
Any system with space-time translational symmetry must conserve momentum and energy according to Noether’s theorem. In the case of a system with charge and current densities the energy-momentum conservation law takes the form [3]:
are space-time coordinates such that , is a partial derivative with respect to the four dimensional coordinates and Einstein’s summation convention is assumed, is a volume element. In the above:
and:
The various terms in the matrix appearing in Equation (2) are defined in terms of the electric field and magnetic flux density as follows. The field energy density is defined such that:
where is the vacuum permittivity (≃). Poynting’s vector is defined as:
where is the vacuum magnetic permeability. is the Maxwell stress tensor:
and is Kronecker’s delta. Equation (3) contains the mechanical energy and momentum and the temporal derivative . Next we shall write the matrix Equation (1) in terms of the spatial and temporal components separately. The spatial components will yield the equation:
In the above, is the i component of the field momentum of the system:
S is a closed surface encapsulating the volume in which the system is located, is a unit vector normal to the surface, is a surface element.
Equation (7) as proved in [3] is a precise statement of momentum conservation in a relativistic engine and from a pure point of view nothing else is needed, however, for the sake of concreteness a specific example for the two current loops relativistic engine was analyses in [8] and will not be repeated here.
To conclude this section we shall look at the zeroth component of Equation (1), which yields the energy conservation equation:
The derivative of the mechanical energy is the power needed to sustain the system and is given by [3]:
where is the current flux density. Hence:
Or:
In the following we will discuss the manifestation of energy conservation as described by Equation (12) for a relativistic engine.
3. The Case of Two Currents Loops of Arbitrary Geometry
Consider two wires having segments of length located at , respectively, and carrying currents (see Figure 2).
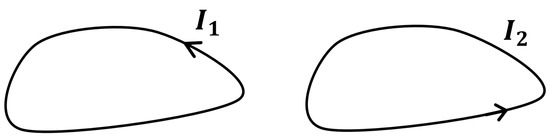
Figure 2.
Two current loops.
According to [14] (Equation (38)), the force on loop generated by loop takes the form:
in which , . is written as a Taylor expansion in the time t and the terms are the derivatives of order n with respect to the variable t. As in all expansions the above equation is valid only for a certain environment of t on the time axis which depends on the function , this environment shall be defined using the convergence radius . That is Equation (13) is valid only in the domain . We note that there is no first order contribution to the force. Hence the next contribution to the force after the quasi-static term is second order. Let us define the dimensionless geometrical factor as:
in the above h is some characteristic distance between the coils. In terms of we can write Equation (13) as:
The force due to coil 2 that acts on coil 1 is:
The total force on the system is thus:
We note that the quasi-static term does not contribute to the sum nor does the term. The fact that the retarded field “corrects” itself to first order in order to “mimic” a non retarded field was already noticed by Feynman [4]. Hence we can write:
We conclude that in general Newton’s third law is not satisfied, taking the leading non-vanishing terms in the above sum we obtain:
This result is correct up to a second order in . Assuming that the total momentum of the system and the current derivatives are null at , we obtain a mechanical linear momentum as follows:
For simplicity, we will from here on assume a direct current in loop 2 hence:
For a calculation of in particular geometries see [14,15,16]. We stress that the mechanical momentum given is of order and higher order terms are neglected. The kinetic mechanical energy associated with this momentum is:
where M is the mass of the relativistic engine and:
is the engine velocity. This indicates that unlike the conservation of momentum [8] which was independent of the mass and therefore of the velocity attained by the system, in the calculations of both the mechanical and electromagnetic energies the systems velocity and mass are of paramount importance. We also note that the expression for mechanical energy is of order , lower order corrections do not exist and higher order corrections are neglected.
We define the relativistic engine effect as a motion of the center of mass of a system due to the interaction of its two subsystems, if there is no motion of the center of mass than the effect is null. It may be that the center of mass is moving due to the motion of each subsystem separately but then, according to the above definition this is not a relativistic engine effect but an effect caused by an external force.
3.1. Proposed Experiment
In the following, we calculate the factor for a geometry of two loops of unit radius and a unit distance placed one atop the other (see Figure 3).
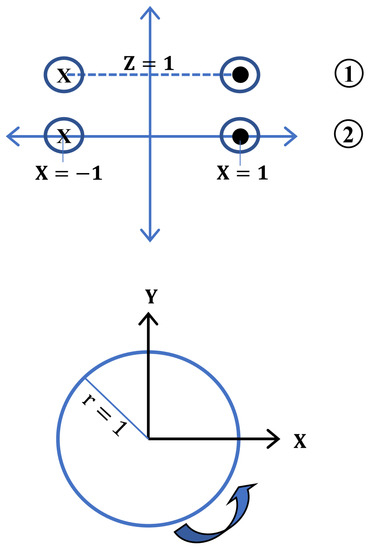
Figure 3.
Two loops of radius 1 and displacement 1. We depict x-z and x-y cross sections. The x-z cross section dot describes current going inside the plane and the symbol x describes a current going outside the plane. In the x-y section the arrow is used to specify the current direction.
According to Equation (14), we obtain by taking (in arbitrary units since is dimensionless).
Every point on loop 1 and 2 has the coordinates and , hence:
Furthermore, thus:
The line elements can be calculated as follows:
Hence:
Inserting Equations (28), (26) and (25) into Equation (14) we arrive at:
We now make a change of variable in the above integral , in terms of the new variable:
In which:
The integrand is periodic with respect to with a period of , we thus write Equation (30) as:
Noticing that:
We arrive at the equation:
Vanishing of the x and y components of the force is expected due to the symmetry. The z components can be calculated analytically, for even values of n one needs elliptic functions, for example:
K values for are given in Table 1.

Table 1.
Table of the geometric factor K values.
Finally notice that for multiple loops we have:
where and are the number of turns in coil 1 and coil 2, respectively.
The Problem of Current Switching
We will address the problem of achieving constant force which is of interest for locomotive applications. A constant force may be achieved by having a direct current in one loop and a current of uniform second derivative on the other . In this case the accelerating force will be according to Equation (19):
Assuming the case of circular loops of the previous subsection we obtain from Equation (35):
For the values given in Table 2 Newton. The switching time may represent some difficulty which one can overcome with advanced enough switching technology, perhaps using low resistivity superconducting materials. Another possibility is using numerous modular solid-state devices each with fast switching and small current such that an appreciable amount of cumulative forcing will result. In any case increasing the current for ever is not possible, but probably can be maintained sufficiently long to allow experimental verification. Changing periodically the current is of course possible but in this case one is led back to the standard piston going up and down as in an ordinary car motor and this type of motion needs to transfer momentum to the road in order to convert circular to linear motion.

Table 2.
The choice of parameters for the force calculation.
4. Field Energy
Consider two sub-systems denoted system and system which are far apart such that their interaction is negligible. In this case, Equation (12) is correct for each sub-system separately, that is:
Next we will put the two loops closer together such that they may interact but without modifying the charge and the current densities of each of the subsystems. The total fields of the combined system are:
Since both the field energy Equation (4) and Poynting’s vector Equation (5) are quadratic in the fields the following result is obtained:
The power invested in the combined system in bilinear in the current flux density and the electric field according to Equation (10). This will lead to the following expression:
Subtracting from Equation (12) the expressions given in Equations (39) and (40):
taking into account Equations (42)–(44) we arrive at:
5. Field Energy of a System of Two Current Loops
We now study the case of two loops of arbitrary geometry as described in Section 3. However, now we assume two time dependencies. One due to the intrinsic time dependence of the current in the loop and another is due to its motion as part of the relativistic engine. Thus, the current density is:
in which is the current density in the moving frame of the relativistic engine and is the velocity of the relativistic engine. The vector potential is [3]:
Which can be written as a power series in in the form:
As in the case of Equation (13) this expansion is only valid in the domain in which being the “convergence radius” of the above series. Hence this is only valid for distances satisfying or:
since c is a big number we will occasionally use Equation (49) for infinite distances while remembering that although may be big it is not infinite. Let us introduce a comoving integration variable: such that: in such a comoving coordinate system we have:
For a thin and uniform current loop this can be written as:
Let us define:
in terms of we may write:
We notice is at least of order but may contain higher order terms. The reason for this is the fact that contains temporal derivatives of which satisfy the equation:
and is proportional to for a relativistic engine according to Equation (23). Thus, may contain terms which are up to order of . We also notice that the zeroth order terms takes the form:
which is just the quasi static approximation to . It also easy to see that the first order term:
as . As contains terms in various orders of , and we will be interested in analyzing the energy problem for a definite order of , we introduce the square bracket notation to denote a quantity of order . Obviously, generally . The electric field can be calculated (in the gauge ) as [3]:
We shall define for computational convenience:
This means that will contain terms coming from but also from as the derivative will create terms which have an additional factor. As for the magnetic field which can be calculated as [3]:
it is easy to see that is the same order as and:
In what follows we will use the above expressions to analyzed the energy transformation order by order starting from and up to which according to Equation (22) is the most relevant for analyzing the energy transfer between the field and the mechanical components of a relativistic engine.
5.1. Normalization
To avoid carrying the factor in numerous calculations we shall define:
Furthermore, hence:
The field energy (see Equation (42)) can be calculated in terms of the new variables as:
where we are reminded that , the Pointing vector (Equation (43)) will take the following form in terms of the new variables:
Finally the mechanical work which is represented by Equation (44) will take the form:
We introduce the following normalization:
In terms of the normalized quantities we may write the relativistic engine energy transformation Equation (46) as:
This can be analyzed order by order in terms of powers of hence:
We notice that because of the pre-factor of the electric field contribution in Equation (68) this term will not contribute to the field energy for the lowest orders: . We also notice that since we are considering a case of two loop currents Equation (69) takes the form:
We are now ready to analyzed the field contribution order by order. In what follow we give the main results the reader who is interested in the details is referred to Appendix A.
5.2.
For we conclude that the energy equation of order zero is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. To be more specific the magnetic field energy is affected by the mechanical work. The power related to the mechanical work is:
in which:
and this is equal to minus the derivative of the field energy:
which is what is expected from Equation (71) for the case that there is no Poynting contribution. We underline that those contributions are not related the relativistic engine effect as none of the terms depends on the engine velocity , and thus the above expression will be valid even if the engine is infinitely massive and no motion occurs.
5.3.
For we conclude that the energy equation of order one is indeed balanced in a trivial way. Equation (71) is satisfied in the sense that . From now on we will disregard in our calculations any field term of order one, as their contribution to any expression is obviously null.
5.4.
We conclude that the energy equation of the second order is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. To be more specific the magnetic field energy is affected by the mechanical work. The power related to the mechanical work is:
and this is equal to minus the derivative of the field energy:
which is what is expected for the case that there is no Poynting contribution. We underline that those contributions are not related the relativistic engine effect as non of the terms depends on the engine velocity , and thus the above expression will be valid even if the engine is infinitely massive and no motion occurs. We do not expect any relativistic engine contributions for orders smaller than . For a phasor current of frequency we obtain a relativistic correction to the classical mutual inductance which is important for large systems with high frequency.
5.5.
We conclude that the energy of the third order is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. To be more specific the magnetic field energy is affected by the mechanical work. The power related to the mechanical work is:
and this is equal to minus the derivative of the volume field energy:
However, for the third order in there is also a surface contribution to the field energy:
in which:
such that the total field energy is:
The change in the field energy through the surface terms results in radiation as described by the Poynting flux:
curiously this flux can be avoided by configuring the loops to be orthogonal to each other [19]. We underline that third order contributions are not related the relativistic engine effect as non of the terms depends on the engine velocity , and thus the above expression will be valid even if the engine is infinitely massive and no motion occurs. We do not expect any relativistic engine contributions for orders smaller than . For a phasor current of frequency the result indicates a resistive relativistic correction to the classical mutual inductance which is important for large systems with high frequency.
5.6.
We conclude that the energy of the fourth order is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. In the fourth order both electric and magnetic field energies are affected by the mechanical work. The power related to the mechanical work is:
it contains both work done by the mutual inductance and on the relativistic engine. This is equal to minus the derivative of the volume field energy:
The total field energy is s made of an electric part:
and a magnetic part:
Moreover, for the fourth order in there is also a surface contribution to the field energy which satisfies:
such that the total field energy is:
The change in the field energy through the surface terms results in radiation as described by the Poynting flux:
We underline that fourth order contributions are the only one that are related to the relativistic engine effect as some of the terms depends on the engine velocity . If the engine is infinitely massive and no motion occurs, we are left with the mutual inductance correction terms and radiation terms which involve higher order derivatives. For a phasor current of frequency we obtain a relativistic correction to the classical mutual inductance which is important for large systems with high frequency.
6. Conclusions
A relativistic engine is not a “perpetuum mobile” it requires energy to operate. The energy needed for its operation comes at the expanse of the electromagnetic field energy. Moreover, we have shown that the total energy required is six times the mechanical energy obtained by the engine as energy must be invested also in driving the needed current for its operation through the loops (see Equations (A182) and (A195)). Two times comes at the expense of the electric field energy and four times at the expense of the magnetic field energy. Notice that we have not taken resistive losses into account but if the coils are not superconductive this should be taken into account as well. As we collected all the terms up to and including we have encountered for most of the time terms that can be thought of as relativistic corrections to the mutual inductance formula and are not connected in any way to the relativistic engine effect. For order there are also radiation losses which may be avoided by cleverly constructing the loop coils orthogonal to each other. For order the nature of our series expansion prevents us from evaluating the radiation flux at infinity and we must suffice with the radiation flux over a sphere of radius which is the distance after which our approximation becomes invalid.
In this work we have only dealt with the energy exchange due to the interaction of two loops but of course even a single loop looses energy due to radiation. Future works will consider other relativistic concepts such as an electric (rather than magnetic) relativistic engine. We will also be interested in studying the relativistic ramifications of small body moving in a large structure generating an “external field”. In such a body we expect additional contribution to the main “classical” force which are due to the relativistic retardation.
Finally we remark that although an energy of seems excessive and inefficient, it is highly efficient with respect to other types of engines which are purely electromagnetic. For example, to reach a momentum p using a photon engine one needs an energy of while for a relativistic engine an energy of will suffice. The ratio is which is a huge number for non relativistic speeds.
Author Contributions
Conceptualization, A.Y.; methodology, S.R. and A.Y.; software, S.R. and A.Y.; validation, S.R., A.Y. and H.Q.; formal analysis and investigation, S.R., A.Y. and H.Q.; data curation, S.R. and A.Y.; writing—original draft preparation, S.R., A.Y. and H.Q.; writing—review and editing, A.Y. and H.Q.; supervision, A.Y.; project administration and funding acquisition, A.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the U.S. Department of Energy (DE-AC02-09CH11466), Shailendra Rajput is thankful to the Israeli Council for Higher Education (CHE) for fellowship.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Asher Yahalom wishes to thank Princeton University for hospitality during the composition of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Energy Balance from n = 0 to n = 4
Appendix A.1. n = 0
Let us look at Equation (71) and study it for the zeroth order in :
Appendix A.1.1. Power
We shall start by calculating , according to Equation (72):
The field can only come from the vector potential as all other are of higher order in n, hence according to Equation (56):
According to Equation (59):
However, the second term in the above equation is of order of and will be dealt with later. Hence:
we notice that the derivative of the integral is of order hence does not contribute to the zeroth order. Now since the second coil has a constant current this leads to the result:
Inserting the above result into Equation (A2) yields:
Inserting Equation (A5) into Equation (A7) will yield the expression:
This can be written in terms of the familiar mutual inductance [3]:
as:
We notice that may be positive or negative according to the relative position of the current loops and current directions, hence, energy can be invested or extracted from the combined system according to the system configuration.
Appendix A.1.2. Field Energy
Turning our attention next to field energy defined in Equation (68):
is calculated according to Equation (61) as:
Now since we may use Equation (56) to obtain:
Inserting Equation (A13) into Equation (A11) will yield:
in which we recall that is time independent. Using a well known identity from vector analysis we may write:
We shall show in the Appendix B that:
Hence:
Now:
Taking into account that [3]:
in which is a three dimensional delta function, we have:
The first term in the right hand side is a divergence. Thus, using Gauss theorem its volume integral will become a surface integral, the second term is a delta function. This means that there is no contribution to the volume integral from the delta term unless . We may now write Equation (A17) as follows:
Let us look at the surface integral and assume that the system is contained inside an infinite sphere. On the surface of such a sphere:
is an infinitesimal solid angle. Now since on the surface and:
it follows that:
up to second order in the infinitesimal quantity . Furthermore, for the same reason:
to the same order. Furthermore, also:
Using the above results we conclude that:
Hence:
And:
where we took advantage of the mutual inductance term defined in Equation (A9).
Appendix A.1.3. Poynting Vector
Finally we shall study the Poynting vector:
Taking into account that is null according to Equation (A6) this simplifies to:
Now the Poynting vector term which is usually associated with radiation only contributes to the energy balance on a surface encapsulating the system under consideration (see Equation (71)). Taking this surface to be spherical and at infinity we deduce that only the asymptotic forms of and are of interest for the purpose of evaluating the Poynting vector contribution. According to Equation (A5):
In which we use the approximation given in Equation (A25) and take into account that . The magnetic field is given in Equation (A13):
in the above we used again the identity . We shall define the quantity:
for future use. From the above it easy to see that:
and thus it is easy to see that:
hence there is no Poynting vector contribution to the energy balance. Thus, is the quasi static approximation there is no radiation losses as expected.
Appendix A.1.4. Intermediate Account
We conclude that the energy equation of order zero is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. To be more specific the magnetic field energy is affected by the mechanical work. The power related to the mechanical work is:
and this is equal to minus the derivative of the field energy:
which is what is expected from Equation (71) for the case that there is no Poynting contribution. We underline that those contributions are not related the relativistic engine effect as none of the terms depends on the engine velocity , and thus the above expression will be valid even if the engine is infinitely massive and no motion occurs.
Appendix A.2. n = 1
Let us look at Equation (71) and study it for the first order in :
Appendix A.2.1. Power
We shall start by calculating , according to Equation (72):
The field can only come from the vector potential . As (see Equation (57)) it follows that and hence by Equation (58):
It then follows that:
Hence no mechanical work is invested nor extracted for a relativistic engine in the first order of .
Appendix A.2.2. Field Energy
Turning our attention next to field energy defined in Equation (68):
is calculated according to Equation (61) as:
Now since we may use Equation (A45) to obtain:
for the magnetic field generated from both coils. Inserting Equation (A46) into Equation (A44) will yield:
Hence there is no contribution from first order terms in to the field energy of a relativistic engine neither.
Appendix A.2.3. Poynting Vector
Finally we shall study the Poynting vector:
According to Equations (A42) and (A46) all the above terms vanish and we have:
Appendix A.2.4. Intermediate Account
We conclude that the energy equation of order one is indeed balanced in a trivial way. Equation (71) is satisfied in the sense that . From now on we will disregard in our calculations any field term of order one, as their contribution to any expression is obviously null.
Appendix A.3. n = 2
Let us look at Equation (71) and study it for the second order in :
Appendix A.3.1. Power
We shall start by calculating , according to Equation (72):
The field can only come from the vector potential and . is given in Equation (A3) while can be deduce from which can be calculated using Equation (53) as:
Or explicitly as:
in which we have used Equation (55). It is clear that contain contributions to but also to and (but not to odd ’s). For now we will only be interested in which is:
Combining the above result with Equations (59) and (A4) yields:
Now since the second coil has a constant current this leads to the result:
Inserting the above results into Equation (A51) yields:
In the above:
Inserting Equation (A58) into Equation (A57) will result in the cancellation of the first two terms:
Hence:
We notice that may be positive or negative according to the relative position of the current loops and current directions and third derivative, hence, energy can be invested or extracted from the combined system according to the system configuration. We also notice that this term has nothing to do with the relativistic engine effect as it is completely independent of the mass of the engine and will exist also for an infinitely heavy motor. This is to be expected as the relativistic engine effect is fourth order in and not second order. We will interpret the double integral in the next subsection dealing with the field energy.
Appendix A.3.2. Field Energy
Turning our attention next to field energy defined in Equation (68) we obtain the following expression for second order terms in :
in which we are reminded that there are no field contributions which are first order in . According to Equation (A6) the zeroth order electric field for the static current second coil is null, hence:
is calculated according to Equation (61) as:
Taking into account Equation (A54) the second order correction to the magnetic field is thus:
Hence for a static coil:
Furthermore, thus:
Inserting Equation (A13) into Equation (A11) will yield:
in which we recall that is time independent. Using a well known identity from vector analysis we may write:
Let us look at the integral expression
This is an expression of the type described in Equation (A305) of Appendix B with and . According to Appendix A the expression in Equation (A69) can be expressed as a surface integral. Assuming that our system is contained in an infinite sphere we have according to Equations (A316) and (A22):
Now:
This can be calculated up to second order in using Equations (A23) and (A24) as:
Similarly according to Equation (A25):
Plugging Equations (A72) and (A73) into Equation (A70) we obtain:
The terms will not contribute in the limit of infinite radius and thus we may write:
multiplying the square brackets explicitly we obtain:
in the limit of large r:
Now we notice that performing a loop integral over a constant we obtain a null result:
Since neither of the terms in the square bracket depends on both and (they depend on either or or non of them) certainly one of the loop integrals of Equation (A77) will vanish (or both), hence and thus Equation (A68) takes the form:
Now:
Taking into account Equation (A19), we have:
The first term in the right hand side is a divergence. Thus, using Gauss theorem its volume integral will become a surface integral, the second term is a delta function. This means that there is no contribution to the volume integral from the delta term unless . We may now write Equation (A79) as follows:
Let us look at the surface integral and assume as usual that the system is contained inside an infinite sphere.
Using Equations (A24) and (A27) this can be written as:
Or also as:
In the limit of large r the terms will not contribute, hence:
multiplying the square brackets explicitly we obtain:
the term will not contribute, hence:
Since neither of the terms in the square bracket depends on both and (they depend on either or or non of them) certainly one of the loop integrals of Equation (A77) will vanish (or both) being a loop integral over a constant vector (see Equation (A78)), hence and thus Equation (A82) takes the simple form:
And:
For a phasor current with frequency :
we obtain a second order correction to the mutual inductance of the form [18]:
Such that:
Obviously the larger the system and the higher the frequency the more important this correction is. We stress that this term is not related to the relativistic engine effect and will exist even for an engine of “infinite” mass.
Appendix A.3.3. Poynting Vector
Finally we shall study the Poynting vector:
Taking into account that is null according to Equation (A6) and is null according to Equation (A65) this simplifies to:
Now the Poynting vector terms which are usually associated with radiation only contributes to the energy balance on a surface encapsulating the system under consideration (see Equation (71)). Taking this surface to be spherical and at infinity we deduce that only the asymptotic forms of and are of interest for the purpose of evaluating the Poynting vector contribution. According to Equation (A55):
Taking into account the asymptotic forms given in Equations (A24) and (A27) and taking into account that ., we arrive at the asymptotic form:
Hence for an asymptotic field created by a time dependent current we have the form:
However, for an asymptotic field created by a time independent current we have the form:
The asymptotic form of the magnetic field is given in Equations (A34) and (A35):
From the above it easy to see that:
of course the contribution from Equation (A99) will go to zero much faster as: . This term is only obtained when is time dependent. It easy to see that:
hence there is no Poynting vector contribution to the energy balance. This is expected as the mechanical work is balanced by the field energy loss exactly in second order terms of .
Appendix A.3.4. Intermediate Account
We conclude that the energy equation of the second order is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. To be more specific the magnetic field energy is affected by the mechanical work. The power related to the mechanical work is according to Equation (A60):
and this is equal to minus the derivative of the field energy Equation (A90):
which is what is expected from Equation (A50) for the case that there is no Poynting contribution. We underline that those contributions are not related the relativistic engine effect as none of the terms depends on the engine velocity , and thus the above expression will be valid even if the engine is infinitely massive and no motion occurs. We do not expect any relativistic engine contributions for orders smaller than . For a phasor current of frequency Equation (A92) indicates a relativistic correction to the classical mutual inductance which is important for large systems with high frequency.
Appendix A.4. n = 3
Let us look at Equation (71) and study it for the third order in :
Appendix A.4.1. Power
We shall start by calculating , according to Equation (72):
The field can only come from the vector potential and . is null according to Equation (57) while can be deduce from which can be calculated using Equation (53). As expected, the higher the frequency the more pronounced the relativistic effect is. A third order correction to the magnetic field in a relativistic motor can be derived from the third term in the sum given in Equation (52):
Now it is clear that this expression contains terms of the order of and higher (including terms of the order and ). However, it is easy to see that there are no third order corrections to the vector potential except:
Now using Equation (58) we arrive at the following equation for :
in which we maintained only terms of the order of but not higher. From which it is clear that:
for a constant current loop. Hence according to Equation (72):
Hence:
We notice that may be positive or negative according to the relative position of the current loops and current directions and fourth derivative, hence, energy can be invested or extracted from the combined system according to the system configuration. We also notice that this term has nothing to do with the relativistic engine effect as it is completely independent of the mass of the engine and will exist also for an infinitely heavy motor. This is to be expected as the relativistic engine effect is fourth order in and not third order. We will interpret the double integral in the next subsection dealing with the field energy.
Appendix A.4.2. Field Energy
Turning our attention next to field energy defined in Equation (68) we obtain the following expression for third order terms in :
in which we are reminded that there are no field contributions which are first order in . is calculated according to Equation (61) as:
Taking into account Equation (A108) the third order correction to the magnetic field is thus:
in which we have used:
Hence for a static coil:
Furthermore, thus:
Inserting Equation (A13) into Equation (A11) will yield:
in which we recall that is time independent. Using a well known identity from vector analysis we may write:
Let us look at the integral expression
Such that:
This is an expression of the type described in Equation (A305) of Appendix B with and . According to Appendix A the expression in Equation (A122) can be expressed as a surface integral. Assuming that our system is contained in an infinite sphere we have according to Equations (A316) and (A22):
Now:
This can be calculated using Equation (A23) as:
Similarly according to Equation (A25):
Plugging Equations (A126) and (A127) into Equation (A128) we obtain:
Now we recall that performing a loop integral over a constant we obtain a null result:
The only term that contribute must depend on both and thus Equation (A128) takes the form:
Furthermore, taking the limit we obtain:
According to [3]:
in which is a Kronecker delta, hence:
Hence although is a surface integral at infinity it does not vanish which indicates radiation. The radiation contribution to the energy balance will be discussed further in the next subsection in which we shall consider the Poynting flux contribution. Let us now look at the first part of the integral:
Such that:
Now:
Taking into account Equation (A19), we have:
The first term in the right hand side is a divergence. Thus, using Gauss theorem its volume integral will become a surface integral, the second term is a delta function. This means that there is no contribution to the volume integral from that terms unless . We may now write Equation (A122) as follows:
Let us look at the surface integral and assume as usual that the system is contained inside an infinite sphere.
We denote:
and show in Appendix C that:
Hence:
Now taking int account Equation (A132) we obtain the result:
Hence:
Now inserting Equations (A144) and (A133) into Equation (A135) will yield:
we will dissect the above expression into volume and surface contributions such that:
And:
It can easily seen that the change in volume energy is balance by the mechanical work done, see Equation (A113). For a phasor current with frequency :
we obtain a second order correction to the mutual inductance of the form [18]:
Such that:
Obviously the larger the system and the higher the frequency the more important this correction is. We note that this term contains a j indicating that this correction is resistive. We stress that this term is not related to the relativistic engine effect and will exist even for an engine of “infinite” mass. Of course we have unbalanced surface terms with field energy:
The only way to balance the derivative of this term in the energy equation is by a Poynting term which signifies the generation of radiation. Finally we notice the vector identity:
and the definition of a oriented Area:
and write Equation (A153) in a compact form:
Hence orthogonal current loops will generate a null surface field contribution.
Appendix A.4.3. Poynting Vector
Finally we shall study the Poynting vector:
Taking into account that is null according to Equation (A6) and is null according to Equation (A118) this simplifies to:
Further more according to Equation (A110) is also null hence:
The above expression can be calculated using Equations (A109) and (A13):
in we have used the definition of given in Equation (A140). Doing some vector algebra we have:
Now let us calculate the Poynting flux on an infinite sphere:
According to Equation (A161) this will take the form:
According to Appendix C this can be calculated using the result of Equation (A333):
Applying Equation (A132) we obtain:
Taking into account Equations (A154) and (A155) we have finally:
Thus, the Poynting radiation flux balances that change in surface field energy given in Equation (A156).
Appendix A.4.4. Intermediate Account
We conclude that the energy Equation (A105) of the third order is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. To be more specific the magnetic field energy is affected by the mechanical work. The power related to the mechanical work is according to Equation (A113):
and this is equal to minus the derivative of the volume field energy Equation (A149):
However, for the third order in there is also a surface contribution to the field energy given in Equation (A156):
such that the total field energy is:
The change in the field energy through the surface terms results in radiation as described by the Poynting flux depicted in Equation (A166):
curiously this flux can be avoided by configuring the loops to be orthogonal to each other [19]. We underline that third order contributions are not related the relativistic engine effect as non of the terms depends on the engine velocity , and thus the above expression will be valid even if the engine is infinitely massive and no motion occurs. We do not expect any relativistic engine contributions for orders smaller than . For a phasor current of frequency Equation (A151) indicates a resistive relativistic correction to the classical mutual inductance which is important for large systems with high frequency.
Appendix A.5. n = 4
Let us look at Equation (71) and study it for the fourth order in :
Appendix A.5.1. Power
We shall start by calculating , according to Equation (72):
The field can only come from the vector potential and . Let us start by analyzing the contribution of the term, according to Equation (A54) this is equal to:
to calculate the electric field contribution to the fourth order according to Equation (58) we shall take the temporal derivative of Equation (A175) but keep only fourth order terms, thus we arrive at:
where we use Equation (55), obviously this is not the only contribution to the electric field of the fourth order and thus it is marked by the index other contributions to the electric field will be marked by . Hence for the static coil we have:
and thus:
Plugging Equation (A176) into Equation (A178) leads to the result:
Using Equation (14) for defining we arrive at the form:
or also:
Taking into account Equation (21) we have:
which is exactly the amount of mechanical power needed to drive the relativistic engine. Unfortunately more power is needed to drive the currents through the coils as will be demonstrated below.
Let us now derive an expression for , the fourth order contribution will come from given in Equation (A53) but also from defined in Equation (53):
We notice that there are no contributions from which contains only odd powers of . It is clear that Equation (A183) contains terms of the order of and higher (including terms of the order , and ). However, it is easy to see that there are no fourth order corrections to the vector potential coming from Equation (A183) except:
Taking into account Equation (A184) and the fourth order contributions from Equation (A53) we obtain the expression:
We shall define:
for future reference. Now using Equation (58) and keeping only fourth order contributions we arrive at the following equation for :
We shall define for future reference the mutual inductance fourth order electric field:
the last equation sign is correct up to the fourth power in . It is clear that for a constant current we have:
We shall write down the total electric field correction to fourth order in for future reference:
Plugging Equations (A187) and (A189) into Equation (A173) will lead to the following expression:
Now since the first and fifth terms cancel. Furthermore, we obtain:
Taking into account the definition of given in Equation (14) we have:
Hence:
Now using the expression for the relativistic engine mechanical momentum given in Equation (21) we have:
Hence the total mechanical work done in the fourth order can be calculated using Equations (A182) and (A195) as:
We notice that power invested is mechanical work to fourth order in has two parts. One which clearly is not related the relativistic engine effect and the other which clearly is. As related to the mechanical power needed to operate the relativistic engine it is six times greater then the change in kinetic energy of the engine itself, the rest of the power is invested in driving the currents through the coils. An additional part which is related to the fifth derivative of the current is not connected to relativistic engine effect and will exist even for an infinitely heavy engine.
Appendix A.5.2. Field Energy
Turning our attention next to field energy defined in Equation (68) we obtain the following expression for fourth order term in :
in which we are reminded that there are no field contributions which are first order in . According to Equation (A6) , and according to Equation (A65) , hence the above equation simplifies as follows:
The field energy can be clearly partitioned to electric field and magnetic field contributions:
We begin with evaluating by using of Equation (A5) and of Equation (A56). Obtaining:
We show in Appendix D (see also [17]) that:
hence:
Taking into account Equation (14) we obtain:
hence:
using the mechanical momentum Equation (21) we thus obtain:
Turning our attention to the magnetic part of the field energy we notice that a fourth order correction of the magnetic field is needed, this can be calculated according to Equation (61) as:
Taking into account Equation (A185) the fourth order correction to the magnetic field is thus:
Hence for a static current:
We shall find it convenient to label the different terms of the magnetic field of the fourth order:
Furthermore, thus the magnetic energy can also be partitioned:
We shall start by evaluating . Using Equations (A13) and (A208) we obtain:
Using a well known identity from vector analysis we may write:
Let us look at the integral expression
This is an expression of the type described in Equation (A305) of Appendix B with and . According to Appendix A the expression in Equation (A213) can be expressed as a surface integral. Assuming that our system is contained in an infinite sphere we have according to Equations (A316) and (A22):
The following asymptotic expressions will now come in handy (see Equations (A72) and (A84)):
Inserting Equations (A215) and (A216) into Equation (A214) and taking the limit will yield:
However, according to Equation (A129) a closed loop integral over a constant is null hence:
Furthermore, Equation (A212) simplifies to:
Now:
Taking into account Equation (A19), we have:
Plugging Equation (A221) into Equation (A219) and using Gauss theorem we obtain:
Let us perform the surface integral on an infinite sphere as usual and look at the integral:
Now Equation (A216) takes the asymptotic form:
Using Equations (A215) and (A224) in Equation (A223) and taking the limit:
However, according to Equation (A129) a closed loop integral over a constant is null hence:
and thus Equation (A222) simplifies
Taking into account the definition Equation (14) this is simplified to the form:
Next we turn our attention to (see Equation (A210)), using Equations (A13) and (A209) we obtain:
However, this integral is the same as the integral given in Equation (A211) with the indices 1 and 2 interchanged. It immediately follows that is equal to right hand side of Equation (A228) with the indices 1 and 2 interchanged, thus:
However, according to Equation (14):
Thus, we obtain:
Furthermore, Equation (A210) simplifies to the form:
this is to be expected as the energy terms should not depend on acceleration but only on velocity. We now turn our attention to defined in Equation (A210). Using Equations (A13) and (A209) we obtain:
Using a well known identity from vector analysis we may write:
Let us look at the integral expression
This is an expression of the type described in Equation (A305) of Appendix B with and . According to Appendix A the expression in Equation (A202) can be expressed as a surface integral. Assuming that our system is contained in an infinite sphere we have according to Equations (A316) and (A22):
Now:
Taking into account the asymptotic expressions in Equations (A215) and (A25) the limit of Equation (A237) takes the following form:
However, according to Equation (A129) a closed loop integral over a constant is null hence:
Furthermore, Equation (A235) simplifies to:
Now:
Taking into account Equation (A19), we have:
Plugging Equation (A242) into Equation (A241) and using Gauss theorem we obtain:
Let us perform the surface integral on an infinite sphere as usual and look at the integral:
Using Equations (A215) and (A224) in Equation (A245) and taking the limit we obtain:
However, according to Equation (A129) a closed loop integral over a constant is null hence:
and thus Equation (A244) simplifies to:
Taking into account the definition in Equation (14) this is simplified to the form:
Hence:
Taking into account the mechanical momentum Equation (21) and the mechanical energy Equation (22) this can be written as:
Finally we turn we turn our attention to defined in Equation (A210), by taking the time derivative of and keeping only terms of the fourth order in :
According to Equations (A206), (A186) and (A188) this can be written as:
However, according to a well known vector analysis identity:
Now to zeroth order in Maxwell equations dictate that:
Thus, we may write:
Plugging Equation (A256) into Equation (A253) and using Gauss theorem we obtain:
Now taking into account Equation (A188) this can be written as:
to the fourth order in we may write:
Hence up to a constant:
We notice that this magnetic energy term has a surface and volume contributions as follows:
In which:
It can easily seen that the change in volume energy is balance by the mechanical work done (see Equation (A196)). For a phasor current with frequency defined in Equation (A150) we obtain a fourth order correction to the mutual inductance of the form
Such that:
Obviously the larger the system and the higher the frequency the more important this correction is. We stress that this term is not related to the relativistic engine effect and will exist even for an engine of “infinite” mass. The surface terms of the field energy are:
We recall that the derivative of this term is:
This term is not balanced by mechanical work and thus the only way to balance the derivative of this term in the energy equation is by a Poynting term which signifies the generation of radiation and will be discussed in the next section. We notice that this term will not exist if but the relativistic engine effect will still exist provided there is a second order derivative to the current.
The total magnetic energy can calculated by plugging Equations (A261) and (A251) into Equation (A233). This will partitioned into a volume and surface terms as follows:
in which:
and:
Finally we may calculate the total field energy by plugging Equations (A267) and (A205) into Equation (A199). The total field energy will partitioned into a volume and surface terms as follows:
in which:
and:
It can easily seen that the change in volume energy is balance by the mechanical work done (see Equation (A196)). However, the surface term remains unbalanced and cannot be balanced with a Poynting flux which indicate radiation. We stress that this term has nothing to do with the relativistic engine effect and will vanish for .
Appendix A.5.3. Poynting Vector
We shall now study the Poynting vector correction of the fourth order in :
Taking into account that is null according to Equation (A6) and is null according to Equation (A65) this simplifies to:
We will find it useful to make the following definitions:
Furthermore, thus:
We shall also find it useful to define the Poynting flux:
The Poynting flux will be calculated on an “infinite” sphere, while recalling that the sphere cannot actually be infinite as we are limited by the convergence radius and can only be “big”, hence:
We will find it convenient to make the following definitions:
Furthermore, thus:
From Equation (A278) it is clear that only the asymptotic expressions of are relevant for the Poynting flux.
Let us start by looking . The asymptotic form of is given in Equation (A33). From Equations (A208) and (A238) we have:
which shall show in Appendix E that for large r:
hence and thus:
on the infinite sphere (see Equation (A278)).
Let us now look at the asymptotic expression for is given in Equation (A34) according to which asymptotically . For the electric field we turn our attention to Equation (A190) and partition the field into relativistic engine terms and mutual inductance (see also Equation (A188)) correction terms:
This in turn will lead to a partition of such that:
Now contain integrals of the type for a constant . It follows from Equation (A345) that asymptotically and thus thus this term will have a null contribution to . Hence:
Plugging into the above equation, Equations (A284) and (A13) will result in:
We shall now use the definition
to write the above equation as:
Using standard vector identities:
This equation is analyzed in Appendix F. Using Equations (A361) and (A370) we obtain the result:
Turning next our attention to we notice that this term involves a cross product of and . According to Equation (A99) decreases as while is given by Equation (A64):
Taking into account Equation (A72) it then follows that decreases asymptotically as and thus decreases asymptotically as . It follows that:
Finally we evaluate . We notice that this term involves a cross product of and . As for , we have already indicated that according to Equation (A34) it behaves asymptotically as: . is defined in Equation (A189), it is of the form type for a spatial constant . It thus follows from Equation (A345) that asymptotically and thus . We conclude that:
Collecting all terms of Poynting flux it follows that:
Or we may write:
This term is clearly not a relativistic engine term and involves a fifth derivative of the current (only a second derivative is needed for a relativistic engine). We underline again that the expansion is valid for large but finite range defined in Equation (50), however, the explicit value of enters explicitly only into the field energy surface terms and the Poynting flux of the fourth order in , for small or null fourth derivative of the current one need not worry about such terms.
Appendix A.5.4. Intermediate Account
We conclude that the energy Equation (A173) of the fourth order is indeed balanced. Mechanical work invested or extracted in the system results in increase or decrease in the field energy accordingly. In the fourth order both electric and magnetic field energies are affected by the mechanical work. The power related to the mechanical work is according to Equation (A196):
it contains both work done by the mutual inductance and on the relativistic engine. This is equal to minus the derivative of the volume field energy Equation (A271):
Moreover, for the fourth order in there is also a surface contribution to the field energy given in Equation (A272) which according to Equation (A266) satisfies:
such that the total field energy is:
The change in the field energy through the surface terms results in radiation as described by the Poynting flux depicted in Equation (A296):
We underline that fourth order contributions are the only one that are related to the relativistic engine effect as some of the terms depend on the engine velocity . If the engine is infinitely massive and no motion occurs, we are left with the mutual inductance correction terms and radiation terms which involve higher order derivatives. For a phasor current of frequency Equation (A263) indicates a relativistic correction to the classical mutual inductance which is important for large systems with high frequency.
Appendix B. On the Nullification of a Certain Integral
We would like to prove the equality:
Which may be written in terms of the Einstein summation convention as follows:
in the above we have used the symbol . To do this let us look at a more general case. Let and be two arbitrary functions. Furthermore, let us evaluate the integral:
The following set of equations follow:
Now since it follows that:
Furthermore, since it follows that:
Summing up the above results we have:
We thus conclude that:
Now for every single valued set of function h and g we have:
Hence:
The above integral contains only gradients which once integrated can only contribute to surface terms as follows:
Now:
according to Equations (A307) and (A311). Hence:
Suppose now that the system is contained in an infinite sphere of radius and suppose that:
Then it follows that:
Furthermore, Equation (A303) is proved. To verify that this is indeed so we only need to substitute and and take into account Equations (A22), (A25) and (A27).
Appendix C. Asymptotic Values
In the limit we may think of:
as a small parameter. In terms of this small parameter we expand defined in Equation (A140):
Inserting Equation (A319) into Equation (A141) will result in:
the terms will cancel in the limit. Obvious the first two terms in right hand side will diverge unless the closed loop integrals vanish. Let us denote:
and
in terms of we may write as:
obviously:
However, since a closed loop integral over a constant vanishes (see Equation (A78)), it follows that:
Now let us calculate to do this we notice the following identities:
Using the above identities we calculate:
Furthermore, thus:
Hence:
because at least one of the two loop integrals is done over a constant. Finally we calculate which leads to a somewhat lengthy but straight forward expression:
From the above expression we calculate as follows:
Obviously only the first term contributes as it depends on both and (and not on each variable alone) and hence:
Finally inserting the results from Equations (A325), (A329) and (A332) into Equation (A320) we obtain
which is identical to Equation (A141).
Appendix D. Q Function Evaluation
We shall now calculate the term:
First let us introduce a change of variables:
Since the integral is calculated at a fixed point it follows that and:
This leads to the following expression for :
This integral is now evaluated using a spherical coordinate system in which the “z” axis point at the direction of . In this case and can be calculated as follows:
Now:
In which we notice that the above expression is not dependent on the azimuthal angle . Moreover, using a cartesian set of unit vectors one may write:
Thus, it can easily be seen that there is component to in the directions as the azimuthal integral vanishes. In the direction the azimuthal integral is trivial and we obtain the result:
Let us make a change of variables and notice that which is a unit vector in the direction of , in terms of those variables we obtain a simpler representation of :
However, we can evaluate analytically the s integral to obtain:
Furthermore, plugging this back into Equation (A342) we obtain:
Appendix E. Asymptotic Form of
Let us write Equation (A72) in the form (keeping only the first order term in ):
in which we define a perpendicular vector to as follows:
Hence we may write up to first order in ):
Let us use the above equation and Equation (A25) in Equation (A281), we obtain:
Now since for a constant loop integral we have:
It follows that:
and Equation (A282) is thus derived.
Appendix F. Evaluating PFb
Let us look at defined in Equation (A288). In terms of the small parameter defined in Equation (A318) we may expand as follows:
Thus, we have:
the terms will cancel in the limit. Obviously the first three terms in right hand side will diverge unless the closed loop integrals vanish. However:
Since a closed loop integral over a constant vanishes (see Equation (A78)), it follows that:
For calculating the derivatives of we shall use computer algebra due to the complexity of the expressions. We shall write down only the values of the derivative in 0 since only those are of interest to us for evaluating the expressions in Equation (A352). For we obtain:
Hence:
because at least one of the two loop integrals is done over a constant. Let us now evaluate :
Obviously only the first term contributes as it depends on both and (and not on each variable alone) thus:
and hence:
Taking into account Equation (A132) we thus have:
As this result is diverging we are reminded that we are not allowed to use our expansion beyond (see Equation (50)) and thus the above integral takes the value:
in which stands for terms which are either independent of or decrease with .
For the same reasons the first two terms in the expansion do not contribute to the second integral of Equation (A290) and we are left with third term. Thus:
will be equal to:
and taking into account Equation (A358) we obtain:
The above expression can be written in terms of Einstein summation notation as:
taking into account Equation (A132) and also the result [3]:
we obtain:
Taking into account that , Equation (A367) takes the form:
or more simply as:
This term is diverging and thus we shall replace the infinite sphere with a sphere which is simply big to the maximum allowable size of the expansion:
References
- Einstein, A. On the Electrodynamics of Moving Bodies. Ann. Phys. 1905, 17, 891–921. [Google Scholar] [CrossRef]
- Maxwell, J.C. A dynamical theory of the electromagnetic field. Philos. Trans. R. Soc. Lond. 1865, 155, 459–512. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd. ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M.L. Feynman Lectures on Physics, Revised 50th Anniversary Edition; Basic Books: New Yrok, NY, USA, 2011. [Google Scholar]
- Heaviside, O. On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1889, 27, 324–339. [Google Scholar] [CrossRef]
- Newton, I. Philosophiae Naturalis Principia Mathematica; Benjamin Motte: London, UK, 1687. [Google Scholar]
- Goldstein, H.; Poole, C.P., Jr.; Safko, J.L. Classical Mechanics, 3rd ed.; Pearson: London, UK, 2001. [Google Scholar]
- Tuval, M.; Yahalom, A. Momentum Conservation in a Relativistic Engine. Eur. Phys. J. Plus 2016, 131, 374. [Google Scholar] [CrossRef]
- Pryce, M.H.L. The mass-centre in the restricted theory of relativity and its connexion with the quantum theory of elementary particles. Proc. Roy. Soc. Lond. Ser. A 1948, 195, 62–81. [Google Scholar]
- SBosanac, S.D. Dynamics of Particles and the Electromagnetic Field; World Scientific: Singapore, 2005; Chapter 6. [Google Scholar]
- Mansuripur, M. Trouble with the Lorentz Law of Force: Incompatibility with Special Relativity and Momentum Conservation. Phys. Rev. Lett. 2012, 108, 193901. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, D.J.; Heald, M.A. Time dependent Generalizations of the Biot-Savart and Coulomb laws. Am. J. Phys. 1991, 59, 111–117. [Google Scholar] [CrossRef]
- Jefimenko, O.D. Electricity and Magnetism, Appleton-Century Crofts, New York, 1966, 2nd ed.; Electret Scientific: Star City, WV, USA, 1989. [Google Scholar]
- Tuval, M.; Yahalom, A. Newton’s Third Law in the Framework of Special Relativity. Eur. Phys. J. Plus 2014, 129, 240. [Google Scholar] [CrossRef]
- Tuval, M.; Yahalom, A. A Permanent Magnet Relativistic Engine. In Proceedings of the Ninth International Conference on Materials Technologies and Modeling (MMT-2016), Ariel, Israel, 5–29 July 2016. [Google Scholar]
- Yahalom, A. Retardation in Special Relativity and the Design of a Relativistic Motor. Acta Phys. Pol. A 2017, 131, 1285–1288. [Google Scholar] [CrossRef]
- Yahalom, A. Preliminary Energy Considerations in a Relativistic Engine. In Proceedings of the Israeli-Russian Bi-National Workshop, The Optimization of Composition, Structure and Properties of Metals, Oxides, Composites, Nano- and Amorphous Materials, Ariel, Israel, 28–31 August 2017; pp. 203–213. [Google Scholar]
- Rajput, S.; Yahalom, A. Preliminary Magnetic Energy Considerations in a Relativistic Engine: Mutual Inductance vs. Kinetic Terms. In Proceedings of the 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE), Eilat, Israel, 12–14 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rajput, S.; Yahalom, A. Material Engineering and Design of a Relativistic Engine: How to Avoid Radiation Losses. Adv. Eng. Forum 2020, 36, 126–131. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).