Bifurcation Analysis of Time-Delay Model of Consumer with the Advertising Effect

Abstract

Given the economic importance of advertising and product promotions, we have developed a diffusion model to describe the impact of advertising on sales. The main message of this study is to show the effect of advertising diffusion to convert potential buyers into actual customers which may result in persistent alteration in marketing over time. This work is devoted to studying the dynamic behavior of a reaction-diffusion model and its delayed version with the advertising effect. For the non-delay model, it is proven the existence of Hopf bifurcation. Moreover, the stability and direction of bifurcation of periodic solutions are detected. On the other hand, we consider there is a lag for responding of potential buyers to the advertising. Therefore, the time delay $\tau$ is deemed as an additional factor in the diffusion model. We have determined the critical values for the delay parameter that yield periodic solutions. Furthermore, the direction and the stability of bifurcating periodic solutions is studied. For supporting the theoretical analysis and demonstrate complex dynamic behaviors, numerical simulations including families of periodic curves are given.

1. Introduction

Advertising has an important role in our life. It mainly affects the determination of the image and method of purchase, and it also affects our thinking towards different and new products. Advertising is connected with brand recognition and choosing measures to build the commercial long-term strategy, while promotion activities are seasonal measures to raise the company’s immediate revenues by directly influence the prices of goods or services.

In view of the economic importance of advertising promotion, it has been discussed in many economic and social studies. In [1], how advertising creativity influences consumer treatment and response has been discussed. In [2], the effect of advertising bans has been studied to limit the spread of tobacco products. However, the results proved the effectiveness of advertising bans on the consumption of tobacco products. In [3], the effect of word of mouth on consumer marketing behavior was examined based on preliminary data collected from the population of some cities, and the results revealed the effect of word of mouth on marketing of various commercial products. For more information and results see [4,5].

Many studies have used the innovation diffusion theory since its appearance due to its great economic importance. Numerous mathematical models have been established to market new products. Sales promotions have been widely discussed in many studies from both mathematical and economic standpoints. Many of these models have been developed to clarify the diffusion of the products amongst potential customers of the population, by taking into account the influence of oral speech, advertising and other means of communication. Since then, these models have been studied and developed in several research perspectives which resulting in important theoretically and practically contributions.

To name a few, we can highlight some of the described diffusion models. In [6], Bass has developed a growth model describing successive purchases by assuming that the number of previous purchases affect the purchase expectations. Which led to good predictions of buying behavior consistent with experimental data. In [7], Dodson and etc. have been developed a model for the interaction process between adopters and non-adopters and the effect of repetitive purchase. Hence, the behavioral assumptions that support the model are clarified.

In [8], Australian scholar Feichtinger established a two-dimensional advertising diffusion model as follows:

$$\left\{\begin{array}{c}{\dot{x}}_1=k_0-\alpha x_1{x}_2^2+\beta x_2,\hfill \\ {\dot{x}}_2=\alpha x_1{x}_2^2-(\beta +ϵ)x_2,\hfill \end{array}\right.$$

(1)

where $x_1,x_2\in R^{+}$ are the number of potential buyers of a specific brand at time t and customers of this brand at that time, respectively. The coefficients in model (1) are illustrated in Table 1.

Table 1. The meaning of the coefficients in the system.

The Symbol	The Meaning
$k_0>0$	individuals stream into the firms market,
$\epsilon >0$	the current customers leaving the market forever,
$\beta \ge 0$	current customers switching to a rival brand,
$\alpha >0$	proportionality measuring of the advertising effectiveness.

In [9], it has been considered the impact of product marketing planning on potential consumers to improve Feichtinger’s model by

$$\left\{\begin{array}{c}{\dot{x}}_1=k_0-\alpha x_1{x}_2^2+\beta x_2-c{x}_1,\hfill \\ {\dot{x}}_2=\alpha x_1{x}_2^2-(\beta +ϵ)x_2+c{x}_1,\hfill \end{array}\right.$$

where c indicates the success rate of marketing planning. In [10], a mathematical model to interpret consumer behavior under the advertising and word-of-mouth effects was proposed, which was studied in both of continuous and discrete versions, for more studies see [11,12].

The theory of dynamism applied to behavior allows us to study and analyze this movement between the condition of current client and the potential one. The trajectory in time that reflects the evolution of both types of clients and their role change can be analyzed by studying the bifurcations of the dynamic model, since they reflect a change in the behavior of the elements studied. The analysis of the independent variables controlled by the organization and the sensitivity of the parametric values that reflect the trend in behavioral changes make it possible to visualize the possible movements in the system.

Recently, the differential equations theory (stability, bifurcation, chaos, etc.) has been used in several fields such as medicine, economics, life science, engineering, technology and sociology [13,14,15,16,17].

The analysis of time-delay differential equations is more realistic to describe the interactions between elements of dynamic systems. The time delays can be regarding to the period of some hidden processes, such as the stages of growth, response and sensitivity to some influences, and the incubation period of the infectious diseases [18,19,20,21,22].

Given the economic importance of the impact of revenue on daily life, we investigate the dynamic behaviors of the effect of ads to give a clearer view and to reveal the influencing factors. Based on [8], in our paper we consider a clear three compartment model which consists of the numbers of potential and actual consumers and the influence of advertising. In modification of [8], we consider that the dynamics of the potential buyers number and buyers are influenced by the advertising effect in Holling type I.

The rest of our article is regulated as follows. Section 2 provides the mathematical model and the equilibria existence. In Section 3 and Section 4 we analyze the dynamical behavior of continuous consumption behavior model and delayed consumption behavior model, respectively, including the numerical simulations. In the last, we conclude the paper with a brief discussion in Section 5.

2. The Mathematical Model and Its Dynamics

Advertising can affect a company’s sales volume in both the short and long term, contingent upon its targets. It is assumed that the rate of the conversion of potential buyers to customers, is proportional to the advertisements effect function. Suppose the advertisement stimulates the increase in the number of consumers represented by the positive nonlinear growth term for potential buyers, which can be conveniently represented by the response function Holling Type 2. Based on description of the dissemination of advertising in [23] the change of advertising influence over time can be described by the logistic curve.

Thus, the flows of individuals are divided into the two different groups $x_1$ and $x_2$ and the influence of advertising $x_3$. can be presented as follows:

$$\left\{\begin{array}{c}{\dot{x}}_1=k_0+\beta x_2-\alpha x_1{x}_2^2-\frac{b{x}_1{x}_3}{x_3+a},\hfill \\ {\dot{x}}_2=\alpha x_1{x}_2^2-(\beta +ϵ)x_2+\frac{b{x}_1{x}_3}{x_3+a},\hfill \\ {\dot{x}}_3=d{x}_3(1-\frac{x_3}{k}),\hfill \end{array}\right.$$

(2)

where a is the half-saturation constant and b is the response rate of the individuals, $x_3\ge 0$, and $k>0,d\ge 0$ are control parameters of logistics curve.

To simplify calculations, we carry out the following transformations:

$$x=\frac{k_0\alpha }{n(n-\beta )}{x}_1, y=\frac{n-\beta }{k_0}{x}_2, z=x_3, t^{\prime }=nt,$$

and

$$n=\beta +ϵ,\gamma =\frac{\alpha k_0^2}{n{(n-\beta )}^2},{\beta }^{\prime }=\frac{\beta }{n},b^{\prime }=\frac{b}{n},d^{\prime }=\frac{d}{n}.$$

For avoiding the abuse of mathematical notation, we still denote $(t^{\prime },{\beta }^{\prime },b^{\prime },d^{\prime })$ by $(t,\beta ,b,d)$, system (2) becomes

$$\left\{\begin{array}{c}\dot{x}=\gamma (1-x{y}^2+\beta (y-1))-\frac{bxz}{a+z},\hfill \\ \dot{y}=-y+x{y}^2+\frac{bxz}{\gamma (a+z)},\hfill \\ \dot{z}=dz-\frac{d{z}^2}{k},\hfill \end{array}\right.$$

(3)

where $\gamma >0$, $0\le \beta <1$.

Due to the previous transformations, systems (2) and (3) are topologically equivalent, so we are going to study system (3) instead of the original system.

Proposition 1.

The following triples are all equilibrium points of system (3)

1.

Semi-trivial equilibrium point $E_1(1,1,0)$,

2.

Nontrivial equilibrium $E_2(a_0,1,k)$, where $a_0=\frac{\gamma (a+k)}{\gamma (a+k)+bk}$.

The Jacobian matrix of system (3) at $E_1(1,1,0)$ takes the form

$$J\left(E_1\right)=\left(\begin{array}{ccc}-\gamma & \gamma (\beta -2)& -\frac{b}{a}\\ 1& 1& \frac{b}{a\gamma }\\ 0& 0& d\end{array}\right),$$

(4)

therefore, the characteristic equation is expressed as [24]

$$(\lambda -d)\left({\lambda }^2+(\gamma -1)\lambda +\gamma (1-\beta )\right)=0.$$

(5)

Which leads to a non negative eigenvalue ${\lambda }_3=d$ and the other two eigenvalues satisfy the following equation

$${\lambda }^2+(\gamma -1)\lambda +\gamma (1-\beta )=0.$$

Lemma 1.

The eigenvalues ${\lambda }_{1,2}$ of $J\left(E_1\right)$ satisfy the following conditions

1.

$Re\left({\lambda }_{1,2}\right)>0$ iff $\gamma <1$;

2.

$Re\left({\lambda }_{1,2}\right)<0$ iff $\gamma >1$;

3.

$Re\left({\lambda }_{1,2}\right)=0$ and $Im\left({\lambda }_{1,2}\right)\ne 0$ iff $\gamma =1$;

4.

${\lambda }_1={\lambda }_2$ iff $\beta =\frac{1}{4}(6-\gamma -\frac{1}{\gamma })$.

The Jacobian matrix of system (3) at $E_2(a_0,1,k)$ takes the form

$$J\left(E_2\right)=\left(\begin{array}{ccc}-\frac{bk}{a+k}-\gamma & \gamma (\beta -\frac{2(a+k)\gamma }{bk+(a+k)\gamma })& -\frac{ab\gamma }{(a+k)(bk+(a+k\left)\gamma \right)}\\ \frac{bk}{(a+k)\gamma }+1& 1-\frac{2bk}{be+(a+k)\gamma }& \frac{ab}{(a+k)(bk+(a+k\left)\gamma \right)}\\ 0& 0& -d\end{array}\right),$$

(6)

therefore, the characteristic equation can be written as

$$(\lambda +d)\left({\lambda }^2+{\mathsf{\Psi }}_1\lambda +{\mathsf{\Psi }}_2\right)=0,$$

(7)

where ${\mathsf{\Psi }}_1=bk(\frac{2}{\gamma (a+k)+bk}+\frac{1}{a+k})+\gamma -1$, ${\mathsf{\Psi }}_2=\frac{(1-\beta )\left(\gamma \right(a+k)+bk)}{a+k}$.

One can verify ${\lambda }_3=-d$ is always a non positive eigenvalue, the other two eigenvalues satisfy the following equation

$${\lambda }^2+{\mathsf{\Psi }}_1\lambda +{\mathsf{\Psi }}_2=0.$$

Lemma 2.

The eigenvalues ${\lambda }_{1,2}$ of $J\left(E_2\right)$ satisfy the following conditions

1.

$Re\left({\lambda }_{1,2}\right)>0$ iff ${\mathsf{\Psi }}_1<0$;

2.

$Re\left({\lambda }_{1,2}\right)<0$ iff ${\mathsf{\Psi }}_1>0$;

3.

$Re\left({\lambda }_{1,2}\right)=0$ and $Im\left({\lambda }_{1,2}\right)\ne 0$ iff ${\mathsf{\Psi }}_1=0$;

4.

${\lambda }_1={\lambda }_2$ iff $\mathsf{\Delta }={\mathsf{\Psi }}_1^2-4{\mathsf{\Psi }}_2=0$.

To analyse the stability of equilibria of system (3) we give the following theorems [25]:

Theorem 1.

The semi-trivial equilibrium point $E_1(1,1,0)$ is

1.

A hyperbolic saddle if $\gamma >1$;

2.

An unstable Equilibrium Point if $\gamma <1$;

3.

A non-hyperbolic point if the parameter satisfies one of the following conditions

(a) 

$\gamma =1$;

(b) 

$d=0$.

Theorem 2.

The non-trivial equilibrium point $E_2(a_0,1,k)$ is

1.

A hyperbolic saddle if ${\mathsf{\Psi }}_1<0$;

2.

A stable Equilibrium Point if ${\mathsf{\Psi }}_1>0$;

3.

A non-hyperbolic Equilibrium Point if ${\mathsf{\Psi }}_1=0$.

3. Stability and Bifurcation Analysis

In this part, we investigate the topological equivalent system (3) of the original system and analyze the $Hopf$ bifurcation.

3.1. Hopf Bifurcation of Semi-Trivial Equilibrium Point $E_1$

For system (3), let $u=x-1,v=y-1,w=z$, then the topologically equivalent system is given by

$$\dot{X}=AX+F\left(X\right)+O\left(X^4\right),$$

(8)

where,

$$X=\left[\begin{array}{c}u\\ v\\ w\end{array}\right], A=\left(\begin{array}{ccc}-\gamma & \gamma (\beta -2)& -\frac{b}{a}\\ 1& 1& \frac{b}{a\gamma }\\ 0& 0& d\end{array}\right), F\left(X\right)=\left[\begin{array}{c}{\chi }_{11}\\ {\chi }_{12}\\ -\frac{d{w}^2}{k}\end{array}\right],$$

and

$${\chi }_{11}=\frac{bw(w-au)}{a(a+w)}-\gamma v(u(v+2)+v),{\chi }_{12}=\frac{bw(au-w)}{a\gamma (a+w)}+v(u(v+2)+v).$$

Theorem 3.

System (8) undergoes Hopf at $E_1$ if $\gamma =1$.

Proof. 

From (5), one can get the eigenvalues of $J\left(E_1\right)$ of system (3) as follows:

$${\lambda }_{1,2}=\frac{-(\gamma -1)\pm \sqrt{{(\gamma -1)}^2-4\gamma (1-\beta )}}{2}, {\lambda }_3=d.$$

To verify the transversality condition. Consider the real part of the complex eigenvalues of the characteristic equation $\mathsf{\Phi }=\frac{-(\gamma -1)}{2}$. Let $\gamma$ be the bifurcation parameter, then suppose that $\gamma ={\gamma }_0$ implies

$$\mathsf{\Phi }\left({\gamma }_0\right)=0, \Rightarrow \gamma =1,$$

Therefore, the eigenvalues of the system (8) become

$${\lambda }_{1,2}=\pm i\sqrt{1-\beta }=\pm i\omega , {\lambda }_3=d,$$

where i denotes an imaginary unit. The transversality condition can be verified as

$$\frac{d\mathsf{\Phi }}{d\gamma }=-\frac{1}{2}.$$

Hence, system (8) undergoes Hopf bifurcation. □

Next, the normal form theory is useful to study the direction and stability of bifurcating periodic solutions for system (8) [26]. Let the eigenvectors corresponding to the eigenvalues ${\lambda }_1$ and ${\lambda }_3$ be $u_1+i{u}_2$ and $u_3$, where $u_1, u_2$ and $u_3$ are real vectors.

By straightforward calculations, we obtain

$$u_1=\left(\begin{array}{c}-1\\ 1\\ 0\end{array}\right), u_2=\left(\begin{array}{c}\omega \\ 0\\ 0\end{array}\right), u_3=\left(\begin{array}{c}-\frac{b\left(d+{\omega }^2\right)}{a\left(d^2+{\omega }^2\right)}\\ \frac{bd}{a\left(d^2+{\omega }^2\right)}\\ 1\end{array}\right).$$

Define

$$P=(u_1 u_2 u_3), \left(\begin{array}{c}u\\ v\\ w\end{array}\right)=P\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right).$$

By straightforward calculations, we get

$$\left\{\begin{array}{c}\dot{X}=\omega Y+F_{Hopf1},\hfill \\ \dot{Y}=-\omega X+F_{Hopf2},\hfill \\ \dot{Z}=dz+\frac{d}{k}{z}^2,\hfill \end{array}\right.$$

(9)

where $F_{Hopf1}={\displaystyle \sum _{i,j,l}^{i+j+l\le 3}}{A}_{i,j,l}{X}^i{Y}^j{Z}^l,F_{Hopf2}=-\frac{bd\omega Z^2}{a{d}^{2}k+ak{\omega }^2}.$

Then, following a similar computation process as in [15] we can calculate the first Lyapunov coefficient of system (3),

$$C_1\left(0\right)=\frac{i}{2\omega }(g_{02}{g}_{11}-2|{g_{11}|}^2-\frac{1}{3}|g_{02}{|}^2)+\frac{1}{2}{g}_{21},$$

(10)

and

$$l_1=\frac{Re\left(C_1\left(0\right)\right)}{\omega }.$$

(11)

For classifying the existence of a generic Hopf bifurcation

• System (3) undergoes supercritical Hopf bifurcation if $l_1<0$;
• System (3) undergoes subcritical Hopf bifurcation if $l_1>0$;
• System (3) undergoes degenerate Hopf bifurcation if $l_1=0$.

3.2. Hopf Bifurcation of Non-Trivial Equilibrium Point $E_2$

Next, we study the bifurcation analysis of system (3) at the equilibrium point $E_2(a_0,1,k)$. By applying the theory of series at the point $E_2(a_0,1,k)$, system (3) can be presented as

$$\left\{\begin{array}{c}\dot{x}=\gamma (1-x{y}^2+\beta (y-1))-b\left(\frac{k}{a+k}+\frac{ax(z-k)}{{(a+k)}^2}-\frac{a{(z-k)}^2}{{(a+k)}^3}\right)x+O\left({(z-k)}^3\right),\hfill \\ \dot{y}=-y+x{y}^2+\frac{b}{\gamma }\left(\frac{k}{a+k}+\frac{a(z-k)}{{(a+k)}^2}-\frac{a{(z-k)}^2}{{(a+k)}^3}\right)x+O\left({(z-k)}^3\right),\hfill \\ \dot{z}=dz-\frac{d{z}^2}{k}.\hfill \end{array}\right.$$

(12)

For system (3), let $u=x-a_0,v=y-1,w=z-k$, then system (12) becomes

$$\dot{X}=AX+F\left(X\right)+O\left(X^4\right),$$

(13)

where

$$X=\left[\begin{array}{c}u\\ v\\ w\end{array}\right], A=\left(\begin{array}{ccc}-\frac{be}{a+k}-\gamma & \gamma \left(\beta -\frac{2(a+k)\gamma }{bk+(a+k)\gamma }\right)& -\frac{ab\gamma }{(a+k)(bk+(a+k\left)\gamma \right)}\\ \frac{bk}{(a+k)\gamma }+1& 1-\frac{2bk}{bk+(a+k)\gamma }& \frac{ab}{(a+k)(bk+(a+k\left)\gamma \right)}\\ 0& 0& -d\end{array}\right),$$

$$F\left(X\right)=\left[\begin{array}{c}{\chi }_{21}\\ {\chi }_{22}\\ de-\frac{d{w}^2}{k}\end{array}\right],$$

${\chi }_{21}=u\left(\frac{ab{w}^2}{{(a+k)}^3}-\frac{abw}{{(a+k)}^2}-\gamma v^2-2\gamma v\right)-\frac{{\gamma }^2{v}^2(a+k)}{\gamma (a+k)+bk}+\frac{ab\gamma w^2}{{(a+k)}^2(\gamma (a+k)+bk)}$,

${\chi }_{22}=u\left(-\frac{ab{w}^2}{\gamma {(a+k)}^3}+\frac{abw}{\gamma {(a+k)}^2}+v^2+2v\right)+\frac{\gamma v^2(a+k)}{\gamma (a+k)+bk}-\frac{ab{w}^2}{{(a+k)}^2(\gamma (a+k)+bk)}$.

Theorem 4.

A $Hopf$ bifurcation occurs at $E_2$ if $\gamma =\frac{(a-2bk+k)\pm \sqrt{{(a+k)}^2-8bk(a+k)}}{2(a+k)}$ and $b<\frac{a+k}{8k}$.

Proof. 

From (7), the two conjugate eigenvalues of $J\left(E_2\right)$ of system (12) satisfy

$${\lambda }^2+{\mathsf{\Psi }}_1\lambda +{\mathsf{\Psi }}_2=0.$$

Consider $\gamma$ as the bifurcation parameter, then suppose that $\gamma ={\gamma }_0$ implies

$${\mathsf{\Psi }}_1\left({\gamma }_0\right)=0, \Rightarrow {\gamma }_0^2-\frac{(a-2bk+k)}{a+k}{\gamma }_0+\frac{bk(a+bk+k)}{{(a+k)}^2}=0,$$

which leads to

$${\gamma }_0=\frac{(a-2bk+k)\pm \sqrt{{(a+k)}^2-8bk(a+k)}}{2(a+k)}>0\iff b\le \frac{a+k}{8k},$$

Therefore, the eigenvalues of the system (8) become

$${\lambda }_{1,2}=\pm i\omega , {\lambda }_3=-d,$$

$$\omega =\sqrt{\frac{(1-\beta )((a+k)\pm \sqrt{(a+k)(a-8bk+k)})}{2(a+k)}}.$$

The transversality condition can be verified as

$$\frac{d{\mathsf{\Psi }}_1}{d\gamma }=1-\frac{8bk(a+k)}{{\left((a+k)\pm \sqrt{{(a+k)}^2-8bk(a+k)}\right)}^2}\ne 0\iff b\ne \frac{a+k}{8k}.$$

Hence, system (13) undergoes Hopf bifurcation. □

As we did in the previous subsection we can get $l_1$ to determine the direction of Hopf bifurcation.

3.3. Numerical Simulations

In this part, a rigorous investigation of the influenced advertising diffusion model by word-of-mouth response to verify the analytical result numerically. The dynamics of system is explored using both of the software packages MATLAB and AUTO by varying different parameters. We select some parameters values to illustrate the existence of the Hopf bifurcation in different equilibrium points. For satisfying the bifurcation conditions, we select the parameters as $\beta =0.1,a=5,b=5,d=1,k=0.1$ and $\gamma$ as a bifurcation parameter. The illustrative simulations are shown as following.

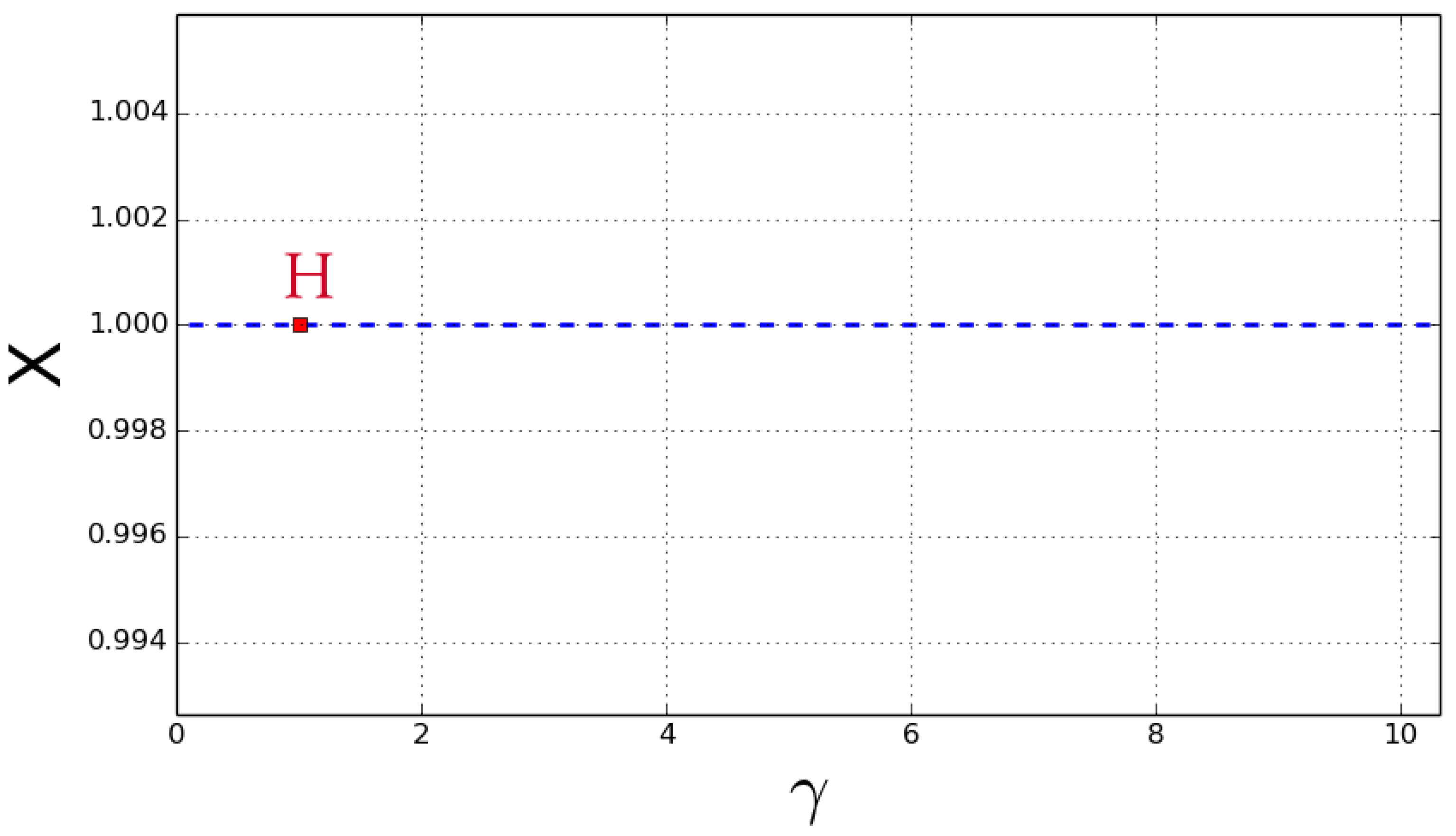
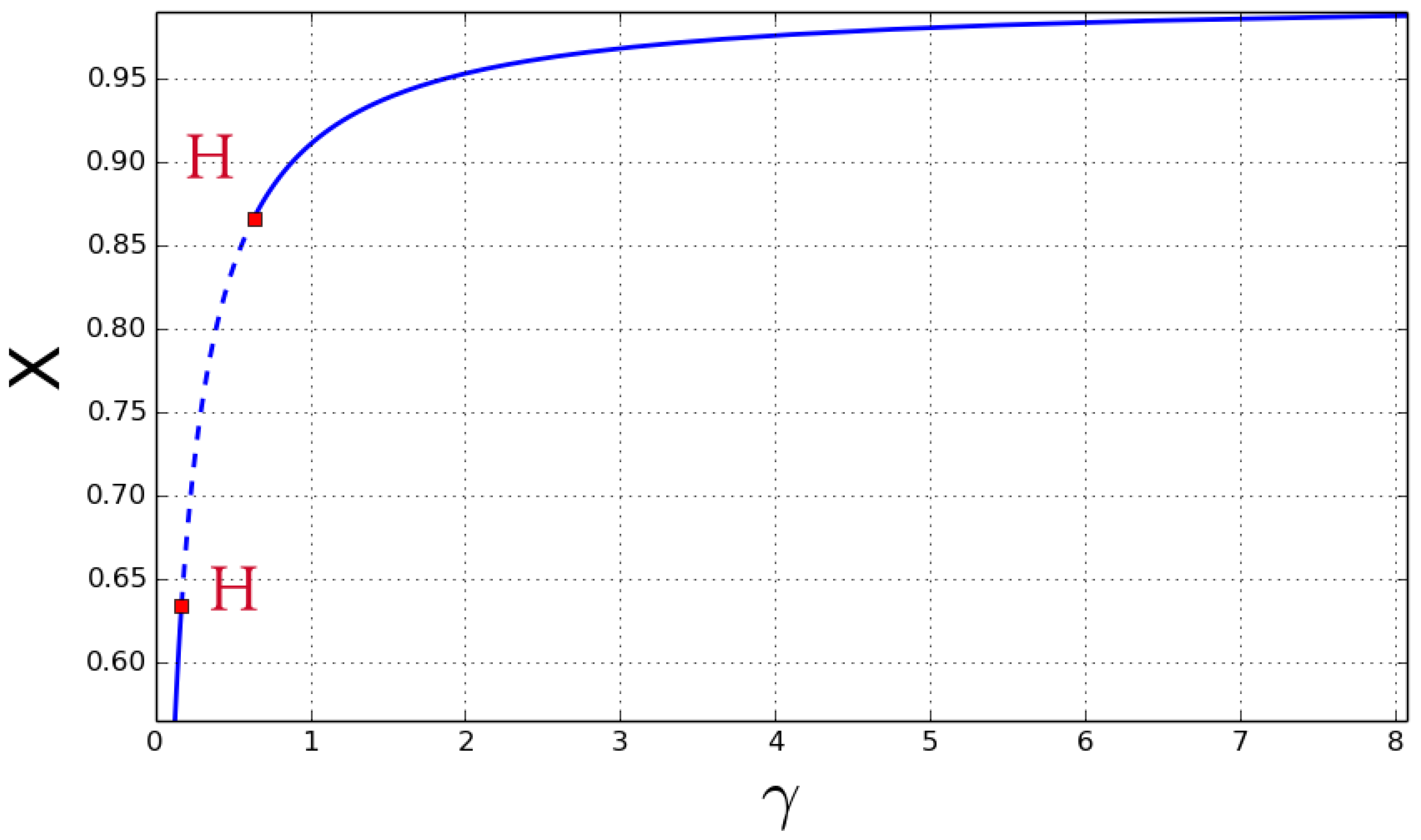
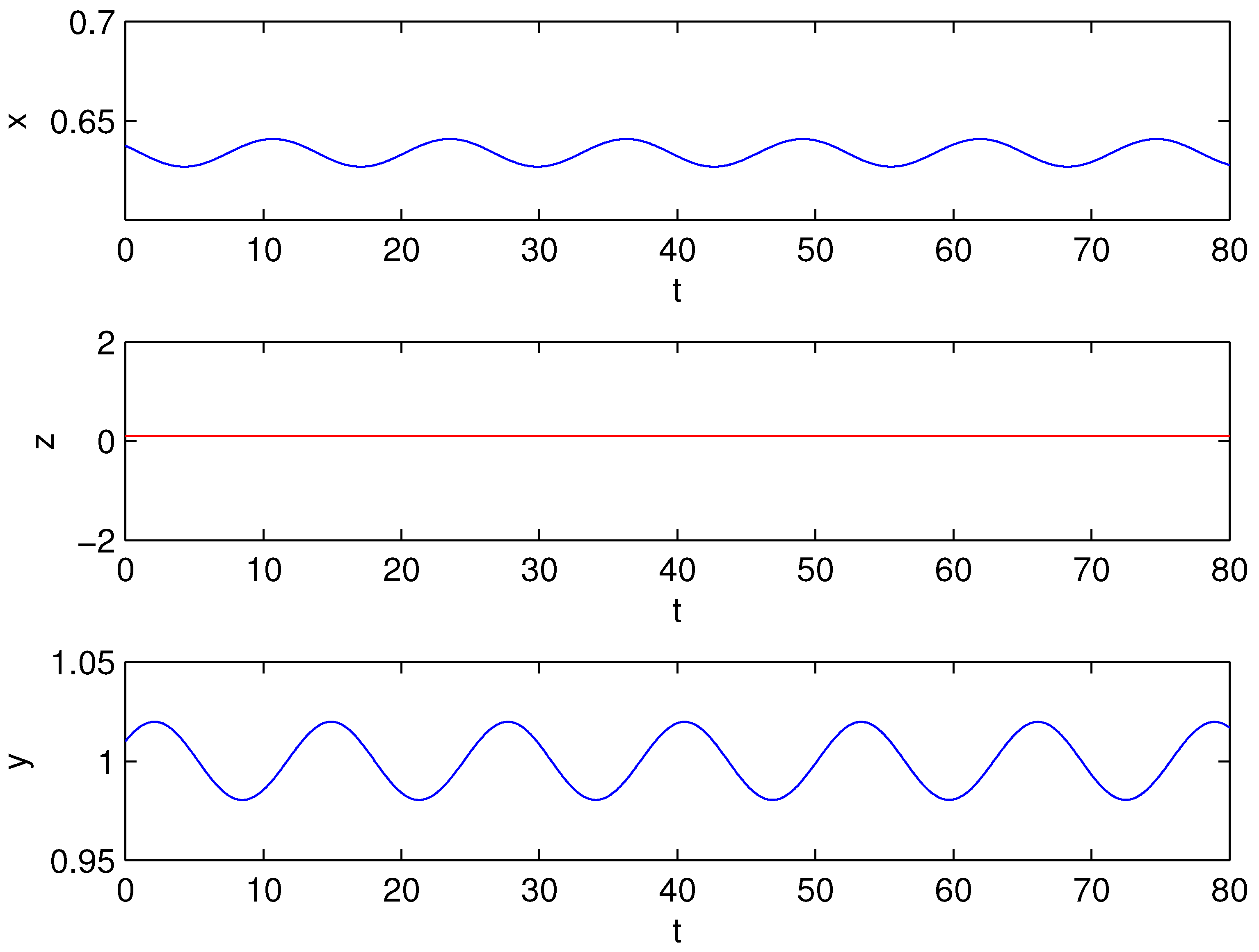
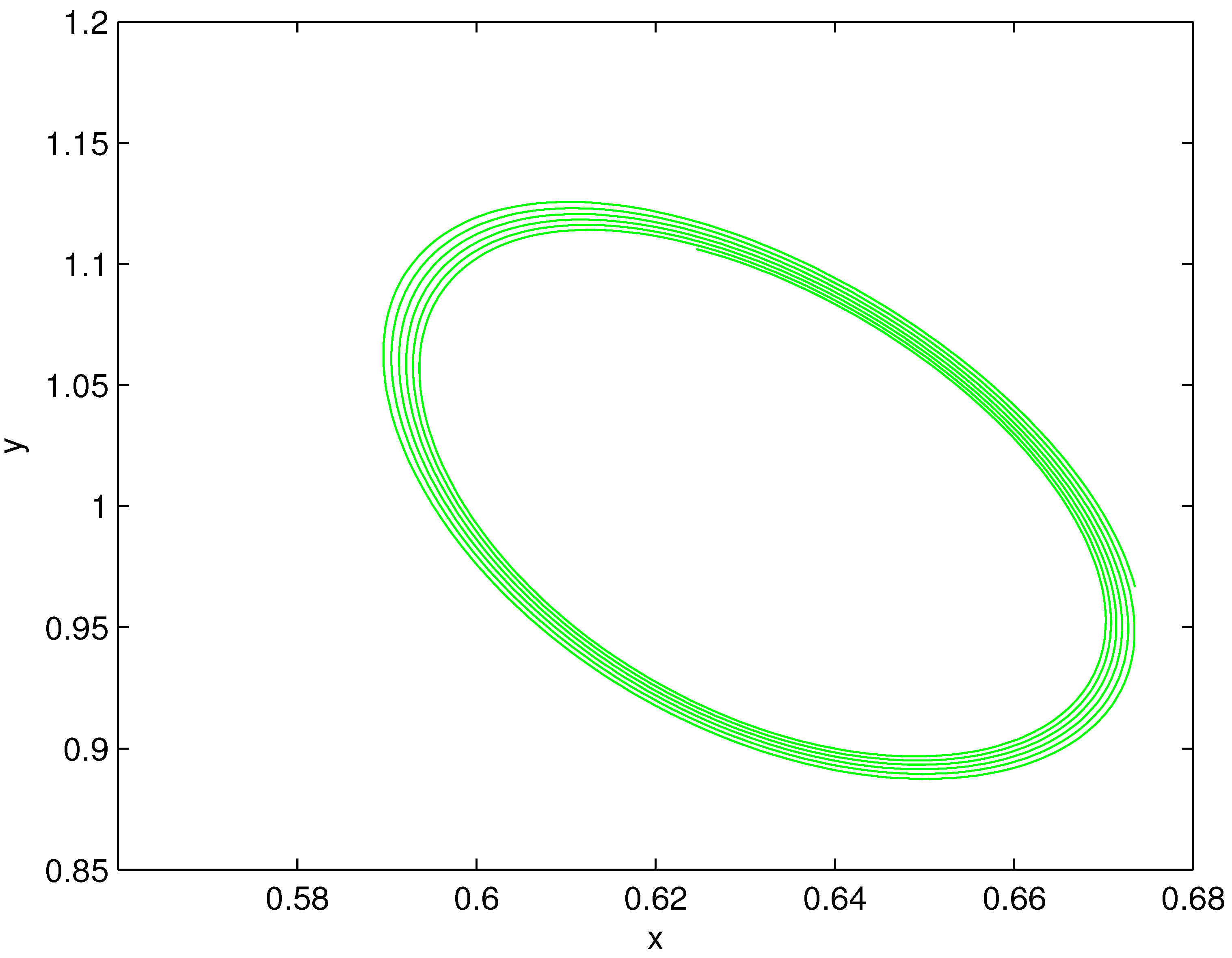
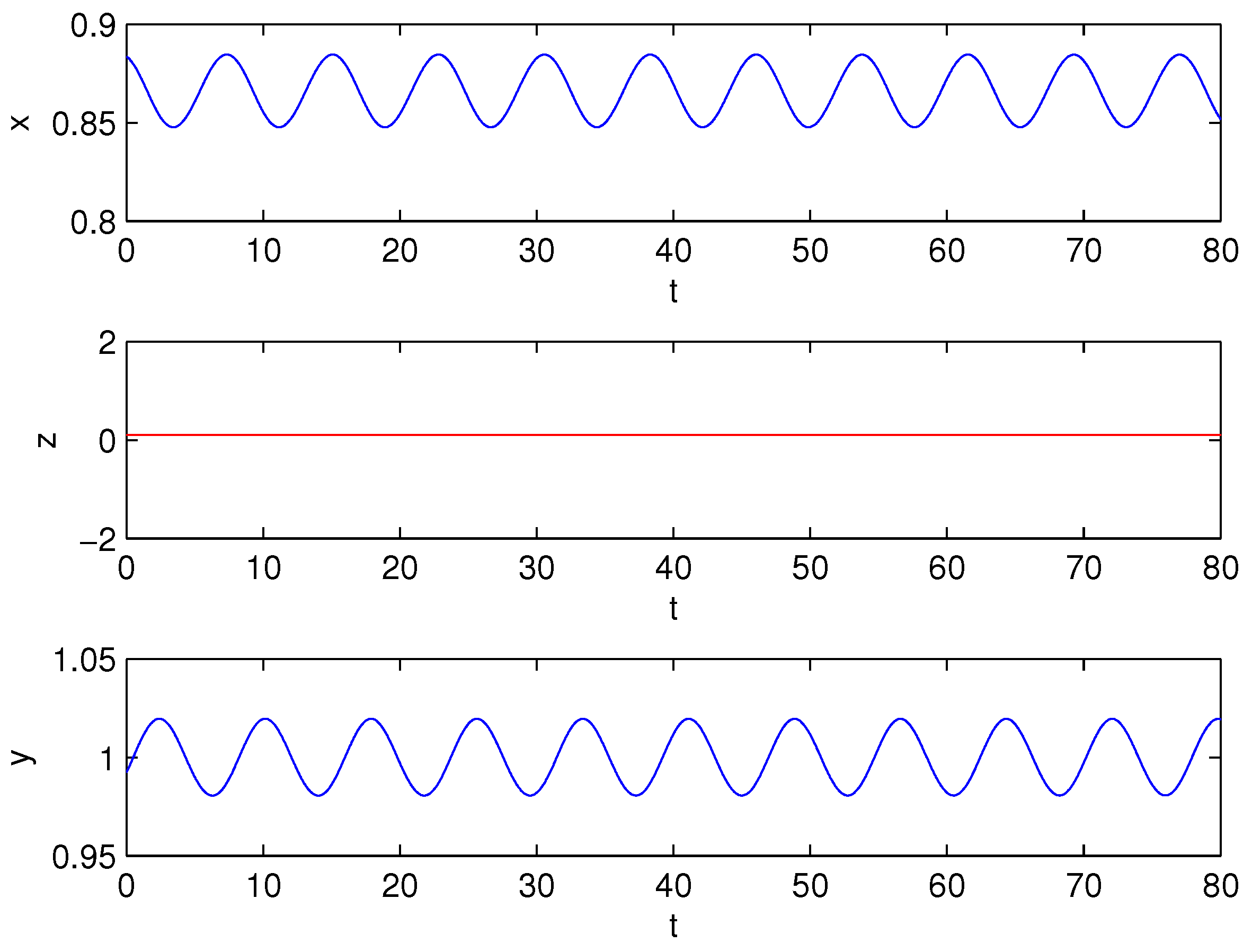
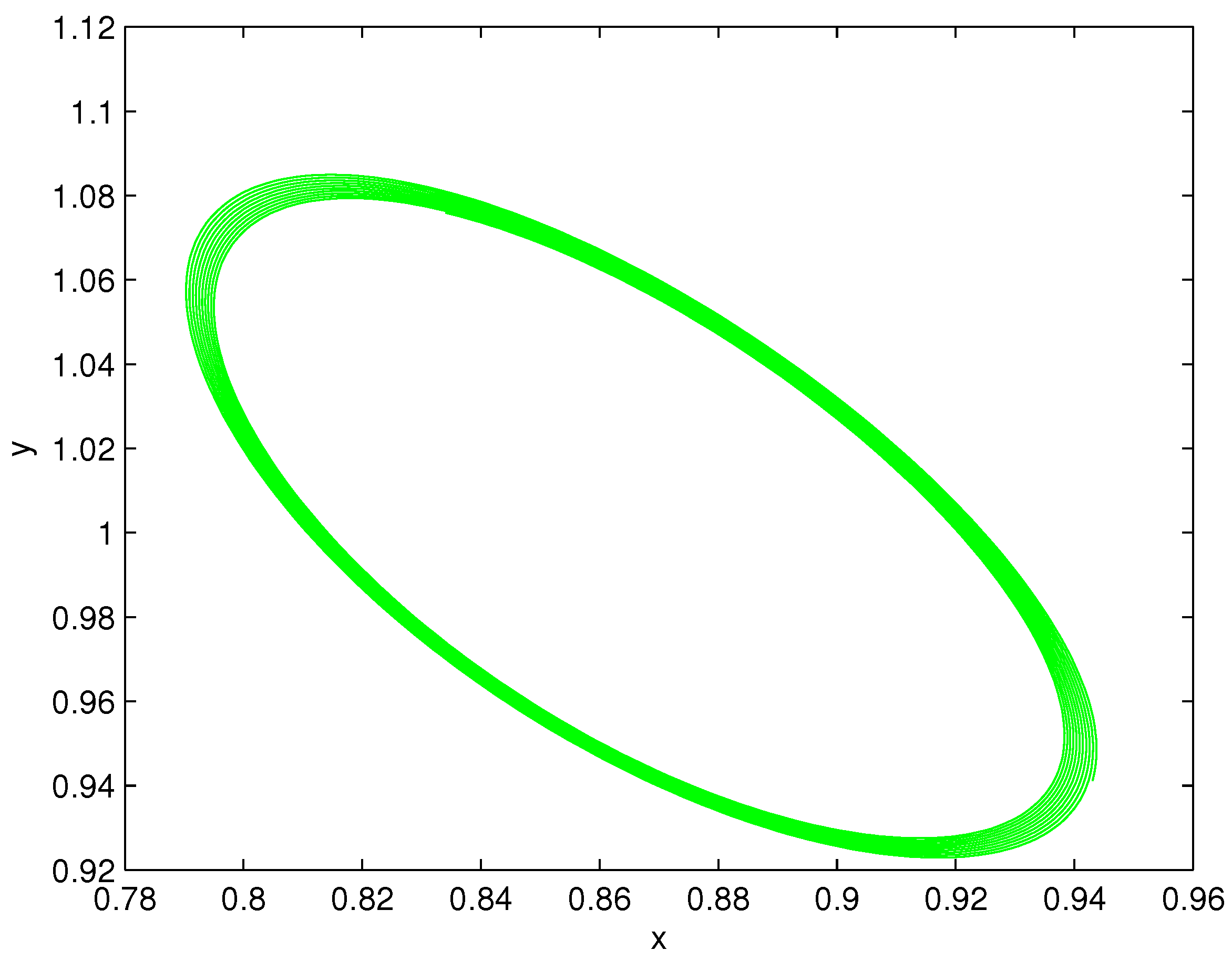
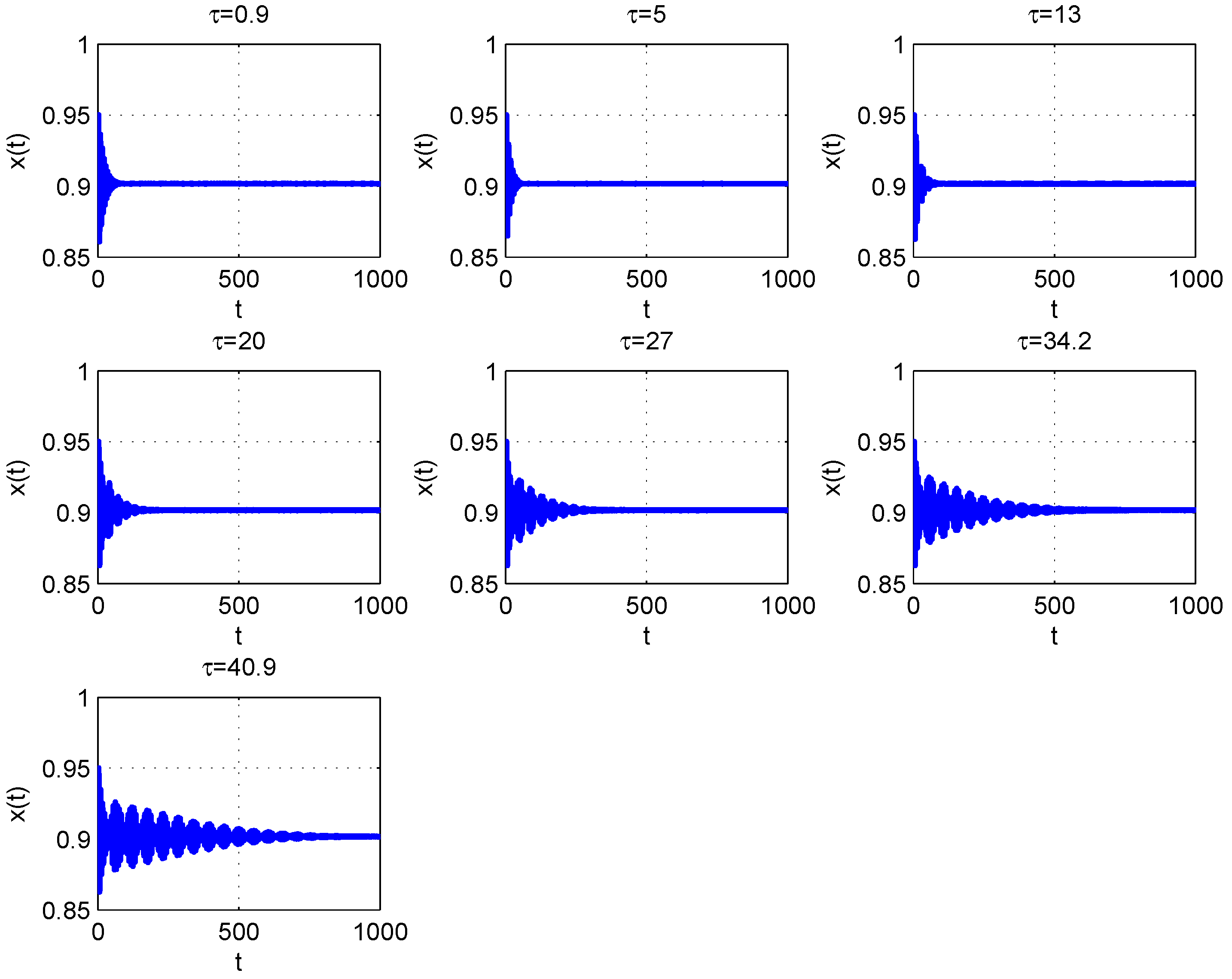
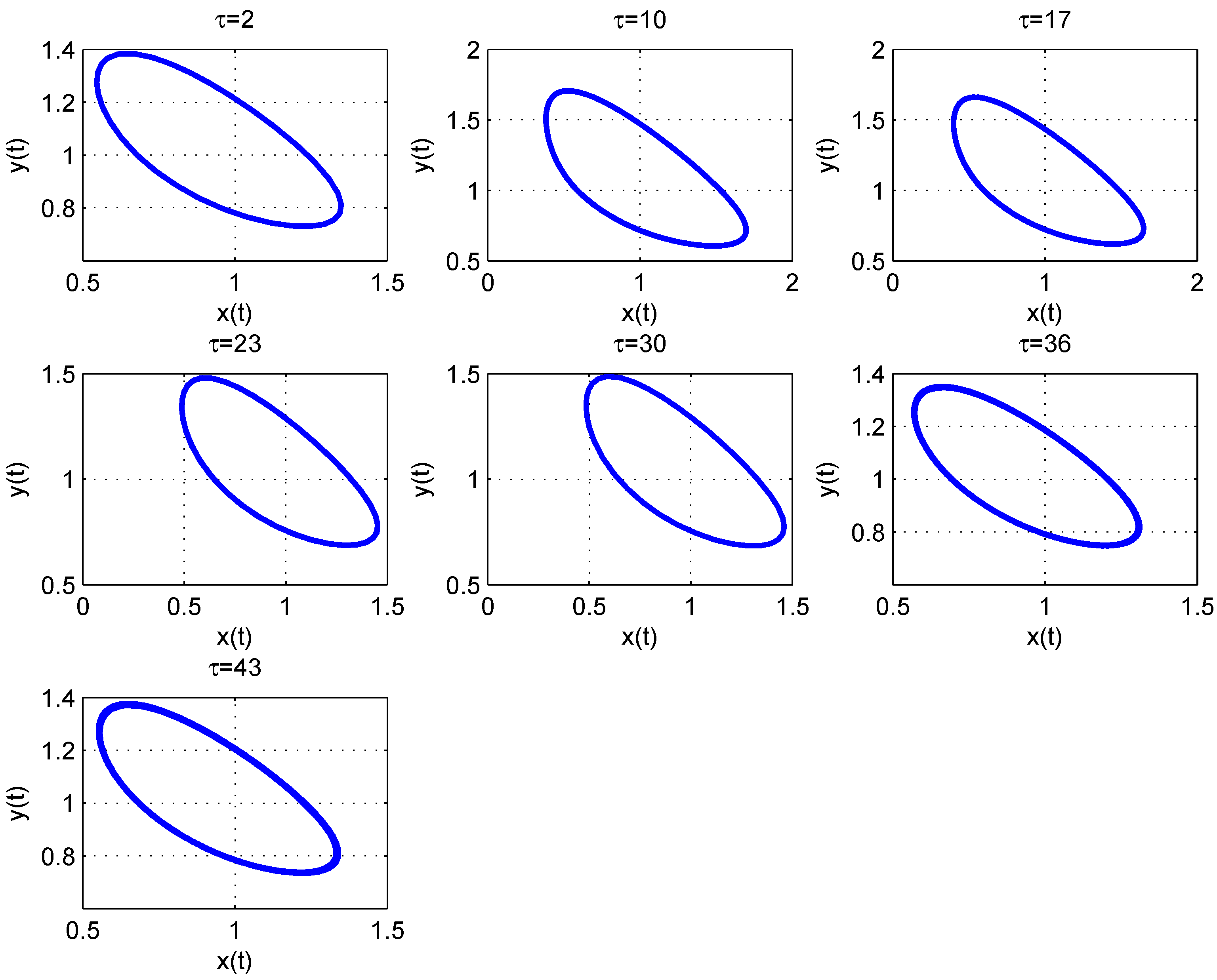
Figure 1 and Figure 2 show the values of $\gamma$ at which Hopf bifurcation occurs. It can be seen from Figure 1 that Hopf bifurcation occurs at $E_1(1,1,0)$ at one value $\gamma =1$, while there are two values ${\gamma }_1=0.169751,{\gamma }_2=0.634171$ at $E_2(a_0,1,k)$. Some phase portraits and time series of limit cycle are given in Figure 3 and Figure 4 at $E_1(1,1,0)$ and in Figure 5, Figure 6, Figure 7 and Figure 8 at $E_2(a_0,1,k)$. By the computation of the AUTO package, we present all the first Lyapunov coefficient of the Hopf points in Table 2.

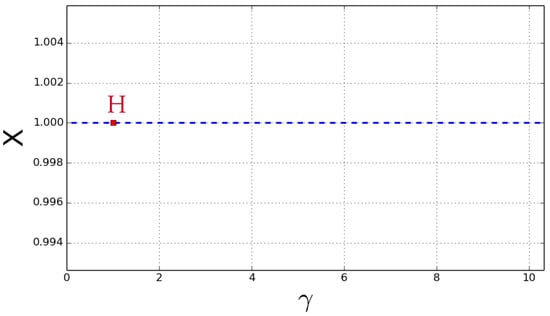
Figure 1. Hopf bifurcation Diagrams of model at $E_1(1,1,0)$ (3) for bifurcation values of $\gamma =1$.

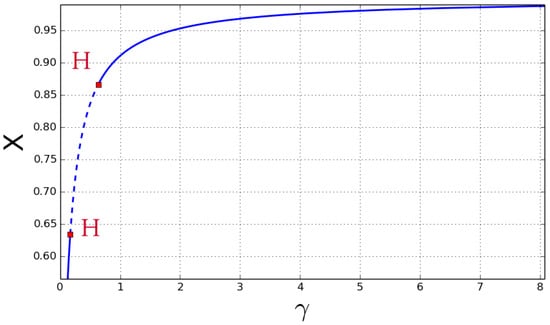
Figure 2. Hopf bifurcation Diagrams of model at $E_2(\frac{5.1\gamma }{0.5+5.1\gamma },1,0.1)$ (3) for bifurcation values of ${\gamma }_1=0.169751,{\gamma }_2=0.634171$.

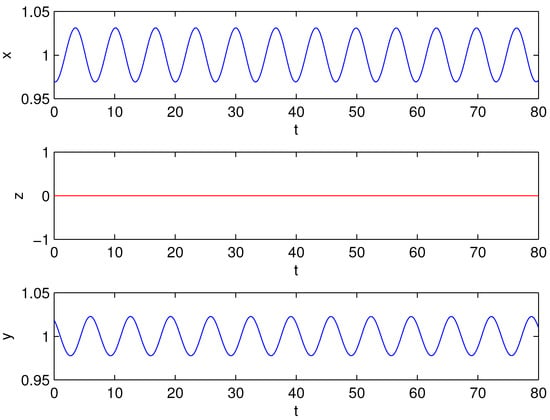
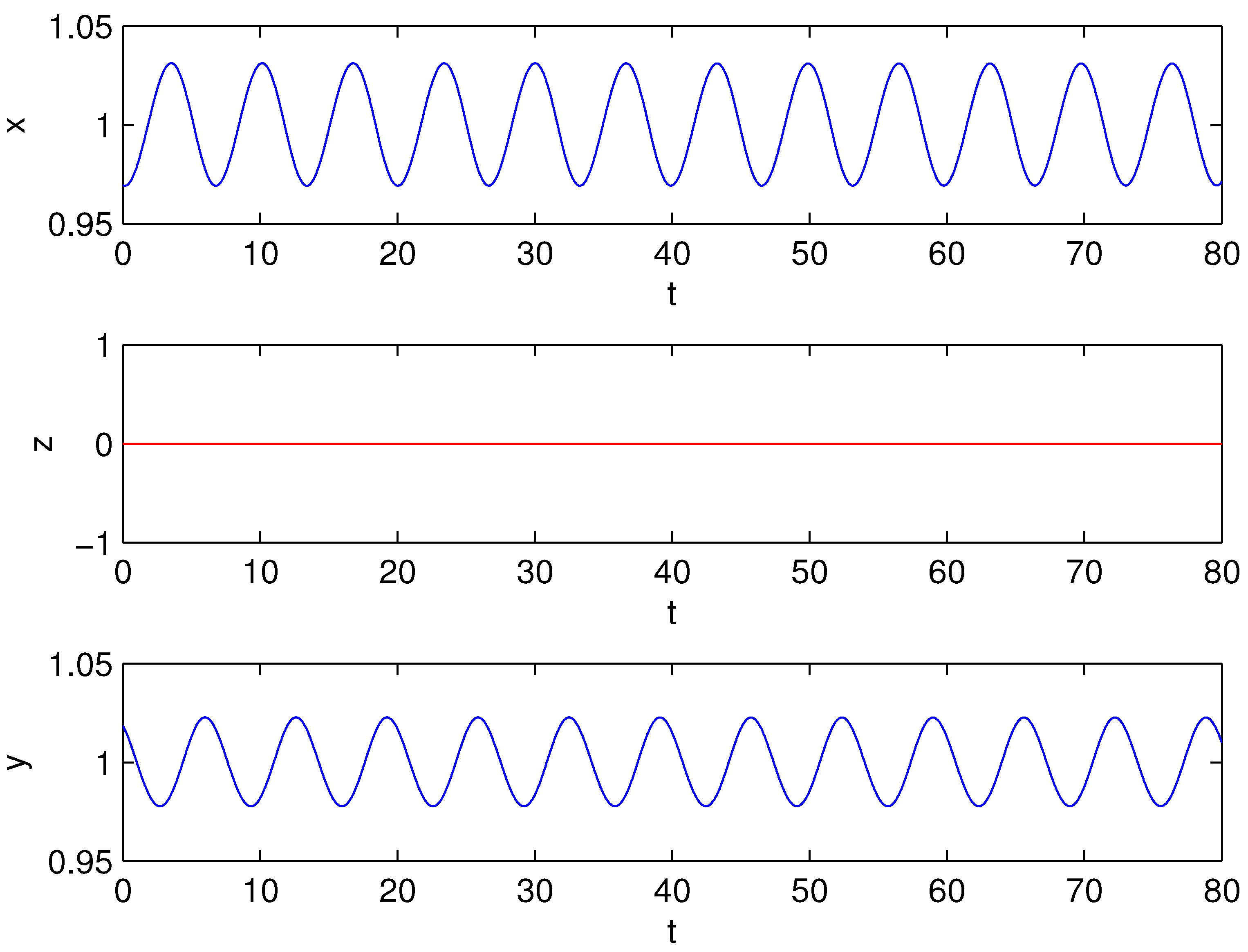
Figure 3. The time series at $E_1(1,1,0)$, $\gamma =1$.

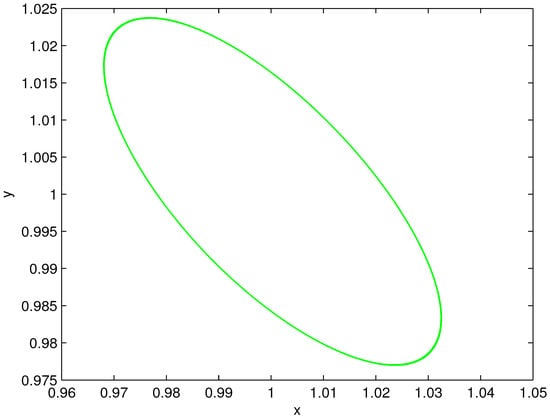
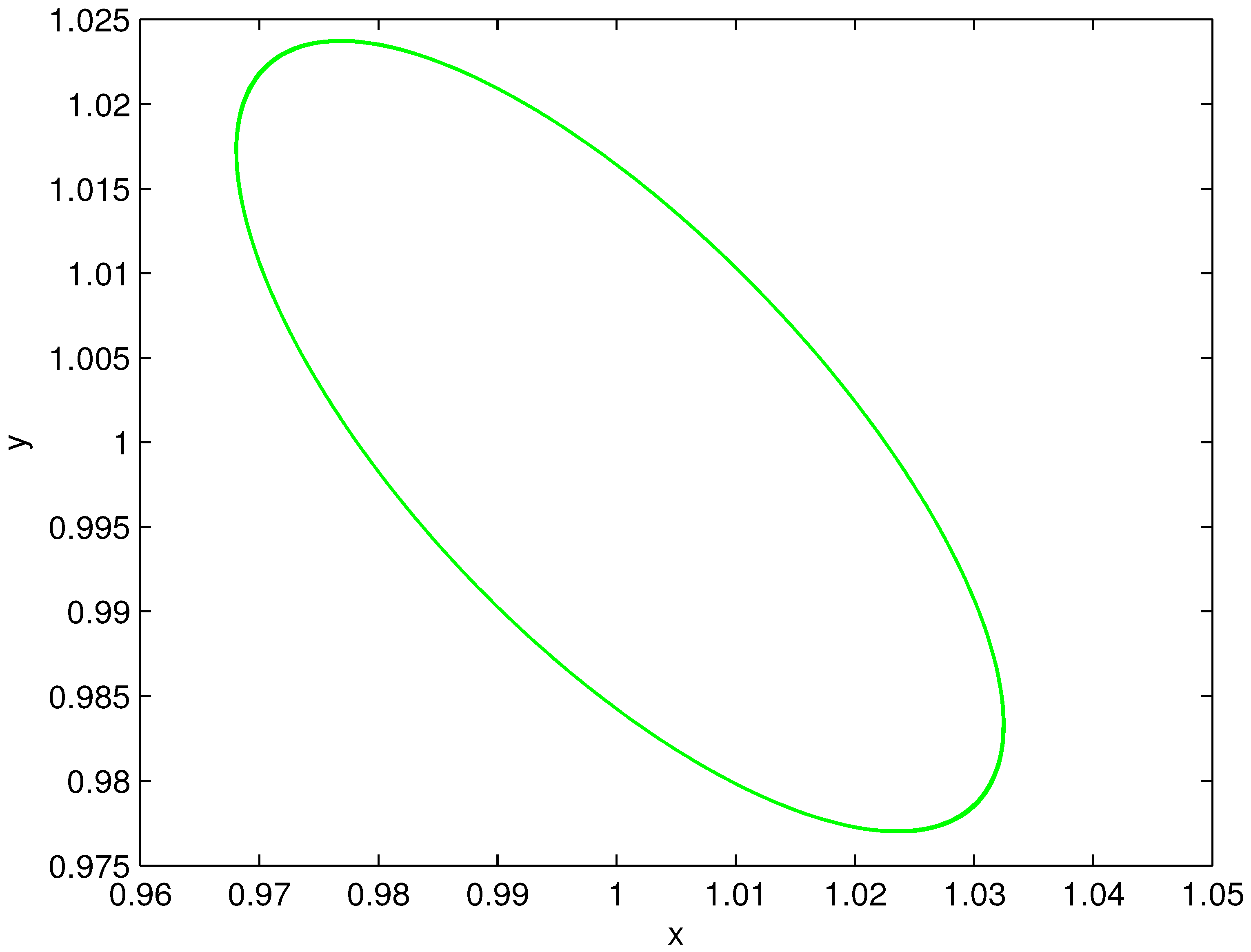
Figure 4. The phase portrait of the limit cycle at $E_1(1,1,0)$, $\gamma =1$.

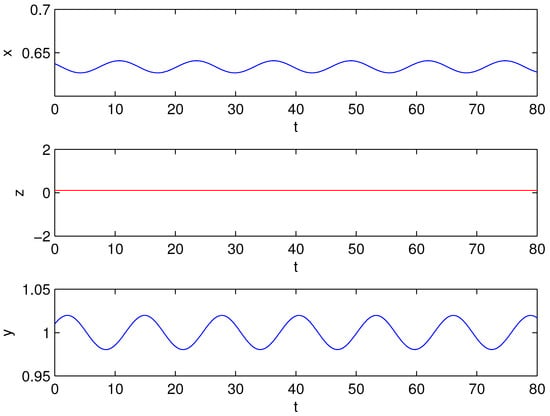
Figure 5. The time series at $E(\frac{5.1\gamma }{0.5+5.1\gamma },1,0.1)$, ${\gamma }_1=0.169751.$

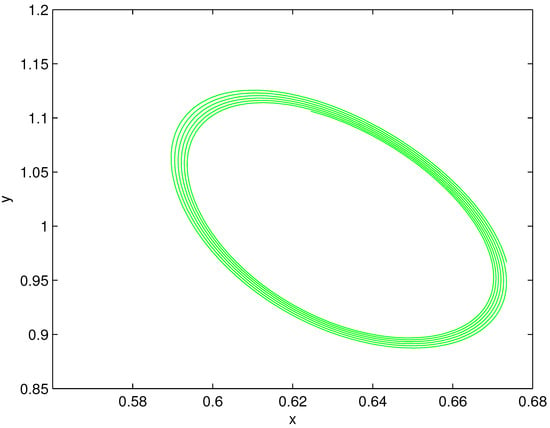
Figure 6. The phase portrait of the limit cycle at $E(\frac{5.1\gamma }{0.5+5.1\gamma },1,0.1)$, ${\gamma }_1=0.169751$.

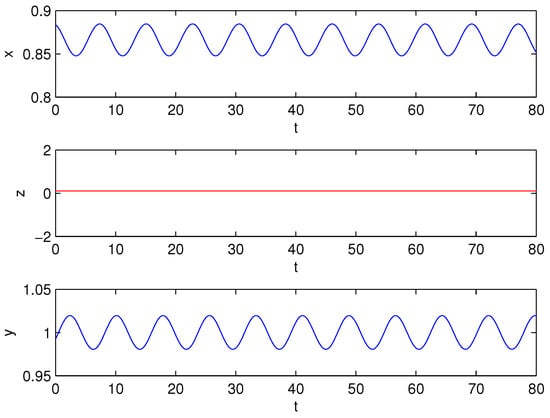
Figure 7. The time series at $E(\frac{5.1\gamma }{0.5+5.1\gamma },1,0.1)$, ${\gamma }_2=0.634171$.

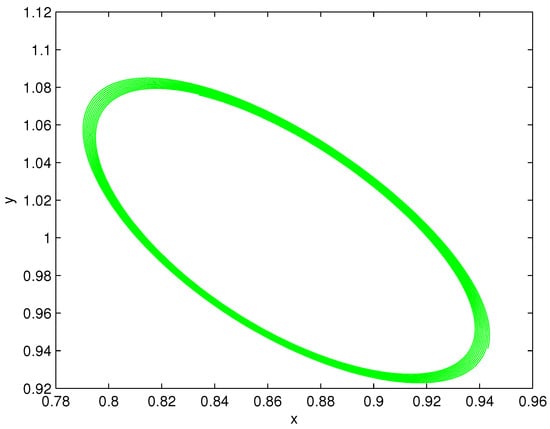
Figure 8. The phase portrait of the limit cycle at $E(\frac{5.1\gamma }{0.5+5.1\gamma },1,0.1)$, ${\gamma }_2=0.634171$.

Table 2. The numerical results.

Fig.	Hopf Bifurcation Point	The First Lyapunov Coefficient
Figure 1	(1,1,0)	$6.2\times {10}^{-9}$
Figure 2	(0.6339,1,0.1)	$8.64328\times {10}^{-6}$
Figure 2	(0.8661,1,0.1)	$2.7982\times {10}^{-6}$

4. Delayed Model and Its Dynamics

Taking into account that the effect of advertising in the non-potential buyers class most probably does not happen instantaneously, it is assumed that the potential buyers takes $\tau$ time for reacting with the advertising. In other words, it is presumed that there is a time delayed $\tau$ in the response of potential buyers to purchase the product under the influence of advertising. Thus, the proportion of potential buyers who became customers due to advertising is $\frac{bx(t-\tau )z}{a+z}$. Consequently, the delayed model of (3) is given by

$$\left\{\begin{array}{c}\dot{x}=\gamma (1-x{y}^2+\beta (y-1))-\frac{bx(t-\tau )z}{a+z},\hfill \\ \dot{y}=-y+x{y}^2+\frac{bx(t-\tau )z}{\gamma (a+z)},\hfill \\ \dot{z}=dz-\frac{d{z}^2}{k}.\hfill \end{array}\right.$$

(14)

By applying the theory of series at the point $(x,y,z^{*})$, system (14) can be expressed as

$$\left\{\begin{array}{c}\dot{x}=\gamma (1-x{y}^2+\beta (y-1))-b\left(\frac{z^{*}}{a+z^{*}}+\frac{a(z-z^{*})}{{(a+z^{*})}^2}-\frac{a{(z-z^{*})}^2}{{(a+z^{*})}^3}\right)x(t-\tau )+O\left({(z-z^{*})}^3\right),\hfill \\ \dot{y}=-y+x{y}^2+\frac{b}{\gamma }\left(\frac{z^{*}}{a+z^{*}}+\frac{a(z-z^{*})}{{(a+z^{*})}^2}-\frac{a{(z-z^{*})}^2}{{(a+z^{*})}^3}\right)x(t-\tau )+O\left({(z-z^{*})}^3\right),\hfill \\ \dot{z}=dz-\frac{d{z}^2}{k}.\hfill \end{array}\right.$$

(15)

4.1. Stability of Equilibria and Bifurcations of Periodic Solutions

Now, we analyze the delay effect on the dynamic behavior of system (15). When $\tau =0$, system (15) returns to the system (3), which has been studied in the previous sections.

Obviously, the equilibria of system (3) still the same for the delayed system (15). From proposition (1), system (15) has two equilibria $E=(x_i^{*},1,z_i^{*})=E_i,i=1,2$ as well. Through the next transformation

$$u\left(t\right)=x\left(t\right)-x^{*},v\left(t\right)=y\left(t\right)-1,w\left(t\right)=z\left(t\right)-z^{*}.$$

The linearized system (15) becomes:

$$\left\{\begin{array}{c}\dot{u}=-\gamma u-\frac{b{z}^{*}}{a+z^{*}}u(t-\tau )+\gamma (\beta -2x^{*})v-\frac{ab{x}^{*}}{{(a+z^{*})}^2}w,\hfill \\ \dot{v}=u+\frac{b{z}^{*}}{\gamma (a+z^{*})}u(t-\tau )+(2x^{*}-1)v+\frac{ab{x}^{*}}{\gamma {(a+z^{*})}^2}w,\hfill \\ \dot{w}=w(d-\frac{2d{z}^{*}}{k}),\hfill \end{array}\right.$$

(16)

which can be written as

$$\frac{d}{dt}\left(\begin{array}{c}u\\ v\\ w\end{array}\right)=M_1\left(\begin{array}{c}u\left(t\right)\\ v\left(t\right)\\ w\left(t\right)\end{array}\right)+M_2\left(\begin{array}{c}u(t-\tau )\\ v(t-\tau )\\ w(t-\tau )\end{array}\right),$$

(17)

where,

$$M_1=\left(\begin{array}{ccc}-\gamma & \gamma (\beta -2x^{*})& -\frac{ab{x}^{*}}{{(a+z^{*})}^2}\\ 1& 2x^{*}-1& \frac{ab{x}^{*}}{{(a+z^{*})}^2\gamma }\\ 0& 0& d-\frac{2d{z}^{*}}{k}\end{array}\right),M_2=\left(\begin{array}{ccc}-\frac{b{z}^{*}}{a+z^{*}}& 0& 0\\ \frac{b{z}^{*}}{(a+z^{*})\gamma }& 0& 0\\ 0& 0& 0\end{array}\right).$$

The characteristic polynomial of the delayed system (15), depending on $\tau$, is expressed as follows:

$$F(\lambda ,\tau ):=det(\lambda I-M_1-e^{-\lambda \tau }{M}_2).$$

A straightforward calculation leads to

$$F(\lambda ,\tau ):=(\lambda +d_1)\left({\lambda }^2+c_1\lambda +c_0+\left(l_1\lambda +l_0\right)e^{-\lambda \tau }\right)=0,$$

(18)

where $d_1=d(\frac{2z^{*}}{k}-1),c_1=\gamma -2x^{*}+1,c_0=\gamma (1-\beta ),l_1=\frac{b{z}^{*}}{a+z^{*}},l_0=l_1(1-\beta ).$

Obviously, ${\lambda }_1=-d_1$ is constantly an eigenvalue and the remain eigenvalues satisfy the following equation

$$P(\lambda ,\tau ):={\lambda }^2+c_1\lambda +c_0+(l_1\lambda +l_0)e^{-\lambda \tau }.$$

(19)

Therefore, we analyze the distribution of the roots of Equation (19).

For $\tau =0,$$F(\lambda ,\tau )$ has roots with negative real parts iff

$$\begin{array}{c}\left(L_1\right)d_1>0,\hfill \\ \left(L_2\right)c_i+l_i>0,\hfill \end{array}$$

(20)

where $i=0,1.$

Now, we consider $\tau >0$. For the occurrence of the Hopf bifurcation, denote $\lambda =\eta \left(\tau \right)+i\omega \left(\tau \right)(\omega >0)$ is the eigenvalue of the characteristic Equation (19), where $\eta$ and $\omega$ depend on the delay $\tau$. A critical time delay $\tau ={\tau }_0$ must exist such that $\lambda \left({\tau }_0\right)=\pm i\omega \left({\tau }_0\right),\omega >0$ and the transversally condition $Re\left(\frac{d\lambda \left(\tau \right)}{d\tau }\right){|}_{\tau ={\tau }_0}\ne 0$ is satisfied.

Assume that the characteristic Equation (19) has a pair of pure imaginary roots $\lambda \left({\tau }_0\right)=\pm i\omega \left({\tau }_0\right),\omega >0$. By setting $\lambda =i\omega$ in (19), one obtains

$$-{\omega }^2+c_1\omega i+c_0+(l_1\omega i+l_0)(cos\left(\omega \tau \right)-isin\left(\omega \tau \right)).$$

Taking the real and imaginary parts, one gets

$$l_{0}cos\left(\omega \tau \right)+\omega l_{1}sin\left(\omega \tau \right)={\omega }^2-c_0,$$

(21)

$$l_{0}sin\left(\omega \tau \right)-\omega l_{1}cos\left(\omega \tau \right)=c_1\omega .$$

(22)

Taking the squares of both equations, we have

$$l_0^2{cos}^2\left(\omega \tau \right)+{\omega }^2{l}_1^2{sin}^2\left(\omega \tau \right)+2l_1{l}_0\omega cos\left(\omega \tau \right)sin\left(\omega \tau \right)={({\omega }^2-c_0)}^2,$$

(23)

$$l_0^2{sin}^2\left(\omega \tau \right)+{\omega }^2{l}_1^2{cos}^2\left(\omega \tau \right)-2l_1{l}_0\omega cos\left(\omega \tau \right)sin\left(\omega \tau \right)={\left(c_1\omega \right)}^2,$$

(24)

which leads to

$$P\left(\omega \right)={\omega }^4+A_1{\omega }^2+A_0=0,$$

(25)

where, $A_0=c_0^2-l_0^2$, $A_1=c_1^2-l_1^2-2c_0.$

Let $\mathsf{\Omega }={\omega }^2$, we get

$$P\left(\mathsf{\Omega }\right)={\mathsf{\Omega }}^2+A_1\mathsf{\Omega }+A_0=0.$$

(26)

Next, we discuss the conditions under which Equation (26) has at least one positive root.

Lemma 3.

For the distribution of the roots of Equation (26), we have

$\left(L_3\right)$

If either $A_0>0$ and $A_1>0$ or $A_1^2<4A_0,$ then Equation (26) does not have any positive roots.

$\left(L_4\right)$

If either $A_0<0$ or $A_1<0$ and $A_1^2=4A_0$ then Equation (26) has one positive root.

$\left(L_5\right)$

If $A_0>0$ and $A_1<0$ and $A_1^2>4A_0$ then Equation (26) has two positive roots.

Generally, it is assumed that Equation (26) has two positive roots ${\omega }_m(m=1,2).$ Then from Equations (23) and (24) we have

$${\tau }_{m,j}=\frac{1}{{\omega }_m}\left[cos{}^{-1}\left(\frac{l_0({\omega }_m^2-c_0)-l_1{c}_1{\omega }_m^2}{l_1{\omega }_m^2+l_0^2}\right)+2\pi j\right],m=1,2;j=0,1,2,\dots$$

(27)

The transversality condition can be verified in the following discussion:

By differentiating Equation (19) w.r.t. $\tau$, we get

$$\frac{d\lambda }{d\tau }\left(\frac{e^{\lambda \tau }(2\lambda +c_1)+l_1}{l_1\lambda +l_0}-\tau \right)=\lambda .$$

To facilitate the calculations, we consider $\mathsf{\Gamma }={\left[\frac{d\lambda }{d\tau }\right]}^{-1}$, thus

$$Re\left(\mathsf{\Gamma }\right)=Re\left(\frac{e^{\lambda \tau }(2\lambda +c_1)+l_1}{\lambda (l_1\lambda +l_0)}-\frac{\tau }{\lambda }\right),$$

we get

$${\left.Re\left(\mathsf{\Gamma }\right)\right|}_{\tau =m,j}=Re\left(\frac{e^{\lambda \tau }(2\lambda +c_1)+l_1}{\lambda (l_1\lambda +l_0)}\right),$$

$${\left.Re\left(\mathsf{\Gamma }\right)\right|}_{\tau =m,j}=Re\left(\frac{2{\omega }^2+c_1^2-l_1^2-2c_0}{l_1^2{\omega }^2+l_0^2}\right),$$

we find

$$sign{\left[Re\left(\mathsf{\Gamma }\right)\right]}_{\tau =m,j}=sign\left(P^{\prime }\left({\omega }^2\right)\right).$$

Therefore, a Hopf bifurcation occurs at the equilibrium E when $\tau ={\tau }_{m,j}$. We have the following theorem for the stability of the fixed point E.

Theorem 5.

Let ${\tau }_{m,j}(m=1,2;j=0,1,2,\dots )$ be defined by Equation (27).

• If the conditions $\left(L_1\right)$ or $\left(L_2\right)$ do not hold, the fixed point E is unstable for all $\tau \ge 0.$
• If the conditions $\left(L_1\right),\left(L_2\right)$ and $\left(L_3\right)$ hold, the fixed point E is stable for all $\tau \ge 0.$
• If the conditions $\left(L_1\right),\left(L_2\right)$ and $\left(L_4\right)$ hold, the equilibrium point E is stable for $\tau \in [0,{\tau }_{1,0})$ and unstable for $\tau >{\tau }_{1,0}.$ Moreover, the Hopf bifurcation occurs when $\tau ={\tau }_{1,0}.$
• If the conditions $\left(L_1\right),\left(L_2\right)$ and $\left(L_5\right)$ hold, there is an integer $p\ge 1$, such that

  $$0<{\tau }_{1,0}<{\tau }_{2,0}<{\tau }_{1,1}<{\tau }_{2,1}<\cdots <{\tau }_{1,p-1}<{\tau }_{1,p}<{\tau }_{2,p-1}<\cdots .$$
  So the equilibrium point E is stable for $\tau \in [0,{\tau }_{1,0})\cup \left({\tau }_{2,j},{\tau }_{1,j+1}\right)$ for $j=0,1,\dots ,p-1$ and unstable for $\tau \in \left({\tau }_{1,j},{\tau }_{2,j}\right)\cup ({\tau }_{1,p},\infty )$ for $j=0,1,\dots ,p-1.$ Moreover, the Hopf bifurcation occurs when $\tau ={\tau }_{1,j}$ and $\tau ={\tau }_{2,j}$ for $j=0,1,\dots ,p.$

4.2. Direction and Stability of the Hopf Bifurcation

In the former section, we obtained the critical value of the time delay ${\tau }_{m,j}(m=1,2;j=0,1,2,\dots )$ at which periodic solutions appear. As pointed out in [26], it is interesting to reveal the direction, stability and period of these bifurcating periodic solutions. Following the idea in [26], then the normal form and the center manifold theory are helpful to determine the properties of the periodic solutions at the critical value of $\tau$. Henceforth, we assume that system (15) undergoes Hopf bifurcations at the equilibrium point $E=(x_i^{*},1,z_i^{*})$ for $\tau ={\tau }_{m,j}(m=1,2;j=0,1,2,\dots )$, then $\pm i{\omega }_m$ is corresponding purely imaginary roots of the characteristic Equation (15) at E.

Let, $x_1\left(t\right)=x\left(t\right)-x_i^{*},x_2\left(t\right)=y\left(t\right)-1,x_3\left(t\right)=z\left(t\right)-z_i^{*}$ and $\tau ={\tau }_{m,j}+\mu$. For avoiding the abuse of mathematical notation, we set ${\tau }_m$ instead of ${\tau }_{m,j}$ and $x^{*},z^{*}$ instead of $x_i^{*},z_i^{*},$ respectively. Thus, $\mu =0$ is the Hopf bifurcation value of system (15). Then system (15) can be written as a functional differential equation in $C=C([-{\tau }_m,0],R^3)$ as the following form

$$\dot{x}=L_{\mu }\left(x_t\right)+f(\mu ,x_t),$$

(28)

where $x\left(t\right)=(x_i\left(t\right),i=1,2,3)\in R^3,L_{\mu }:C\to R$ and $f:R\times C\to R$ are given, respectively, as

$$L_{\mu }\left(\varphi \right)=({\tau }_m+\mu )M_1\left(\begin{array}{c}{\varphi }_1\left(0\right)\\ {\varphi }_2\left(0\right)\\ {\varphi }_3\left(0\right)\end{array}\right)+({\tau }_m+\mu )M_2\left(\begin{array}{c}{\varphi }_1(-{\tau }_m)\\ {\varphi }_2(-{\tau }_m)\\ {\varphi }_3(-{\tau }_m)\end{array}\right),$$

(29)

and

$$f(\tau ,\varphi )=({\tau }_m+\mu )\left(\begin{array}{c}{f}_1\\ f_2\\ -\frac{d}{k}{\varphi }_3^2\left(0\right)\end{array}\right),$$

(30)

where,

$f_1=\left(\frac{ab{\varphi }_1(-{\tau }_m)}{{(a+z^{*})}^3}+\frac{ab{x}^{*}}{{(a+z^{*})}^3}\right){\varphi }_3^2\left(0\right)-\frac{ab{\varphi }_1(-{\tau }_m){\varphi }_3\left(0\right)}{{(a+z^{*})}^2}-\gamma {\varphi }_1\left(0\right)\left({\varphi }_2^2\left(0\right)+2{\varphi }_2\left(0\right)\right)-\gamma x^{*}{\varphi }_2^2\left(0\right)$,

$f_2=-\left(\frac{ab{\varphi }_1(-{\tau }_m)}{\gamma {(a+z^{*})}^3}+\frac{ab{x}^{*}}{\gamma {(a+z^{*})}^3}\right){\varphi }_3^2\left(0\right)+\frac{ab{\varphi }_1(-{\tau }_m){\varphi }_3\left(0\right)}{\gamma {(a+z^{*})}^2}+{\varphi }_1\left(0\right)\left({\varphi }_2^2\left(0\right)+2{\varphi }_2\left(0\right)\right)+{\varphi }_2^2\left(0\right)x^{*}.$

According to Riesz representation theorem, there is a bounded variation function $\eta (\theta ,\mu )$ in $\theta \in [-{\tau }_m,0]$, such that

$$L_{\mu }\varphi ={\int }_{-{\tau }_m}^{0}d\eta (\theta ,0)\varphi \left(\theta \right), \mathrm{for}\varphi \in C.$$

(31)

In fact, $\eta (\theta ,\mu )$ can be written as

$$\eta (\theta ,\mu )=({\tau }_m+\mu )M_1\delta \left(\theta \right)-({\tau }_m+\mu )M_2\delta (\theta +1),$$

(32)

where $\delta$ is the Dirac delta function. For $\varphi \in C^1([-{\tau }_m,0],R^3)$, define

$$A\left(\mu \right)\varphi =\left\{\begin{array}{cc}\frac{d\varphi \left(\theta \right)}{d\theta },\hfill & \theta \in [-{\tau }_m,0),\hfill \\ \hfill & \\ {\int }_{-{\tau }_m}^{0}d\eta (\mu ,s)\varphi \left(s\right),\hfill & \theta =0,\hfill \end{array}\right.$$

(33)

and

$$R\left(\mu \right)\varphi =\left\{\begin{array}{cc}0,\hfill & \theta \in [-{\tau }_m,0),\hfill \\ f(\mu ,\varphi ),\hfill & \theta =0.\hfill \end{array}\right.$$

(34)

In order to facilitate, system (28) can be written into an operator equation

$$\dot{x_t}=A\left(\mu \right)x_t+R\left(\mu \right)x_t,$$

(35)

where $x_t\left(\theta \right)=x(t+\theta )$ for $\theta \in [-{\tau }_m,0)$. For $\psi \in C^1([0,{\tau }_m],R^{3*})$, the adjoint operator $A^{*}$ of A is defined as:

$$A^{*}\left(\mu \right)\left(\psi \left(s\right)\right)=\left\{\begin{array}{cc}\frac{-d\varphi \left(s\right)}{ds},\hfill & s\in (0,{\tau }_m],\hfill \\ {\int }_{-{\tau }_m}^{0}d{\eta }^T(t,0)\psi (-t),\hfill & s=0.\hfill \end{array}\right.$$

(36)

For normalization of the eigenvector of A and its adjoint $A^{*}$, we define the bilinear inner product

$$⟨\psi \left(s\right),\varphi \left(\theta \right)⟩=\overline{\psi }\left(0\right)\varphi \left(0\right)-{\int }_{-{\tau }_m}^0{\int }_{\zeta =0}^{\theta }\overline{\psi }(\zeta -\theta )d\eta \left(\theta \right)\varphi \left(\zeta \right)d\zeta ,$$

(37)

where $\eta \left(\theta \right)=\eta (\theta ,0).$

By the discussion in the previous subsection, it is known that $\pm i{\omega }_m$ are eigenvalues of $A\left(0\right)$ and also the eigenvalues of $A^{*}$. First, we compute the eigenvector of $A\left(0\right)$ and $A^{*}$ corresponding to $i{\omega }_m$ and $-i{\omega }_m$, respectively.

Consider $q\left(\theta \right)={(1,\rho ,\sigma )}^T{e}^{i\theta {\omega }_m}$ is the eigenvector of $A\left(0\right)$ corresponding to $i{\omega }_m$. Therefore

$$A\left(0\right)q\left(0\right)=i{\omega }_{m}q\left(\theta \right).$$

Then

$$\left(\begin{array}{ccc}\frac{b{e}^{-i{\tau }_m{\omega }_m}{z}^{*}}{a+z^{*}}+\gamma +i{\omega }_m& \gamma (2x^{*}-\beta )& \frac{ab{x}^{*}}{{(a+z^{*})}^2}\\ -\frac{b{e}^{-i{\tau }_m{\omega }_m}{z}^{*}}{(a+z^{*})\gamma }& -2x^{*}+i{\omega }_m+1& -\frac{ab{x}^{*}}{{(a+z^{*})}^2\gamma }\\ 0& 0& \frac{2d{z}^{*}}{k}+i{\omega }_m\end{array}\right)q\left(0\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),$$

one can get

$$\rho =\frac{\gamma (a+z^{*})+b{z}^{*}{e}^{-i{\tau }_{m}o{\omega }_m}}{\gamma (a+z^{*})(-2x^{*}+i{\omega }_m+1)},\sigma =0.$$

(38)

Similarly, assume that the eigenvector of $A^{*}$ corresponding to $-i{\omega }_m$ is $q^{*}$ which can be written as

$$q^{*}\left(\theta \right)=D{(1,{\rho }^{*},{\sigma }^{*})}^T{e}^{i\theta {\omega }_m},$$

then from the definition of $A^{*}$ we can compute

$$\begin{array}{ccc}\hfill {\rho }^{*}& =& \frac{\gamma (2x^{*}-\beta )}{2x^{*}+i{\omega }_m-1},\hfill \\ \hfill {\sigma }^{*}& =& \frac{abk{x}^{*}({\omega }_m-i\beta +i)}{{(a+z^{*})}^2(2x^{*}+i{\omega }_m-1)(k{\omega }_m-id(k-2z^{*}))}.\hfill \end{array}$$

(39)

For $⟨q^{*},q⟩=1,$ it is needed to determine the value of D. From (37) we have

$$\begin{array}{cc}\hfill ⟨q^{*},q⟩& =⟨{\overline{q}}^{*}\left(0\right),q\left(0\right)⟩-{\int }_{-{\tau }_m}^0{\int }_0^{\theta }\overline{q}(\zeta -\theta )d\eta \left(\theta \right)q\left(\zeta \right)d\zeta \hfill \\ \hfill & =\overline{D}\{1+\rho {\overline{\rho }}^{*}-{\int }_{-{\tau }_m}^0{\int }_0^{\theta }(1,\overline{{\rho }^{*}},\overline{{\sigma }^{*}})e^{-i(\zeta -\theta ){\omega }_m}d\eta \left(\theta \right){(1,\rho ,0)}^T{e}^{i\zeta {\omega }_m}d\zeta \}\hfill \\ \hfill & =\overline{D}\{\frac{b{z}^{*}{\tau }_m({\overline{\rho }}^{*}-\gamma )e^{-i{\tau }_m{\omega }_m}}{\gamma (a+z^{*})}+{\overline{\rho }}^{*}\rho +{\overline{\sigma }}^{*}\sigma +1\}.\hfill \end{array}$$

(40)

Thus, we have

$$D=\frac{\gamma (a+z^{*})}{\gamma (a+z^{*})({\rho }^{*}\overline{\rho }+1)-b{\tau }_m{z}^{*}(\gamma -{\rho }^{*})e^{i{\tau }_m{\omega }_m}}.$$

(41)

Next, we study the stability of bifurcating periodic solution. As in [26], the bifurcating periodic solutions $Z(t,\mu (ϵ\left)\right)$ have the amplitude $O\left(ϵ\right)$ and nonzero Floquet exponent $\beta \left(ϵ\right)$ with $\beta \left(0\right)=0$. Then, $\mu$, $\beta$ are given by

$$\mu ={\mu }_2{ϵ}_2+{\mu }_4{ϵ}_4+\cdots ,$$

$$\beta ={\beta }_2{ϵ}_2+{\beta }_4{ϵ}_4+\cdots .$$

The sign of ${\mu }_2$ indicates the direction of bifurcation while ${\beta }_2$ determines the stability of $Z(t,\mu (ϵ\left)\right)$, which is stable if ${\beta }_2<0$ and unstable if ${\beta }_2>0.$ In the following, we construct the coordinates to describe a center manifold $C_0$ near $\mu =0$, which is a local invariant, attracting a two-dimensional manifold [26].

Let $x_t$ be the solution of Equation (28) when $\mu =0$. Define

$$z\left(t\right)=⟨q^{*},x_t⟩,W(t,\theta )=x_t\left(\theta \right)-2Re\left\{z\left(t\right)q\left(\theta \right)\right\}.$$

(42)

On the center manifold $C_0$ we have

$$W(t,\theta )=W(z\left(t\right),\overline{z}\left(t\right),\theta ),$$

where

$$W(z,\overline{z},\theta )=W_{20}\left(\theta \right)\frac{z^2}{2}+W_{11}\left(\theta \right)z\overline{z}+W_{02}\left(\theta \right)\frac{{\overline{z}}^2}{2}+\cdots ,$$

where $z,\overline{z}$ are local coordinates for center manifold $C_0$ in the direction of $q^{*}$ and ${\overline{q}}^{*}$. Note that W is real if $x_t$ is real. We consider only real solutions. For the solution $x_t\in C_0$ of Equation (28), since $\mu =0$, we have

$$\begin{array}{c}\dot{z}=i{\omega }_{m}z+{\overline{q}}^{*}\left(\theta \right)f(0,W(z,\overline{z},\theta )+2Re\left\{zq\left(\theta \right)\right\})\hfill \\ =i{\omega }_{m}z+{\overline{q}}^{*}\left(0\right)f(0,W(z,\overline{z},0)+2Re\left\{zq\left(0\right)\right\}),\hfill \end{array}$$

(43)

which can written as

$$\dot{z}=i{\omega }_{m}z\left(t\right)+g(z,\overline{z}),$$

where

$$g(z,\overline{z})={\overline{q}}^{*}{f}_0(z,\overline{z})=g_{20}\frac{z^2}{2}+g_{11}z\overline{z}+g_{02}\frac{{\overline{z}}^2}{2}+g_{21}\frac{z^2\overline{z}}{2}+\cdots .$$

(44)

Hence

$$x_t\left(\theta \right)=(x_{1t}\left(\theta \right),x_{2t}\left(\theta \right),x_{3t}\left(\theta \right))=W(t,\theta )+z\left(t\right)q\left(\theta \right)+\overline{z}\left(t\right)\overline{q}\left(\theta \right),$$

then

$$\begin{array}{c}{x}_{1t}\left(\theta \right)=z{e}^{i{\omega }_m\theta }+\overline{z}{e}^{-i{\omega }_m\theta }+W_{20}^{\left(1\right)}\left(\theta \right)\frac{z^2}{2}+W_{11}^{\left(1\right)}\left(\theta \right)z\overline{z}+W_{02}^{\left(1\right)}\left(\theta \right)\frac{{\overline{z}}^2}{2}+O(\parallel (z,\overline{z}){\parallel }^3),\\ x_{2t}\left(\theta \right)=\rho z{e}^{i{\omega }_m\theta }+\overline{\rho }\overline{z}{e}^{-i{\omega }_m\theta }+W_{20}^{\left(2\right)}\left(\theta \right)\frac{z^2}{2}+W_{11}^{\left(2\right)}\left(\theta \right)z\overline{z}+W_{02}^{\left(2\right)}\left(\theta \right)\frac{{\overline{z}}^2}{2}+O(\parallel (z,\overline{z}){\parallel }^3),\\ x_{3t}\left(\theta \right)=\sigma z{e}^{i{\omega }_m\theta }+\overline{\sigma }\overline{z}{e}^{-i{\omega }_m\theta }+W_{20}^{\left(3\right)}\left(\theta \right)\frac{z^2}{2}+W_{11}^{\left(3\right)}\left(\theta \right)z\overline{z}+W_{02}^{\left(3\right)}\left(\theta \right)\frac{{\overline{z}}^2}{2}+O(\parallel (z,\overline{z}){\parallel }^3),\end{array}$$

(45)

By substituting in Equation (44), we get

$$g(z,\overline{z})={\overline{q}}^{*}\left(0\right)f_0(z,\overline{z})=\overline{D}(1,{\overline{\rho }}^{*},{\overline{\sigma }}^{*})f_0(z,\overline{z}).$$

(46)

Comparing the coefficients of equations (44) and (46), we get

$$\begin{array}{cc}\hfill g_{20}& =-2{\tau }_m\overline{D}\rho (2+x^{*}\rho )(\gamma -{\overline{\rho }}^{*}),\hfill \\ \hfill g_{11}& =-2{\tau }_m\overline{D}(\rho +\overline{\rho }+x^{*}\rho \overline{\rho })(\gamma -{\overline{\rho }}^{*}),\hfill \\ \hfill g_{02}& =-2{\tau }_m\overline{D}\overline{\rho }(2+x^{*}\overline{\rho })(\gamma -{\overline{\rho }}^{*}),\hfill \\ \hfill g_{21}& =\overline{D}(\gamma -{\overline{\rho }}^{*})(-4W_{11}^{\left(2\right)}\left(0\right)-2\rho (\rho +2(W_{11}^{\left(1\right)}\left(0\right)+x^{*}{W}_{11}^{\left(2\right)}\left(0\right)))-2W_{20}^{\left(2\right)}\left(0\right)-\hfill \\ \hfill & 2{\overline{\rho }}^{*}(2\rho +W_{20}^{\left(1\right)}\left(0\right)+x^{*}{W}_{20}^{\left(2\right)}\left(0\right))-\frac{ab{e}^{-i{\omega }_m{\tau }_m}(2W_{11}^{\left(3\right)}\left(0\right)+e^{2i{\omega }_m{\tau }_m}{W}_{20}^{\left(3\right)}\left(0\right))}{{(a+z^{*})}^2\gamma }),\hfill \end{array}$$

(47)

where $W_{20}\left(\theta \right)=(W_{20}^{\left(1\right)},W_{20}^{\left(2\right)},W_{20}^{\left(3\right)})$, $W_{11}\left(\theta \right)=(W_{11}^{\left(1\right)},W_{11}^{\left(2\right)},W_{11}^{\left(3\right)})$,

$$W_{20}\left(\theta \right)=\frac{i{g}_{20}}{{\omega }_m}q\left(0\right)e^{i\theta {\omega }_m}+\frac{i{\overline{g}}_{02}}{3{\omega }_m}\overline{q}\left(0\right)e^{-i\theta {\omega }_m}+{\mathsf{\Delta }}_1{e}^{2i\theta {\omega }_m},$$

(48)

$$W_{11}\left(\theta \right)=-\frac{i{g}_{11}}{{\omega }_m}q\left(0\right)e^{i\theta {\omega }_m}+\frac{i{\overline{g}}_{11}}{3{\omega }_m}\overline{q}\left(0\right)e^{-i\theta {\omega }_m}+{\mathsf{\Delta }}_2,$$

(49)

Furthermore, $\mathsf{\Delta },\mathsf{\Lambda }\in {\mathbb{C}}^3$ are constant vectors, which can be computed through the relations [27,28]

$$\left(\begin{array}{ccc}-2i{\omega }_m-\gamma -\frac{b{e}^{-2i{\omega }_m{\tau }_m}{z}^{*}}{a+z^{*}}& (\beta -2x^{*})\gamma & -\frac{ab{x}^{*}}{{(a+z^{*})}^2}\\ \frac{b{e}^{-2i{\omega }_m{\tau }_m}{z}^{*}}{(a+z^{*})\gamma }+1& -2i{\omega }_m+2x^{*}-1& \frac{ab{x}^{*}}{{(a+z^{*})}^2\gamma }\\ 0& 0& -\frac{2z^{*}d}{k}+d-2i{\omega }_m\end{array}\right)·{\mathsf{\Delta }}_1={\chi }_1\left(\begin{array}{c}\gamma \\ -1\\ 0\end{array}\right),$$

(50)

$$\left(\begin{array}{ccc}-\gamma -\frac{b{z}^{*}}{a+z^{*}}& (\beta -2x^{*})\gamma & -\frac{ab{x}^{*}}{{(a+z^{*})}^2}\\ \frac{b{z}^{*}}{(a+z^{*})\gamma }+1& 2x^{*}-1& \frac{ab{x}^{*}}{{(a+z^{*})}^2\gamma }\\ 0& 0& -\frac{2z^{*}d}{k}+d\end{array}\right)·{\mathsf{\Delta }}_2=\left(\begin{array}{c}-\gamma \\ 1\\ 0\end{array}\right),$$

(51)

where

$$\begin{array}{c}{\chi }_1=2{\tau }_m\rho (2+x^{*}\rho ),\hfill \\ {\chi }_2=(Re\left\{\rho \right\}+x^{*}\rho \overline{\rho })\hfill \end{array}$$

(52)

Using Equation (47) we can compute the following values [27]:

$$\begin{array}{c}{C}_1\left(0\right)=\frac{i}{2{\omega }_m}(g_{02}{g}_{11}-2|g_{11}{|}^2-\frac{1}{3}|g_{02}{|}^2)+\frac{1}{2}{g}_{21},\hfill \\ {\mu }_2=\frac{-Re\left(C_1\left(0\right)\right)}{2Re({\lambda }^{\prime }\left(0\right))},\hfill \\ {\beta }_2=2\Re \left(C_1\left(0\right)\right).\hfill \end{array}$$

(53)

which determine the quantities of bifurcating periodic solutions in the center manifold at the critical value ${\tau }_m;$

• If ${\mu }_2>0(<0)$, the direction of bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for $\tau >{\tau }_m(\tau <{\tau }_m)$,
• If ${\beta }_2>0(<0)$, the solutions of bifurcating periodic solutions are orbitally stable (unstable),
• If ${\tau }_2>0(<0)$, the periods of bifurcating periodic solutions increase (decrease).

Remark 1.

In [10], the authors discussed continuous and discrete systems by using a linear function to describe the response to the advertising effect. In the present article, we mainly focus on the stability of the equilibria and the existence of Hopf bifurcation of diffusion model by using Holling type II to describe the response, which generalizes and advances the outcome of the response description. In addition to analysis of the time delay model. The research method and theoretical findings are different from those in [10]. From this viewpoint, the present paper developed the proceeded work of article [10].

4.3. Numerical Simulations

In order to support our theoretical analysis, we shall carry out the numerical simulations. Model (14) involves six parameters, including the delay $\tau$ which can be chosen $\gamma =0.9,a=5,b=5,d=1,k=0.1$ and vary $\beta \in [0,1).$ Regarding to the semi-trivial equilibrium point $E_1(1,1,0)$, the characteristic Equation (18) can be written as

$$(\lambda -1)({\lambda }^2-0.1\lambda +0.9(1-\beta ))=0,$$

therefore the condition $\left(L_1\right)$ does not satisfied where $d_1=-1<0.$ Based on the first item of Theorem 5, $E_1(1,1,0)$ is unstable for all $\tau \ge 0$.

On the other hand, for the nontrivial equilibrium, we have $E_2(0.901768,1,0.1)$ and by simple calculations the coefficients of (18) we get

$$d_1=-1,c_1=0.0964637,c_0=0.9(1-\beta ),l_1=0.0980392,l_0=0.0980392(1-\beta ).$$

From Equation (25) we have

$$\begin{array}{ccc}\hfill A_1& =& 1.8\beta -1.80031,\hfill \\ \hfill A_0& =& 0.800388{(1-\beta )}^2>0,\hfill \end{array}$$

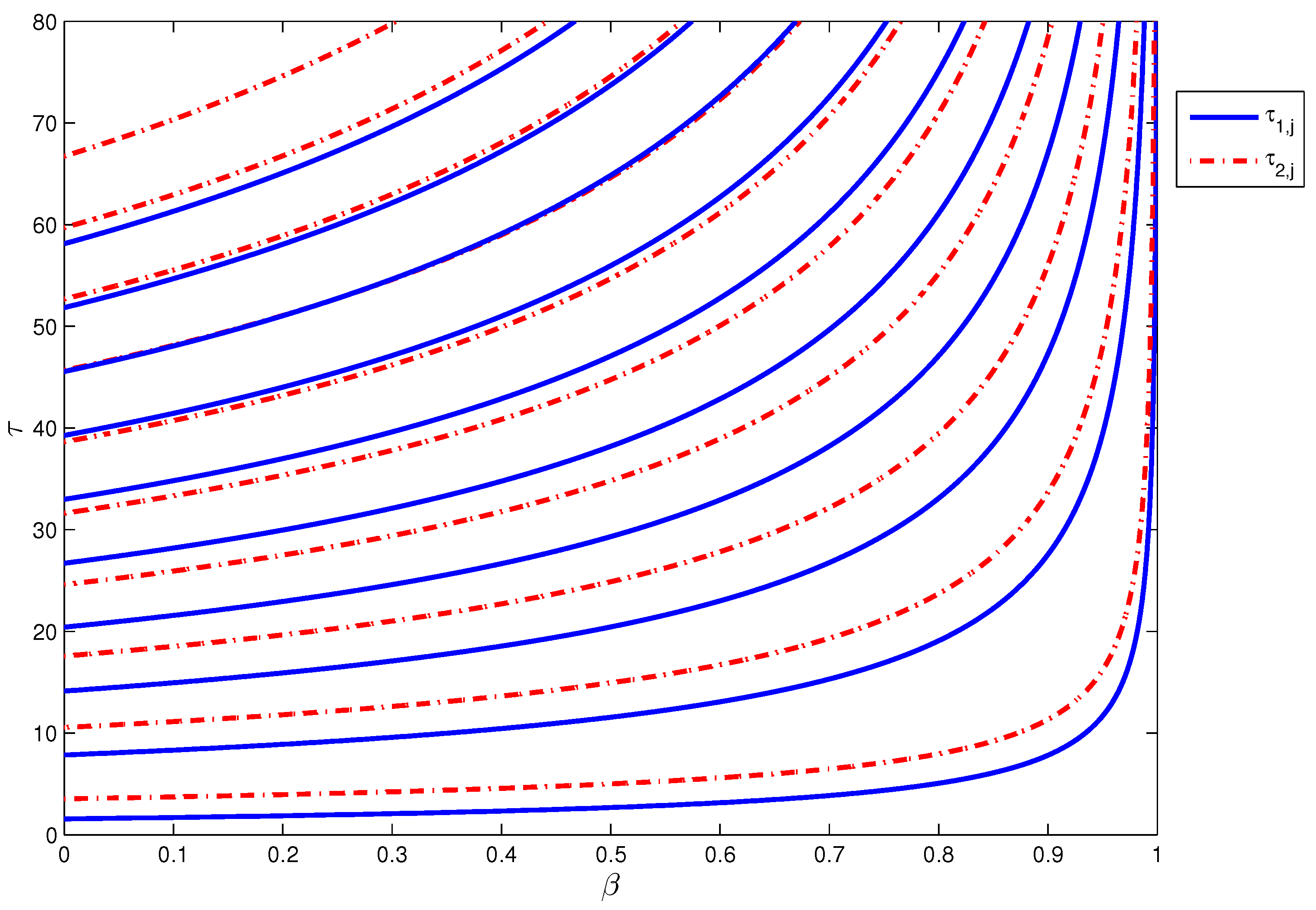
so according to Lemma 3, Equation (26) has two positive roots for $\beta \in [0,1)$. We simulate the critical time delays ${\tau }_{1,j}$ (blue curves) and ${\tau }_{2,j}$ (red dash curves) for system (14) with $\beta$ by using Equations (25) and (27) in Figure 9, $j=0,1, \dots ,10$. As seen in this figure, there are finite stability domains for $E_2.$ Furthermore, by fixing $\beta =0.1$, we have two positive roots

$${\omega }_1=0.94857, P^{\prime }\left({\omega }^2\right)>0,$$

$${\omega }_2=0.848836,P^{\prime }\left({\omega }^2\right)<0,$$

then from (27) we have

$$\begin{array}{ccc}\hfill {\tau }_{1,j}& =& 1.69365+6.62385j,\hfill \\ \hfill {\tau }_{2,j}& =& 3.71879+7.40212j,\hfill \end{array}$$

for $j=0,1,2, \dots$ Consequently,

$$\begin{array}{ccc}\hfill {\tau }_{1,0}& =& 1.69365<{\tau }_{2,0}=3.71879<{\tau }_{1,1}=8.3175<{\tau }_{2,1}=11.1209<{\tau }_{1,2}=14.9414<\hfill \\ \hfill {\tau }_{2,2}& =& 18.5230<{\tau }_{1,3}=21.5652<{\tau }_{2,3}=25.925<{\tau }_{1,4}=28.1891<{\tau }_{2,4}=33.3273<\hfill \\ \hfill {\tau }_{1,5}& =& 34.8129<{\tau }_{2,5}=40.7293<\hfill \\ \hfill {\tau }_{1,6}& =& 41.4368<\left({\tau }_{2,6}=48.1315\nless \right.\hfill \\ \hfill {\tau }_{1,7}& =& \left.48.06061\right)<\hfill \\ \hfill {\tau }_{2,7}& =& 55.5336.\hfill \end{array}$$

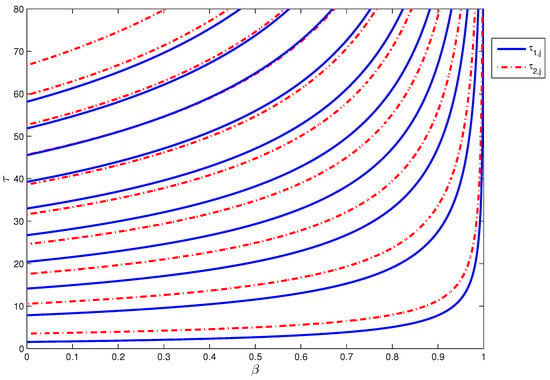
Figure 9. The critical time delays ${\tau }_{1,j}$ (blue curves) and ${\tau }_{2,j}$ (red dash curves) for system (14) against $\beta$.

So, the equilibrium $E_2$ is stable for

$$[0,{\tau }_{1,0})\cup ({\tau }_{2,0},{\tau }_{1,1})\cup ({\tau }_{2,1},{\tau }_{1,2})\cup \cdots \cup \left({\tau }_{2,5},{\tau }_{1,6}\right),$$

and otherwise it is unstable. Moreover, the Hopf bifurcation occurs when $\tau ={\tau }_{1,j}$ and $\tau ={\tau }_{2,j+1}$ for $j=0,1, \dots ,5.$ As discussed in Section 4.2, for ${\tau }_{1,j}(j=0,1, \dots ,5),$ we find that $Re\left(C_1\left(0\right)\right)<0$ and $\frac{d\left(Re\lambda \left({\tau }_{1,j}\right)\right)}{d\tau }>0$. Thus, we get ${\mu }_2>0$ and ${\beta }_2<0$, hence, the system undergoes supercritical Hopf bifurcation at the equilibrium $E_2$ and the bifurcating periodic solution is stable. As seen in Figure 10, delayed model (14) approaches stable fixed points for $\tau \in [0,{\tau }_{1,0})\cup \left({\tau }_{2,j},{\tau }_{1,j+1}\right)$ for $j=0,1, \dots ,5,$ for example $\tau =0.9,5,13,20,27,34.2$ and $40.9.$ Moreover, the delayed model (14) has periodic solution when $\tau \in \left({\tau }_{1,j},{\tau }_{2,j}\right)\cup ({\tau }_{1,6},\infty )$ for $j=0,1, \dots ,5$ as shown in Figure 11.

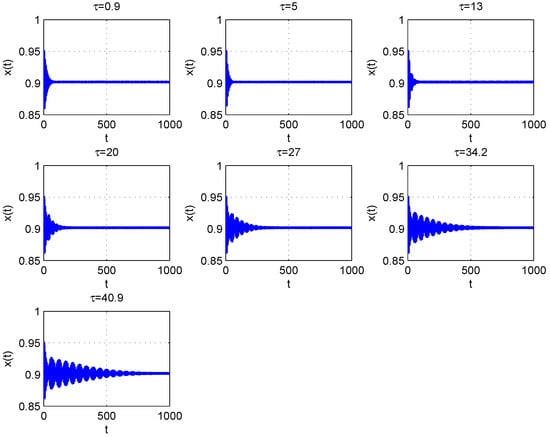
Figure 10. The stable solution of system (14) with different values of $\tau$.

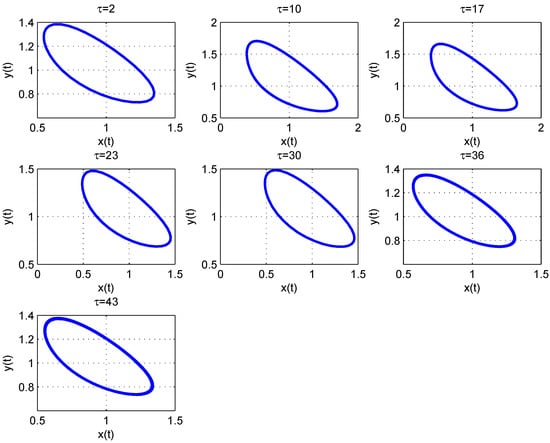
Figure 11. Periodic solutions of system (14) with different values of $\tau$.

5. Discussion

As compared to the marketing strategies, advertising has striking advantages, for instance, the cost of it is significantly lower and its propagation is much faster especially on social media. It is supposed that the product information disseminates thanks to twice ways: word-of-mouth among people’s direct contacts and advertising. We investigated the effect of advertising diffusion to convert potential buyers into actual customers in order reveal the frequent fluctuations in sales and advertising over time. For the sake of completion the study, we must not lose sight of the period of influence of advertisements on individuals. It is expected that it will be encountered by a time delay in the duration of the effect. Therefore, model has been divided into continuous and delayed versions to analyze the dynamic behavior extensively.

In order to analyze the dynamics of system it is noted that system (3) has two kinds of equilibria, semi-trivial and nontrivial equilibria which exist for all values of parameters. The local stability behavior was carried out of the system around each equilibria for both delayed (15) and non-delayed (3) systems. According to the concepts of theory of Hopf bifurcation, the continuous system undergoes supercritical Hopf bifurcation under specific conditions, and the formula for critical value of the bifurcation parameter was derived. However, this result illustrates that advertising has a periodic effect on the consumers. Therefore, businesses deem the investment tradeoff between advertising and product services, rationally optimizes resource allocation from service level, product quality, creative advertising, packaging design, etc., to ameliorate its market share and maximize their enterprize profits.