Abstract
In the present paper, we examine the quantum entanglement for more general states of two-qubit system in the context of spin coherent states (SCSs). We consider the concurrence as a quantifier of entanglement and express it in terms of SCSs. We determine new set of maximally entangled conditions that provide the maximal amount of entanglement for certain values of the amplitudes of SCSs for the case of pure states. Finally, we examine the entanglement of a class of mixed states of the two qubits and provide the range in which the entanglement value is maximal with respect to the values of the amplitudes of SCSs.
PACS:
03.67.-a; 03.65.Yz; 03.65.Ud
1. Introduction
Recently, the physical features of the entanglement of quantum states has been recognized as a key resource in different domains of the quantum information processing and transmission (QIPT). This phenomenon introduces various applications, such as cryptography, quantum computation, quantum communication, quantum teleportation, etc. [1,2,3,4]. The task of determining the degree of entanglement of the quantum states is significant for QIPT, and, therefore, numerous entanglement measures have been developed, such as entanglement of formation [5,6], distillation [7], relative entropy [8], and negativity [9,10,11,12]. Several aspects of entanglement have not been explored yet, even if this phenomenon is well characterized and quantified for a quantum system in a low-dimensional Hilbert space, namely, a system of two qubits for which Wootters identified the entanglement of formation [6].
For bipartite systems, the entanglement of pure states is unambiguous. On the contrary, the entanglement of a mixed state has not been defined well yet because entanglement is not represented by a linear operator in Hilbert space. In this case, quantifying entanglement is more complicated when its measures are hard to estimate analytically. The measures of the entanglement of a mixed state are the average of entanglement of a set of pure states that represent the mixed state, minimized over all decompositions of the mixed state. Researchers are preoccupied with finding this minimization. In some instances, several minimizations may undergo analysis. However, this problem is not solved mathematically and poses several open questions. Special status of mixed states has to be conferred to those that, for a given value of the entropy [11], contain the highest entanglement [13,14]. These quantum states can be viewed as generalizations of mixed states of the Bell states; the latter have the maximum entanglement of the pure states of two qubits. Ishizaka and Hiroshima developed the term maximally-entangled mixed states [15] in a strongly linked setting, namely that of mixed states with two qubits whose quantum entanglement can be maximized at fixed eigenvalues rather than at fixed entropy as indicated by the density operator. The quantum entanglement of the mixed states introduced by Ishizaka and Hiroshima is hard to increase by any unitary transformations. Concerning those states, the maximality property is obtained under a global unitary operation by considering relative entropy, entanglement of formation, and negativity [16].
Another significant concept that has received a lot of interest in the theory of quantum information is the concept of coherent states. These states have been regarded as a mathematical tool for describing quantum systems in many branches of physics [15,16,17,18,19]. The large number of their applications has led to exploring new quantum features of particular quantum systems for which coherent states are involved. The coherent states were firstly introduced by Schrödinger in 1926 in the framework of the harmonic oscillators and have been largely examined in physics [20]. In 1965, these states played a substantial role in the development of quantum optics by the work of Roy J. Glauber [21], who introduced an eigenket of the annihilation operator with the property of minimizing the uncertainty in the conjugate variables. In 1972, Perelomov developed the SCSs that are constructed from the SU(2) group [22,23]. These states prescribes a large set of quantum systems with many applications in condensed matter physics, statistical mechanics, and quantum optics [24,25,26].
The present paper aims at quantifying the entanglement of more general non-orthogonal states with two qubits within the SCSs that are important in several tasks of transmitting and processing of quantum information. For measuring entanglement, we derive the concurrence and give the requirements of the maximal and minimal entanglement for mixed and pure states. We determine the families of maximally entangled mixed states that possess the ultimate entanglement for certain values of the amplitudes of SCSs [27,28,29,30]. Those states can benefit the processing of quantum information with noise because they possess the highest entanglement made possible by a proper choice of the amplitudes of SCSs.
The paper is organized as follows. In Section 1, we display the entanglement measure of an arbitrary state of two qubits. In Section 2, we write the entanglement measure in terms of the amplitudes of SCSs and explore its performance for the cases of more general non-orthogonal states. Section 3 covers the conclusion.
2. Entanglement of an Arbitrary State of a System of Two Qubits
Generally, the normalized pure state of a system of two qubits is defined on the computational basis and takes the form of
with the condition of normalization
The pure state (1) is an entangled state if it does not take the form of a product of states of each qubit.
The concurrence of the state is defined as [31]
where “” is the “spin-flip” operation, . Here, represents the complex conjugate of and defines the second Pauli matrix. The concurrence is 0 for separable states and equals 1 for states with maximal entanglement.
For the case of mixed states, the system of two qubits is described by a density matrix, , that can be represented as a statistical mixture of a set of pure states as
in which represents the states of the two qubits with the probabilities . The mixed state is said to be entangled if it cannot be represented as a set of separable pure states, i.e., where represents the reduced matrices of each qubit.
The concurrence of the mixed state of the two-qubit system was introduced by Wootters and Hill as [8]
where represent the square roots in descending order of the eigenvalues of the operator in decreasing order. As in the case of pure states, the state is a separable state when and it is a maximally entangled state when .
Generally, for a two-qubit mixed state having only two eigenvalues, there is a simplified expression of Wootters concurrence [7]
where the pure states corresponding to eigenvalues and are given by
The concurrence of the state is
where
represents the concurrence of the state and
represents the concurrence of the pure state . and represent the complex concurrences.
3. More General Non-Orthogonal States of Two Qubits in the Context of SCSs
In the present section, we display the states of the two qubits within the coherent states and explore their entanglement degree.
Let us introduce a more general pure state of the two qubits as
where is the normalization factor for which and with being the SCS for a particle with spin-1/2 [32,33,34,35]. Substituting , into Equation (11), the pure state can be expressed as functions of the amplitudes of SCSs as
in which
with
Using Equation (3), the concurrence of a two-qubit state in the representation of the coherent states is given by
Then, the pure state (11) is disentangled (i.e., ) if and only if one of the following is true: , , or . When , the concurrence attains its maximal, which corresponds to a pure state with maximum entanglement.
To simplify the issue, we consider the state (11) with the conditions and and assume and . The concurrence is simplified to
where
The concurrence reaches its maximal value when that corresponds to a maximally entangled state.
In Figure 1 and Figure 2, we show the variation of the concurrence as a function of with fixed values of . The blue dotted line is for , the red dotted-dashed line is for , the black dashed line is for , and the green line is for . In the figures, we can observe that the behavior and amount of the concurrence is very sensitive to the values of the parameters and . Interestingly, high values of with accompanied by small values of for which the entanglement is maximal (). Moreover, the amount of the entanglement depends on the values of the parameters a and b.
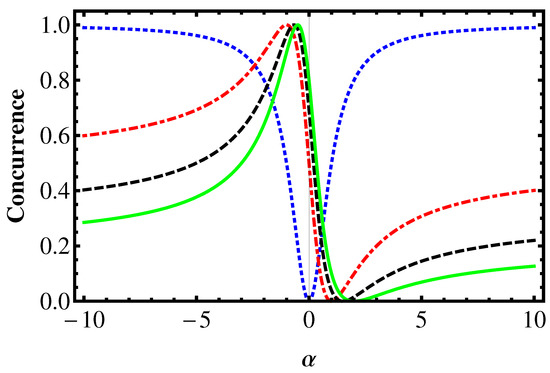
Figure 1.
The variation of the concurrence of the state in terms of with various values of for . The maximum is attained for .
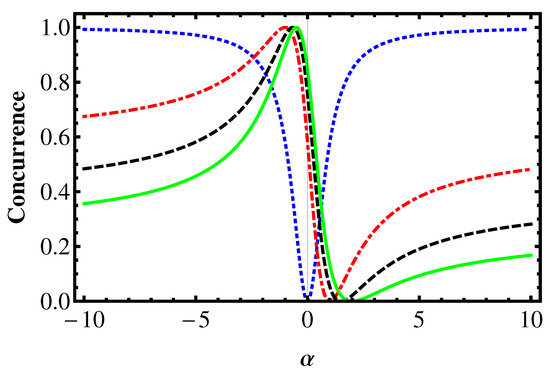
Figure 2.
The variation of the concurrence of the state in terms of with various values of for and . The maximum is attained for .
Now, we investigate the degree of entanglement for a mixed state defined as a statistical mixture of more general pure states by exploiting the advantages of the simplified expression of Wootters concurrence. We consider the following two-qubit mixed state
where
with
where the coefficients , and can be obtained from Equation (14). Based on the concurrence formula given by Equation (8), the entanglement of the mixed state can be quantized in terms of amplitudes of SCSs as
where
and
The concurrence expression depends on and . In the limits or , this expression of the concurrence reduces to the definition given by Equation (3).
We assume the case in which one of the pure states of two qubits is an unentangled state (i.e., or ). In this way, the concurrence of the mixed state is given in terms of amplitudes of SCSs and probability as
Equation (23) illustrates that the state and its probability have information about the mixed state’s entanglement. For simplicity, we take into account the case and . The concurrence is reduced to
where can be obtained from Equation (17). We focus on the study of the concurrence in terms of the parameters , and .
We distinguish two significant limit cases:
- (1)
- , which displays a mixed state with zero entanglement ().
- (2)
- , which corresponds to a mixed state defined as a statistical mixture of a maximally entangled state and a separable state with concurrence
In Figure 3 and Figure 4, we display the variation of the concurrence of the mixed state in terms of the amplitudes of SCSs for and , respectively. In the figures, it is clear that the control of the amount of the entanglement of the mixed state can be achieved by an appropriate choice the main physical parameters.
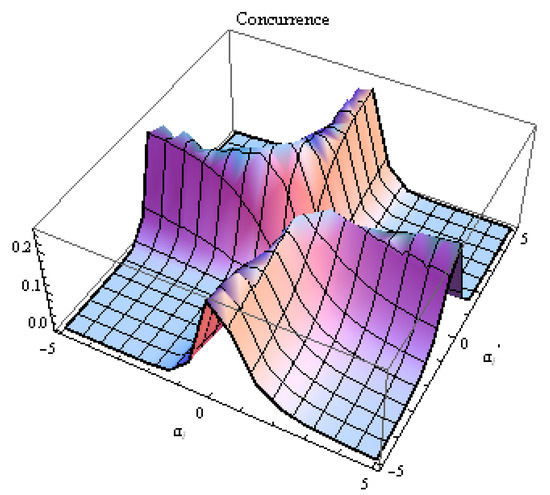
Figure 3.
The variation of the concurrence of the state in terms of and for and .
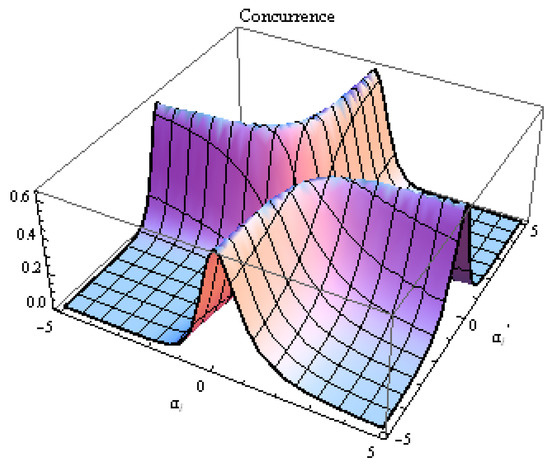
Figure 4.
The variation of the concurrence of the state in terms of and for and .
These kinds of two-qubit mixed states are a significant set of quantum states [36,37,38] that are extensively utilized in QIPT and more recently in the study of quantum discord phenomenon [39].
4. Conclusions
In the present research paper, we express the concurrence of more general two-qubit non-orthogonal states in terms of the amplitudes of SCSs. Then, we examine them and consider the concurrence that helps define the conditions for maximum and minimum entanglement. The findings show that the SCSs benefit quantifying and measuring the degree of entanglement. These states are easy and convenient to use and generate experimentally [40]. Finally, we analyze the concurrence performance as a role of new parameters for a class of mixed states with two qubits characterized by a statistical mixture of separable and Bell states, using a simplified manifestation of concurrence in Wootters’ measure of entanglement. We provide the range in which the entanglement value is maximal with respect to the amplitudes of SCSs. We define families of maximally entangled mixed states, namely frontier states that have the highest entanglement for given values of the amplitudes of SCSs. These states can help process quantum information when having noise because they have the highest entanglement by a proper choice of the values of the amplitudes.
Author Contributions
Writing—original draft preparation, S.A.-K. and K.B.; and writing—review and editing, E.M.K., F.A. All authors have read and agreed to the published version of the manuscript.
Funding
Taif University Researchers Supporting Project number (TURSP-2020/154), Taif University, Taif, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschafen 1935, 23, 807. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Fort. Phys. 2000, 48, 9. [Google Scholar]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Hill, S.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S.; Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046. [Google Scholar] [CrossRef]
- Peres, A. Separability Criterion for Density Matrices. Phys. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef]
- Ali, M.; Rau, A.R.P.; Alber, G. Quantum discord for two-qubit X states. Phys. Rev. A 2010, 81, 042105. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1. [Google Scholar] [CrossRef]
- Berrada, K.; Eleuch, H. Noncommutative deformed cat states under decoherence. Phys. Rev. D 2019, 100, 016020. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S. Entanglement of atom–field interaction for nonlinear optical fields. Phys. E Low-Dimens. Syst. Nanostruct. 2011, 44, 628–634. [Google Scholar] [CrossRef]
- Ishizaka, S.; Hiroshim, T. Maximally entangled mixed states under nonlocal unitary operations in two qubits. Phys. Rev. A 2000, 62, 022310. [Google Scholar] [CrossRef]
- Verstraete, F.; Audenaert, K.; De Moor, B. Maximally entangled mixed states of two qubits. Phys. Rev. A 2001, 64, 012316. [Google Scholar] [CrossRef]
- Eleuch, H.; Bennaceur, R. Nonlinear dissipation and the quantum noise of light in semiconductor microcavities. J. Opt. B Quantum Semiclass. Opt. 2004, 6, 189. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Ooi, C.H.R. Beam splitter entangler for nonlinear bosonic fields. Laser Phys. 2014, 22, 1449–1454. [Google Scholar] [CrossRef]
- Abbott, A.A.; Alzieu, P.-L.; Hall, M.J.W.; Branciard, C. Tight State-Independent Uncertainty Relations for Qubits. Mathematics 2016, 4, 8. [Google Scholar] [CrossRef]
- Schrödinger, E. Der stetige Übergang von der Mikro- zur Makromechanik. Naturwissenschafter 1926, 14, 664. [Google Scholar]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222. [Google Scholar] [CrossRef]
- Perelomov, A.M. Generalized Coherent States and Their Applications; Springer: New York, NY, USA, 1986. [Google Scholar]
- Klauder, J.R.; Skagertam, B. Coherent States: Application in Physics and Mathematical Physics; World Scientific: Singapore, 1985. [Google Scholar]
- Zhang, W.-M.; Feng, D.H. Coherent states: Theory and some applications. Rev. Mod. Phys. 1990, 62, 867. [Google Scholar] [CrossRef]
- Inomata, A.; Kuratsuji, H.; Gerry, C. Path Integrals and Coherent States of SU(2) and SU(1; 1); World Scientific: Singapore, 1992. [Google Scholar]
- Loh, Y.L.; Kim, M. Visualizing spin states using the spin coherent state representation. Am. J. Phys. 2014, 83, 30–35. [Google Scholar] [CrossRef]
- Valencia, N.H.; Goel, S.; McCutcheon, W.; Defienne, H.; Malik, M. Unscrambling entanglement through a complex medium. Nat. Phys. 2020, 16, 1112–1116. [Google Scholar] [CrossRef]
- Berrada, K.; Chafik, A.; Eleuch, H.; Hassouni, Y. Concurrence in the framework of coherent states. Quantum Inf. Process. 2010, 9, 13–26. [Google Scholar] [CrossRef]
- Berrada, K.; El Baz, M.; Eleuch, H.; Hassouni, Y. A comparative study of negativity and concurrence based on spin coherent states. Inter. J. Mod. Phys. C 2010, 21, 291. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation and concurrence. Quantum Inf. Comput. 2001, 1, 27. [Google Scholar]
- Ma, J.; Wang, X.; Sun, C.P.; Nori, F. Quantum spin squeezing. Phys. Rep. 2011, 509, 89. [Google Scholar] [CrossRef]
- Bergeron, M. Coherent State Path Integral for the Harmonic Oscillator and a Spin Particle in a Constant Magnetic Field; University of British Columbia: Vancouver, BC, Canada, 1989. [Google Scholar]
- Gerry, C.C.; Benmoussa, A.; Hach, E.E.; Albert, J. Maximal violations of a Bell inequality by entangled spin-coherent states. Phys. Rev. A 2009, 79, 022111. [Google Scholar] [CrossRef]
- Gerry, C.C.; Benmoussa, A. Spin squeezing via ladder operations on an atomic coherent state. Phys. Rev. A 2008, 77, 062341. [Google Scholar] [CrossRef]
- Eisert, J.; Plenio, M. A comparison of entanglement measure. J. Mod. Opt. 1999, 46, 145–154. [Google Scholar] [CrossRef]
- Miranowicz, A.; Ishizaka, S.; Horst, B.; Grudka, A. Comparison of the relative entropy of entanglement and negativity. Phys. Rev. A 2008, 78, 052308. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Quantum Information: An Introduction to Basic Theoretical Concept and Experiments; Springer: Berlin/Heidelberg, Germany, 2001; p. 151. [Google Scholar]
- Liang, J.; Zhang, C. Study on Non-Commutativity Measure of Quantum Discord. Mathematics 2019, 7, 543. [Google Scholar] [CrossRef]
- Ali, S.T.; Antoine, J.-P.; Gazeau, J.-P. Coherent States, Wavelets and Their Generalization; Springer: New York, NY, USA, 2000. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).