Abstract
This work is about the use of some classical spectral collocation methods as well as with the new software system Chebfun in order to compute the eigenpairs of some high order Sturm–Liouville eigenproblems. The analysis is divided into two distinct directions. For problems with clamped boundary conditions, we use the preconditioning of the spectral collocation differentiation matrices and for hinged end boundary conditions the equation is transformed into a second order system and then the conventional ChC is applied. A challenging set of “hard” benchmark problems, for which usual numerical methods (FD, FE, shooting, etc.) encounter difficulties or even fail, are analyzed in order to evaluate the qualities and drawbacks of spectral methods. In order to separate “good” and “bad” (spurious) eigenvalues, we estimate the drift of the set of eigenvalues of interest with respect to the order of approximation N. This drift gives us a very precise indication of the accuracy with which the eigenvalues are computed, i.e., an automatic estimation and error control of the eigenvalue error. Two MATLAB codes models for spectral collocation (ChC and SiC) and another for Chebfun are provided. They outperform the old codes used so far and can be easily modified to solve other problems.
Keywords:
Sturm–Liouville; clamped; hinged boundary condition; spectral collocation; Chebfun; chebop; eigenpairs; preconditioning; drift; error control MSC:
34B09; 34B40; 34L16; 65L15; 65L20; 65L60; 65L70
1. Introduction
Due to the spectacular evolution of advanced programming environments, a special curiosity arose in the numerical analysis of a classical problem, that of accurate solving of high order SL eigenproblems. It seems that quantum mechanics is the richest source of self-adjoint problems, while non-self-adjoint problems arise in hydrodynamic and magnetohydrodynamic stability theory (see for instance [1] and the vast literature quoted there). The need to compute accurately and efficiently a large set of eigenvalues and eigenfunctions, including those of high index, is now an utmost task.
Our main interest here is to evaluate the capabilities of the new Chebfun package as well as those of conventional spectral methods in meeting these requirements. The latter work in the classical mode, i.e., “discretize-then-solve”. On the contrary, the Chebfun spirit consists in the continuous mode, i.e., “solve-then-discretize” (see [2] p. 302).
The effort expended by both classes of methods is also of real interest. It can be assessed in terms of the ease of implementation of the methods as well as in terms of computer resources required to achieve a specified accuracy.
Some FORTRAN software packages have been designed over time to solve various regular and singular SL problems. These seem to be the first attempts to solve numerically (automatically) eigenvalue problems.The most important would be SLEDGE [3,4], the NAG’s code SL02F [5,6], SLEIGN and SLEIGN2 [7,8], and later MATSLISE. The SLDRIVER interactive package supports exploration of a set of SL problems with the first four previously mentioned packages. The SLEDGE, SL02F, SLEIGN2, and NAG’s D02KDF are “automatic” for eigenvalues and not for eigenfunctions. They have built in error estimation and from that they achieve error control. They adjust the accuracy of the discretization so that the delivered eigenvalue has estimated error below a user-supplied tolerance.
Essentially, the numerical method used in these software packages replaces the coefficients in the equation by a step function approximation. Their most important drawback remains the impossibility to compute the eigenfunctions and a slow convergence in case of some singular eigenproblems.
The MATSLISE code introduced in [9] can solve some Schrödinger eigenvalue problems by a constant perturbation method of a higher order. Very recently, this code has been improved (see [10]) but it remains for Schrödinger issues which are outside the scope of this paper.
There is also a class of semi-analytical methods which includes the variational iteration method, the homotopy perturbation method, homotopy analysis method, and Adomian decomposition (see for instance [11]) for solving eigenvalue problems. Their accuracy is far from what spectral collocation methods can provide.
In [12], the authors set up an ambitious method based on the Lie group method along with the Magnus expansion in order to solve any order of SL problem with arbitrary boundary conditions.
We believe that spectral collocation methods can contribute to the systematic clarification of some still open issues related to the numeric aspects of SL problems. The most important aspect is how many computed eigenpairs (eigenvalues and eigenfunctions) can we trust when solving a high order SL? This is the outstanding, not completely resolved research issue, we want to address in this paper.
Thus, we will argue that generally Chebfun would provide a greater flexibility in solving various differential problems than the classical spectral methods. This fact is fully true for regular problems. A Chebfun code contains a few lines in which the differential operator is defined along with the boundary conditions and then a subroutine to solve the algebraic eigenproblem. It provides useful information on the optimal order of approximation of eigenvectors and the degree to which the boundary conditions have been satisfied.
Unfortunately, in the presence of various singularities or for problems of higher order than 4, the maximum order of approximation of the unknowns can be reached () and then Chebfun issues a message that warns about the possible inaccuracy of the results provided.
Alternative use of conventional spectral collocation methods generally helps to overcome this difficulty.
As a matter of fact, in order to resolve a singularity on one end of the integration interval, Chebfun uses only the truncation of the domain. Classical spectral methods can also use this method, but it is not recommended because much more sophisticated methods are at hand in this case. For singular points at finite distances (mainly origin) we will use the so-called removing technique of independent boundary conditions (see for a review of this technique our monograph [13] p. 91). The boundary conditions at infinity can be enforced using basis functions that asymptotically satisfy these conditions (Laguerre, Hermite, sinc).
A Chebfun code and two MATLAB codes, one for ChC and another for the SiC method, are provided in order to exemplify. With minor modifications they could be fairly useful for various numerical experiments. These codes are very easy to implement, efficient, and reliable. All our numerical experiments have been carried out using MATLAB R2020a on an Intel (R) Xeon (R) CPU E5-1650 0 @ 3.20 GHz.
The main purpose of this paper was to argue that Chebfun, along with the spectral collocation methods, can be a very feasible alternative to the above software packages regarding accuracy, robustness as well as simplicity of implementation. In addition, these methods can calculate exactly the “ whole” set of eigenvectors approximating eigenfunctions and provide automatic estimation and control of the eigenvalue error. For self-adjoint problems, checking the orthonormality of computed eigenvectors gives us valuable information on the accuracy of the calculation of these vectors.
The structure of this work is as follows. In Section 2, we recall some specific issues for the regular as well as singular Sturm–Liouville eigenproblems. In Section 3, we review briefly the conventional ChC method as well as Chebfun, the relative drift of a set of eigenvalues and the preconditioning of Chebyshev differentiation matrices. Section 4 is the core part of our study. By analyzing one set of hinged problems and another one of clamped problems, we want to evaluate the applicability of the two classes of methods as well as their performances in terms of the accuracy of the outcomes they produce. There is also a subsection that contains problems equipped with boundary conditions that are a mixture of these two types, clamped and hinged. We end up with Section 5 devoted to conclusions and open problems.
2. 2nd-Order Sturm–Liouville Eigenproblems
The 2nd-order SL equation reads
along with separated, (self-adjoint) boundary conditions. We shall assume that all coefficient functions are real valued. The technical conditions for the problem to be non singular are: the interval is finite; the coefficient functions , , the weight w and are in ; and the essential infima of and w are both positive. Under these assumptions, the eigenvalues are bounded below (see for instance [14]).
The eigenvalues can be ordered in the usual form: such that In this sequence, each eigenvalue has multiplicity at most n (so for all k). The restriction on the multiplicity arises from the fact that for each there are at most n linearly independent solutions of the differential equation satisfying either of the endpoint conditions which we shall consider below.
Some of the problems we deal with are also found in the monographic paper [15]. It contains over 50 challenging examples from mathematical physics and applied mathematics along with a summary of SL theory, differential operators, Hilbert function spaces, classification of interval endpoints, and boundary condition functions.
3. Chebfun vs. Conventional Spectral Collocation
3.1. Chebfun
For details on Chebfun we refer to [2,16,17,18]. The Chebfun system, in object-oriented MATLAB, contains algorithms which amount to spectral collocation methods on Chebyshev grids of automatically determined resolution. This is the main difference compared to conventional spectral methods in which the resolution (order of approximation) is imposed almost arbitrarily. Its properties are briefly summarized in [17]. In [16] the authors explain that chebops are the fundamental Chebfun tools for solving ordinary, partial differential or integral equations.
The implementation of chebops combines the numerical analysis idea of spectral collocation with the computer science idea of lazy or delayed evaluation of the associated spectral discretization matrices. The grammar of chebops along with a lot of illustrative examples is displayed in the above quoted papers as well as in the text [2]. Thus, one can get a suggestive image of what they can do working with Chebfun.
Moreover, in ([16] p. 12) the authors explain clearly how the Chebfun works, i.e., it solves the eigenproblem for two different orders of approximation, automatically chooses a reference eigenvalue and checks the convergence of the process. At the same time, it warns about the possible failures due to the high non-normality of the analyzed operator (matrix).
Actually, we want to show in this paper that Chebfun along with chebops can do much more, i.e., can accurately solve high order SL problems.
3.2. Spectral Collocation Methods
Spectral methods have been shown to provide exponential convergence for a large variety of problems, generally with smooth solutions, and are often preferred [19]. In all spectral collocation methods designed so far, we have used the collocation differentiation matrices from the seminal paper [20]. We preferred this MATLAB differentiation suite for the accuracy, efficiency as well as for the ingenious way of introducing various boundary conditions.
In order to impose (enforce) the boundary conditions we have used the boundary bordering, which is a simplified variant of the above mentioned removing technique of independent boundary conditions, as well as the basis recombination. We have used the first technique in the large majority of our papers except [21] where the latter technique has been employed. In the last quoted paper a modified ChT method based on basis recombination has been used in order to solve an Orr-Sommerfeld problem with an eigenparameter dependent boundary condition.
Once eigenvectors are calculated in physical space they are transposed into the space of coefficients using FCT. In this way, it is possible to estimate the way in which their coefficients decrease.
3.3. The Drift of Eigenvalues
Two techniques are used in order to eliminate the “bad” eigenvalues as well as to estimate the stability (accuracy) of ChC or Chebfun computations. The first one is the drift, with respect to the order of approximation or the scaling factor, of a set of eigenvalues of interest. The second one is based on the check of the eigenvectors’ orthogonality.
In other words, we want to separate the “good” eigenvalues from the “bad” ones, i.e., inaccurate eigenvalues. An obvious way to achieve this goal is to compare the eigenvalues computed for different orders of some parameters such as the approximation order (cut-off parameter) N or the scaling factor (length of integration interval). Only those whose difference or “resolution-dependent drift” is “small” can be believed. In this connection, in the paper [22], the so called absolute (ordinal) drift with respect to the order of approximation has been introduced. We extend this definition in our recent paper [23] and will use it without repeating it here.
Whenever the exact eigenvalues of a problem are known, the relative drift is reduced to the relative error.
At this point, the following observation is extremely important. In the highly cited monograph [24], the author makes a subtle analysis of spectral methods in solving linear eigenproblems. Among others, he states the so called Boyd’s Eigenvalues Rule-of-Thumb in which he notices that in solving such a problem with a spectral method using terms in the truncated spectral series, the lowest eigenvalues are usually accurate to within a few percent, while the larger numerical eigenvalues differ from those of the differential equation by such large amounts as to be useless.
3.4. Preconditioning
To simplify the introduction of a preconditioner, we use the differential operator
subject to clamped boundary conditions
and
where , and are positive integers such that
It is well known that for general collocation points the first order differentiation matrix has a condition number of order and the second order differentiation matrix has a condition number of order as We comment on the preconditioner introduced in [25]. These authors show that the preconditioning matrix
applied to ChC as well as to Chebfun discretization of differential operator produces matrices of an inferior condition number, namely
4. Numerical Experiments
4.1. Hinged Ends or Simply Supported Boundary Conditions
4.1.1. The Viola’s Eigenproblem-Revisited
Let us consider now the so called Viola’s eigenproblem. It is encountered in porous stability problems (see [1], Chapter 9) and reads
It is singular as in accordance with the definition introduced in Section 2.
By straightforward variational arguments, we have shown in ([13] p. 50) that the lowest eigenvalue is positive. In this text, we have solved the above problem by ChC using the so called strategy which involves the change of variables
The main deficiency of this strategy is the fact that it produces a lot of numerical spurious eigenvalues (at infinity).
In spite of this, we succeeded in stating the conjecture according to which the lowest eigenvalue of the problem (4), approaches 1 as
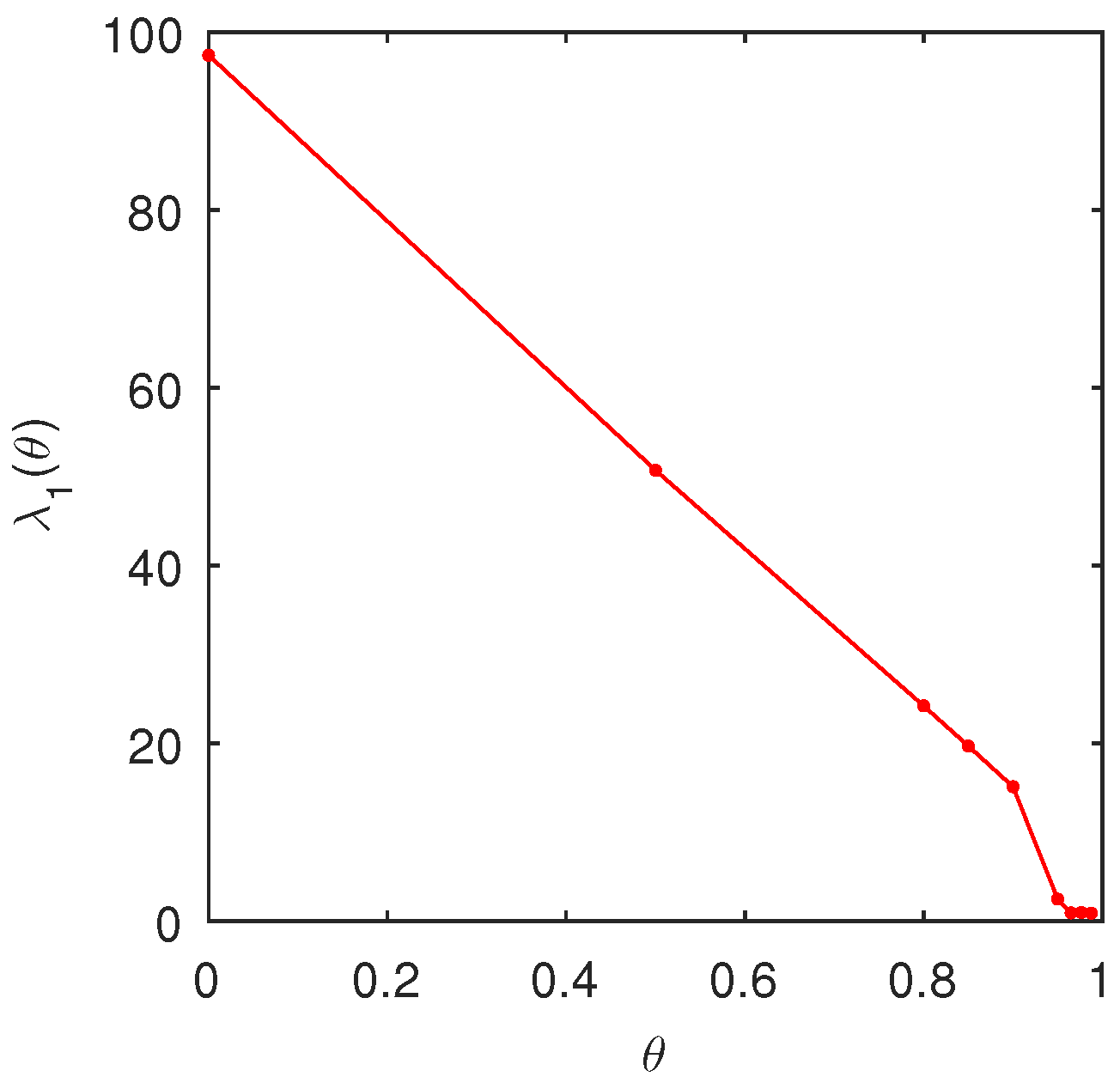
Now, taking advantage of Chebfun we solve directly problem (4). Thus, the dependence of the lowest eigenvalue of the problem (4), computed by Chebfun, on the parameter is depicted in Figure 1. Actually, we have obtained
which only partly confirms the above conjecture.
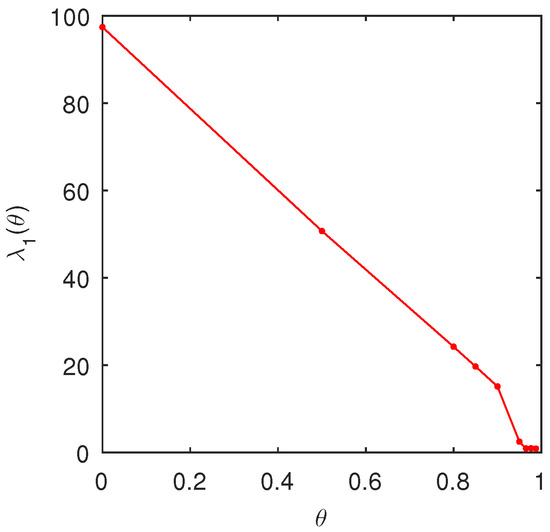
Figure 1.
The dependence of the lowest eigenvalue of the Viola’s eigenproblem (4), computed by Chebfun, on the parameter
As a validation issue for our computations we have obtained the known value
within an approximation of a thousand.
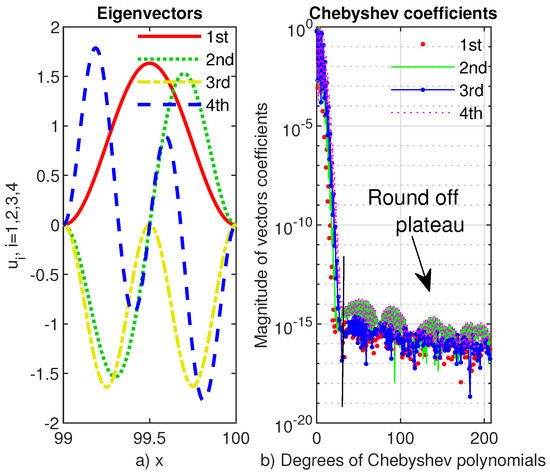
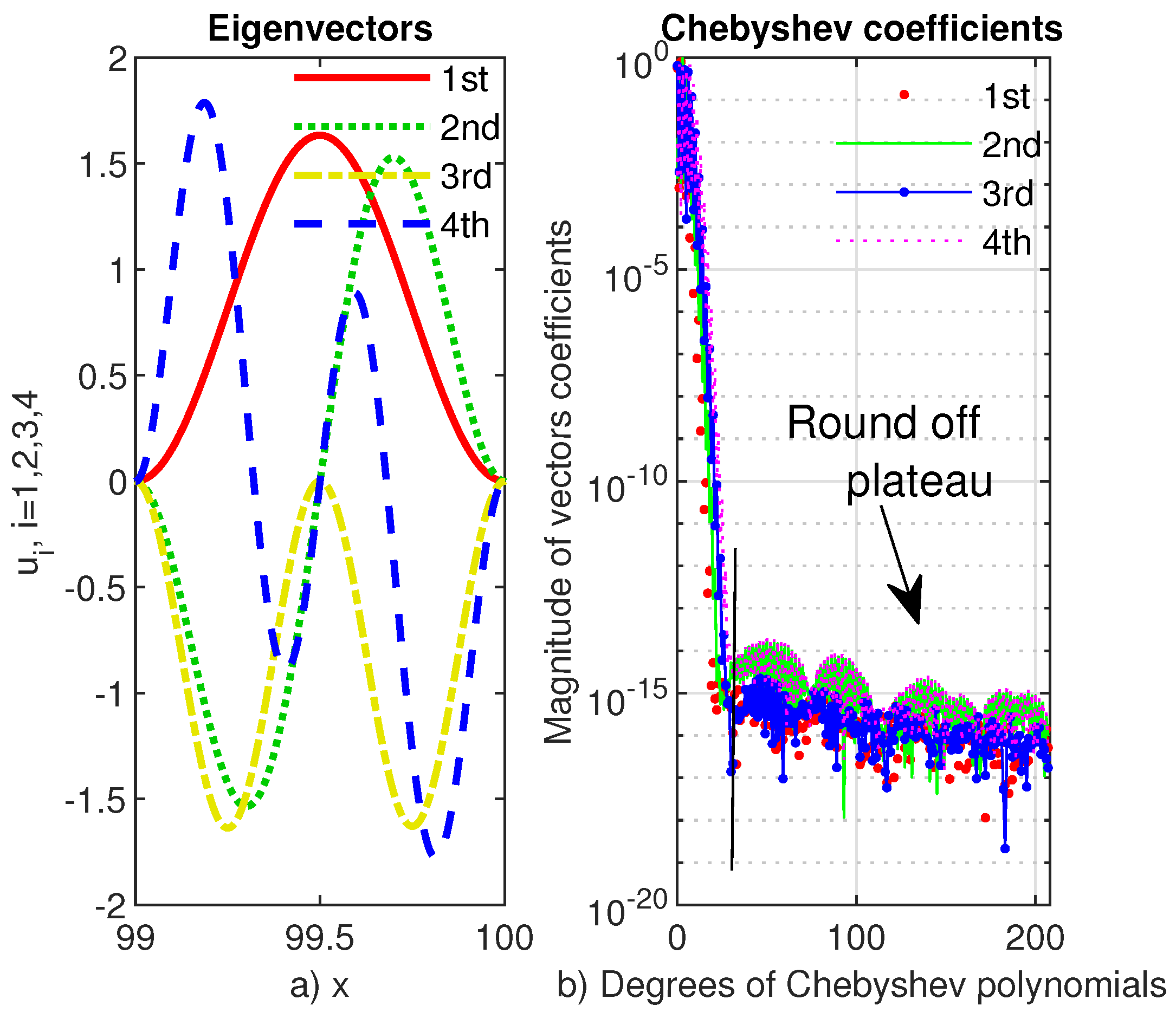
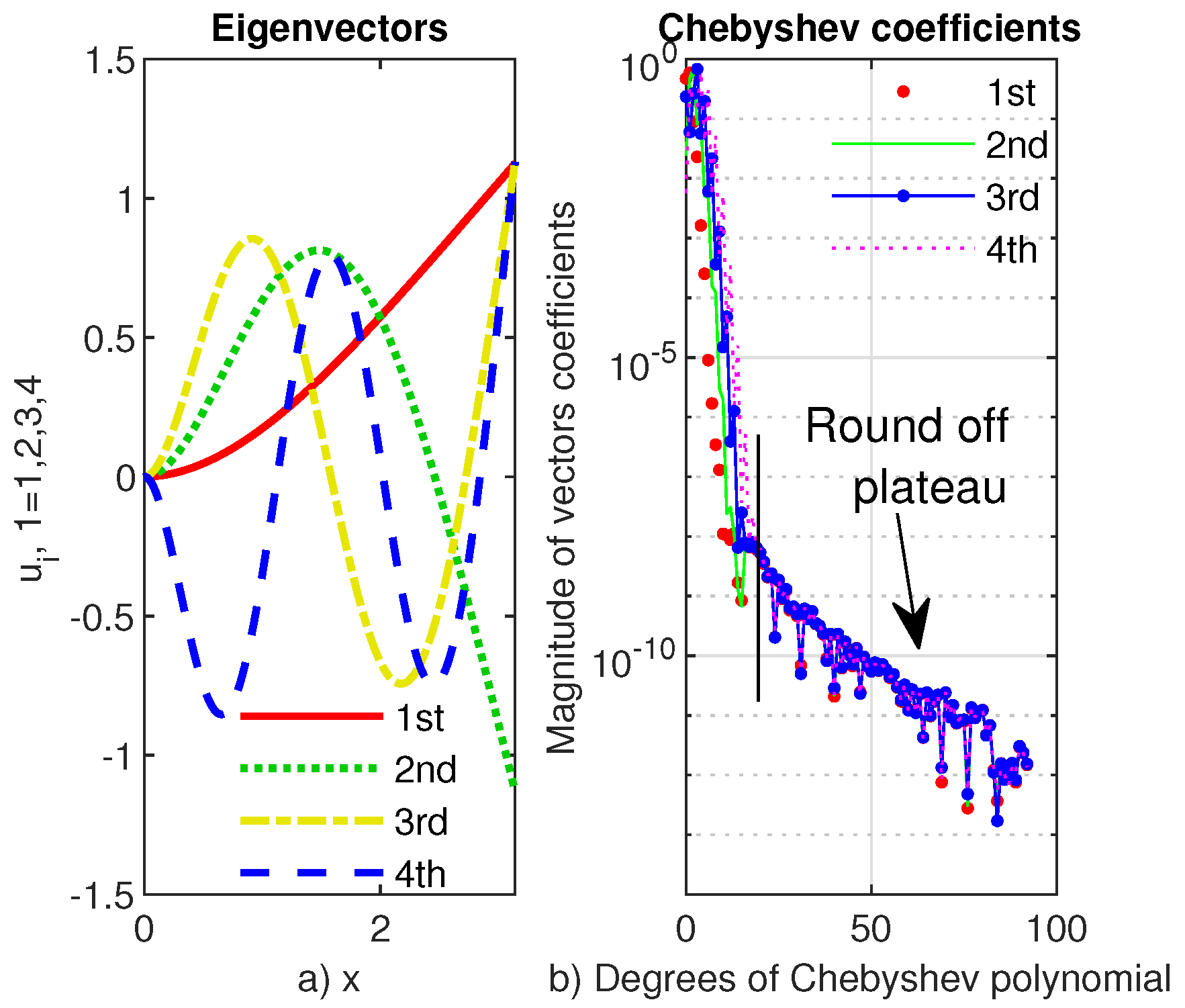
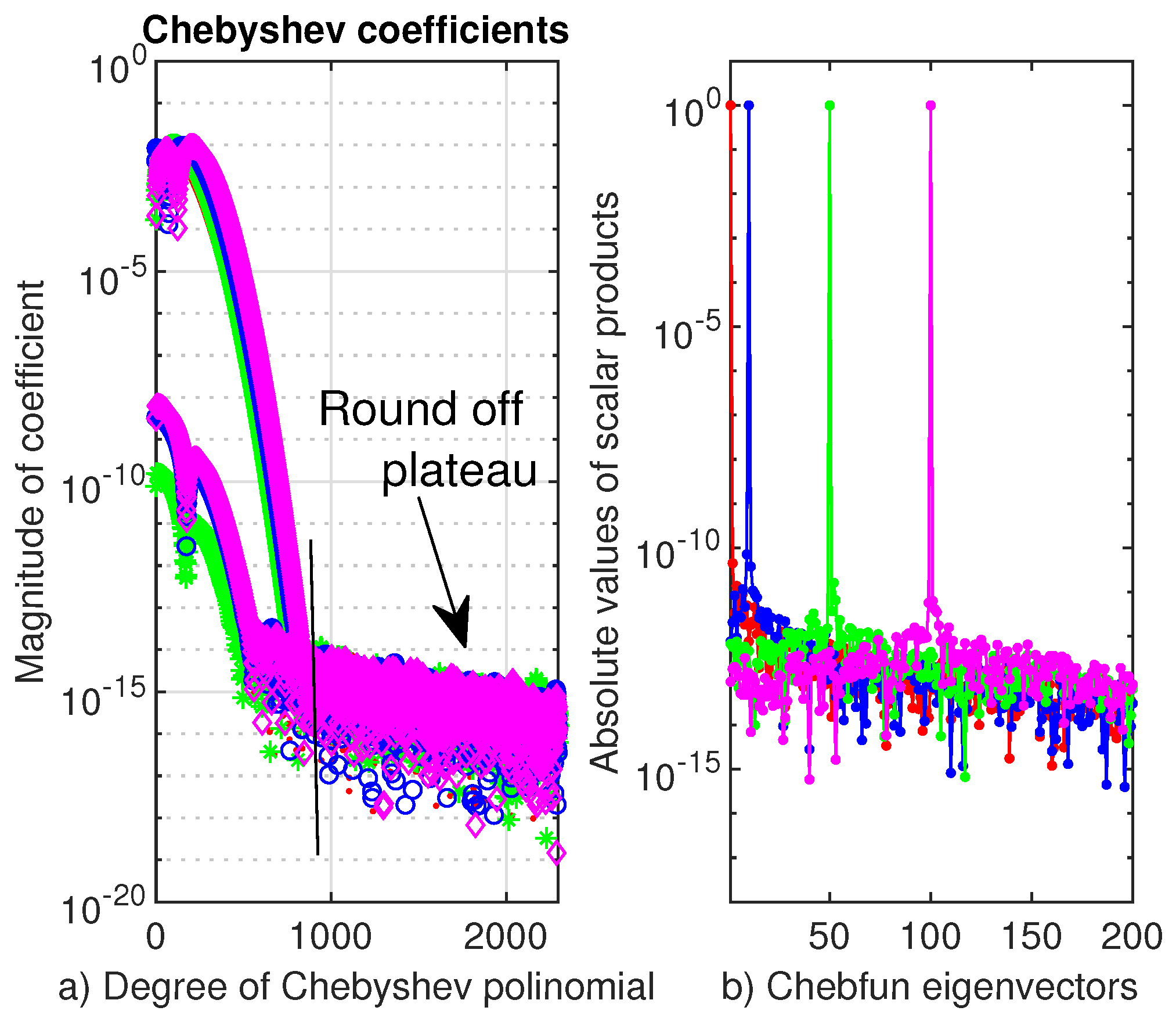
For the highest computable value of parameter , we display in Figure 2 the first four eigenvectors of problem (4) and in Figure 3 the Chebyshev coefficients of these eigenvectors.
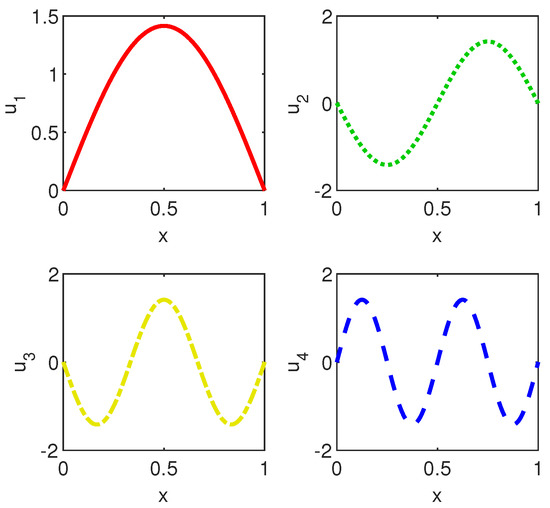
Figure 2.
From upper left to lower right we display the first four eigenvectors of the Viola’s eigenproblem (4) computed by Chebfun with
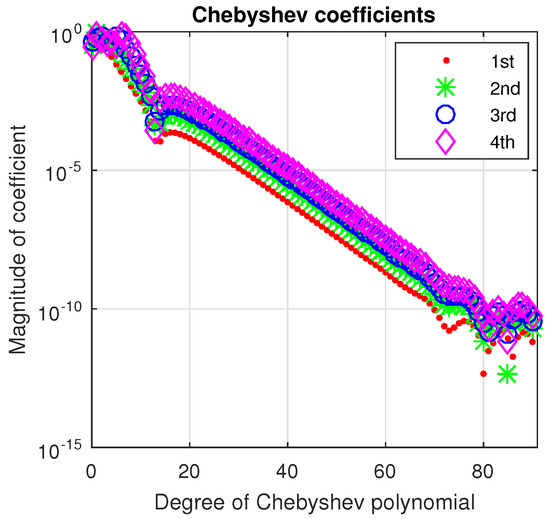
Figure 3.
The Chebyshev coefficients of the first four eigenvectors of the Viola’s eigenproblem (4) computed by Chebfun with A very narrow rounding-off plateau can be seen.
We have to mention that the singularity in the right end becomes more prominent as the tends to 1. This is confirmed by increasing the degree of the Chebfun approximation. For instance, when only a 25 degree Chebyshev polynomial uses it and when the degree of approximation grows to more than 80 (see Figure 3). It is also worth mentioning that only for growing very close to 1 a truncation of the domain along with the use of the option splitting have been necessary when Chebfun has been used.
We have to observe that the problem (4) has been solved by compound matrix method in [26] for The author asserts that other methods have to be used in order to resolve the singularity in this problem. We hope that the above analysis sheds some light in this direction.
4.1.2. The Bénard Stability Problem
A simplified form of the Bénard stability problem supplied with self-adjoint boundary conditions reads (see for instance [14,27])
The constant is regarded as a parameter which typically can take the values
All our attempts to solve this problem using Chebfun have failed, so we have resorted to the old strategy.
Thus, we rewrite problem (5) as a homogeneous Dirichlet one attached to a second order differential system, namely
Now we apply to each line the ChC discretization. It leads to the generalized and singular eigenpencil
where the block matrices are defined by
and
The factor 4 in front of comes from the shift of interval to the canonical Chebyshev interval and the matrix signifies the second order Chebyshev differentiation matrix with the homogeneous Dirichlet boundary conditions enforced. The matrices I and Z stand respectively for the identity and zeros matrices of the same dimension as
The following short MATLAB code has been used to solve (6):
N=256; % order of approximation nu=-(1+4*(pi^2))-sqrt(1+4*(pi^2)); % parameter \nu [x,D]=chebdif(N,2); D2=D(2:N-1,2:N-1,2); % differentiation matrices I=eye(size(D2)); Z=zeros(size(D2)); A=[ 4*D2 -I Z; Z 4*D2 -I; -(nu^2+2*nu+2)*I (nu^2+4*nu+3)*I 4*D2-(2*nu+3)*I]; B=[Z Z Z; Z Z Z; I Z Z]; % block matrices in pencil k = 8; % number of computed eigs E=eigs( @(x)(A\(B*x)), size(A,1),k, ’SM’) % Arnoldi method
When the order of approximation is N, both matrices in (7) have order This tripling of the dimensions of the matrices involved is not a major disadvantage. On the contrary, if we use Henrici’s number as a measure of normality (see for instance our text [13] pp. 22–23), we see from the inequality
that matrix is more normal than .
In our previous paper [28], we have analyzed various methods to solve singular eigenproblems attached to pencils of the form (7). For the problem at hand we have used the Arnoldi method with the MATLAB sequence eigs() and with the above code obtained the eigenvalue reported in Table 1. It is very clear that for the values of considered, the block matrix is non singular and the block matrix is singular and independent of

Table 1.
The first two eigenvalues of Bénard problem (5) for various computed by strategy along with ChC.
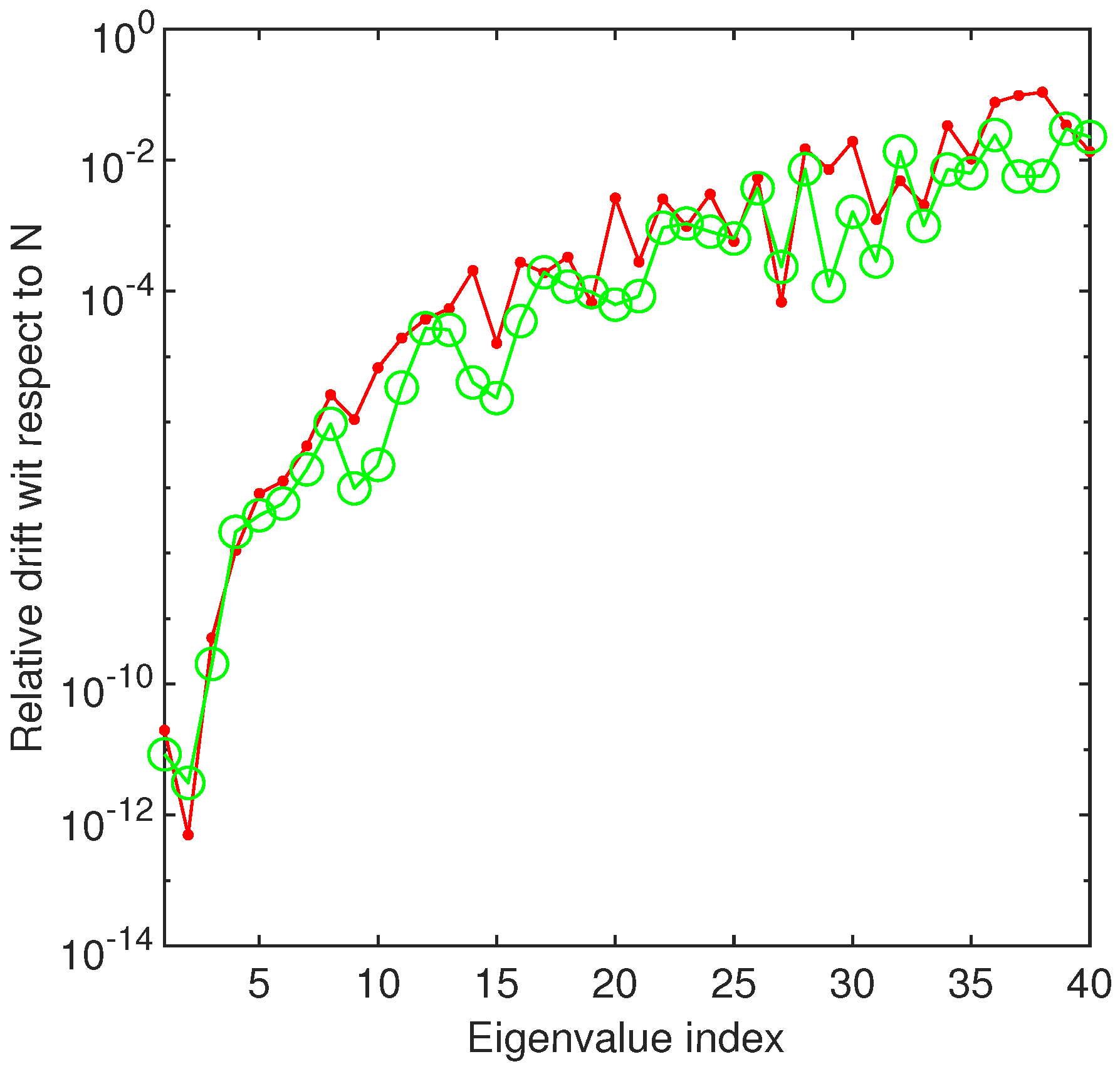
It is extremely important to point out that for the first two values of the parameter in Table 1 our results are very close to those reported in [14]. For the other parameter values this no longer happens. A similar situation occurs even for the second eigenvalue. Then, to decide over the accuracy of our outcomes, we resorted to drift. The relative drift, with respect to the order of approximation of the first forty eigenvalues when is displayed in Figure 4. It suggests that the first two eigenvalues are computed with an accuracy of at least and the first forty with an accuracy of at least . This leads us to believe that we have produced much better approximations for these eigenvalues than those reported in [14] as well as [27]. Actually, in [14] the authors use the SLEUTH code and accept that “it is clear that the code is not very accurate on this problem”.
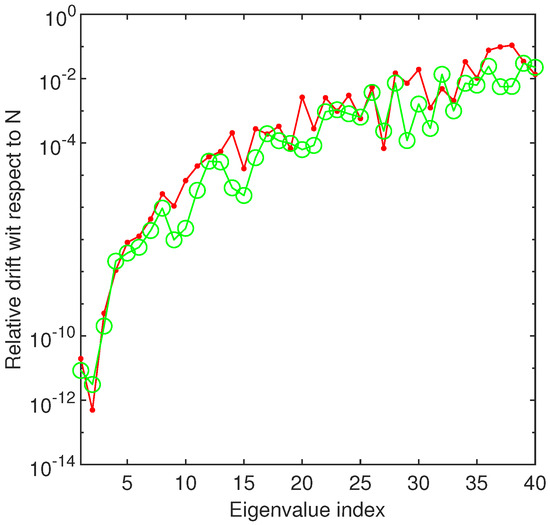
Figure 4.
The relative drift of the first forty eigenvalues of Bénard problem is displayed when -red dotted line when and and green circled line when and
4.1.3. A Self-Adjoint Eighth-Order Problem
The eigenproblem of the highest order we consider in this paper is the following
with exact eigenvalues
All our attempts to solve this problem with Chebfun have failed. The abortion message referred to the extremely small conditioning of the eight order Chebyshev collocation differentiation matrix (of the order ).
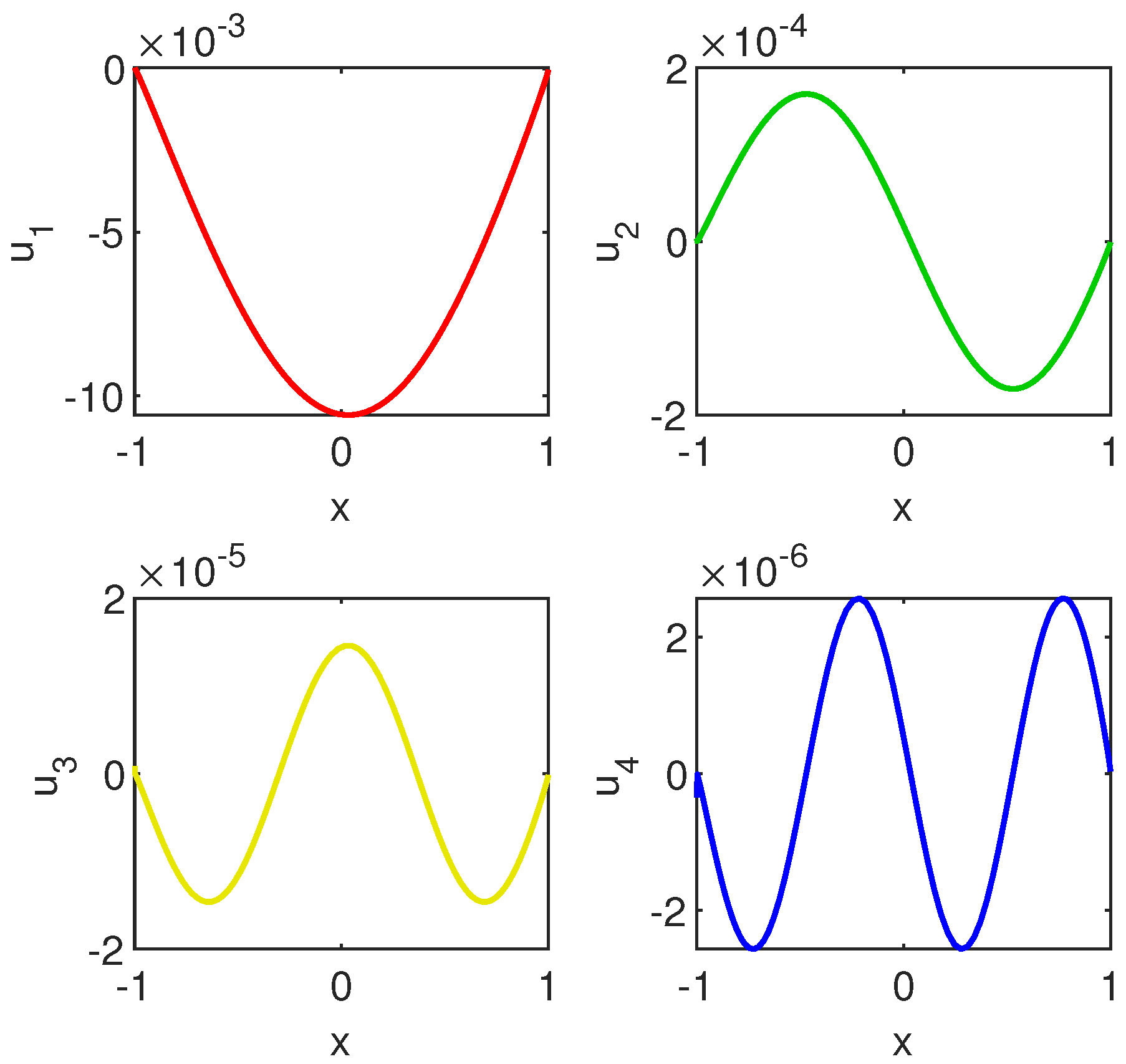
Instead, the strategy along with ChC worked well and produced vectors from Figure 5.
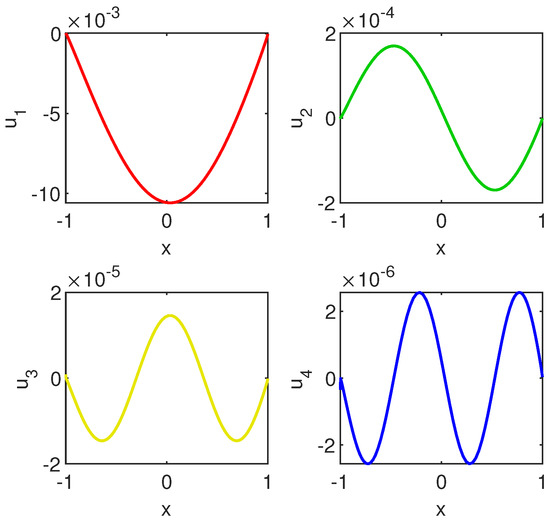
Figure 5.
From upper left to lower right we display the first four eigenvectors of problem (8) computed by ChC along with method when the order of approximation has been .
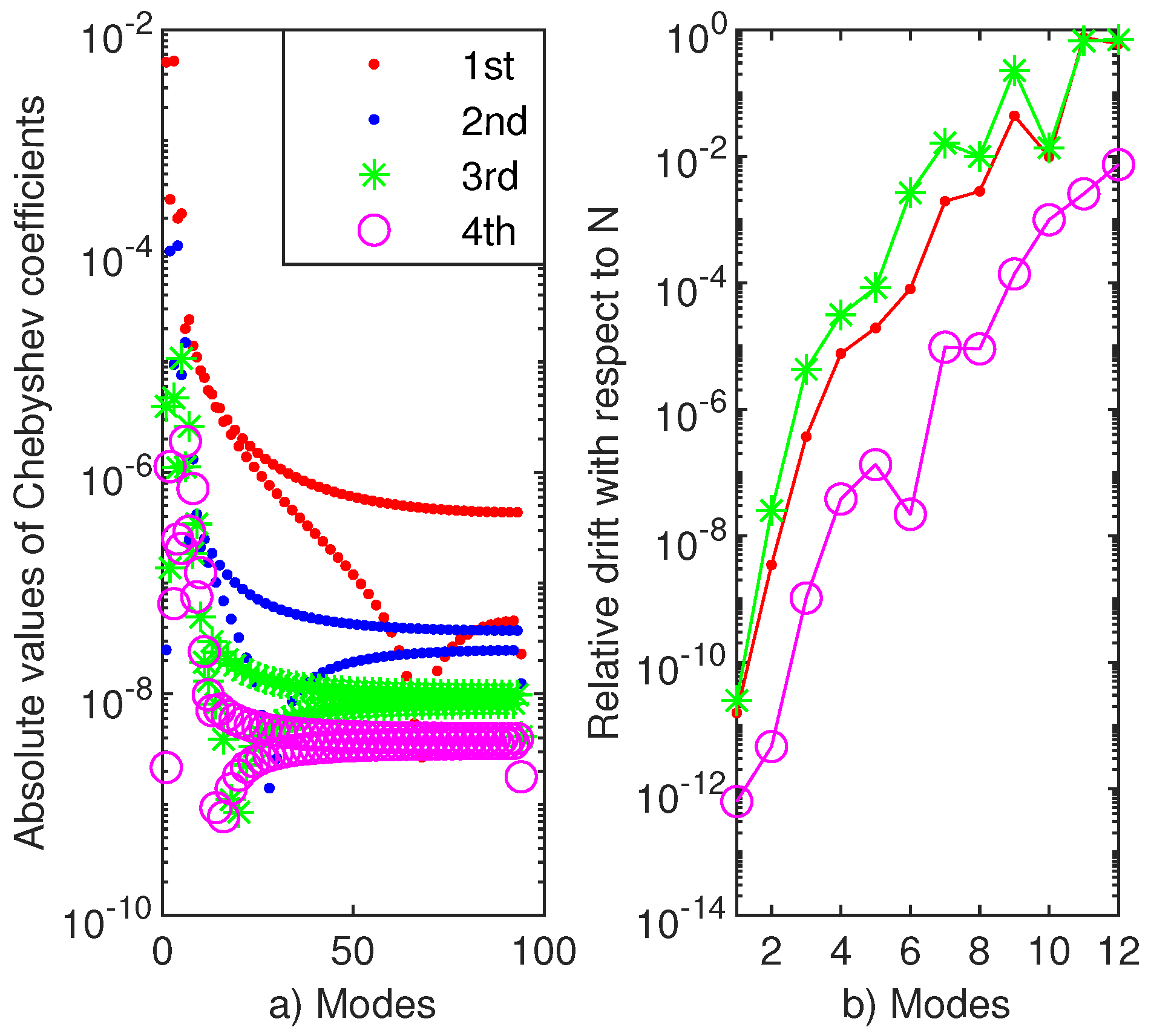
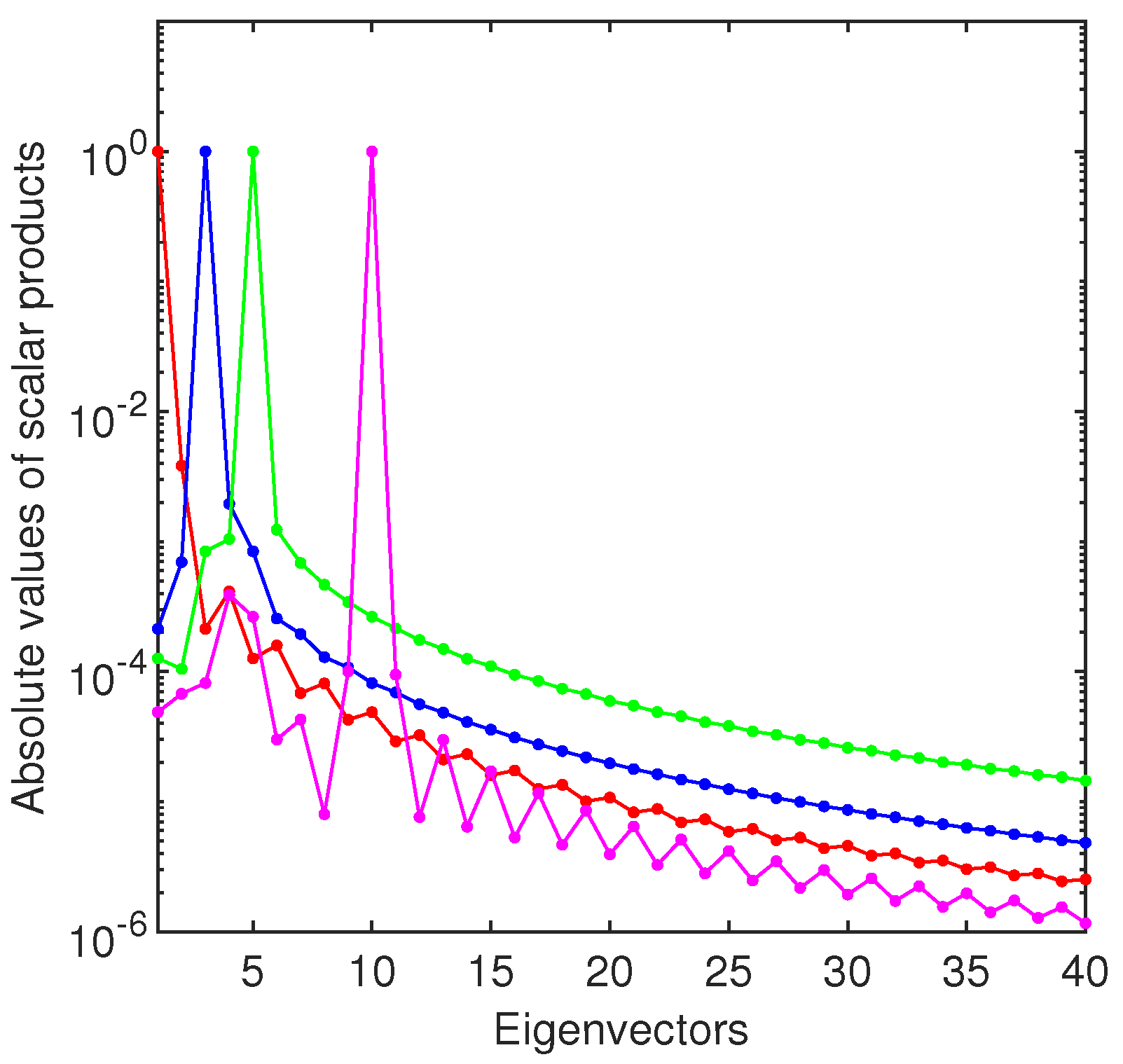
In order to estimate the error with which the eigenvalues were calculated, we display in Figure 6b the relative drift of the first twelve eigenvalues for different approximation orders. As a result that we know the exact eigenvalues, we also display the relative errors. It is very clear that the first eigenvalue is computed with better accuracy than . Unfortunately, this means a lower performance by three decimals than that of Magnus expansion reported in Table 10 from [12].
Moreover, this means that we cannot trust more than twelve eigenvalues for this problem.
It is clear that ChC along with the method have the potential to find the first eigenvalues of an SL problem of arbitrary (even) order with good accuracy. In addition to the Magnus method, this strategy calculates its eigenfunctions (eigenvectors) with reasonable accuracy as can be seen in Figure 6a. We use FCT to compute the Chebyshev coefficients of the eigenvectors.
4.2. Clamped Boundary Conditions
4.2.1. A Fourth Order Problem with a Third Derivative Term
With this first example we have to highlight the importance of preconditioning in improving the accuracy of Chebfun. In the papers [25,29], as well as in the monograph [30], the following eigenproblem is carefully studied. It consists of the fourth order differential equation
supplied with the clamped boundary conditions
The eigencondition for this problem is
Problems similar to this appear, for example, in linearized stability analysis in fluid dynamics. In [29], the authors noticed spurious eigenvalues when the problem (9) and (10) is solved by ChT method. These spurious eigenvalues appears in the right-half plane suggesting physical instabilities that do not exist.
We have solved the problems (9) and (10) by Chebfun with and without preconditioning. The numerical outcomes are displayed in Table 2. Boldfaced digits in the computed eigenvalues show the extent of agreement with the exact values. Thus, it is very clear that preconditioning Chebfun can considerably improve its accuracy.
4.2.2. A Fourth Order Eigenproblem from Spherical Geometry
In [29], the authors consider the eigenproblem
where the operator D is defined by
and l is a positive integer. They solve this problem by a modified ChT method in order to avoid spurious eigenvalues. We have solved this problem by ChC and obtained for the fist two eigenvalues the numerical values
which agree up to the fourth decimal with the the true values (determined from the eigencondition.
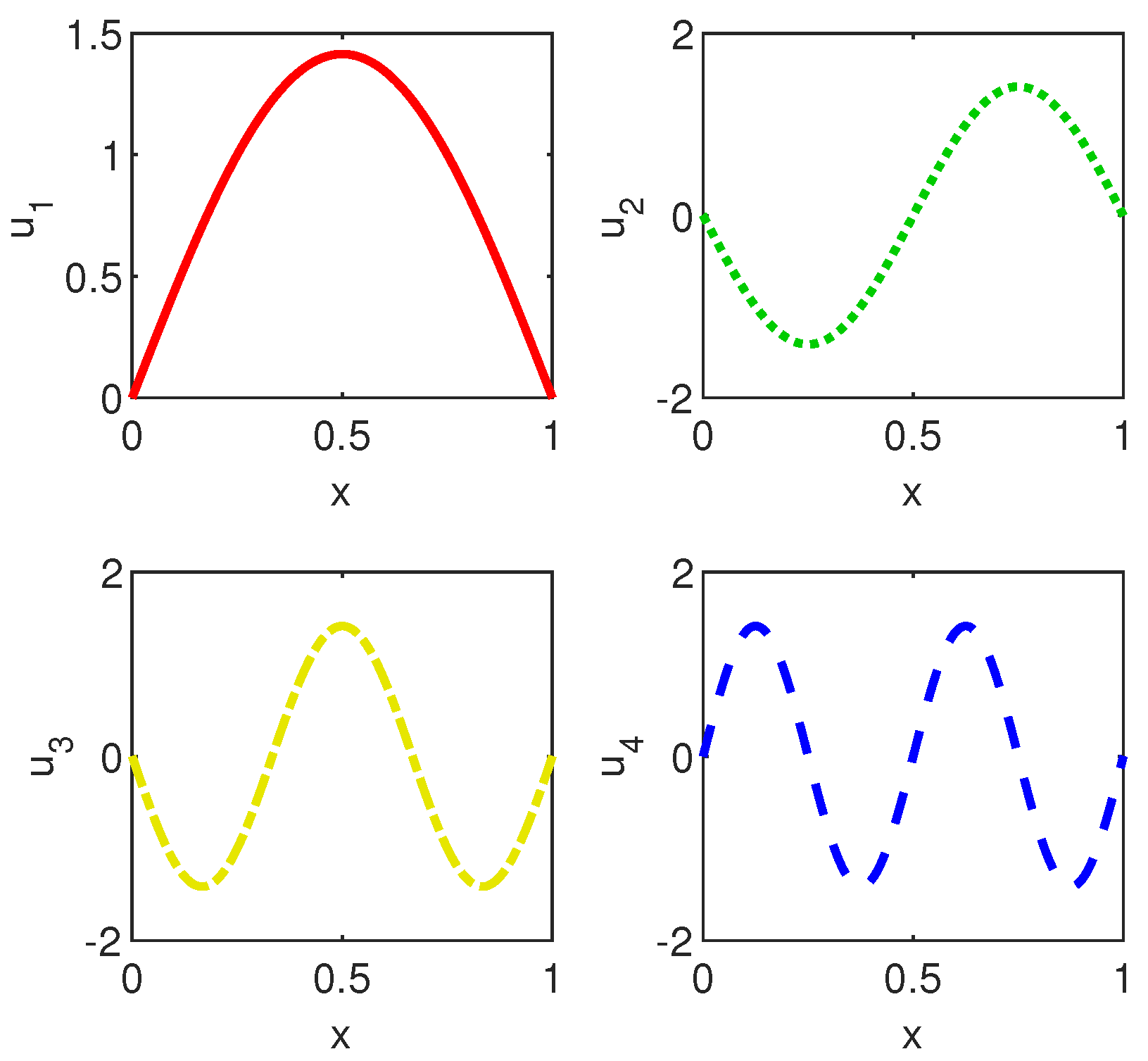
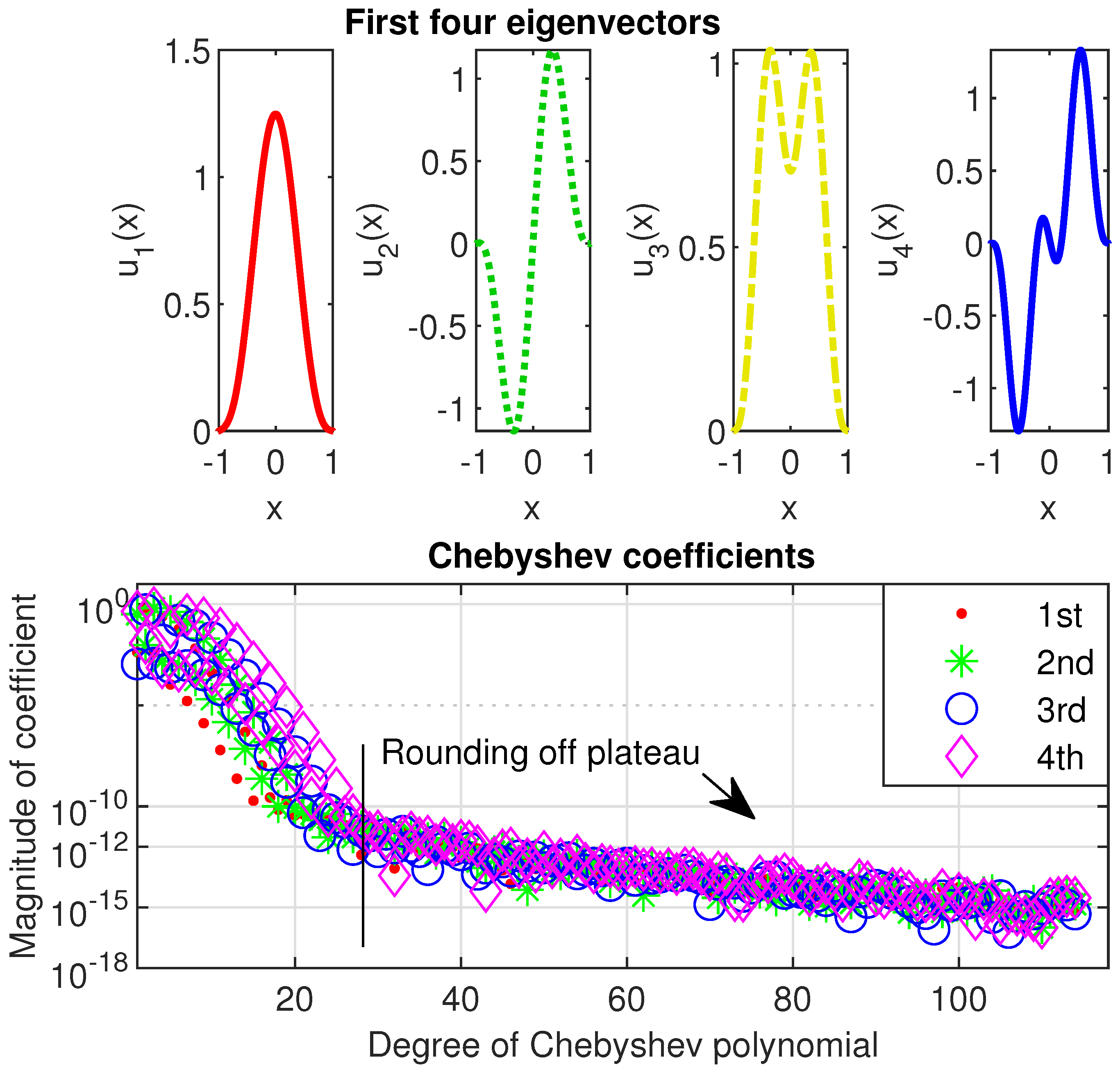
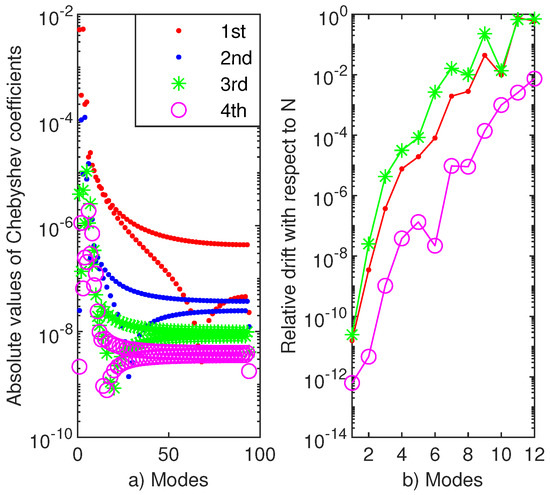
The first four vectors to problem (12) computed by Chebfun are depicted in Figure 7a. It is visible that they satisfy the boundary conditions. Their Chebyshev coefficients are displayed Figure 7b. About the first twenty coefficients of the first four eigenvectors decrease just as abruptly and smoothly.
4.2.3. A Set of Sixth Order Eigenproblems
In [31], the authors consider the following sixth order eigenproblems
and introduce an extremely simple modification to the ChT method which eliminates the spurious eigenvalues when such high order eigenproblems are solved.
We have tried to solve problem (13) with by Chebfun but all our attempts failed due to the very small conditioning of matrix involved, i.e., around The situation became much better with the preconditioner introduced in Section 3.4.
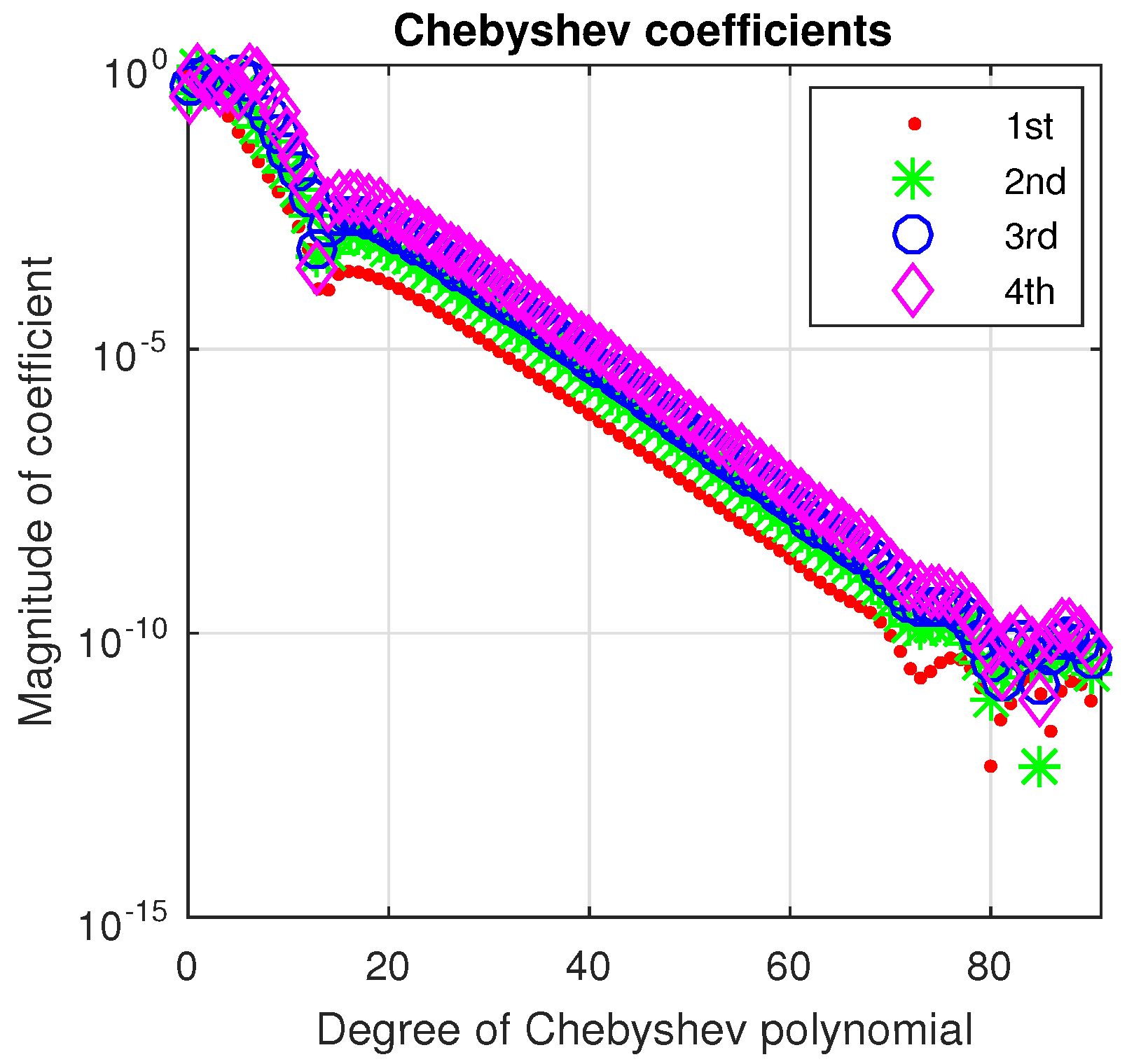
Thus, the first four eigenvectors along with their Chebyshev coefficients are depicted in Figure 8. As it is apparent from the lower panel of this figure the coefficients of degree up to 30 drop sharply to an absolute value below and then slowly decrease to machine accuracy. This happens at an degree around
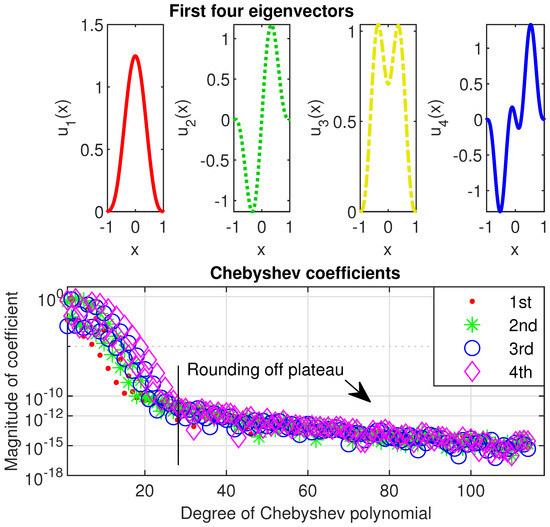
Figure 8.
The first four eigenvectors of problem (13) with computed by Chebfun, are reported in the the upper panels and their Chebyshev coefficients are displayed in the lower panel.
The eigenvalues computed by Chebfun agree up to the first three digits with those provided in ([25] p. 405).
4.3. Problems with Mixed Boundary Conditions
4.3.1. The Free Lateral Vibration of a Uniform Clamped–Hinged Beam
The fourth order eigenproblem
is considered in [32] and is solved by a non conventional spectral collocation method. In this paper, the author shows that the eigenvalues satisfy the transcendental equation
It is extremely important to observe that neither preconditioning nor strategy can handle the mixture of boundary conditions in (14). Thus, this problem tests how well the Chebfun can cope with various boundary conditions.
As the eigenvalues computed from (15) are compared with those obtained by Magnus expansion in [12], we report in Table 3 the latter eigenvalues compared with those provided by Chebfun. A coincidence of at least three decimals can be observed.

Table 3.
The first five eigenvalues to problem (14) computed by Chebfun and compared with those provided by Magnus expansion.
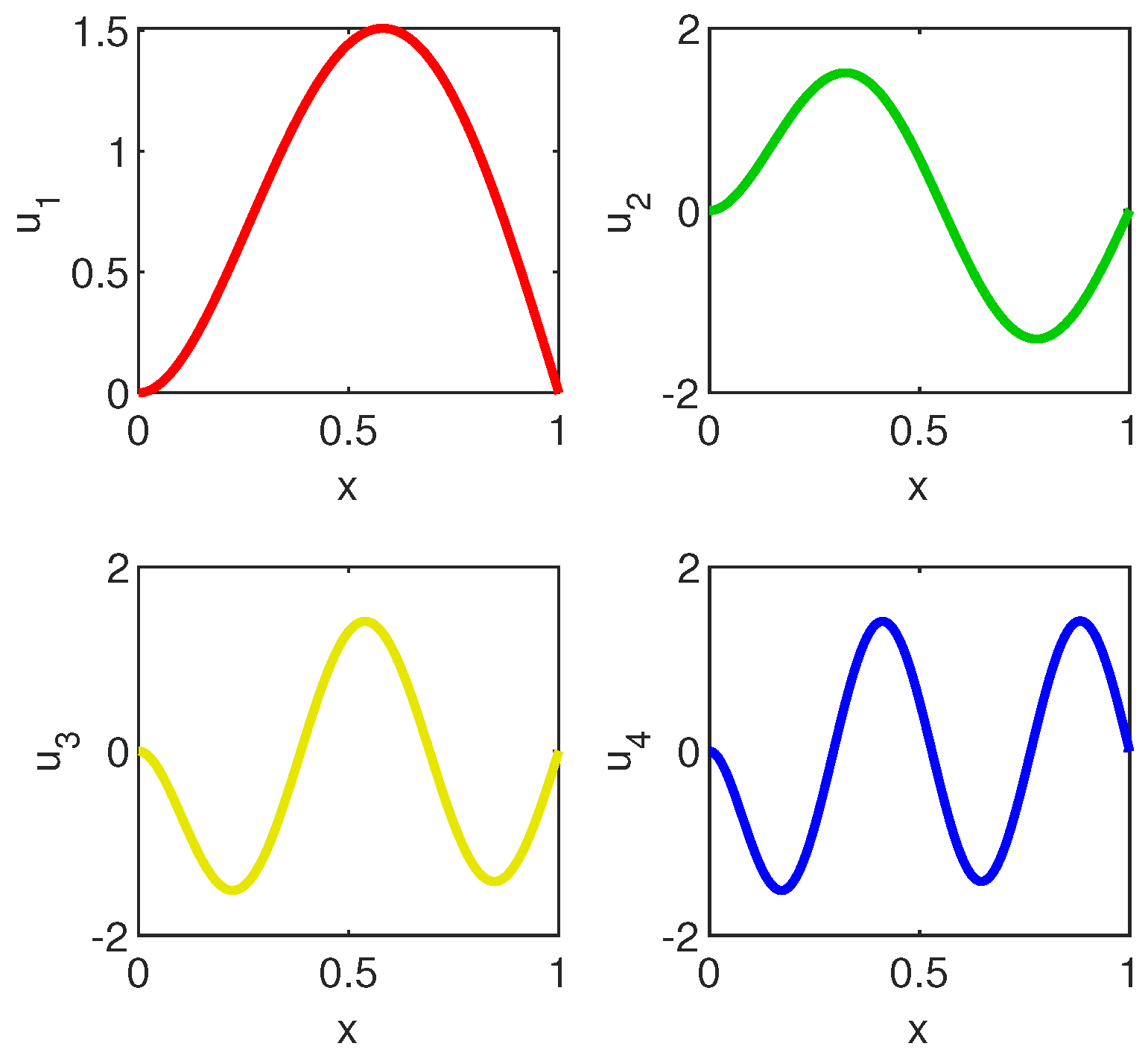
The first four eigenvectors to problem (14) computed by Chebfun are displayed in Figure 9. It is perfectly visible that they satisfy the boundary conditions assumed in this problem.
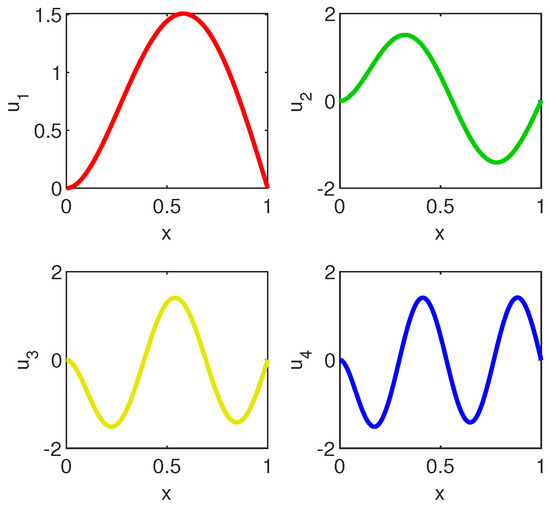
Figure 9.
From upper left to lower right we display the first four eigenvectors to problem (14) computed by Chebfun.
The Chebyshev coefficients of the first four eigenvectors to problem (14) computed by Chebfun are displayed in Figure 10. They decrease smoothly to somewhere around which is an argument in favor of the accuracy of numerical results.
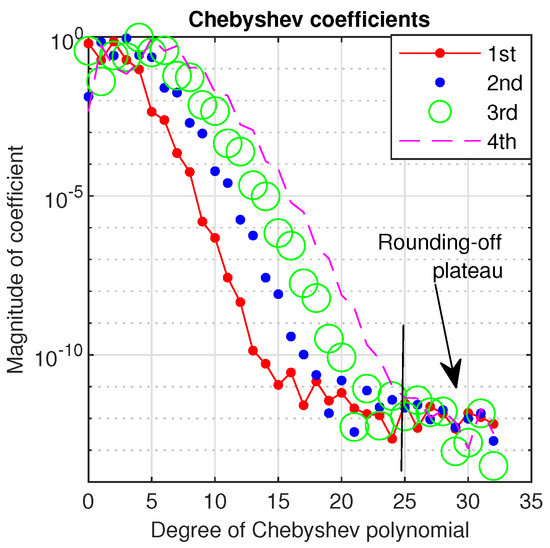
Figure 10.
In a log-linear plot we display the Chebyshev coefficients of the first four eigenvectors to problem (14) computed by Chebfun.
4.3.2. A Fourth Order Eigenproblem with Higher Order Boundary Conditions
In order to show again the Chebfun versatility in introducing boundary conditions, we consider the following problem called the cantilevered beam in Euler–Bernouilli theory (see for instance [33]). The equation simply reads
and is equipped with the following boundary conditions
The first two boundary conditions state that the beam is clamped in 0 and the last two state that the bean is free in the right hand end. The eigenvalues satisfy the eigencondition
Actually, the problems (16) and (17) are self-adjoint. Without going into details, we will notice that the first eigenvalue of this eigenproblem is the solution of the minimization problem
where, roughly, V is a space of continuous functions satisfying the boundary conditions in (17). This Ritz formulation, as well as a weak (variational) formulation can be obtained by multiplying the equation with a function v from V and a double integration by parts.
Again, these boundary conditions are not treatable by preconditioning or strategy.
The following simple and short Chebfun code solves the problems (16) and (17).
% Cantilevered beam in Euler-Bernouilli theory dom=[0,pi];x=chebfun(’x’,dom); % the domain L = chebop(dom); L.op = @(x,y) diff(y,4); % the operator L.lbc = @(y)[y; diff(y,1)]; % fixed b. c. L.rbc = @(y)[diff(y,2); diff(y,3)];% free b. c. [U,D]=eigs(L,40,’SM’); % first six eigs. % Sorted eigenpairs (eigenvalues and eigenvectors) D=diag(D); [t,o]=sort(D); D=D(o); disp((D.^(1/4))) U=U(:,o);
In Table 4, the first four eigenvalues computed by Chebfun and by Magnus expansion are reported. A satisfactory agreement is observed.

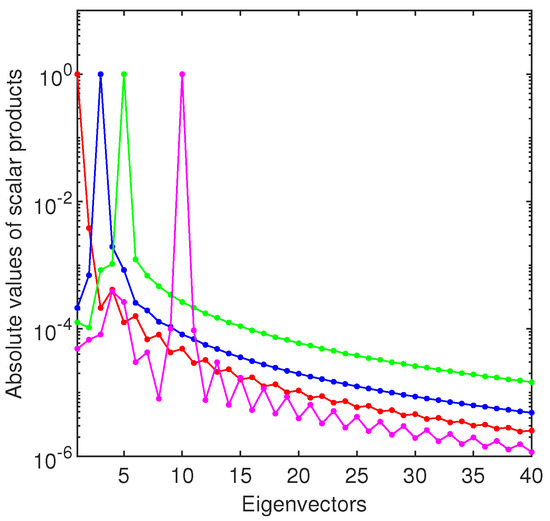
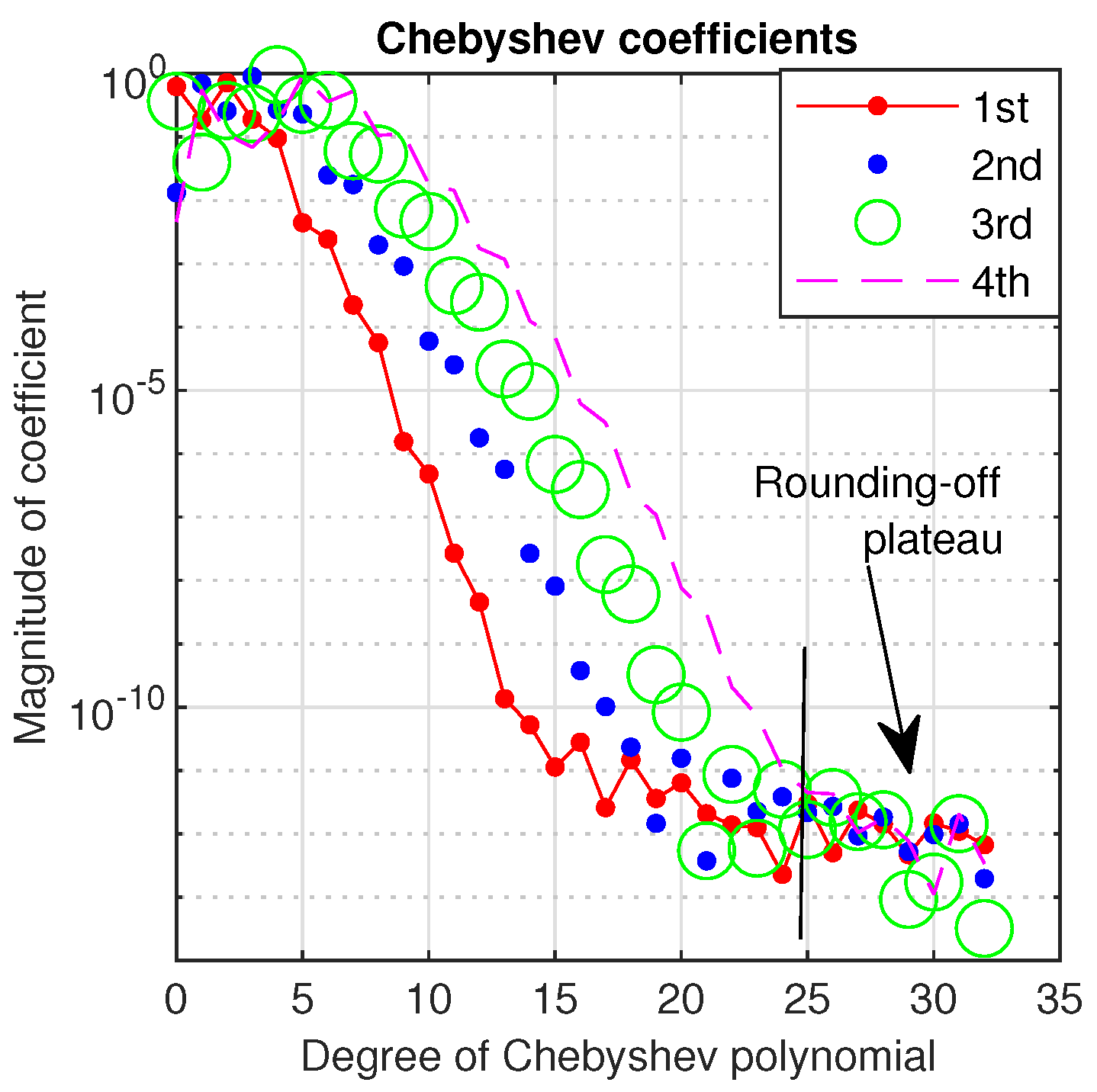
The first four eigenvectors are displayed in Figure 11a and their Chebyshev coefficients are displayed in the same figure panel b. It is clear that Chebfun uses Chebyshev polynomials of slightly lower degree than 20 and from this level only a sharply decreasing rounding-off plateau follows.
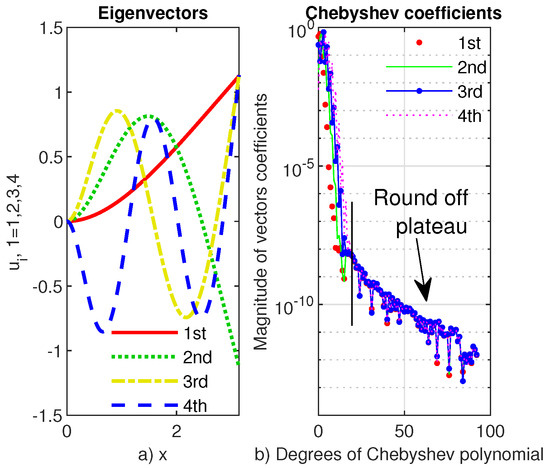
The first four eigenvectors approximating the eigenfunctions are in very good agreement with those exposed in literature. Using the definition of the scalar product of two vectors u and v, namely , we can easily check the orthonormality of eigenvectors.
The curves in Figure 12 clearly show that the eigenvectors of this problem computed by Chebfun are orthonormal.
4.3.3. The Harmonic Oscillator and Its Second and Third Powers
We wanted to test our strategy on a problem whose differential equation exhibits stiffness in at least part of the range. Thus, along with the well known harmonic oscillator operator
we will consider its second and third powers, namely
and
Actually we want to solve the fourth order eigenvalue problem for namely
and the sixth order eigenvalue problem
corresponding to the cube of the harmonic oscillator operator. The eigenvalues of the harmonic oscillator are and those of and are the second and the third powers, respectively of According to the definition for classification of SL problems, given in this Section 2, the eigenproblems (19) and (20) are singular.
We have to observe that no boundary conditions are needed because the problem is of limit-point type [15]: the requirement that the eigenfunctions be square integrable suffices as a boundary condition. In [14] the problem (20) is solved by a SLEUTH code along with domain truncation. Actually the authors truncate this problem to the interval , and impose the simplest boundary conditions at Along with these boundary conditions the eigenproblem becomes self-adjoint.
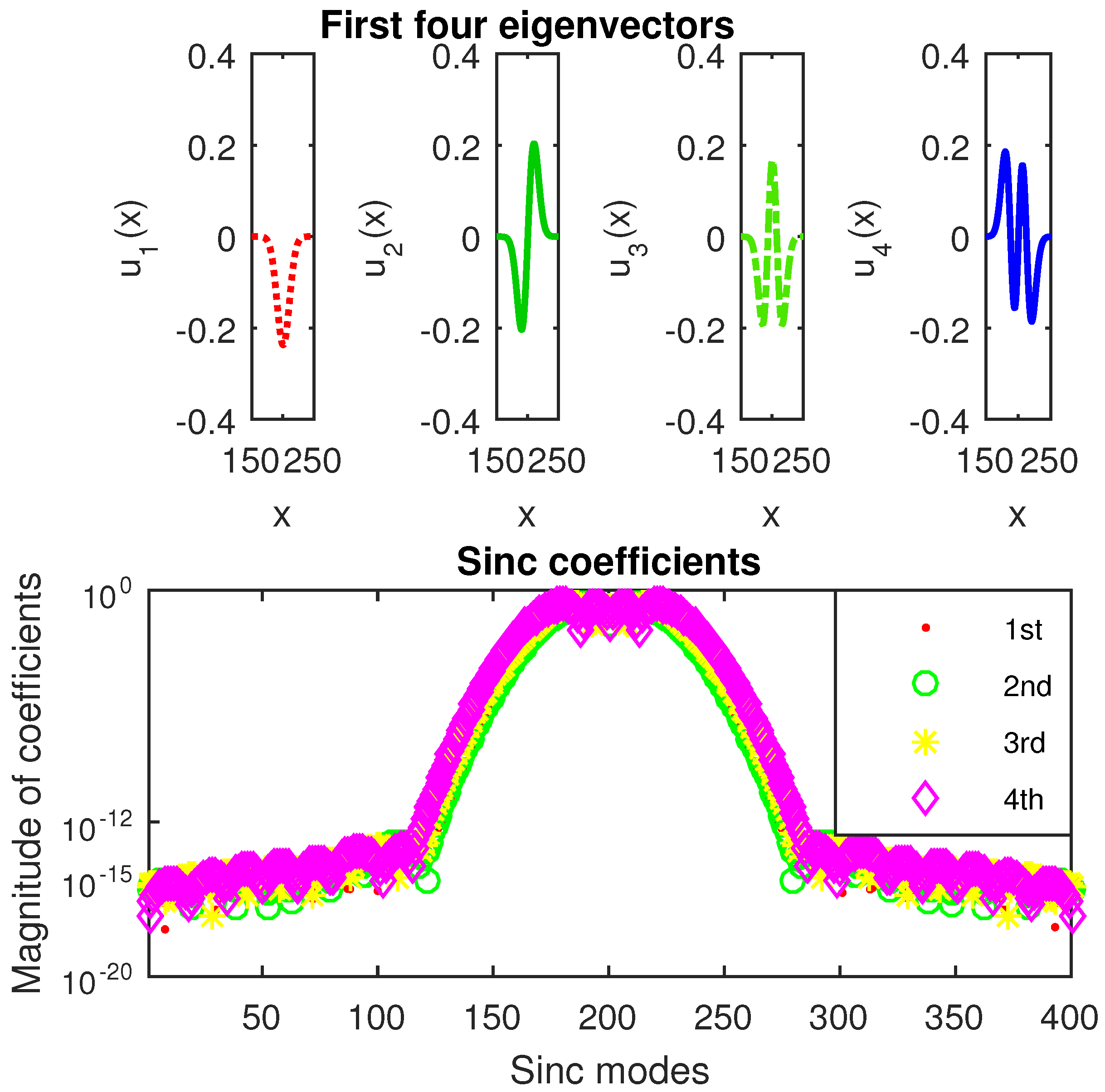
The first four eigenvectors of the cube of harmonic oscillator computed by SiC are displayed in the upper panels of Figure 13. Their sinc coefficients are displayed in the lower panel of the same figure. Roughly speaking, it guarantees us an accuracy of at least in the computation of these eigenvectors.
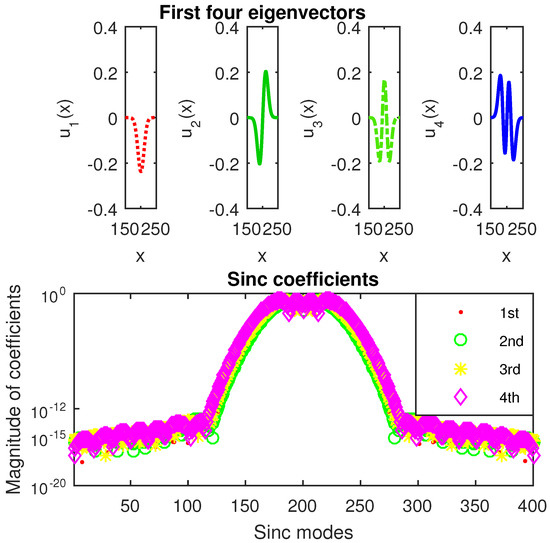
Figure 13.
A zoom in on the first four eigenvectors of the cube of harmonic oscillator (20) computed by SiC is displayed in the upper panels and the sinc coefficients of eigenvectors are reported in the lower panel.
SiC computes the integers with an accuracy of at least six digits.
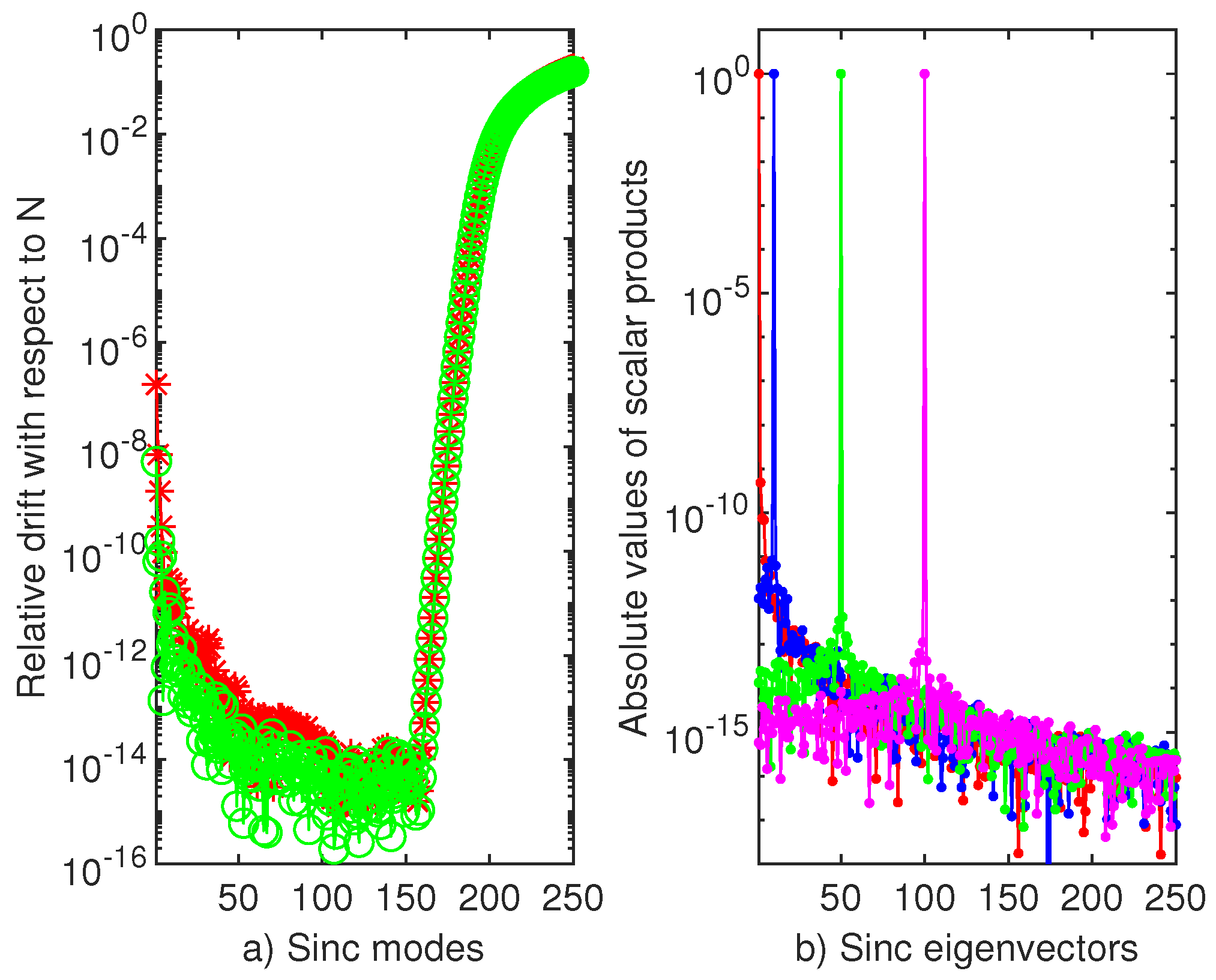
The relative drift, with respect to of the first 250 eigenvalues of the cube of harmonic oscillator computed by SiC are displayed in Figure 14a). It tells us that the first 200 eigenvalues are “good" within an accuracy of approximately It also means the “highest” confirmation of Boyd’s Eigenvalues Rule-of-Thumb (see Section 3.3).
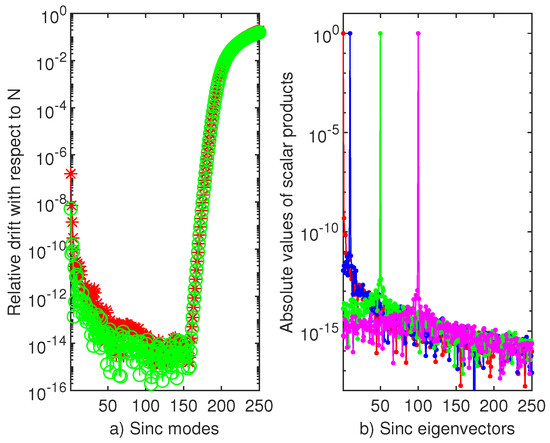
Figure 14.
(a)The relative drift of the first 250 eigenvalues of the cube of harmonic oscillator computed by SiC. Red stared line compares the exact values with the eigenvalues computed with and the circled green line compares the latter eigenvalues with those computed when in SiC In both cases, the scaling factor h equals . (b) The orthonormality of the first 250 eigenvectors, i.e., the scalar products, red dotted line, blue dotted line, green dotted line and magenta dotted line, .
Trying to explain this spectacular phenomenon we cannot forget the fact that the derivation matrices of SiC are symmetric. This leads to normal matrices (operators) whose eigenpairs are properly computable.
If we compare this result with Table 10 from [14], where the best accuracy in computing of the first eigenvalue is , we can speak of a total superiority of SiC method over SLEUTH.
In Figure 14b, we display the scalar product of some eigenvectors. They prove that the SiC computed eigenvectors are orthonormal. This means that we can trust at least the first 200 eigenpairs computed by SiC. The following few lines of MATLAB compute the above eigenpairs:
% The sinc differentiation matrices [Weideman & Reddy] N=400;M=6;h=0.1; %Orders of approximation and differentiation and scaling factor [x, D] = sincdif(N, M, h); D1=D(:,:,1);D2=D(:,:,2);D6=D(:,:,6); % The cube of the "harmonic oscillator" operator L=-D6+D2*(3*diag(x.^2)*D2)+D1*(diag(8-3*(x.^4))*D1)+diag(x.^6-14*(x.^2)); % Finding eigenpairs of L [U,S]=eigs(L,250,0); S=diag(S); [t,o]=sort(S); S=S(o);
Unfortunately, Chebfun along with domain truncation fails in solving the sixth order problem (20) with or without preconditioning. Actually, a warning concerning the very bad conditioning of the matrix is issued.
However, Chebfun behaves fairly well in solving the fourth order problem (19), i.e., computes the corresponding integers with the same accuracy as SiC. We have solved the Equation (19) on the truncated interval for various X along with the boundary conditions The Chebyshev coefficients of the first four eigenvectors of eigenproblem (19) computed by Chebfun are displayed in Figure 15a). An important aspect must be highlighted, namely the first about 1000 polynomial coefficients decrease steeply and smoothly to about after which up to the order of 2500 follows a wide rounding-off plateau.This is the polynomial of the highest degree that Chebfun has used in our numerical experiments. The curves in Figure 15b) show the orthonormality of Chebfun eigenvectors.
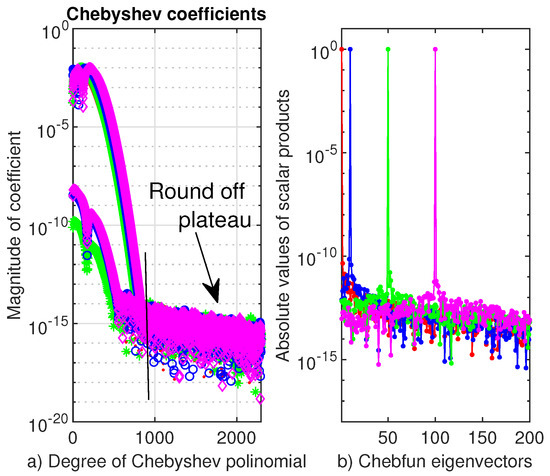
Figure 15.
(a) We display the Chebyshev coefficients of the first four eigenvectors of eigenproblem (19); red dotted line-first vector, green stared line-second, blue circles-third and magenta diamonds-fourth vector. (b) In a log-linear plot we display the scalar products —red dotted line, —blue dotted line, —green dotted line and —magenta dotted line, when the eigenproblem (19) is solved by Chebfun.
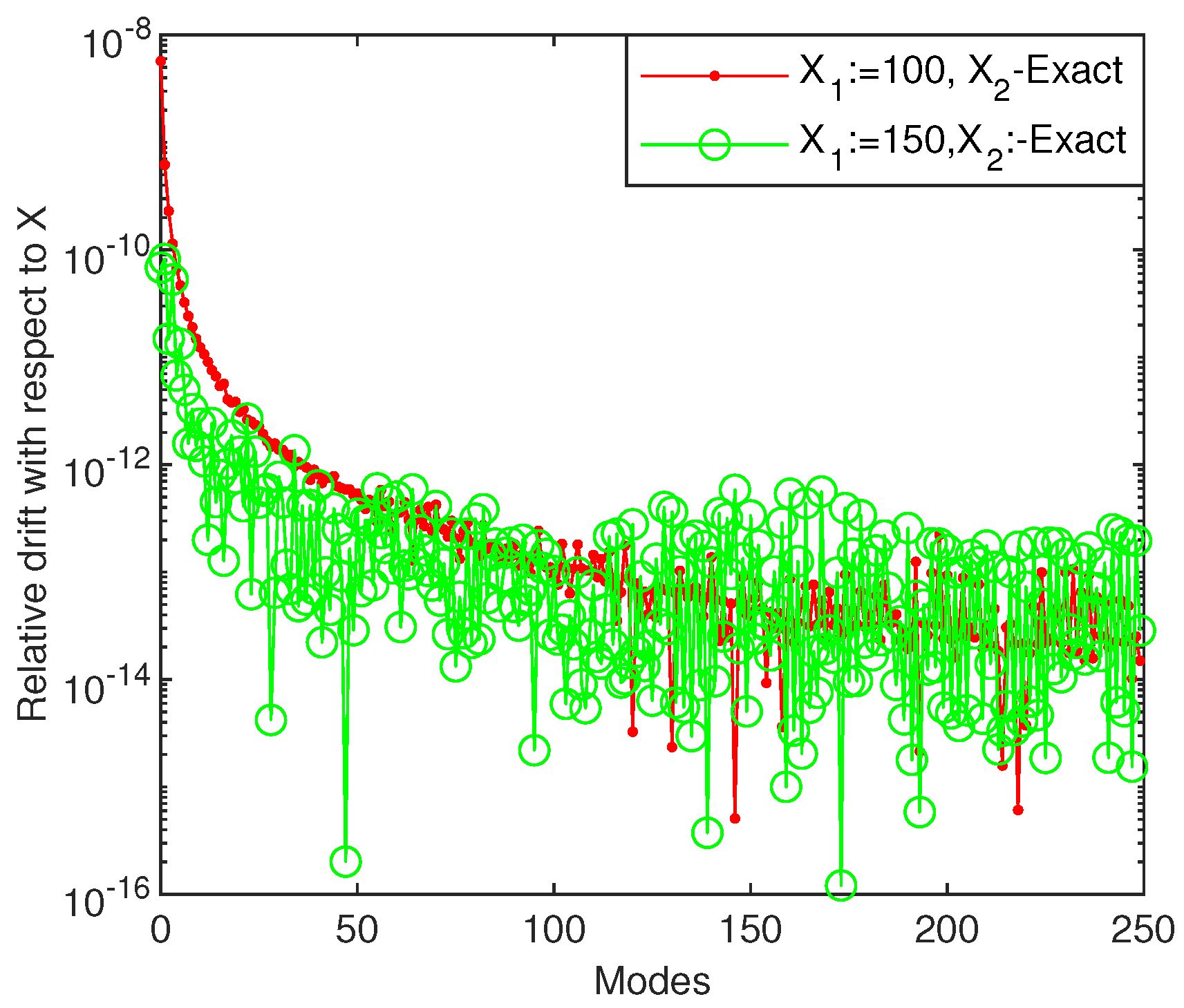
The relative drift with respect to the length of integration interval X of the first 250 eigenvalues to problem (19), when it is solved by Chebfun, is displayed in Figure 16. It means that the numerical stability is lost for larger X than 100 and a set of small eigenvalues can be computed with an accuracy better than .
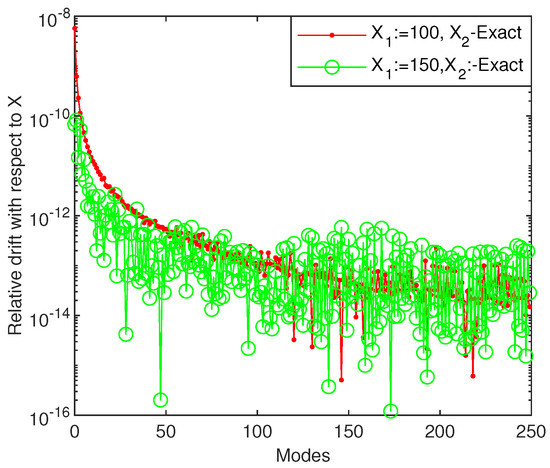
Figure 16.
The relative drift (errors) with respect to X of the first 250 eigenvalues of second order harmonic oscillator operator .
5. Conclusions and Open Problems
After analyzing these challenging problems, some firm conclusions can be drawn.
First of all, Chebfun can easily handle any type of boundary condition. This is a significant advantage. Thus, for fourth order eigenproblems, the direct application of Chebfun is versatile in handling various high order boundary conditions and produces reliable outcomes. Furthermore, for problems with clamped boundary conditions both methods, Chebfun as well as ChC, improve their results with two, three decimals by preconditioning.
For sixth order eigenproblems, the Chebfun situation is not so encouraging. Its direct application is very uncertain. Matrices whose conditioning order drops to appear, which most often lead to inaccurate results. For problems of this order or more, subjected to hinged boundary conditions, the reduction to second-order systems and then the application of the ChC method is the best strategy. In this way, we managed to establish a conjecture for the Viola’s problem regarding its lowest eigenvalue.
For fourth order problems on the real line Chebfun along with the truncation of the domain worked fairly well as was the case with the second power harmonic oscillator. As an absolute novelty, we have established in this case the numerical stability with respect to the length of the integration interval. Instead, for the sixth order eigenproblems on the real line, the SiC method remains the unique feasible alternative.
In fact, this method is the best in the sense that we can trust the first half of computed eigenpairs. To our knowledge, no software package has reached this performance so far.
An open problem remains for finding preconditioning methods for the case of hinged boundary conditions or some other types of boundary conditions.
This paper comes shortly after when in another one (see [23]) we have approached, with the same two classes of methods, singular Schröedinger eigenproblems. In this situation we can appreciate that ChC along with Chebfun are a better alternative in some respects to other existing methods for a very wide range of eigenproblems. Both compute eigenvectors (approximating eigenfunctions) and by drift estimation demonstrate numerical stability. In addition, the drift with respect to N shows the degree of accuracy up to which a set of eigenvalues is computed. The situation when both types of methods can be applied to the same problem is the ideal one and the one that produces the safest results.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank the reviewers for their thoughtful comments and efforts towards improving our manuscript.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ChC | Chebyshev collocation method |
| ChT | Chebyshev tau method |
| strategy to reduce a 2nd-order equation to a second order system | |
| FCT | fast Chebyshev transform |
| FD | finite difference method |
| FE | finite element method |
| MATSLISE | a MATLAB package for the numerical solution of SL and Schröedinger equations |
| SiC | sinc spectral collocation |
| SL | Sturm–Liouville |
| SLEDGE | Sturm–Liouville estimates determined by global errors |
| SLEUTH | Sturm–Liouville Eigenvalues using Theta Matrices |
References
- Straughan, B. Stability of Wave Motion in Porous Media; Springer Science+Business Media: New York, NY, USA, 2008. [Google Scholar]
- Trefethen, L.N.; Birkisson, A.; Driscoll, T.A. Exploring ODEs; SIAM: Philadelphia, PA, USA, 2018. [Google Scholar]
- Pruess, S.; Fulton, C.T. Mathematical Software for Sturm-Liouville Problem. ACM Trans. Math. Softw. 1993, 19, 360–376. [Google Scholar] [CrossRef]
- Pruess, S.; Fulton, C.T.; Xie, Y. An Asymptotic Numerical Method for a Class of Singular Sturm-Liouville Problems. ACM SIAM J. Numer. Anal. 1995, 32, 1658–1676. [Google Scholar] [CrossRef]
- Marletta, M.; Pryce, J.D. LCNO Sturm-Liouville problems. Computational difficulties and examples. Numer. Math. 1995, 69, 303–320. [Google Scholar] [CrossRef]
- Pryce, J.D.; Marletta, M. A new multi-purpose software package for Schrödinger and Sturm–Liouville computations. Comput. Phys. Comm. 1991, 62, 42–54. [Google Scholar] [CrossRef]
- Bailey, P.B.; Everitt, W.N.; Zettl, A. Computing Eigenvalues of Singular Sturm-Liouville Problems. Results Math. 1991, 20, 391–423. [Google Scholar] [CrossRef]
- Bailey, P.B.; Garbow, B.; Kaper, H.; Zettl, A. Algorithm 700: A FORTRAN software package for Sturm-Liouville problems. ACM Trans. Math. Softw. 1991, 17, 500–501. [Google Scholar] [CrossRef]
- Ledoux, V.; Van Daele, M.; Vanden Berghe, G. MATSLISE: A MATLAB Package for the Numerical Solution of Sturm-Liouville and Schrödinger Equations. ACM Trans. Math. Softw. 2005, 31, 532–554. [Google Scholar] [CrossRef]
- Baeyens, T.; Van Daele, M. The Fast and Accurate Computation of Eigenvalues and Eigenfunctions of Time-Independent One-Dimensional Schrödinger Equations. Comput. Phys. Commun. 2021, 258, 107568. [Google Scholar] [CrossRef]
- Abbasb, Y.S.; Shirzadi, A. A new application of the homotopy analysis method: Solving the Sturm—Liouville problems. Commun. Nonlinear. Sci. Numer. Simulat. 2011, 16, 112–126. [Google Scholar] [CrossRef]
- Perera, U.; Böckmann, C. Solutions of Direct and Inverse Even-Order Sturm-Liouville Problems Using Magnus Expansion. Mathematics 2019, 7, 544. [Google Scholar] [CrossRef]
- Gheorghiu, C.I. Spectral Methods for Non-Standard Eigenvalue Problems: Fluid and Structural Mechanics and Beyond; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Greenberg, G.; Marletta, M. Oscillation Theory and Numerical Solution of Sixth Order Sturm-Liouville Problems. SIAM J. Numer. Anal. 1998, 35, 2070–2098. [Google Scholar] [CrossRef]
- Everitt, W.N. A Catalogue of Sturm-Liouville Differential Equations. In Sturm-Liouville theory: Past and Present; Amrein, W.O., Hinz, A.M., Hinz, D.B., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2005; pp. 271–331. [Google Scholar]
- Driscoll, T.A.; Bornemann, F.; Trefethen, L.N. The CHEBOP System for Automatic Solution of Differential Equations. BIT 2008, 48, 701–723. [Google Scholar] [CrossRef]
- Driscoll, T.A.; Hale, N.; Trefethen, L.N. Chebfun Guide; Pafnuty Publications: Oxford, UK, 2014. [Google Scholar]
- Driscoll, T.A.; Hale, N.; Trefethen, L.N. Chebfun-Numerical Computing with Functions. Available online: http://www.chebfun.org (accessed on 15 November 2019).
- Gheorghiu, C.I. Spectral Collocation Solutions to Problems on Unbounded Domains; Casa Cărţii de Ştiinţă Publishing House: Cluj-Napoca, Romania, 2018. [Google Scholar]
- Weideman, J.A.C.; Reddy, S.C. A MATLAB Differentiation Matrix Suite. ACM Trans. Math. Softw. 2000, 26, 465–519. [Google Scholar] [CrossRef]
- Gheorghiu, C.I.; Pop, I.S. A Modified Chebyshev-Tau Method for a Hydrodynamic Stability Problem. In Proceedings of the International Conference on Approximation and Optimization; Stancu, D.D., Coman, G., Breckner, W.W., Blaga, P., Eds.; Transilvania Press: Cluj-Napoca, Romania, 1996; Volume II, pp. 119–126. [Google Scholar]
- Boyd, J.P. Traps and Snares in Eigenvalue Calculations with Application to Pseudospectral Computations of Ocean Tides in a Basin Bounded by Meridians. J. Comput. Phys. 1996, 126, 11–20. [Google Scholar] [CrossRef]
- Gheorghiu, C.I. Accurate Spectral Collocation Computation of High Order Eigenvalues for Singular Schrödinger Equations. Computation 2021, 9, 2. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Dover Publications: New York, NY, USA, 2000; pp. 127–158. [Google Scholar]
- Huang, W.; Sloan, D.M. The Pseudospectral Method for Solving Differential Eigenvalue Problems. J. Comput. Phys. 1994, 111, 399–409. [Google Scholar] [CrossRef]
- Straughan, B. The Energy Method, Stability, and Nonlinear Convection; Springer: New York, NY, USA, 1992; pp. 218–222. [Google Scholar]
- Lesnic, D.; Attili, S. An Efficient Method for Sixth-order Sturm-Liouville Problems. Int. J. Sci. Technol. 2007, 2, 109–114. [Google Scholar]
- Gheorghiu, C.I.; Rommes, J. Application of the Jacobi-Davidson method to accurate analysis of singular linear hydrodynamic stability problems. Int. J. Numer. Meth. Fluids 2013, 71, 358–369. [Google Scholar] [CrossRef]
- Gardner, D.R.; Trogdon, S.A.; Douglass, R.W. A Modified Spectral Tau Method That Eliminates Spurious Eigenvalues. J. Comput. Phys. 1989, 80, 137–167. [Google Scholar] [CrossRef]
- Fornberg, B. A Practical Guide to Pseudospectral Methods; Cambridge University Press: Cambridge, UK, 1998; pp. 89–90. [Google Scholar]
- McFadden, G.B.; Murray, B.T.; Boisvert, R.F. Elimination of Spurious Eigenvalues in the Chebyshev Tau Spectral Method. J. Comput. Phys. 1990, 91, 228–239. [Google Scholar] [CrossRef]
- Mai-Duy, N. An effective spectral collocation method for the direct solution of high-order ODEs. Commun. Numer. Methods Eng. 2006, 22, 627–642. [Google Scholar] [CrossRef]
- Zhao, S.; Wei, G.W.; Xiang, Y. DSC analysis of free-edged beams by an iteratively matched boundary method. J. Sound. Vib. 2005, 284, 487–493. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).