A Model Free Adaptive Scheme for Integrated Control of Civil Aircraft Trajectory and Attitude
Abstract
1. Introduction
2. Data Generation
3. MIMO MFAC Method with Saturation Constraint
4. MIMO MFAC Method with Hard Constraints
5. Control Scheme with Mixed Constraints
- (1)
- Estimate the value of PPJM by Formula (23).
- (2)
- Reset the value of when the following conditions are satisfied:if or or , , thenif or , , thenwhere is a small value, and , . is the initial value of .
- (3)
- Calculate the current control input using the estimated value of PPJM .; ; ; , . According to Equation (21), impose the saturation constraint on the control input.
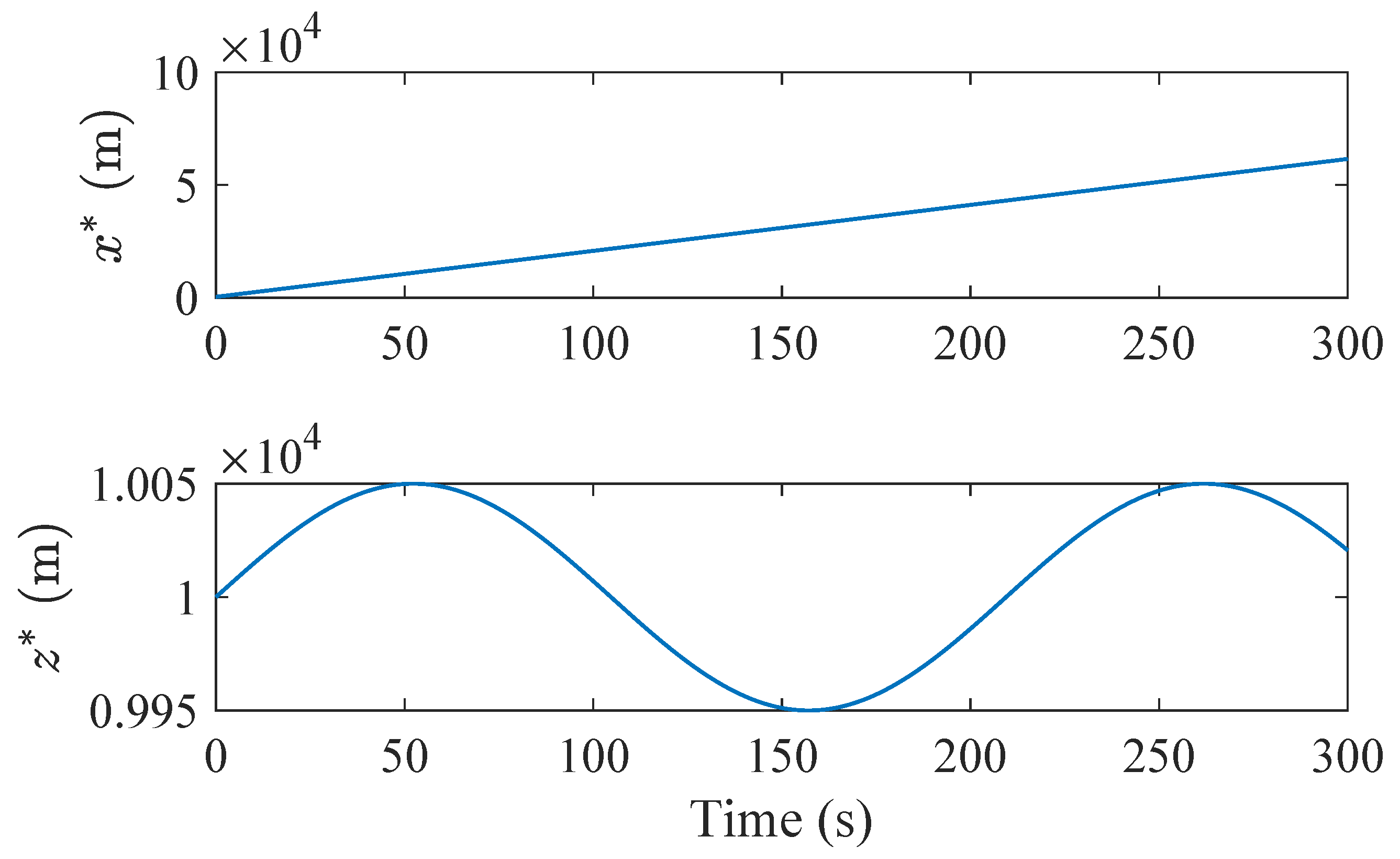
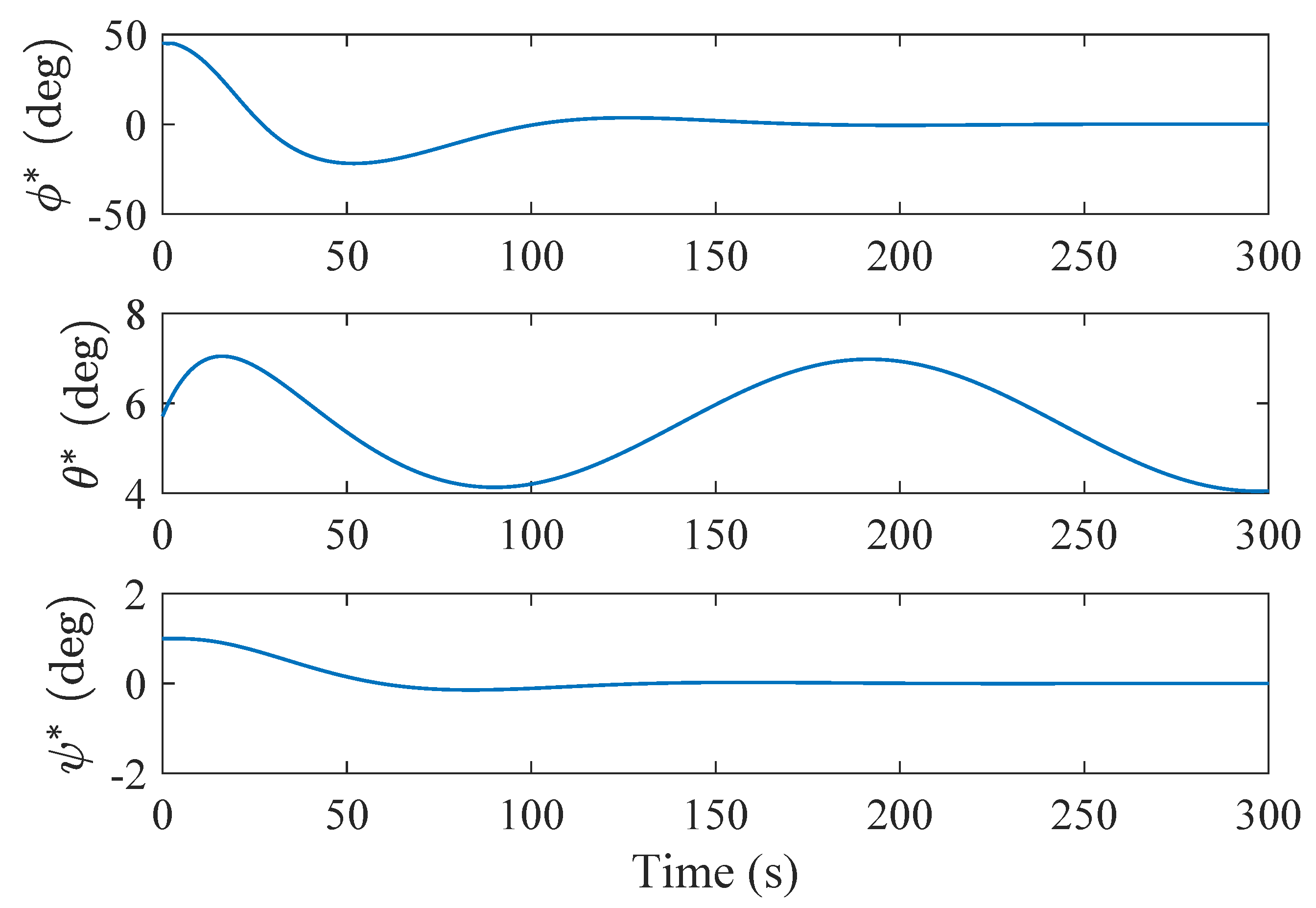
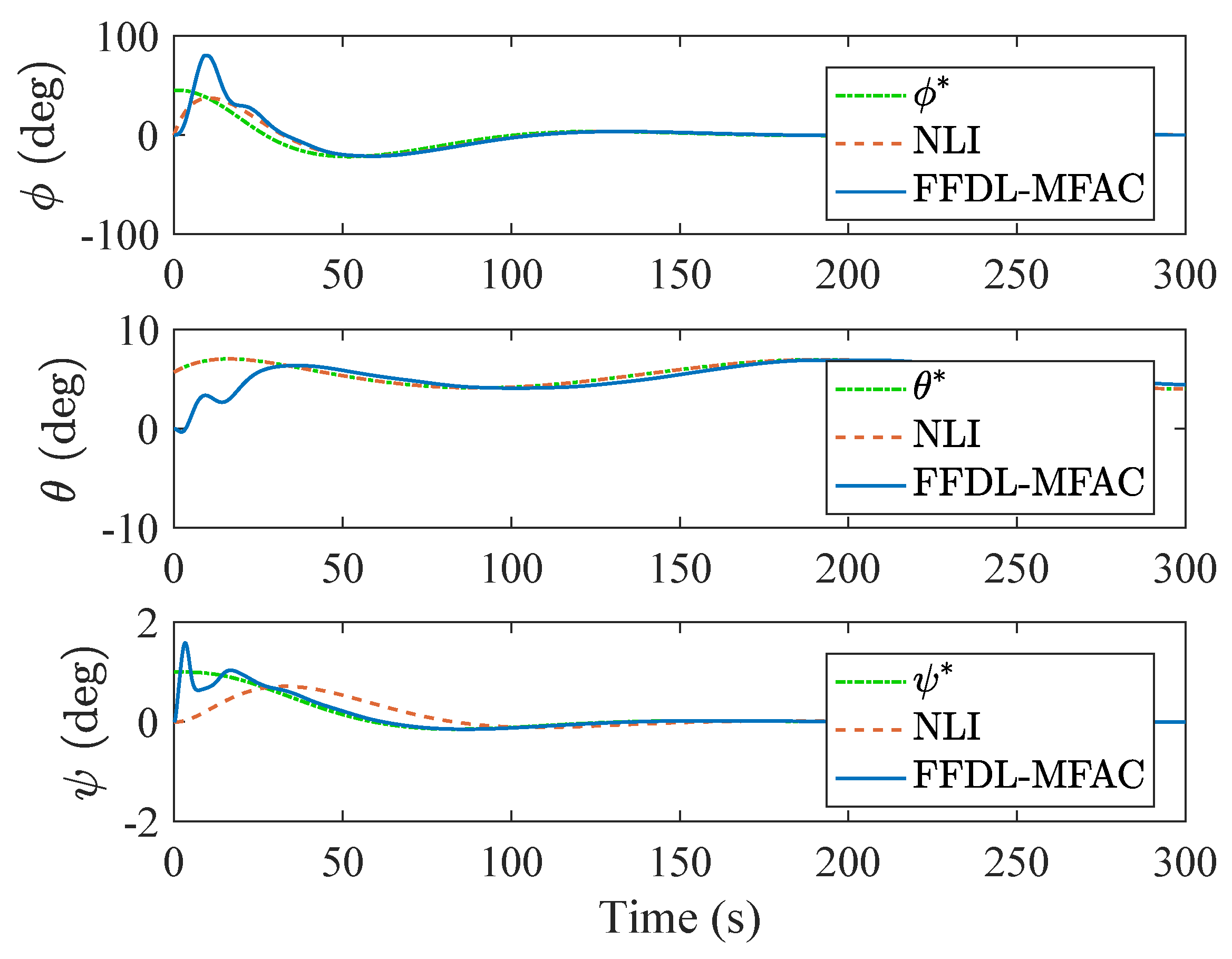
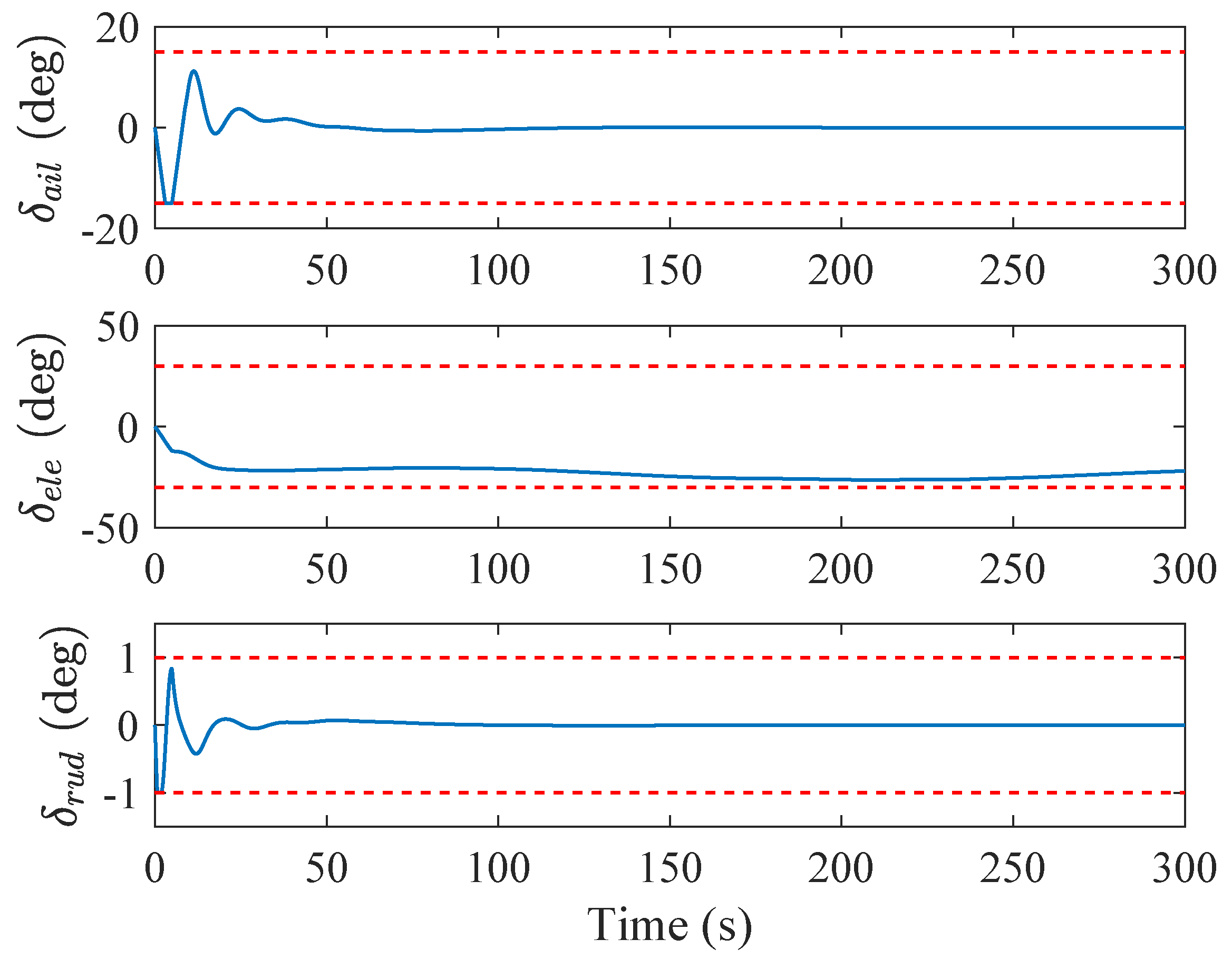
6. Simulation Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MIMO | Multi-input multi-output |
| MFAC | Model free adaptive control |
| NextGen | Next generation air traffic transportation system |
| SESAR | Single european sky air traffic management research |
| UAV | Unmanned aerial vehicle |
| PID | Proportion integration differentiation |
| NLI | Non-linear inversion |
| I/O | Input / Output |
| SPSA | Simultaneous perturbation stochastic approximation |
| UC | Unfalsified control |
| IFT | Iterative feedback tuning |
| VRFT | Virtual reference feedback tuning |
| FFDL | Full-format dynamic linearization |
| PPJM | Pseudo partitioned Jacobian matrix |
| MBC | Model-based control |
| DDC | Data-driven control |
References
- FAA. NextGen Implementation Plan; Technical Report; Federal Aviation Administration: Washington, DC, USA, 2018.
- SESAR. SESAR Solutions Catalogue 2019, 3rd ed.; Technical Report; SESAR Joint Undertaking: Luxembourg, 2019. [Google Scholar]
- Al-Hiddabi, S.A.; McClamroch, N.H. Aggressive longitudinal aircraft trajectory tracking using nonlinear control. J. Guid. Control Dyn. 2002, 25, 26–32. [Google Scholar] [CrossRef]
- Bouadi, H. Contribution to Flight Control Law Design and Aircraft Trajectory Tracking. Ph.D. Thesis, INSA de Toulouse, Toulouse, France, 2014. [Google Scholar]
- Nuñez, H.E. Contribution To Flight Guidance In High Density Traffic. Ph.D. Thesis, National School of Civil Aviation, Toulouse, France, 2018. [Google Scholar]
- Dong, W.; Gu, G.; Zhu, X.; Ding, H. High-performance trajectory tracking control of a quadrotor with disturbance observer. Sens. Actuators A Phys. 2014, 211, 67–77. [Google Scholar] [CrossRef]
- Su, Z.; Wang, H.; Shao, X.; Huang, Y. A robust back-stepping based trajectory tracking controller for the tanker with strict posture constraints under unknown flow perturbations. Aerosp. Sci. Technol. 2016, 56, 34–45. [Google Scholar] [CrossRef]
- Bouadi, H.; Mora-Camino, F. Modeling and adaptive flight control for quadrotor trajectory tracking. J. Aircr. 2018, 55, 666–681. [Google Scholar] [CrossRef]
- Bousson, K.; Machado, P. 4D trajectory generation and tracking for waypoint-based aerial navigation. WSEAS Trans. Syst. Control 2013, 8, 105–119. [Google Scholar]
- Stastny, T.; Dash, A.; Siegwart, R. Nonlinear MPC for fixed-wing UAV trajectory tracking: Implementation and flight experiments. In AIAA Guidance, Navigation, and Control Conference; AIAA: Grapevine, TX, USA, 2017; pp. 1–14. [Google Scholar]
- Emami, S.A.; Rezaeizadeh, A. Adaptive model predictive control-based attitude and trajectory tracking of a VTOL aircraft. IET Control Theory Appl. 2018, 12, 2031–2042. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, J.; Zhu, B.; Qin, K. Synchronised trajectory tracking for a network of MIMO non-minimum phase systems with application to aircraft control. IET Control Theory Appl. 2018, 12, 1543–1552. [Google Scholar] [CrossRef]
- Wang, X.; Sang, Y.; Zhou, G. Combining stable inversion and H-infinity synthesis for trajectory tracking and disturbance rejection control of civil aircraft autolanding. Appl. Sci. 2020, 10, 1224. [Google Scholar] [CrossRef]
- Buelta, A.; Olivares, A.; Staffetti, E. Iterative learning control for precise aircraft trajectory tracking in continuous climb operations. In Thirteenth USA/Europe Air Traffic Management Research and Development Seminar; EUROCONTROL and the U.S. Federal Aviation Administration: Vienna, Austria, 2019. [Google Scholar]
- Buelta, A.; Olivares, A.; Universidad, E.S. Iterative learning control for precise aircraft trajectory tracking in continuous descent approaches. In Proceedings of the 8th European Conference for Aeronautics and Aerospace Sciences, EUCASS Association, Madrid, Spain, 1–4 July 2019. [Google Scholar]
- Munoz, F.; Espinoza, E.S.; Gonzalez-Hernandez, I.; Salazar, S.; Lozano, R. Robust trajectory tracking for unmanned aircraft systems using a nonsingular terminal modified super-twisting sliding mode controller. J. Intell. Robot. Syst. 2019, 93, 55–72. [Google Scholar] [CrossRef]
- Panathula, C.B.; Rosales, A.; Shtessel, Y.B.; Fridman, L.M. Closing gaps for aircraft attitude higher order sliding mode control certification via practical stability margins identification. IEEE Trans. Control Syst. Technol. 2018, 26, 2020–2034. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, Y.; Ai, J. Full-altitude attitude angles envelope and model predictive control-based attitude angles protection for civil aircraft. Aerosp. Sci. Technol. 2016, 55, 292–306. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, B.; Zhang, Y. A novel robust attitude control for quadrotor aircraft subject to actuator faults and wind gusts. IEEE/CAA J. Autom. Sin. 2018, 5, 292–300. [Google Scholar] [CrossRef]
- Liang, S.; Song, B.; Xuan, J. Active disturbance rejection attitude control for a bird-like flapping wing micro air vehicle during automatic landing. IEEE Access 2020, 8, 171359–171372. [Google Scholar] [CrossRef]
- Zhang, S.; Han, W.; Zhang, Y. Finite time convergence incremental nonlinear dynamic inversion-based attitude control for flying-wing aircraft with actuator faults. Actuators 2020, 9, 70. [Google Scholar] [CrossRef]
- Poksawat, P.; Wang, L.; Mohamed, A. Gain scheduled attitude control of fixed-wing UAV with automatic controller tuning. IEEE Trans. Control Syst. Technol. 2018, 26, 1192–1203. [Google Scholar] [CrossRef]
- Duan, L.; Hou, Z.; Yu, X.; Jin, S.; Lu, K. Data-driven model-free adaptive attitude control approach for launch vehicle with virtual reference feedback parameters dining method. IEEE Access 2019, 7, 54106–54116. [Google Scholar] [CrossRef]
- Li, C.; Zhang, T.; Yang, J. Attitude control of aircraft using only synthetic jet actuators when stall occurs. IEEE Access 2018, 6, 37910–37917. [Google Scholar] [CrossRef]
- He, Q.; Tan, Y.; Liu, X.; Jia, Q.; Liu, J. Reconfigurable nonlinear dynamic inversion for attitude control of a structurally damaged aircraft. IEEE Access 2020, 8, 199931–199943. [Google Scholar] [CrossRef]
- Guo, T.; Hou, Z.; Zhu, B. Dynamic modeling and active morphing trajectory-attitude separation control approach for gull-wing aircraft. IEEE Access 2017, 5, 17006–17019. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, X.; Li, Q.; Ren, Z. Integrated 4D trajectory and attitude adaptive controller for civil aircraft. Acta Aeronaut. Et Astronaut. Sin. 2019, 40, 522437. [Google Scholar]
- Hou, Z.S.; Xu, J.X. On data-driven control theory: The state of the art and perspective. Acta Autom. Sin. 2009, 35, 650–667. [Google Scholar] [CrossRef]
- Hou, Z. Parameter Identification, Adaptive Control and Model-Free Learning Adaptive Control. Ph.D. Thesis, Northeastern University, Shenyang, China, 1994. [Google Scholar]
- Hou, Z.; Jin, S. Model Free Adaptive Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Jin, S. On Model Free Learning Adaptive Control and Applications. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2008. [Google Scholar]
- Hou, Z.; Wang, Z. From model-based control to data-driven control: Survey, classification and perspective. Inf. Sci. 2013, 235, 3–35. [Google Scholar] [CrossRef]
- Hou, Z.; Chi, R.; Gao, H. An overview of dynamic-linearization-based data-driven control and applications. IEEE Trans. Ind. Electron. 2017, 64, 4076–4090. [Google Scholar] [CrossRef]
- Hou, Z.; Gao, H.; Lewis, F.L. Data-driven control and learning systems. IEEE Trans. Ind. Electron. 2017, 64, 4070–4075. [Google Scholar] [CrossRef]
- Javadi, A.; Pezeshki, S. A new model- free adaptive controller versus non-linear H-infinity controller for levitation of an electromagnetic system. Trans. Inst. Meas. Control 2013, 35, 321–329. [Google Scholar] [CrossRef]
- Bai, L.; Feng, Y.W.; Li, N.; Xue, X.F.; Cao, Y. Data-driven adaptive iterative learning method for active vibration control based on imprecise probability. Symmetry 2019, 11, 746. [Google Scholar] [CrossRef]
- Hou, Z.; Jin, S. A novel data-driven control approach for a class of discrete-time nonlinear systems. IEEE Trans. Control Syst. Technol. 2011, 19, 1549–1558. [Google Scholar] [CrossRef]
- Meng, Q.; Hou, Z. Data-driven multi-inverter cooperative control for voltage tracking and current sharing in islanded AC microgrids. Trans. Inst. Meas. Control 2019, 41, 3145–3157. [Google Scholar] [CrossRef]
- Lei, T.; Hou, Z.; Ren, Y. Data-driven model free adaptive perimeter control for multi-region urban traffic networks with route choice. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2894–2905. [Google Scholar] [CrossRef]
- Jiang, G.; Hou, Z. A data-driven approach for trajectory-based aircraft operation with controlled time of arrival and along-track wind effects. Trans. Inst. Meas. Control 2020, 42, 2166–2177. [Google Scholar] [CrossRef]
- Núñez, H.E.; Camino, F.M.; Bouadi, H. Towards 4D trajectory tracking for transport aircraft. IFAC-PapersOnLine 2017, 50, 8196–8201. [Google Scholar] [CrossRef]


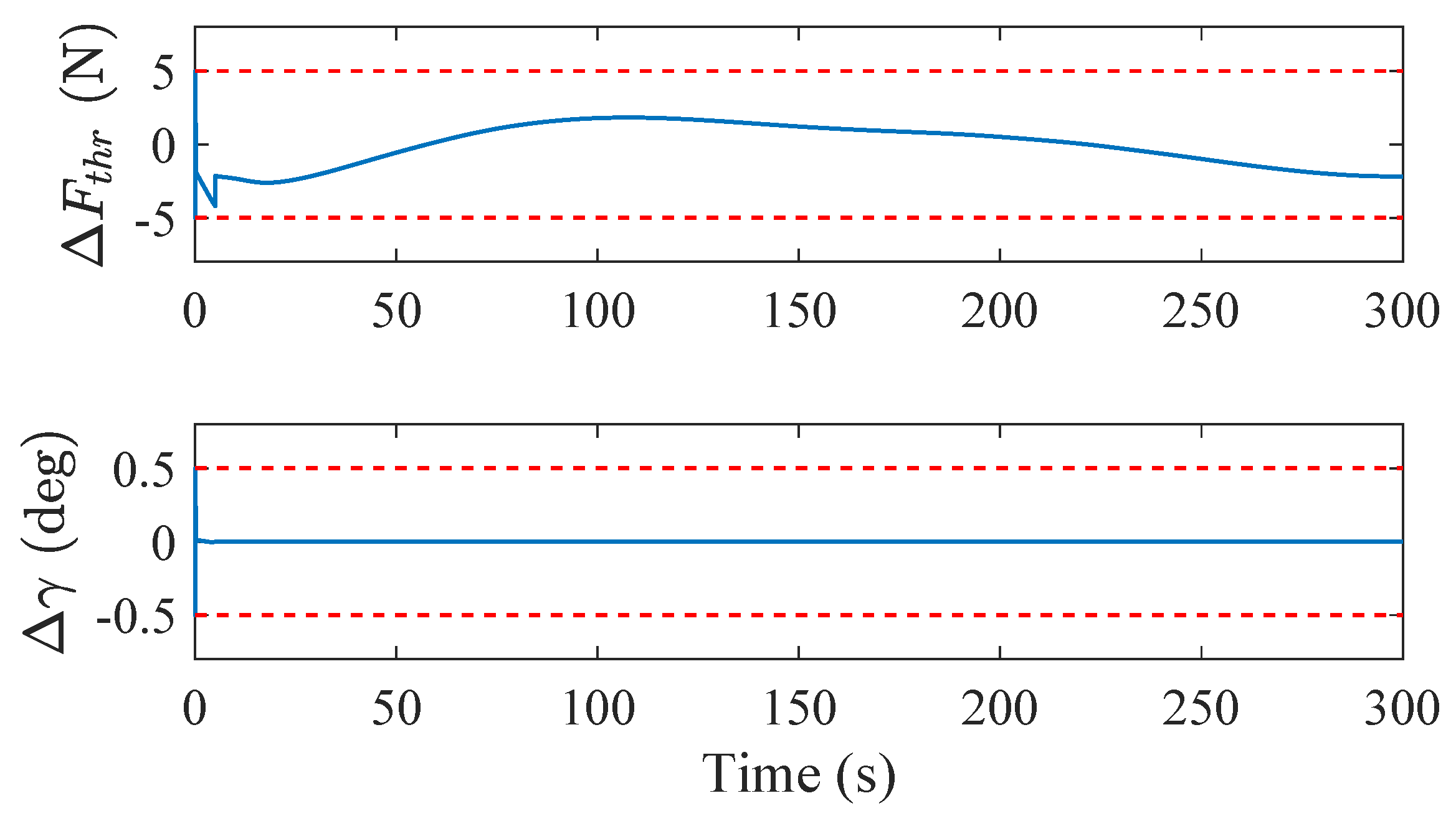
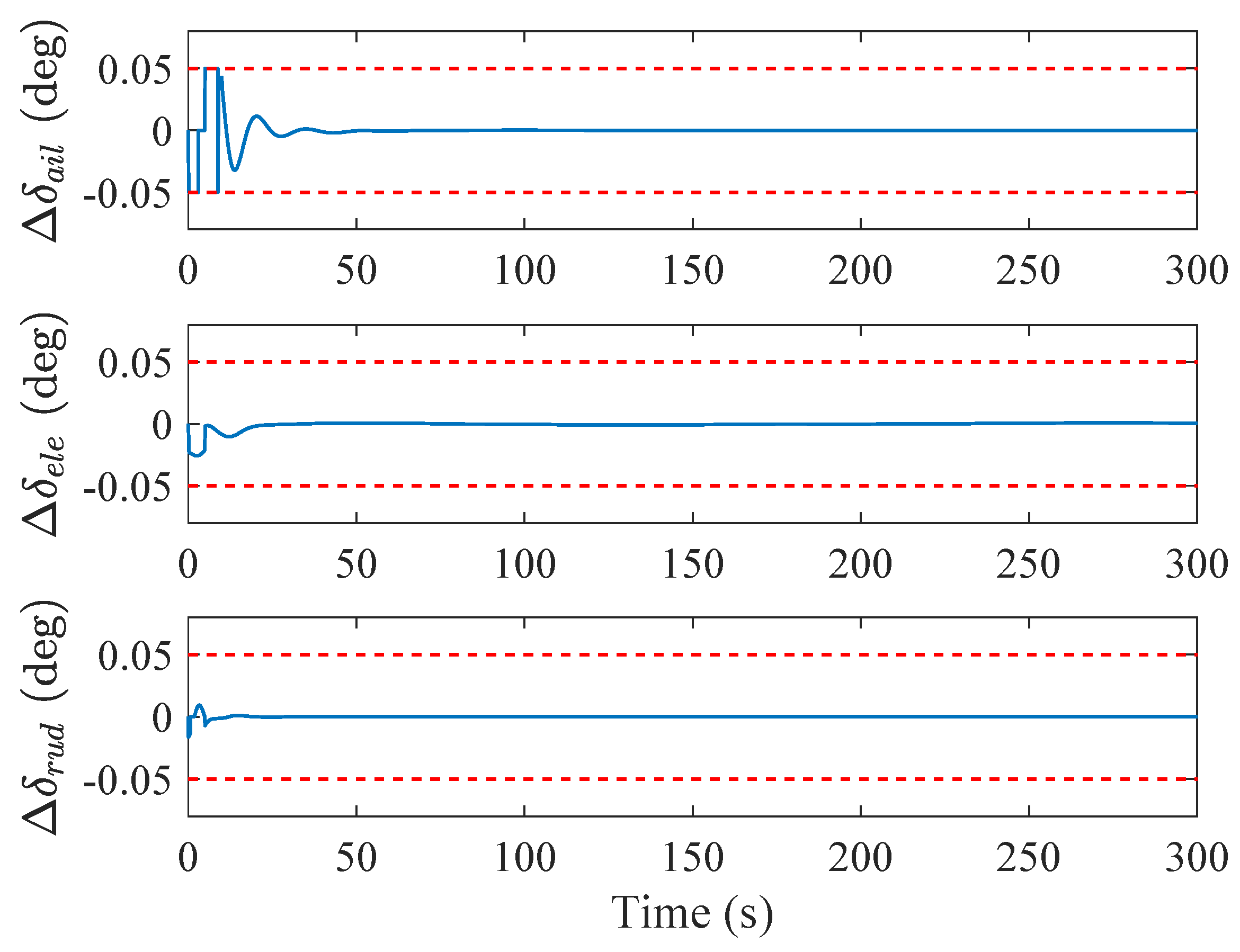
| Aircraft Parameters | Controller Parameters |
|---|---|
| m = 48,000 kg | |
| m | |
| m | |
| A = 1,278,369.56 | |
| B = 3,781,267.79 | |
| C = 4,877,649.98 | |
| E = 135,588.17 | |
| Control Input Increment | Control Input |
|---|---|
| NLI | 4.82 | 0.00 | 0.23 | 120.28 | 24.65 |
| FFDL-MFAC | 8.36 | 1.27 | 0.09 | 881.43 | 2.22 |
| NLI | 0.35 | 14.21 | 0.00 | 153,239.35 | 0.00 |
| FFDL-MFAC | 2.34 | 0.37 | 0.03 | 64,522.67 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Liu, G.; Yu, H. A Model Free Adaptive Scheme for Integrated Control of Civil Aircraft Trajectory and Attitude. Symmetry 2021, 13, 347. https://doi.org/10.3390/sym13020347
Jiang G, Liu G, Yu H. A Model Free Adaptive Scheme for Integrated Control of Civil Aircraft Trajectory and Attitude. Symmetry. 2021; 13(2):347. https://doi.org/10.3390/sym13020347
Chicago/Turabian StyleJiang, Gaoyang, Genfeng Liu, and Hansong Yu. 2021. "A Model Free Adaptive Scheme for Integrated Control of Civil Aircraft Trajectory and Attitude" Symmetry 13, no. 2: 347. https://doi.org/10.3390/sym13020347
APA StyleJiang, G., Liu, G., & Yu, H. (2021). A Model Free Adaptive Scheme for Integrated Control of Civil Aircraft Trajectory and Attitude. Symmetry, 13(2), 347. https://doi.org/10.3390/sym13020347






