Abstract
In this paper, a 2-gyrogroup of order , , is constructed in which every proper subgyrogroup is either a cyclic or a dihedral group. It is proved that the subgyrogroup lattice and normal subgyrogroup lattice of are isomorphic to the subgroup lattice and normal subgroup lattice of the dihedral group of order , which causes us to use the name dihedral gyrogroup for this class of gyrogroups of order . Moreover, all proper subgyrogroups of are subgroups.
MSC:
Primary 20N05; Secondary 20F99; 20D99
1. Basic Concept and History
A pair consisting of a nonempty set G and a binary operation is called a groupoid. A bijection from the groupoid G to itself is called an automorphism of G if , for all . The set of all automorphisms of G is denoted by . It is straightforward to check that forms a group under composition of function.
A groupoid is called a gyrogroup if the following conditions are satisfied:
- there exists an element such that for all , ;
- for each , there exists such that ;
- (gyroassociative law) there exists a function such that for every , , where ;
- for each , =.
The gyrogroup G is called gyrocommutative if and only if for all , =. The function , , is called the gyroautomorphism generated by a and b. Note that the axioms of a gyrogroup apply their right counterpart. Suppose G is a group and , where denotes the trivial automorphism and are arbitrary elements of G. Then it is easy to see that G will have the structure of a gyrogroup. This shows that gyrogroup is a generalization of the classical notion of a group.
Abraham Ungar in his seminal paper [1] initiated a new approach to special theory of relativity and in [2], he employed the Thomas precession and its interplay with Einstein’s addition to formally defines gyrogroups. In 2001, Ungar published a book containing many results about gyrogroups and gyrovector spaces [2]. In [3], he applied gyrogroups and gyrovector spaces to introduce an interesting analogy between three models in hyperbolic geometry: the Poincar ball model, the Beltrami ball model and the PV space model. In [4], it is shown that the gyrocommutative gyrogroups and their resulting gyrovector spaces in hyperbolic geometry have the role as vector spaces in Euclidean geometry. In 2009, Ungar published another book in which he presented his idea that Thomas gyration turns Euclidean geometry into hyperbolic geometry, and what philosophical analogies the two geometries share [5]. Ungar published four other books [6,7,8,9] and some survey articles like [10] in which he explained the history and philosophy of his theory.
In this paper, we present an algebraic approach to constructing new gyrogroups. We will construct a gyrogroup , of order by considering a cyclic group of order . It is proved that all proper subgyrogroups of are either cyclic or dihedral groups. The structure of the subgyrogroup lattice of will also be given.
2. Preliminaries
In this section we introduce some useful lemmas which are crucial in our main results. We refer to [11,12] for the main properties of the subgyrogroups, gyrogroup homomorphisms and quotient gyrogroup. Our calculations are done with the aid of GAP [13].
Throughout this paper , and , where is a natural number. It is clear that is a cyclic group under addition modulo and . This shows that . Define the binary operation ⊕ on as follows:
and are the following non-negative integers:
Suppose the greatest common divisor of positive integers r and s is denoted by . It is obvious that the operation ⊕ is well-defined, and if and are simultaneously in or , then .
Lemma 1.
Suppose is defined as:
where and . Then A is an automorphism of .
Proof.
It is clear that the mapping A is well defined, one to one and onto mapping on . To prove A is a homomorphism, we assume are arbitrary elements. If , then it is obvious that . Our main proof will consider three separate cases as follows:
- 1.
- 2.
- 3.
This completes our argument. □
Set , , and . Define the map as follows:
where I is the identity automorphism of and A is the automorphism defined in Lemma 1.
3. Main Results
The aim of this section is to construct finite gyrogroups of order by cyclic group , for .
Theorem 1.
is a gyrogroup.
Proof.
By Lemma 1, . By definition of ⊕, and so 0 is the identity element of . It is easy to see that the inverse of each element can be computed by the following formula:
in which is the inverse of x in .
Now we will prove the loop property. Suppose is an arbitrary element of . We will have four separate cases as follows:
- 1.
- . In this case, . Clearly . Thus, by definition of , as desired.
- 2.
- . In this case, and
- 3.
- . In this case, andIf , then by Equation (8), we have the following two subcases:
- (a)
- and . In this case, and by definition of , .
- (b)
- and . In this case, . For every , if , then If , then such that .
If , then by Equation (8), we have the following two subcases:- (a)
- and . In this case . The proof is now similar to the subcase (a).
- (b)
- and . In this case . The proof of this subcase is similar to the subcase (b).
- 4.
- . In this case, and The proof of this case is similar to (3) and so it is omitted.
Therefore, the loop property is valid. Finally, we investigate the left gyroassociative law. To do this, we have four separate cases as follows:
- 1.
- . In this case and . If , then and by definition of ⊕, we have:This proves that . If , then and by definition of ⊕,Therefore, , which proves the left gyroassociative law for this case.
- 2.
- . In this case, andin which . We consider two subcases as follows:
- 3.
- . In this case, andWe consider two subcases as follows:
- (a)
- . In this subcase, and if , then . Now by definition ⊕,By Equation (14), . If , then and by definition of ⊕,By the last equalities, .
- (b)
- . In this subcase, . If , then and . A similar argument as Equation (14) shows that . If , then , and . Apply again definition of ⊕ to deduce thatBy the last equalities, .
- 4.
- . In this case, and =A, when ; and I, otherwise. We now consider the following two subcases:
Hence the result. □
Example 1.



In this example, we investigate the gyrogroup of order 8 constructed by the cyclic group . By definition, and the binary operation ⊕ is defined as follows:
in which , and . Also,
Therefore, the addition table and the gyration table for are presented in Table 1 in which A is the unique nonidentity gyroautomorphism of given by . Also, the addition table and the gyration table for are presented in Table 2 and Table 3 in which A is the unique nonidentity gyroautomorphism of given by .

Table 1.
The addition and Gyration Tables of . (a) The addition table of . (b) The gyration table of such that .

Table 2.
The addition table of .

Table 3.
The gyration table of such that .
Theorem 2.
The gyrogroup is non-gyrocommutative.
Proof.
We know , for . If , then by Example 1, and . Therefore, in this case is non-gyrocommutative. For , suppose that is gyrocommutative. So, for every , the following equality is satisfied:
Suppose and . By definition, , and . Also, , such that and . Thus and . By these relations and Equation (16), =. This proves that and so . Therefore, and hence which is a contradiction. □
Theorem 3.
Let be the dihedral 2-gyrogroup of order . B is a subgyrogroup of if and only if it has one of the following forms:
- 1.
- ;
- 2.
- B is a subgroup of ;
- 3.
- , where ;
- 4.
- There are integers r and s such that , and , where .
Proof.
Suppose B is a proper subgyrogroup of . We first assume that . Since the restriction of ⊕ to B is the group addition of , B will be a subgroup of , as desired. We next assume that . Since can be partitioned by and , we can write the subgyrogroup B as in which and . It is easy to see is a subgroup of . Suppose and . By an easy calculation one can see that () if and only if () if and only if () if and only if (). Since , . This shows that and , for some . Therefore, B has the form of . Finally, suppose that , . We will prove that , for some s, . Choose arbitrary elements . By definition and there exists an integer k such that and so . Suppose x is the least element of , then in which . If , then and so . This shows that . Next fix an element . Define two one to one mappings and by and . This proves that and so , as desired.
Conversely, it is obvious that is a subgyrogroup of itself. Suppose H is a subgroup of , then by (Proposition 23) [14] it will be a subgyrogroup of . We now assume that , where . By definition of , and by (Proposition 22) [14], H is a subgyrogroup of . Finally, we assume that , where r and s are positive integers such that and . If then . If and , then there are integers such that , and === . Hence, =. A similar calculations shows that if , or then . This completes the proof. □
4. Concluding Remarks
Miller [15] characterized the non-abelian and non-dihedral finite group G with this property that all non-abelian subgroups of G are dihedral. In this paper, we continue an earlier work of some of us [16] to construct a 2-gyrogroup of order , , such that all non-abelian subgyrogroups are dihedral. The structure of the subgyrogroups and normal subgyrogroups are completely determined. As a consequence, the subgyrogroup lattice and the normal subgyrogroup lattices of are isomorphic to the subgroup and normal subgroup lattices of , respectively. Therefore, all non-abelian subgroups of G are dihedral. This is a research problem for future to characterize non-degenerate gyrogroups for which all subgyrogroups are subgroups and non-abelian subgroups of this gyrogroup are dihedral.
Suppose denotes as usual the subgyrogroup generated by the set . By Theorem 3, it is easy to prove that , , ⋯, , , , , . In Figure 1, the subgyrogroup and normal subgyrogroup lattices of are depicted. In this figure, the circled subgyrogroups are denoted the normal subgyrogroups of . Because of this similarity between the dihedral group and the gyrogroup of order , we like to use the name dihedral gyrogroup of order for . Moreover, all proper subgyrogroups of , are subgroups, see Figure 2.
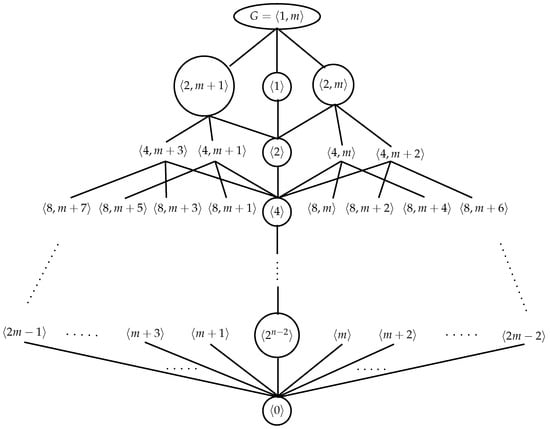
Figure 1.
The subgyrogroup and normal subgyrogroup lattices of .
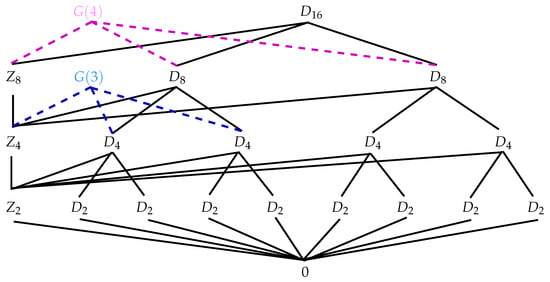
Figure 2.
The subgyrogroup lattice of , , and in one frame.
We end this paper with the following question:
Question 1.
Is it possible to apply the same method for constructing a gyrogroup of order , , in which the the subgyrogroup and normal subgyrogroup lattices of are isomorphic to the subgroup and normal subgroup lattices of respectively?
Note that for every integer n, , A is an automorphism of order two and so is a group of order 2.
Author Contributions
S.M., A.R.A., M.A.S., and A.A.U. contributed equally to this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ungar, A.A. Thomas rotation and parametrization of the Lorentz transformation group. Found. Phys. Lett. 1988, 1, 57–89. [Google Scholar] [CrossRef]
- Ungar, A.A. Beyond the Einstein Addition Law and Its Gyroscopic Thomas Precession: The Theory of Gyrogroups and Gyrovector Spaces; Fundamental Theories of Physics; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 2001; Volume 117. [Google Scholar]
- Ungar, A.A. Analytic Hyperbolic Geometry: Mathematical Foundations and Applications; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2005. [Google Scholar]
- Ungar, A.A. Analytic Hyperbolic Geometry and Albert Einstein’s Special Theory of Relativity; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2008. [Google Scholar]
- Ungar, A.A. A Gyrovector Space Approach to Hyperbolic Geometry; Synthesis Lectures on Mathematics and Statistics; Morgan & Claypool Publishers: Williston, VT, USA, 2009; Volume 4. [Google Scholar]
- Ungar, A.A. Beyond Pseudo-Rotations in Pseudo-Euclidean Spaces: An Introduction to the Theory of Bi-Gyrogroups and Bi-Gyrovector Spaces; Mathematical Analysis and Its Applications; Academic Press: London, UK, 2018. [Google Scholar]
- Ungar, A.A. Analytic Hyperbolic Geometry in N Dimensions: An Introduction; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Ungar, A.A. Barycentric Calculus in Euclidean and Hyperbolic Geometry: A Comparative Introduction; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2010. [Google Scholar]
- Ungar, A.A. Hyperbolic Triangle Centers: The Special Relativistic Approach; Fundamental Theories of Physics; Springer: Dordrecht, The Netherlands, 2010; Volume 166. [Google Scholar]
- Ungar, A.A. The intrinsic beauty, harmony and interdisciplinarity in Einstein velocity addition law: Gyrogroups and gyrov, ector spaces. Math. Interdisc. Res. 2016, 1, 5–51. [Google Scholar]
- Suksumran, T.; Wiboonton, K. Lagranges theorem for gyrogroups and the Cauchy property. Quasigroups Relat. Syst. 2014, 22, 283–294. [Google Scholar]
- Suksumran, T.; Wiboonton, K. Isomorphism theorems for gyrogroups and L-subgyrogroups. J. Geom. Symmetry Phys. 2015, 37, 67–83. [Google Scholar]
- The GAP Team. GAP—Groups, Algorithms, and Programming. Version 4.5.5. 2012. Available online: http://www.gap-system.org (accessed on 12 February 2021).
- Suksumran, T. The algebra of gyrogroups: Cayley’s theorem, Lagrange’s theorem, and isomorphism theorems. In Essays in Mathematics and Its Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 369–437. [Google Scholar]
- Miller, G.A. Groups in which every subgroup is either abelian or dihedral. Trans. Am. Math. Soc. 1907, 29, 289–294. [Google Scholar] [CrossRef]
- Mahdavi, S.; Ashrafi, A.R.; Salahshour, M.A. Construction of new gyrogroups and the structure of their subgyrogroups. Algebr. Struct. Appl. 2020. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).