Abstract
Given the tunability of their optical properties over the UV–Visible–Near IR spectral range, ligand-capped quantum dots (QDs) are employed for the design of optical biosensors with low detection threshold. Thanks to non-linear optical spectroscopies, the absorption properties of QDs are indeed used to selectively enhance the local vibrational response of molecules located in their vicinity. Previous studies led to assume the existence of a vibroelectronic QD–molecule coupling based on dipolar interaction. However, no systematic study on the strength of this coupling has been performed to date. In order to address this issue, we use non-linear optical Two-Color Sum-Frequency Generation (2C-SFG) spectroscopy to probe thick QD layers deposited on calcium fluoride (CaF) prisms previously functionalized by a self-assembled monolayer of phenyltriethoxysilane (PhTES) molecules. Here, 2C-SFG is performed in Attenuated Total Reflection (ATR) configuration. By comparing the molecular vibrational enhancement measured for QD–ligand coupling and QD–PhTES coupling, we show that the spatial dependence of the QD–molecule interactions (∼1/r, with r the QD–molecule distance) is in agreement with the hypothesis of a dipole–dipole interaction.
1. Introduction
As semiconductor nanoparticles, colloidal quantum dots (QDs) evince unique optical and electronic properties deriving from the quantum confinement of their laser-excited electron-hole pairs. With diameters ranging between 1 and 10 nm, QDs are able to absorb and emit light over the visible range [,,,,]. Hence, they are largely employed within various scientific fields such as photovoltaics [,], photocatalysis [,,], fluorescence spectroscopy [,], biomedical imaging [,,], and biosensing [,,,,,]. In the later case, QDs are often used as fluorescent probes. Indeed, their spectral and temporal emission properties are highly sensitive to their chemical environment, including capping ligands, solvent, pH, ion concentration, cross-linking molecules, and biomolecules [,,,,,,,,]. As a result, the literature extensively reports how the chemical medium of QDs influence their optical properties, especially within the framework of biosensors.
For some years now, our team has investigated the possibility of a reciprocal coupling enabling to use the optical and electronic behavior of QDs in order to influence their molecular surroundings [,]. Since then, the aim is to design biosensors wherein QDs are employed as optoelectronic enhancers instead of fluorescent probes. Thanks to non-linear Two-color Sum-Frequency Generation (2C-SFG) spectroscopy combining a visible and an infrared laser beams, we previously proved that the amplitude of the vibrational response of the ligands (over the IR range) was modulated by the linear optical susceptibility of the QDs (over the visible range), []. To evidence such a vibroelectronic correlation, we performed 2C-SFG spectroscopy on thick layers of QDs deposited on CaF prisms. From the symmetry rules proper to second-order optical processes [], 2C-SFG spectroscopy is actually surface-specific and then constitutes an ideal tool to study the interactions occurring at the interface between QDs and molecules, both immobilized on a solid substrate. Besides, CaF prisms benefit from favorable Local Field correction factors (reflectivity) in ATR configuration (Figure 1a) as explained in Section 3.1. In this way, we succeeded in measuring the vibrational spectrum of the QD ligands (from 3.2 to 3.6 m, i.e., 2800 to 3000 cm) under a visible excitation whose wavelength varied between 450 and 620 nm. This previous study thus demonstrated a spectral correlation between the ligand vibration amplitudes and []. On a theoretical point of view, we assumed it arose from a dipolar interaction between the QDs, on one side, and the molecules, on the other side. However, this assumption has not been experimentally attested so far. Especially, our aim here is to assess the spatial dependence of the vibroelectronic coupling with respect to the distance between QDs and molecules.
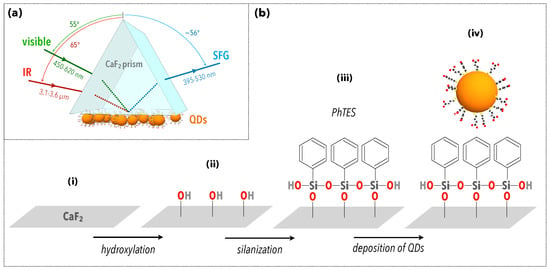
Figure 1.
(a) Scheme of the experimental configuration used to perform SFG spectroscopy on a quantum dot (QD) layer deposited on a CaF prism. The surface of the prism is first functionalized by PhTES molecules. (b) Description of the different steps of the chemical preparation of the sample. (i) The prism initially has a surface layer of CaF, which is mainly oxidized. (ii) Hydroxylation then leads to the activation of silanol groups that serve as the attachment base for (iii) the grafting of PhTES molecules. (iv) The deposition of QDs is then obtained by drop-casting. (See Materials and Methods for details.)
In this paper, we chose to study the interaction between, on the one hand, a thick layer of colloidal CdTeS QDs capped with mercaptocarboxylic acids and, on the other hand, a self-assembled monolayer of phenyltriethoxysilane molecules (PhTES), both deposited or grafted on a CaF prism. PhTES actually displays two great advantages for our study: first, it can be grafted on CaF in the form of a monolayer and be used as a molecular probe to assess the strength and the range of the vibroelectronic coupling induced by the overlying QDs; second, the IR vibrational response of its aromatic rings is characterized by CH stretching modes located at ∼3060 cm [], which is out of the range of the QD ligands (from 2800 to 3000 cm) []. Thanks to this approach, we show that the vibroelectronic coupling already seen between QDs and their ligands, chemically bound to their surface and thus very close to them, can also be observed with molecules which are further from their surface. First, this teaches us that the coupling is not mediated by strong chemical bounds. Second, compared to the ligands, the intensity of the coupling proves to be two times lower in the case of PhTES. This ratio is consistent with a spatial dependence of the coupling following , where r is the QD–molecule distance, therefore compatible with the hypothesis of a dipole–dipole interaction.
2. Materials and Methods
Preparation of CdTeS QD. CdTe (cadmium telluride) QDs were purchased from Sigma-Aldrich (Saint-Quentin-Fallavier, France): Ref. 777935 CdTe core-type 25 mg (www.sigmaaldrich.com/catalog/product/aldrich/777935, accessed on January 2021). These commercial QDs are coated with carboxylic acid functional ligands (COOH) and are provided through water-soluble powders. According to Ref. [], their mean radius is nm. The stock solution was prepared in Milli-Q water (18 Mcm, Millipore, France) for a QD density m (i.e., ∼0.6M). Previous works [,] have shown that the nanocrystals are CdTeS alloys and that the ligands are HS-(CH)-COOH, with .
Preparation of Prism/PhTES/QD interface. To graft PhTES molecules and deposit QDs on an equilateral CaF prism (Fichou, flatness: at 633 nm, sample base size: 25 mm), we first washed the prism in acetone (99.8%, Sigma-Aldrich) and ethanol (99.8%, Sigma-Aldrich) using a sonication bath, and then we cleaned it with a piranha solution (HO 30%:HSO 96%, 1:2, Sigma-Aldrich). It was rinsed with Milli-Q water (18 Mcm, Millipore, France) and dried under nitrogen gas flow. For the grafting of the PhTES monolayer, we prepared a 5% solution of phenyltriethoxysilane (679291-50G Triethoxyphenylsilane, ≥98%, Sigma-Aldrich) in anhydrous methanol (MeOH, 99.9%,VWR). One percent solution is equivalent to 1 g of PhTES in 100 mL of methanol. The prism was immersed in 4 mL of this solution for 1 h and 30 min under a fume hood at 20 °C, then rinsed in methanol under sonication (four baths of 1 min), and finally dried under nitrogen flow. The result of this process is shown in Figure 1b, step iii. The deposition of QDs then consisted of spreading a droplet (50 L) of the stock solution on one face of the prism and drying it with nitrogen.
UV–visible spectroscopy. UV–visible absorbance spectra of the Prism/PhTES/QD sample was recorded using a Cary-5000 spectrophotometer (Agilent) in transmission. A bare CaF prism was used as reference. The absorbance curve was thus obtained by differential measurement.
Non-linear 2C-SFG spectroscopy. Vibrational SFG spectra were acquired thanks to a home-made setup described in Ref. []. A pulsed IR laser source (Nd:YVO, 1064 nm, 7.5 ps, HighQ laser) was coupled to an acousto-optic modulator (AA Opto-Electronic, 62.5 MHz micropulse repetition rate, 2 s train, 25 Hz macropulse repetition rate) and underwent a power amplification step based on the successive double round-trip passage of the incident beam through two successive water-cooled Nd:YVO crystals (Quantel flash pump laser system); this step temporally widened the pulse up to 12 ps with 1.3 W mean power at the output. The latter was therefore used to pump two optical parametric oscillators (OPO) with a pump power ratio of 35% and 65% for the IR and visible OPOs described, respectively as follows: (i) the IR OPO based on a lithium niobate (LiNBO) non-linear crystal continuously tunable in the 2500–4000 cm spectral range (spectral resolution fixed to 3 cm thanks to a Fabry–Perot slide inserted inside the OPO cavity in a direction normal to the beam propagation; output mean power at 3.45 µm: 30 mW) and, (ii) the visible OPO based on a non-linear BBO (-BaBO) crystal continuously tunable between 440 and 710 nm (spectral resolution fixed to 6 cm thanks to a Fabry–Perot slide inserted inside the OPO cavity in a direction normal to the beam propagation; output mean power at 520 nm: 20 mW) for which we selected five specific wavelengths in the SFG experiments: 450, 488, 520, 568, and 612 nm, respectively. It is worth noting that the BBO crystal inside the visible OPO cavity was pumped by an ultraviolet beam (wavelength: 355 nm, mean power: 200 mW) obtained after frequency conversion of the pump beam from successive passage through two non-linear crystals: (i) a BBO crystal that converts a part of the incident IR beam (1064 nm) into a green visible beam (532 nm) by frequency doubling, (ii) a LBO (lithium triborate, LiBO) crystal that mixes the green beam and the remaining part of the incident IR beam, giving rise to the ultraviolet beam by a sum-frequency generation process. The infrared and visible beams were then coherently mixed at the same point of the functionalized surface of the prism, as illustrated in Figure 1a. Both beams were in Gaussian beam mode with 2 mm diameter on the sample surface in order to avoid sample damage. The two input beams were -polarized, and the -component of the SFG output beam was collected by photomultipliers after spatial and spectral filtering through Raman filters (Kaiser Optical Systems, for each of the five incident corresponding visible wavelengths) and a monochromator (Princeton Instruments, Acton SpectraPro SP-2500, 500 nm triple grating imaging spectrometer). Besides, in order to compensate for the intensity fluctuations of the laser source, the SFG signal of a reference ZnS crystal was acquired in the same conditions and used to normalize the SFG intensity of the sample. 2C-SFG measurements were performed at ambient air in a dark experimental room with temperature fixed at 22 °C. All the laser, OPO, and spectroscopic setups were embedded in a protective box on the optical table with a monitored humidity less than 10% thanks to the presence of a circulating nitrogen flow under the box during measurements, which minimized IR OPO absorption in the probed spectral range.
3. Results
3.1. Structural and Chemical Characterizations of the QD/Molecule Interface
In order to probe the vibroelectronic coupling between QDs and phenyltriethoxysilane (PhTES), the CaF prism was first functionalized by an organic monolayer of PhTES, as depicted in Figure 1b (steps i to iii). The QD layer was then deposited through drop-casting, by drying 50 L of a QD colloidal solution under nitrogen (Figure 1b, step iv). The UV–visible absorption spectrum of this Prism/PhTES/QD sample is given in Figure 2a. The semiconductor gap of the CdTeS QDs was characterized by a first absorption peak located at 488 nm. Thanks to a mathematical model developed in previous works [,], it is possible to extract the surface density of QDs, which was here up to 7.68 nm, and to estimate a layer thickness of 300 nm. This dense QD layer is expected to contribute to the vibrational SFG signal through the vibration modes of the ligands: mercaptocarboxylic acids, HS-(CH)-COOH, with . The SFG spectrum of Figure 2b indeed exhibits the five vibration modes of mercaptocarboxylic acids between 2800 and 3000 cm. They correspond to []: the symmetric (2856 cm), asymmetric (2929 cm), and exotic (2910 cm) stretching modes of CH; the symmetric (2883 cm) and asymmetric (2871 cm) stretching modes of CH [,]. This spectrum also shows a new, intense peak located at 3062 cm that can be ascribed to the CH stretching modes of PhTES aromatic rings and, thus, proves how efficient the chemical grafting of PhTES on the prism is. Indeed, such aromatic modes revealed to be hardly observable by SFG spectroscopy on metals [,], especially compared with CH and CH stretching modes. Here, we show that the combination of the ATR configuration and the QD layer deposition enhanced the signal associated to aromatic CH stretching modes. The ATR configuration allowed the coupling of light with the PhTES/QD layer through the generation of an evanescent electromagnetic wave at the interface. This evanescent wave had a decreasing intensity through the QD layer in the z-direction normal to the sample surface. The ATR coupling configuration is efficient on a distance related to the wavelength of the beams. In the present case, the visible and incident beams were in total reflection, generating two evanescent waves whose the intensity was significant at least until 450 nm deep in the z-direction because it corresponds to the lowest visible beam wavelength used in the process (while the IR one being around 3 µm is 10 times greater). In both cases, the penetration depth was greater than the sample layer thickness of 300 nm mentioned before. ATR configuration is thus of particular interest in SFG spectroscopy because the surface-specificity of the probe relies on the breaking of symmetry induced by the CaF prism in terms of spatial symmetry (existence of an interface) and local electric field symmetry (existence of a dielectric gap), leading thus to evanescent waves at the sample interface []. Moreover, given that SFG is sensitive to the symmetry of the sample in the z-direction pointing out of the interface, the presence of such an intense peak means that the PhTES layer is very well ordered, with a great isotropy of the PhTES monolayer in the plane parallel to the prism surface. As a result, PhTES constitutes a very good molecular probe to assess the strength and the range of the vibroelectronic coupling induced by the QDs beyond their ligands.
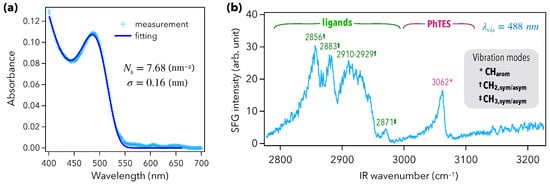
Figure 2.
(a) UV–visible absorption spectra of the Prism/PhTES/QD sample. The continuous curve is a fit to the data. The fitting procedure is only based on two parameters: the surface density of QDs, and their size dispersion (radius). (b) Vibrational SFG spectrum of the Prism/PhTES/QD sample performed at a fixed visible wavelength of 488 nm.
3.2. Vibroelectronic Correlation between QDs and Aromatic Rings
Benefiting from a tunable visible laser beam, we acquired five vibrational SFG spectra for five different fixed visible wavelengths: 450, 488, 520, 568, and 612 nm (Figure 3a). In order to get a greater precision on the measurement of the vibration amplitude associated to PhTES at 3062 cm, we optimized the spatial overlap between the visible and IR beams, at the sample point, over the range 3000–3100 cm. This explains why the amplitudes of the aromatic mode (resp. of the ligand modes) were higher (resp. lower) than those of Figure 2b. As expected, the vibration amplitude of the aromatic CH stretching mode was maximum when the visible wavelength coincided with the first peak of excitonic absorption at 488 nm. It evidences that the vibroelectronic coupling previously observed with the ligands (chemically bound to the QD surface) was also efficient and above all quantifiable according to the distance, with molecules which are not located within the direct chemical environment of the QDs (and not chemically bound to their surface) as calculated below in Section 4. This was not possible to be calculated in disorganized monolayers made of APTES (3-aminopropyltriethoxysilane) []. Here again, the vibration amplitude of the aromatic rings was driven by the linear susceptibility of the QDs, which was resonant around the semiconductor gap at 488 nm, proving the generality of the first observations []. However, contrary to the ligand modes which vanish when the visible wavelength deviated from 488 nm (Figure 3a, 2900–3000 cm IR spectral range), the vibration amplitude was much less altered at the other four visible wavelengths (Figure 3a, 3062 cm IR wave number). This means that the ability of the QDs to modulate the vibrational response of PhTES was weaker than for the ligands.
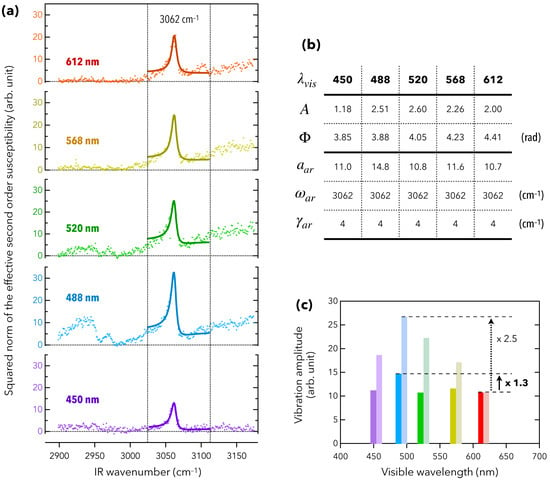
Figure 3.
(a) SFG spectra of the Prism/PhTES/QD interface. These spectra consist in performing the vibrational spectroscopy of the sample over the IR range 2900–3200 cm for five different fixed visible wavelengths, as indicated in nanometers on the left. The bold curves are fits to the experimental data. (b) Table gathering the fitting parameters corresponding to the fit curves of Figure 3a. They refer to Equation (1). (c) Superposition of, i, the vibration amplitudes of aromatic rings (left-handed color bars), extracted from the fitting procedure, and, ii, the mean vibration amplitudes of the five vibration modes of ligands (right-handed color bars), extracted from []. To be compared to , the vibration amplitudes are rescaled so that .
Arising from a second-order optical process, SFG is driven by the second-order susceptibility tensor of the sample, , with . Taking into account the planar geometry of the Prism/PhTES/QD interface, it is possible to reduce this tensor to only four components , which combine themselves into an effective second-order susceptibility [,,]. Indeed, as calculated in Ref. [], in [:] polarization combination (for SFG, Vis, IR beams, respectively), only the -Local Field factor prevailed in such experiments with an ATR prism; the three other Local Field factors involved were significantly weaker, and their values were almost constant over the entire visible spectral range. In these conditions, only the -component was considered in order to distinguish it from the vibroelectronic coupling between QDs and molecules in our calculations of the vibration mode amplitudes from 2C-SFG experimental data. It is quite logical because this Local Field factor is associated to the z-electric field components of the IR and Visible beams, which are the only ones that probe the sample layer in depth, in the normal direction to the prism base, including therefore the QDs. This leads to consider the well-known following expression of the effective second-order susceptibility to fit the SFG data:
thus modeled as the sum of a non IR-resonant term associated to the substrate, whose amplitude and phase are A and , and an IR-resonant term associated to the PhTES molecules, consisting in a Lorentzian function centered at cm with the amplitude and the damping constant . From the SFG spectra of Figure 3a that give as a function of , it is possible to extract the vibration amplitudes of the aromatic rings for the five visible wavelengths. The results of the fitting procedure are gathered in Figure 3b. Figure 3c then reports the five values of with respect to the visible wavelength (left-handed color bars). According to the UV-visible absorption spectrum of Figure 2a, the QDs did not absorb at 612 nm, so that we can choose as a reference value for which there is no enhancement due to the optoelectronic activity of QDs. The enhancement factor at 488 nm is written as follows:
which is 1.9 times lower than that of the ligands established in Ref. [] (Figure 3c).
4. Discussion
In order to explain the spectral correlation between and , we assume the existence of a dipolar coupling between QDs and molecules, stating that the molecules feel the local electric field produced by the QDs as a response of their excitation by the visible laser beam []:
where the tensor relates the local electric field produced by the QDs to their dipole moment p:
and is the electric field of the input visible beam: . The dipole–dipole interaction is thus encoded by the tensor , depending on the distance r between QDs and molecules. Considering the QDs are isotropic, it is then possible to demonstrate that the vibration amplitudes of the surrounding molecules follow []:
Consequently,
First, we can estimate the QD–ligand distance by the mean radius nm of QDs [], and the QD–PhTES distance by , where is the length of mercaptocarboxylic acids. Second, the ratio between the two linear susceptibilities is not equal to 1. Indeed, they are the macroscopic susceptibilities of the QD layers (not the polarizability of an individual QD), and are thus proportional to the QD density within the thick layer. From UV–visible measurements, we extracted a coverage density of 7.68 nm for the Prism/PhTES/QD sample. In Ref. [], we measured a density of 6.6 nm for a Prism/QD sample. Hence,
Since , Equation (6) then leads to
Given that the QD ligands are mercaptocarboxylic acids of type HS-(CH)-COOH, with , this value of 0.51 nm must be compared to the lengths of thioglycolic acid, 0.43 nm (), mercaptopropionic acids, 0.54 nm (), and mercaptobutyric acid, 0.65 nm (). As a result, our estimation of nm, based on the hypothesis of a dipolar interaction between QD and molecules, is compatible with the chain length of mercaptopropionic acid, which is actually the most commonly used [,,]. In addition, studying the general case of an -dependence, Figure 4 tells us that the couple of parameters is the most consistent. These constitute decisive arguments in favor of an -dependence of the vibroelectronic coupling occurring at QD/molecule interface.
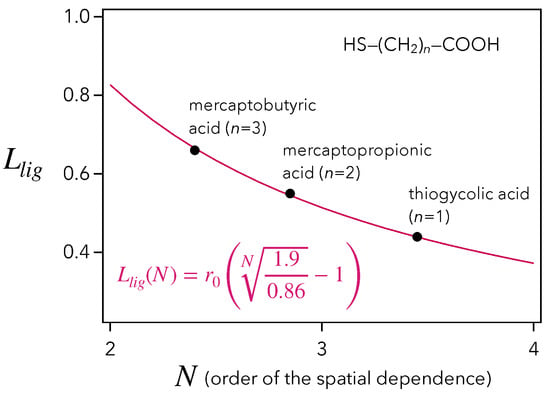
Figure 4.
Drawing of the QD ligand chain length (nm) as a function of the order N of the spatial dependence (red curve). The black dots indicate the lengths of the mercaptocarboxylic acids HS-(CH)-COOH ().
5. Conclusions
The strength of a dipolar coupling between semiconductor nanocrystals and phenyl probe molecules was quantified thanks to 2C-SFG spectroscopy performed in ATR configuration. From the measurement of the amplitudes of specific molecular vibration modes as functions of the distance between the QDs and, first, their chemical ligands then, second, a further PhTES monolayer, this study quantitatively evidenced the spatial dependence in ∼1/r of the dipole–dipole interaction. As a collateral result from this observation, 2C-SFG allowed to deduce that, in the present case, the QD ligands are mercaptopropionic acids, information not always given or known by the suppliers whatever the investigated system. Therefore, 2C-SFG spectroscopy proved to be well-suited for molecular recognition by taking profit of such a dipolar coupling from excitons to molecular vibrations. However, it also confirms that neat synthesis protocols and control experiments are mandatory when ligand-capped QDs are operated at the industrial level. Besides, in these extreme conditions, 2C-SFG spectroscopy revealed its potential to be used as an analytical probe for biosensing applications at the nanoscale level. Such an optical technique could therefore be used in the future for any type of sensor based on metal, semiconductor, or hybrid nanocrystals.
Author Contributions
T.N., L.D. and C.H. designed the sample configuration for UV–vis and 2C-SFG spectroscopy, and performed the 2C-SFG measurements. T.N. performed the UV–visible measurements, analyzed all the data, and wrote the original draft. T.N. also derived the analytical calculation of the dipole–dipole interaction to account for 2C-SFG measurements. T.N., L.D., A.T. and C.H. participated in the analysis and interpretation of the data and contributed to discussions and corrections during the writing process. L.D. and C.H. initiated and supervised the project. All authors have read and agreed to the published version of the manuscript.
Funding
Research leading to these results has received funding from the International Scientific Cooperation Program of the CNRS (Centre National de la Recherche Scientifique) under Grant agreement number PICS07339.
Data Availability Statement
The data presented in this study are available on reasonable request from the corresponding author.
Acknowledgments
The authors acknowledge Assistant Engineer B. Rieul (Université Paris-Saclay, Institut de Chimie Physique, CNRS, 91405 Orsay, France) for his technical assistance on the pilot control development of the SFG spectroscopy setup.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QD | Quantum Dot |
| 2C-SFG | Two-color Sum-Frequency Generation |
| ATR | Attenuated Total Reflection |
| PhTES | Triethoxyphenylsilane |
| APTES | 3-aminopropyltriethoxysilane |
References
- Brus, L.E. Electron-electron and electron-hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic states. J. Chem. Phys. 1984, 80, 4403–4409. [Google Scholar] [CrossRef]
- Masumoto, Y.; Sonobe, K. Size-dependent energy levels of CdTe quantum dots. Phys. Rev. B 1997, 56, 9734–9737. [Google Scholar] [CrossRef]
- Wang, X.; Yu, W.W.; Zhang, J.; Aldana, J.; Peng, X.; Xiao, M. Photoluminescence upconversion in colloidal CdTe quantum dots. Phys. Rev. B 2003, 68, 125318–125323. [Google Scholar] [CrossRef]
- Wuister, S.F.; Swart, I.; van Driel, F.; Hickey, S.G.; de Mello Donegá, C. Highly Luminescent Water-Soluble CdTe Quantum Dots. Nano Lett. 2003, 3, 503–507. [Google Scholar] [CrossRef]
- Sapra, S.; Sarma, D.D. Evolution of the electronic structure with size in II-VI semiconductor nanocrystals. Phys. Rev. B 2004, 69, 125304–125310. [Google Scholar] [CrossRef]
- Law, M.; Beard, M.C.; Choi, S.; Luther, J.M.; Hanna, M.C.; Nozik, A.J. Determining the Internal Quantum Efficiency of PbSe Nanocrystal Solar Cells with the Aid of an Optical Model. Nano Lett. 2008, 8, 3904–3910. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Fan, Z.; Liang, H.; Selopal, G.S.; Gonfa, B.A.; Jin, L.; Soudi, A.; Cui, D.; Enrichi, F.; Natile, M.M.; et al. Controlling photoinduced electron transfer from PbS@CdS core@shell quantum dots to metal oxide nanostructured thin films. Nanoscale 2014, 6, 7004. [Google Scholar] [CrossRef]
- Cao, S.W.; Yuan, Y.P.; Fang, J.; Shahjamali, M.M.; Boey, F.Y.C.; Barber, J.; Loo, S.C.J.; Xue, C. In-situ growth of CdS quantum dots on g-C3N4 nanosheets for highly efficient photocatalytic hydrogen generation under visible light irradiation. Int. J. Hydrog. Energy 2013, 38, 1258–1266. [Google Scholar] [CrossRef]
- Xiao, F.X.; Miao, J.; Liu, B. Layer-by-Layer Self-Assembly of CdS Quantum Dots/Graphene Nanosheets Hybrid Films for Photoelectrochemical and Photocatalytic Applications. J. Am. Chem. Soc. 2014, 136, 1559–1569. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Navarro-Pardo, F.; Selopal, G.S.; Sun, S.; Wang, Z.M.; Zhao, H.; Rosei, F. Hybrid surface passivation of PbS/CdS quantum dots for efficient photoelectrochemical hydrogen generation. Appl. Surf. Sci. 2020, 530, 147252. [Google Scholar] [CrossRef]
- Heuff, R.F.; Swift, J.L.; Cramb, D.T. Fluorescence correlation spectroscopy using quantum dots: Advances, challenges and opportunities. Phys. Chem. Chem. Phys. 2007, 9, 1870–1880. [Google Scholar] [CrossRef]
- Hottechamps, J.; Noblet, T.; Brans, A.; Humbert, C.; Dreesen, L. How Quantum Dots Aggregation Enhances Förster Resonant Energy Tranfer. ChemPhysChem 2020, 21, 853–862. [Google Scholar] [CrossRef] [PubMed]
- Medintz, I.L.; Uyeda, H.T.; Goldman, E.R.; Mattoussi, H. Quantum dot bioconjugates for imaging, labelling and sensing. Nat. Mater. 2005, 4, 435–446. [Google Scholar] [CrossRef]
- Yong, K.T.; Law, W.C.; Roy, I.; Jing, Z.; Huang, H.; Swihart, M.T.; Prasad, P.N. Aqueous phase synthesis of CdTe quantum dots for biophotonics. J. Biophotonics 2011, 4, 9–20. [Google Scholar] [CrossRef]
- Li, J.; Zhu, J.J. Quantum dots for fluorescent biosensing and bio-imaging applications. Analyst 2013, 138, 2506–2515. [Google Scholar] [CrossRef]
- Tyrakowski, C.M.; Snee, P.T. A primer on synthesis, water-solubilization, and functionalization of quantum dots, their use as biological sensing agents, and present status. Phys. Chem. Chem. Phys. 2014, 16, 837–855. [Google Scholar] [CrossRef]
- Wegner, K.D.; Hildebrandt, N. Quantum dots: Bright and versatile in vitro and in vivo fluorescence imaging biosensors. Chem. Soc. Rev. 2015, 44, 4792–4834. [Google Scholar] [CrossRef]
- Dubertret, B. Quantum dots: DNA detectives. Nat. Mater. 2005, 4, 797–798. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Wang, Q.; Li, X. Studies on CdSe/L-cysteine Quantum Dots Synthesized in Aqueous Solution for Biological Labeling. J. Phys. Chem. C 2009, 113, 7670–7676. [Google Scholar] [CrossRef]
- Zahavy, E.; Freeman, E.; Lustig, S.; Keysary, A.; Yitzhaki, S. Double Labeling and Simultaneous Detection of B- and T Cells Using Fluorescent Nano-Crystal (q-dots) in Paraffin-Embedded Tissues. J. Fluoresc. 2005, 15, 661. [Google Scholar] [CrossRef] [PubMed]
- Goldman, E.R.; Clapp, A.R.; Anderson, G.P.; Uyeda, H.; Mauro, J.M.; Medintz, I.L.; Mattoussi, H. Multiplexed Toxin Analysis Using Four Colors of Quantum Dot Fluororeagents. Anal. Chem. 2004, 76, 684–688. [Google Scholar] [CrossRef] [PubMed]
- Susha, A.S.; Javier, A.M.; Parak, W.J.; Rogach, A.L. Luminescent CdTe nanocrystals as ion probes and pH sensors in aqueous solutions. Colloids Surfaces A Physicochem. Eng. Asp. 2006, 281, 40–43. [Google Scholar] [CrossRef]
- Generalova, A.N.; Oleinikov, V.A.; Zarifullina, M.M.; Lankina, E.V.; Sizova, S.V.; Artemyev, M.V.; Zubov, V.P. Optical sensing quantum dot-labeled polyacrolein particles prepared by layer-by-layer deposition technique. J. Colloid Interface Sci. 2011, 357, 265–272. [Google Scholar] [CrossRef]
- Mrad, R.; Poggi, M.; Chaâbane, R.B.; Negrerie, M. Role of surface defects in colloidal cadmium selenide (CdSe) nanocrystals in the specificity of fluorescence quenching by metal cations. J. Colloid Interface Sci. 2020, 571, 368–377. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhou, Z.; Yang, B. The Influence of Carboxyl Groups on the Photoluminescence of Mercaptocarboxylic Acid-Stabilized CdTe Nanoparticles. J. Phys. Chem. B 2003, 107, 8–13. [Google Scholar] [CrossRef]
- Frederick, M.T.; Amin, V.A.; Weiss, E.A. Optical Properties of Strongly Coupled Quantum Dot-Ligand Systems. J. Phys. Chem. Lett. 2013, 4, 634–640. [Google Scholar] [CrossRef]
- Liang, Y.; Thorne, J.E.; Parkinson, B.A. Controlling the Electronic Coupling between CdSe Quantum Dots and Thiol Capping Ligands via pH and Ligand Selection. Langmuir 2012, 28, 11072–11077. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Harris, R.D.; Lau, B.; Aruda, K.O.; Amin, V.A.; Weiss, E.A. Enhanced Rate of Radiative Decay in CdSe Quantum Dots upon Adsorption of an Exciton-Delocalizing Ligand. Nano Lett. 2014, 14, 5323–5328. [Google Scholar] [CrossRef] [PubMed]
- Noblet, T.; Dreesen, L.; Boujday, S.; Méthivier, C.; Busson, B.; Tadjeddine, A.; Humbert, C. Semiconductor quantum dots reveal dipolar coupling from exciton to ligand vibration. Commun. Chem. 2018, 1, 76. [Google Scholar] [CrossRef]
- Noblet, T.; Boujday, S.; Méthivier, C.; Erard, M.; Hottechamps, J.; Busson, B.; Humbert, C. Two-Dimensional Layers of Colloidal CdTe Quantum Dots: Assembly, Optical Properties, and Vibroelectronic Coupling. J. Phys. Chem. C 2020, 124, 25873–25883. [Google Scholar] [CrossRef]
- Humbert, C.; Noblet, T. A Unified Mathematical Formalism for First to Third Order Dielectric Response of Matter: Application to Surface-Specific Two-Colour Vibrational Optical Spectroscopy. Symmetry 2021, 13, 153. [Google Scholar] [CrossRef]
- Barbillon, G.; Noblet, T.; Busson, B.; Tadjeddine, A.; Humbert, C. Localised detection of thiophenol with gold nanotriangles highly structured as honeycombs by nonlinear Sum Frequency Generation spectroscopy. J. Mater. Sci. 2018, 53, 4554–4562. [Google Scholar] [CrossRef]
- Noblet, T.; Dreesen, L.; Hottechamps, J.; Humbert, C. A global method for handling fluorescence spectra at high concentration derived from the competition between emission and absorption of colloidal CdTe quantum dots. Phys. Chem. Chem. Phys. 2017, 19, 26559–26565. [Google Scholar] [CrossRef]
- Dalstein, L.; Haddada, M.B.; Barbillon, G.; Humbert, C.; Tadjeddine, A.; Boujday, S.; Busson, B. Revealing the Interplay between Adsorbed Molecular Layers and Gold Nanoparticles by Linear and Nonlinear Optical Properties. J. Phys. Chem. C 2015, 119, 17146–17155. [Google Scholar] [CrossRef]
- Humbert, C.; Pluchery, O.; Lacaze, E.; Tadjeddine, A.; Busson, B. Optical spectroscopy of functionalized gold nanoparticles assemblies as a function of the surface coverage. Gold Bull. 2013, 46, 299–309. [Google Scholar] [CrossRef]
- Tourillon, G.; Dreesen, L.; Volcke, C.; Sartenaer, Y.; Thiry, P.A.; Peremans, A. Total internal reflection sum-frequency generation spectroscopy and dense gold nanoparticles monolayer: A route for probing adsorbed molecules. Nanotechnology 2007, 18, 415301–415307. [Google Scholar] [CrossRef]
- Chen, F.; Gozdzialski, L.; Hung, K.K.; Stege, U.; Hore, D.K. Assessing the Molecular Specificity and Orientation Sensitivity of Infrared, Raman, and Vibrational Sum-Frequency Spectra. Symmetry 2021, 13, 42. [Google Scholar] [CrossRef]
- Zhuang, X.; Miranda, P.B.; Kim, D.; Shen, Y.R. Mapping molecular orientation and conformation interfaces by surface nonlinear optics. Phys. Rev. B 1999, 59, 12632–12640. [Google Scholar] [CrossRef]
- Sperling, R.A.; Parak, W.J. Surface modification, functionalization and bioconjugation of colloidal inorganic nanoparticles. Phil. Trans. R. Soc. A 2010, 368, 1333–1383. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).