A Novel Threshold Changeable Secret Image Sharing Scheme
Abstract
1. Introduction
2. Related Work
3. Preliminaries
3.1. Two-Variable One-Way Function
3.2. Yuan et al.’s Secret Sharing Scheme with a Changeable Threshold
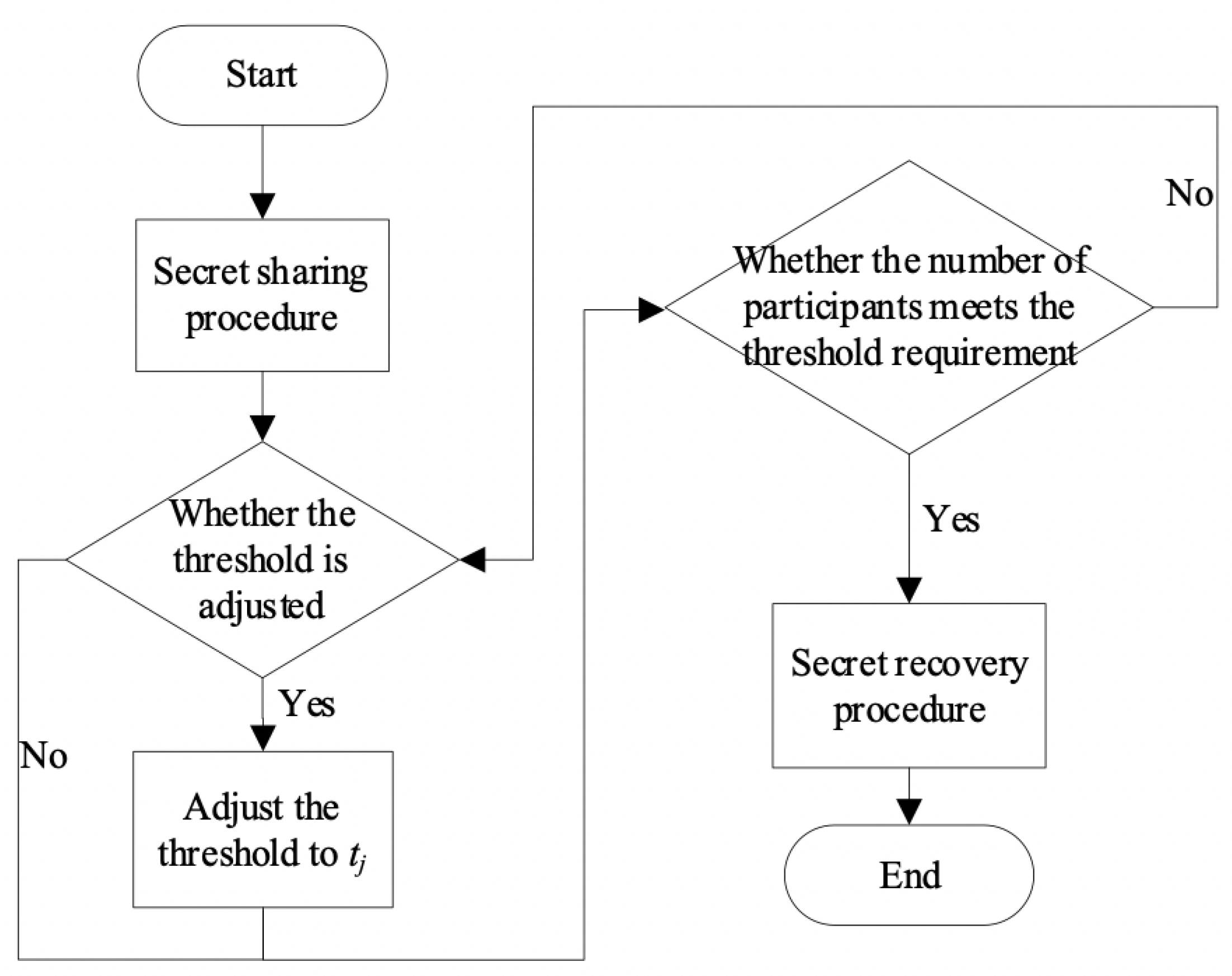
3.2.1. Sharing Procedure
3.2.2. Recovering Procedure
4. Proposed Scheme
4.1. Secret Sharing Procedure
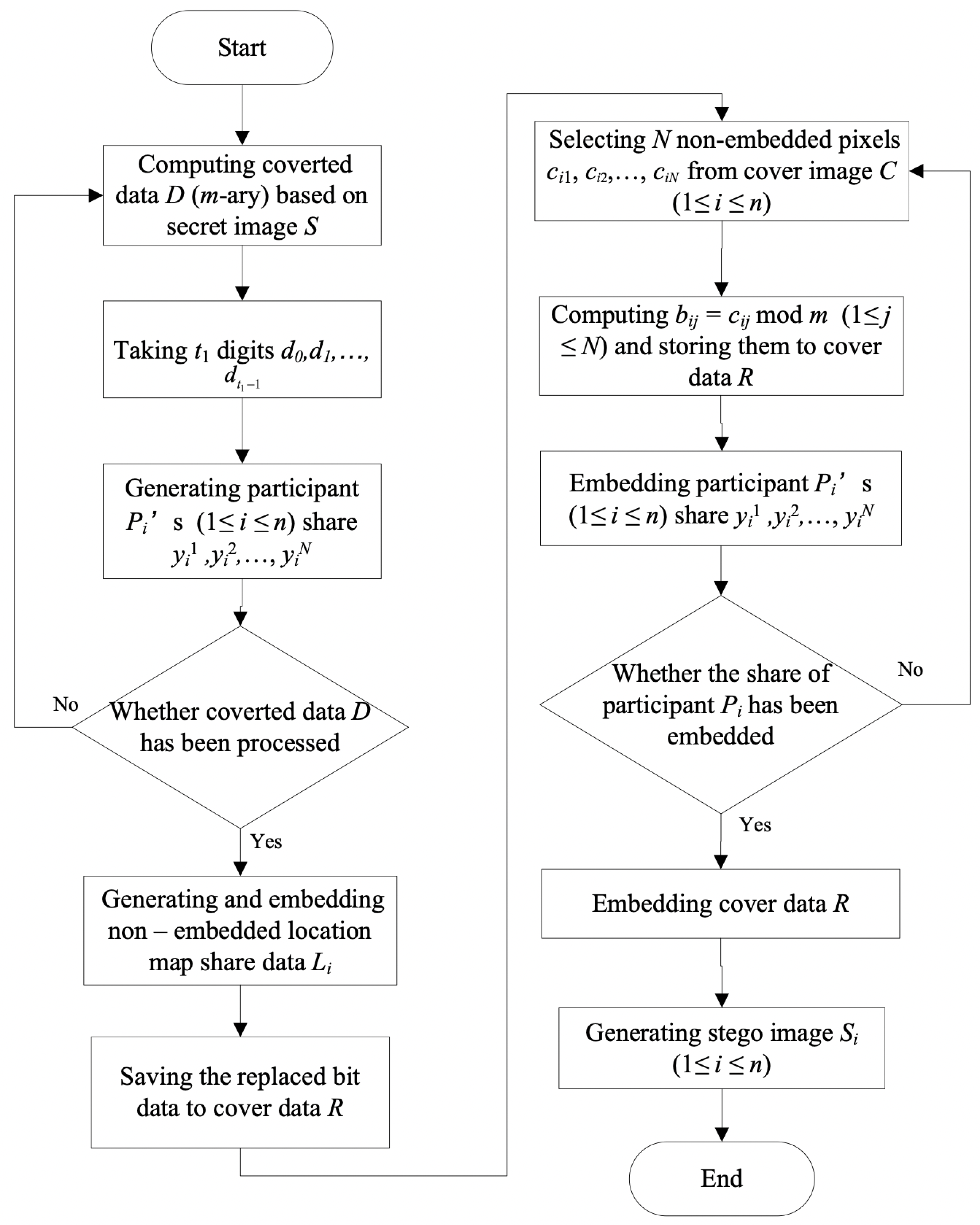
4.1.1. Share Generation Phase
| Algorithm 1 Polynomial generator. |
| Input:, j, , |
| Output: |
| ; |
| ; |
| while do |
| end while |
4.1.2. Stego Images Generation Phase
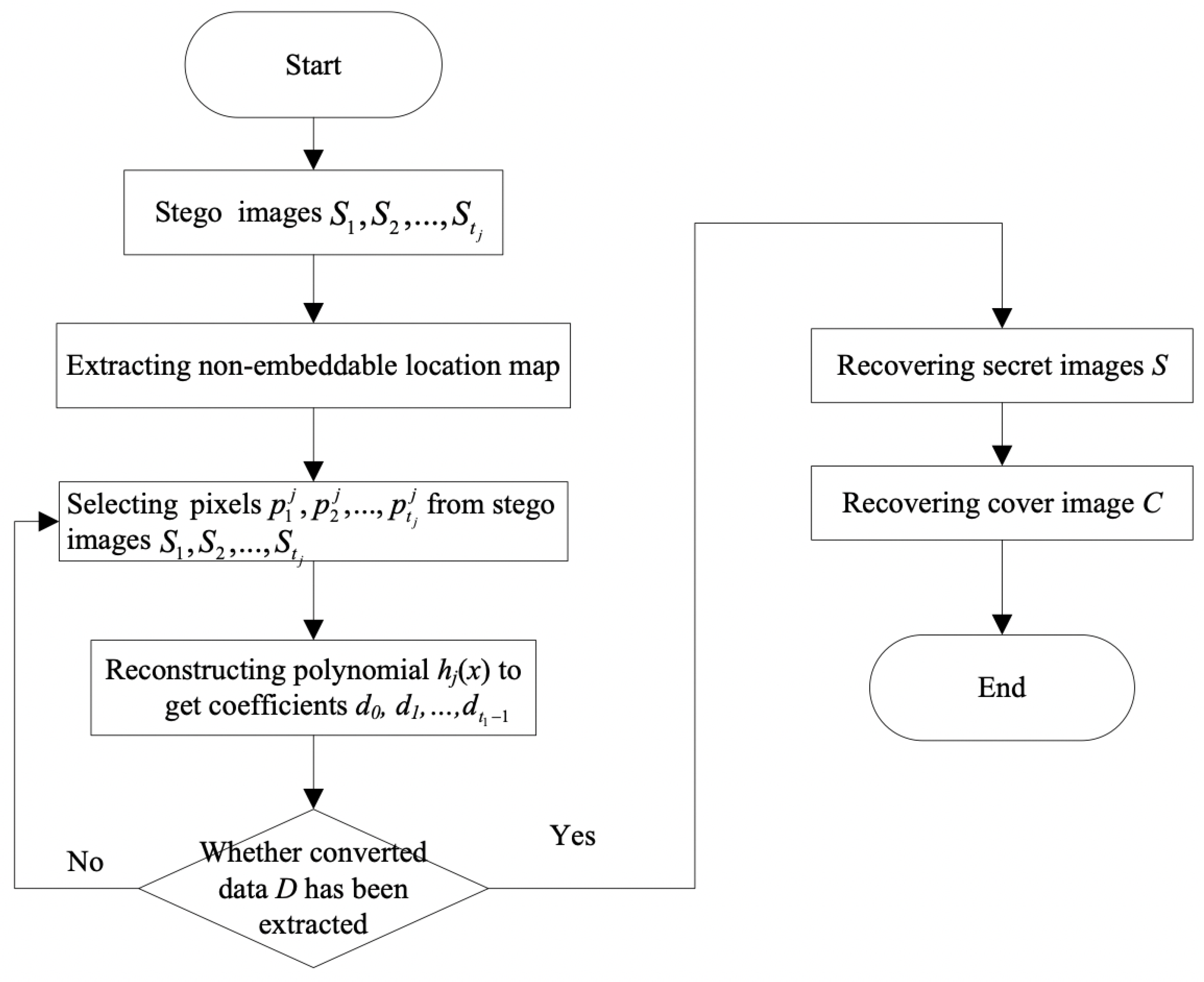
4.2. Recovery Procedure
5. Experiment and Analysis
5.1. Simulation Results
5.2. Performance Analysis
5.3. Security Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, C.; Jia, J.; Jie, Y.; Liu, C.Z.; Choo, K.R. Enabling Secure Cross-Modal Retrieval Over Encrypted Heterogeneous IoT Databases With Collective Matrix Factorization. IEEE Internet Things J. 2020, 7, 3104–3113. [Google Scholar] [CrossRef]
- Guo, C.; Jiang, X.; Choo, K.K.R.; Jie, Y. R-Dedup: Secure client-side deduplication for encrypted data without involving a third-party entity. J. Netw. Comput. Appl. 2020, 162, 102664. [Google Scholar] [CrossRef]
- Guo, C.; Jia, J.; Choo, K.K.R.; Jie, Y. Privacy-preserving image search (PPIS): Secure classification and searching using convolutional neural network over large-scale encrypted medical images. Comput. Secur. 2020, 99, 102021. [Google Scholar] [CrossRef]
- Shamir, A. How to Share a Secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the 1979 International Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, 4–7 June 1979; pp. 313–318. [Google Scholar]
- Naor, M.; Shamir, A. Visual Cryptography. In Workshop on the Theory and Application of of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1994; Volume 950, pp. 1–12. [Google Scholar]
- Lin, C.C.; Tsai, W.H. Secret image sharing with steganography and authentication. J. Syst. Softw. 2004, 73, 405–414. [Google Scholar] [CrossRef]
- Lin, P.Y.; Chan, C.S. Invertible secret image sharing with steganography. Pattern Recognit. Lett. 2010, 31, 1887–1893. [Google Scholar] [CrossRef]
- Guo, C.; Chang, C.C.; Qin, C. A multi-threshold secret image sharing scheme based on MSP. Pattern Recognit. Lett. 2012, 33, 1594–1600. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, H.; Song, Q.; Li, M. A multi-threshold secret image sharing scheme based on the generalized Chinese reminder theorem. Multimed. Tools Appl. 2015, 75, 11577–11594. [Google Scholar] [CrossRef]
- Liu, Y.N.; Zhong, Q.; Xie, M.; Chen, Z.B. A novel multiple-level secret image sharing scheme. Multimed. Tools Appl. 2018, 77, 6017–6031. [Google Scholar] [CrossRef]
- Zarepour-Ahmadabadi, J.; Shiri Ahmadabadi, M.; Latif, A. An adaptive secret image sharing with a new bitwise steganographic property. Inf. Sci. 2016, 369, 467–480. [Google Scholar] [CrossRef]
- Yuan, L.; Li, M.; Guo, C.; Choo, K.K.R.; Ren, Y. Novel Threshold Changeable Secret Sharing Schemes Based on Polynomial Interpolation. PLoS ONE 2016, 11, e0165512. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, H.; Fu, Z.; Feng, B.; Li, M. A novel proactive secret image sharing scheme based on LISS. Multimed. Tools Appl. 2017, 77, 19569–19590. [Google Scholar] [CrossRef]
- Laih, C.S.; Harn, L.; Lee, J.Y.; Hwang, T. Dynamic Threshold Scheme Based on the Definition of Cross-Product in an N-Dimensional Linear Space. In Advances in Cryptology—CRYPTO’ 89 Proceedings; Brassard, G., Ed.; Springer: New York, NY, USA, 1990; pp. 286–298. [Google Scholar]
- Desmedt, Y.; Jajodia, S. Redistributing Secret Shares to New Access Structures and Its Applications; Technical Report; Citeseer: State College, PA, USA, 1997. [Google Scholar]
- Martin, K.; Pieprzyk, J.; Safavi Naini, R.; Wang, H. Changing Thresholds in the Absence of Secure Channels. Aust. Comput. J. 1999, 31, 34–43. [Google Scholar]
- Barwick, S.G.; Jackson, W.; Martin, K.M. Updating the parameters of a threshold scheme by minimal broadcast. IEEE Trans. Inf. Theory 2005, 51, 620–633. [Google Scholar] [CrossRef]
- Zhang, Z.; Chee, Y.M.; Ling, S.; Liu, M.; Wang, H. Threshold changeable secret sharing schemes revisited. Theor. Comput. Sci. 2012, 418, 106–115. [Google Scholar] [CrossRef]
- Pilaram, H.; Eghlidos, T. A lattice-based changeable threshold multi-secret sharing scheme and its application to threshold cryptography. Sci. Iran. 2017, 24, 1448–1457. [Google Scholar] [CrossRef]
- Jia, X.; Wang, D.; Nie, D.; Luo, X.; Sun, J.Z. A new threshold changeable secret sharing scheme based on the Chinese Remainder Theorem. Inf. Sci. 2019, 473, 13–30. [Google Scholar] [CrossRef]
- Yang, C.N.; Chen, T.S.; Yu, K.H.; Wang, C.C. Improvements of image sharing with steganography and authentication. J. Syst. Softw. 2007, 80, 1070–1076. [Google Scholar] [CrossRef]
- Guo, C.; Chang, C.C.; Qin, C. A hierarchical threshold secret image sharing. Pattern Recognit. Lett. 2012, 33, 83–91. [Google Scholar] [CrossRef]
- Pakniat, N.; Noroozi, M.; Eslami, Z. Secret image sharing scheme with hierarchical threshold access structure. J. Vis. Commun. Image Represent. 2014, 25, 1093–1101. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Y.; Jia, X. A novel hierarchical secret image sharing scheme with multi-group joint management. Mathematics 2020, 8, 448. [Google Scholar] [CrossRef]
- Ulutas, M.; Ulutas, G.; Nabiyev, V.V. Invertible secret image sharing for gray level and dithered cover images. J. Syst. Softw. 2013, 86, 485–500. [Google Scholar] [CrossRef]
- Chen, C.C.; Chen, J.L. A new Boolean-based multiple secret image sharing scheme to share different sized secret images. J. Inf. Secur. Appl. 2017, 33, 45–54. [Google Scholar] [CrossRef]
- Nag, A.; Singh, J.P.; Singh, A.K. An efficient Boolean based multi-secret image sharing scheme. Multimed. Tools Appl. 2019, 79, 16219–16243. [Google Scholar] [CrossRef]
- Deshmukh, M.; Nain, N.; Ahmed, M. An (n, n)-multi secret image sharing scheme using boolean XOR and modular arithmetic. In Proceedings of the 2016 IEEE 30th International Conference on Advanced Information Networking and Applications (AINA), Taipei, Taiwan, 27–29 March 2016; pp. 690–697. [Google Scholar]
- Azza, A.; Lian, S. Multi-secret image sharing based on elementary cellular automata with steganography. Multimed. Tools Appl. 2020, 79, 21241–21264. [Google Scholar] [CrossRef]
- Yuan, L.; Li, M.; Guo, C.; Hu, W.; Luo, X. Secret Image Sharing Scheme with Threshold Changeable Capability. Math. Probl. Eng. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Thien, C.C.; Lin, J.C. Secret image sharing. Comput. Graph. 2002, 26, 765–770. [Google Scholar] [CrossRef]
- Liu, Y.X.; Yang, C.N.; Wu, C.M.; Sun, Q.D.; Bi, W. Threshold changeable secret image sharing scheme based on interpolation polynomial. Multimed. Tools Appl. 2019, 78, 18653–18667. [Google Scholar] [CrossRef]
- Chien, H.Y.; Jan, J.K.; Tseng, Y.M. A practical (t, n) multi-secret sharing scheme. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2000, E83-A, 2762–2765. [Google Scholar]
- He, J.; Dawson, E. Multi secret-sharing scheme based on one-way function. Electron. Lett. 1995, 31, 93–95. [Google Scholar] [CrossRef]
- Goldwasser, S.; Micali, S.; Rivest, R.L. A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 1988, 17, 281–308. [Google Scholar] [CrossRef]
- Naor, M.; Yung, M. Universal One-Way Hash Functions and their Cryptographic Applications. In Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 15–17 May 1989; pp. 33–43. [Google Scholar]
- Waring, E. Vii. problems concerning interpolations. Philos. Trans. R. Soc. Lond. 1779, 59–67. [Google Scholar] [CrossRef]
- Kyriakopoulos, K.; Parish, D.J. A live system for wavelet compression of high speed computer network measurements. In Proceedings of the International Conference on Passive and Active Network Measurement, Louvain-la-Neuve, Belgium, 5–6 April 2007; pp. 241–244. [Google Scholar]



| Notation | Meaning |
|---|---|
| S | Gray-scale secret image S |
| C | Gray-scale cover image C |
| and are the width and height of secret image S | |
| and is the width and height of cover image C | |
| n | The number of participants |
| Participant i | |
| The stego images holed by participant | |
| N | The number of changeable thresholds |
| The value of the changeable threshold | |
| m | A prime number, and |
| The polynomial corresponding to threshold | |
| A two-variable one-way function | |
| The identification of participant | |
| The key corresponding to threshold | |
| Coefficient operator. If , then | |
| The ceiling function | |
| The flooring function | |
| D | Converted data of secret image |
| R | Cover data of the cover image |
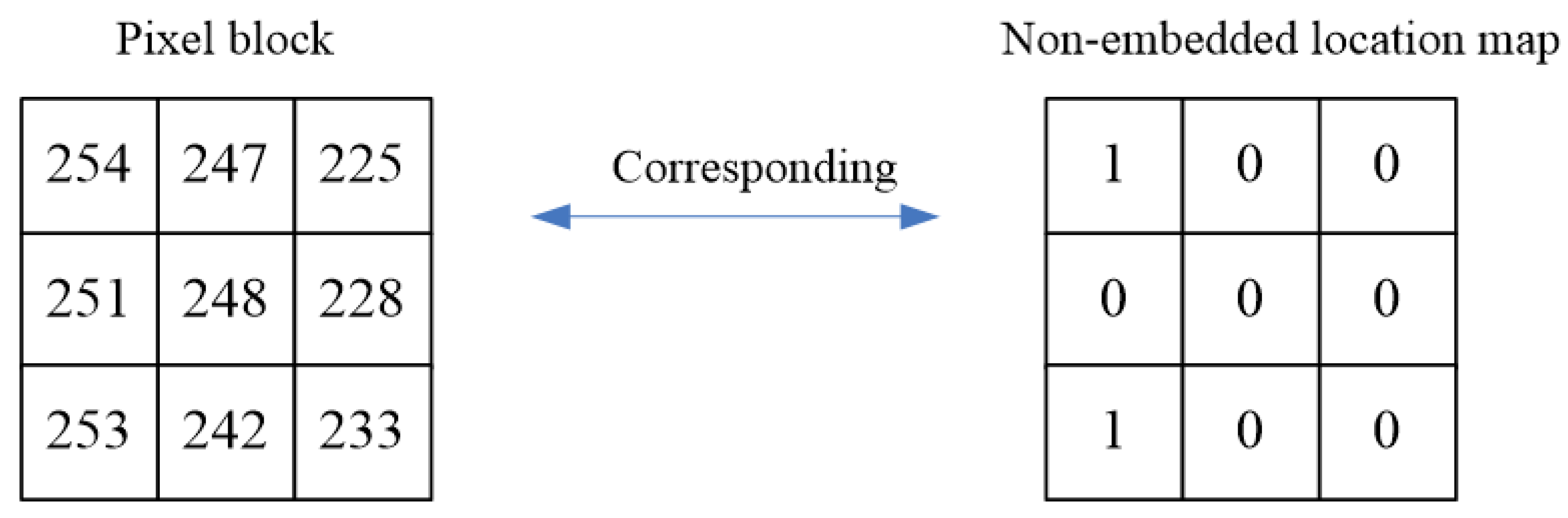
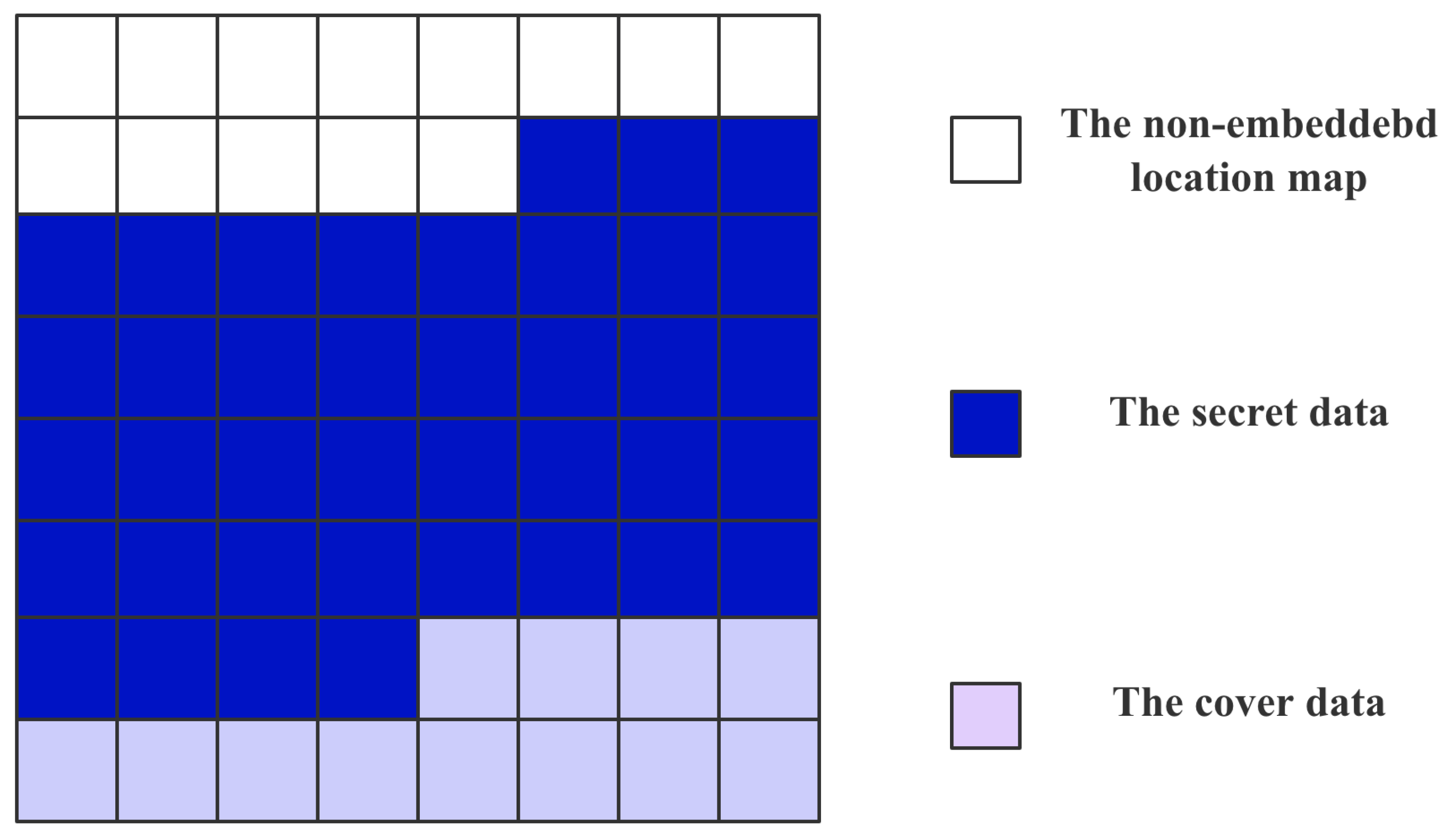
| M | Non-embedded location map m-ary data |
| Location map share data of participan |
| Cover Images | Stego 1 | Stego 2 | Stego 3 | Stego 4 | Stego 5 | Stego 6 | Average |
|---|---|---|---|---|---|---|---|
| Lena | 47.14 | 47.13 | 47.16 | 47.17 | 47.13 | 47.14 | 47.15 |
| Peppers | 47.20 | 47.19 | 47.22 | 47.20 | 47.23 | 47.22 | 47.21 |
| Boat | 47.22 | 47.13 | 47.22 | 47.24 | 47.15 | 47.20 | 47.19 |
| Fruits | 47.03 | 47.12 | 47.00 | 47.14 | 47.03 | 47.10 | 47.07 |
| Couple | 47.15 | 47.22 | 47.22 | 47.13 | 47.15 | 47.22 | 47.18 |
| Crowd | 47.17 | 47.16 | 47.15 | 47.17 | 47.13 | 47.15 | 47.15 |
| Airplane | 47.11 | 47.12 | 47.13 | 47.13 | 47.12 | 47.11 | 47.12 |
| Tiffany | 47.03 | 47.14 | 47.11 | 47.14 | 47.06 | 47.03 | 47.08 |
| Barbara | 47.16 | 47.19 | 47.19 | 47.18 | 47.17 | 47.20 | 47.18 |
| m | Pixel Change Range | PSNR |
|---|---|---|
| 7 | [−3, 3] | 47.15 |
| 11 | [−5, 5] | 43.32 |
| 13 | [−6, 6] | 41.81 |
| 17 | [−8, 8] | 39.33 |
| 19 | [−9, 9] | 38.34 |
| 23 | [−11, 11] | 36.55 |
| Number | Thresholds | PSNR (dB) |
|---|---|---|
| 1 | {2, 3, 4} | 44.25 |
| 2 | {2, 4, 7} | 44.24 |
| 3 | {3, 4, 5} | 47.15 |
| 4 | {3, 5, 7} | 47.15 |
| 5 | {6, 7, 8} | 51.18 |
| Functionality | Yang et al. [22] 2007 | Lin et al. [7] 2010 | Ulutas et al. [26] 2013 | Yuan et al. [31] 2016 | Guo et al. [14] 2018 | Liu et al. [33] 2019 | Ours |
|---|---|---|---|---|---|---|---|
| Threshold | |||||||
| Threshold changeability | No | No | No | Yes | No | Yes | Yes |
| Collusion Attack Resistance | Yes | Yes | Yes | Yes | Yes | No | Yes |
| Number of recovering polynomials | 1 | 1 | 1 | − | 1 | 1 | |
| Meaningful stego image | Yes | Yes | Yes | Yes | Yes | No | Yes |
| Quality of stego images | 46.0 dB | 48.36 dB | 52.79 dB | 46.02 dB | 48.0 dB | − | 46.65 dB |
| Lossless secret image | Yes | Yes | Yes | Yes | Yes | No | Yes |
| Lossless cover image | No | Yes | Yes | No | No | No | Yes |
| Maximum capacity (pixels) | − | * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Wang, M.; Wang, Q.; Yao, Y.; Yuan, L.; Miao, G. A Novel Threshold Changeable Secret Image Sharing Scheme. Symmetry 2021, 13, 286. https://doi.org/10.3390/sym13020286
Wu G, Wang M, Wang Q, Yao Y, Yuan L, Miao G. A Novel Threshold Changeable Secret Image Sharing Scheme. Symmetry. 2021; 13(2):286. https://doi.org/10.3390/sym13020286
Chicago/Turabian StyleWu, Guohua, Mingyao Wang, Qiuhua Wang, Ye Yao, Lifeng Yuan, and Gongxun Miao. 2021. "A Novel Threshold Changeable Secret Image Sharing Scheme" Symmetry 13, no. 2: 286. https://doi.org/10.3390/sym13020286
APA StyleWu, G., Wang, M., Wang, Q., Yao, Y., Yuan, L., & Miao, G. (2021). A Novel Threshold Changeable Secret Image Sharing Scheme. Symmetry, 13(2), 286. https://doi.org/10.3390/sym13020286







