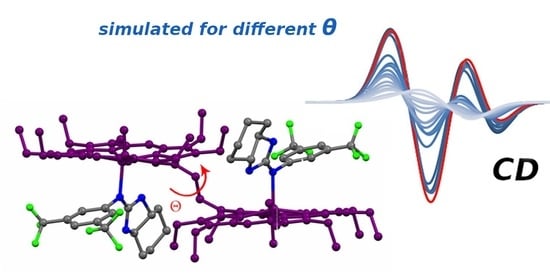
Supramolecular Chirogenesis in Bis-Porphyrin: Crystallographic Structure and CD Spectra for a Complex with a Chiral Guanidine Derivative
Abstract
1. Introduction
2. Materials and Methods
3. Results
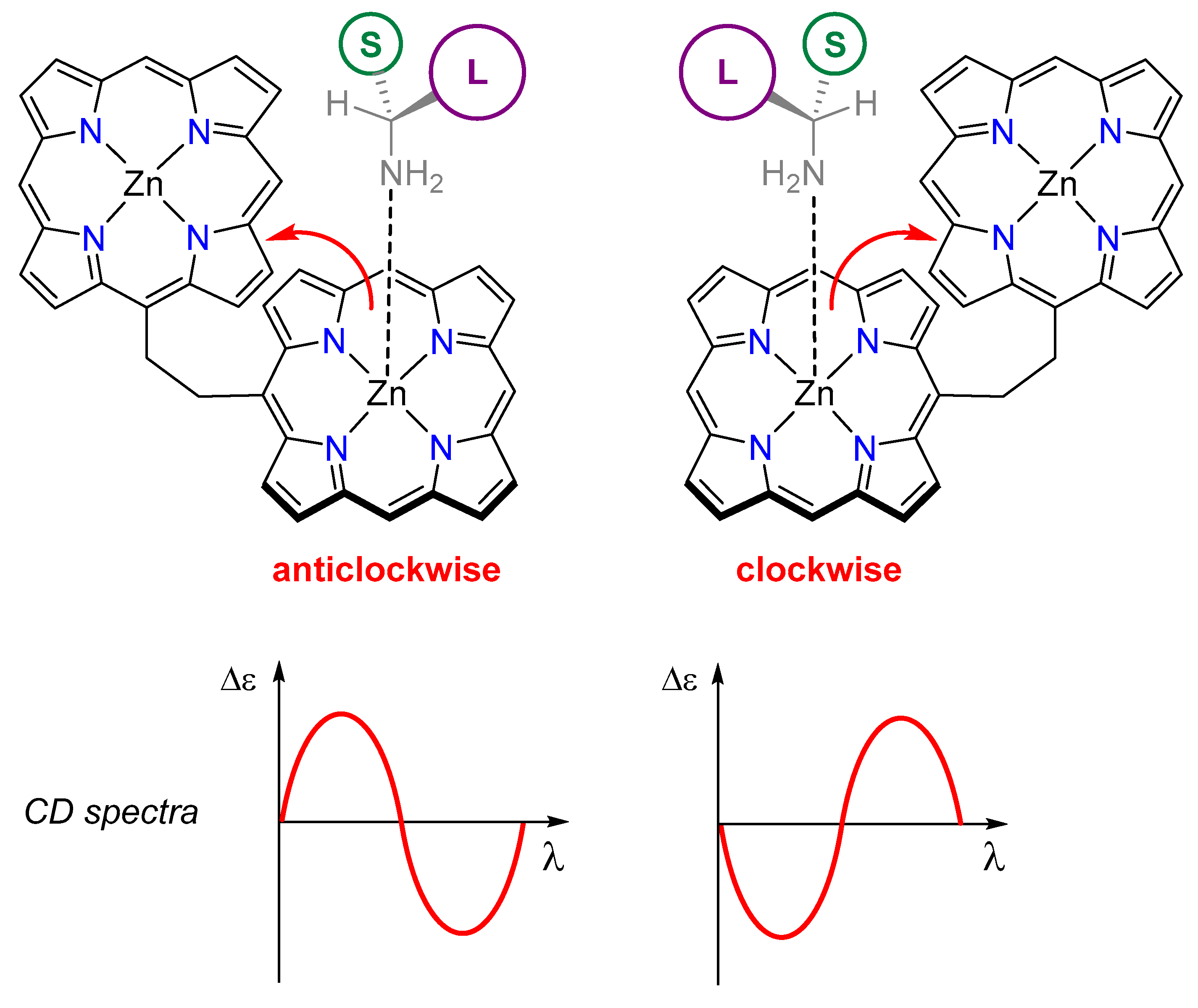
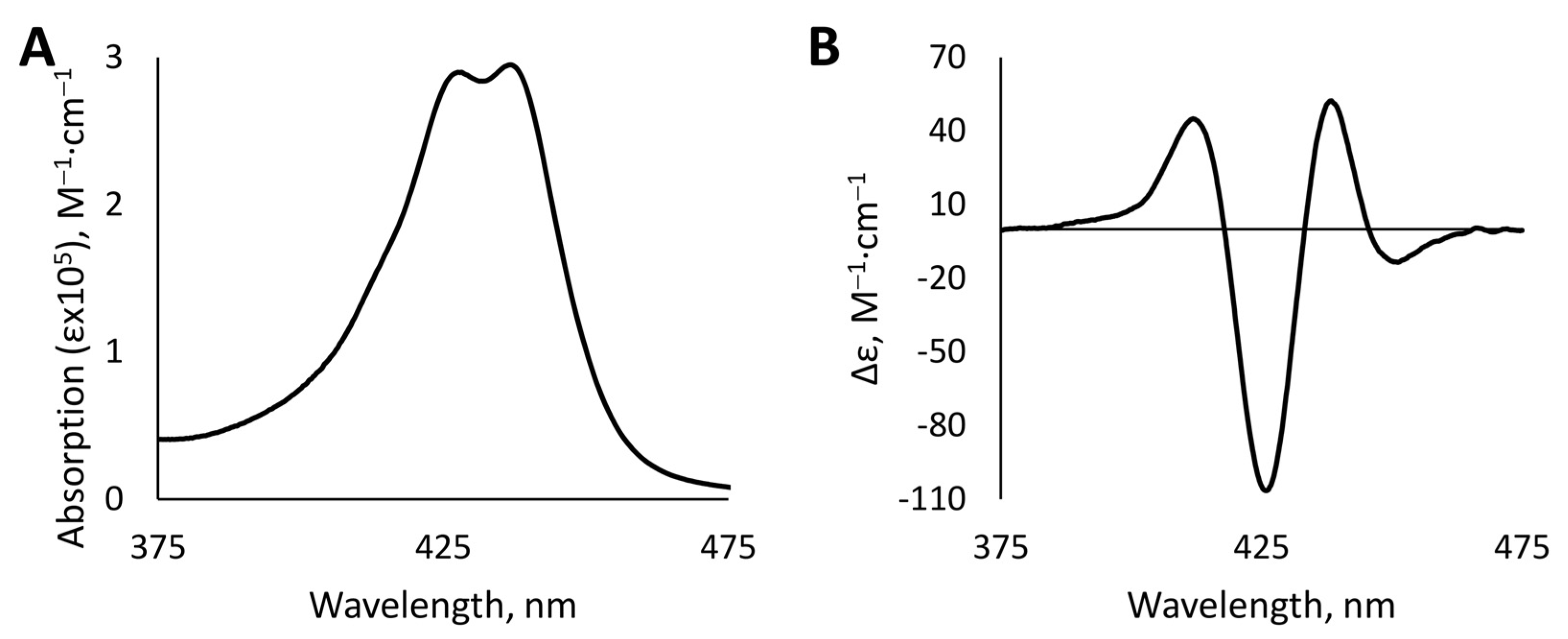
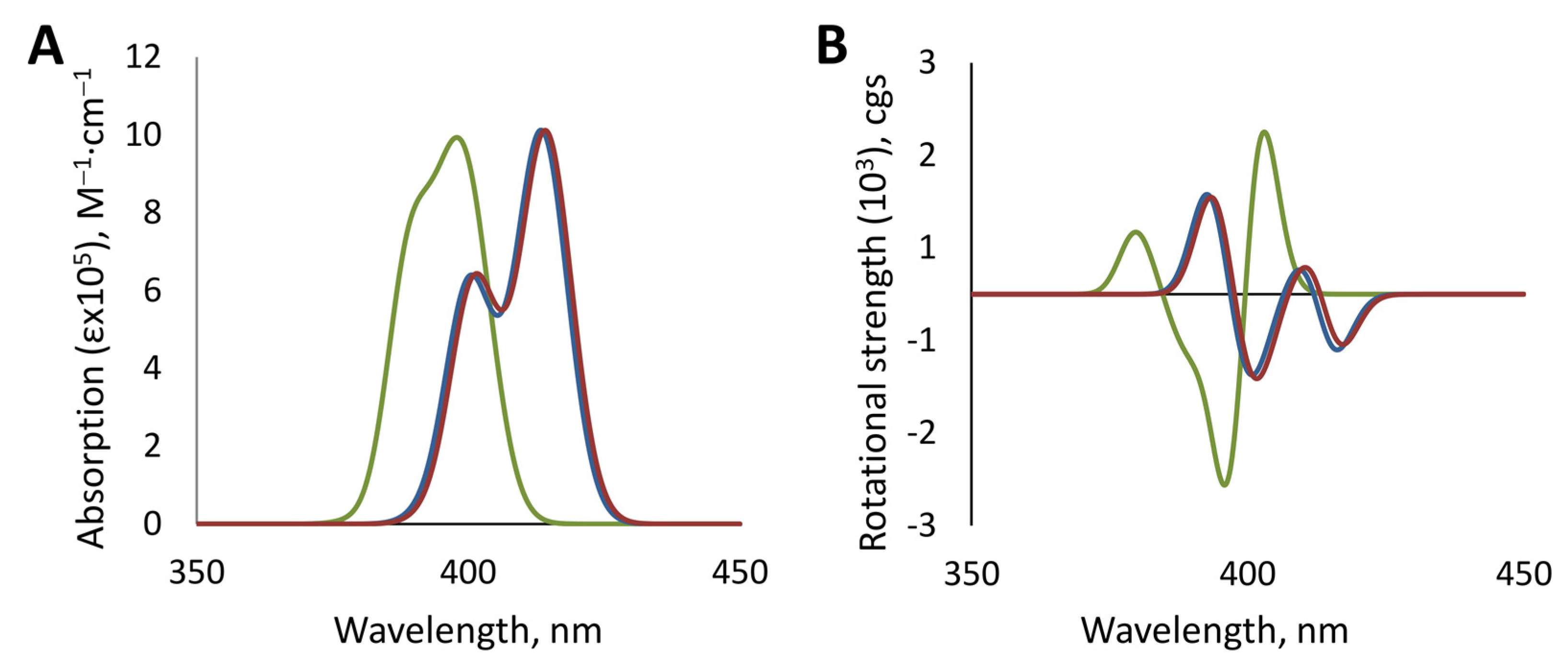
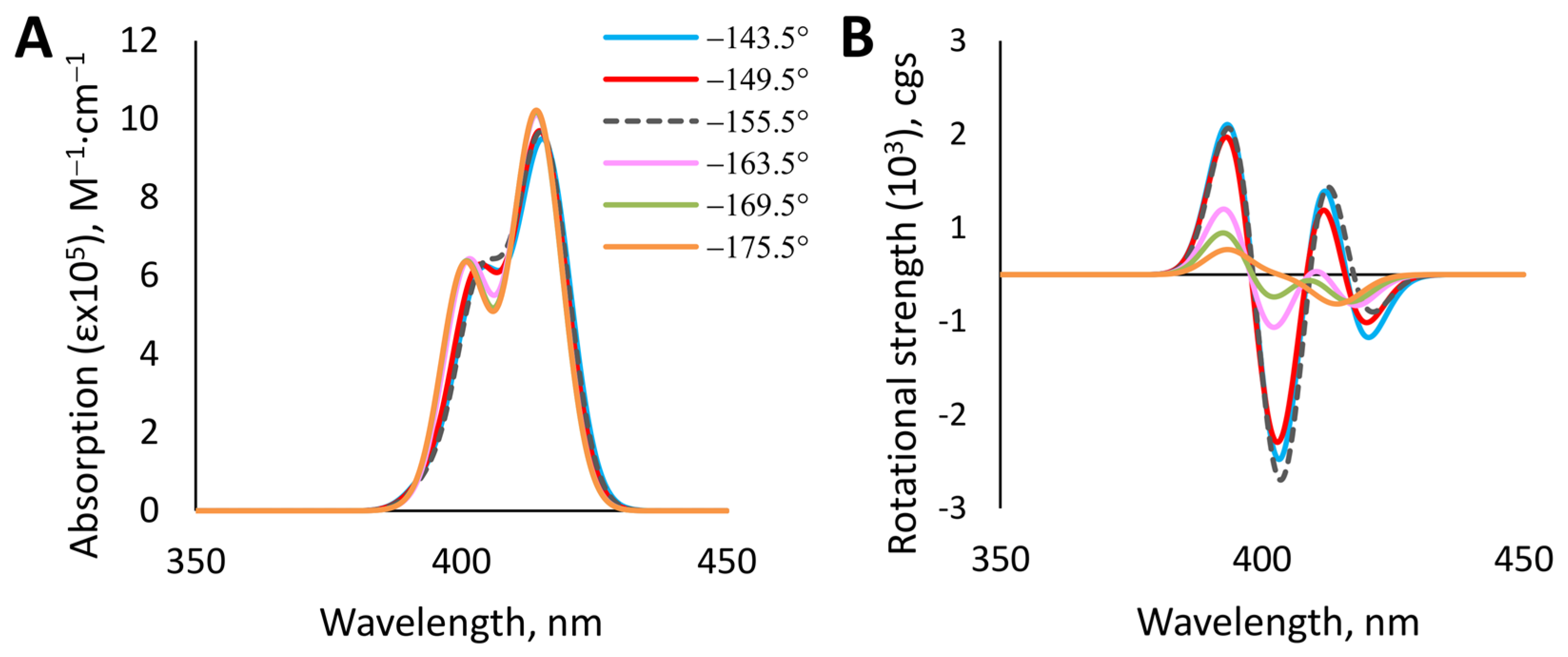
3.1. Absorption UV-Vis and CD Spectroscopy
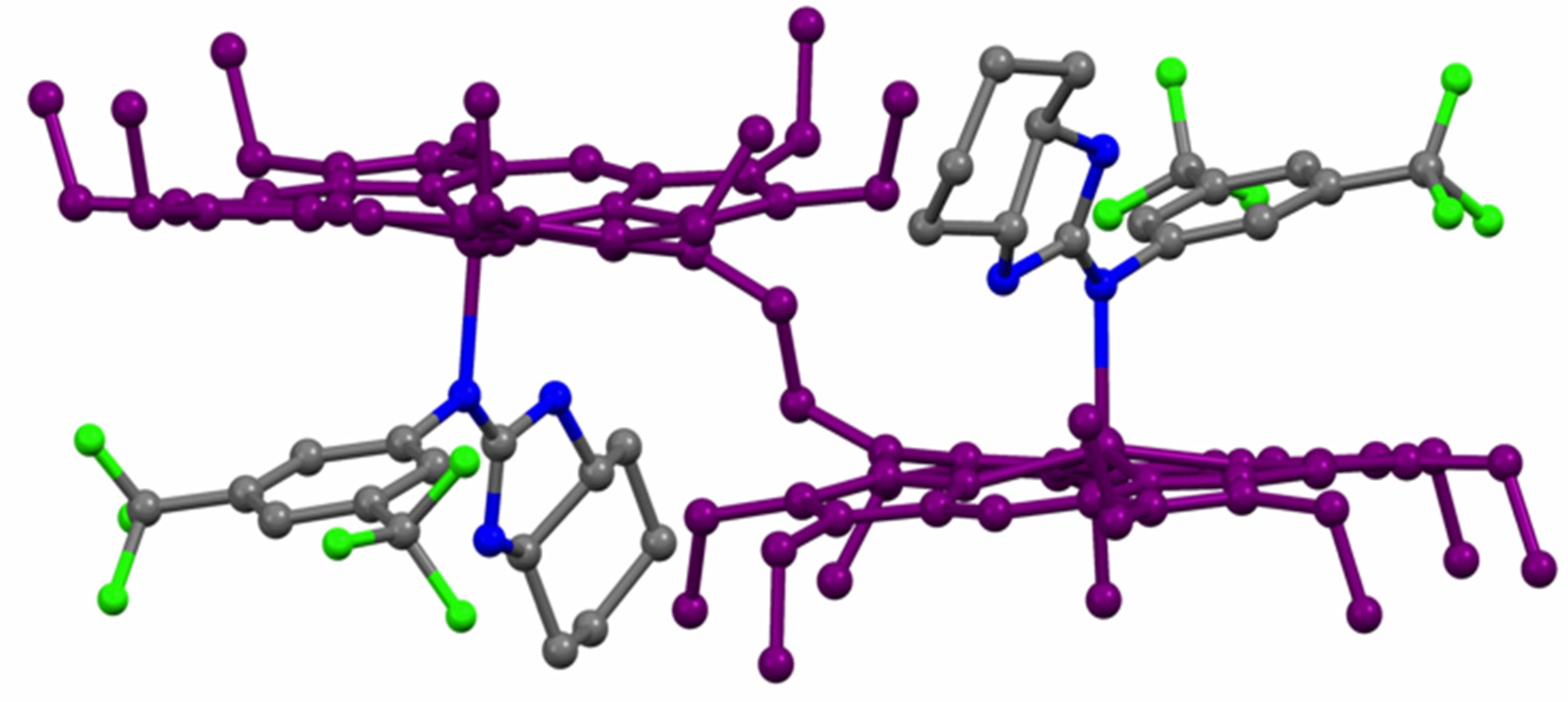
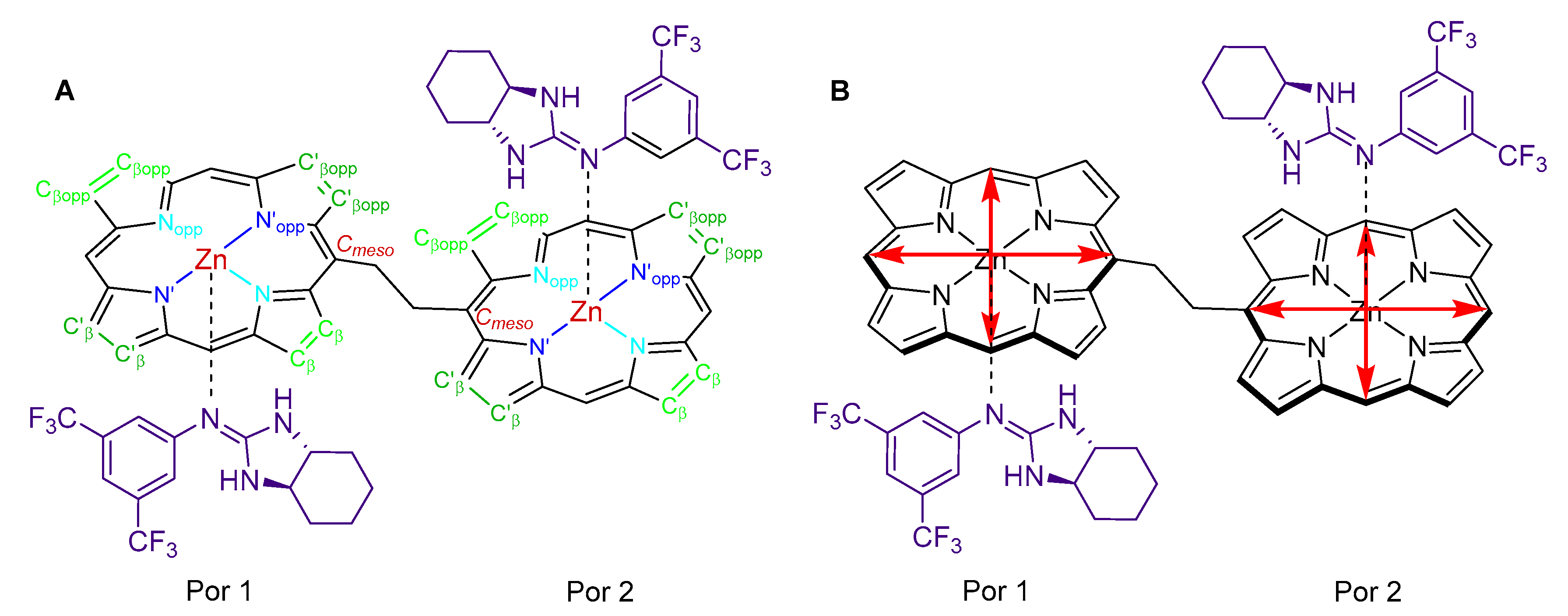
3.2. Single Crystal X-ray Structure
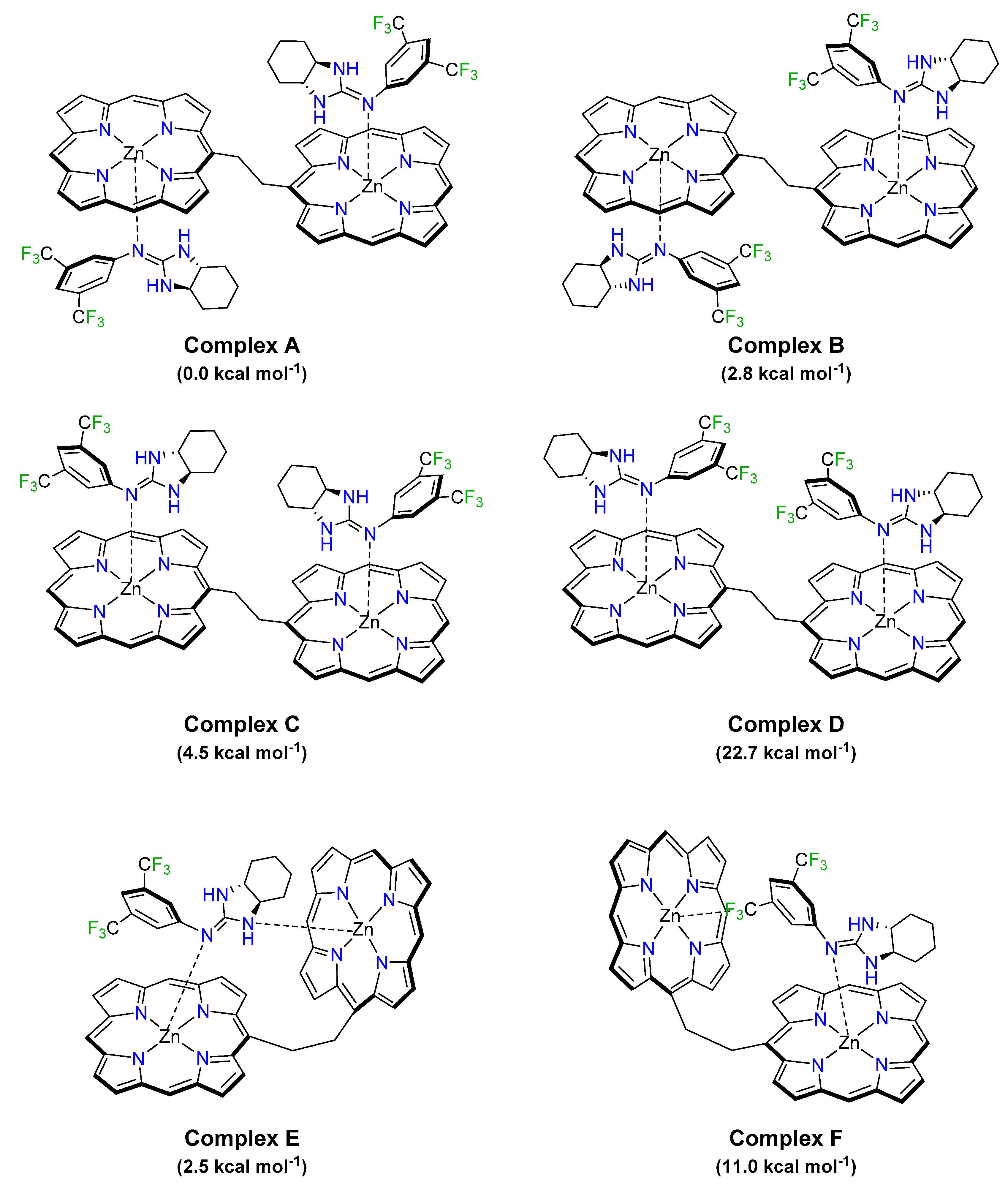
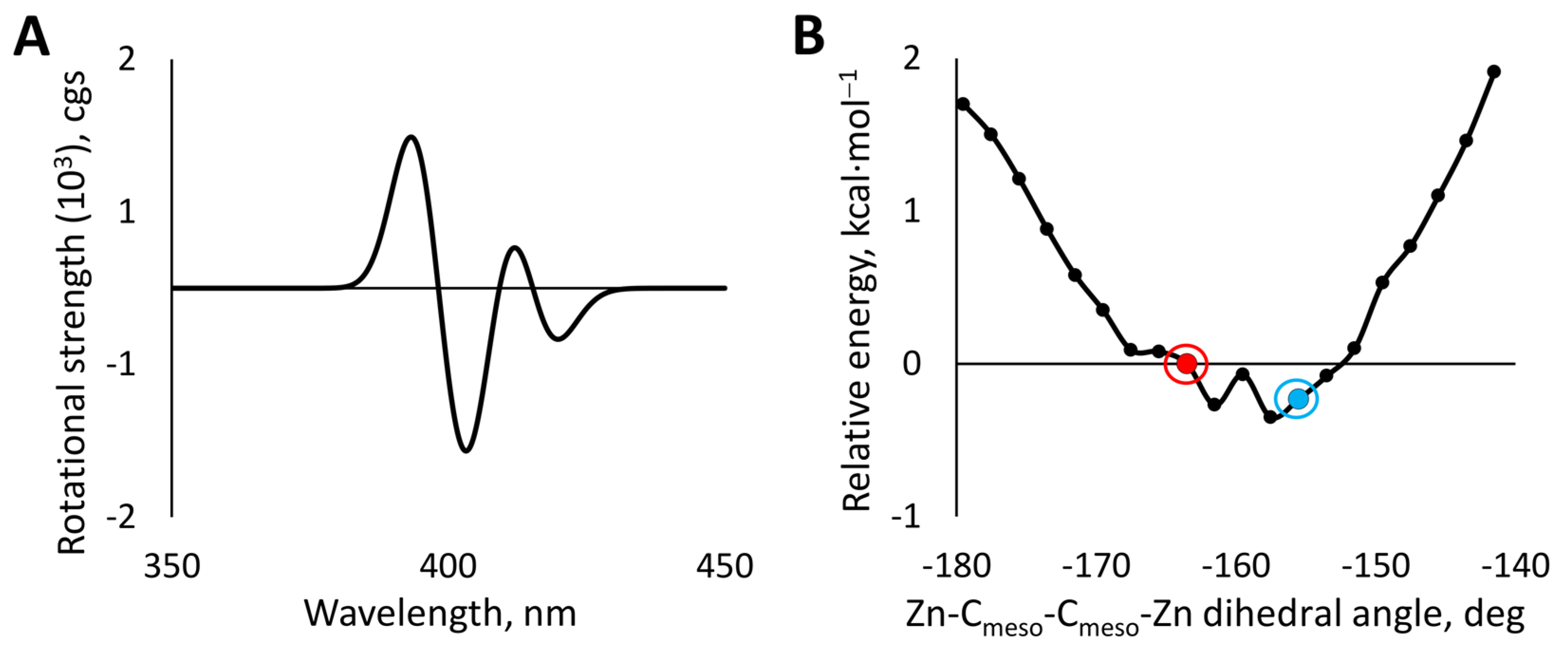
3.3. DFT Modelling of the Complex
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Che, C.-M.; Lo, V.K.-Y.; Zhou, C.-Y.; Huang, J.-S. Selective functionalisation of saturated C–H bonds with metalloporphyrin catalysts. Chem. Soc. Rev. 2011, 40, 1950–1975. [Google Scholar] [CrossRef] [PubMed]
- Barona-Castaño, J.C.; Carmona-Vargas, C.C.; Brocksom, T.J.; De Oliveira, K.T.; Graça, M.; Neves, P.M.S.; Amparo, M.; Faustino, F. Porphyrins as catalysts in scalable organic reactions. Molecules 2016, 21, 310. [Google Scholar] [CrossRef] [PubMed]
- Meunier, B. Metalloporphyrins as versatile catalysts for oxidation reactions and oxidative DNA cleavage. Chem. Rev. 1992, 92, 1411–1456. [Google Scholar] [CrossRef]
- Walter, M.G.; Rudine, A.B.; Wamser, C.C. Porphyrins and phthalocyanines in solar photovoltaic cells. J. Porphyr. Phthalocyanines 2010, 14, 759–792. [Google Scholar] [CrossRef]
- Martínez-Díaz, M.V.; de la Torre, G.; Torres, T. Lighting porphyrins and phthalocyanines for molecular photovoltaics. Chem. Commun. 2010, 46, 7090–7108. [Google Scholar] [CrossRef] [PubMed]
- Bottari, G.; Trukhina, O.; Ince, M.; Torres, T. Towards artificial photosynthesis: Supramolecular, donor–acceptor, porphyrin- and phthalocyanine/carbon nanostructure ensembles. Coord. Chem. Rev. 2012, 256, 2453–2477. [Google Scholar] [CrossRef]
- Günsel, A.; Güzel, E.; Bilgiçli, A.T.; Şişman, İ.; Yarasir, M.N. Synthesis of non-peripheral thioanisole-substituted phthalocyanines: Photophysical, electrochemical, photovoltaic, and sensing properties. J. Photochem. Photobiol. A Chem. 2017, 348, 57–67. [Google Scholar] [CrossRef]
- Xue, X.; Lindstrom, A.; Li, Y. Porphyrin-Based Nanomedicines for Cancer Treatment. Bioconjug. Chem. 2019, 30, 1585–1603. [Google Scholar] [CrossRef]
- Cieplik, F.; Deng, D.; Crielaard, W.; Buchalla, W.; Hellwig, E.; Al-Ahmad, A.; Maisch, T. Antimicrobial photodynamic therapy—What we know and what we don’t. Crit. Rev. Microbiol. 2018, 44, 571–589. [Google Scholar] [CrossRef]
- Tsolekile, N.; Nelana, S.; Oluwafemi, O.S. Porphyrin as diagnostic and therapeutic agent. Molecules 2019, 24, 2669. [Google Scholar] [CrossRef]
- Drain, C.M.; Varotto, A.; Radivojevic, I. Self-Organized Porphyrinic Materials. Chem. Rev. 2009, 109, 1630–1658. [Google Scholar] [CrossRef] [PubMed]
- Borovkov, V. Effective Supramolecular Chirogenesis in Ethane-Bridged Bis-Porphyrinoids. Symmetry 2010, 2, 184–200. [Google Scholar] [CrossRef]
- Borovkov, V. Supramolecular chirality in porphyrin chemistry. Symmetry 2014, 6, 256–294. [Google Scholar] [CrossRef]
- Borovkov, V.; Inoue, Y. A Versatile Bisporphyrinoid Motif for Supramolecular Chirogenesis. Eur. J. Org. Chem. 2009, 2, 189–197. [Google Scholar] [CrossRef]
- Chmielewski, P.J.; Siczek, M.; Stępień, M. Bis(N-Confused Porphyrin) as a Semirigid Receptor with a Chirality Memory: A Two-Way Host Enantiomerization through Point-to-Axial Chirality Transfer. Chem. A Eur. J. 2015, 21, 2547–2559. [Google Scholar] [CrossRef]
- Paolesse, R.; Nardis, S.; Monti, D.; Stefanelli, M.; Di Natale, C. Porphyrinoids for Chemical Sensor Applications. Chem. Rev. 2017, 117, 2517–2583. [Google Scholar] [CrossRef]
- Mathew, P.T.; Fang, F. Advances in Molecular Electronics: A Brief Review. Engineering 2018, 4, 760–771. [Google Scholar] [CrossRef]
- Cook, L.; Brewer, G.; Wong-Ng, W. Structural aspects of porphyrins for functional materials applications. Crystals 2017, 7, 223. [Google Scholar] [CrossRef]
- Chaudhri, N.; Sankar, M. Colorimetric “naked eye” detection of CN−, F−, CH3COO− and H2PO4− ions by highly nonplanar electron deficient perhaloporphyrins. RSC Adv. 2015, 5, 3269–3275. [Google Scholar] [CrossRef]
- Hembury, G.A.; Borovkov, V.V.; Inoue, Y. Chirality-Sensing Supramolecular Systems. Chem. Rev. 2008, 108, 1–73. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, W.-H.; Xie, Y. Development of Ion Chemosensors Based on Porphyrin Analogues. Chem. Rev. 2017, 117, 2203–2256. [Google Scholar] [CrossRef]
- Carvalho, C.M.B.; Brocksom, T.J.; de Oliveira, K.T. Tetrabenzoporphyrins: Synthetic developments and applications. Chem. Soc. Rev. 2013, 42, 3302–3317. [Google Scholar] [CrossRef]
- Geraci, G.; Parkhurst, L.J.B.T.-M. Circular dichroism spectra of hemoglobins. In Methods in Enzymology; Academic Press: Cambridge, MA, USA, 1981; Volume 76, pp. 262–275. [Google Scholar]
- Ishiwari, F.; Fukasawa, K.; Sato, T.; Nakazono, K.; Koyama, Y.; Takata, T. A Rational Design for the Directed Helicity Change of Polyacetylene Using Dynamic Rotaxane Mobility by Means of Through-Space Chirality Transfer. Chem. A Eur. J. 2011, 17, 12067–12075. [Google Scholar] [CrossRef]
- Balaz, M.; De Napoli, M.; Holmes, A.E.; Mammana, A.; Nakanishi, K.; Berova, N.; Purrello, R. A Cationic Zinc Porphyrin as a Chiroptical Probe for Z-DNA. Angew. Chem. 2005, 117, 4074–4077. [Google Scholar] [CrossRef]
- Lu, H.; Kobayashi, N. Optically Active Porphyrin and Phthalocyanine Systems. Chem. Rev. 2016, 116, 6184–6261. [Google Scholar] [CrossRef]
- Ito, S.; Hiroto, S.; Ousaka, N.; Yashima, E.; Shinokubo, H. Control of Conformation and Chirality of Nonplanar π-Conjugated Diporphyrins Using Substituents and Axial Ligands. Chem. Asian J. 2016, 11, 936–942. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Fujioka, N.; Pescitelli, G.; Koehn, F.E.; Williamson, R.T.; Nakanishi, K.; Berova, N. Absolute Configurational Assignments of Secondary Amines by CD-Sensitive Dimeric Zinc Porphyrin Host. J. Am. Chem. Soc. 2002, 124, 10320–10335. [Google Scholar] [CrossRef] [PubMed]
- Borovkov, V.V.; Inoue, Y. Supramolecular Chirogenesis in Host-Guest Systems Containing Porphyrinoids. In Supramolecular Chirality; Crego-Calama, M., Reinhoudt, D.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 625, pp. 89–146. [Google Scholar]
- Borovkov, V.V.; Lintuluoto, J.M.; Inoue, Y. Supramolecular Chirogenesis in Bis(zinc porphyrin): An Absolute Configuration Probe Highly Sensitive to Guest Structure. Org. Lett. 2000, 2, 1565–1568. [Google Scholar] [CrossRef] [PubMed]
- Borovkov, V.V.; Lintuluoto, J.M.; Inoue, Y. Supramolecular Chirogenesis in Zinc Porphyrins: Mechanism, Role of Guest Structure, and Application for the Absolute Configuration Determination. J. Am. Chem. Soc. 2001, 123, 2979–2989. [Google Scholar] [CrossRef]
- Borovkov, V.V.; Lintuluoto, J.M.; Inoue, Y. Stoichiometry-Controlled Supramolecular Chirality Induction and Inversion in Bisporphyrin Systems. Org. Lett. 2002, 4, 169–171. [Google Scholar] [CrossRef] [PubMed]
- Olsson, S.; Schäfer, C.; Blom, M.; Gogoll, A. Exciton-Coupled Circular Dichroism Characterization of Monotopically Binding Guests in Host−Guest Complexes with a Bis(zinc porphyrin) Tweezer. ChemPlusChem 2018, 83, 1169–1178. [Google Scholar] [CrossRef] [PubMed]
- Takeda, S.; Hayashi, S.; Noji, M.; Takanami, T. Chiroptical Protocol for the Absolute Configurational Assignment of Alkyl-Substituted Epoxides Using Bis(zinc porphyrin) as a CD-Sensitive Bidentate Host. J. Org. Chem. 2019, 84, 645–652. [Google Scholar] [CrossRef] [PubMed]
- Borovkov, V.V.; Fujii, I.; Muranaka, A.; Hembury, G.A.; Tanaka, T.; Ceulemans, A.; Kobayashi, N.; Inoue, Y. Rationalization of Supramolecular Chirality in a Bisporphyrin System. Angew. Chem. Int. Ed. 2004, 43, 5481–5485. [Google Scholar] [CrossRef] [PubMed]
- Borovkov, V.V.; Lintuluoto, J.M.; Inoue, Y. Synthesis of Zn-, Mn, and Fe-containing mono- and heterometallated ethanediyl-bridged porphyrin dimers. Helv. Chim. Acta 1999, 82, 919–934. [Google Scholar] [CrossRef]
- Dudziński, K.; Pakulska, A.M.; Kwiatkowski, P. An Efficient Organocatalytic Method for Highly Enantioselective Michael Addition of Malonates to Enones Catalyzed by Readily Accessible Primary Amine-Thiourea. Org. Lett. 2012, 14, 4222–4225. [Google Scholar] [CrossRef]
- Cotton, F.A.; Murillo, C.A.; Wang, X.; Wilkinson, C.C. Strong reducing agents containing dimolybdenum Mo24+ units and their oxidized cations with Mo25+/6+ cores stabilized by bicyclic guanidinate anions with a seven-membered ring. Dalton Trans. 2006, 38, 4623–4631. [Google Scholar] [CrossRef]
- Online Tools for Supramolecular Chemistry Research and Analysis. Available online: http://supramolecular.org/ (accessed on 7 January 2021).
- Hirose, K. A Practical Guide for the Determination of Binding Constants. J. Incl. Phenom. 2001, 39, 193–209. [Google Scholar] [CrossRef]
- Hibbert, D.B.; Thordarson, P. The death of the Job plot, transparency, open science and online tools, uncertainty estimation methods and other developments in supramolecular chemistry data analysis. Chem. Commun. 2016, 52, 12792–12805. [Google Scholar] [CrossRef]
- Rigaku Oxford Diffraction. CrysAlisPro Software System, Version 38.46; Rigaku Corporation: Oxford, UK, 2017. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Cryst. 2008, A64, 112–122. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXL13. Program Package for Crystal Structure Determination from Single Crystal Diffraction Data; University of Göttingen: Göttingen, Germany, 2013. [Google Scholar]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, C71, 3–8. [Google Scholar]
- Hirshfeld, F.L. Can X-ray data distinguish bonding effects from vibrational smearing? Acta Cryst. 1976, A32, 239–244. [Google Scholar] [CrossRef]
- Thorn, A.; Dittrich, B.; Sheldrick, G.M. Enhanced rigid-bond restraints. Acta Cryst. 2012, A68, 448–451. [Google Scholar] [CrossRef]
- Eichkorn, K.; Treutler, O.; Öhm, H.; Häser, M.; Ahlrichs, R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995, 240, 283–290. [Google Scholar] [CrossRef]
- Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc. 1997, 97, 119–124. [Google Scholar] [CrossRef]
- Sierka, M.; Hogekamp, A.; Ahlrichs, R. Fast evaluation of the Coulomb potential for electron densities using multipole accelerated resolution of identity approximation. J. Chem. Phys. 2003, 118, 9136–9148. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- TURBOMOLE V7.0 2015, A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, Since 2007. Available online: http://www.turbomole.com (accessed on 7 January 2021).
- Martynov, A.G.; Mack, J.; May, A.K.; Nyokong, T.; Gorbunova, Y.G.; Tsivadze, A.Y. Methodological Survey of Simplified TD-DFT Methods for Fast and Accurate Interpretation of UV–Vis–NIR Spectra of Phthalocyanines. ACS Omega 2019, 4, 7265–7284. [Google Scholar] [CrossRef] [PubMed]
- Osadchuk, I.; Borovkov, V.; Aav, R.; Clot, E. Benchmarking computational methods and influence of guest conformation on chirogenesis in zinc porphyrin complexes. Phys. Chem. Chem. Phys. 2020, 22, 11025–11037. [Google Scholar] [CrossRef]
- Conradie, J.; Ghosh, A. Energetics of Saddling versus Ruffling in Metalloporphyrins: Unusual Ruffled Dodecasubstituted Porphyrins. ACS Omega 2017, 2, 6708–6714. [Google Scholar] [CrossRef]
- Andzelm, J.; Kölmel, C.; Klamt, A. Incorporation of solvent effects into density functional calculations of molecular energies and geometries. J. Chem. Phys. 1995, 103, 9312–9320. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Stratmann, R.E.; Scuseria, G.E.; Frisch, M.J. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules. J. Chem. Phys. 1998, 109, 8218–8224. [Google Scholar] [CrossRef]
- Casida, M.E.; Jamorski, C.; Casida, K.C.; Salahub, D.R. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J. Chem. Phys. 1998, 108, 4439–4449. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Peterson, K.A.; Woon, D.E.; Dunning, T.H. Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H+H2→H2+H reaction. J. Chem. Phys. 1994, 100, 7410–7415. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Konrad, N.; Meniailava, D.; Osadchuk, I.; Adamson, J.; Hasan, M.; Clot, E.; Aav, R.; Borovkov, V.; Kananovich, D. Supramolecular chirogenesis in zinc porphyrins: Complexation with enantiopure thiourea derivatives, binding studies and chirality transfer mechanism. J. Porphyr. Phthalocyanines 2019, 24, 840–849. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Borovkov, V.V.; Lintuluoto, J.M.; Inoue, Y. Syn-Anti Conformational Changes in Zinc Porphyrin Dimers Induced by Temperature-Controlled Alcohol Ligation. J. Phys. Chem. B 1999, 24, 5151–5156. [Google Scholar] [CrossRef]
- Borovkov, V.V.; Lintuluoto, J.M.; Sugeta, H.; Fujiki, M.; Arakawa, R.; Inoue, Y. Supramolecular Chirogenesis in Zinc Porphyrins: Equilibria, Binding Properties, and Thermodynamics. J. Am. Chem. Soc. 2002, 124, 2993–3006. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, D.; Guchhait, T.; Rath, S.P. Spin Modulation in Highly Distorted FeIII Porphyrinates by Using Axial Coordination and Their π-Cation Radicals. Eur. J. Inorg. Chem. 2016, 21, 3441–3453. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, M.; Chen, D.; Lin, B.; Zhou, Z.; Liu, Q. Horizontal and Vertical Push Effects in Saddled Zinc Porphyrin Complexes: Implications for Heme Distortion. Inorg. Chem. 2019, 58, 2627–2636. [Google Scholar] [CrossRef]
- Guberman-Pfeffer, M.J.; Greco, J.A.; Samankumara, L.P.; Zeller, M.; Birge, R.R.; Gascón, J.A.; Brückner, C. Bacteriochlorins with a Twist: Discovery of a Unique Mechanism to Red-Shift the Optical Spectra of Bacteriochlorins. J. Am. Chem. Soc. 2017, 139, 548–560. [Google Scholar] [CrossRef]
- Hajizadeh, F.; Reisi-Vanani, A.; Azar, Y.T. Theoretical design of Zn-dithiaporphyrins as sensitizer for dye-sensitized solar cells. Curr. Appl. Phys. 2018, 18, 1122–1133. [Google Scholar] [CrossRef]
- Sánchez-Bojorge, N.A.; Zaragoza-Galán, G.; Flores-Holguín, N.R.; Chávez-Rojo, M.A.; Castro-García, C.; Rodríguez-Valdez, L.M. Theoretical analysis of the electronic properties in Zinc-porphyrins derivatives. J. Mol. Struct. 2019, 1191, 259–270. [Google Scholar] [CrossRef]
- Thomassen, I.K.; Vazquez-Lima, H.; Gagnon, K.J.; Ghosh, A. Octaiodoporphyrin. Inorg. Chem. 2015, 54, 11493–11497. [Google Scholar] [CrossRef] [PubMed]
- Farley, C.; Bhupathiraju, N.V.S.D.K.; John, B.K.; Drain, C.M. Tuning the Structure and Photophysics of a Fluorous Phthalocyanine Platform. J. Phys. Chem. A 2016, 120, 7451–7746. [Google Scholar] [CrossRef] [PubMed]
- Harada, N.; Nakanishi, K. Circular Dichroic Spectroscopy. Exciton Coupling in Organic Stereochemistry; University Science Books: Mill Valley, CA, USA, 1983; pp. 1–406. [Google Scholar]


| Angles | Experimental (Solid-State) | Fully Optimized (Gas) | Fully Optimized (CH2Cl2 Solution) |
|---|---|---|---|
| N-Zn-Nopp (Por 1) | 160.6° | 162.9° | 160.8° |
| 161.2° | 163.5° | 161.0° | |
| Cβ-Cβ-Cβopp-Cβopp (Por 1) | 9.4° | 18.4° | 18.1° |
| −9.3° | −16.4° | −15.2° | |
| N-Zn-Nopp (Por 2) | 160.9° | 164.0° | 161.0° |
| 160.8° | 163.5° | 161.0° | |
| Cβ-Cβ-Cβopp-Cβopp (Por 2) | 11.6° | 10.9° | 10.7° |
| −13.5° | −11.7° | −11.9° | |
| Nguest-Zn-Nguest-Zn | 0.0° | 6.4° | 6.1° |
| Zn-Cmeso-Cmeso-Zn | 179.0° | −162.2° | −163.5° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osadchuk, I.; Konrad, N.; Truong, K.-N.; Rissanen, K.; Clot, E.; Aav, R.; Kananovich, D.; Borovkov, V. Supramolecular Chirogenesis in Bis-Porphyrin: Crystallographic Structure and CD Spectra for a Complex with a Chiral Guanidine Derivative. Symmetry 2021, 13, 275. https://doi.org/10.3390/sym13020275
Osadchuk I, Konrad N, Truong K-N, Rissanen K, Clot E, Aav R, Kananovich D, Borovkov V. Supramolecular Chirogenesis in Bis-Porphyrin: Crystallographic Structure and CD Spectra for a Complex with a Chiral Guanidine Derivative. Symmetry. 2021; 13(2):275. https://doi.org/10.3390/sym13020275
Chicago/Turabian StyleOsadchuk, Irina, Nele Konrad, Khai-Nghi Truong, Kari Rissanen, Eric Clot, Riina Aav, Dzmitry Kananovich, and Victor Borovkov. 2021. "Supramolecular Chirogenesis in Bis-Porphyrin: Crystallographic Structure and CD Spectra for a Complex with a Chiral Guanidine Derivative" Symmetry 13, no. 2: 275. https://doi.org/10.3390/sym13020275
APA StyleOsadchuk, I., Konrad, N., Truong, K.-N., Rissanen, K., Clot, E., Aav, R., Kananovich, D., & Borovkov, V. (2021). Supramolecular Chirogenesis in Bis-Porphyrin: Crystallographic Structure and CD Spectra for a Complex with a Chiral Guanidine Derivative. Symmetry, 13(2), 275. https://doi.org/10.3390/sym13020275