A Modified PRP-CG Type Derivative-Free Algorithm with Optimal Choices for Solving Large-Scale Nonlinear Symmetric Equations

Abstract

Inspired by the large number of applications for symmetric nonlinear equations, this article will suggest two optimal choices for the modified Polak–Ribiére–Polyak (PRP) conjugate gradient (CG) method by minimizing the measure function of the search direction matrix and combining the proposed direction with the default Newton direction. In addition, the corresponding PRP parameters are incorporated with the Li and Fukushima approximate gradient to propose two robust CG-type algorithms for finding solutions for large-scale systems of symmetric nonlinear equations. We have also demonstrated the global convergence of the suggested algorithms using some classical assumptions. Finally, we demonstrated the numerical advantages of the proposed algorithms compared to some of the existing methods for nonlinear symmetric equations.

1. Introduction

Consider the problem

$$G\left(x\right)=0,x\in R^n,$$

(1)

where $G:R^n⟶R^n$ is continuously differentiable mapping and its Jacobian is symmetric, i.e., $J\left(x\right)=J{\left(x\right)}^T$. Generally, the system of nonlinear equations has various applications in modern science and technology, some examples of nonlinear problems that are symmetrical in nature include “the discretized two-point boundary value problem, the gradient mapping of unconstrained optimization problem, the Karush-Kuhn-Tucker (KKT) of equality constrained optimization problems, the saddle point problem, and the discretized elliptic boundary value problem” see [1,2,3] for more details. There are different methods for solving symmetric nonlinear equations. Starting from the classic work of Li and Fukushima [1], where they proposed a Gauss-Newton-based Broyden-Fletcher-Goldfarb-Shanno (BFGS) method for the symmetric nonlinear equations. Subsequent improvements on the performance of [1] were discussed in [2,3,4,5,6] and the references therein. However, these methods are cost-effective in computing and storing the Jacobian approximate and therefore could not handle large-scale symmetric systems efficiently. These inspired researchers to develop methods that could adequately deal with large-scale problems. The conjugate gradient (CG) method is an iterative scheme of the form:

$$x_0\in R^n,x_{k+1}=x_k+t_k{h}_k,k=0,1,\dots ,$$

(2)

where $t>0$ is a stepsize to be determined by some line search techniques and $h_k$ is the CG search direction defined by

$$h_0=-G_0,h_{k+1}=-G_{k+1}+{\beta }_k{h}_k,k=0,1,\dots ,$$

(3)

$G_k=G\left(x_k\right)$, and ${\beta }_k$ is the CG parameter [7]. Moreover, the efficiency of the CG method is based on the appropriate selection of the parameter ${\beta }_k$, see [7,8,9]. As dictated in the survey paper proposed by Hager and Zhang [7], one of the most effective CG parameters is the one suggested by Polak, Ribiére and Polyak (PRP) [8] with an outstanding restart feature given by

$${\beta }_k^{PRP}=\frac{G_{k+1}^T{y}_k}{∥G_k∥},$$

(4)

where $y_k=G_{k+1}-G_k$ and $∥.∥$ represents the Euclidean norm. However, despite the effectiveness and efficiency of the PRP method, the direction generated by the PRP method is not descent, i.e., it does not fulfill the condition

$$G_k^T{h}_k<0,\forall k\ge 0.$$

(5)

This prompted Zhang et al. [10] to propose the following modification of the PRP CG parameter given by

$${\beta }_k^{DPRP}={\beta }_k^{PRP}-\frac{G_{k+1}^T{h}_k}{{∥G_k∥}^2}.$$

(6)

The modified CG parameter (6) met the following sufficient descent condition

$$G_k^T{h}_k\le -\gamma {∥G_k∥}^2,\forall k\ge 0,$$

(7)

with $\gamma$ as positive constant.

Furthermore, in the same vein as Zhang et al [10], Babaie-Kafaki and Ghanbari [11] have recently studied the following extension of the PRP method based on the Dai and Liao [12] strategies,

$${\beta }_k^{EPRP}={\beta }_k^{PRP}-\eta \frac{G_{k+1}^T{h}_k}{{∥G_k∥}^2},$$

(8)

$\eta$ is specified as a nonnegative constant. They considered the computation of $\eta$ in (8) as an open problem in nonlinear CG methods. They also pointed out that their adaptive formula for selecting $\eta$ for each iteration is better than a fixed selection [11].

Now, researchers have focused their attention on solving the symmetric systems of nonlinear equations using CG methods. Li and Wang [13] have suggested the modified Fletcher-Reeves-type (FR) CG method for solving symmetric equations. The method is a derivative and matrix-free method, therefore it could handle large dimensions of symmetric nonlinear equations efficiently. Besides, Zhou and Shen have suggested an inexact version of the PRP CG method for the systems of symmetric nonlinear equations [14]. Since then, different CG methods for the solution of symmetric nonlinear systems have been presented, see [15,16,17,18,19,20,21,22,23] for more details. Moreover, motivated by the efficiency of the extended PRP method [11] and the robustness of CG methods in solving large-scale symmetric nonlinear systems, we want to propose two optimal relations for the computation of $\eta$ in (8) and use the corresponding modified PRP parameters to propose algorithms for solving large-scale symmetric nonlinear systems without using the exact gradient information.

The rest of this paper is organized as follows. In Section 2, we present the modified PRP CG-type algorithm for solving symmetric nonlinear equations. In Section 3, the proposed algorithm is shown to converge globally. Section 4 provides computational experiments to demonstrate its practical performance. The paper is concluded in Section 5.

2. Modified PRP CG-Type with Optimal Choices

Li and Fukushima [1] observed that when the Jacobian $\nabla G\left(x_k\right)$ is symmetric, then the following relation holds:

$$G(x_k+t_k{G}_k)-G_k=t_k{\int }_0^1\nabla G(x_k+r{t}_k{G}_k)G_{k}dr,$$

(9)

where $t_k$ is an arbitrary scalar. They utilized (9) and approximated the gradient of the function $G_k$ as

$$p_k=\frac{G(x_k+t_k{G}_k)-G_k}{t_k},$$

(10)

and the step size $t_k$ is to be determined as $t_k=max\left\{1,a,a^2,\cdots \right\}$ such that

$$g(x_k+t_k{h}_k)-g\left(x_k\right)\le -{\zeta }_1\left|\right|t_{k}G\left(x_k\right){\left|\right|}^2-{\zeta }_2\left|\right|t_k{h}_k{\left|\right|}^2+{\varphi }_{k}g\left(x_k\right),$$

(11)

where ${\zeta }_1>0$, ${\zeta }_2>0$, $a\in (0,1)$ are real constants and $\left\{{\varphi }_k\right\}$ is a positive sequence such that

$$\sum _{k=0}^{\infty }{\varphi }_k<\infty .$$

(12)

It is important to state that the function $g:R^n⟶R$ is a merit function defined by

$$g\left(x\right)=\frac{1}{2}{∥G\left(x\right)∥}^2.$$

(13)

Byrd and Nocedal [24] presented the following measure function given by

$$\phi \left(Q_k\right)=Tr\left(Q_k\right)-ln(det\left(Q_k\right))$$

(14)

where “$Q_k$” is a positive definite matrix, “$Tr\left(Q_k\right)$” is the trace of the matrix $Q_k$, “ln” denotes the natural logarithm, and “$det\left(Q_k\right)$” is the determinant of $Q_k$. The function $\phi$ works with the trace and the determinant of the matrix $Q_k$ and it involves all the eigenvalues of $Q_k$ [24]. Now, using (8) and (11) we suggest the following modified PRP CG-type parameter

$${\beta }_k^{MPRP}=\frac{p_{k+1}^T{y}_k}{∥p_k∥}-{\eta }_k^{*}\frac{p_{k+1}^T{h}_k}{{∥p_k∥}^2},$$

(15)

where ${\eta }_k^{*}$ is the optimal choice of $\eta$ and $y_k=p_{k+1}-p_k$. In what follows, we are going to propose two optimal choices for the nonnegative constant ${\eta }_k^{*}$ at every iteration.

2.1. The First Optimal Choice for ${\eta }_k^{*}$

This subsection will presents the first optimal choice by minimizing the major function of the proposed search direction matrix over ${\eta }_k^{*}$. Now, considering Perry’s point of view [25], and Equations (3), (10) and (15), we write the search directions of the MPRP CG method as follows:

$$h_{k+1}=Q_{k+1}{p}_{k+1},k=0,1,\cdots ,$$

(16)

with $Q_{k+1}$ being the search direction matrix defined by

$$Q_{k+1}=I-\frac{h_k{y}_k^T}{{∥p_k∥}^2}+{\eta }_k^{*}\frac{h_k{h}_k^T}{{∥p_k∥}^2}.$$

(17)

The major function of the search directions matrix $Q_{k+1}$ is defined by

$$\phi \left(Q_{k+1}\right)=tr\left(Q_{k+1}\right)-ln(det\left(Q_{k+1}\right)).$$

(18)

Since the matrix $Q_{k+1}$ is a rank 2 update, its determinant is given by

$$det\left(Q_{k+1}\right)=1-\frac{h_k^T{y}_k}{{∥p_k∥}^2}+{\eta }_k^{*}\frac{{∥h_k∥}^2}{{∥p_k∥}^2},$$

(19)

and it trace as

$$tr\left(Q_{k+1}\right)=n-\frac{h_k^T{y}_k}{{∥p_k∥}^2}+{\eta }_k^{*}\frac{{∥h_k∥}^2}{{∥p_k∥}^2}$$

(20)

respectively. Now, using (19) and (20) the major fuction of $Q_{k+1}$ is

$$\phi \left(Q_{k+1}\right)=n-\frac{h_k^T{y}_k}{{∥p_k∥}^2}+{\eta }_k^{*}\frac{{∥h_k∥}^2}{{∥p_k∥}^2}-ln\left(1-\frac{h_k^T{y}_k}{{∥p_k∥}^2}+{\eta }_k^{*}\frac{{∥h_k∥}^2}{{∥p_k∥}^2}\right).$$

(21)

Differentiating (21) with respect to ${\eta }_k^{*}$ to have

$$\frac{d\phi \left(Q_{k+1}\right)}{d{\eta }_k^{*}}=\frac{{∥h_k∥}^2}{{∥p_k∥}^2}-\frac{1}{1-\frac{h_k^T{y}_k}{{∥p_k∥}^2}+{\eta }_k^{*}\frac{{∥h_k∥}^2}{{∥p_k∥}^2}}\frac{{∥h_k∥}^2}{{∥p_k∥}^2}.$$

(22)

Hence, by setting $\frac{d\phi \left(Q_{k+1}\right)}{d{\eta }_k^{*}}=0$, and solving for ${\eta }_k^{*}$ to get the first optimal choice for ${\eta }_k^{*}$ as

$${\eta }_k^{1*}=\frac{h_k^T{y}_k}{{∥h_k∥}^2}.$$

(23)

Therefore the modified PRP CG-type parameter (15) becomes

$${\beta }_k^{MPRP}=\frac{p_{k+1}^T{y}_k}{∥p_k∥}-{\eta }_k^{1*}\frac{p_{k+1}^T{h}_k}{{∥p_k∥}^2},$$

(24)

2.2. The Second Optimal Choice for ${\eta }_k^{*}$

Now, for the second optimal choice of the parameter ${\eta }_k$ in (15). Recall that using the approximate gradient (10) the Newton direction is given by

$$h_{k+1}=-J_{k+1}^{-1}{p}_{k+1}.$$

(25)

Moreover, the search direction for the modified PRP CG-type method (15) can be written as

$$h_{k+1}=-p_{k+1}+\left(\frac{p_{k+1}^T{y}_k}{{∥p_k∥}^2}-{\eta }_k^{*}\frac{p_{k+1}^T{h}_k}{{∥p_k∥}^2}\right)h_k.$$

(26)

Newton direction is considered to be among the most robust schemes [7]. Therefore by Equating (25) with (26), we get

$$-J_{k+1}^{-1}{p}_{k+1}=-p_{k+1}+\left(\frac{p_{k+1}^T{y}_k}{{∥p_k∥}^2}-{\eta }_k^{*}\frac{p_{k+1}^T{h}_k}{{∥p_k∥}^2}\right)h_k.$$

(27)

Now, assuming that the Jacobian of $G_k$ is symmetric and multiplying the both sides of (27) by $s_k^T{J}_{k+1}$ to obtain

$$-s_k^T{p}_{k+1}=-s_k^T{J}_{k+1}{p}_{k+1}+s_k^T{J}_{k+1}\left(\frac{p_{k+1}^T{y}_k}{{∥p_k∥}^2}-{\eta }_k^{*}\frac{p_{k+1}^T{h}_k}{{∥p_k∥}^2}\right)h_k.$$

(28)

Recall that, the secant equation is given by

$$y_k=J_{k+1}{s}_k.$$

(29)

From the fact that $J_{k+1}=J_{k+1}^T$ and the vitue of the secant equation, we rewrite (28) as

$$-s_k^T{p}_{k+1}=-y_k^T{p}_{k+1}+y_k^T\left(\frac{p_{k+1}^T{y}_k}{{∥p_k∥}^2}-{\eta }_k^{*}\frac{p_{k+1}^T{h}_k}{{∥p_k∥}^2}\right)h_k.$$

(30)

After simple algebraic simplifications we get the second optimal choice as

$${\eta }_k^{*}=\frac{{\left(s_k-y_k\right)}^T{p}_{k+1}{∥p_k∥}^2}{p_{k+1}^T{h}_k{y}_k^T{h}_k}+\frac{p_{k+1}^T{y}_k}{p_{k+1}^T{h}_k}.$$

(31)

Now, for the prove of the global convergence of propose algorithm and promising numerical result, we selected our second optimal choice to be given as

$${\eta }_k^{2*}=min\left\{1,\frac{{\left(s_k-y_k\right)}^T{p}_{k+1}{∥p_k∥}^2}{p_{k+1}^T{h}_k{y}_k^T{h}_k}+\frac{p_{k+1}^T{y}_k}{p_{k+1}^T{h}_k}\right\}.$$

(32)

Therefore, the modified PRP CG-type parameter with second optimal choice becomes

$${\beta }_k^{MPRP}=\frac{p_{k+1}^T{y}_k}{{∥p_k∥}^2}-{\eta }_k^{2*}\frac{p_{k+1}^T{h}_k}{{∥p_k∥}^2}.$$

(33)

Below is the modified PRP CG-type algorithm for solving large system of nonlinear symmetric equations.

3. Global Convergence

To start with the optimal choice ${\eta }_k^{1*}$, we define the level set by

$$\Psi =\left\{x|g\left(x\right)\le {exp}^{\varphi }g\left(x_0\right)\right\},$$

(34)

where $\varphi$ satisfies (12).

Lemma 1.

Let $\left\{x_k\right\}$ be generated by the MPRP Algorithm 1. Then $\left\{x_k\right\}\in \Psi$. In addition, $\left\{G_k\right\}$ converges.

Algorithm 1: MPRP Algorithm

step 0 Choose $x_0\in R^n$, $t_0,ϵ>0$, $\zeta \in \left(0,1\right)$, $h_0=-p_0$ and set $k=0$.  step 1 Check if $∥G\left(x_k\right)∥\le ϵ$ is satisfied, else go to step 2.  step 2 Determine the stepsize $t_k$ by using (11).  step 3 Compute $x_{k+1}=x_k+t_k{h}_k$  step 4 Determine the CG direction as $$h_{k+1}=-p_{k+1}+{\beta }_k^{MPRP}{h}_k,$$ (35)  using any of the optimal choices in (23) or (32).  step 5 Set $k=k+1$ and go back to step 1.

Proof. 

From (11), we have $∥G_{k+1}∥\le {(1+\varphi )}^{\frac{1}{2}}∥G_k∥$ for all k. As $\varphi$ fulfills (12), we conclude that $\left\{∥G_k∥\right\}$ converges from Lemma 3.3 in [26]. In fact, we have for all k

$$\begin{array}{cc}\hfill \parallel G_{k+1}\parallel & \le {(1+{\varphi }_k)}^{\frac{1}{2}}\parallel G_k\parallel \hfill \\ \hfill & ⋮\hfill \\ \hfill & \le \prod _{i=0}^k{(1+{\varphi }_k)}^{\frac{1}{2}}\parallel G_0\parallel \hfill \\ \hfill & \le \parallel G_0\parallel {\left[\frac{1}{k+1}\sum _{i=0}^k(1+{\varphi }_i)\right]}^{\frac{k+1}{2}}\hfill \\ \hfill & \le \parallel G_0\parallel {\left[1+\frac{1}{k+1}\sum _{i=0}^k{\varphi }_i\right]}^{\frac{k+1}{2}}\hfill \\ \hfill & \le \parallel G_0\parallel {\left(1+\frac{\varphi }{k+1}\right)}^{\frac{k+1}{2}}\hfill \\ \hfill & \le \parallel G_0\parallel {\left(1+\frac{\varphi }{k+1}\right)}^{k+1}\hfill \\ \hfill & \le e^{\varphi }\parallel G_0\parallel .\hfill \end{array}$$

(36)

This means $\left\{x_k\right\}\in \Psi$. □

We make the following assumptions, which in the rest of this section will be frequently used.

Assumption A1.

(i) 

The set Ψ is bounded.

(ii) 

The Jacobian is Lipschitz in some neighbourhood $x\in {\Psi }_1$ of Ψ. The positive constant M exists, such that

$$∥J\left(x\right)-J\left(y\right)∥\le M∥x-y∥,\forall x,y\in {\Psi }_1.$$

(37)

Assumptions (i) and (ii) mean that there are constants $M>m>0$ such that for all $x\in {\Psi }_1$

$$∥G\left(x\right)∥\le C_1,∥J\left(x\right)∥\le C_2\forall x\in {\Psi }_1.$$

(38)

$$∥\nabla g\left(x\right)-\nabla g\left(y\right)∥\le M_1∥x-y∥,\forall x,y\in {\Psi }_1.$$

(39)

Lemma 2.

Let Assumption K holds. Then we have

$$\underset{k\to \infty }{lim}∥t_k{h}_k∥=\underset{k\to \infty }{lim}\left|\right|s_k\left|\right|=0,$$

(40)

and

$$\underset{k\to \infty }{lim}∥t_k{G}_k∥=0.$$

(41)

Proof. 

This comes directly from (11) and (12). Now,

$${\zeta }_1{∥t_{k}G\left(x_k\right)∥}^2+{\zeta }_2{∥t_k{h}_k∥}^2\le g\left(x_k\right)-g\left(x_{k+1}\right)+{\varphi }_{k}g\left(x_k\right),$$

(42)

when we sum up the k inequality above, then we get:

$$\sum _{i=0}^m{\zeta }_1{∥t_{k}G\left(x_k\right)∥}^2+{\zeta }_2{∥t_k{h}_k∥}^2\le g\left(x_1\right)-g\left(x_m\right)+\sum _{i=0}^m{\varphi }_{i}g\left(x_k\right).$$

(43)

So, from hypothesis K and that $\left\{{\varphi }_k\right\}$ satisfies (12) the results will follow. □

The theorem below shows that MPRP algorithm converge globally.

Theorem 1.

Let Assumption K holds. Then the MPRP Algorithm 1 generated sequence $\left\{x_k\right\}$ converges globally, that is,

$$\underset{k\to \infty }{lim\; inf}∥\nabla g\left(x_k\right)∥=0.$$

(44)

Proof. 

We prove this theorem by contradiction. Suppose that (44) is not true, then there exists a positive constant $\alpha$ such that

$$∥\nabla g\left(x_k\right)∥\ge \alpha ,\forall k\ge 0.$$

(45)

Since $\nabla g\left(x_k\right)=J_k^T$, then (45) implies that there exists a positive constant ${\alpha }_1$ satisfying

$$∥G_k∥\ge {\alpha }_1,\forall k\ge 0.$$

(46)

CASE I:${lim\; sup}_{k\to \infty }{t}_k>0$, then by (41), we have ${lim\; sup}_{k\to \infty }∥G_k∥=0$. This and Lemma 2 show that ${lim}_{k\to \infty }∥G_k∥=0$, which contradicts with (46).

CASE II:${lim\; sup}_{k\to \infty }{t}_k=0$. Since $t_k\ge 0$, this case implies that

$$\underset{k\to \infty }{lim}{t}_k=0.$$

(47)

By definition of $p_k$ in (10) and the symmetry of the Jacobian, we have

$$\begin{array}{cc}\hfill ∥p_k-\nabla g\left(x_k\right)∥& =∥\frac{G(x_k+t_k{G}_k)-G_k}{t_k}∥-J_k{G}_k\hfill \\ \hfill & =∥{\oint }_0^1\left(J(x_k+s{t}_k{G}_k)-J_k\right)ds{G}_k∥\hfill \\ \hfill & \le t_{k}M{C}_1^2,\hfill \end{array}$$

(48)

where we used the Lipschitz assumption on the Jacobian and the boundedness on $G_k$ as well in the last inequality. However, (45) and (47) show that there exist a constant ${\alpha }_2>0$ such that

$$∥p_k∥\ge {\alpha }_2,\forall k\ge 0.$$

(49)

By considering (10) and the boundness of $J_k$ and $G_k$

$$∥p_k∥=∥{\int }_0^{1}J(x_k+s{t}_k{G}_k)G_{k}ds∥\le M{C}_1,\forall k\ge 0.$$

(50)

Now, from Equaton (48) and the Lipschitz assuption on $\nabla g\left(x\right)$

$$\begin{array}{cc}\hfill ∥y_k∥& =∥p_{k+1}-p_k∥\hfill \\ \hfill & \le ∥p_{k+1}-\nabla g\left(x_{k+1}\right)∥+∥p_k-\nabla g\left(x_k\right)∥+∥\nabla g\left(x_{k+1}\right)-\nabla g\left(x_k\right)∥\hfill \\ \hfill & \le M{C}_1\left(t_{k+1}-t_k\right)+M_1∥s_k∥.\hfill \end{array}$$

(51)

This together with (40) and (47) show that ${lim}_{k\to \infty }{y}_k=0$. Then from (49) and (50) we get

$$\begin{array}{cc}\hfill \left|{\beta }_k^{MPRP}\right|& \le \frac{∥p_{k+1}∥∥y_k∥}{{\alpha }_2^2}+\frac{∥h_k∥∥y_k∥}{{∥h_k∥}^2}\frac{∥p_{k+1}∥∥h_k∥}{{\alpha }_2^2}\hfill \\ \hfill & \le 2\frac{M{C}_1}{{\alpha }_2^2}∥y_k∥⟶0,\hfill \end{array}$$

(52)

which means that there exists a constant $\tau \in (0,1)$ such that for sufficiently large k,

$$\left|{\beta }_k^{MPRP}\right|\le \tau .$$

(53)

We assume that the inequality (52) is true for all $k>0$ without any loss of generality. Then from (3) and (50), we get

$$\begin{array}{cc}\hfill ∥h_{k+1}∥& \le ∥p_{k+1}∥+\left|{\beta }_{k+1}\right|∥h_k∥\le M{C}_1+\tau ∥h_k∥,\hfill \\ \hfill & \le M{C}_1\left(1+\tau +{\tau }^2+\cdots +{\tau }^k\right)+{\tau }^k∥h_0∥,\hfill \\ \hfill & \le \frac{M{C}_1}{1-\tau }+M{C}_1=\frac{M{C}_1(2-\tau )}{1-\tau },\hfill \end{array}$$

(54)

this shows that the sequence $\left\{h_{k+1}\right\}$ is bounded. Because of ${lim}_{k\to \infty }{t}_k=0$, then $t_k^{\prime }=\frac{t_k}{a}$ is not satisfied (11), that is to say,

$$g(x_k+t_k^{\prime }{h}_k)-g\left(x_k\right)>-{\zeta }_1{∥t_k^{\prime }G\left(x_k\right)∥}^2-{\zeta }_2{∥t_k^{\prime }{h}_k∥}^2+{\varphi }_{k}g\left(x_k\right),$$

(55)

which means that

$$\frac{g(x_k+t_k^{\prime }{h}_k)-g\left(x_k\right)}{t_k^{\prime }}>-{\zeta }_1{t}_k^{\prime }{∥G\left(x_k\right)∥}^2-{\zeta }_2{t}_k^{\prime }{∥h_k∥}^2.$$

(56)

By means of the mean value theorem, $\delta \in (0,1)$ exists in such a way as

$$\frac{g(x_k+t_k^{\prime }{h}_k)-g\left(x_k\right)}{t_k^{\prime }}=\nabla g{(x_k+\delta t_k^{\prime }{h}_k)}^T{h}_k.$$

(57)

Because $x\in \Psi$ is bounded, We assume that $x_k\to x^{*}$ and have the following result using (48) and the boundedness of $h_{k+1}$

$$\underset{k\to \infty }{lim}{h}_{k+1}=-\underset{k\to \infty }{lim}{p}_{k+1}+\underset{k\to \infty }{lim}{\beta }_{k+1}{h}_k=-\nabla g\left(x^{*}\right).$$

(58)

We have, on the other hand,

$$\underset{k\to \infty }{lim}\nabla g(x_k+\delta t_k^{\prime }{h}_k)=\nabla g\left(x^{*}\right).$$

(59)

Hence, using (58) and (59) in (57) we get $-\nabla g{\left(x^{*}\right)}^T\nabla g\left(x^{*}\right)\ge 0$. Which implies $∥\nabla g\left(x^{*}\right)∥=0$. This is in contradiction with (45). This complete the proof of the theorem. □

4. Numerical Experiments

In this section, we compare the numerical performances of the modified PRP CG-type algorithm using the proposed optimal choice with the norm descent derivative-free algorithm (NDDA) [21] and the ICGM algorithm [22] for solving the nonlinear symmetric Equation (1). For the MPRP algorithm, we set: $\zeta ={10}^{-4}$, $a=0.4$, $t_0=0.01$ and ${\varphi }_k=\frac{1}{{({10}^4+k)}^2}$. While for the remaining two methods we adopted the same parameter as in their respective papers. The codes were written in Matlab R2014a and run on a personal computer with a 1.6 GHz CPU and 8 GB RAM. If the total number of iterations exceeds 1000 or $∥G\left(x_k\right)∥\le {10}^{-5}$, then the iteration is stopped. On the following eight test problems, we tested all three methods with different initial points and n values:

Problem 1

([1]).

• $G\left(x_i\right)=4x_i+(x_{i+1}-2x_i)-\frac{x_{i+1}^2}{3}$, for $i=1,2,\dots ,n-1$.
• $G\left(x_n\right)=4x_n+(x_{n-1}-2x_n)-\frac{x_{n-1}^2}{3}$,

Problem 2

([1]).

• $G_1\left(x\right)=x_1(x_1^2+x_2^2)-1$
• $G_i\left(x\right)=x_i(x_{i-1}^2+2x_i^2+x_{i+1}^2)-1,i=2,3,\cdots ,n-1,$
• $G_n\left(x\right)=x_n(x_{n-1}^2+x_n^2)$

Problem 3

([14]).

• $G_i\left(x\right)=x_i-{(1-\frac{c}{2n}{\sum }_{j=1}^n\frac{{\mu }_i{x}_j}{{\mu }_i+{\mu }_j})}^{-1},$ for $i=1,2,\cdots ,n,$ $\mu =\frac{i-0.5}{n}$, $c=0.9$

Problem 4

([27]).

• $G\left(x_i\right)=2x_i-sin\left|x_i\right|$, for $i=1,2,\dots ,n$

Problem 5

([27]).

• $G_1\left(x\right)=h{x}_1+x_2-1,$
• $G_i\left(x\right)=x_{i-1}+h{x}_i+x_{i-1}-1,$ for $i=2,3,\dots ,n-1$, $h=2.5$
• $G_n\left(x\right)=x_{n-1}+h{x}_n-1$

Problem 6

([27]).

• $G_1\left(x\right)=x_1+exp(cos(h{x}_1+x_2)),$
• $G_i\left(x\right)=x_i+exp(cos(h{x}_{i-1}+x_i+x_{i+1})),$ for $i=2,3,\dots ,n-1$, $h=\frac{1}{n+1}$
• $G_n\left(x\right)=x_n+exp(cos(h{x}_{n-1}+x_n))$

Problem 7

([15]).

• $G_1\left(x\right)=2x_1-x_2+u{h}^{2}log\left(cosh(x_1-1)\right)-1,$
• $G_i\left(x\right)=2x_i-x_{i-1}+u{h}^{2}log\left(cosh(x_i-1)\right)-1,$ for $i=2,3,\dots ,n-1$, $h=\frac{1}{n-1}$
• $G_i\left(x\right)=2x_n-x_{n-1}+uhlog\left(cosh(x_n-1)\right)-1,$

Problem 8

([26]).

• $G\left(x\right)=\left(\begin{array}{ccccc}\frac{5}{2}& 1& & & \\ 1& \frac{5}{2}& 1& & \\ & \ddots & \ddots & \ddots & \\ & & \ddots & \ddots & 1\\ & & & 1& \frac{5}{2}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ \\ \\ x_n\end{array}\right)+\left(\begin{array}{c}1\\ 1\\ ⋮\\ \\ \\ 1\end{array}\right)$

Table 1, Table 2, Table 3 and Table 4 contained the numerical results of the three methods for the test problems with the eight different initial points namely; $x_1=(1,1,\dots ,1)$, $x_2=(1,\frac{1}{2},\frac{1}{3},\dots ,\frac{1}{n})$, $x_3=(0.1,0.1,\dots ,0.1)$, $x_4=(\frac{1}{n},\frac{2}{n},\dots ,1)$, $x_5=(1-\frac{1}{n},1-\frac{2}{n},\dots ,0)$, $x_6=(-1,-1,\dots ,-1)$, $x_7=(n-\frac{1}{n},n-\frac{2}{n},\dots ,n-1)$ and $x_8=(\frac{1}{2},1,\frac{2}{3},\dots ,\frac{2}{n})$.

Table 1. Numerical Comparisons of MPRP, NDDA [21] and ICGM [22].

PROBLEM 1
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
50,000	$x_1$	31	93	1.51757	7.72 × 10${}^{-6}$	11	44	0.517181	5.84 × 10${}^{-6}$	19	95	0.602169	8.39 × 10${}^{-6}$	13	39	0.394323	6.33 × 10${}^{-6}$
	$x_2$	25	75	1.182817	7.05 × 10${}^{-6}$	22	88	0.825475	8.39 × 10${}^{-7}$	21	105	0.641815	7.71 × 10${}^{-6}$	18	54	0.531024	4.16 × 10${}^{-6}$
	$x_3$	33	99	1.604626	8.78 × 10${}^{-6}$	11	44	0.503097	4.82 × 10${}^{-6}$	18	90	0.558197	7.96 × 10${}^{-6}$	19	57	0.58265	4.37 × 10${}^{-6}$
	$x_4$	39	117	1.894566	5.22 × 10${}^{-6}$	30	120	1.348329	5.4 × 10${}^{-6}$	20	100	0.608259	6.12 × 10${}^{-6}$	27	81	0.830261	4.49 × 10${}^{-6}$
	$x_5$	39	117	1.737297	5.31 × 10${}^{-6}$	28	112	1.227482	5.55 × 10${}^{-6}$	20	100	0.614197	8.51 × 10${}^{-6}$	27	81	0.82587	6.28 × 10${}^{-6}$
	$x_6$	43	129	1.95166	8.01 × 10${}^{-6}$	19	76	0.938165	9.28 × 10${}^{-6}$	21	105	0.643514	5.89 × 10${}^{-6}$	21	63	0.663403	5.11 × 10${}^{-6}$
	$x_7$	39	117	1.561943	5.31 × 10${}^{-6}$	28	112	1.237306	5.55 × 10${}^{-6}$	20	100	0.611944	8.51 × 10${}^{-6}$	27	81	0.817997	6.28 × 10${}^{-6}$
	$x_8$	24	72	0.866136	5.98 × 10${}^{-6}$	17	68	0.578612	7.32 × 10${}^{-7}$	25	125	0.744996	6.89 × 10${}^{-6}$	26	78	0.801215	2.77 × 10${}^{-6}$
100,000	$x_1$	33	99	2.503401	4.79 × 10${}^{-6}$	11	44	1.060649	8.26 × 10${}^{-6}$	20	100	1.261737	4.86 × 10${}^{-6}$	13	39	0.824816	8.95 × 10${}^{-6}$
	$x_2$	25	75	1.828535	7.05 × 10${}^{-6}$	22	88	1.748833	8.39 × 10${}^{-7}$	21	105	1.29851	7.71 × 10${}^{-6}$	18	54	1.103288	5.3 × 10${}^{-6}$
	$x_3$	35	105	2.51006	5.45 × 10${}^{-6}$	11	44	1.062033	6.82 × 10${}^{-6}$	19	95	1.200428	4.61 × 10${}^{-6}$	19	57	1.206809	6.18 × 10${}^{-6}$
	$x_4$	39	117	2.825586	7.37 × 10${}^{-6}$	30	120	2.821417	7.3 × 10${}^{-6}$	20	100	1.258583	8.6 × 10${}^{-6}$	28	84	1.74041	6.85 × 10${}^{-6}$
	$x_5$	39	117	2.623883	7.38 × 10${}^{-6}$	28	112	2.570306	7.91 × 10${}^{-6}$	20	100	1.236652	9.1 × 10${}^{-6}$	29	87	1.816512	6.83 × 10${}^{-6}$
	$x_6$	45	135	3.021735	4.97 × 10${}^{-6}$	21	84	2.200632	1.13 × 10${}^{-6}$	21	105	1.268213	8.33 × 10${}^{-6}$	21	63	1.341347	7.22 × 10${}^{-6}$
	$x_7$	39	117	2.603868	7.38 × 10${}^{-6}$	28	112	2.621052	7.91 × 10${}^{-6}$	20	100	1.17081	9.1 × 10${}^{-6}$	29	87	1.804864	6.83 × 10${}^{-6}$
	$x_8$	24	72	1.63477	5.98 × 10${}^{-6}$	17	68	1.197102	7.63 × 10${}^{-7}$	25	125	1.476767	6.89 × 10${}^{-6}$	26	78	1.619349	2.77 × 10${}^{-6}$
PROBLEM 2
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
50,000	$x_1$	170	510	7.931493	8.93 × 10${}^{-6}$	150	600	4.737454	8.27 × 10${}^{-6}$	382	1910	11.20393	9.75 × 10${}^{-6}$	237	711	7.620697	9.98 × 10${}^{-6}$
	$x_2$	141	423	5.058762	6.93 × 10${}^{-6}$	269	1076	9.397728	9.33 × 10${}^{-6}$	155	775	4.362288	8.76 × 10${}^{-6}$	244	732	7.83738	9.88 × 10${}^{-6}$
	$x_3$	102	306	2.842245	8.74 × 10${}^{-6}$	137	548	4.299041	8.93 × 10${}^{-6}$	384	1920	8.689407	9.91 × 10${}^{-6}$	211	633	4.873246	9.22 × 10${}^{-6}$
	$x_4$	324	972	9.531927	5.72 × 10${}^{-6}$	309	1236	10.46505	9.73 × 10${}^{-6}$	619	3095	12.28244	9.99 × 10${}^{-6}$	1000	3000	22.33118	10.91535
	$x_5$	244	732	6.331992	5.68 × 10${}^{-6}$	268	1072	7.62583	8.86 × 10${}^{-6}$	455	2275	8.708046	9.02 × 10${}^{-6}$	1000	3000	19.49895	10.68423
	$x_6$	67	201	1.95987	7.29 × 10${}^{-6}$	122	488	3.443245	9.85 × 10${}^{-6}$	352	1760	6.605092	9.02 × 10${}^{-6}$	324	972	6.04279	9.73 × 10${}^{-6}$
	$x_7$	276	828	9.354755	8.37 × 10${}^{-6}$	278	1112	8.543894	8.97 × 10${}^{-6}$	455	2275	9.163612	9.02 × 10${}^{-6}$	1000	3000	21.8643	10.68423
	$x_8$	207	621	6.630383	7.9 × 10${}^{-6}$	157	628	4.880471	6.37 × 10${}^{-6}$	288	1440	6.438931	8.97 × 10${}^{-6}$	166	498	3.764327	9.71 × 10${}^{-6}$
100,000	$x_1$	152	456	9.113001	7.61 × 10${}^{-6}$	148	592	8.525471	9.9 × 10${}^{-6}$	383	1915	15.44497	9.74 × 10${}^{-6}$	91	273	4.354032	9.74 × 10${}^{-6}$
	$x_2$	163	489	10.66124	9.28 × 10${}^{-6}$	223	892	15.55174	9.09 × 10${}^{-6}$	155	775	6.307293	9.95 × 10${}^{-6}$	399	1197	17.15205	9.74 × 10${}^{-6}$
	$x_3$	77	231	3.928872	4.92 × 10${}^{-6}$	127	508	6.798184	7.22 × 10${}^{-6}$	388	1940	14.24754	9.96 × 10${}^{-6}$	260	780	10.00556	7.72 × 10${}^{-6}$
	$x_4$	317	951	16.27087	9.79 × 10${}^{-6}$	292	1168	14.8396	6.16 × 10${}^{-6}$	614	3070	22.54226	9.65 × 10${}^{-6}$	1000	3000	38.68036	10.18736
	$x_5$	278	834	14.69331	9.92 × 10${}^{-6}$	296	1184	15.86248	7.74 × 10${}^{-6}$	547	2735	19.97045	8.39 × 10${}^{-6}$	1000	3000	37.66586	13.37156
	$x_6$	114	342	5.378932	9.74 × 10${}^{-6}$	110	440	5.0539	7.91 × 10${}^{-6}$	354	1770	12.81065	8.79 × 10${}^{-6}$	258	774	11.08156	7.29 × 10${}^{-6}$
	$x_7$	274	822	13.97211	6.32 × 10${}^{-6}$	275	1100	15.80533	8.28 × 10${}^{-6}$	546	2730	19.73994	8.9 × 10${}^{-6}$	1000	3000	37.19552	13.37156
	$x_8$	208	624	12.82466	8.67 × 10${}^{-6}$	144	576	9.141726	6.49 × 10${}^{-6}$	160	800	7.659241	9.25 × 10${}^{-6}$	516	1548	21.02884	9.86 × 10${}^{-6}$

Table 2. Numerical Comparisons of MPRP, NDDA [21] and ICGM [22].

PROBLEM 3
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
50,000	$x_1$	11	33	0.322182	5.17 × 10${}^{-6}$	10	40	0.400361	5.96 × 10${}^{-6}$	599	2995	12.23839	8.38× 10${}^{-7}$	13	39	0.241657	3.49 × 10${}^{-6}$
	$x_2$	16	48	0.607104	7.34 × 10${}^{-6}$	20	80	0.686698	8.82 × 10${}^{-6}$	58	290	1.276429	8.28 × 10${}^{-6}$	10	30	0.211414	6.37 × 10${}^{-6}$
	$x_3$	11	33	0.320112	4.62 × 10${}^{-6}$	15	60	0.505286	7.15× 10${}^{-7}$	495	2475	10.54336	9.96 × 10${}^{-6}$	10	30	0.240468	9.4 × 10${}^{-6}$
	$x_4$	9	27	0.292944	8.08 × 10${}^{-6}$	6	24	0.372806		764	3820	13.48614	7.08 × 10${}^{-6}$	14	42	0.410652	9.06 × 10${}^{-6}$
	$x_5$	15	45	0.588793	3.6 × 10${}^{-6}$	15	60	0.664088	3.97 × 10${}^{-6}$	252	1260	4.319963	4.89 × 10${}^{-6}$	12	36	0.377217	9.45 × 10${}^{-6}$
	$x_6$	11	33	0.448889	5.17 × 10${}^{-6}$	10	40	0.60674	5.96 × 10${}^{-6}$	599	2995	11.48276	8.38× 10${}^{-7}$	13	39	0.437431	3.49 × 10${}^{-6}$
	$x_7$	15	45	0.60361	3.6 × 10${}^{-6}$	15	60	0.713857	3.97 × 10${}^{-6}$	252	1260	3.986961	4.89 × 10${}^{-6}$	12	36	0.399796	9.45 × 10${}^{-6}$
	$x_8$	14	42	0.873261	9.37 × 10${}^{-6}$	11	44	0.432592	8.11 × 10${}^{-6}$	61	305	1.189075	5.05 × 10${}^{-6}$	8	24	0.234699	3.02 × 10${}^{-6}$
100,000	$x_1$	6	18	0.609567	6.69 × 10${}^{-6}$	5	20	0.322736	1.14 × 10${}^{-6}$	15	75	0.647448	5.11 × 10${}^{-6}$	10	30	0.5706	1.66 × 10${}^{-6}$
	$x_2$	12	36	1.599188	7.4 × 10${}^{-6}$	11	44	0.893855	9.9 × 10${}^{-6}$	76	380	3.81177	5.42 × 10${}^{-6}$	8	24	0.481089	4.31 × 10${}^{-6}$
	$x_3$	10	30	0.793137	8.9 × 10${}^{-6}$	13	52	1.784466	9.06 × 10${}^{-6}$	909	4545	28.60394	8.29 × 10${}^{-6}$	11	33	0.773752	2.2 × 10${}^{-6}$
	$x_4$	12	36	0.977956	6.37 × 10${}^{-6}$	13	52	1.161575	4.14 × 10${}^{-6}$	404	2020	14.25168	2.02 × 10${}^{-6}$	12	36	0.857321	4.46 × 10${}^{-6}$
	$x_5$	14	42	1.261941	9.15 × 10${}^{-6}$	11	44	0.940573	7.49 × 10${}^{-6}$	516	2580	15.59973	7.95 × 10${}^{-6}$	12	36	0.842963	6.33 × 10${}^{-6}$
	$x_6$	6	18	0.614141	6.69 × 10${}^{-6}$	5	20	0.310198	1.14 × 10${}^{-6}$	15	75	0.482139	2.5 × 10${}^{-6}$	10	30	0.58923	1.66 × 10${}^{-6}$
	$x_7$	14	42	1.242289	9.15 × 10${}^{-6}$	11	44	0.93746	7.49 × 10${}^{-6}$	516	2580	17.44822	7.95 × 10${}^{-6}$	12	36	0.8428	6.33 × 10${}^{-6}$
	$x_8$	13	39	1.664243	3.68 × 10${}^{-6}$	13	52	1.209169	1.86 × 10${}^{-6}$	75	375	2.555772	8.69 × 10${}^{-6}$	8	24	0.49346	7.81 × 10${}^{-6}$
PROBLEM 4
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
50,000	$x_1$	9	27	0.212201	9.28 × 10${}^{-6}$	11	44	0.247058	4.22 × 10${}^{-6}$	38	190	0.483188	8.05 × 10${}^{-6}$	12	36	0.22417	3.58 × 10${}^{-6}$
	$x_2$	14	42	0.321678	5.07 × 10${}^{-6}$	11	44	0.263394	5.47 × 10${}^{-6}$	27	135	0.398743	8.23 × 10${}^{-6}$	22	66	0.394745	6.26 × 10${}^{-6}$
	$x_3$	9	27	0.202813	1.19 × 10${}^{-6}$	9	36	0.215252	1.46 × 10${}^{-6}$	26	130	0.436246	8.17 × 10${}^{-6}$	8	24	0.147041	6.88 × 10${}^{-6}$
	$x_4$	23	69	0.593432	8.53 × 10${}^{-6}$	21	84	0.50064	5.56 × 10${}^{-6}$	39	195	0.690833	8.04 × 10${}^{-6}$	36	108	0.63236	9.86 × 10${}^{-6}$
	$x_5$	23	69	0.578756	4.6 × 10${}^{-6}$	20	80	0.491674	3.58× 10${}^{-7}$	39	195	0.714213	8.04 × 10${}^{-6}$	39	117	0.705334	9.49 × 10${}^{-6}$
	$x_6$	17	51	0.45665	9.68× 10${}^{-8}$	19	76	0.595362	3.48× 10${}^{-8}$	37	185	0.682459	8.44 × 10${}^{-6}$	12	36	0.219326	2.67 × 10${}^{-6}$
	$x_7$	23	69	0.586717	4.6 × 10${}^{-6}$	20	80	0.488278	3.58× 10${}^{-7}$	39	195	0.732293	8.04 × 10${}^{-6}$	39	117	0.698136	9.52 × 10${}^{-6}$
	$x_8$	18	54	0.47571	4.21 × 10${}^{-6}$	32	128	0.906585	7.41× 10${}^{-7}$	28	140	0.51624	8.54 × 10${}^{-6}$	27	81	0.479781	4.96 × 10${}^{-6}$
100,000	$x_1$	11	33	0.476225	1.02× 10${}^{-7}$	11	44	0.484772	5.96 × 10${}^{-6}$	39	195	1.445101	7.29 × 10${}^{-6}$	12	36	0.438499	5.06 × 10${}^{-6}$
	$x_2$	14	42	0.633407	5.06 × 10${}^{-6}$	11	44	0.527568	5.47 × 10${}^{-6}$	27	135	1.000728	8.23 × 10${}^{-6}$	19	57	0.675121	9.94 × 10${}^{-6}$
	$x_3$	9	27	0.406597	1.69 × 10${}^{-6}$	9	36	0.42648	2.06 × 10${}^{-6}$	27	135	0.974066	7.39 × 10${}^{-6}$	8	24	0.291315	9.73 × 10${}^{-6}$
	$x_4$	24	72	1.218071	8.4 × 10${}^{-6}$	21	84	1.017136	1.52 × 10${}^{-6}$	40	200	1.431425	7.28 × 10${}^{-6}$	30	90	1.037708	2.42 × 10${}^{-6}$
	$x_5$	23	69	1.171541	7.52 × 10${}^{-6}$	20	80	0.960639	4.96 × 10${}^{-6}$	40	200	1.427526	7.28 × 10${}^{-6}$	43	129	1.466193	7.58 × 10${}^{-6}$
	$x_6$	17	51	0.901294	1.37× 10${}^{-7}$	19	76	1.156228	4.92× 10${}^{-8}$	38	190	1.339707	7.63 × 10${}^{-6}$	12	36	0.446339	3.78 × 10${}^{-6}$
	$x_7$	23	69	1.171954	7.52 × 10${}^{-6}$	20	80	0.942363	4.96 × 10${}^{-6}$	40	200	1.419573	7.28 × 10${}^{-6}$	43	129	1.472821	7.58 × 10${}^{-6}$
	$x_8$	18	54	0.958594	4.21 × 10${}^{-6}$	25	100	1.289564	8.32 × 10${}^{-6}$	28	140	1.009042	8.54 × 10${}^{-6}$	26	78	0.900203	8.57 × 10${}^{-6}$

Table 3. Numerical Comparisons of MPRP, NDDA [21] and ICGM [22].

PROBLEM 5
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
50,000	$x_1$	69	207	2.267497	9.33 × 10${}^{-6}$	105	420	3.891633	7.84 × 10${}^{-6}$	191	955	4.947418	9.93 × 10${}^{-6}$	135	405	3.611205	9.12 × 10${}^{-6}$
	$x_2$	87	261	2.940586	8.23 × 10${}^{-6}$	109	436	3.97732	8.31 × 10${}^{-6}$	207	1035	5.307014	9.87 × 10${}^{-6}$	220	660	5.912201	9.97 × 10${}^{-6}$
	$x_3$	86	258	2.994068	9.81 × 10${}^{-6}$	79	316	2.592411	9.4 × 10${}^{-6}$	214	1070	5.430976	9.9 × 10${}^{-6}$	998	2994	21.5748	9.96 × 10${}^{-6}$
	$x_4$	79	237	2.599857	7.72 × 10${}^{-6}$	101	404	3.660022	7.37 × 10${}^{-6}$	205	1025	4.680842	9.23 × 10${}^{-6}$	152	456	2.266204	9.89 × 10${}^{-6}$
	$x_5$	80	240	2.659913	9.52 × 10${}^{-6}$	111	444	3.90133	9.93 × 10${}^{-6}$	205	1025	4.295369	9.23 × 10${}^{-6}$	704	2112	12.14497	9.93 × 10${}^{-6}$
	$x_6$	86	258	2.632166	9.8 × 10${}^{-6}$	114	456	4.071767	9.07 × 10${}^{-6}$	224	1120	4.554054	9.19 × 10${}^{-6}$	1000	3000	15.05272	2.1 × 10${}^{-5}$
	$x_7$	79	237	2.337165	8.46 × 10${}^{-6}$	103	412	3.302599	9.43 × 10${}^{-6}$	205	1025	3.89815	9.23 × 10${}^{-6}$	719	2157	12.18638	9.86 × 10${}^{-6}$
	$x_8$	86	258	2.501353	6.97 × 10${}^{-6}$	122	488	3.74481	4.86 × 10${}^{-6}$	216	1080	4.080285	9.5 × 10${}^{-6}$	172	516	2.941251	7.99 × 10${}^{-6}$
100,000	$x_1$	80	240	4.991337	6.4 × 10${}^{-6}$	93	372	5.303749	8.04 × 10${}^{-6}$	192	960	7.479403	9.02 × 10${}^{-6}$	656	1968	21.91715	9.86 × 10${}^{-6}$
	$x_2$	86	258	5.350999	9.84 × 10${}^{-6}$	104	416	5.60915	9.53 × 10${}^{-6}$	207	1035	7.35847	9.01 × 10${}^{-6}$	713	2139	22.61809	9.95 × 10${}^{-6}$
	$x_3$	80	240	4.52125	7.67 × 10${}^{-6}$	94	376	4.548221	7.97 × 10${}^{-6}$	212	1060	7.260601	9.45 × 10${}^{-6}$	758	2274	25.39184	9.98 × 10${}^{-6}$
	$x_4$	82	246	4.482321	8.53 × 10${}^{-6}$	83	332	3.911853	9.59 × 10${}^{-6}$	205	1025	8.032846	9.62 × 10${}^{-6}$	197	591	6.705366	9.9 × 10${}^{-6}$
	$x_5$	81	243	4.063491	8.48 × 10${}^{-6}$	79	316	4.167463	8.7 × 10${}^{-6}$	205	1025	7.737062	9.62 × 10${}^{-6}$	173	519	6.832254	9.52 × 10${}^{-6}$
	$x_6$	83	249	4.060558	6.42 × 10${}^{-6}$	104	416	6.16264	8.65 × 10${}^{-6}$	214	1070	7.483374	9.19 × 10${}^{-6}$	790	2370	27.09478	9.86 × 10${}^{-6}$
	$x_7$	82	246	4.173369	7.61 × 10${}^{-6}$	85	340	4.378839	8.54 × 10${}^{-6}$	205	1025	7.096066	9.62 × 10${}^{-6}$	431	1293	14.45969	9.87 × 10${}^{-6}$
	$x_8$	87	261	4.104345	9.47 × 10${}^{-6}$	114	456	6.210763	9.51 × 10${}^{-6}$	215	1075	7.667577	9.88 × 10${}^{-6}$	150	450	4.905177	5.81 × 10${}^{-6}$
PROBLEM 6
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
50,000	$x_1$	3	9	0.081907	1.46 × 10${}^{-6}$	3	12	0.074954	1.46 × 10${}^{-6}$	32	160	0.510629	6.43 × 10${}^{-6}$	2	6	0.04543	2.36 × 10${}^{-6}$
	$x_2$	1	3	0.033824	8 × 10${}^{-6}$	1	4	0.032205	8.08 × 10${}^{-6}$	1	5	0.032867	8 × 10${}^{-6}$	1	3	0.031592	8 × 10${}^{-6}$
	$x_3$	1	3	0.033946	8.57 × 10${}^{-6}$	1	4	0.032505	8.64 × 10${}^{-6}$	1	5	0.032653	8.57 × 10${}^{-6}$	1	3	0.03293	8.57 × 10${}^{-6}$
	$x_4$	1	3	0.034092	9.94 × 10${}^{-6}$	1	4	0.035	9.99 × 10${}^{-6}$	1	5	0.033783	9.94 × 10${}^{-6}$	1	3	0.036741	9.94 × 10${}^{-6}$
	$x_5$	1	3	0.037075	9.94 × 10${}^{-6}$	1	4	0.037857	9.99 × 10${}^{-6}$	1	5	0.037706	9.94 × 10${}^{-6}$	1	3	0.037229	9.94 × 10${}^{-6}$
	$x_6$	1	3	0.037861	1.3 × 10${}^{-6}$	1	4	0.036916	1.16 × 10${}^{-6}$	1	5	0.038647	1.3 × 10${}^{-6}$	1	3	0.03646	1.3 × 10${}^{-6}$
	$x_7$	1	3	0.037923	9.94 × 10${}^{-6}$	1	4	0.039097	9.99 × 10${}^{-6}$	1	5	0.038561	9.94 × 10${}^{-6}$	1	3	0.038467	9.94 × 10${}^{-6}$
	$x_8$	1	3	0.037427	8.01 × 10${}^{-6}$	1	4	0.03926	8.08 × 10${}^{-6}$	1	5	0.040607	8.01 × 10${}^{-6}$	1	3	0.037036	8.01 × 10${}^{-6}$
100,000	$x_1$	1	3	0.077721	3.79 × 10${}^{-6}$	1	4	0.075644	3.8 × 10${}^{-6}$	1	5	0.075443	3.79 × 10${}^{-6}$	1	3	0.073561	3.79 × 10${}^{-6}$
	$x_2$	1	3	0.079765	2.83 × 10${}^{-6}$	1	4	0.076144	2.86 × 10${}^{-6}$	1	5	0.077985	2.83 × 10${}^{-6}$	1	3	0.076044	2.83 × 10${}^{-6}$
	$x_3$	1	3	0.077061	3.03 × 10${}^{-6}$	1	4	0.076729	3.05 × 10${}^{-6}$	1	5	0.076138	3.03 × 10${}^{-6}$	1	3	0.074692	3.03 × 10${}^{-6}$
	$x_4$	1	3	0.081273	3.52 × 10${}^{-6}$	1	4	0.075837	3.53 × 10${}^{-6}$	1	5	0.075578	3.52 × 10${}^{-6}$	1	3	0.078154	3.52 × 10${}^{-6}$
	$x_5$	1	3	0.081851	3.52 × 10${}^{-6}$	1	4	0.076603	3.53 × 10${}^{-6}$	1	5	0.075728	3.52 × 10${}^{-6}$	1	3	0.076166	3.52 × 10${}^{-6}$
	$x_6$	1	3	0.077072	4.59× 10${}^{-7}$	1	4	0.076258	4.1× 10${}^{-7}$	1	5	0.075658	4.59× 10${}^{-7}$	1	3	0.075048	4.59× 10${}^{-7}$
	$x_7$	1	3	0.07455	3.52 × 10${}^{-6}$	1	4	0.075514	3.53 × 10${}^{-6}$	1	5	0.076933	3.52 × 10${}^{-6}$	1	3	0.074581	3.52 × 10${}^{-6}$
	$x_8$	1	3	0.087563	2.83 × 10${}^{-6}$	1	4	0.077531	2.86 × 10${}^{-6}$	1	5	0.074854	2.83 × 10${}^{-6}$	1	3	0.074646	2.83 × 10${}^{-6}$

Table 4. Numerical Comparisons of MPRP, NDDA [21] and ICGM [22].

PROBLEM 7
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
50,000	$x_1$	0	0	0.011313	0	0	0	0.01209	0	0	0	0.016223	0	0	0	0.012003	0
	$x_2$	87	261	2.348944	9.16 × 10${}^{-6}$	79	316	2.273501	8.88 × 10${}^{-6}$	154	770	4.291607	9.45 × 10${}^{-6}$	1000	3000	26.32372	0.016563
	$x_3$	14	42	0.516938	7.44 × 10${}^{-6}$	6	24	0.220502	4.02 × 10${}^{-6}$	3	15	0.080141	4.41 × 10${}^{-6}$	5	15	0.084522	6.44 × 10${}^{-6}$
	$x_4$	34	102	0.926885	8.95 × 10${}^{-6}$	33	132	0.980913	8.11 × 10${}^{-6}$	41	205	1.188357	9.99 × 10${}^{-6}$	1000	3000	27.79381	3.13 × 10${}^{-5}$
	$x_5$	36	108	1.009782	8.7 × 10${}^{-6}$	36	144	1.084175	7.95 × 10${}^{-6}$	49	245	1.316967	9.56 × 10${}^{-6}$	1000	3000	45.34329	3.2 × 10${}^{-5}$
	$x_6$	18	54	0.660205	8.81 × 10${}^{-6}$	8	32	0.29928	9.78 × 10${}^{-6}$	4	20	0.114832	1.58 × 10${}^{-6}$	7	21	0.221179	8.72 × 10${}^{-6}$
	$x_7$	36	108	1.03182	8.7 × 10${}^{-6}$	36	144	1.087501	7.95 × 10${}^{-6}$	49	245	1.318538	9.56 × 10${}^{-6}$	936	2808	42.23109	NaN
	$x_8$	90	270	2.548954	9.86 × 10${}^{-6}$	88	352	2.584854	7.43 × 10${}^{-6}$	163	815	4.589919	9.82 × 10${}^{-6}$	1000	3000	29.78786	0.037358
100,000	$x_1$	0	0	0.016449	0	0	0	0.017713	0	0	0	0.019086	0	0	0	0.014114	0
	$x_2$	87	261	4.427758	8.58 × 10${}^{-6}$	80	320	4.971012	9.72 × 10${}^{-6}$	154	770	7.208364	9.4 × 10${}^{-6}$	1000	3000	49.27	0.017351
	$x_3$	12	36	0.706042	6.35 × 10${}^{-6}$	6	24	0.4356	1.65 × 10${}^{-6}$	3	15	0.121382	2.2 × 10${}^{-6}$	4	12	0.164811	7.8 × 10${}^{-6}$
	$x_4$	26	78	1.188328	9.34 × 10${}^{-6}$	30	120	1.787787	9.37 × 10${}^{-6}$	34	170	1.501828	9.85 × 10${}^{-6}$	925	2775	48.35269	NaN
	$x_5$	29	87	1.375369	9.64 × 10${}^{-6}$	31	124	1.774428	9.55 × 10${}^{-6}$	45	225	1.998629	9.4 × 10${}^{-6}$	1000	3000	53.17642	2.14 × 10${}^{-5}$
	$x_6$	16	48	1.08696	7.41 × 10${}^{-6}$	6	24	0.420024	5.49 × 10${}^{-6}$	3	15	0.144028	7.36 × 10${}^{-6}$	6	18	0.221337	4.8 × 10${}^{-6}$
	$x_7$	29	87	1.496431	9.64 × 10${}^{-6}$	31	124	1.761076	9.55 × 10${}^{-6}$	45	225	2.231545	9.4 × 10${}^{-6}$	1000	3000	54.97467	1.99 × 10${}^{-5}$
	$x_8$	92	276	4.563438	9.67 × 10${}^{-6}$	85	340	4.913522	8.77 × 10${}^{-6}$	163	815	7.319916	9.37 × 10${}^{-6}$	1000	3000	48.95704	0.032224
PROBLEM 8
		MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{1}\mathbf{*}}$)				MPRP(${\mathit{\eta }}_{\mathit{k}}^{\mathbf{2}\mathbf{*}}$)				NDDA				ICGM
DIMENSION	INITIAL POINT	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM	ITER	FVAL	TIME	NORM
1000	$x_1$	82	246	0.455454	9.96 × 10${}^{-6}$	105	420	0.597806	8.96 × 10${}^{-6}$	224	1120	0.94912	9.83 × 10${}^{-6}$	135	405	0.58535	9.26 × 10${}^{-6}$
	$x_2$	88	264	0.59479	9.39 × 10${}^{-6}$	98	392	0.576119	8.76 × 10${}^{-6}$	228	1140	1.088754	9.84 × 10${}^{-6}$	148	444	0.678534	9.94 × 10${}^{-6}$
	$x_3$	76	228	0.447432	8.79 × 10${}^{-6}$	107	428	0.625566	8.22 × 10${}^{-6}$	215	1075	1.036161	9.92 × 10${}^{-6}$	953	2859	4.435764	9.97 × 10${}^{-6}$
	$x_4$	83	249	0.571694	8.7 × 10${}^{-6}$	84	336	0.544969	7.1 × 10${}^{-6}$	218	1090	1.264795	9.9 × 10${}^{-6}$	952	2856	5.6264	9.97 × 10${}^{-6}$
	$x_5$	74	222	0.714045	7.74 × 10${}^{-6}$	100	400	0.991748	9.97 × 10${}^{-6}$	218	1090	1.652656	9.9 × 10${}^{-6}$	722	2166	5.116361	1 × 10${}^{-5}$
	$x_6$	78	234	0.864799	9.45 × 10${}^{-6}$	104	416	1.442508	6.02 × 10${}^{-6}$	188	940	1.717357	1 × 10${}^{-5}$	114	342	0.906444	8.28 × 10${}^{-6}$
	$x_7$	74	222	0.872029	7.75 × 10${}^{-6}$	93	372	1.332749	8.21 × 10${}^{-6}$	218	1090	2.532429	9.9 × 10${}^{-6}$	151	453	1.475109	7.62 × 10${}^{-6}$
	$x_8$	90	270	1.006991	7.67 × 10${}^{-6}$	117	468	1.869405	8.9 × 10${}^{-6}$	236	1180	2.831446	9.84 × 10${}^{-6}$	162	486	1.559799	8.39 × 10${}^{-6}$
2000	$x_1$	82	246	1.001497	9.96 × 10${}^{-6}$	91	364	1.851274	8.63 × 10${}^{-6}$	223	1115	3.376192	9.27 × 10${}^{-6}$	787	2361	10.66835	9.86 × 10${}^{-6}$
	$x_2$	88	264	1.205998	9.39 × 10${}^{-6}$	90	360	1.751596	9.71 × 10${}^{-6}$	228	1140	3.306594	9.9 × 10${}^{-6}$	750	2250	6.84631	1 × 10${}^{-5}$
	$x_3$	76	228	1.125966	8.79 × 10${}^{-6}$	92	368	1.842185	9.36 × 10${}^{-6}$	214	1070	3.016198	9.96 × 10${}^{-6}$	159	477	1.140194	9.44 × 10${}^{-6}$
	$x_4$	83	249	1.167799	8.7 × 10${}^{-6}$	144	576	3.194961	8.2 × 10${}^{-6}$	219	1095	2.994653	9.73 × 10${}^{-6}$	885	2655	8.149794	9.97 × 10${}^{-6}$
	$x_5$	74	222	1.045681	7.74 × 10${}^{-6}$	109	436	2.276981	9.94 × 10${}^{-6}$	219	1095	2.892295	9.75 × 10${}^{-6}$	396	1188	3.821894	9.98 × 10${}^{-6}$
	$x_6$	78	234	1.174389	9.45 × 10${}^{-6}$	82	328	1.611686	9.42 × 10${}^{-6}$	190	950	2.546115	9.85 × 10${}^{-6}$	108	324	1.188268	8.95 × 10${}^{-6}$
	$x_7$	74	222	1.069987	7.75 × 10${}^{-6}$	114	456	2.431602	9.96 × 10${}^{-6}$	219	1095	2.956538	9.75 × 10${}^{-6}$	682	2046	6.50311	9.86 × 10${}^{-6}$
	$x_8$	90	270	1.224429	7.67 × 10${}^{-6}$	117	468	2.359865	7.39 × 10${}^{-6}$	235	1175	3.148771	9.56 × 10${}^{-6}$	272	816	3.325016	1 × 10${}^{-5}$

In Table 1, Table 2, Table 3 and Table 4, “ITER” indicates the number of iteration; “TIME” for the CPU time; “FEV” for the number of function evaluations, and “NORM” indicate the norm of the function at the stopping point. Table 1 contained Problems 1 and 2, although for the number of iterations MPRP with the optimal choice ${\eta }_k^{2*}$ is the winner, followed by the NDDA methods and then the remaining two other algorithms. For the number of function evaluations and the CPU time, the proposed algorithms are also promising. The same observations can be made throughout the remaining tables concerning the number of iterations, CPU time, and the number of function evaluations.

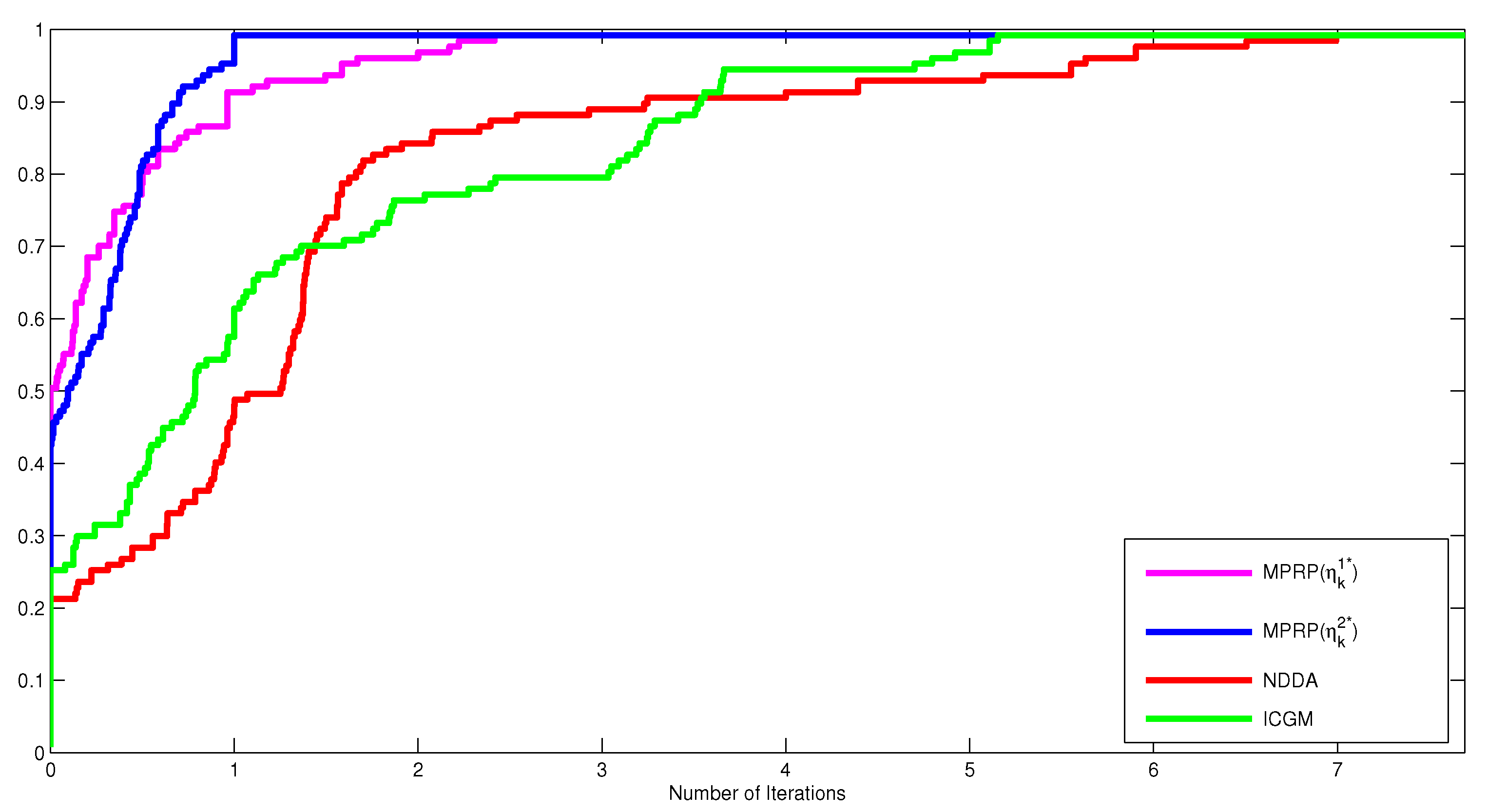
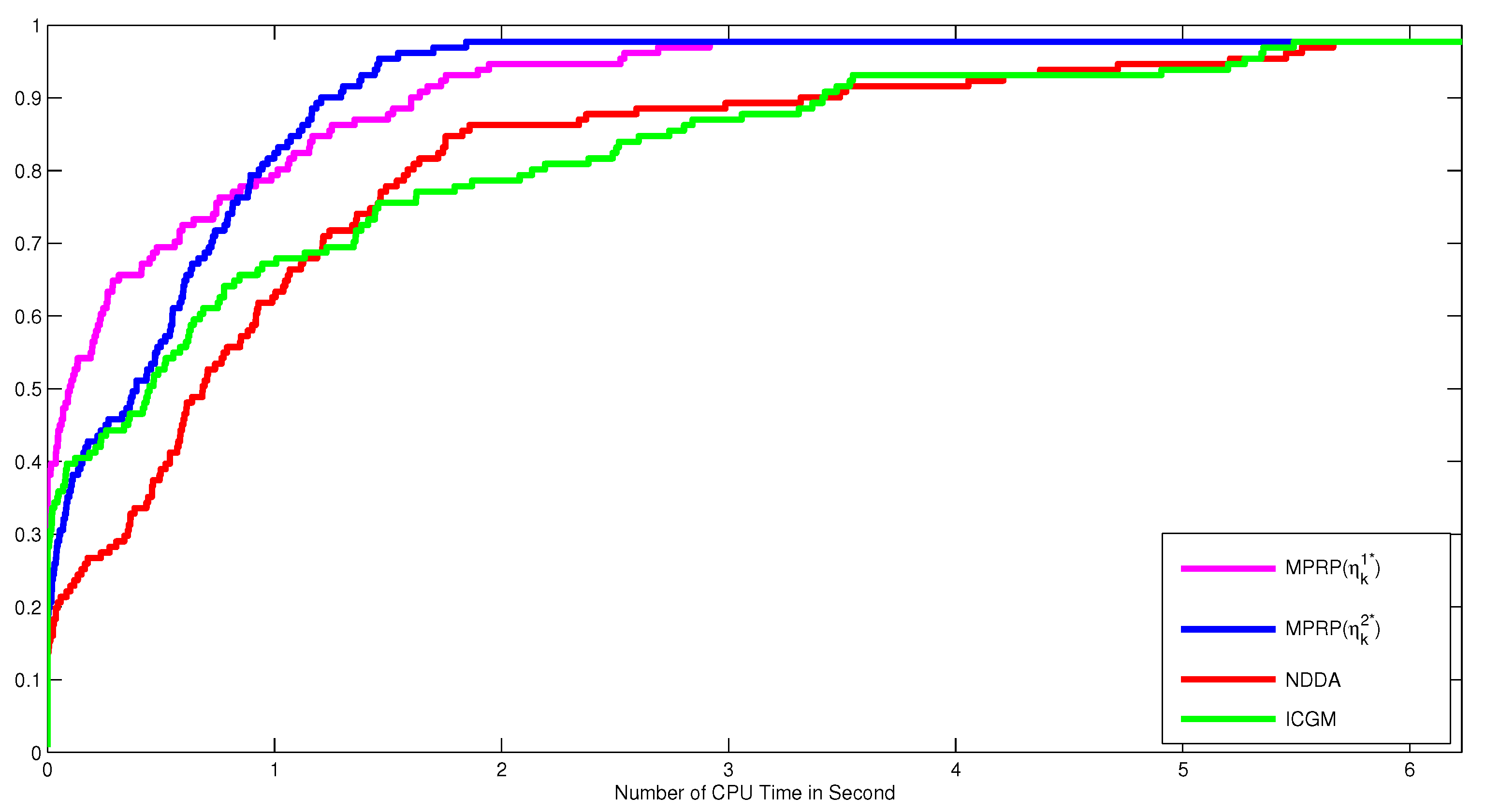
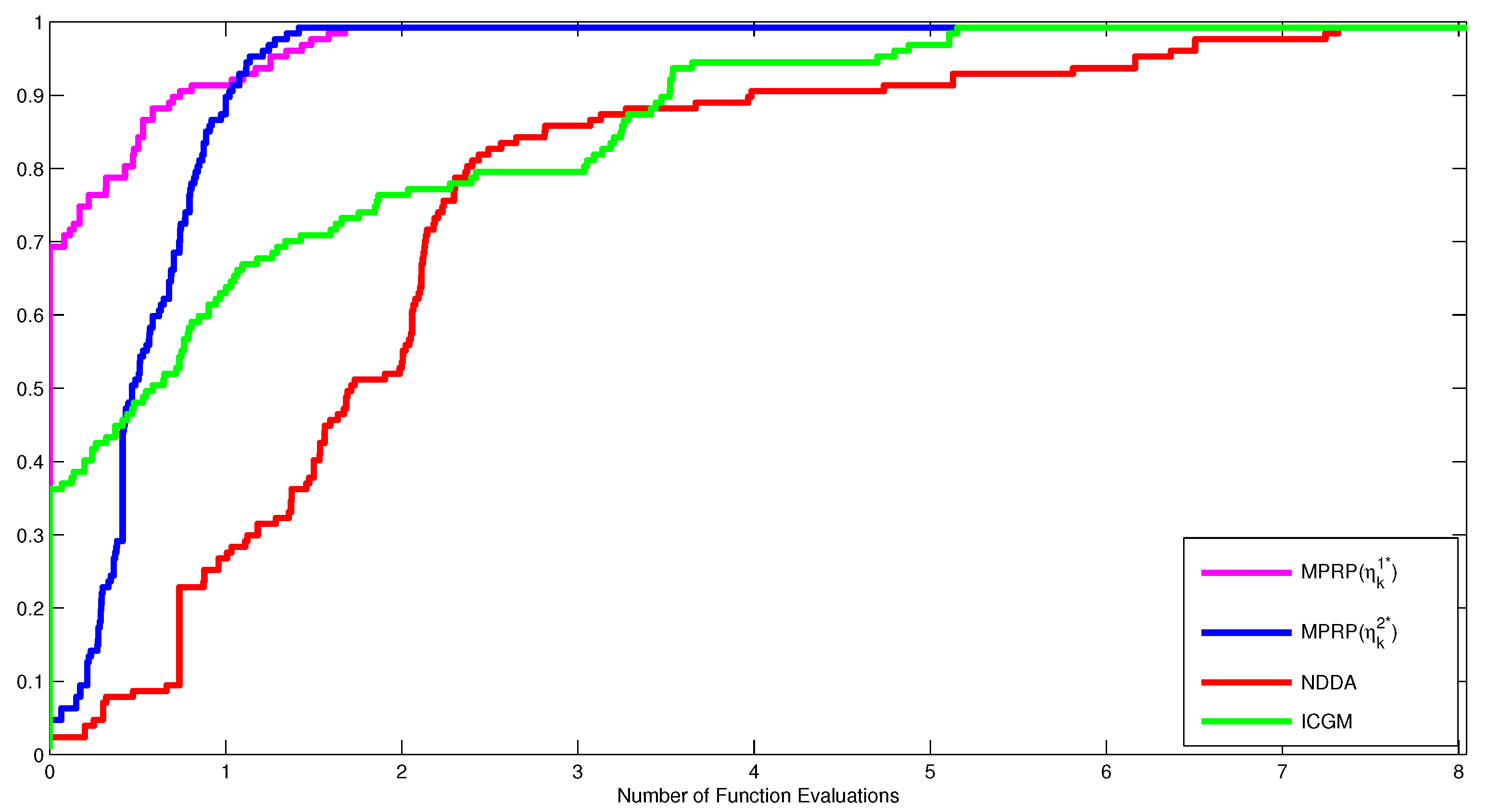
Moreover, to clearly show the performance of these algorithms, Figure 1, Figure 2 and Figure 3 were plotted according to the data in Table 1, Table 2, Table 3 and Table 4 using the Dolan and Moré performance profiles [28]. According to the Dolan and Moré performance profiles [28], the most efficient method is the one whose curve is at the top left of all curves. Therefore, We concluded from Figure 1, Figure 2 and Figure 3, that the MPRP with the optimal choice ${\eta }_k^{2*}$ is the most effective for the number of iterations, followed by the MPRP with optimal choice ${\eta }_k^{1*}$, NDDA algorithm, and lastly the ICGM algorithm. Similarly, the proposed algorithm remained the most stable algorithms concerning the number of CPU time and the number of function evaluations as their curves correspond to the top left curves.

Figure 1. Performance profiles of MPRP, NDDA [21] and ICGM [22] for number of iterations.

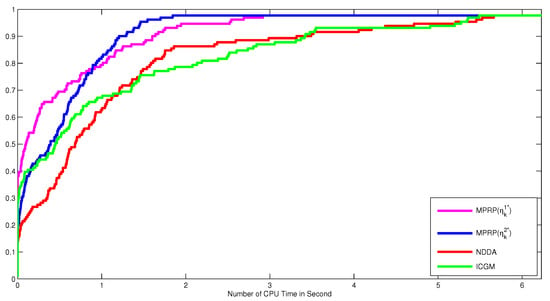
Figure 2. Performance profiles of MPRP, NDDA [21] and ICGM [22] for the CPU time in second.

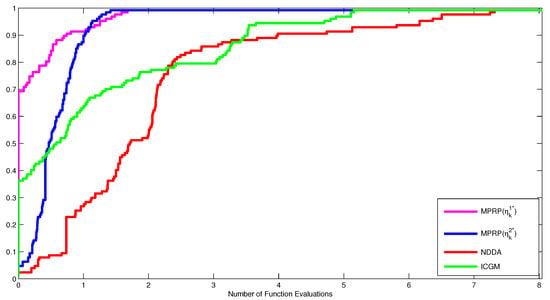
Figure 3. Performance profiles of MPRP, NDDA [21] and ICGM [22] for number of function evaluations.

5. Conclusions

In this paper, we provided a derivative-free PRP CG-type algorithm for solving the symmetric nonlinear equations and proved its global convergence by using the backtracking type line search. No information on the Jacobian matrix of G is used in the entire process of the proposed algorithm. The proposed algorithm is therefore appropriate for solving large-scale symmetric nonlinear systems. Computational outcomes also show that the proposed algorithm is robust and performs better than the NDDA [21] and ICGM [22] schemes for the symmetric nonlinear equations in number of iterations and the CPU time in seconds. This is because our algorithm makes full use of the optimal choice ${\eta }_k^{*}$ at every iteration.