Numerical Solution for Crack Phenomenon in Dissimilar Materials under Various Mechanical Loadings

Abstract

A new mathematical model is developed for the analytical study of two cracks in the upper plane of dissimilar materials under various mechanical loadings, i.e., shear, normal, tearing and mixed stresses with different geometry conditions. This problem is developed into a new mathematical model of hypersingular integral equations (HSIEs) by using the modified complex potentials (MCPs) function and the continuity conditions of the resultant force and displacement with the crack opening displacement (COD) function as the unknown. The newly obtained mathematical model of HSIEs are solved numerically by utilizing the appropriate quadrature formulas. Numerical computations and graphical demonstrations are carried out to observe the profound effect of the elastic constants ratio, mode of stresses and geometry conditions on the dimensionless stress intensity factors (SIFs) at the crack tips.

1. Introduction

Study on the vigor of materials and engineering structures provides a broad sense which is related to a review of the carrying capacity of a body with and without consideration of initial cracks. In order to predict the stress state or stress intensity in the vicinity of the crack tip due to the mechanical loading or residual stresses, one needs to determine very important factors, i.e., stress intensity factors (SIFs). The SIF is a fundamental parameter in fracture mechanics, and it is an important factor for safety analysis of the materials, structural stability and design analysis. Complex potential function (CPF) method introduced by Muskhelishvili [1] is the simplest and most rigorous method to investigate the behavior of SIFs, measured at the tip of cracks to determine the stability behavior of bodies or materials containing cracks or flaws. Many researchers used CPF methods to investigate the crack problems in an infinite plane [2,3,4], finite plane [5,6] and half plane [7,8,9]. Gray et al. [2] and Nik Long et al. [3] established the relevant hypersingular integral equations (HSIEs) using CPF method in calculating the SIFs with Green’s function, and crack opening displacement (COD) function as the unknown, respectively. Liu et al. [4] analyzed SIFs for two unequal-length collinear cracks using weight functions method with COD function as the unknown. Lai and Schijve [5] analyzed a single hole-edge crack in a finite plane using CPF methods with the treatment of boundary condition with the minimum potential energy principle. Moreover, Zhang et al. [6] analyzed multiple cracks in a finite plane by numerically solved a system of singular integral equations with the Gauss–Chebyshev quadrature, and evaluating the SIFs. Legros et al. [7] performed the analysis of multiple circular inclusions in an elastic half plane based on complex singular integral equation with the unknown tractions at each circular boundary approximated by a truncated complex Fourier series. Liu and Guo [8] used the CPF method to calculate the SIFs for the interaction between a screw dislocation and an oblique edge crack in a half plane with the help of Cauchy integral formula. Elfakhakhre et al. [9] investigated the behavior of the SIFs at the crack tips in half plane elasticity using the modified complex potentials (MCPs) with the distribution dislocation as the unknown function. As per the authors’ knowledge, no mathematical model of the HSIEs has been made to date to develop and study the crack phenomenon in dissimilar materials under various mechanical loadings using CPF method.

Many different methods were applied by the researchers to investigate the crack problems in dissimilar materials. Chen [10] used the Fredholm integral equations to evaluate the dimensionless SIFs for multiple inclined cracks in dissimilar materials under shear stress. It was obtained that the mathematical model for the multiple cracks in dissimilar materials were reduced to the model in an infinite plane when $G_1=G_2$. According to Chen and Hasebe [11], the values of dimensionless SIFs depend on the elastic constant ratio and crack geometric. They used the mixed boundary value problems to obtain a logarithmic singular kernel for a circular arc crack in the upper plane of dissimilar materials. Isida and Noguchi [12] analyzed the crack problems in dissimilar materials by using the continuous distributions of the body force method along the cracks but excluded the interface cracks and singularity problems for cracks terminating at the interface. Zhou et al. [13] found that the dimensionless SIFs for an arbitrary crack problems in dissimilar materials depends on the thickness of the strip, crack configuration and the existence of the crack near the punch foundation. They used a system of complex Cauchy type singular integral equations. Long and Xu [14] applied the combination of direct boundary integral method and displacement discontinuity method to solve the crack problems in dissimilar materials. The result showed that the proposed method was efficient especially for the scaled thin layers in the application of practical hydraulic fracturing simulations. Hamzah et al. [15,16] used the HSIEs to calculate the dimensionless SIFs for multiple cracks in the upper plane and both upper and lower planes of dissimilar materials subjected to shear stress. They expanded their study to analyze the behavior of dimensionless SIFs under various mechanical loadings, however it focused on a single crack in the upper plane of dissimilar materials [17].

The present mathematical model is a novel investigation of dimensionless SIFs at the crack tip of the two cracks in the upper plane of dissimilar materials under various mechanical loadings such as shear, normal, tearing and mixed stresses with different geometry conditions. By using CPF method, the problem is formulated into HSIEs. The noticeable impact of elastic constants ratio, mechanical loading and geometry conditions on SIFs for dissimilar materials has been depicted by means of numerical computations and graphical demonstrations. Moreover, a comparative analysis is carried out for dimensionless SIFs in dissimilar materials under various mechanical loadings to elucidate the unrevealed facts. The present findings may assist engineers in investigating the stability behavior of the perfectly bonded dissimilar structures or materials under various mechanical loadings.

2. Mathematical Model of the Problem

The CPF method plays an important role in solving the crack problems in plane elasticity [1]. In this method, the stress components $({\sigma }_x,{\sigma }_y,{\sigma }_{xy})$, resultant force function $f(X,Y)$ and displacements $(u,v)$ are related to two complex potentials $\mathsf{\Phi }\left(z\right)={\varphi }^{\prime }\left(z\right)$ and $\mathsf{\Omega }\left(z\right)={\omega }^{\prime }\left(z\right)$ as follows

$$\begin{array}{cc}\hfill {\sigma }_y-i{\sigma }_{xy}& =\mathsf{\Phi }\left(z\right)+(z-\overline{z})\overline{{\mathsf{\Phi }}^{\prime }\left(z\right)}+\mathsf{\Omega }\left(\overline{z}\right),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill f=-Y+iX& =\varphi \left(z\right)+(z-\overline{z})\overline{{\mathsf{\Phi }}^{\prime }\left(z\right)}+\omega \left(\overline{z}\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill 2G(u+iv)& =\kappa \varphi \left(z\right)-(z-\overline{z})\overline{\mathsf{\Phi }\left(z\right)}-\omega \left(\overline{z}\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \omega \left(z\right)& =z\overline{\mathsf{\Phi }}\left(z\right)+\overline{\psi }\left(z\right),\hfill \end{array}$$

(4)

where $z=x+iy$, G is shear modulus of elasticity, $\kappa =(3-v)/(1+v)$ for plane stress, $\kappa =3-4v$ for plane strain and v is Poisson’s ratio. The derivative of Equation (2) with respect to z gives

$$\frac{d}{dz}\left\{-Y+iX\right\}=\mathsf{\Phi }\left(z\right)+(z-\overline{z})\overline{{\mathsf{\Phi }}^{″}\left(z\right)}\frac{d\overline{z}}{dz}+\mathsf{\Omega }\left(\overline{z}\right)\frac{d\overline{z}}{dz}=N+iT$$

(5)

where the traction $N+iT$ denotes the normal and tangential components along the crack segment $\overline{z,z+dz}$. Note that the traction $N+iT$ depends on the position of point z and the direction of the segment $d\overline{z}/dz$.

According to Nik Long and Eshkuvatov [3], the complex potentials for a crack L in an infinite plane can be expressed by

$$\begin{array}{c}{\varphi }_{}\left(z\right)=\frac{1}{2\pi }{\int }_L\frac{g\left(t\right)dt}{t-z},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \omega \left(z\right)& =\frac{1}{2\pi }{\int }_L\frac{z\overline{g\left(t\right)}d\overline{t}}{{(\overline{t}-z)}^2}+\frac{1}{2\pi }{\int }_L\frac{\overline{g\left(t\right)}dt}{\overline{t}-z}+\frac{1}{2\pi }{\int }_L\frac{g\left(t\right)d\overline{t}}{\overline{t}-z}-\frac{1}{2\pi }{\int }_L\frac{t\overline{g\left(t\right)}d\overline{t}}{{(\overline{t}-z)}^2},\hfill \end{array}$$

(7)

where $g\left(t\right)$ is COD function defined by

$$g\left(t\right)=\frac{2G}{i(\kappa +1)}[{(u\left(t\right)+iv\left(t\right))}^{+}-{(u\left(t\right)+iv\left(t\right))}^{-}],$$

(8)

${(u\left(t\right)+iv\left(t\right))}^{+}$ and ${(u\left(t\right)+iv\left(t\right))}^{-}$ denote the displacements at point t of the upper and lower crack faces, respectively. Note that COD function has the following properties

$$g\left(t\right)=O\left[\sqrt{t-t_{A_j}}\right],$$

(9)

at the crack tip $A_j$, where $j=1,2$.

Consider a crack in upper plane of dissimilar materials under various mechanical loadings; see Figure 1.

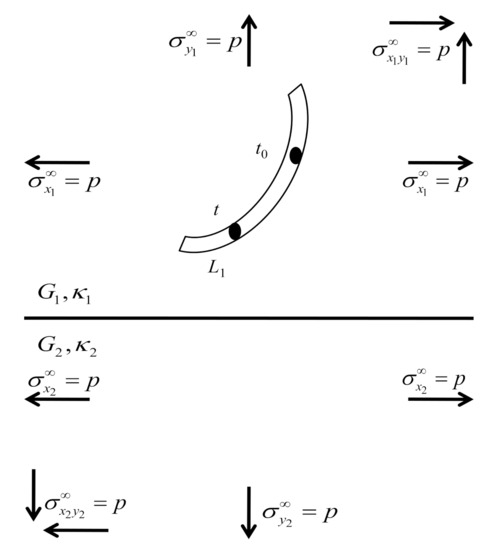
Figure 1. A crack $L_1$ in dissimilar materials under various mechanical loadings.

The conditions for strain components $\epsilon$ in dissimilar materials are

$${\epsilon }_{x_1}={\epsilon }_{x_2},{\epsilon }_{y_1}={\epsilon }_{y_2},{\epsilon }_{x_1{y}_1}={\epsilon }_{x_2{y}_2}\mathrm{and}{\epsilon }_{x_1}={\epsilon }_{x_2}={\epsilon }_{y_1}={\epsilon }_{y_2}$$

(10)

where subscripts 1 and 2 are the strain components for the upper and lower planes of dissimilar materials, respectively. Those strains can be defined by Young’s modulus of elasticity E and stress components $\sigma$ as

$$\begin{array}{ccc}\hfill {\epsilon }_{x_1}=\frac{1}{E_1}({\sigma }_{x_1}^{\infty }-v_1{\sigma }_{y_1}^{\infty }),& & {\epsilon }_{x_2}=\frac{1}{E_2}({\sigma }_{x_2}^{\infty }-v_2{\sigma }_{y_2}^{\infty }),\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\epsilon }_{y_1}=\frac{1}{E_1}({\sigma }_{y_1}^{\infty }-v_1{\sigma }_{x_1}^{\infty }),& & {\epsilon }_{y_2}=\frac{1}{E_2}({\sigma }_{y_2}^{\infty }-v_2{\sigma }_{x_2}^{\infty }),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\epsilon }_{x_1{y}_1}=\frac{1+v_1}{E_1}{\sigma }_{x_1{y}_1}^{\infty },& & {\epsilon }_{x_2{y}_2}=\frac{1+v_2}{E_2}{\sigma }_{x_2{y}_2}^{\infty },\hfill \end{array}$$

(13)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\epsilon }_{x_1}& ={\epsilon }_{y_1}=\frac{1-v_1}{E_1}{\sigma }_{x_1}^{\infty }=\frac{1-v_1}{E_1}{\sigma }_{y_1}^{\infty },\hfill \\ \hfill {\epsilon }_{x_2}& ={\epsilon }_{y_2}=\frac{1-v_2}{E_2}{\sigma }_{x_2}^{\infty }=\frac{1-v_2}{E_2}{\sigma }_{y_2}^{\infty },\hfill \end{array}\end{array}$$

(14)

where $E_i=2G_i(1+v_i)$ and $i=1,2$. For the shear stress, we have ${\sigma }_{x_1}={\sigma }_{x_2}=p$, ${\sigma }_{y_1}^{\infty }=0$, ${\sigma }_{y_2}^{\infty }=0$ and applying condition Equation (10), Equation (11) is reduced to

$$\frac{1}{E_1}{\sigma }_{x_1}^{\infty }=\frac{1}{E_2}{\sigma }_{x_2}^{\infty }.$$

(15)

For normal stress, we have ${\sigma }_{y_1}={\sigma }_{y_2}=p$, ${\sigma }_{x_1}^{\infty }=0$, ${\sigma }_{x_2}^{\infty }=0$ and applying condition Equation (10), Equation (12) is reduced to

$$\frac{1}{E_1}{\sigma }_{y_1}^{\infty }=\frac{1}{E_2}{\sigma }_{y_2}^{\infty }.$$

(16)

For tearing stress, we have ${\sigma }_{x_1{y}_1}={\sigma }_{x_2{y}_2}=p$ and applying condition Equation (10), Equation (13) is reduced to

$$\frac{1+v_1}{E_1}{\sigma }_{x_1{y}_1}^{\infty }=\frac{1+v_2}{E_2}{\sigma }_{x_2{y}_2}^{\infty }.$$

(17)

Whereas for mixed stress, we have ${\sigma }_{x_1}={\sigma }_{x_2}={\sigma }_{y_1}={\sigma }_{y_2}=p$ and applying condition Equation (10), Equation (14) is reduced to

$$\begin{array}{ccc}\hfill \frac{1-v_1}{E_1}{\sigma }_{x_1}^{\infty }=\frac{1-v_2}{E_2}{\sigma }_{x_2}^{\infty }& \mathrm{or}& \frac{1-v_1}{E_1}{\sigma }_{y_1}^{\infty }=\frac{1-v_2}{E_2}{\sigma }_{y_2}^{\infty }.\hfill \end{array}$$

(18)

According to Chen and Hasebe [11], the MCPs for the crack in the upper plane of dissimilar materials are defined as

$$\begin{array}{ccc}\hfill {\varphi }_1\left(z\right)={\varphi }_{1p}\left(z\right)+{\varphi }_{1c}\left(z\right),& & {\psi }_1\left(z\right)={\psi }_{1p}\left(z\right)+{\psi }_{1c}\left(z\right)\hfill \end{array}$$

(19)

where ${\varphi }_{1p}\left(z\right)$ and ${\psi }_{1p}\left(z\right)$ are the principal parts and ${\varphi }_{1c}\left(z\right)$ and ${\psi }_{1c}\left(z\right)$ are the complementary parts of the complex potentials. The complex potentials for the lower plane are represented by ${\varphi }_2\left(z\right)$ and ${\psi }_2\left(z\right)$. Note that ${\varphi }_{1p}\left(z\right)$ and ${\psi }_{1p}\left(z\right)$ are similar to the complex potentials for cracks in an infinite material. The continuity conditions for the resultant force (2) and displacement functions (3), yields

$$\begin{array}{cc}\hfill {\{-Y+iX\}}^{+}& ={\{-Y+iX\}}^{-},\hfill \\ \hfill {\{{\varphi }_1\left(t\right)+(t-\overline{t})\overline{{\mathsf{\Phi }}_1^{\prime }\left(t\right)}+{\omega }_1\left(\overline{t}\right)\}}^{+}& ={\{{\varphi }_2\left(t\right)+(t-\overline{t})\overline{{\mathsf{\Phi }}_2^{\prime }\left(t\right)}+{\omega }_2\left(\overline{t}\right)\}}^{-},\hfill \end{array}$$

(20)

and

$$\begin{array}{cc}\hfill {\{u+iv\}}^{+}& ={\{u+iv\}}^{-},\hfill \\ \hfill G_2{\left\{{\kappa }_1{\varphi }_1\left(t\right)-(t-\overline{t})\overline{{\Phi }_1\left(t\right)}-{\omega }_1\left(\overline{t}\right)\right\}}^{+}& =G_1{\left\{{\kappa }_2{\varphi }_2\left(t\right)-(t-\overline{t})\overline{{\Phi }_2\left(t\right)}-{\omega }_2\left(\overline{t}\right)\right\}}^{-},\hfill \end{array}$$

(21)

where $t\in L_j$, $(j=1,2)$ and + and − signs represent the upper and lower planes of dissimilar materials, respectively. Apply Equations (19) and (4) into Equations (20) and (21), the following expressions are obtainable

$$\begin{array}{cc}\hfill {\varphi }_{1c}\left(z\right)={\beta }_1(z\overline{{\varphi }_{1p}^{\prime }}\left(z\right)+\overline{{\psi }_{1p}}\left(z\right)),& z\in S_1+L_b\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\psi }_{1c}\left(z\right)={\beta }_2\overline{{\varphi }_{1p}}\left(z\right)-{\beta }_1(z\overline{{\varphi }_{1p}^{\prime }}\left(z\right)+z^2\overline{{\varphi }_{1p}^{\prime \prime }}\left(z\right)+z\overline{{\psi }_{1p}^{\prime }}\left(z\right)),& z\in S_1+L_b\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\varphi }_2\left(z\right)=(1+{\beta }_2){\varphi }_{1p}\left(z\right),& z\in S_2+L_b\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\psi }_2\left(z\right)=({\beta }_1-{\beta }_2)z{\varphi }_{1p}^{\prime }\left(z\right)+(1+{\beta }_1){\psi }_{1p},& z\in S_2+L_b\hfill \end{array}$$

(25)

where $\overline{{\varphi }_{1p}}\left(z\right)=\overline{{\varphi }_{1p}\left(\overline{z}\right)}$. Note that $L_b$ is boundary of dissimilar materials, $S_1$ and $S_2$ are upper and lower planes of dissimilar materials, respectively, and ${\beta }_1$, ${\beta }_2$ are elastic constants defined as

$$\begin{array}{ccc}\hfill {\beta }_1=\frac{G_2-G_1}{G_1+{\kappa }_1{G}_2},& & {\beta }_2=\frac{{\kappa }_1{G}_2-{\kappa }_2{G}_1}{G_2+{\kappa }_2{G}_1}.\hfill \end{array}$$

Consider two cracks $L_1$ and $L_2$ in the upper plane of dissimilar materials under various mechanical loadings; see Figure 2.

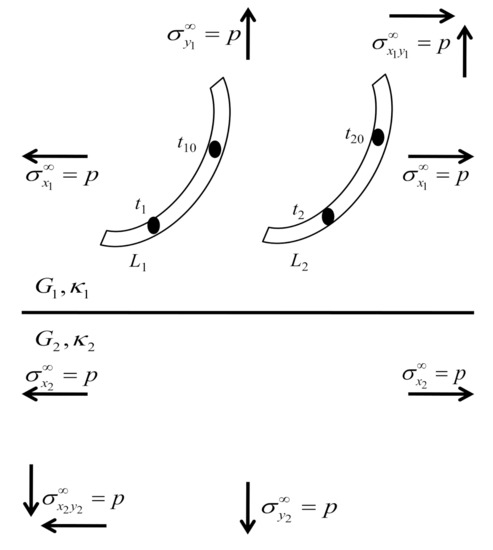
Figure 2. Two cracks $L_1$ and $L_2$ in the upper plane of dissimilar materials.

In order to develop the new mathematical model of HSIEs for two cracks in the upper plane of dissimilar materials, we need to define four traction components ${\{N\left(t_{10}\right)+iT\left(t_{10}\right)\}}_{11}$, ${\{N\left(t_{10}\right)+iT\left(t_{10}\right)\}}_{12}$, ${\{N\left(t_{20}\right)+iT\left(t_{20}\right)\}}_{22}$ and ${\{N\left(t_{20}\right)+iT\left(t_{20}\right)\}}_{21}$ which consist of two groups of $N+iT$ by using Equation (5). The first two tractions ${\{N\left(t_{10}\right)+iT\left(t_{10}\right)\}}_{11}$ and ${\{N\left(t_{20}\right)+iT\left(t_{20}\right)\}}_{21}$ are obtained when the observation point is placed at the point $t_{10}\in L_1$ and $t_{20}\in L_2$, respectively, caused by $g_1\left(t_1\right)$ at $t_1\in L_1$. Whereas, the second two tractions ${\{N\left(t_{10}\right)+iT\left(t_{10}\right)\}}_{12}$ and ${\{N\left(t_{20}\right)+iT\left(t_{20}\right)\}}_{22}$ are obtained when the observation point is placed at the point $t_{10}\in L_1$ and $t_{20}\in L_2$, respectively, caused by $g_2\left(t_2\right)$ at $t_2\in L_2$. Since both cracks lie in the upper part of dissimilar materials, we need to combine four traction components which consist of the principal ${\{N\left(t_{\mathrm{j}0}\right)+iT\left(t_{\mathrm{j}0}\right)\}}_{\mathrm{jp}}$$(j=1,2)$ and complementary parts ${\{N\left(t_{\mathrm{j}0}\right)+iT\left(t_{\mathrm{j}0}\right)\}}_{\mathrm{jc}}$$(j=1,2)$. By using the superposition principle, the new mathematical model of HSIEs for two cracks in the upper plane of dissimilar materials can be obtained as follows

$$\begin{array}{cc}\hfill {\{N\left(t_{10}\right)+iT\left(t_{10}\right)\}}_1& ={\{N\left(t_{10}\right)+iT\left(t_{10}\right)\}}_{11}+{\{N\left(t_{10}\right)+iT\left(t_{10}\right)\}}_{12}\hfill \\ \hfill & {\displaystyle =\frac{1}{\mathsf{\pi }}{⨎}_{L_1}\frac{g_1\left(t_1\right)d{t}_1}{{(t_1-t_{10})}^2}+\frac{1}{2\mathsf{\pi }}{\int }_{L_1}{K}_1(t_1,t_{10})g_1\left(t_1\right)d{t}_1+\frac{1}{2\mathsf{\pi }}{\int }_{L_1}{K}_2(t_1,t_{10})\overline{g_1\left(t_1\right)}d{t}_1}\hfill \\ \hfill & +\frac{1}{\mathsf{\pi }}{\int }_{L_2}\frac{g_2\left(t_2\right)d{t}_2}{{(t_2-t_{10})}^2}+\frac{1}{2\mathsf{\pi }}{\int }_{L_2}{K}_1(t_2,t_{10})g_2\left(t_2\right)d{t}_2+\frac{1}{2\mathsf{\pi }}{\int }_{L_2}{K}_2(t_2,t_{10})\overline{g_2\left(t_2\right)}d{t}_2,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\{N\left(t_{20}\right)+iT\left(t_{20}\right)\}}_2& ={\{N\left(t_{20}\right)+iT\left(t_{20}\right)\}}_{22}+{\{N\left(t_{20}\right)+iT\left(t_{20}\right)\}}_{21}\hfill \\ \hfill & {\displaystyle =\frac{1}{\mathsf{\pi }}{⨎}_{L_2}\frac{g_2\left(t_2\right)d{t}_2}{{(t_2-t_{20})}^2}+\frac{1}{2\mathsf{\pi }}{\int }_{L_2}{K}_1(t_2,t_{20})g_2\left(t_2\right)d{t}_2+\frac{1}{2\mathsf{\pi }}{\int }_{L_2}{K}_2(t_2,t_{20})\overline{g_2\left(t_2\right)}d{t}_2}\hfill \\ \hfill & +\frac{1}{\mathsf{\pi }}{\int }_{L_1}\frac{g_1\left(t_1\right)d{t}_1}{{(t_1-t_{20})}^2}+\frac{1}{2\pi }{\int }_{L_1}{K}_1(t_1,t_{20})g_1\left(t_1\right)d{t}_1+\frac{1}{2\mathsf{\pi }}{\int }_{L_1}{K}_2(t_1,t_{20})\overline{g_1\left(t_1\right)}d{t}_1,\hfill \end{array}$$

(27)

where

$$\begin{array}{cc}\hfill K_1(t_{\mathrm{i}},t_{\mathrm{j}0})& =\frac{1}{{(t_{\mathrm{i}}-t_{\mathrm{j}0})}^2}\left(\frac{{(t_{\mathrm{i}}-t_{\mathrm{j}0})}^2}{{({\overline{t}}_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}\frac{d{\overline{t}}_{\mathrm{i}}}{d{t}_{\mathrm{i}}}\frac{d{\overline{t}}_{\mathrm{j}0}}{d{t}_{\mathrm{j}0}}-1\right)+{\beta }_1(\frac{1}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}+\frac{2({\overline{t}}_{\mathrm{j}0}-{\overline{t}}_{\mathrm{i}})}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^3}\hfill \\ \hfill & +\frac{d{\overline{t}}_{\mathrm{j}0}}{d{t}_{\mathrm{j}0}}\left(\frac{2(2t_{\mathrm{j}0}-3{\overline{t}}_{\mathrm{j}0}+{\overline{t}}_{\mathrm{i}})}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^3}-\frac{6({\overline{t}}_{\mathrm{j}0}-{\overline{t}}_{\mathrm{i}})({\overline{t}}_{\mathrm{j}0}-t_{\mathrm{j}0})}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^4}-\frac{1}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}\right))+{\beta }_2\frac{d{\overline{t}}_{\mathrm{j}0}}{d{t}_{\mathrm{j}0}}\frac{1}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}\hfill \\ \hfill & +{\beta }_1\left(\frac{1}{{({\overline{t}}_{\mathrm{i}}-t_{\mathrm{j}0})}^2}+\frac{1}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}-\frac{d{\overline{t}}_{\mathrm{j}0}}{d{t}_{\mathrm{j}0}}\left(\frac{1}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}+\frac{2({\overline{t}}_{\mathrm{j}0}-t_{\mathrm{j}0})}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^3}\right)\right)\frac{d{\overline{t}}_{\mathrm{i}}}{d{t}_{\mathrm{i}}},\hfill \\ \hfill K_2(t_{\mathrm{i}},t_{\mathrm{j}0})& =\frac{t_{\mathrm{i}}-t_{\mathrm{j}0}}{{({\overline{t}}_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^3}\left(\frac{({\overline{t}}_{\mathrm{i}}-\overline{t_{\mathrm{j}0}})}{(t_{\mathrm{i}}-t_{\mathrm{j}0})}\left(\frac{d{\overline{t}}_{\mathrm{i}}}{d{t}_{\mathrm{i}}}+\frac{d{\overline{t}}_{\mathrm{j}0}}{d{t}_{\mathrm{j}0}}\right)-2\frac{d{\overline{t}}_{\mathrm{i}}}{d{t}_{\mathrm{i}}}\frac{d{\overline{t}}_{\mathrm{j}0}}{d{t}_{\mathrm{j}0}}\right)+{\beta }_1(\frac{1}{{({\overline{t}}_{\mathrm{i}}-t_{\mathrm{j}0})}^2}+\frac{1}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}\hfill \\ \hfill & -\frac{d{\overline{t}}_{\mathrm{j}0}}{d{t}_{\mathrm{j}0}}\left(\frac{1}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^2}+\frac{2({\overline{t}}_{\mathrm{j}0}-t_{\mathrm{j}0})}{{(t_{\mathrm{i}}-{\overline{t}}_{\mathrm{j}0})}^3}\right))+{\beta }_1\left(\frac{1}{{({\overline{t}}_{\mathrm{i}}-t_{\mathrm{j}0})}^2}+\frac{2(t_{\mathrm{j}0}-t_{\mathrm{i}})}{{({\overline{t}}_{\mathrm{i}}-t_{\mathrm{j}0})}^3}\right)\frac{d{\overline{t}}_{\mathrm{i}}}{d{t}_{\mathrm{i}}},\hfill \end{array}$$

and $i,j=1,2$. In Equation (26), the first three integrals on the right hand side represent the traction influence on crack $L_1$ caused by COD function $g_1\left(t_1\right)$ on crack $L_1$. The next three integrals represent the traction influence on crack $L_1$ caused by COD function $g_2\left(t_2\right)$ on crack $L_2$. Whereas in Equation (27), the first three integrals on the right hand side represent the traction influence on crack $L_2$ caused by COD function $g_2\left(t_2\right)$ on crack $L_2$. The next three integrals represent the traction influence on crack $L_2$ caused by COD function $g_1\left(t_1\right)$ on crack $L_1$. Note that the first integral with the equal sign in Equations (26) and (27) represents the hypersingular integral and must be defined as a finite part integral. If $G_2=0$, then ${\beta }_1={\beta }_2=-1$, Equations (26) and (27) reduce to the HSIEs for the two cracks in a half plane elasticity [18]. Whereas, if $G_1=G_2$, then ${\beta }_1={\beta }_2=0$, Equations (26) and (27) reduce to the HSIEs for the two cracks in an infinite plane [3].

In order to solve the new mathematical model of HSIEs, the curved length coordinate method is used. Let

$$H\left(s\right)=\frac{h\left(s\right)}{\sqrt{a^2-s^2}},{h\left(s\right)=g\left(t\right)|}_{t=t\left(s\right)}.$$

(28)

Then the following quadrature formulas can be applied [19,20,21,22]

$${\displaystyle \frac{1}{\pi }{⨎}_{-a}^a\frac{\sqrt{a^2-s^2}H\left(s\right)ds}{{(s-s_0)}^2}\simeq \sum _{j=1}^{M+1}{W}_j\left(s_0\right)H\left(s_j\right),}$$

(29)

and

$$\frac{1}{\pi }{\int }_{-a}^a\sqrt{a^2-s^2}H\left(s\right)ds\simeq \frac{1}{M+2}\sum _{j=1}^{M+1}(a^2-s_0^2)H\left(s_j\right),$$

(30)

where $H\left(s\right)$ is a given function, $M\in {\mathbb{Z}}^{+}$,

$$s_j=acos\left(\frac{j\pi }{M+2}\right),j=1,2,...,M+1,$$

and

$$W_j\left(s_0\right)=-\frac{2}{M+2}\sum _{n=0}^M(n+1)sin\left(\frac{j\pi }{M+2}\right)sin\left(\frac{(n+1)j\pi }{M+2}\right)U_n\left(\frac{s_{j0}}{a}\right),$$

and the observation points

$$s_0=s_{0,k}=acos\left(\frac{k\pi }{M+2}\right),k=1,2,...,M+1.$$

Here, $U_n\left(t\right)$ is a Chebyshev polynomial of the second kind, defined by

$$U_n\left(t\right)=\frac{sin\left(\right(n+1\left)\theta \right)}{sin\theta },\mathrm{where}t=cos\theta .$$

(31)

The normal and tangential components $N+iT$ of the HSIEs for the shear stress ${\sigma }_{x_1}={\sigma }_{x_2}=p$, normal stress ${\sigma }_{y_1}={\sigma }_{y_2}=p$, tearing stress ${\sigma }_{x_1{y}_1}={\sigma }_{x_2{y}_2}=p$ and mixed stress ${\sigma }_{x_1}={\sigma }_{x_2}={\sigma }_{y_1}={\sigma }_{y_2}=p$ with an angle of the crack $\alpha$ are defined as follows

$$\begin{array}{c}\hfill N+iT=-p{sin}^2\alpha -ipsin\alpha cos\alpha ,\end{array}$$

(32)

$$\begin{array}{c}\hfill N+iT=-p{cos}^2\alpha +ipsin\alpha cos\alpha ,\end{array}$$

(33)

$$\begin{array}{c}\hfill N+iT=2psin\alpha cos\alpha +ip({cos}^2\alpha -{sin}^2\alpha ),\end{array}$$

(34)

$$\begin{array}{c}\hfill N+iT=-p+i0.\end{array}$$

(35)

In order to investigate the behavior of dimensionless SIFs for two cracks in the upper plane of dissimilar materials under various mechanical loadings, we define the SIFs at the crack tips $A_j$ and $B_j$ as follows

$$\begin{array}{cc}\hfill K_{A_j}={(K_1-i{K}_2)}_{A_j}=\sqrt{2\pi }\underset{t\to t_{A_j}}{lim}\sqrt{|t-t_{A_j}|}{g}_1^{\prime }\left(t_1\right),& j=1,2,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill K_{B_j}={(K_1-i{K}_2)}_{B_j}=\sqrt{2\pi }\underset{t\to t_{B_j}}{lim}\sqrt{|t-t_{B_j}|}{g}_2^{\prime }\left(t_2\right),& j=1,2,\hfill \end{array}$$

(37)

where $g_1^{\prime }\left(t_1\right)$ and $g_2^{\prime }\left(t_2\right)$ are defined as follows

$$g_k^{\prime }\left(t_k\right){|}_{t_k=t_k\left(s_k\right)}=\frac{-s_k{H}_k\left(s_k\right)}{\sqrt{a_k^2-s_k^2}}{e}^{-i{\theta }_{A_j}},H_k^{\prime }\left(s_k\right)=0,$$

(38)

and $k=1,2$. Therefore, the dimensionless SIFs at crack tips $A_j$ and $B_j$ are defined as follows

$$\begin{array}{c}\hfill K_{A_j}={(K_1-i{K}_2)}_{A_j}=\sqrt{2\pi }\underset{s\to s_{A_j}}{lim}\sqrt{|s-s_{A_j}|}\left[\frac{-s_1{H}_1\left(s_1\right)}{\sqrt{a_1^2-s_1^2}}{e}^{-i{\theta }_{A_j}}\right]=\sqrt{a_1\pi }{F}_{A_j},\end{array}$$

(39)

$$\begin{array}{c}\hfill K_{B_j}={(K_1-i{K}_2)}_{B_j}=\sqrt{2\pi }\underset{s\to s_{B_j}}{lim}\sqrt{|s-s_{B_j}|}\left[\frac{-s_2{H}_2\left(s_2\right)}{\sqrt{a_2^2-s_2^2}}{e}^{-i{\theta }_{B_j}}\right]=\sqrt{a_2\pi }{F}_{B_j},\end{array}$$

(40)

where

$$\begin{array}{c}\hfill F_{A_j}=H_1(-a_1)e^{-i{\theta }_{A_j}}=F_{1A_j}+i{F}_{2A_j},\\ \hfill F_{B_j}=H_2(-a_2)e^{-i{\theta }_{B_j}}=F_{1B_j}+i{F}_{2B_j}.\end{array}$$

$F_{1A_j}$ and $F_{1B_j}$ are the Mode I dimensionless SIFs at crack tips $A_j$ and $B_j$, respectively, and characterizes the amplitude of normal stress singularity. Whereas $F_{2A_j}$ and $F_{2B_j}$ are the Mode II dimensionless SIFs at crack tips $A_j$ and $B_j$, respectively, and describe the amplitude of the shear stress singularity. Note that the crack propagates if the value of dimensionless SIFs is greater than or equal to the value of critical dimensionless SIFs [23]. The strength of the materials is getting weaker as the value of dimensionless SIFs increases [24]. Whereas the negative values of dimensionless SIFs were obtained for some geometric problems, implicatively insinuating the possible use of unknown contact and frictional stresses between the closed crack surfaces, thereby invalidating the presumption of a frictionless open crack model [25].

3. Numerical Results and Discussion

In this section, numerical computations and graphical demonstrations are carried out to show the effects of the elastic constants ratio, mode of stresses and geometry conditions on the dimensionless SIFs for crack problems in the upper plane of dissimilar materials. To validate the proposed mathematical model, we compared our numerical results with a crack parallel to the boundary of dissimilar materials investigated by Isida and Noguchi [12] in Table 1, and two cracks in the upper plane of dissimilar materials presented by Chen [10] in Table 2.

Table 1. Stress intensity factors (SIFs) for a crack parallel to the boundary of dissimilar materials (Figure 3a).

SIF	$\mathit{h}/2\mathit{R}$
	$\mathbf{0}.\mathbf{1}$	$\mathbf{0}.\mathbf{2}$	$\mathbf{0}.\mathbf{3}$	$\mathbf{0}.\mathbf{4}$	$\mathbf{0}.\mathbf{5}$	$\mathbf{0}.\mathbf{6}$	$\mathbf{0}.\mathbf{7}$
$F_{1A_1}$*	0.8083	0.8357	0.8568	0.8752	0.8920	0.9071	0.9203
$F_{2A_1}$*	0.1119	0.0811	0.0634	0.0500	0.0391	0.0304	0.0236
$F_{1A_2}$*	0.8083	0.8357	0.8568	0.8752	0.8920	0.9071	0.9203
$F_{1A_2}$**	0.8080	0.8360	0.8570	0.8750	0.8920	0.9070	0.9200
$F_{2A_2}$*	−0.1119	−0.0811	−0.0634	−0.0500	−0.0391	−0.0304	−0.0236
$F_{2A_2}$**	−0.1120	−0.0810	−0.0630	−0.0500	−0.0390	−0.0300	−0.0240

* Present study, ** Isida and Noguchi [12].

Table 2. SIFs for two cracks in the upper plane of dissimilar materials under various mechanical loadings (Figure 3b).

Stress	${\mathit{G}}_2/{\mathit{G}}_1$	SIF
		${\mathit{F}}_{\mathbf{1}{\mathit{A}}_{\mathbf{1}}}$	${\mathit{F}}_{\mathbf{2}{\mathit{A}}_{\mathbf{1}}}$	${\mathit{F}}_{\mathbf{1}{\mathit{A}}_{\mathbf{2}}}$	${\mathit{F}}_{\mathbf{2}{\mathit{A}}_{\mathbf{2}}}$	${\mathit{F}}_{\mathbf{1}{\mathit{B}}_{\mathbf{1}}}$	${\mathit{F}}_{\mathbf{2}{\mathit{B}}_{\mathbf{1}}}$	${\mathit{F}}_{\mathbf{1}{\mathit{B}}_{\mathbf{2}}}$	${\mathit{F}}_{\mathbf{2}{\mathit{B}}_{\mathbf{2}}}$
Shear	0.2 *	0.4634	−0.3358	0.0612	−0.1974	1.2272	−0.0336	1.1004	0.0510
	0.2 **	0.4670	−0.3333	0.0420	−0.2010	1.2140	−0.0180	1.1010	0.0650
	1.0 *	0.4250	−0.3226	0.0420	−0.2341	0.8909	−0.0364	0.9844	0.0536
	1.0 **	0.4250	−0.3230	0.0420	−0.2360	0.8910	−0.0360	0.9850	0.0530
	5.0 *	0.4219	−0.3000	0.0571	−0.2352	0.6666	−0.0486	0.9128	0.0472
	5.0 **	0.4020	−0.2830	0.0370	−0.2400	0.6600	−0.0440	0.9030	0.0460
Normal	0.2 *	0.7333	0.5407	0.5561	0.6535	−0.1501	−0.1375	0.1483	−0.0758
	1.0 *	0.5177	0.4920	0.4833	0.5594	−0.1097	−0.0805	0.1152	−0.0270
	5.0 *	0.3974	0.4609	0.4327	0.5093	−0.0649	−0.0472	0.1122	−0.0079
Tearing	0.2 *	−1.3748	0.2490	−1.0732	0.0420	0.4691	−1.1090	−0.0698	−1.1981
	1.0 *	−1.1290	0.1528	−0.9643	0.0614	0.3696	−0.7944	−0.0589	−1.1132
	5.0 *	−0.9501	0.0443	−0.8446	0.0524	0.2347	−0.5754	−0.0770	−1.0218
Mixed	0.2 *	1.1967	0.2050	0.6173	0.4562	1.0771	−0.1711	1.2488	−0.0247
	1.0 *	0.9427	0.1694	0.5253	0.3254	0.7812	−0.1169	1.0996	0.0266
	5.0 *	0.8194	0.1609	0.4898	0.2741	0.6017	−0.0958	1.0250	0.0393

* Present study, ** Chen [10].

Consider the geometry conditions for crack problems in the upper plane of dissimilar materials under various mechanical loadings; see Figure 3.

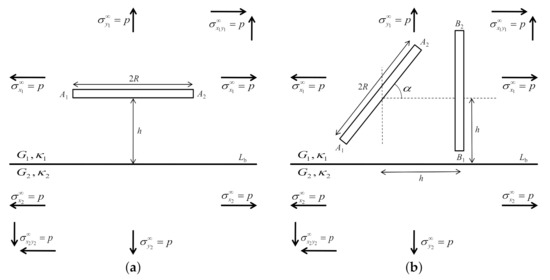
Figure 3. The geometry conditions for crack problems in the upper plane of dissimilar materials. (a) A crack parallel to the boundary; (b) Two cracks in the upper plane.

Table 1 shows the dimensionless SIFs for a crack parallel to the boundary of dissimilar materials under normal stress when elastic constant ratio $G_2/G_1=4.0$ and $h/2R$ varies (Figure 3a). Our numerical results totally agree with those of Isida and Noguchi [12]. We observed that $F_1$ at crack tip $A_1$ is equal to $F_1$ at crack tip $A_2$. Whereas $F_2$ at crack tip $A_1$ is equal to the negative of $F_2$ at crack tip $A_2$. This is due to the equivalence of the stress acting at the tips of the cracks.

Table 2 shows the dimensionless SIFs for two cracks in the upper plane of dissimilar materials under various mechanical loadings when $\alpha ={45}^{\circ }$ and $R/h=0.9$ (Figure 3b). For shear stress, our numerical results agree with those of Chen [10]. For other stresses, the value of dimensionless SIFs are displayed in Figure 4, Figure 5, Figure 6, Figure 7. The dimensionless SIFs with black lines at crack tips $A_1$ and $B_1$, and with blue lines at crack tips $A_2$ and $B_2$ under shear stress are delineated in Figure 4. It is found that as $G_2/G_1$ increases, $F_1$ decreases at all cracks tips. However $F_2$ increases when $\alpha >{40}^{\circ }$ at tip $A_1$ and decreases at tip $A_2$. As $\alpha$ increases, $F_1$ increases at crack tips $A_1$ and $A_2$. These numerical evidences show that the materials become weaker as $\alpha$ increases and more stable as $G_2/G_1$ increases.

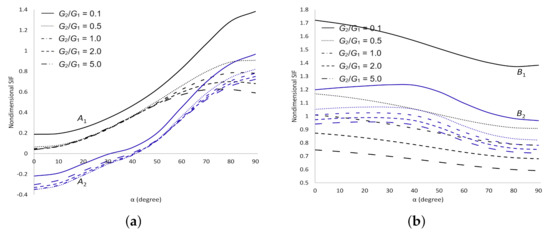
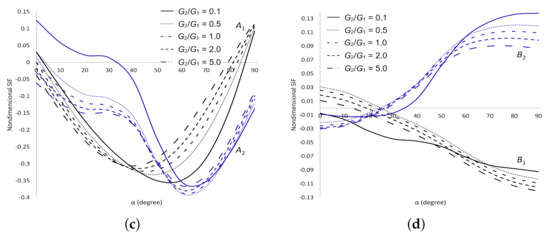
Figure 4. SIFs for two cracks in the upper plane of dissimilar materials under shear stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $A_2$; (b) Dimensionless SIF $F_1$ at crack tips $B_1$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $A_2$; (d) Dimensionless SIF $F_2$ at crack tips $B_1$ and $B_2$.

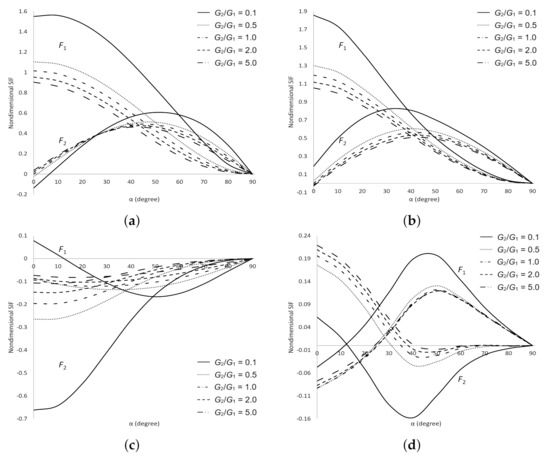
Figure 5. SIFs for two cracks in the upper plane of dissimilar materials under normal stress. (a) Crack tip $A_1$; (b) Crack tip $A_2$; (c) Crack tip $B_1$; (d) Crack tip $B_2$.

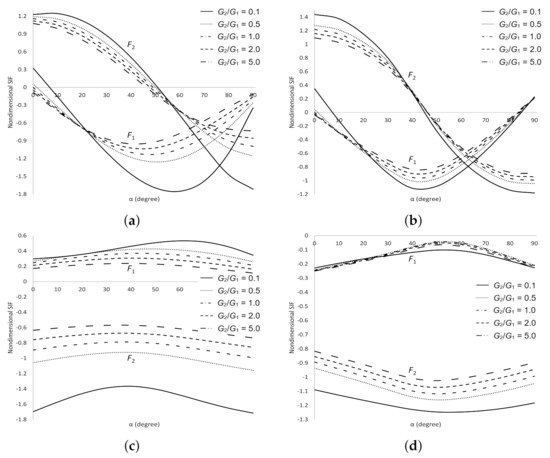
Figure 6. SIFs for two cracks in the upper plane of dissimilar materials under tearing stress. (a) Crack tip $A_1$; (b) Crack tip $A_2$; (c) Crack tip $B_1$; (d) Crack tip $B_2$.

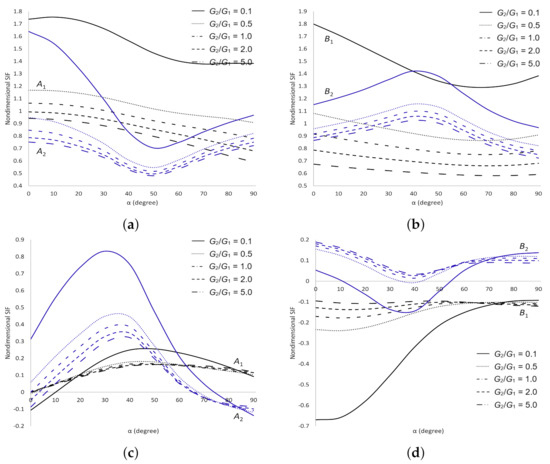
Figure 7. SIFs for two cracks in the upper plane of dissimilar materials under mixed stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $A_2$; (b) Dimensionless SIF $F_1$ at crack tips $B_1$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $A_2$; (d) Dimensionless SIF $F_2$ at crack tips $B_1$ and $B_2$.

The dimensionless SIFs under normal stress are delineated in Figure 5. It is observed that as $G_2/G_1$ increases $F_1$ decreases at cracks tips $A_1$, $A_2$ and $B_2$, and increases at tip $B_1$. As $\alpha$ increases $F_1$ decreases at crack tips $A_1$ and $A_2$. Whereas as $\alpha ={90}^{\circ }$, the values of $F_1$ and $F_2$ are equal to zero at all cracks tips, due to the stress acting parallel to the geometric of the cracks. These observations show that the materials are more stable as $\alpha$ and $G_2/G_1$ increase. The dimensionless SIFs under tearing stress are delineated in Figure 6. It demonstrates that as $G_2/G_1$ increases, $F_1$ increases at cracks tips $A_1$, $A_2$ and $B_1$ but $F_2$ only increases at tips $B_1$ and $B_2$. As $\alpha$ increases, $F_2$ decreases at crack tips $A_1$ and $A_2$. These results indicate that the strength of the materials depends on $\alpha$ and $G_2/G_1$. The dimensionless SIFs with black lines at crack tips $A_1$ and $B_1$, and with blue lines at crack tips $A_2$ and $B_2$ under mixed stress are delineated in Figure 7. It portrays that as $G_2/G_1$ increases $F_1$ decreases at all cracks tips. As $\alpha$ increases, $F_1$ decreases at crack tips $A_1$ and $B_1$. These results enable us to conclude that the materials are more stable as $G_2/G_1$ increases.

Consider the geometry conditions for two cracks in the upper plane of dissimilar materials under various mechanical loadings as depicted in Figure 8.

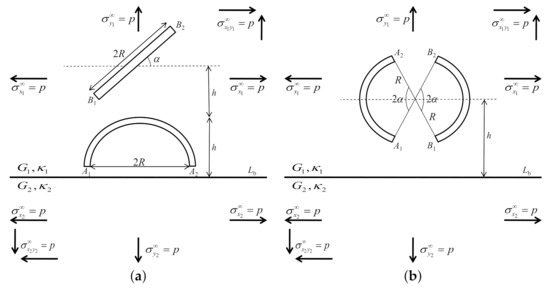
Figure 8. The geometry conditions for two cracks in the upper plane of dissimilar materials. (a) A semi circular arc crack and an inclined crack; (b) Two equal circular arc cracks on the same circle.

The dimensionless SIFs with black lines at crack tips $A_1$ and $B_1$, and with blue lines at crack tips $A_2$ and $B_2$ for a semi circular arc crack and an inclined crack in the upper plane of dissimilar materials under various mechanical loadings when $h=1.5R$ and $\alpha$ varies are plotted in Figure 9, Figure 10, Figure 11 and Figure 12 (Figure 8a).

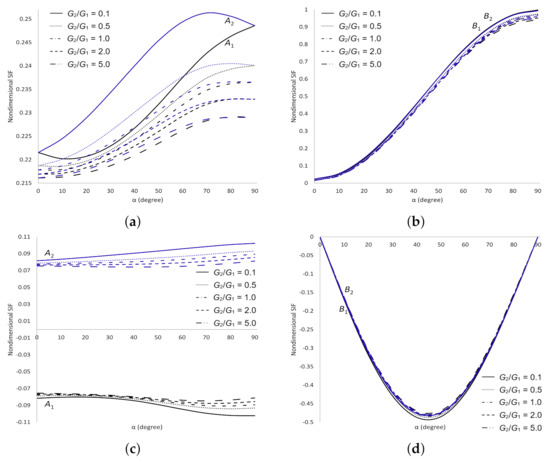
Figure 9. SIFs for two cracks in the upper plane of dissimilar materials under shear stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $A_2$; (b) Dimensionless SIF $F_1$ at crack tips $B_1$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $A_2$; (d) Dimensionless SIF $F_2$ at crack tips $B_1$ and $B_2$.

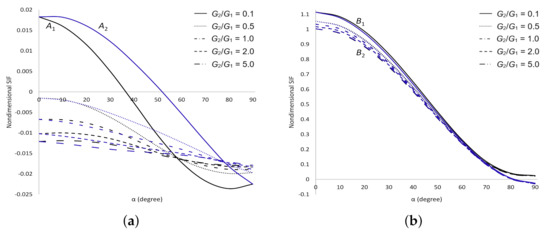
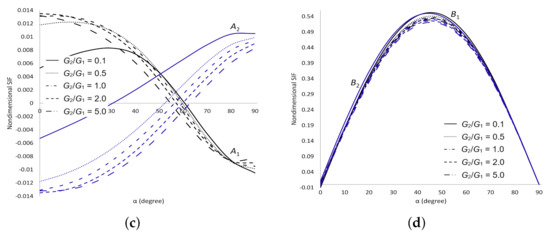
Figure 10. SIFs for two cracks in the upper plane of dissimilar materials under normal stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $A_2$; (b) Dimensionless SIF $F_1$ at crack tips $B_1$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $A_2$; (d) Dimensionless SIF $F_2$ at crack tips $B_1$ and $B_2$.

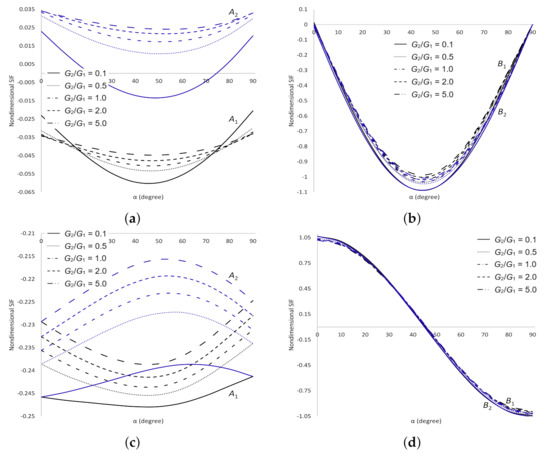
Figure 11. SIFs for two cracks in the upper plane of dissimilar materials under tearing stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $A_2$; (b) Dimensionless SIF $F_1$ at crack tips $B_1$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $A_2$; (d) Dimensionless SIF $F_2$ at crack tips $B_1$ and $B_2$.

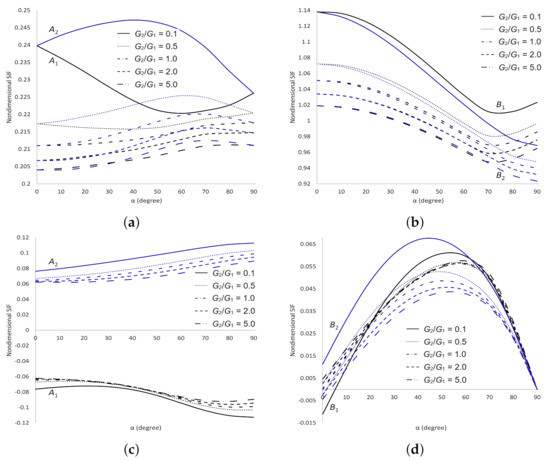
Figure 12. SIFs for two cracks in the upper plane of dissimilar materials under mixed stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $A_2$; (b) Dimensionless SIF $F_1$ at crack tips $B_1$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $A_2$; (d) Dimensionless SIF $F_2$ at crack tips $B_1$ and $B_2$.

The dimensionless SIFs under shear stress are delineated in Figure 9. It is found that as $G_2/G_1$ and $\alpha$ increase $F_1$ decreases and increases, respectively at all cracks tips. As $G_2/G_1$ increases, $F_2$ increases at crack tip $A_1$, decreases at tip $A_2$ and does not show any significant difference at tips $B_1$ and $B_2$. These numerical evidences show that the materials are more stable as $G_2/G_1$ increases and are getting weaker as $\alpha$ increases. The dimensionless SIFs under normal stress are delineated in Figure 10. It can be seen that as $G_2/G_1$ increases $F_1$ decreases at cracks tips $B_1$ and $B_2$ but at tips $A_1$ when $\alpha <{55}^{\circ }$ and $A_2$ when $\alpha <{80}^{\circ }$. As $\alpha$ increases, $F_1$ decreases at all cracks tips. These observations show that the materials are more stable as $G_2/G_1$ and $\alpha$ increase. The dimensionless SIFs under tearing stress are delineated in Figure 11. It portrays that as $G_2/G_1$ increases $F_1$ increases at all cracks tips. As $\alpha$ increases, $F_1$ decreases when $\alpha <{45}^{\circ }$ at all cracks tips. These results show that the strength of the materials depends on the values of $G_2/G_1$ and $\alpha$. For mixed stress, the dimensionless SIFs are displayed in Figure 12. It is observed that as $G_2/G_1$ increases $F_1$ decreases at all cracks tips and $F_2$ decreases at crack tips $A_2$ and $B_2$. As $\alpha$ increases, $F_1$ does not show any significant difference at all cracks tips. These results enable us to conclude that the materials are more stable as $G_2/G_1$ increases.

Figure 13 shows a comparison of the dimensionless SIFs for two equal circular arc cracks on the same circle in the upper plane of dissimilar materials under shear stress when $G_2/G_1=1.0$, $h=1.5R$ and $\alpha$ varies (Figure 8b). Our numerical results agree with those of Chen and Hasebe [26]. We observed that the value of $F_1$ is equal at all crack tips. Whereas $F_2$ at crack tips $A_1$ and $A_2$ are equal to the negative of $F_2$ at crack tips $B_1$ and $B_2$, respectively. This is due to the equivalence of the stress acting at the tips of the cracks.

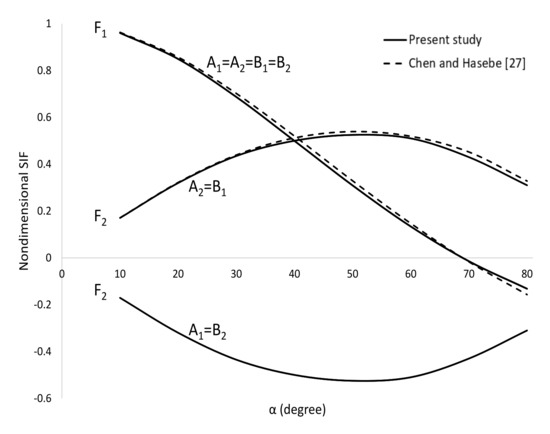
Figure 13. Comparison of dimensionless SIFs between present study and Chen and Hasebe [26] at all crack tips.

For other values of dimensionless SIFs under various mechanical loadings are presented in Figure 14, Figure 15, Figure 16 and Figure 17. The dimensionless SIFs under shear stress are delineated in Figure 14. It is observed that $F_1$ at crack tips $A_1$ and $A_2$ are equal to $F_1$ at tips $B_1$ and $B_2$, respectively. Whereas $F_2$ at crack tips $A_1$ and $A_2$ are equal to the negative of $F_2$ at tips $B_1$ and $B_2$, respectively. As $G_2/G_1$ and $\alpha$ increase, $F_1$ decreases at all cracks tips. As $G_2/G_1$ increases, $F_2$ increases at crack tips $A_1$ and $B_2$, and decreases at tips $A_2$ and $B_1$. These observations show that the materials are more stable as $G_2/G_1$ and $\alpha$ increase.

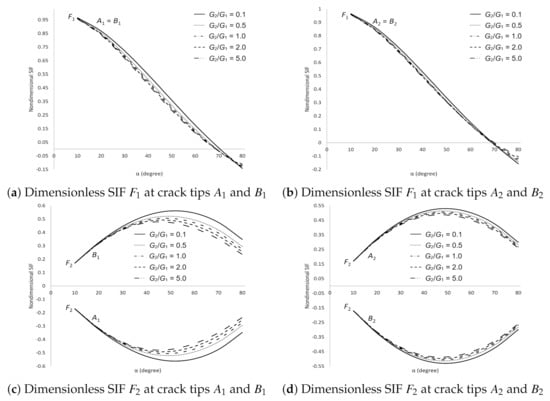
Figure 14. SIFs for two cracks in the upper plane of dissimilar materials under shear stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $B_1$; (b) Dimensionless SIF $F_1$ at crack tips $A_2$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $B_1$; (d) Dimensionless SIF $F_2$ at crack tips $A_2$ and $B_2$.

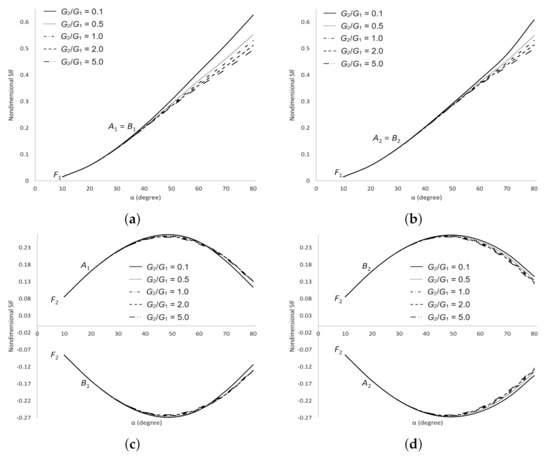
Figure 15. SIFs for two cracks in the upper plane of dissimilar materials under normal stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $B_1$; (b) Dimensionless SIF $F_1$ at crack tips $A_2$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $B_1$; (d) Dimensionless SIF $F_2$ at crack tips $A_2$ and $B_2$.

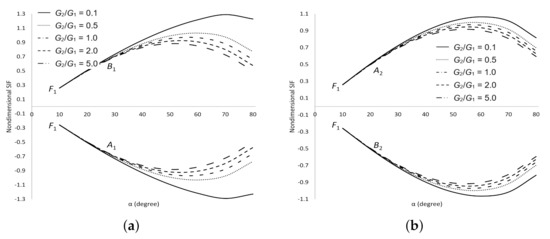
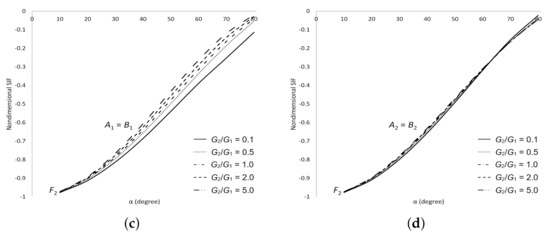
Figure 16. SIFs for two cracks in the upper plane of dissimilar materials under tearing stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $B_1$; (b) Dimensionless SIF $F_1$ at crack tips $A_2$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $B_1$; (d) Dimensionless SIF $F_2$ at crack tips $A_2$ and $B_2$.

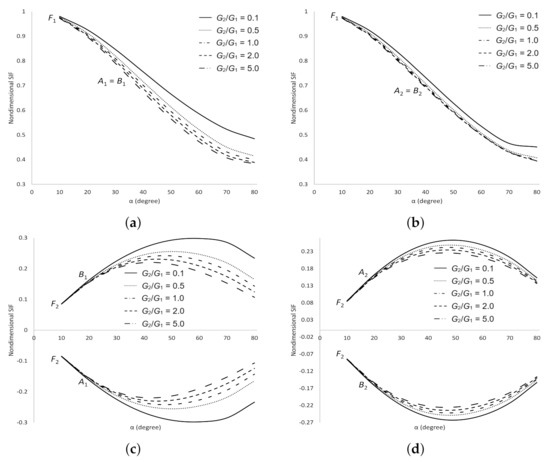
Figure 17. SIFs for cracks in the upper plane of dissimilar materials under mixed stress. (a) Dimensionless SIF $F_1$ at crack tips $A_1$ and $B_1$; (b) Dimensionless SIF $F_1$ at crack tips $A_2$ and $B_2$; (c) Dimensionless SIF $F_2$ at crack tips $A_1$ and $B_1$; (d) Dimensionless SIF $F_2$ at crack tips $A_2$ and $B_2$.

The dimensionless SIFs under normal stress are delineated in Figure 15. It demonstrates that $F_1$ at crack tips $A_1$ and $A_2$ are equal to $F_1$ at tips $B_1$ and $B_2$, respectively. Whereas $F_2$ at crack tips $A_1$ and $A_2$ are equal to the negative of $F_2$ at tips $B_1$ and $B_2$, respectively. As $G_2/G_1$ and $\alpha$ increase, $F_1$ decreases and increases, respectively at all cracks tips. As $\alpha$ increases, $F_2$ increases at crack tips $A_1$ and $B_2$ when $\alpha <{45}^{\circ }$, and decreases at tips $A_2$ and $B_1$ when $\alpha <{45}^{\circ }$. These results show that the materials are more stable as $G_2/G_1$ increases and become weaker as $\alpha$ increases. The dimensionless SIFs under tearing stress are delineated in Figure 16. It is found that $F_2$ at crack tips $A_1$ and $A_2$ are equal to $F_2$ at tips $B_1$ and $B_2$, respectively. Whereas $F_1$ at crack tips $A_1$ and $A_2$ are equal to the negative of $F_1$ at tips $B_1$ and $B_2$, respectively. As $G_2/G_1$ increases, $F_1$ increases at crack tips $A_1$ and $B_2$, and decreases at tips $A_2$ and $B_1$. As $\alpha$ increases, $F_1$ decreases at crack tips $A_1$ and $B_2$ when $\alpha <{50}^{\circ }$, and increases at tips $A_2$ and $B_1$ when $\alpha <{50}^{\circ }$. Whereas $F_2$ increases at all cracks tips as $\alpha$ increases. These numerical evidences show that the materials are more stable as $G_2/G_1$ increases and become weaker as $\alpha$ increases. The dimensionless SIFs under mixed stress are delineated in Figure 17. It is obtained that $F_1$ at crack tips $A_1$ and $A_2$ are equal to $F_1$ at tips $B_1$ and $B_2$, respectively. Whereas $F_2$ at crack tips $A_1$ and $A_2$ are equal to the negative of $F_2$ at tips $B_1$ and $B_2$, respectively. As $G_2/G_1$ and $\alpha$ increase, $F_1$ decreases at all cracks tips. $F_2$ increases at crack tips $A_1$ and $B_2$, and decreases at tips $A_2$ and $B_1$ as $G_2/G_1$ increases. These numerical results show that the materials are more stable as $G_2/G_1$ and $\alpha$ increase.

4. Conclusions

The present mathematical model is focused on the analytical investigation of dimensionless SIFs at the crack tip of two cracks problems in the upper plane of dissimilar materials under various mechanical loadings such as shear, normal, tearing and mixed stresses with different geometry conditions. The problem was formulated into a new mathematical model of HSIEs by using the MCPs function and the continuity conditions of the resultant force and displacement with the crack opening displacement (COD) function as the unknown. The substantial effect of the elastic constant ratio $G_2/G_1$, mode of stresses and geometry conditions of the cracks on dimensionless SIFs have been delineated by means of numerical computation and graphical demonstration. Moreover, the major outcomes of the present analysis can be attributed as follows:

• For $G_2=0$ and $G_1=G_2$, the elementary solution of HSIEs is reduced to two cracks in half plane and infinite plane problems, respectively.
• The equivalence of the stress acting at the crack tip due to the geometric of the cracks resulted in equal values of dimensionless SIFs.
• The value of $G_2/G_1$, types of stresses and geometry conditions of the crack affect the strength of the materials for two cracks in the upper part of dissimilar materials.

For future developments, the approach used in this paper could be extended to investigate the behavior of dimensionless SIFs for others geometry conditions in dissimilar materials under various mechanical loadings. It also can be extended to the three-dimensional cracks problems in dissimilar materials with guided work from Chen and Lee [27].