Comparative Analysis of the Life-Cycle Cost of Robot Substitution: A Case of Automobile Welding Production in China
Abstract
1. Introduction
2. Theoretical Background
2.1. Cost Breakdown Structure of LCC
2.2. Cost Factors Related to the LCC of Robot Substitution
2.3. Cost Measurement and Estimation Methods
3. Materials and Methods
3.1. Comparative LCC Model of Robot Substitution
3.2. Cost Allocation and Variables Estimation
3.3. Data Resources
3.4. Case Analysis and Simulation
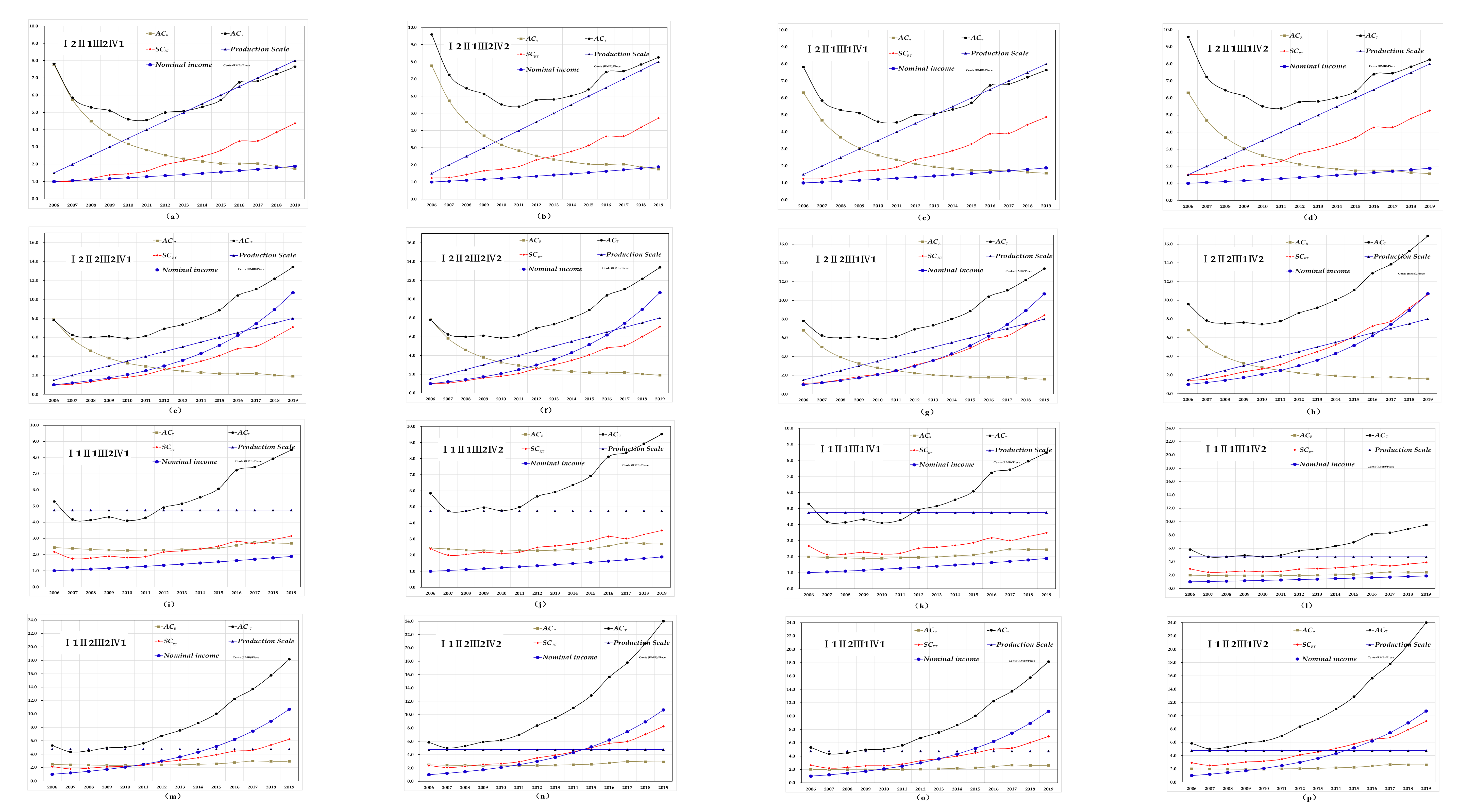
4. Results
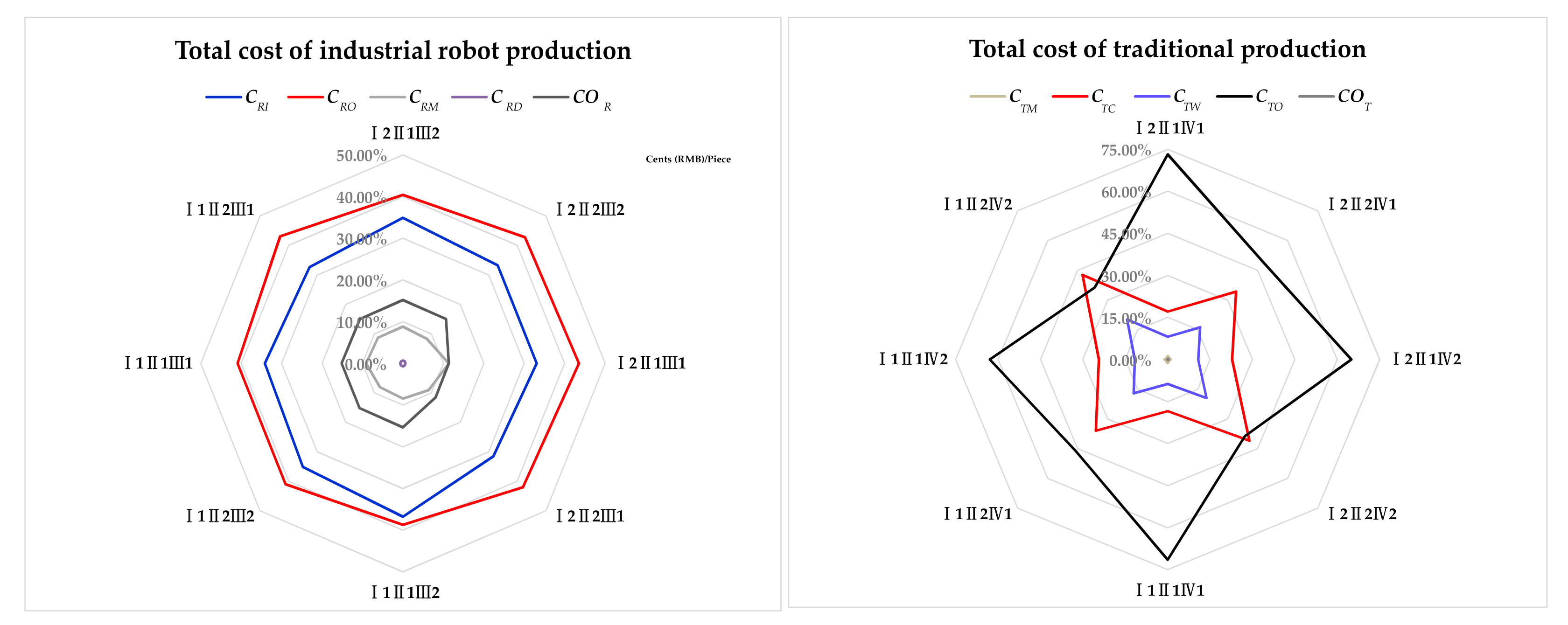
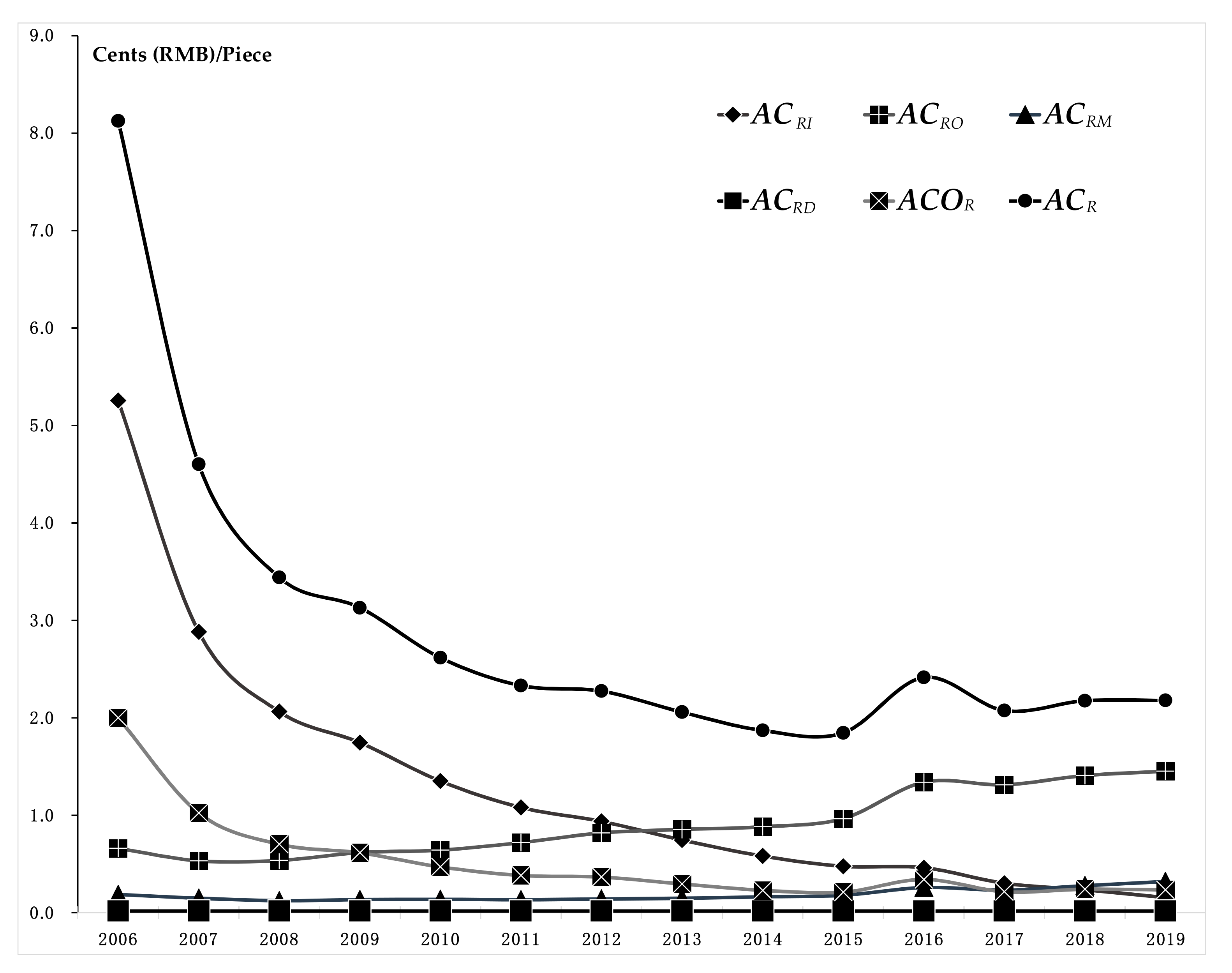
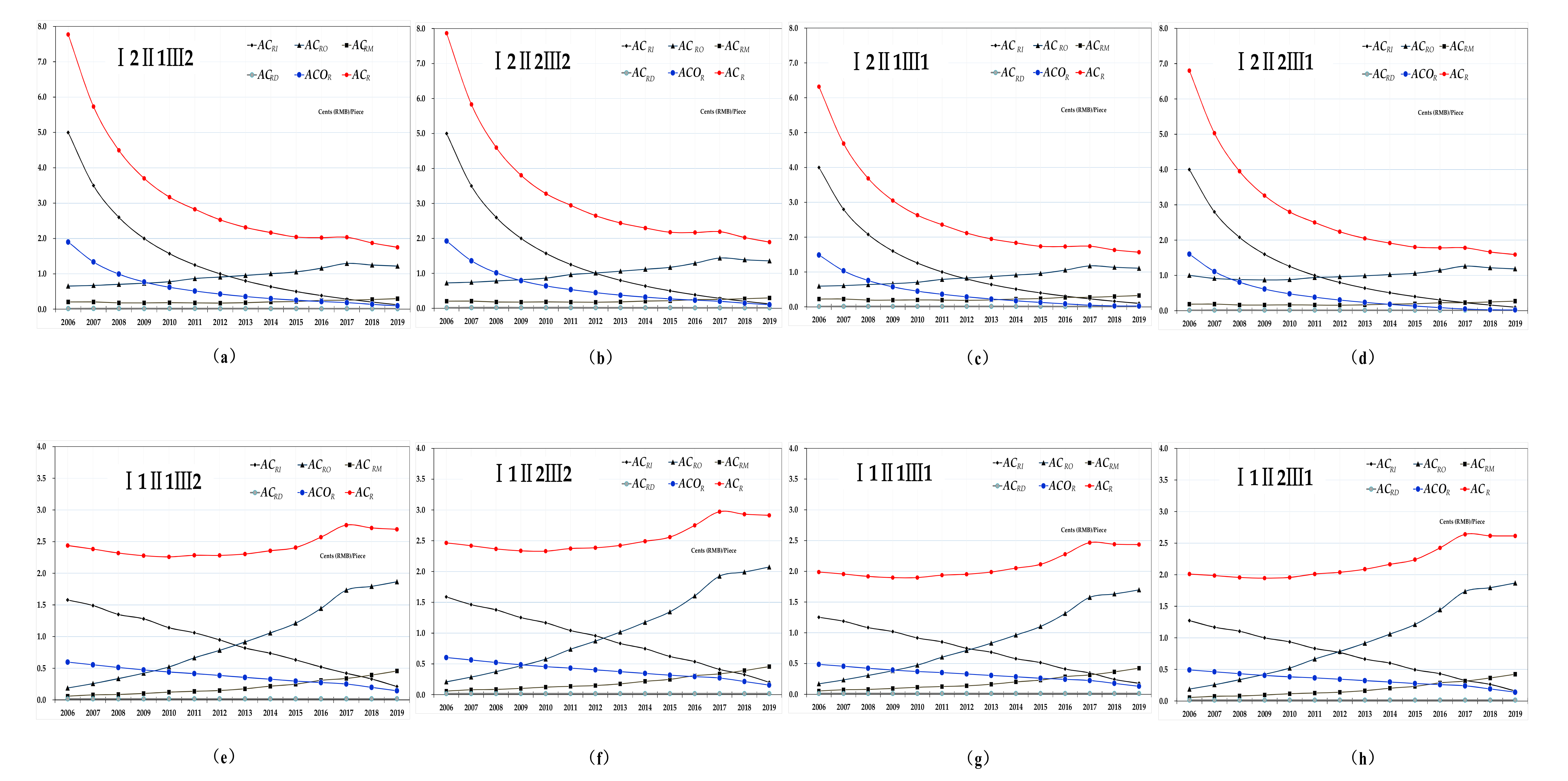
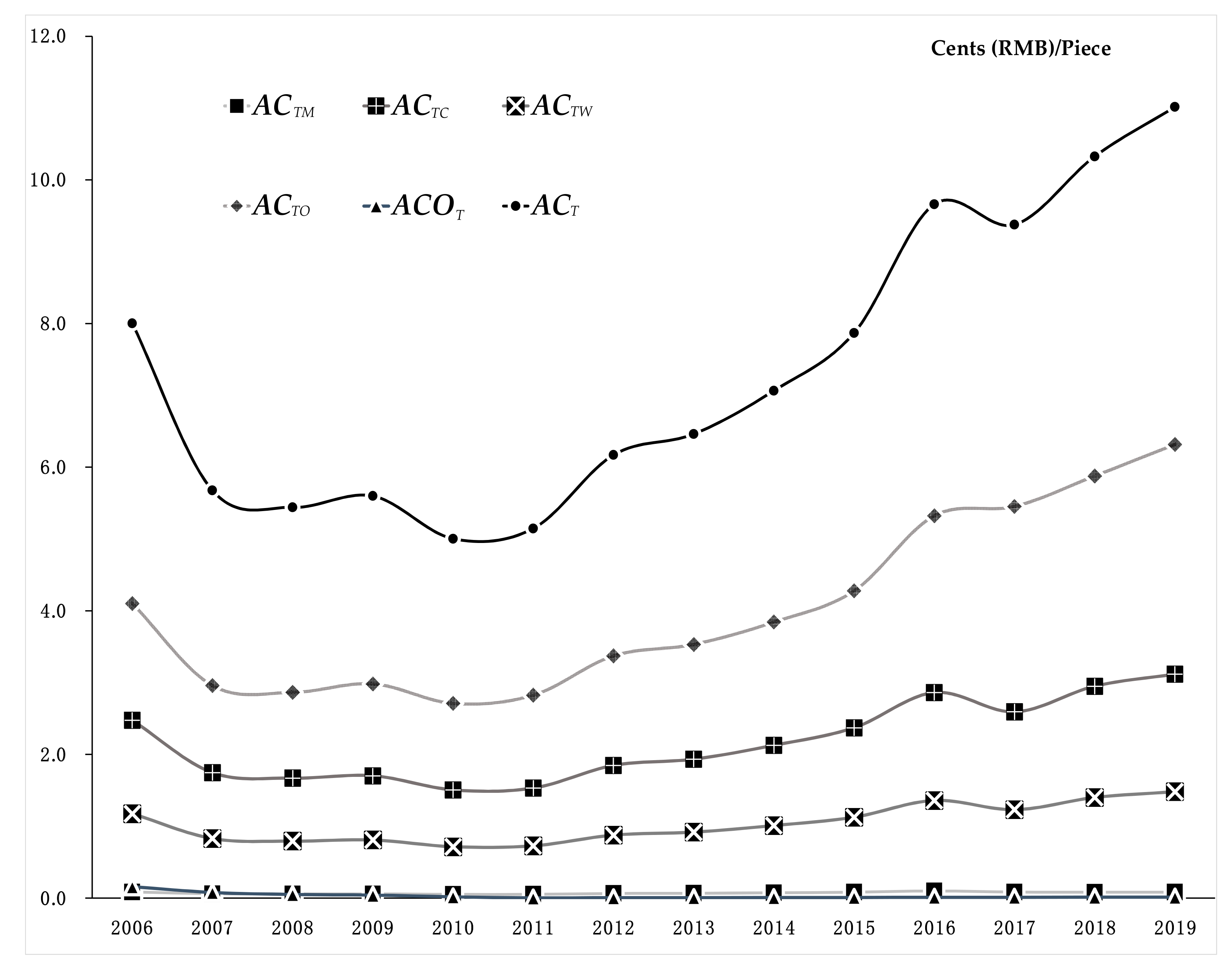
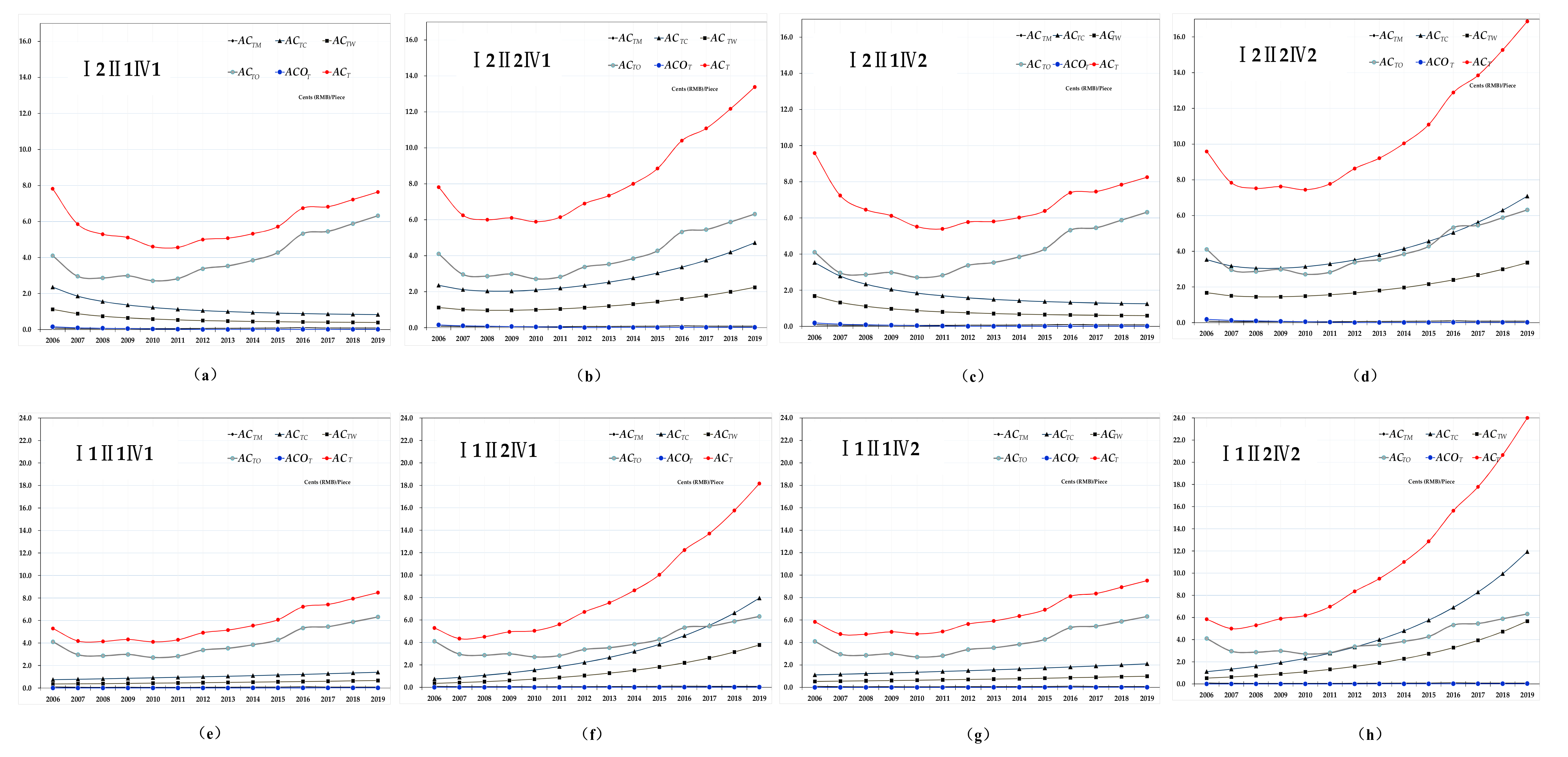
4.1. Comparison of the Total Cost
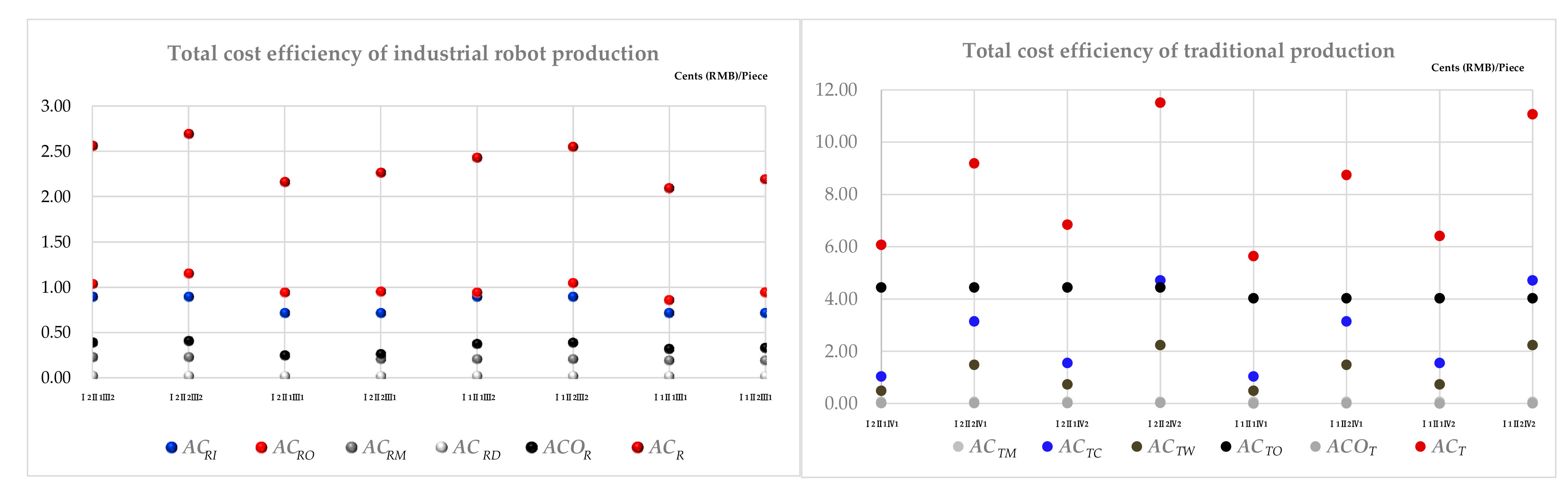
4.2. Comparison of Total Cost Efficiency
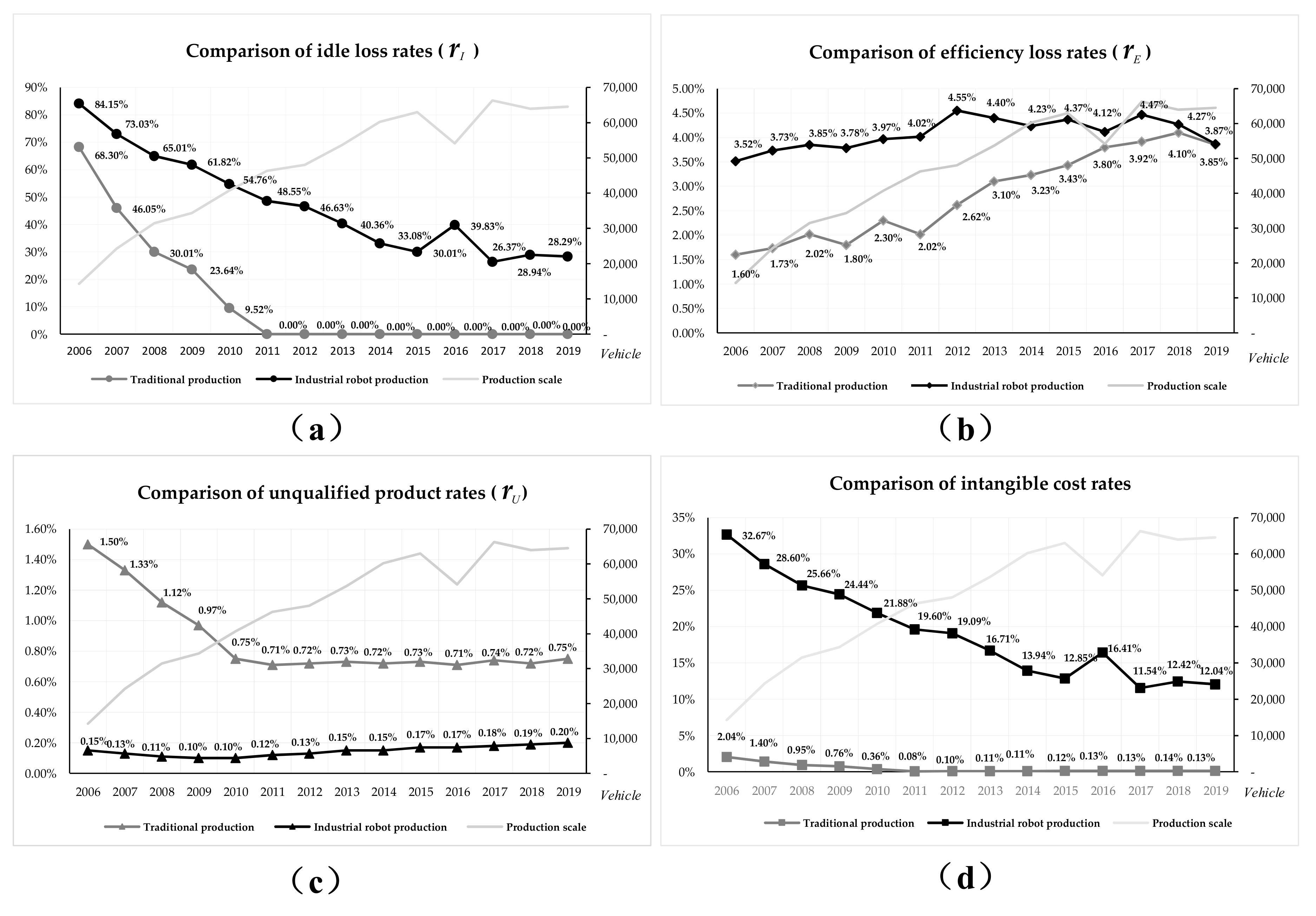
4.3. Comparison of Intangible Cost Factors
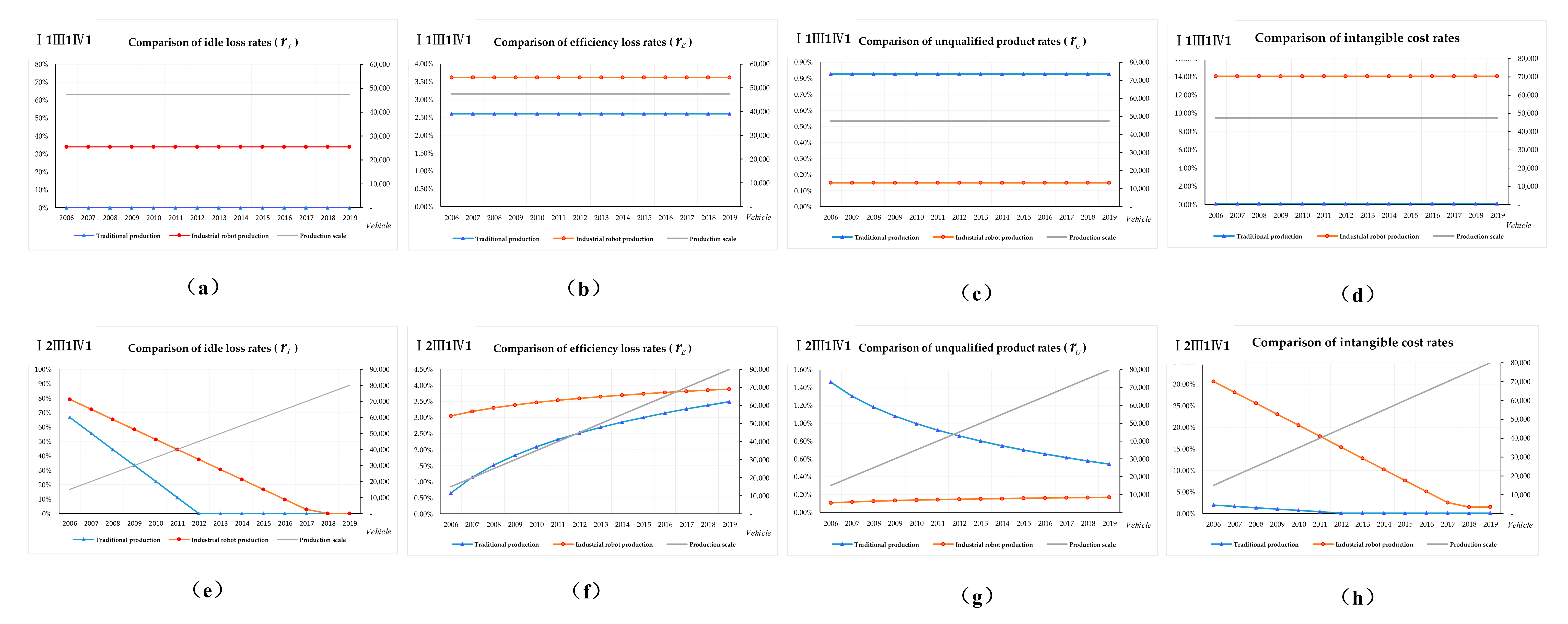
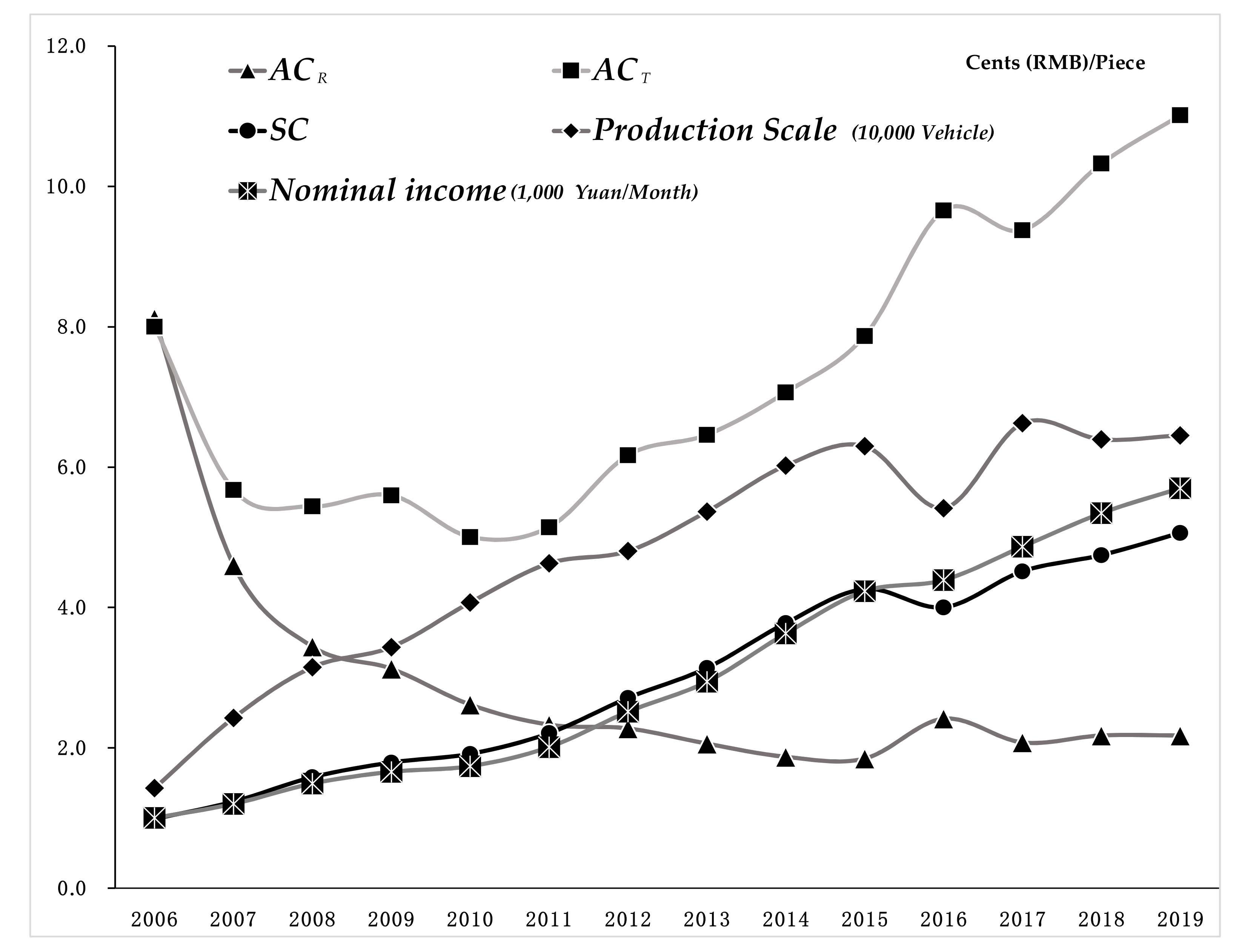
4.4. Comparison of the Dynamic Cost Efficiency
5. Discussion
5.1. Rising Labor Costs Promote Robot Substitution
5.2. Increasing Demand Gives Rise to Robot Substitution
5.3. Robot Substitution Requires a Sustained and Effective Investment of Resources
5.4. The Risks of Robotic Substitution Require Attention
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- International Federation of Robotics (IFR). Robot Density Rises Globally Report. 2018. Available online: http://www.dpaonthenet.net/article/151080/Robot-density-rises-globally.aspx (accessed on 15 December 2020).
- China Robotics Industry Alliance (CRIA). China Industrial Robot Industry Market Report. 2017. Available online: http://cria.mei.net.cn/news.asp?vid=3744 (accessed on 15 December 2020).
- Cheng, H.; Jia, R.; Li, D.; Li, H. The rise of robots in China. J. Econ. Perspect. 2019, 33, 71–88. [Google Scholar] [CrossRef]
- Landscheidt, S.; Kans, M. Method for assessing the total cost of ownership of industrial robots. Procedia CIRP 2016, 57, 746–751. [Google Scholar] [CrossRef]
- Sherif, Y.S.; Kolarik, W.J. Life cycle costing: Concept and practice. Omega 1981, 9, 287–296. [Google Scholar] [CrossRef]
- El-Akruti, K.; Dwight, R.; Zhang, T. The strategic role of engineering asset management. Int. J. Prod. Econ. 2013, 146, 227–239. [Google Scholar] [CrossRef]
- Saccani, N.; Perona, M.; Bacchetti, A. The total cost of ownership of durable consumer goods: A conceptual model and an empirical application. Int. J. Prod. Econ. 2017, 183, 1–13. [Google Scholar] [CrossRef]
- Mandolini, M.; Marilungo, E.; Germani, M. A TCO model for supporting the configuration of industrial plants. Procedia Manuf. 2017, 11, 1940–1949. [Google Scholar] [CrossRef]
- Ellram, L.M. Total cost of ownership: An analysis approach for purchasing. Int. J. Phys. Distrib. Logist. Manag. 1995, 25, 4–23. [Google Scholar] [CrossRef]
- Dietz, T. Knowledge-Based Cost-Benefit Analysis of Robotics for SME-Like Manufacturing; Fraunhofer Verlag: Stuttgart, Germany, 2019. [Google Scholar]
- Dietz, T.; Pott, A.; Hägele, M.; Verl, A. A New, Uncertainty-Aware Cost-Model for Cost-Benefit Assessment of Robot Systems. In Proceedings of the IEEE ISR 2013, Seoul, Korea, 24–26 October 2013; pp. 1–6. [Google Scholar]
- Zwicker, C.; Hammerstingl, V.; Possin, C.; Reinhart, G. Life cycle cost estimation of robot systems in an early production planning phase. Procedia CIRP 2016, 44, 322–327. [Google Scholar] [CrossRef][Green Version]
- Landscheidt, S. Life Cycle Cost Analysis in the Swedish Automation Industry: A Case Study for Developing a Total Cost of Ownership Model for Industrial Robots. Available online: http://www.diva-portal.org. (accessed on 15 December 2020).
- Gołda, G.; Kampa, A.; Paprocka, I. Analysis of human operators and industrial robots performance and reliability. Manag. Prod. Eng. Rev. 2018, 9, 24–33. [Google Scholar]
- Barosz, P.; Gołda, G.; Kampa, A. Efficiency analysis of manufacturing line with industrial robots and human operators. Appl. Sci. 2020, 10, 2862. [Google Scholar] [CrossRef]
- Caputo, A.C.; Pelagagge, P.M.; Salini, P. A model for planning and economic comparison of manual and automated kitting systems. Int. J. Prod. Res. 2020, 9, 1–24. [Google Scholar] [CrossRef]
- Sabelli, H.; Lawandow, A.; Kopra, A.; Zeraoulia, E. Asymmetry, symmetry and beauty. Symmetry 2010, 2, 1591–1624. [Google Scholar] [CrossRef]
- Ellram, L. Total cost of ownership: Elements and implementation. Int. J. Purch. Mater. Manag. 1993, 29, 2–11. [Google Scholar] [CrossRef]
- Fabrycky, W.J.; Blanchard, B.S. Life-Cycle Cost and Economic Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Asiedu, Y.; Gu, P. Product life cycle cost analysis: State of the art review. Int. J. Prod. Res. 1998, 36, 883–908. [Google Scholar] [CrossRef]
- Seif, J.; Rabbani, M. Component based life cycle costing in replacement decisions. J. Qual. Maint. Eng. 2014, 20, 436–452. [Google Scholar] [CrossRef]
- Roda, I.; Macchi, M.; Albanese, S. Building a Total Cost of Ownership model to support manufacturing asset lifecycle man-agement. Prod. Plan. Control 2020, 31, 19–37. [Google Scholar] [CrossRef]
- Waghmode, L.Y.; Sahasrabudhe, A.D. Modelling maintenance and repair costs using stochastic point processes for life cycle costing of repairable systems. Int. J. Comput. Integr. Manuf. 2012, 25, 353–367. [Google Scholar] [CrossRef]
- Roda, I.; Garetti, M. TCO evaluation in physical asset management: Benefits and limitations for industrial adoption. In IFIP International Conference on Advances in Production Management Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 216–223. [Google Scholar]
- Fraser, K.; Hvolby, H.-H.; Tseng, T.-L. Maintenance management models: A study of the published literature to identify em-pirical evidence: A greater practical focus is needed. Int. J. Qual. Reliab. Manag. 2015, 32, 635–664. [Google Scholar]
- Popesko, B. How to calculate the costs of idle capacity in the manufacturing industry. Glob. Bus. Manag. Res. 2009, 1, 19–26. [Google Scholar]
- Kampa, A.; Gołda, G.; Paprocka, I. Discrete event simulation method as a tool for improvement of manufacturing systems. Computers 2017, 6, 10. [Google Scholar] [CrossRef]
- Chen, S.; Keys, L.K. A cost analysis model for heavy equipment. Comput. Ind. Eng. 2009, 56, 1276–1288. [Google Scholar] [CrossRef]
- Ahmed, N.U. A design and implementation model for life cycle cost management system. Inf. Manag. 1995, 28, 261–269. [Google Scholar] [CrossRef]
- Prabhakar, V.J.; Sandborn, P. A part total cost of ownership model for long life cycle electronic systems. Int. J. Comput. Integr. Manuf. 2012, 25, 384–397. [Google Scholar] [CrossRef]
- Walterbusch, M.; Martens, B.; Teuteberg, F. Evaluating cloud computing services from a total cost of ownership perspective. Manag. Res. Rev. 2013, 36, 613–638. [Google Scholar] [CrossRef]
- International Organization for Standardization. Robots and Robotic Devices; ISO: Geneva, Switzerland, 2012; ISO 8373:2012. [Google Scholar]
- Kuss, A.; Hollmann, R.; Dietz, T.; Hägele, M. Manufacturing Knowledge for Industrial Robot Systems: Review and Synthesis of Model Architecture. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016; pp. 348–354. [Google Scholar]
- Dietz, T.; Pott, A.; Verl, A. Practice for planning and realization of advanced industrial robot systems. In Proceedings of the IEEE ISR 2013, Seoul, Korea, 24–26 October 2013; pp. 1–4. [Google Scholar]
- Dahlén, P.; Bolmsjö, G.S. Life-cycle cost analysis of the labor factor. Int. J. Prod. Econ. 1996, 46, 459–467. [Google Scholar] [CrossRef]
- Dahlén, P.G.; Wernersson, S. Human factors in the economic control of industry. Int. J. Ind. Ergon. 1995, 15, 215–221. [Google Scholar] [CrossRef]
- Adegbola, Y.U.; Fisher, P.R.; Hodges, A.W. Benchmarking the efficiency of transplanting plant cuttings at large young plant greenhouse operations. HortScience 2018, 53, 1133–1138. [Google Scholar] [CrossRef]
- Adegbola, Y.U.; Fisher, P.R.; Hodges, A.W. Economic evaluation of transplant robots for plant cuttings. Sci. Hortic. 2019, 246, 237–243. [Google Scholar] [CrossRef]
- Hansen, D.R.; Mowen, M.M. Cost Management: Accounting and Control; LEAP Publishing Services: Stow, OH, USA, 2006. [Google Scholar]
- Foster, G.; Gupta, M. Manufacturing overhead cost driver analysis. J. Account. Econ. 1990, 12, 309–337. [Google Scholar] [CrossRef]
- Taschner, A.; Charifzadeh, M. Management and Cost Accounting; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Chrysafis, K.A.; Papadopoulos, B.K. Decision making for project appraisal in uncertain environments: A fuzzy-possibilistic approach of the expanded NPV method. Symmetry 2021, 13, 27. [Google Scholar] [CrossRef]
- Durairaj, S.K.; Tan, R.B.H. Evaluation of life cycle cost analysis methodologies. Corp. Environ. Strategy 2002, 9, 30–39. [Google Scholar] [CrossRef]
- Locascio, A. Manufacturing cost modeling for product design. In Information-Based Manufacturing; Springer: Berlin/Heidelberg, Germany, 2001; pp. 315–325. [Google Scholar]
- Berliner, C.; Brimson, J.A.X. Cost Management for Today’s Advanced Manufacturing: The CAM-I Conceptual Design; Harvard Business School Press: Boston, MA, USA, 1988. [Google Scholar]
- International Organization for Standardization (ISO). Asset Management: Overview, Principles and Terminology; International Organization for Standardization (ISO): Geneva, Switzerland, 2014; ISO 55000:2014. [Google Scholar]
- Hansen, R.C. Overall Equipment Effectiveness: A Powerful Production/Maintenance Tool for Increased Profits; Industrial Press Inc.: New York, NY, USA, 2001. [Google Scholar]
- Gramlich, E.M.; Gramlich, E.M. A Guide to Benefit-Cost Analysis; Prentice-Hall Englewood: Cliffs, NJ, USA, 1990. [Google Scholar]
- Ganorkar, A.B.; Lakhe, R.R.; Agrawal, K.N. Cost and productivity analysis of the manufacturing industry using TDABC & MOST. S. Afr. J. Ind. Eng. 2019, 30, 196–208. [Google Scholar]
- El-Akruti, K.; Dwight, R.; Zhang, T.; Al-Marsumi, M. The role of life cycle cost in engineering asset management. In Engineering Asset Management-Systems, Professional Practices and Certification; Springer: Berlin/Heidelberg, Germany, 2015; pp. 173–188. [Google Scholar]
- Glaser, A. Industrial Robotics; Industrial Press: New York, NY, USA, 2008. [Google Scholar]
- Pires, J.N. Productive robotics in Europe: Evolution, trends and challenges. Ind. Robot Int. J. 2011, 38, 216–228. [Google Scholar]
- Schmitt, J.; Shierholz, H.; Mishel, L. Don’t Blame the Robots: Assessing the Job Polarization Explanation of Growing Wage Inequality; Economic Policy Institute: Washington, DC, USA, 2013; Available online: http://www.epi.org/publication/technology-inequality-dont-blame-the-robots (accessed on 15 December 2020).
- Jung, J.H.; Lim, D.-G. Industrial robots, employment growth, and labor cost: A simultaneous equation analysis. Technol. Forecast. Soc. Chang. 2020, 159, 120202. [Google Scholar] [CrossRef]
- Hägele, M.; Nilsson, K.; Pires, J.N.; Bischoff, R. Industrial robotics. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1385–1422. [Google Scholar]
- Dhillon, B.; Aleem, M. A report on robot reliability and safety in Canada: A survey of robot users. J. Qual. Maint. Eng. 2000, 6, 61–74. [Google Scholar] [CrossRef]
- Jocanović, M.T.; Agarski, B.; Karanović, V.V.; Orosnjak, M.; Micunovic, M.I.; Ostojić, G.; Stankovski, S. LCA/LCC model for evaluation of pump units in water distribution systems. Symmetry 2019, 11, 1181. [Google Scholar] [CrossRef]
- Litzenberger, G. World Robotics Industrial Robots 2015; IFR Statictical Department: Frankfurt, Germany, 2015; pp. 45–47. [Google Scholar]
- Ciszak, O.; Juszkiewicz, J.; Suszynski, M. Programming of industrial robots using the recognition of geometric signs in flexible welding process. Symmetry 2020, 12, 1429. [Google Scholar] [CrossRef]
| Source | Source | ||||
|---|---|---|---|---|---|
| Investment Cost | Equipment price | [5,9,12,13,14] | Management Cost | Recruitment expenditure | [36,37,40,41,42] |
| () | Transaction cost | [5,13,14] | () | Training expenditure | [36,37,38,39,40,41,42] |
| Loan interest | [5,9,14] | Labor protection expense | [36,37,38,39,40,41,42] | ||
| Taxes minus subsidies | [5,14] | Office expense | [40,41,42] | ||
| After-sales fee | [9,12] | ||||
| Operation Cost | Operator’s remuneration | [5,9,12,13,14] | Compensation Cost | Basic salary | [36,37,38,39] |
| () | Training expenditure | [5,9,12,14] | () | Performance bonus | [36,37,38,39] |
| Spend on pace | [9,12] | Overtime pay | [36,37,38,39] | ||
| Accessories charge | [5,9,14] | Work subsidy | [36,37,38,39] | ||
| Energy consumption | [5,9,12,13,14] | ||||
| Maintenance Cost | Service fee | [5,9,12,14] | Welfare Cost | Social security charges | [36,37,38,39] |
| () | Replacing parts price | [5,9,14] | () | Housing fund | [36,37,38,39] |
| Consumables charge | [9,12] | Trade union funds | [36,37,38,39] | ||
| Annual inspection fee | [5,9,14] | Daily welfare expenses | [36,37,38,39] | ||
| Disposal Cost | Demolition expenses minus residual value | [5,9,14] | Operation Cost | Equipment depreciation | [40,41,42] |
| () | () | Equipment maintenance | [40,41,42] | ||
| Material consumption | [40,41,42] | ||||
| Energy consumption | [40,41,42] | ||||
| Spend on pace | [40,41,42] | ||||
| Tool amortization | [40,41,42] | ||||
| Intangible Cost | Production idle loss | [15,16,17] | Intangible Cost | Production idle loss | [15,16,17] |
| () | Product efficiency loss | [15,16,17] | () | Product efficiency loss | [15,16,17] |
| ⎕ | Product defect loss | [15,16,17] | ⎕ | Product defect loss | [15,16,17] |
| Key Factors | Condition 1 | Condition 2 |
|---|---|---|
| Factor I: the fluctuation of production scale | Uniform and stable an annual output of 47,500 Vehicle from 2006 to 2019. | With a sustained growth an annual increase of 5000 Vehicle, from 15,000 in 2006 to 80,000 in 2019. |
| Factor II: the rise of labor costs | With a moderate growth: an annual growth of 5%. | With a rapid growth: an annual growth of 20%. |
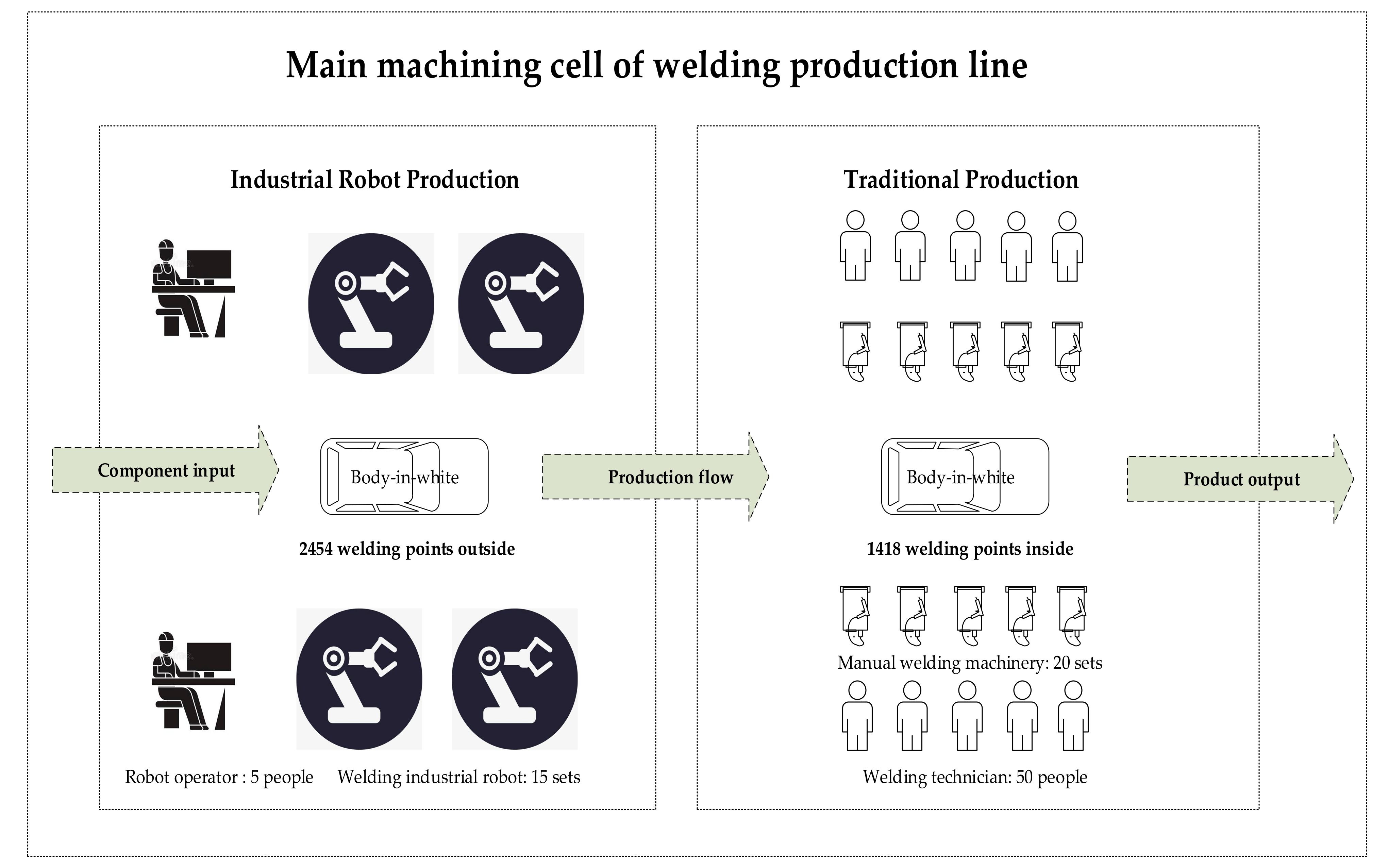
| Factor III: the number of robots input in industrial robot production | Smaller scale: 12 sets of welding industrial robots and 4 operators. | Larger scale 15 sets of welding industrial robots and 5 operators. |
| Factor IV: the front-line workers input in traditional production | Smaller scale: 50 welding technicians and 20 manual welding machineries. | Larger scale 75 welding technicians and 30 manual welding machineries. |
| Sort | Industrial Robot Production | Traditional Production | Unit | ||
|---|---|---|---|---|---|
| Subject | Value | Subject | Value | ||
| Total Output | Auto | 665,248.00 | Auto | 665,248.00 | Vehicle |
| Solders /vehicle | 2454 | Solders /vehicle | 1418 | Piece | |
| 1,632,518,592.00 | 943,321,664.00 | Piece | |||
| Total Cost | 14,595,221.08 | 700,062.84 | CNY | ||
| 16,242,726.13 | 21,392,950.98 | CNY | |||
| 3,180,830.59 | 10,161,651.25 | CNY | |||
| 272,648.91 | 40,418,716.83 | CNY | |||
| 34,291,426.72 | 72,673,381.90 | CNY | |||
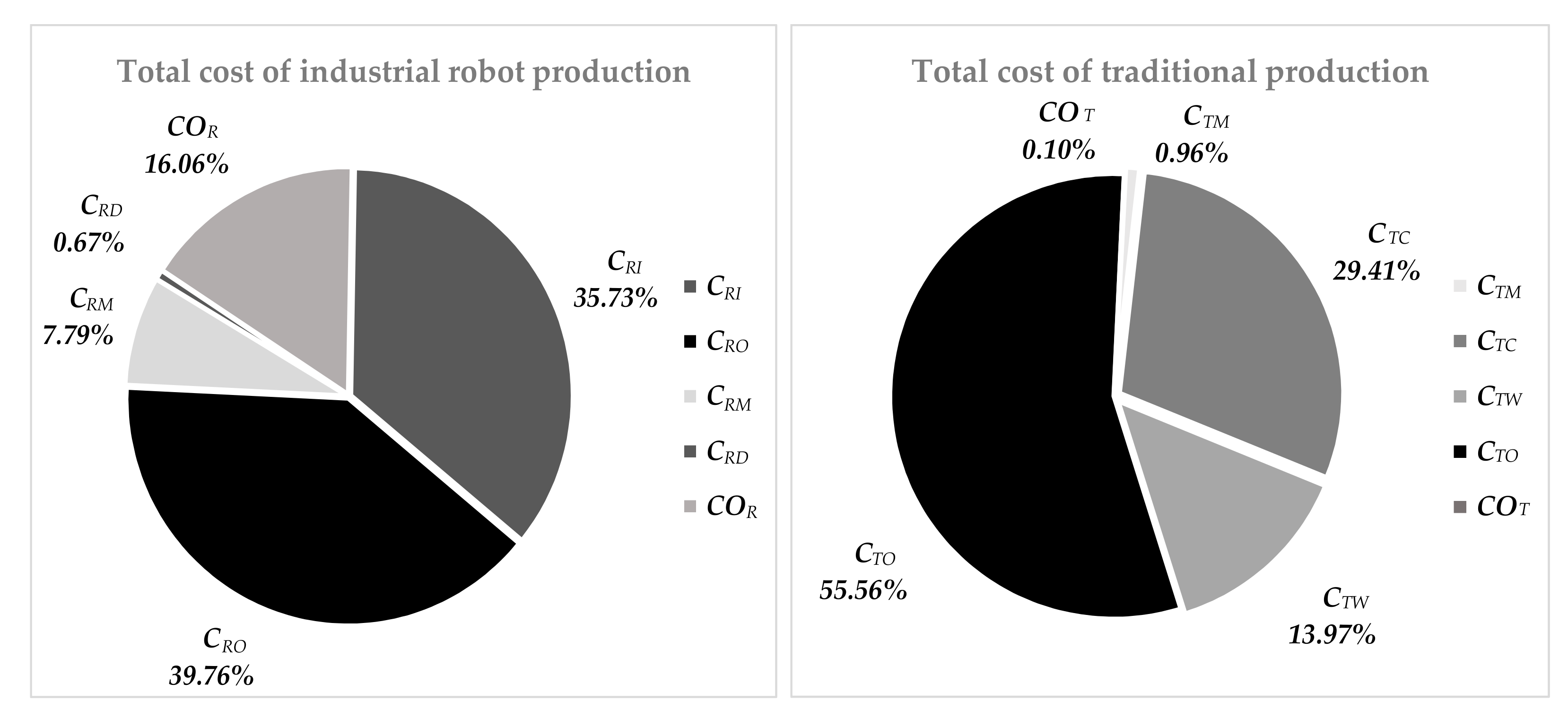
| 0.472 | 0.000 | Rate | |||
| 0.041 | 0.028 | Rate | |||
| 0.002 | 0.008 | Rate | |||
| 0.372 | 0.029 | Rate | |||
| 6,561,502.17 | 75,249.26 | CNY | |||
| 40,852,928.89 | 72,748,631.16 | CNY | |||
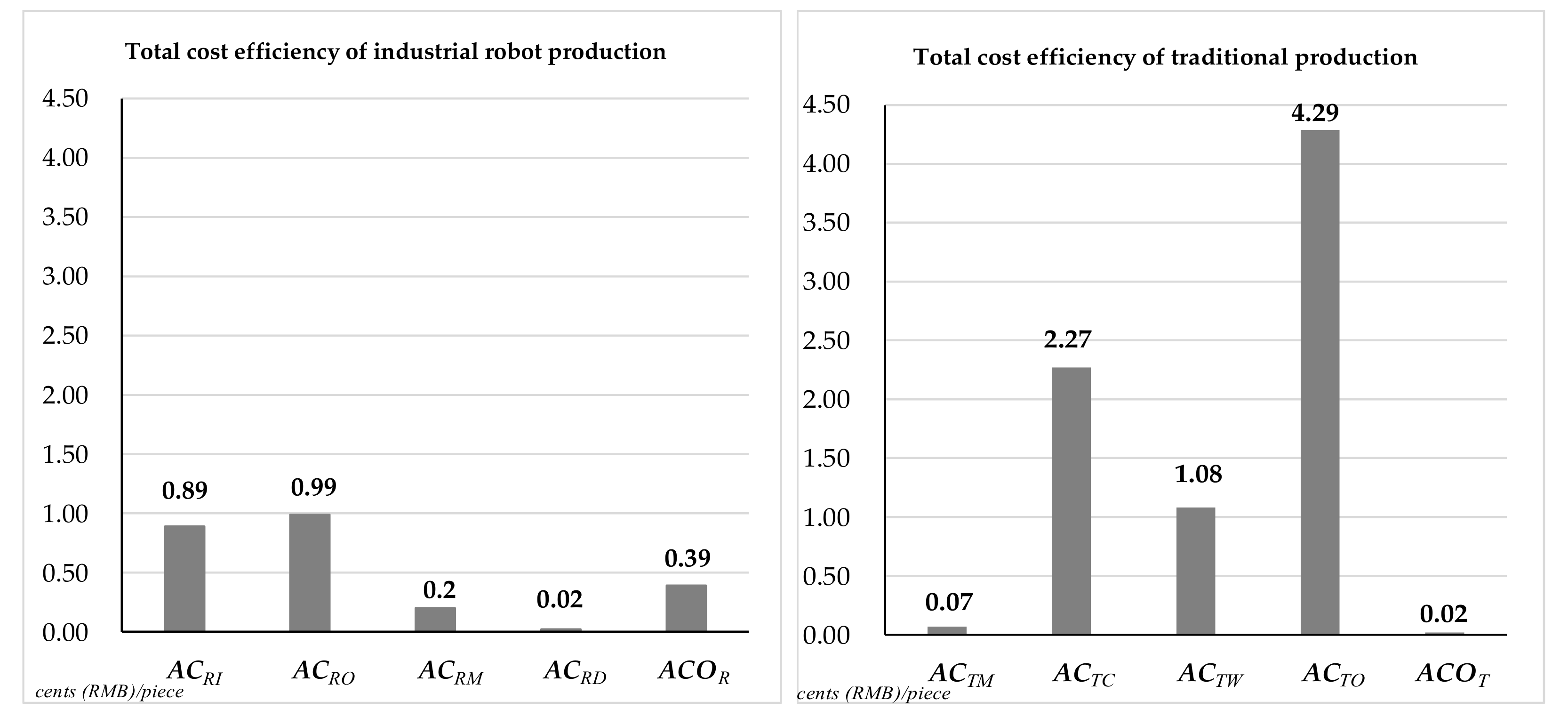
| Cost efficiency | 0.89 | 0.07 | Cent/Piece | ||
| 0.99 | 2.27 | Cent/Piece | |||
| 0.20 | 1.08 | Cent/Piece | |||
| 0.02 | 4.29 | Cent/Piece | |||
| 2.10 | 7.70 | Cent/Piece | |||
| 0.39 | 0.02 | Cent/Piece | |||
| 2.49 | 7.72 | Cent/Piece | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Wu, C.; Liu, D. Comparative Analysis of the Life-Cycle Cost of Robot Substitution: A Case of Automobile Welding Production in China. Symmetry 2021, 13, 226. https://doi.org/10.3390/sym13020226
Zhao X, Wu C, Liu D. Comparative Analysis of the Life-Cycle Cost of Robot Substitution: A Case of Automobile Welding Production in China. Symmetry. 2021; 13(2):226. https://doi.org/10.3390/sym13020226
Chicago/Turabian StyleZhao, Xuyang, Cisheng Wu, and Duanyong Liu. 2021. "Comparative Analysis of the Life-Cycle Cost of Robot Substitution: A Case of Automobile Welding Production in China" Symmetry 13, no. 2: 226. https://doi.org/10.3390/sym13020226
APA StyleZhao, X., Wu, C., & Liu, D. (2021). Comparative Analysis of the Life-Cycle Cost of Robot Substitution: A Case of Automobile Welding Production in China. Symmetry, 13(2), 226. https://doi.org/10.3390/sym13020226






