Solid Particle Erosion Area of Rotor Blades: Application on Small-Size Unmanned Helicopters
Abstract
1. Introduction
2. Numerical Analysis
2.1. Mathematical Model
2.2. Erosion Model
3. Results and Discussion
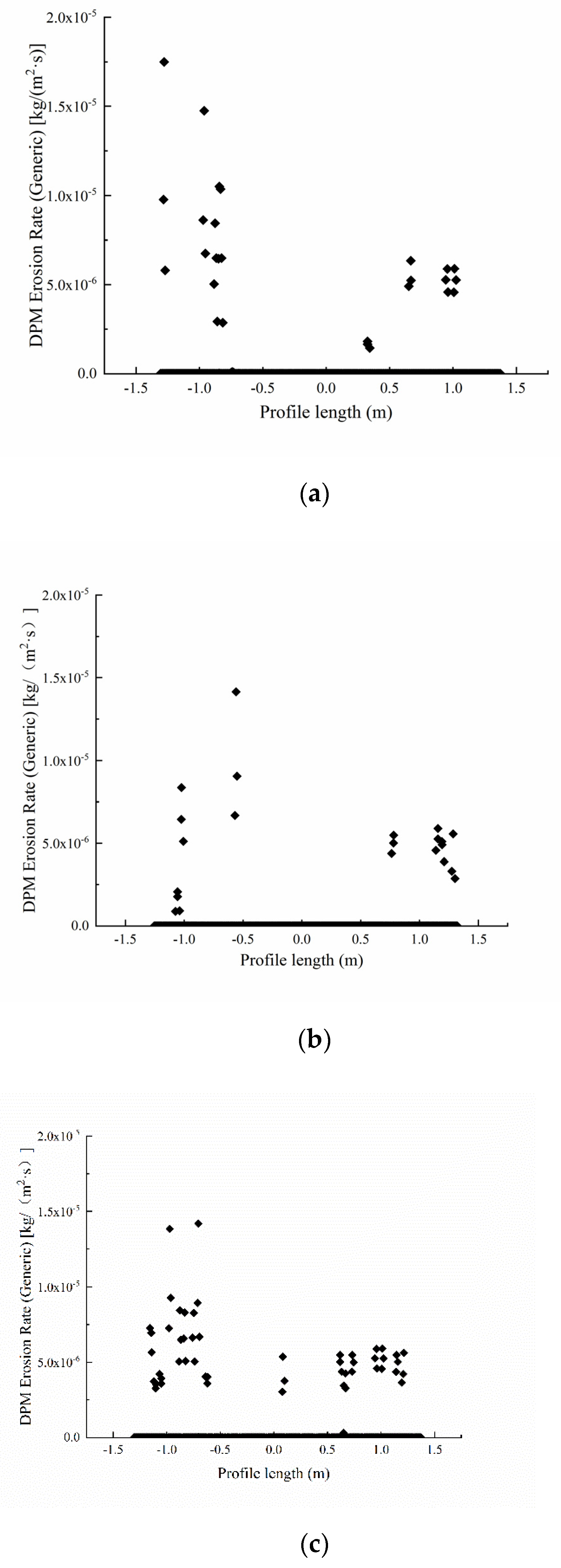
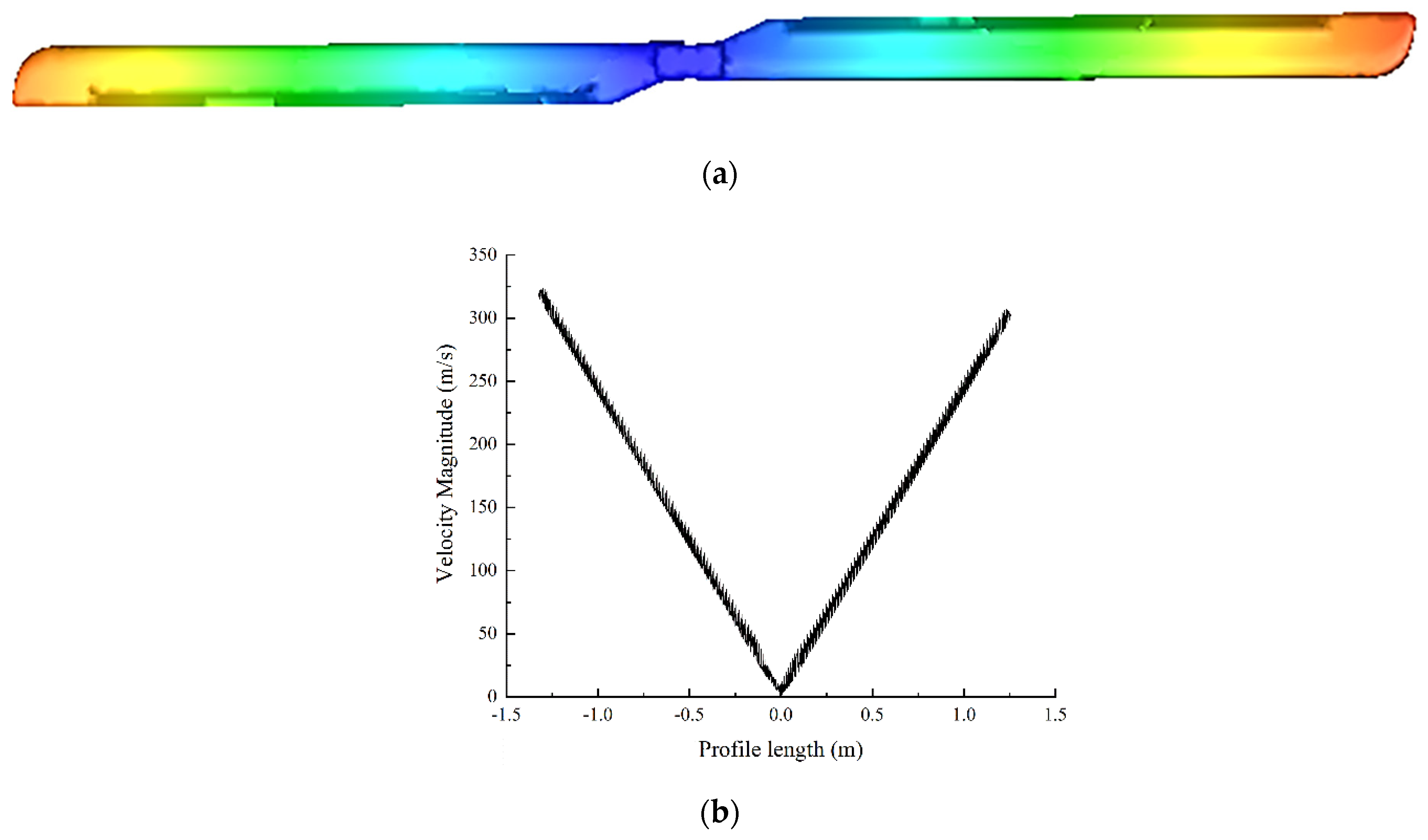
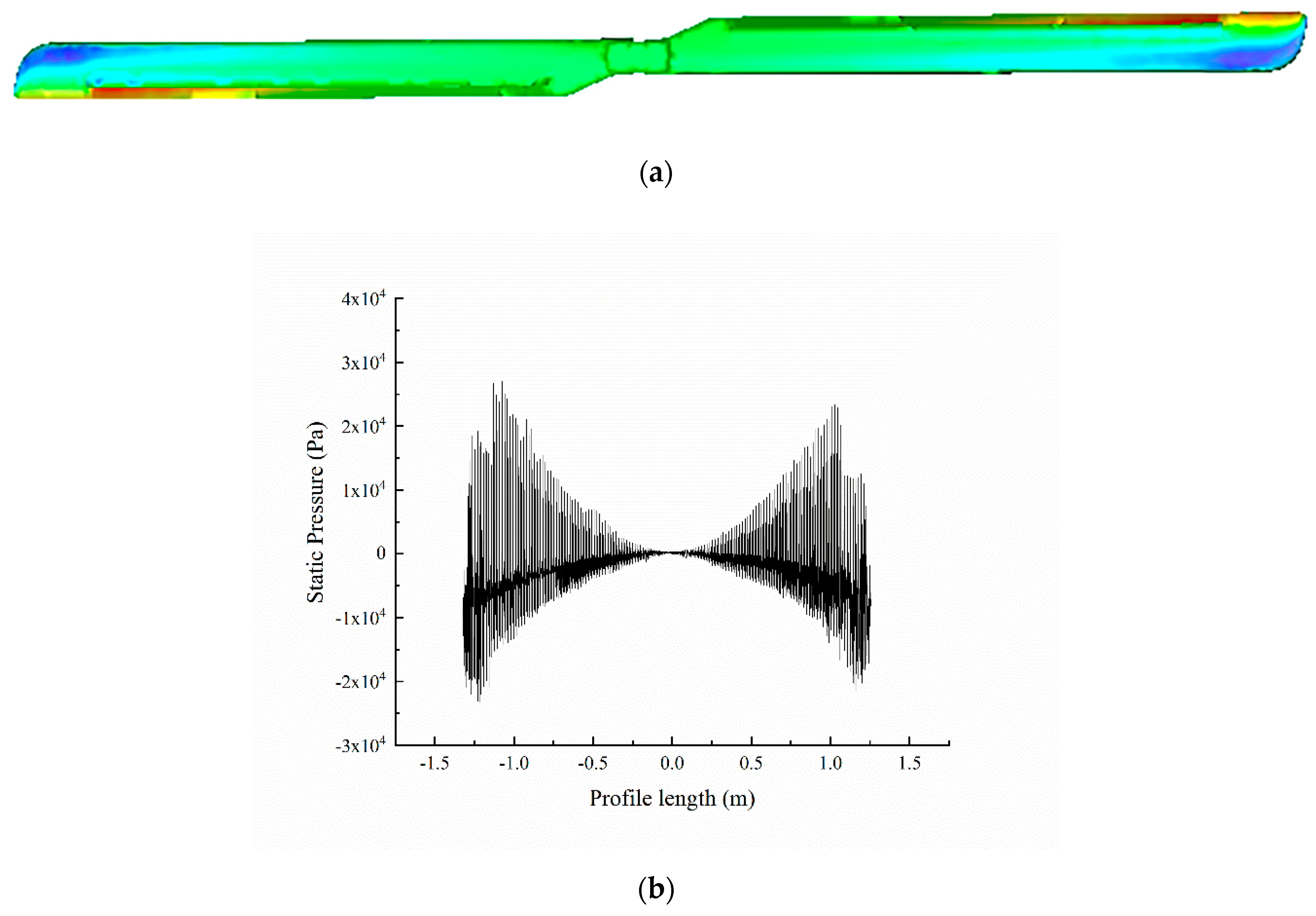
3.1. Blade Erosion at Different Speeds
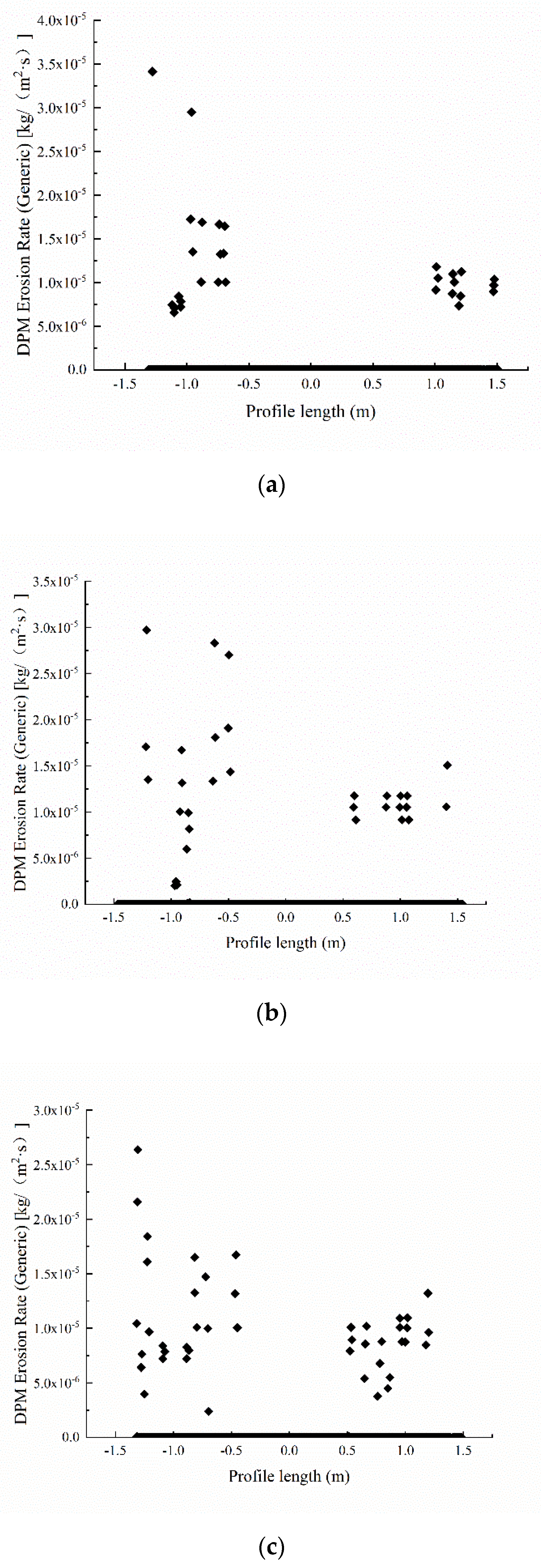
3.2. Blade Erosion at Different Particle Mass Flow Rates
3.3. Eroded Area
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hutchings, I.M.; Winter, R.E. Particle erosion of ductile metals: A mechanism of material removal. Wear 1974, 27, 121–128. [Google Scholar] [CrossRef]
- Mazur, Z.; Amezcua, R.C.; Beltrán, G.U.; Gutiérrez, A.G. Numerical 3D simulation of the erosion due to solid particle impact in the main stop valve of a steam turbine. App. Therm. Eng. 2004, 24, 1877–1891. [Google Scholar] [CrossRef]
- Xinba, Y.; Kazumichi, S.; Hideto, M.; Kitsudo, T.; Momono, T. Erosive wear characteristics of spheroidal carbides cast iron. Wear 2008, 264, 947–957. [Google Scholar]
- Bai, X.; Yao, Y.; Han, Z.; Zhang, J.; Zhang, S. Study of Solid Particle Erosion on Helicopter Rotor Blades Surfaces. App. Sci. 2020, 10, 977. [Google Scholar] [CrossRef]
- Chen, C.W.; Lu, Y.F. Computational Fluid Dynamics Study of Water Entry Impact Forces of an Airborne-Launched, Axisymmetric, Disk-Type Autonomous Underwater Hovering Vehicle. Symmetry 2019, 11, 1100. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, W. Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion. Symmetry 2019, 11, 397. [Google Scholar] [CrossRef]
- Haider, G.; Arabnejad, H.; Shirazi, S.A.; Mclaury, B.S. A mechanistic model for stochastic rebound of solid particles with application to erosion predictions. Wear 2017, 376–377, 615–624. [Google Scholar] [CrossRef]
- Wang, Y.F.; Yang, Z.G. A coupled finite element and meshfree analysis of erosive wear. Tribol. Int. 2009, 42, 373–377. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, F.; Cao, L.; Hu, P.; Li, Y. Research on characteristics of solid particle erosion in governing stage of a 600 MW supercritical steam turbine. App. Therm. Eng. 2017, 118, 471–479. [Google Scholar] [CrossRef]
- Qi, H.; Fan, J.; Wang, J.; Li, H. Impact erosion by high velocity micro-particles on a quartz crystal. Tribol. Int. 2015, 82, 200–210. [Google Scholar] [CrossRef]
- Hadavi, V.; Arani, N.H.; Papini, M. Numerical and experimental investigations of particle embedment during the incubation period in the solid particle erosion of ductile materials. Tribol. Int. 2019, 129, 38–45. [Google Scholar] [CrossRef]
- Solnordal, C.B.; Wong, C.Y. Predicting Surface Profifile Evolution Caused by Solid Particle Erosion. In Proceedings of the Ninth International Conference On CFD in the Minerals and Process Industries, CSIRO, Melbourne, Australia, 10–12 December 2012. [Google Scholar]
- Smith, N.A.S.; Fry, A.T.; Crocker, L.E.; Cernuschi, F.; Lorenzoni, L. Design and optimisation of the nozzle of an innovative high temperature solid particulate erosion testing system using finite element modelling. App. Math. Comp. 2017, 301, 60–69. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Bitter, J.G.A. A study of erosion phenomena, part I. Wear 1962, 6, 5–21. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. An Experiment Study of Certain Aerodynamic Effects on Erosion; Department of Aerospace Engineering Technical Report 72-28; University of Cincinnati: Cincinnati, OH, USA, July 1972; pp. 128–135. [Google Scholar]
- Shin, B.G. Prediction of Sand Particle Trajectories and Sand Erosion Damage on Helicopter Rotor Blades. Ph.D. Thesis, Pennsylvania State University, State College, PA, USA, 2010. [Google Scholar]
- Azimian, M.; Bart, H.J. Computational analysis of erosion in a radial inflow steam turbine. Eng. Fail. Anal. 2016, 64, 26–43. [Google Scholar] [CrossRef]
- Slot, H.M.; Gelinck, E.R.M.; Rentrop, C.; Heide, E. Leading edge erosion of coated wind turbine blades: Review of coating life models. Renew. Energy 2015, 80, 837–848. [Google Scholar] [CrossRef]
- Özen, I.; Gedikli, H. Solid Particle Erosion on Shield Surface of a Helicopter. Aerospace Eng. 2019, 32, 1–14. [Google Scholar]
- Clevenger, B.; Tabakoff, W. Erosion in Radial Inflow Turbines—Volume IV. Erosion Rates on Internal Surfaces; University of Cincinnati: Cincinnati, OH, USA, 1975. [Google Scholar]
- Kyle, R.; Wang, F.; Forbes, B. The effect of a leading edge erosion shield on the aerodynamic performance of a wind turbine blade. Wind Energy 2020, 23, 953–966. [Google Scholar] [CrossRef]
- Roul, R.; Kumar, A. Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation. Symmetry 2020, 12, 1467. [Google Scholar] [CrossRef]
- Amezcua, A.C.; Muñoz, A.G.; Romero, C.A.; Czerwiec, Z.M.; Amezcua, R.C. Numerical investigation of the solid particle erosion rate in a steam turbine nozzle. App. Therm. Eng. 2007, 27, 2394–2403. [Google Scholar] [CrossRef]
- Fluent. ANSYS Fluent Theory Guide; ANSYS: Canonsburg, PA, USA, 2010. [Google Scholar]
- Kim, J.H.; Joo, H.G.; Lee, K.Y. Simulation of solid particle erosion in WC-Ni coated wall using CFD. Mater. Process. Technol. 2015, 224, 240–245. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Heat and Mass Transfer; Begell House: New York, NY, USA, 2003. [Google Scholar]
- Oka, Y.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 1: Effects of impact parameters on a predictive equation. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Taslim, M.E.; Khanicheh, A.; Spring, S. A numerical study of sand separation applicable to engine inlet particle separator systems. J. Am. Helicopter Soc. 2009, 54, 42001. [Google Scholar] [CrossRef]
- Caruso, H. MIL-STD-810F, Test Method Standard for Environmental Engineering Considerations and Laboratory Tests. J. IEST 2001, 44, 30–34. [Google Scholar] [CrossRef]
- Arashpour, M.; Ngob, T.; Lic, H. Scene understanding in construction and buildings using image processing methods: A comprehensive review and a case study. J. Buil. Eng. 2021, 33, 1–10. [Google Scholar] [CrossRef]

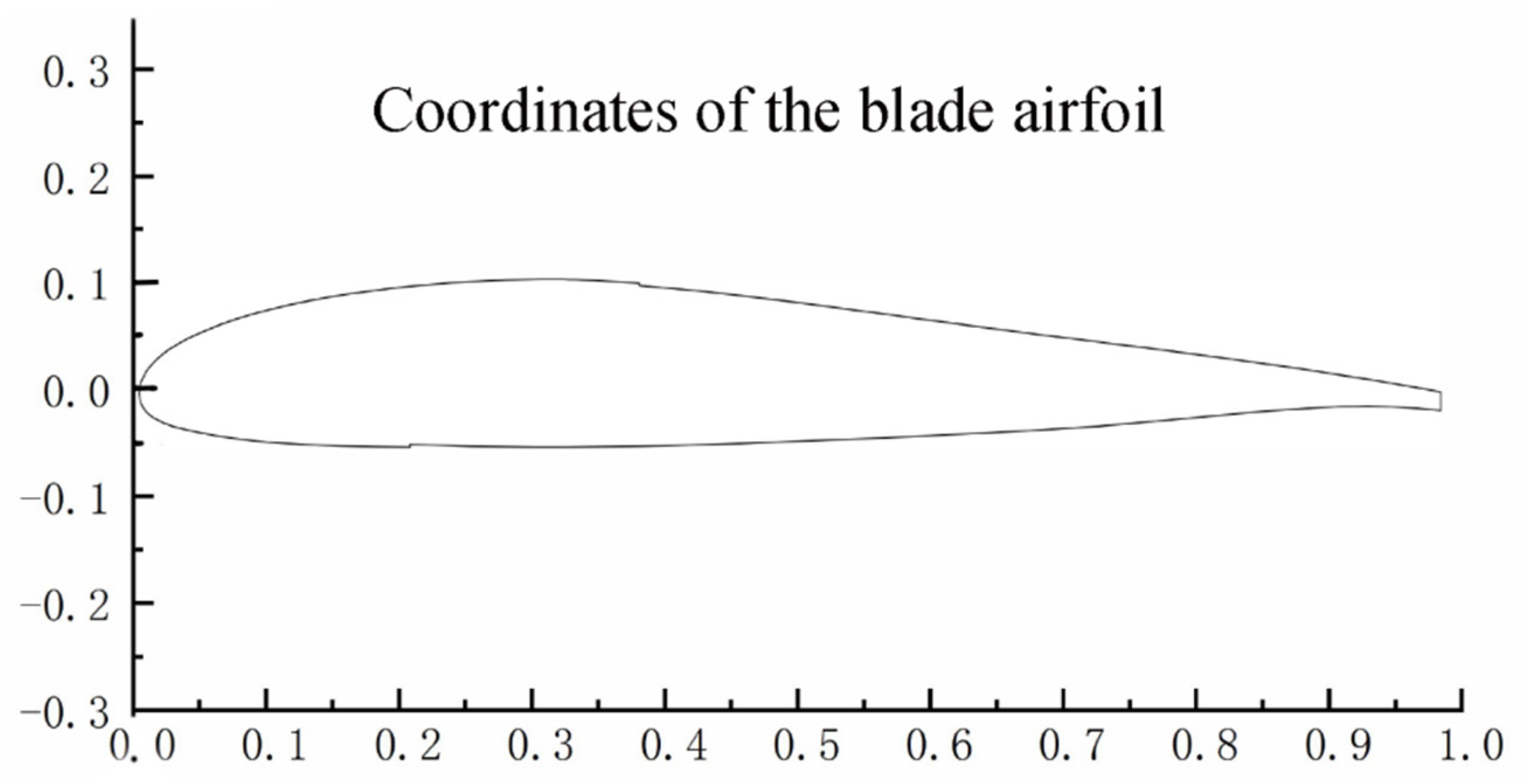

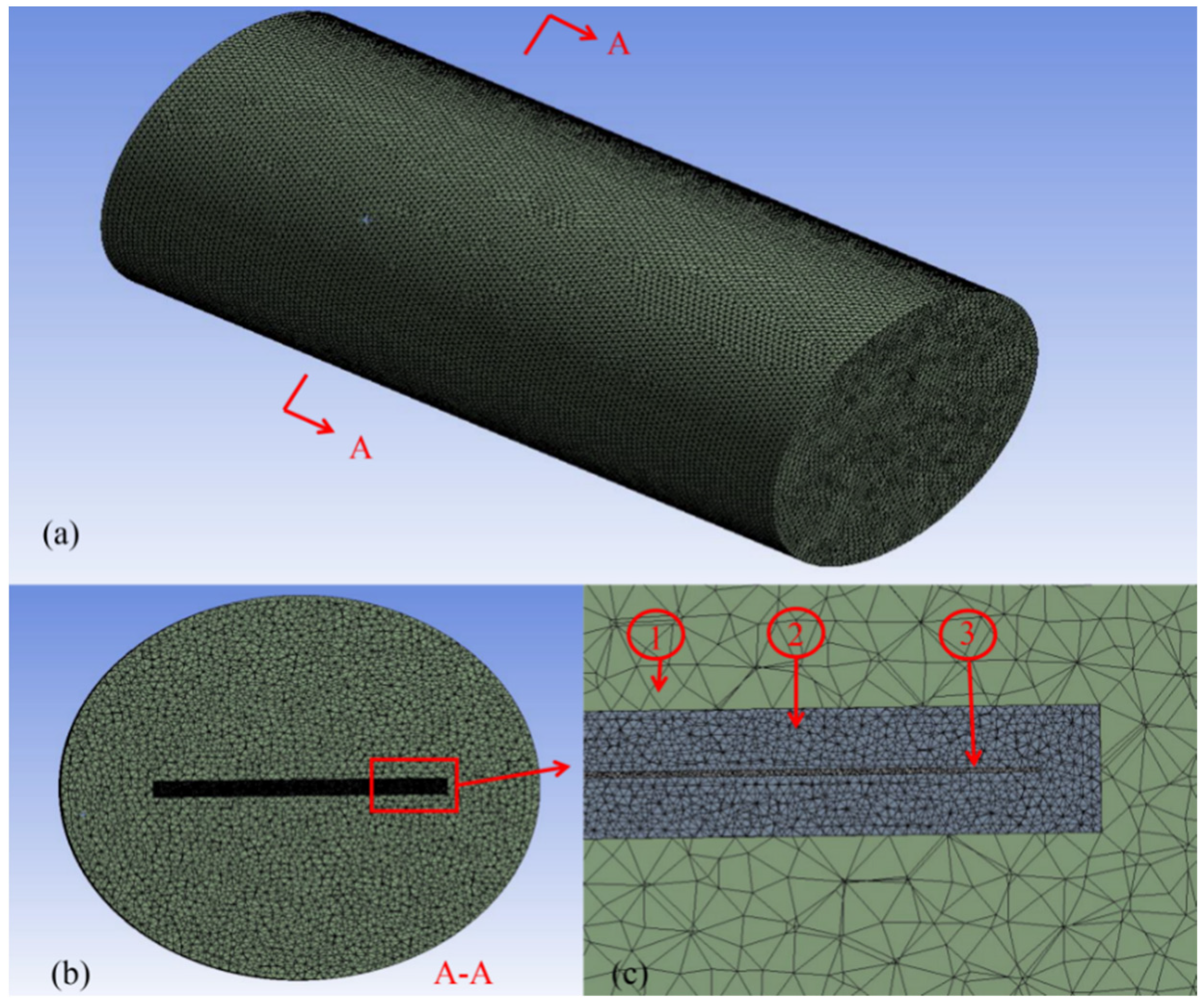
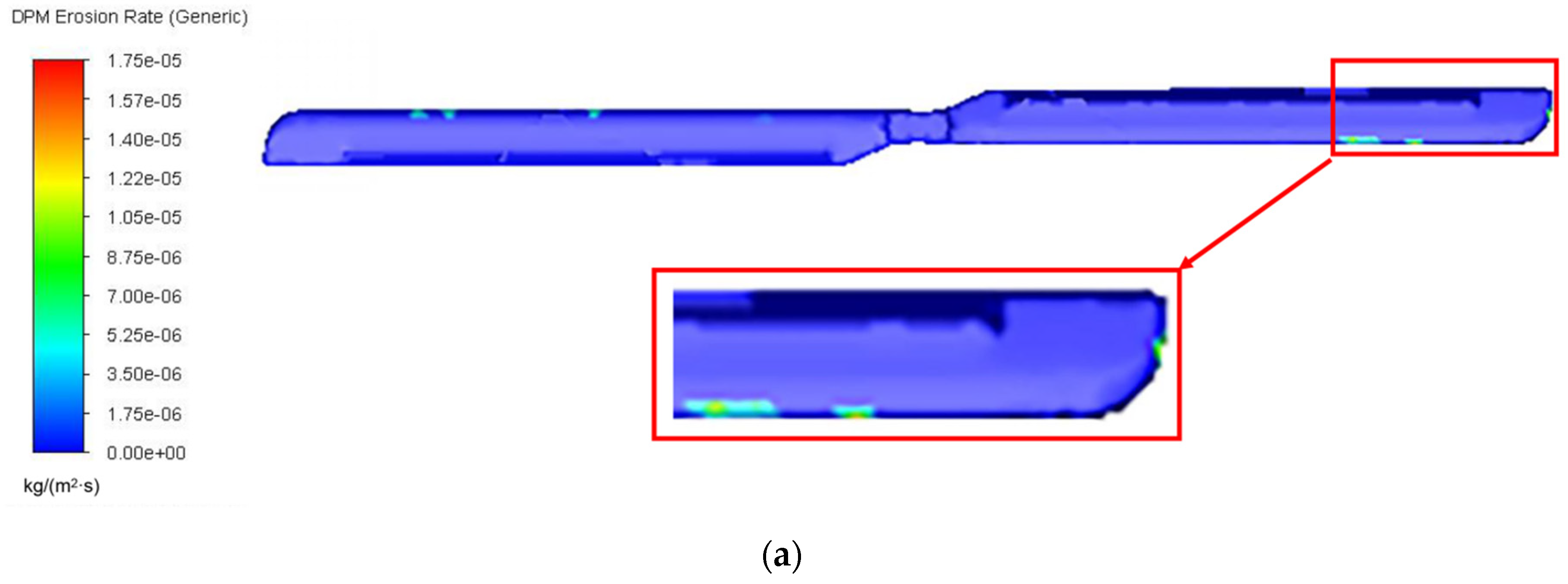
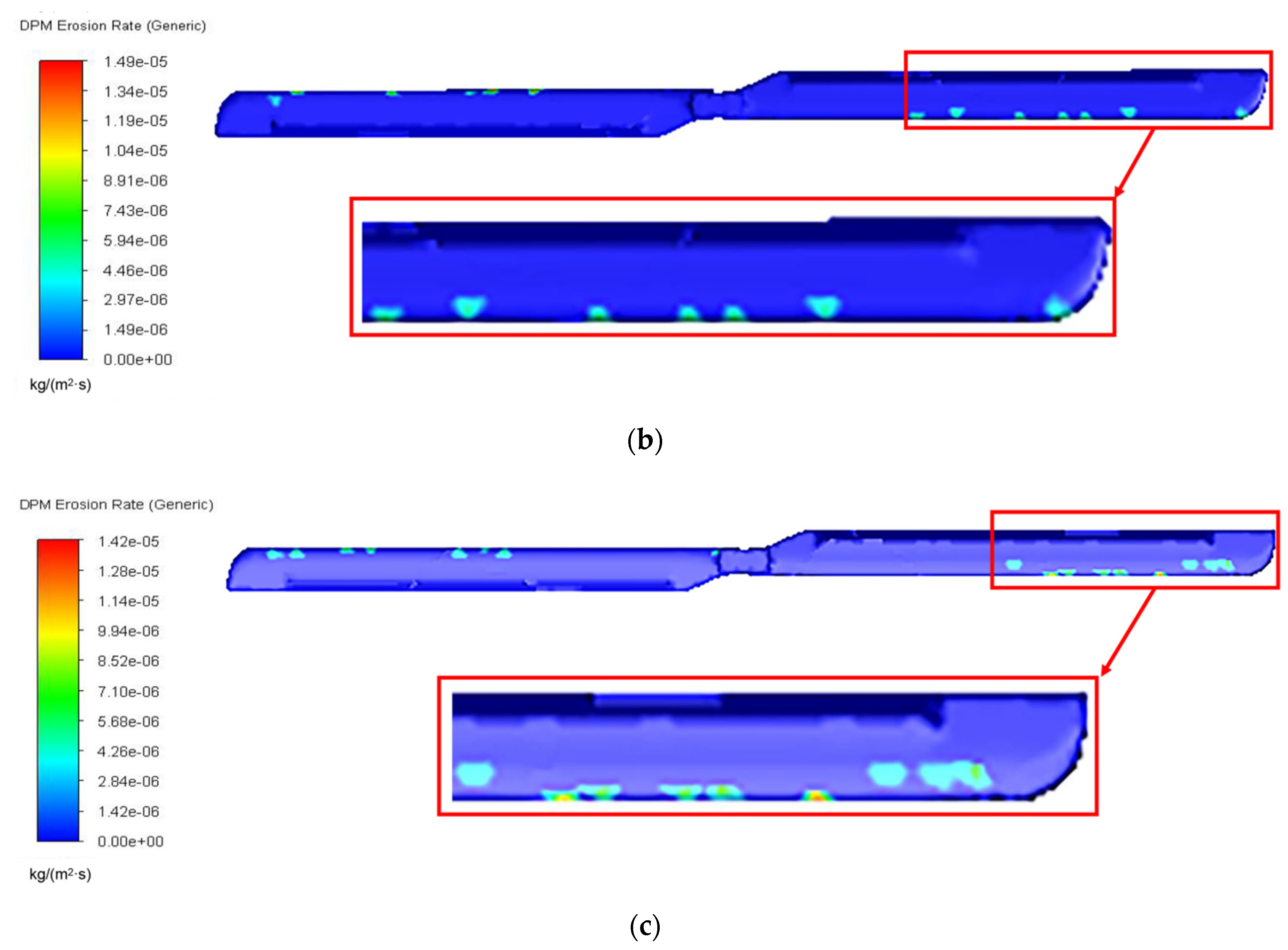



| Ti | Al | Mn | O | Others | |
|---|---|---|---|---|---|
| Ti-4Al-1.5Mn | Balance | 3.5–5.0 | 0.8–2.0 | 0.15 | 0.55 |
| Density (kg/m3) | Hardness (Vickers) | Young’s Modulus (Pa) | Bulk Modulus (Pa) | Shera Modulus (Pa) | |
| 4500 | 330 | 9.6 × 1010 | 1.14 × 1011 | 3.53 × 1010 |
| Mesh Area | Element Average Size | Total Number of Notes | Total Number of Elements | Skewness |
|---|---|---|---|---|
| 1 | 100 mm | 358,570 | 2,060,721 | 0.33 |
| 2 | 20 mm | 360,363 | 2,001,113 | 0.21 |
| 3 | 10 mm | 11,841 | 41,368 | 0.20 |
| Materials | Ti-4Al-1.5Mn | ||
|---|---|---|---|
| Sand Size (µm) | 100 | 100 | 100 |
| Particle velocity (m/s) | 20 | 20 | 20 |
| Speed (rpm) | 500 | 1000 | 2000 |
| Flow Rate (kg/s) | 0.5 | 1 | 1.5 |
| i1 | Flow Rate, Blade Speed | AL (mm2) | PL | AR (mm2) | PR | ||
|---|---|---|---|---|---|---|---|
| 1 | 0.5 kg/s, 500 rpm | 1335.51 | 0.67% | 1967.91 | 1.03% | 3303.42 | |
| 2 | 0.5 kg/s, 1000 rpm | 3095.17 | 1.62% | 4356.17 | 2.28% | 7451.34 | 1.26 |
| 3 | 0.5 kg/s, 2000 rpm | 4738.29 | 2.48% | 7413.12 | 3.88% | 12,151.41 | 0.63 |
| i2 | Flow Rate, Blade Speed | AL (mm2) | PL | AR (mm2) | PR | ||
|---|---|---|---|---|---|---|---|
| 1 | 1.0 kg/s, 500 rpm | 1485.53 | 0.78% | 1719.53 | 0.90% | 3205.06 | |
| 2 | 1.0 kg/s, 1000 rpm | 2674.84 | 1.40% | 4298.85 | 2.25% | 6973.69 | 1.17 |
| 3 | 1.0 kg/s, 2000 rpm | 4700.07 | 2.46% | 7069.22 | 3.70% | 11,176.29 | 0.68 |
| i3 | Flow Rate, Blade Speed | AL (mm2) | PL | AR (mm2) | PR | ||
|---|---|---|---|---|---|---|---|
| 1 | 1.5 kg/s, 500 rpm | 1318.31 | 0.69% | 1757.75 | 0.92% | 3076.06 | |
| 2 | 1.5 kg/s, 1000 rpm | 3228.91 | 1.69% | 4451.70 | 2.33% | 7680.61 | 1.50 |
| 3 | 1.5 kg/s, 2000 rpm | 5426.10 | 2.84% | 7125.53 | 3.73% | 12,551.61 | 0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Bai, X.; Liu, H.; Li, T.; Liu, J.; Zhou, G. Solid Particle Erosion Area of Rotor Blades: Application on Small-Size Unmanned Helicopters. Symmetry 2021, 13, 178. https://doi.org/10.3390/sym13020178
Yao Y, Bai X, Liu H, Li T, Liu J, Zhou G. Solid Particle Erosion Area of Rotor Blades: Application on Small-Size Unmanned Helicopters. Symmetry. 2021; 13(2):178. https://doi.org/10.3390/sym13020178
Chicago/Turabian StyleYao, Yongming, Xupeng Bai, Huiying Liu, Tianyu Li, Jianbo Liu, and Guangli Zhou. 2021. "Solid Particle Erosion Area of Rotor Blades: Application on Small-Size Unmanned Helicopters" Symmetry 13, no. 2: 178. https://doi.org/10.3390/sym13020178
APA StyleYao, Y., Bai, X., Liu, H., Li, T., Liu, J., & Zhou, G. (2021). Solid Particle Erosion Area of Rotor Blades: Application on Small-Size Unmanned Helicopters. Symmetry, 13(2), 178. https://doi.org/10.3390/sym13020178







