Extending Friedmann Equations Using Fractional Derivatives Using a Last Step Modification Technique: The Case of a Matter Dominated Accelerated Expanding Universe
Abstract
1. Introduction
2. Standard Cosmology
3. Fractional Friedmann Equation
Matter Dominated Universe
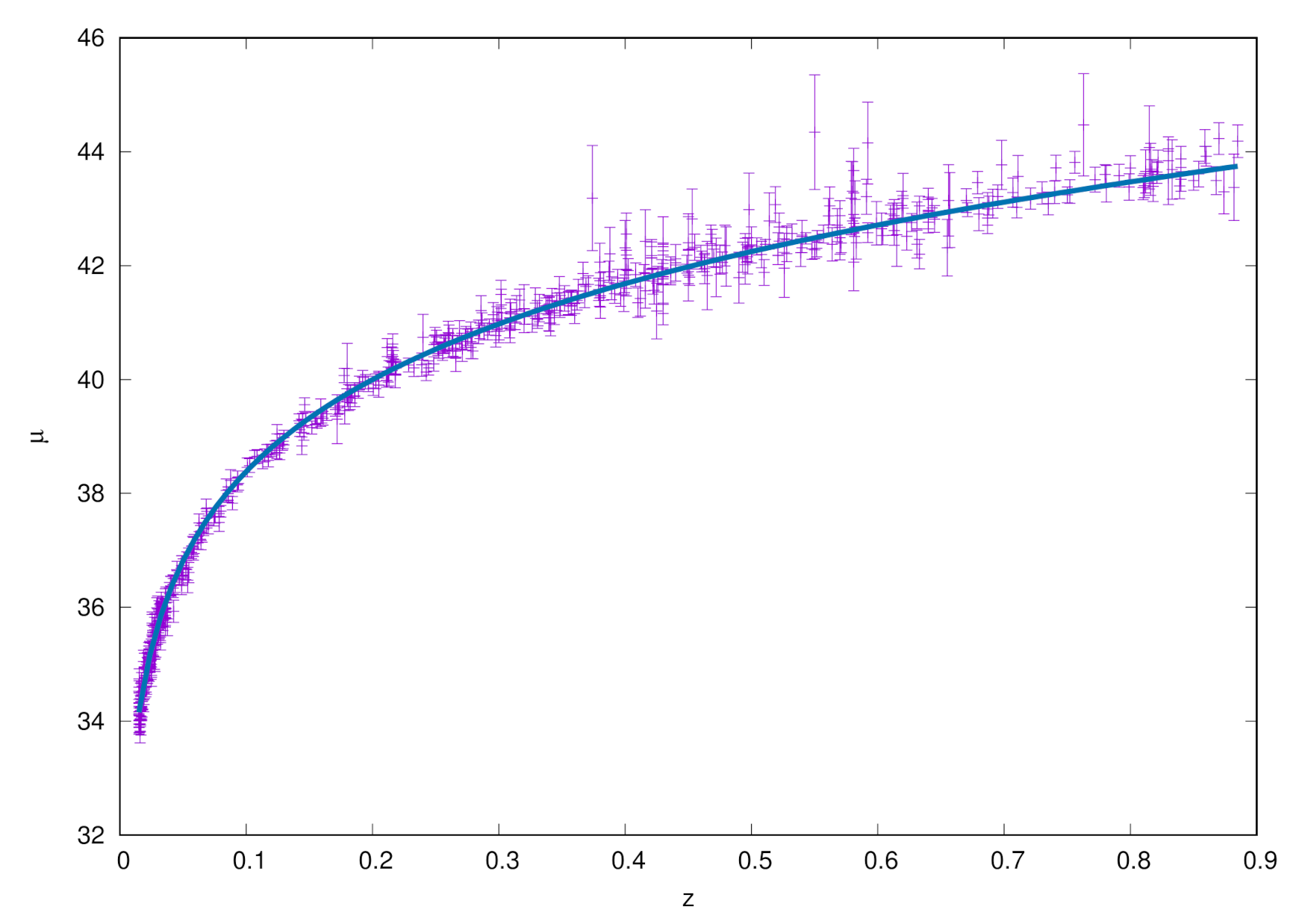
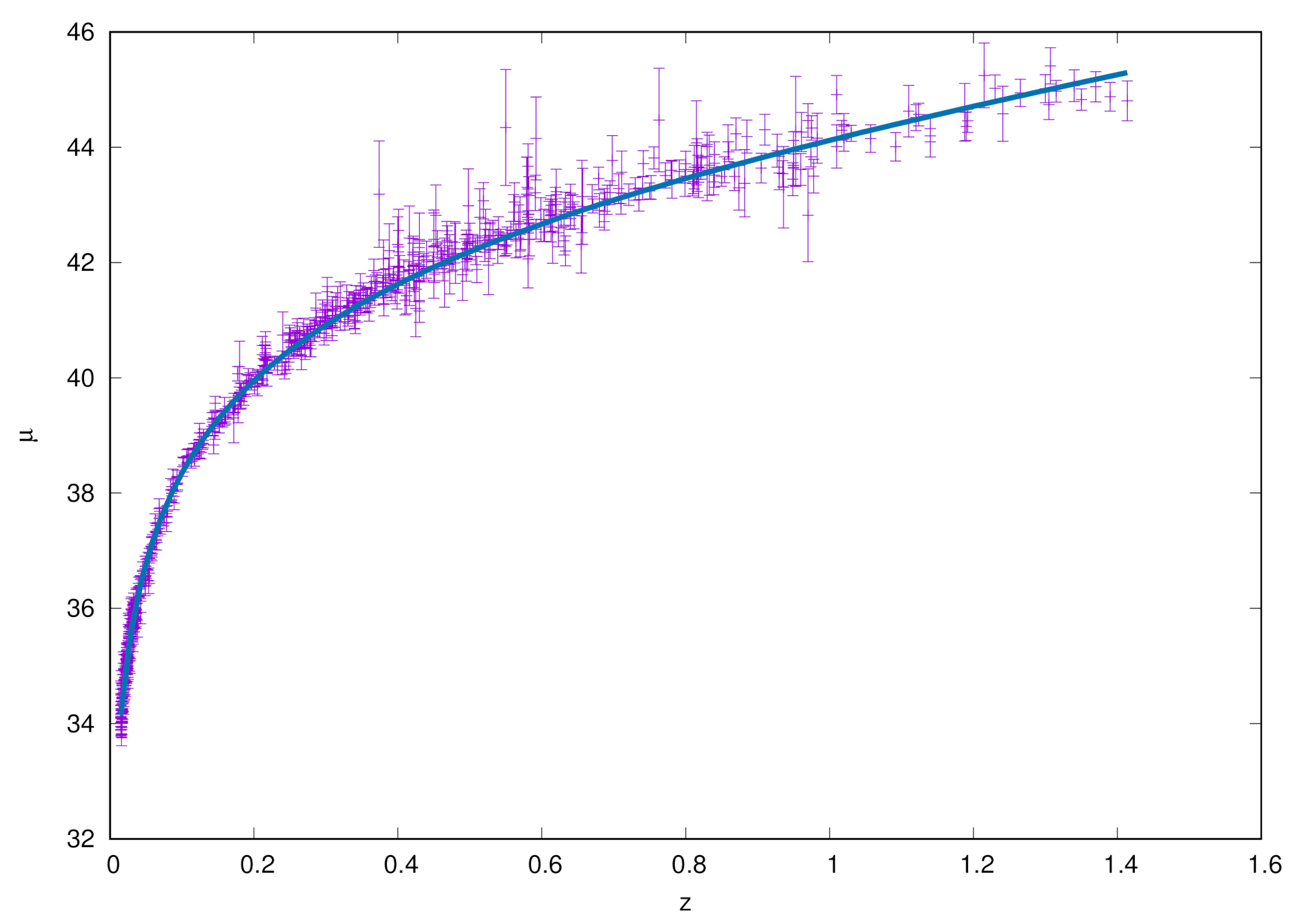
4. SN Ia Fits
5. Results
6. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
Appendix A. Fractional Calculus: A Simple Introduction
Appendix B. ΛCDM Standard Cosmology
| Planck | SN Ia | Local | |
|---|---|---|---|
| Asymptotic Error | |||
| SSR | |||
| p-value | <0.0001 | <0.0001 |
References
- Will, C.M. Theory and Experiment in Gravitational Physics; Will, C.M., Ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Dyson, F.W.; Eddington, A.S.; Davidson, C. A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919. Philos. Trans. R. Soc. Lond. Ser. A 1920, 220, 291–333. [Google Scholar] [CrossRef]
- Pound, R.V.; Rebka, G.A. Apparent. Weight. Photons Phys. Rev. Lett. 1960, 4, 337–341. [Google Scholar] [CrossRef]
- Reasenberg, R.D.; Shapiro, I.I.; MacNeil, P.E.; Goldstein, R.B.; Breidenthal, J.C.; Brenkle, J.P.; Cain, D.L.; Kaufman, T.M.; Komarek, T.A.; Zygielbaum, A.I. Viking relativity experiment—Verification of signal retardation by solar gravity. APJL 1979, 234, L219–L221. [Google Scholar] [CrossRef]
- Anderson, J.D.; Gross, M.; Nordtvedt, K.L.; Turyshev, S.G. The Solar Test of the Equivalence Principle. Astrophys. J. 1996, 459, 365. [Google Scholar] [CrossRef][Green Version]
- Chandler, J.; Pearlman, M.; Reasenberg, R.; Degnan, J. Solar-System Dynamics and Tests of General Relativity with Planetary Laser Ranging. In Proceedings of the 14th International Workshop on Laser Ranging, San Fernando, Spain, 7–11 June 2004. [Google Scholar]
- Ciufolini, I.; Pavlis, E.; Chieppa, F.; Fernandes-Vieira, E.; Perez-Mercader, J. Test of General Relativity and Measurement of the Lense-Thirring Effect with Two Earth Satellites. Science 1998, 279, 2100. [Google Scholar] [CrossRef] [PubMed]
- de Sitter, W. On Einstein’s theory of gravitation and its astronomical consequences. Second paper. MNRAS 1916, 77, 155–184. [Google Scholar] [CrossRef]
- Eubanks, T.M.; Matsakis, D.N.; Martin, J.O.; Archinal, B.A.; McCarthy, D.D.; Klioner, S.A.; Shapiro, S.; Shapiro, I.I. Advances in Solar System Tests of Gravity. In Proceedings of the APS April Meeting Abstracts, Washington, DC, USA, 18–21 April 1997; p. K11.05. [Google Scholar]
- Nordtvedt, K. Testing Relativity with Laser Ranging to the Moon. Phys. Rev. 1968, 170, 1186–1187. [Google Scholar] [CrossRef]
- Nordtvedt, K. Post-Newtonian Gravitational Effects in Lunar Laser Ranging. Phys. Rev. D 1973, 7, 2347–2356. [Google Scholar] [CrossRef]
- Nordtvedt, K., Jr.; Will, C.M. Conservation Laws and Preferred Frames in Relativistic Gravity. II. Experimental Evidence to Rule Out Preferred-Frame Theories of Gravity. Astrophys. J. 1972, 177, 775. [Google Scholar] [CrossRef]
- Schiff, L.I. Motion of a Gyroscope According to Einstein’s Theory of Gravitation. Proc. Natl. Acad. Sci. USA 1960, 46, 871–882. [Google Scholar] [CrossRef]
- Shapiro, I.I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 789–791. [Google Scholar] [CrossRef]
- Mendoza, S. MOND as the basis for an extended theory of gravity. Can. J. Phys. 2015, 93, 217–231. [Google Scholar] [CrossRef]
- Starobinsky, A. Spectrum of relict gravitational radiation and the early state of the universe. JETP Lett. 1979, 30, 682–685. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified non-local-F(R) gravity as the key for the inflation and dark energy. Phys. Lett. B 2008, 659, 821–826. [Google Scholar] [CrossRef]
- Shamir, M.F.; Fayyaz, I. Effect of f(R)-Gravity Models on Compact Stars. Theor. Math. Phys. 2020, 202, 112–125. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflationary attractors in F(R) gravity. Phys. Lett. B 2020, 807, 135576. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K.; Popov, A.A. Propagation of gravitational waves in Chern-Simons axion F(R) gravity. Phys. Dark Universe 2020, 28, 100514. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gravity with ln R Terms and Cosmic Acceleration. Gen. Relativ. Gravit. 2004, 36, 1765–1780. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. B Solid State 2003, 68, 123512. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N. f(R,Lm) gravity. Eur. Phys. J. C 2010, 70, 373–379. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. B Solid State 2011, 84, 024020. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Minazzoli, O. Extended f(R,Lm) gravity with generalized scalar field and kinetic term dependences. Phys. Rev. B Solid State 2013, 87, 047501. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Otalora, G.; Saridakis, E.N. Nonminimal torsion-matter coupling extension of f(T) gravity. Phys. Rev. B Solid State 2014, 89, 124036. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Harko, T. Extended f(R,L_m) theories of gravity. ArXiv 2012, arXiv:1211.0426. [Google Scholar]
- Bertolami, O.; Böhmer, C.G.; Harko, T.; Lobo, F.S.N. Extra force in f(R) modified theories of gravity. Phys. Rev. B Solid State 2007, 75, 104016. [Google Scholar] [CrossRef]
- Barrientos, E.; Mendoza, S. MOND as the weak field limit of an extended metric theory of gravity with a matter-curvature coupling. Phys. Rev. B Solid State 2018, 98, 084033. [Google Scholar] [CrossRef]
- Bernal, T.; Capozziello, S.; Hidalgo, J.C.; Mendoza, S. Recovering MOND from extended metric theories of gravity. Eur. Phys. J. C 2011, 71, 1794. [Google Scholar] [CrossRef]
- Mendoza, S.; Bernal, T.; Hernandez, X.; Hidalgo, J.C.; Torres, L.A. Gravitational lensing with f(χ) = χ3/2 gravity in accordance with astrophysical observations. MNRAS 2013, 433, 1802–1812. [Google Scholar] [CrossRef]
- Barrientos, E.; Mendoza, S. A relativistic description of MOND using the Palatini formalism in an extended metric theory of gravity. Eur. Phys. J. Plus 2016, 131, 367. [Google Scholar] [CrossRef]
- Barrientos, E.; Bernal, T.; Mendoza, S. Relativistic extensions of MOND using metric theories of gravity with curvature-matter couplings and their applications to the accelerated expansion of the Universe without dark components. arXiv 2020, arXiv:2008.01800. [Google Scholar]
- Mashhoon, B. Nonlocal theory of accelerated observers. Phys. Rev. A Gen. Phys. 1993, 47, 4498–4501. [Google Scholar] [CrossRef] [PubMed]
- Mashhoon, B. Gravitation and Nonlocality. arXiv 2001, arXiv:gr-qc/0112058. [Google Scholar]
- Chicone, C.; Mashhoon, B. Nonlocal gravity: Modified Poisson’s equation. J. Math. Phys. 2012, 53, 42501. [Google Scholar] [CrossRef]
- Chicone, C.; Mashhoon, B. Nonlocal gravity in the solar system. Class. Quantum Gravity 2016, 33, 75005. [Google Scholar] [CrossRef]
- Chicone, C.; Mashhoon, B. Nonlocal Newtonian cosmology. J. Math. Phys. 2016, 57, 072501. [Google Scholar] [CrossRef]
- Blome, H.J.; Chicone, C.; Hehl, F.W.; Mashhoon, B. Nonlocal modification of Newtonian gravity. Phys. Rev. B Solid State 2010, 81, 65020. [Google Scholar] [CrossRef]
- Maggiore, M.; Mancarella, M. Nonlocal gravity and dark energy. Phys. Rev. B Solid State 2014, 90, 023005. [Google Scholar] [CrossRef]
- Hehl, F.W.; Mashhoon, B. Nonlocal gravity simulates dark matter. Phys. Lett. B 2009, 673, 279–282. [Google Scholar] [CrossRef]
- Foffa, S.; Maggiore, M.; Mitsou, E. Cosmological dynamics and dark energy from nonlocal infrared modifications of gravity. Int. J. Mod. Phys. A 2014, 29, 1450116. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering, Academic Press: London, UK, 1999. [Google Scholar]
- Kochubei, A.; Luchko, Y. Basic Theory; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar] [CrossRef]
- Kochubei, A.; Luchko, Y. Fractional Differential Equations; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar] [CrossRef]
- Karniadakis, G.E. Numerical Methods; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar] [CrossRef]
- Tarasov, V.E. Applications in Physics, Part A; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar] [CrossRef]
- Petráš, I. Applications in Control; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar] [CrossRef]
- Bǎleanu, D.; Lopes, A.M. Applications in Engineering, Life and Social Sciences, Part A; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Cosmological Models with Fractional Derivatives and Fractional Action Functional. Commun. Theor. Phys. 2011, 56, 389–396. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Cosmic Evolution in Fractional Action Cosmology. Discontinuitynlinearity Complex. 2013, 2, 115–123. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Testing fractional action cosmology. Eur. Phys. J. Plus 2016, 131, 256. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Fractional Einstein-Hilbert Action Cosmology. Mod. Phys. Lett. A 2013, 28, 1350056. [Google Scholar] [CrossRef]
- Roberts, M.D. Fractional Derivative Cosmology. arXiv 2009, arXiv:0909.1171. [Google Scholar] [CrossRef]
- Vacaru, S.I. Fractional Dynamics from Einstein Gravity, General Solutions, and Black Holes. Int. J. Theor. Phys. 2012, 51, 1338–1359. [Google Scholar] [CrossRef]
- Rami, E.N.A. Fractional Unstable Euclidean Universe. Electron. J. Theor. Phys. 2005, 2, 1–11. [Google Scholar]
- Frederico, G.S.F.; Torres, D.F.M. Constants of motion for fractional action-like variational problems. arXiv 2006, arXiv:math/0607472. [Google Scholar]
- Baleanu, D. Fractional variational principles and their applications. Proc. Appl. Math. Mech. 2007, 7. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A.; Torres, D.F.M. Fractional actionlike variational problems. J. Math. Phys. 2008, 49, 053521. [Google Scholar] [CrossRef]
- Herzallah, M.; Baleanu, D. Fractional-order Euler–Lagrange equations and formulation of Hamiltonian equations. Nonlinear Dyn. 2009, 58, 385–391. [Google Scholar] [CrossRef]
- Baleanu, D.; Muslih, S.I. Lagrangian Formulation of Classical Fields within Riemann-Liouville Fractional Derivatives. Phys. Scr. 2005, 72, 119–121. [Google Scholar] [CrossRef]
- El-Nabulsi, R. Non-standard fractional Lagrangians. Nonlinear Dyn. 2013, 74. [Google Scholar] [CrossRef]
- Peacock, J.A. Cosmological Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Longair, M.S. Galaxy Formation. In Evolution of Galaxies: Astronomical Observations; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Li, E.K.; Du, M.; Xu, L. General cosmography model with spatial curvature. MNRAS 2020, 491, 4960–4972. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Liddle, A. An Introduction to Modern Cosmology; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Dodelson, S. Modern Cosmology; Academic Press (Londyn; 1941–1969); Elsevier Science: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Visser, M. Cosmography: Cosmology without the Einstein equations. Gen. Rel. Grav. 2005, 37, 1541–1548. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z > 1 and Building an Early-type-hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Giusti, A. MOND-like fractional Laplacian theory. Phys. Rev. B Solid State 2020, 101, 124029. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. The MOND paradigm. arXiv 2008, arXiv:0801.3133. [Google Scholar]
- Bernal, T.; Capozziello, S.; Cristofano, G.; de Laurentis, M. Mond’s Acceleration Scale as a Fundamental Quantity. Mod. Phys. Lett. A 2011, 26, 2677–2687. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Dover books on mathematics; Dover Publications: New York, NY, USA, 2006. [Google Scholar]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef]
- Mukherjee, S.; Ghosh, A.; Graham, M.J.; Karathanasis, C.; Kasliwal, M.M.; Magaña Hernandez, I.; Nissanke, S.M.; Silvestri, A.; Wandelt, B.D. First measurement of the Hubble parameter from bright binary black hole GW190521. arXiv 2020, arXiv:2009.14199. [Google Scholar]
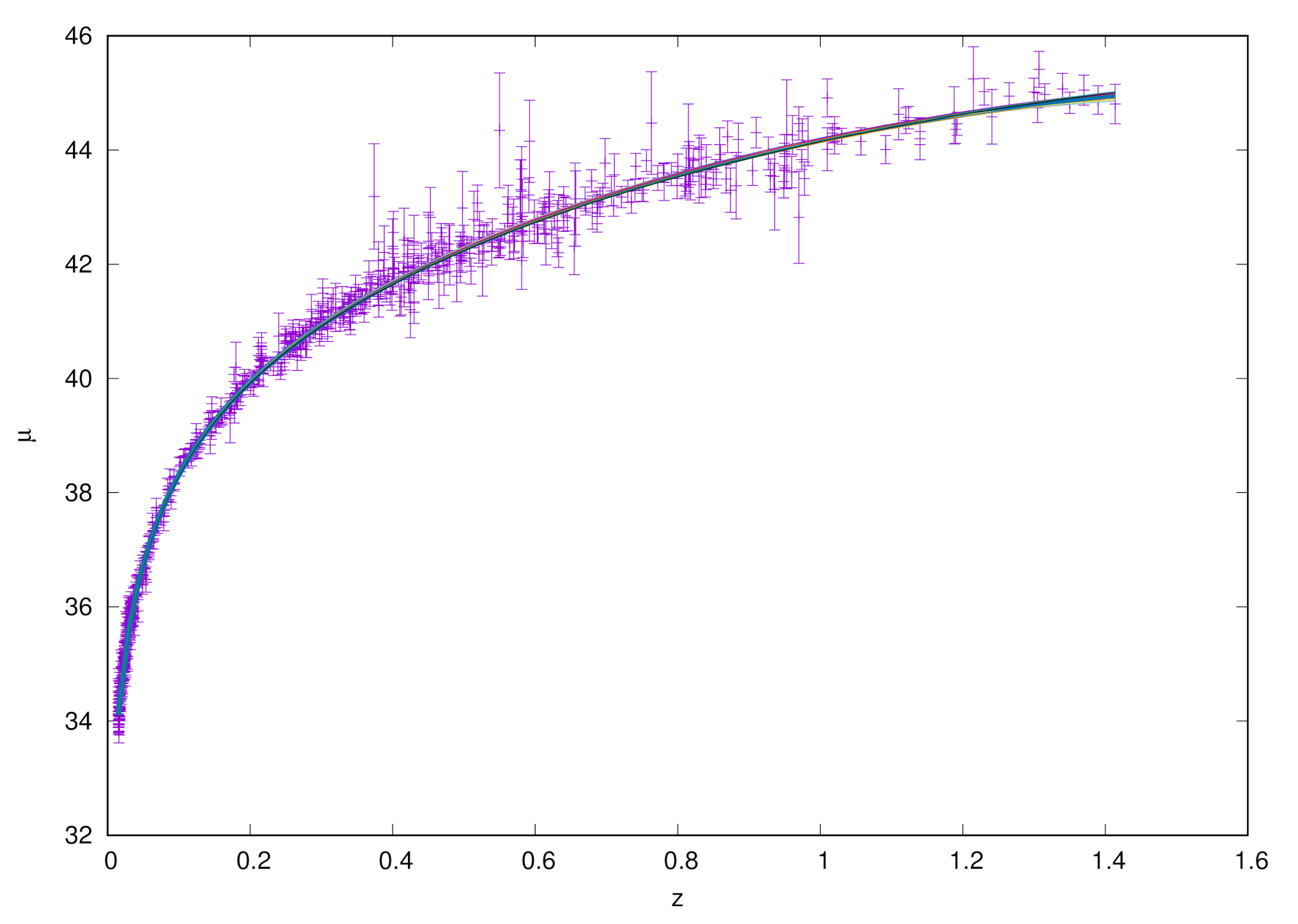
| γ | 1.7254 ± 0.043 |
| ΩM | 11.6273 ± 1.583 |
| n | 0.9306 ± 0.846 |
| γ | ΩM | n | |
| γ | 1.000 | ||
| ΩM | 0.999 | 1.000 | |
| n | 0.995 | 0.995 | 1.000 |
| γ | 1.4937 ± 0.0003 |
| ΩM | 5.4220 ± 0.0243 |
| n | 0.5539 ± 0.0046 |
| γ | ΩM | n | |
| γ | 1.000 | ||
| ΩM | 0.273 | 1.000 | |
| n | −0.140 | 0.587 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrientos, E.; Mendoza, S.; Padilla, P. Extending Friedmann Equations Using Fractional Derivatives Using a Last Step Modification Technique: The Case of a Matter Dominated Accelerated Expanding Universe. Symmetry 2021, 13, 174. https://doi.org/10.3390/sym13020174
Barrientos E, Mendoza S, Padilla P. Extending Friedmann Equations Using Fractional Derivatives Using a Last Step Modification Technique: The Case of a Matter Dominated Accelerated Expanding Universe. Symmetry. 2021; 13(2):174. https://doi.org/10.3390/sym13020174
Chicago/Turabian StyleBarrientos, Ernesto, Sergio Mendoza, and Pablo Padilla. 2021. "Extending Friedmann Equations Using Fractional Derivatives Using a Last Step Modification Technique: The Case of a Matter Dominated Accelerated Expanding Universe" Symmetry 13, no. 2: 174. https://doi.org/10.3390/sym13020174
APA StyleBarrientos, E., Mendoza, S., & Padilla, P. (2021). Extending Friedmann Equations Using Fractional Derivatives Using a Last Step Modification Technique: The Case of a Matter Dominated Accelerated Expanding Universe. Symmetry, 13(2), 174. https://doi.org/10.3390/sym13020174





