Abstract
In this manuscript, we examine the dynamical behavior of the coherence in open quantum systems using the norm. We consider a two-qubit system that evolves in the framework of Kossakowski-type quantum dynamical semigroups (KTQDSs) of completely positive maps (CPMs). We find that the quantum coherence can be asymptotically maintained with respect to the values of the system parameters. Moreover, we show that the quantum coherence can resist the effect of the environment and preserve even in the regime of long times. The obtained results also show that the initially separable states can provide a finite value of the coherence during the time evolution. Because of such properties, several states in this type of environments are good candidates for incorporating quantum information and optics (QIO) schemes. Finally, we compare the dynamical behavior of the coherence with the entire quantum correlation.
Keywords:
open quantum systems; asymptotic states; master equation; quantum coherence; total quantum correlation PACS:
03.67.-a; 03.65.Yz; 03.65.Ud
1. Introduction
In recent years, both theoretically and experimentally, several quantum phenomena have been considered as resources for the implementation of different tasks of quantum information and optics (QIO). In general, quantum correlations require the development of coherent superpositions of quantum states [1,2,3,4,5,6,7]. Its origins may be traced back to Einstein, Podolsky, and Rosen’s (EPR) concept of the “EPR paradox” [8]. They claimed that quantum physics is being used to describe “spooky action at a distance”. The ability of local measurements to govern a quantum system without access to it was explored by E. Schrödinger [9]. Subsequently, Bell introduced the so-called Bell inequality to demonstrate that this “spooky action” is responsible for creating a nonclassical correlation that defies any classical description [10]. Quantum coherence underlies various quantum effects in nanomaterials [11,12], quantum measurements and quantum metrology [13,14,15,16,17], applications of quantum mechanics to biological objects [18,19,20], etc. In keeping with the fundamental importance of quantum coherence, an accurate theory of coherence has only recently been defined with the necessary constraints to ensure that quantum coherence is a physical source [21]. As a result, unique quantum measures based on the -norm and relative entropy [21] have been developed to check these limitations. Furthermore, nonlocal correlation or the convex-roof construction can be utilized to identify the amount of coherence [22,23], and an operational theory of coherence has been presented [24].
Quantum coherence has recently attracted much attention to the development of an experimental technique with the control and observation of quantum phenomena in different quantum systems. Realistic quantum systems are always unavoidably interacting with their environment, which results in the decoherence during their dynamical evolution [25]. In the past few decades, the relaxation and dephasing in open quantum systems have been largely studied in the literature with Markovian and non-Markovian dynamics. The dynamics are interesting features of quantum systems, which makes the time component interesting in itself [26]. In most models that describe open quantum systems, the amount of coherence decreases asymptotically to zero and the entanglement dynamics emphasize the phenomenon of sudden death for decoherent environments [27]. From this perspective, the asymptotic dynamics of many quantum quantities provide us with ideal systems for comprehending quantum characteristics, which play an important role in QIO. Quantum dot systems [28,29,30,31,32], impurity systems [33,34,35,36,37], trapped ions [38,39,40], and other quantum systems can be used to implement many of these quantum systems. The performance of quantum qualities is frequently identified by the external noise reflected in physical quantum systems. As a result, methods for estimating the noise level must be developed and discovered in order to avoid the decay phenomenon in the presence of decoherence. Identifying the parameters of a quantum system’s environment will be a crucial step in minimizing its impact.
Recently, coherence trapping has attracted much attention and has been studied within the open quantum systems considering the information backflow in dephasing qubits [41] and particle indistinguishability in noisy quantum networks [42]. The quantum coherence of two-qubit systems through noisy channels is also studied, where several types of quantum channels with memory are considered [43]. Moreover, the phenomenon of coherence in multiqubit systems traversing the correlated quantum channels is considered and two remarkable quantum phenomena that can be used for protecting and controlling the quantum coherence are demonstrated [44]. In the present manuscript, we examine the phenomenon of coherence for a class of two-qubit states using Kossakowski-type quantum dynamical semigroups (KTQDSs) of completely positive maps (CPMs). These dynamics exhibits quantum states with a finite value of the coherence with respect to the initial states, including separable and entangled states. Such quantum states can be considered to execute logical operations, and perform a universal quantum computation and information. We examine how the coherence evolves in this type of the present model by showing the phenomenon of the coherence trapping where the coherence can be preserved even in the regime of long times. These characteristics make quantum states a suitable option for implementing different QIO schemes in this type of environment. Furthermore, we show that the norm of coherence may be used to reveal the quantum correlation during the dynamics.
The present manuscript is structured as follows. In Section 1, we describe the physical model for the open quantum system in the framework of KTQDSs of CPMs. Furthermore, we give a review of the quantum coherence using the norm. In Section 2, we provide the major findings and discuss them. The comparison of coherence and total quantum correlation in asymptotic dynamics is the subject of Section 3. The conclusion is provided in the last section.
2. Open Quantum System and Coherence
In the section, we display the physical model that describes the open system in the framework of KTQDS of CPMs as well as the measure of quantum coherence using the norm.
We assume a quantum system consisting of two qubits that are submerged in an environment within the techniques of a weak-coupling limit [45]. Here, the irreversible dynamics are characterized by using one-parameter semigroups of the linear maps, the so-called dynamical semigroups that are realized from . These dynamics can be governed through the master equation of the density operator W: where the generator considers the effect of the environment by using the different elements of the Kossakowski matrix [45,46,47]:
where is the frequency of the system, are the Pauli matrices, represents the identity matrix and the matrix M is given by
For all , the semigroup generated by Equation (1) consists of CPMs .
The dissipative contribution to the generator can be written as [48]
with the help of the matrices for for . By using the Pauli matrices of each qubit, and , the dissipative terms reads
where are the Kraus operators with and , and the Kossakowski matrix is given by
From the open system theory [45,49], the elements can be obtained by using the Fourier transforms of the time correlation function according to the equilibrium state of environment , , where the operator represents the interaction between the system and environment. The symmetry in the matrix (5) occurs when the two qubits are linearly related to the operators of the bath such that and .
For simplicity, we consider the initial states of the two-qubit system in the form:
where , and are real numbers satisfying the unit trace and positivity condition. The set defines an orthonormal basis that is aligned to the standard basis of two qubits by
The density operator can be represented in the standard basis as
The state (8) is entangled if and only if or . This state includes large classes of two-qubit states, such as Bell states, Horodecki states [50], Werner states [51], etc.
The density operator, , of two qubits at time t is given by
where
with
It is generally known that connecting a system with its own environment does not have to destroy quantum coherence in an open system, but can instead produce it in certain circumstances. This can happen in the present model and the environment’s ability to generate coherence is due to the Kossakowski generator of the system dynamics.
The fundamental properties of coherence depend on the nondiagonal elements of the system density operator. The norm of coherence detects the coherence by using the absolute value of the nondiagonal elements. The norm of coherence is introduced as
where describes the set of incoherent states. The parameters i and j represent the row and column index, respectively. The measure verifies the monotony for all of the quantum states. We mention that the norm of coherence of the quantum system is evaluated with respect to the standard basis.
When the time t goes to infinity, the elements of the density matrix (9) are given by
and the coherence tends to reach the value
3. Asymptotic Dynamics of Quantum Coherence in Open Quantum System Systems
We have chosen vast classes of initial states defined by Equation (8) exploiting separable and nonseparable states to investigate the effect of initial parameters on the asymptotic dynamical behavior of quantum coherence in open quantum systems.
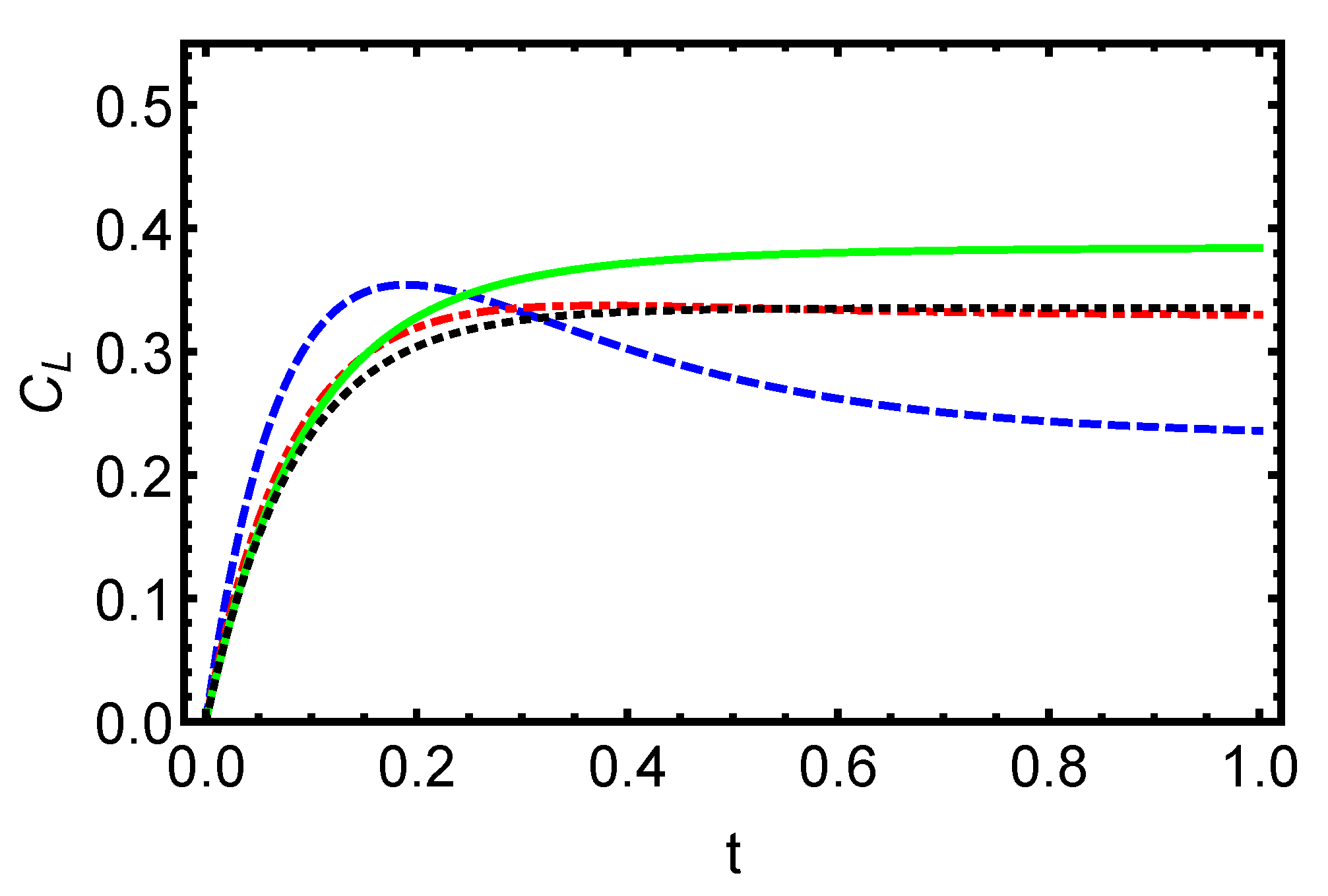
In Figure 1, we display the variation of the measure versus the time t for different values of the parameter m considering initially separable states. The dashed blue () and dash-dotted red () lines correspond to an initially separable pure state ; the solid green () and dotted black () lines correspond to an initially separable mixed state, . In general, we find that the environment has a comparable effect on the measure , with dissipation being able to increase and create the amount of coherence in the system, which subsequently achieves a stable value and persists even over extended periods of time. Interestingly, we can observe that the revival rate of the amount of coherence may take place by adjusting the parameter m. These results provide additional evidence that the initially separable states of the input state can be considered as good candidates for implementation of different tasks of QIO.
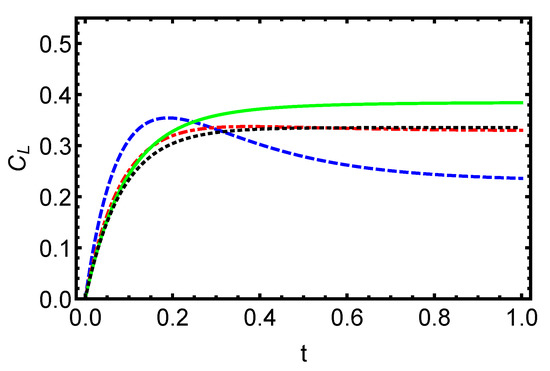
Figure 1.
Dynamics of the coherence for initially separable states is displayed versus the time t for different values of the parameter m. The dashed blue () and dash-dotted red () lines correspond to an initially separable pure state ; the solid green () and dotted black () lines correspond to an initially separable mixed state, . The influence of the environment on the measure of coherence is obtained to be similar, and that the dissipation can be able to enhance the amount of the quantum coherence during the dynamics; then, the function reaches a constant value and is preserved even in the regime of long times. Furthermore, the revival rate of the function depends on the choice of the parameter m.
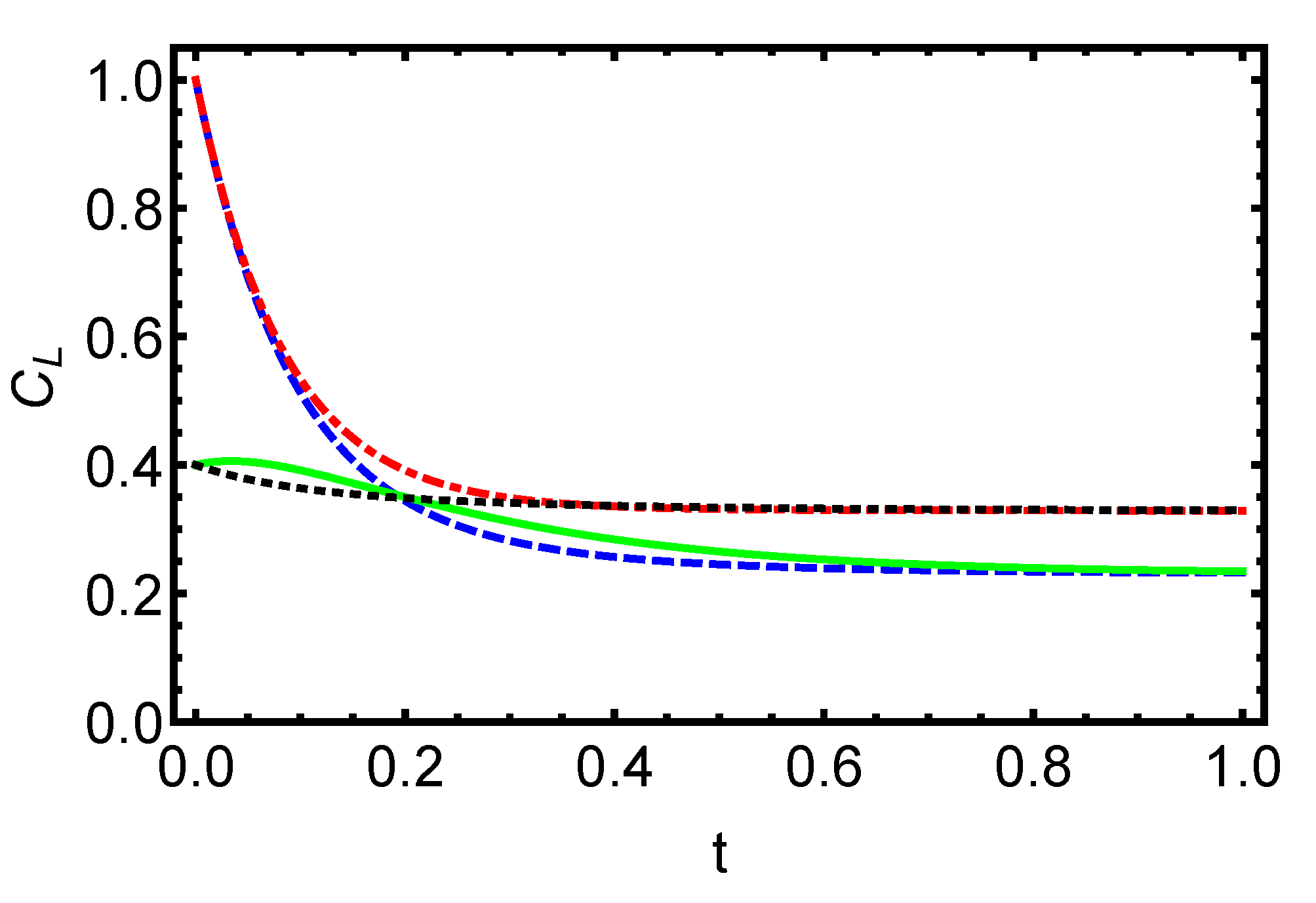
In Figure 2, we display the time evolution of the function as a function of time t for initially entangled states. The dashed blue () and dash-dotted red () lines correspond to an initially maximally pure state, ; the solid green () and dotted black () lines correspond to an initially Horodecki state, , with . It is evident that the dynamics of the function depends on the initial conditions. We note that for the initial Bell state, the amount of the coherence decays almost monotonously with the time t from the maximal value at . For the Horodecki state and by a proper choice of the parameter m, the function can be firstly raised from a finite value at to its maximal value and then attains the asymptotic value. The dependence of the measure on the initial conditions demonstrates that an adequate choice of the system parameters can raise and preserve the coherence amount during the dynamics.
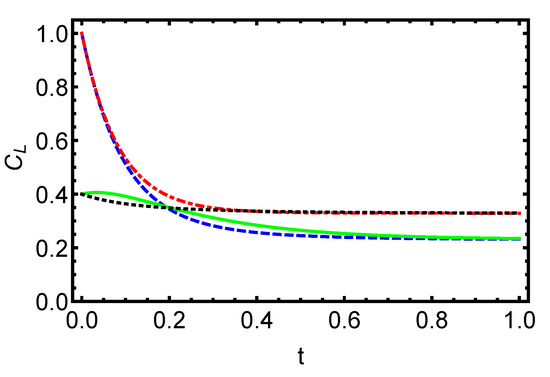
Figure 2.
Dynamics of the coherence for initially entangled quantum states is displayed versus the time t for different values of the parameter m. The dashed blue () and dash-dotted red () lines correspond to an initially maximally pure state, ; the solid green () and dotted black () lines correspond to an initial Horodecki state, , with . The influence of the environment on the function is obtained to be similar for initially entangled states, so the function tends to attain a constant value and is preserved even in the regime of long times. The dependence of the quantum coherence on the initial conditions clearly demonstrates that an appropriate choice of system parameters can lead to the enhancement and preservation of quantum coherence during the dynamics.
From the obtained results, we obtain that the amount of quantum coherence under KTQDSs, which represents a rich set of asymptotic quantum states, may be controlled and preserved during the evolution. The environment’s influence should not only have a negative impact on the quantity of coherence, but it can also be able to grow and asymptotically sustain it even over extended periods of time. This is possible in the current model, where the improvement of quantum coherence is owing to the dissipative contribution (4), in which the Hamiltonian of two qubits does not include coupling terms and hence cannot be seen as a source to produce and increase the quantity of coherence during dynamics. Because the off-diagonal contributions in the matrix (5) couple a system of two qubits, this is possible. This is only necessary, but not sufficient, to provide a long-term improvement in coherence and durability.
4. Coherence and Total Quantum Correlation
In the present section, we compare the dynamics of the quantum coherence with the total quantum correlation for separable and nonseparable states.
Currently, the total quantum correlation is a useful physical resource and its concept depends on the local uncertainty (LU), which is a full-fledged discord-like [52] family of quantifiers of total quantum correlations. It is defined by [53]
where the parameter describes the spectrum of , the amount I represents the skew information, where the minimization over a spectrum of observables leads to a specific measurement of the family. The LU is defined by
with representing the maximum eigenvalue of the symmetric H with the matrix elements
For pure states, the LU is normalized to 1 and coincides with the value of the linear entropy.
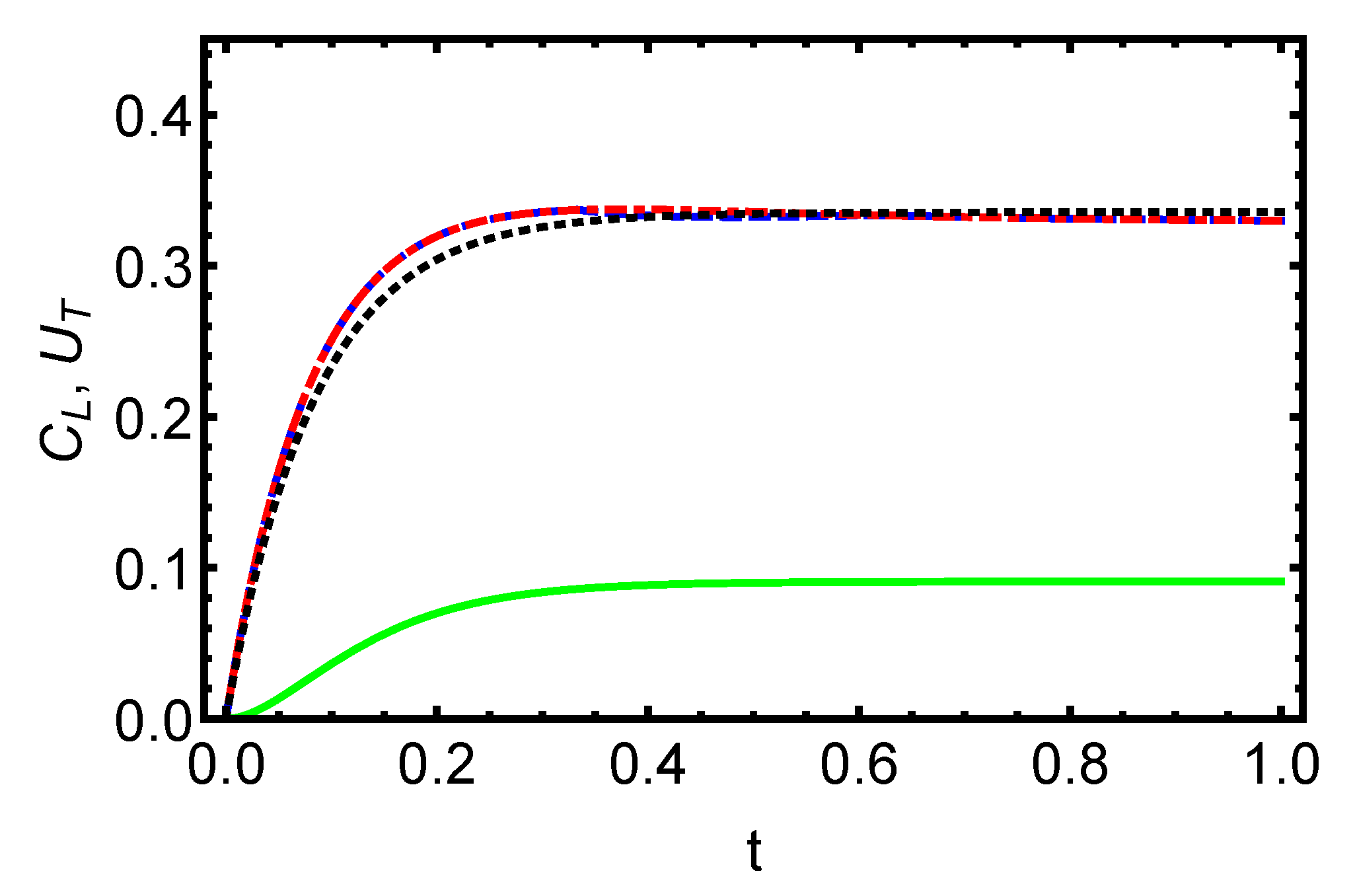
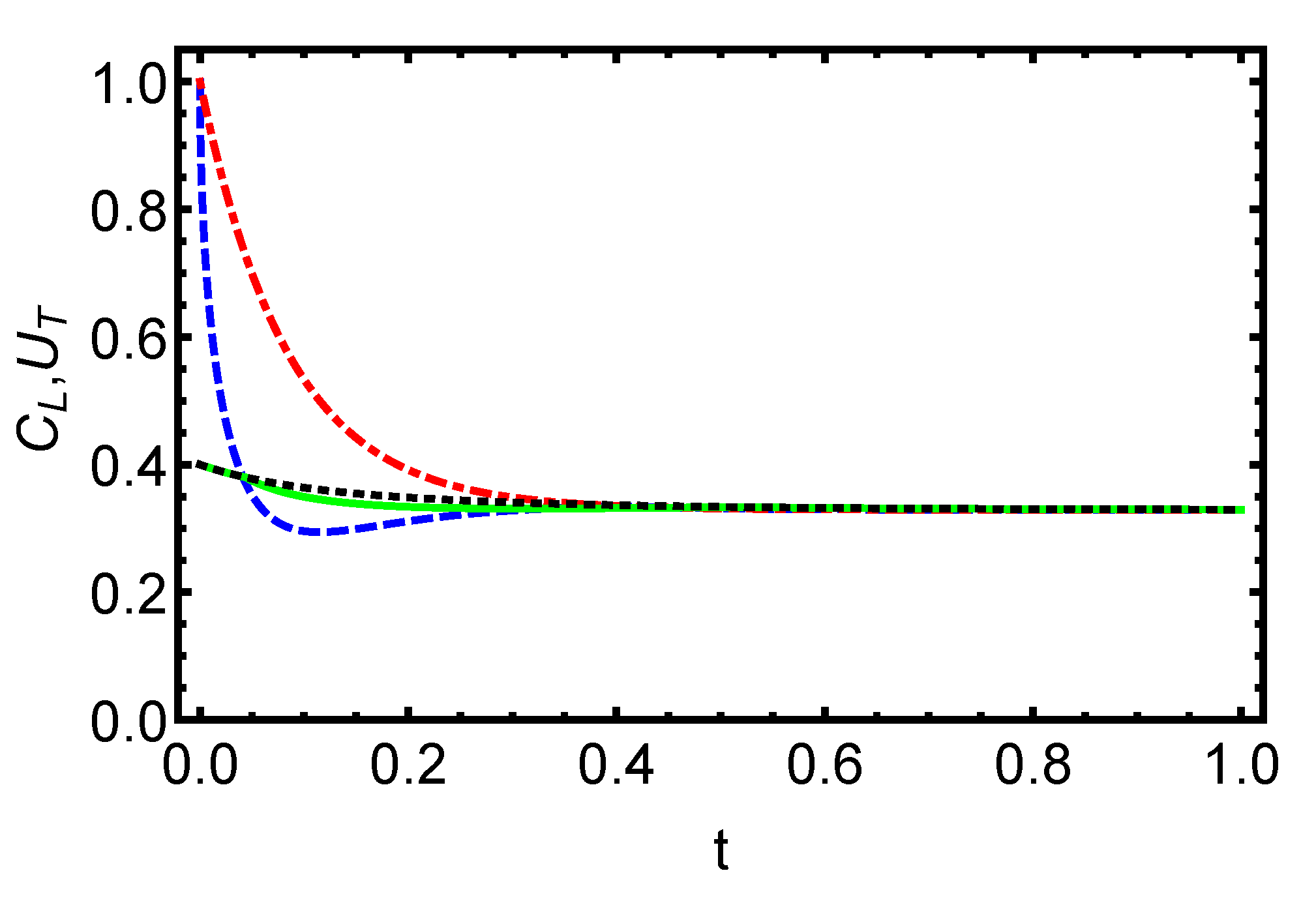
In Figure 3 and Figure 4, we have plotted the time variation of the functions and for initially separable and entangled states. In general, we can see that the behavior of quantum coherence and total quantum correlation is obtained to be similar with respect to the parameters involved in the quantum states. These characteristics make the quantum coherence a suitable candidate for detecting the information content in the open quantum systems, and exploit it in multiple tasks of QIO.
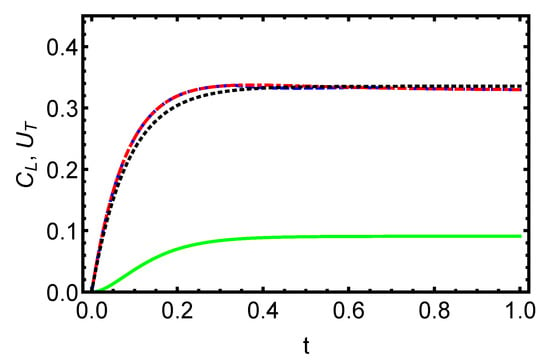
Figure 3.
Dynamics of the total quantum correlation and coherence for initially separable states is displayed versus the time t with . The dashed blue (total quantum correlation) and dash-dotted red (quantum coherence) lines correspond to an initially separable pure state ; the solid green (total quantum correlation) and dotted black (quantum coherence) lines correspond to an initially separable mixed state, . The asymptotic behavior of the functions and is shown to be comparable according to the various parameters that are involved in the state of two qubits, and the quantifiers exhibit the same behavior and maintain their value even over extended periods of time.
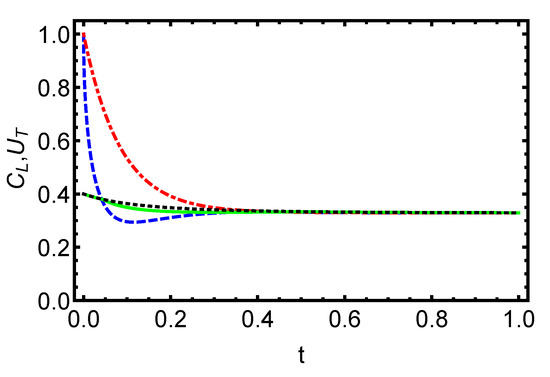
Figure 4.
Dynamics of the total quantum correlation and coherence for initially entangled states is displayed versus the time with . The dashed blue (total quantum correlation) and dash-dotted red (quantum coherence) lines correspond to an initially maximally pure state, ; the solid green (total quantum correlation) and dotted black (quantum coherence) lines correspond to an initial Horodecki state, , with . The asymptotic behavior of the functions and is shown to be comparable according to the various parameters that are involved in the state of two qubits, and the quantifiers exhibit the same behavior and maintain their value even over extended periods of time.
5. Conclusions
We have examined in detail the behavior of the quantum coherence in open systems using the norm. We have considered a two-qubit system that evolves in the framework of KTQDSs of CPMs. We have obtained that the quantum coherence can be asymptotically maintained with respect to the values of the initial parameters. We have proven that quantum coherence can withstand the effects of the environment and persist even over lengthy periods of time. We have observed that during an evolution, the initial separable states can give a limited value of coherence. Because of these characteristics, quantum systems in this type of environment are good candidates for implementing different QIO schemes. Finally, we have demonstrated that the -norm of coherence and quantum correlation exhibit the same behavior during dynamics. From a phenomenological standpoint, the current work may be more helpful in understanding specific experimental measurements of quantum coherence dissipation under real conditions, as well as providing more hints for future research in this area.
Author Contributions
Writing—original draft preparation, K.B. and H.E.; writing—review and editing, M.A. and S.A.-K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Taif University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Taif University Researchers Supporting Project number (TURSP-2020/154), Taif University, Taif, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715. [Google Scholar] [CrossRef] [Green Version]
- Wen-Long, Y.; Yimin, W.; Tian-Cheng, Y.; Chengjie, Z.; Oleś Andrzej, M. Quantum coherence in a compass chain under an alternating magnetic field. Phys. Rev. B 2018, 97, 224420. [Google Scholar]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef] [Green Version]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar]
- Nath Bera, M.; Acín, A.; Kuś, M.; Mitchell, M.; Lewenstein, M. Randomness in quantum mechanics: Philosophy, physics and technology. Rep. Prog. Phys. 2017, 80, 124001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castelano, L.K.; Fanchini, F.F.; Berrada, K. Open quantum system description of singlet-triplet qubits in quantum dots. Phys. Rev. B 2016, 94, 235433. [Google Scholar] [CrossRef] [Green Version]
- Berrada, K.; Eleuch, H. Noncommutative deformed cat states under decoherence. Phys. Rev. D 2019, 100, 016020. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef] [Green Version]
- Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschafen 1935, 23, 807. [Google Scholar]
- Bell, J.S. Physics Long Island City. N. Y. 1964, 195, 1. [Google Scholar]
- Lostaglio, M.; Jennings, D.; Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karlström, O.; Linke, H.; Karlström, G.; Wacker, A. Increasing thermoelectric performance using coherent transport. Phys. Rev. B 2011, 84, 113415. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330. [Google Scholar] [CrossRef] [Green Version]
- Berrada, K. Quantum metrology with SU(1,1) coherent states in the presence of nonlinear phase shifts. Phys. Rev. A 2013, 88, 013817. [Google Scholar] [CrossRef]
- Berrada, K. Quantum metrology with classical light states in non-Markovian lossy channels. J. Opt. Soc. Am. B 2017, 34, 1912. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Ooi, C.H.R. Quantum metrology with entangled spin-coherent states of two modes. Phys. Rev. A 2012, 86, 033823. [Google Scholar] [CrossRef] [Green Version]
- Berrada, K. High precision regions of phase sensitivity for the superposition of coherent fields. Laser Phys. Lett. 2014, 11, 105202. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10, 113019. [Google Scholar] [CrossRef]
- Lloyd, S. Quantum coherence in biological systems. J. Phys. Conf. Ser. 2011, 302, 012037. [Google Scholar] [CrossRef]
- Li, C.-M.; Lambert, N.; Chen, Y.-N.; Chen, G.-Y.; Nori, F. Witnessing Quantum Coherence: From solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [Green Version]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring Quantum Coherence with Entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, X.; Zhou, H.; Cao, Z.; Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 2015, 92, 022124. [Google Scholar] [CrossRef] [Green Version]
- Winter, A.; Yang, D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef] [Green Version]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge U.P.: New York, NY, USA, 1997. [Google Scholar]
- Tsang, M. Quantum transition-edge detectors. Phys. Rev. A 2013, 88, 021801(R). [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Eberly, J.H. Quantum Open System Theory: Bipartite Aspects. Phys. Rev. Lett. 2006, 97, 140403. [Google Scholar] [CrossRef] [Green Version]
- Shulman, M.D.; Dial, O.E.; Harvey, S.P.; Bluhm, H.; Umansky, V.; Yacoby, A. Demonstration of Entanglement of Electrostatically Coupled Singlet-Triplet Qubits. Science 2012, 336, 202. [Google Scholar]
- Schuetz, M.J.A.; Kessler, E.M.; Vandersypen, L.M.K.; Cirac, J.I.; Giedke, G. Nuclear spin dynamics in double quantum dots: Multistability, dynamical polarization, criticality, and entanglement. Phys. Rev. B 2014, 89, 195310. [Google Scholar] [CrossRef] [Green Version]
- Borras, A.; Blaauboer, M. Detecting entanglement of two-electron spin qubits with witness operators. Phy. Rev. B 2011, 84, 033301. [Google Scholar] [CrossRef] [Green Version]
- Hiltunen, T.; Harju, A. Maximal tripartite entanglement between singlet-triplet qubits in quantum dots. Phys. Rev. B 2014, 89, 115322. [Google Scholar]
- Culcer, D.; Cywiński, Ł.; Li, Q.; Hu, X.; Sarma, S.D. Realizing singlet-triplet qubits in multivalley Si quantum dots. Phys. Rev. B 2009, 80, 205302. [Google Scholar] [CrossRef] [Green Version]
- Kennes, D.M.; Meden, V.; Vasseur, R. Universal quench dynamics of interacting quantum impurity systems. Phys. Rev. B 2014, 90, 115101. [Google Scholar] [CrossRef] [Green Version]
- Vasseur, R.; Trinh, K.; Haas, S.; Saleur, H. Crossover physics in the nonequilibrium dynamics of quenched quantum impurity systems. Phys. Rev. Lett. 2013, 110, 240601. [Google Scholar] [CrossRef] [PubMed]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863. [Google Scholar] [CrossRef]
- Vidal, G. Efficient Simulation of One-Dimensional Quantum Many-Body Systems. Phys. Rev. Lett. 2004, 93, 040502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schollwock, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96. [Google Scholar] [CrossRef] [Green Version]
- Porras, D.; Cirac, J.I. Effective Quantum Spin Systems with Trapped Ions. Phys. Rev. Lett. 2004, 92, 207901. [Google Scholar] [CrossRef] [Green Version]
- Leibfried, D.; DeMarco, B.; Meyer, V.; Lucas, D.; Barrett, M.; Britton, J.; Itano, W.M.; Jelenković, B.; Langer, C.; Rosenband, T.; et al. Experimental demonstration of a robust, high-fidelity geometric two ion-qubit phase gate. Nature 2003, 422, 412. [Google Scholar] [CrossRef]
- Schmidt-Kaler, F.; Häffner, H.; Riebe, M.; Gulde, S.; Lancaster, G.P.; Deuschle, T.; Becher, C.; Roos, C.F.; Eschner, J.; Blatt, R. Realization of the Cirac–Zoller controlled-NOT quantum gate. Nature 2003, 422, 408. [Google Scholar] [CrossRef] [PubMed]
- Addis, C.; Brebner, G.; Haikka, P.; Maniscalco, S. Coherence trapping and information backflow in dephasing qubits. Phys. Rev. 2014, 89, 024101. [Google Scholar] [CrossRef] [Green Version]
- Perez-Leija, A.; Guzmán-Silva, D.; León-Montiel, R.D.J.; Gräfe, M.; Heinrich, M.; Moya-Cessa, H.; Busch, K.; Szameit, A. Endurance of quantum coherence due to particle indistinguishability in noisy quantum networks. NPJ Quantum. Inf. 2018, 4, 45. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.-N.; Tian, Q.-L.; Zeng, K.; Li, Z.-d. Microwave photonics with superconducting quantum circuits. Quantum. Inf. Process. 2017, 16, 310. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.L.; Fan, H. Quantum coherence of multiqubit states in correlated noisy channels. Sci. China-Phys. Mech. Astron. 2020, 63, 230322. [Google Scholar] [CrossRef] [Green Version]
- Alicki, R.; Lendi, K. Quantum Dynamical Semigroups and Applications; Lecture Notes in Physics; Springer: Berlin, Germany, 2007; p. 717. [Google Scholar]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Benatti, F.; Liguori, A.M.; Pluzzano, G. Entanglement and entropy rates in open quantum systems. J. Phys. A Math. Theor. 2010, 43, 045304. [Google Scholar] [CrossRef] [Green Version]
- Benatti, F.; Floreanini, R. Open Quantum Dynamics: Complete Positivity and Entanglement. Int. J. Mod. Phys. 2005, B 19, 3063. [Google Scholar] [CrossRef] [Green Version]
- Spohn, H. Kinetic equations from Hamiltonian dynamics: Markovian limits. Rev. Mod. Phys. 1980, 52, 569. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Quantum Information: An Introduction to Basic Theoretical Concepts and Experiments; Springer: Berlin/Heidelberg, Germany, 2001; p. 151. [Google Scholar]
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.L.; Hu, X.; Wang, J.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762, 1. [Google Scholar] [CrossRef] [Green Version]
- Girolami, D.; Tufarelli, T.; Adesso, G. Characterizing Nonclassical Correlations via Local Quantum Uncertainty. Phys. Rev. Lett. 2013, 110, 240402. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).