An Investigation on Weak Concepts in Ordered Hyperstructures

Abstract

The class of weak pseudoorders and left weak interior hyperideals in ordered hyperstructures is a generalization of pseudoorders and interior hyperideals. In this work, we study the concept of weak pseudoorders and left weak interior hyperideals in ordered hyperstructures and explore some results concerning the new defined concepts for ordered hyperrings and ordered Γ-semihypergroups. In this regards, we intend to concentrate our efforts on the relationship between the left weak interior hyperideal and interior hyperideal of an ordered hyperstructure. A characterization of a regular ordered hyperstructure via a left weak interior hyperideal is given. Finally, we characterize the notion of left weak interior simple ordered hyperstructures in terms of left weak interior hyperideals.

1. Introduction

Ordered semihypergroups are algebraic hyperstructures equipped with hyperoperation and (partial) order relation that satisfy the monotone condition. In [1] the pseudoorders were applied to ordered semihypergroups and the authors highlighted the relationship between ordered hyperstructures and ordered structures. The concept of ordered regular equivalence relation in the framework of ordered semihypergroups was considered by Gu and Tang [2] in 2016 and recently by Tang et al. in [3]. Expository and survey definitions on ordered hyperstructures have been published by Heidari and Davvaz [4] in 2011. The notion of hypergroups were initially introduced by Marty [5] in 1934.

In [6], Anvariyeh et. al. introduced an algebraic hyperstructure namely $\mathsf{\Gamma }$-semihypergroups. The weak $\mathsf{\Gamma }$-semihypergroups were introduced by Zare et al. [7] as a generalization of $\mathsf{\Gamma }$-semihypergroups. The quasi-$\mathsf{\Gamma }$-hyperideals are generalization of (left) $\mathsf{\Gamma }$-hyperideals. By using pseudoorders, we can connect ordered $\mathsf{\Gamma }$-semihypergroups to ordered $\mathsf{\Gamma }$-semigroups.

There is a considerable amount of work on the ordered hyperstructures. Recently, in [8] Rao et al. deal with almost interior hyperideals on ordered $\mathsf{\Gamma }$-semihypergroups. Tang et al. in [3] obtained some results on the ordered semihypergroups connected with weak pseudoorders. Tang et al. [9] introduced the notion of (fuzzy) interior $\mathsf{\Gamma }$-hyperideal in ordered $\mathsf{\Gamma }$-semihypergroups. In [10], the concept of uni-soft interior $\mathsf{\Gamma }$-hyperideals of ordered $\mathsf{\Gamma }$-semihypergroups are investigated. In [11], M. M. K. Rao introduced and studied the concept of fuzzy weak interior ideals of $\mathsf{\Gamma }$-semirings.

In the paper of Rao et al. [8], a lot of constructions of quotient ordered hyperstructures are provided with details. In the present work we also provide constructions for quotient ordered hyperrings by using weak concepts. Section 2 will aim for the summarizing the fundamental notions on (ordered) hyperstructures. Almost all topics explained here are already contained in several papers on ordered hyperstructures including Davvaz et al. [1], Kou et al. [12], Rao et al. [8] and etc. Section 3 discusses one of the most weak concepts on quotient ordered hyperrings. This concept is introduced in the works of [3,8]. Weak pseudoorder nowadays has proven to be one of the most important tools in the study of ordered hyperstructures. Section 3 offers basic concepts on left weak interior hyperideals in ordered hyperstructure. Motivated by the above-mentioned studies [8,11], in this paper we establish relationship between interior hyperideals and left weak interior hyperideals and characterize regular and simple ordered hyperstructures. Also, we give some examples to compare left weak interior hyperideals with interior hyperideals. We discuss in detail a number of results on left weak interior hyperideals. At last, in Section 4, we present some conclusions and future works.

2. Preliminaries

In this section, we present some notions that we will need in this study.

Definition 1.

An ordered Γ-semihypergroup is an algebraic hyperstructure $(S,\mathsf{\Gamma },\le )$ such that (1) $(S,\mathsf{\Gamma })$ is a Γ-semihypergroup; (2) $(S,\le )$ is a partially ordered set; (3) $x\le y$ implies $z\gamma x⪯z\gamma y$ and $x\gamma z⪯y\gamma z$ for all $x,y,z\in S$ and $\gamma \in \mathsf{\Gamma }$. Here, $U⪯V$ means that for any $u\in U$, there exists $v\in V$ such that $u\le v$, for all non-empty subsets U and V of S. If $\mathsf{\Gamma }=\{\circ \}$, then $(S,\mathsf{\Gamma },\le )$ is an ordered semihypergroup.

A non-empty subset K of an ordered $\mathsf{\Gamma }$-semihypergroup S is called a subsemihypergroup if $u\gamma v\subseteq K$ for every $u,v\in K$ and $\gamma \in \mathsf{\Gamma }$. If $\varnothing \ne K\subseteq S$, then

$$\left(K\right]:=\{x\in S|x\le k\mathrm{for}\mathrm{some}k\in K\}.$$

A non-empty subset K of an ordered $\mathsf{\Gamma }$-semihypergroup S is called a left (resp. right) hyperideal of S if (1) $S\mathsf{\Gamma }K\subseteq K$ (resp. $K\mathsf{\Gamma }S\subseteq K$); (2) $\left(K\right]\subseteq K$. A non-empty subset K of S is called a hyperideal of S if it is both a left and a right hyperideal of S. A non-empty subset K of S is called a quasi-hyperideal if (1) $\left(K\mathsf{\Gamma }S\right]\cap \left(S\mathsf{\Gamma }K\right]\subseteq K$; (2) $\left(K\right]\subseteq K$. A subsemihypergroup K of an ordered $\mathsf{\Gamma }$-semihypergroup S is called an interior hyperideal of S [9] if (1) $S\mathsf{\Gamma }K\mathsf{\Gamma }S\subseteq K$; (2) $\left(K\right]\subseteq K$. If $\varnothing \ne M,N\subseteq S$, then (1) $M\subseteq \left(M\right]$; (2) If $M\subseteq N$, then $\left(M\right]\subseteq \left(N\right]$; (3) $\left(M\right]\mathsf{\Gamma }\left(N\right]\subseteq \left(M\mathsf{\Gamma }N\right]$ and $\left(\right(M\left]\mathsf{\Gamma }\right(N\left]\right]=\left(M\mathsf{\Gamma }N\right]$; (4) $\left(\right(M\left]\right]=\left(M\right]$. An ordered $\mathsf{\Gamma }$-semihypergroup S is called regular if $A\subseteq \left(A\mathsf{\Gamma }S\mathsf{\Gamma }A\right]$ for every $A\subseteq S$.

Theorem 1.

An ordered Γ-semihypergroup $(S,\mathsf{\Gamma },\le )$ is regular if and only if for every right hyperideal M and every left hyperideal N of S, we have

$$M\cap N=\left(M\mathsf{\Gamma }N\right].$$

An algebraic system $(R,+,·)$ is said to be a (general) hyperring [13], if $(R,+)$ is a hypergroup, $(R,·)$ is a semihypergroup and “·” is distributive over the “+”. The definition of ordered hyperrings is based on the definition of ordered semihypergroups. The ordered hyperrings are a generalization of ordered rings. An algebraic hypersructure $(R,+,·,\le )$ is said to be an ordered hyperring if for all $a,b,x\in R$, (1) $(R,+,·)$ is a hyperring; (2) $(R,\le )$ is a poset; (3) $a\le b$ implies $a+x⪯b+x$ and $x+a⪯x+b$; (4) $a\le b$ implies $a·x⪯b·x$ and $x·a⪯x·b$. Here, a relation $M⪯N$ is only possible if for any $m\in M$ there exists $n\in N$ such that $m\le n$.

Let $\sigma$ be an equivalence relation on an ordered hyperring R. If $\varnothing \ne M,N\subseteq R$, then

(1)

$M\overrightarrow{\sigma }N\iff \forall m\in M,\exists n\in N;m\sigma n$.

(2)

$M\overleftarrow{\sigma }N\iff \forall n^{\prime }\in N,\exists m^{\prime }\in M;m^{\prime }\sigma n^{\prime }$.

(3)

$M\tilde{\sigma }N\iff \forall m\in M,\exists n\in N;m\sigma n$ and $n\sigma m\&\forall n^{\prime }\in N,\exists m^{\prime }\in M;n^{\prime }\sigma m^{\prime }$ and $m^{\prime }\sigma n^{\prime }$.

(4)

$M\overline{\sigma }N\iff M\overrightarrow{\sigma }N$ and $M\overleftarrow{\sigma }N$.

(5)

$M\overline{\overline{\sigma }}N\iff \forall m\in M,\forall n\in N,m\sigma n$.

The relation $\sigma$ is said to be regular if for all $a,b,x\in R$, (1) $a\sigma b\Rightarrow (a+x)\overline{\sigma }(b+x)\mathrm{and}$$(x+a)\overline{\sigma }(x+b)$; (2) $a\sigma b\Rightarrow (a·x)\overline{\sigma }(b·x)\mathrm{and}(x·a)\overline{\sigma }(x·b)$. Also, $\sigma$ is strongly regular if (i) $a\sigma b\Rightarrow (a+x)\overline{\overline{\sigma }}(b+x)\mathrm{and}(x+a)\overline{\overline{\sigma }}(x+b)$; (ii) $a\sigma b\Rightarrow (a·x)\overline{\overline{\sigma }}(b·x)\mathrm{and}(x·a)\overline{\overline{\sigma }}(x·b)$. Let $(R,+,·,{\le }_R)$ and $(T,\oplus ,\odot ,{\le }_T)$ be two ordered hyperrings. A mapping $\phi :R\to T$ is called a homomorphism [12] if for all $a,b\in R$, (1) $\phi (a+b)\subseteq \phi \left(a\right)\oplus \phi \left(b\right)$; (2) $\phi (a·b)\subseteq \phi \left(a\right)\odot \phi \left(b\right)$; (3) $a{\le }_{R}b$ implies $\phi \left(a\right){\le }_T\phi \left(b\right)$.

3. Main Results

First of all, we aim to study weak pseudoorders in quotient ordered hyperrings and give some results. A relation $\sigma$ on an ordered hyperring $(R,+,·,\le )$ is called a weak pseudoorder if for all $a,b,x\in R$, (1) $\le \subseteq \sigma$; (2) $a\sigma b$ and $b\sigma x$ imply $a\sigma x$; (3) $a\sigma b$ implies $(a+x)\overrightarrow{\sigma }(b+x)$ and $(x+a)\overrightarrow{\sigma }(x+b)$; (4) $a\sigma b$ implies $(a·x)\overrightarrow{\sigma }(b·x)$ and $(x·a)\overrightarrow{\sigma }(x·b)$; (5) $a\sigma b$ and $b\sigma a$ imply $(a+x)\tilde{\sigma }(b+x)$ and $(x+a)\tilde{\sigma }(x+b)$; (6) $a\sigma b$ and $b\sigma a$ imply $(a·x)\tilde{\sigma }(b·x)$ and $(x·a)\tilde{\sigma }(x·b)$. Note that the (partial) order relation ≤ on an ordered hyperring R is a weak pseudoorder. By $R/{\sigma }^{*}$ we mean the set of all equivalence classes with respect to ${\sigma }^{*}$, i.e., $R/{\sigma }^{*}=\left\{{\sigma }^{*}\left(x\right)\right|x\in R\}$. Let $\sigma$ be a weak pseudoorder on an ordered hyperring $(R,+,·,\le )$. Then, there exists a regular equivalence relation

$${\sigma }^{*}=\{(x,y)\in R\times R|x\sigma y\mathrm{and}y\sigma x\}$$

on R such that $(R/{\sigma }^{*},\oplus ,\odot ,⪯)$ is an ordered hyperring, where

$$⪯:=\{({\sigma }^{*}\left(x\right),{\sigma }^{*}\left(y\right))\in R/{\sigma }^{*}\times R/{\sigma }^{*}|\exists a\in {\sigma }^{*}\left(x\right),\exists b\in {\sigma }^{*}\left(y\right)\mathrm{such}\mathrm{that}(a,b)\in \sigma \}.$$

Theorem 2.

Let $\phi :R\to T$ be a homomorphism between two ordered hyperrings $(R,+,·,\le )$ and $(T,\oplus ,\odot ,⪯)$. Then, the relation

$$\sigma :=\left\{\right(x,y)\in R\times R|\phi \left(x\right)⪯\phi \left(y\right)\}$$

on R is a weak pseudoorder.

Proof. 

Assume that $(x,y)\in \le$. Since $\phi$ is a homomorphism, we obtain

$$\left(\phi \right(x),\phi (y\left)\right)\in ⪯.$$

So, $(x,y)\in \sigma$. It implies that $\le \subseteq \sigma$.

Let $(x,y)\in \sigma$ and $(y,z)\in \sigma$. Then, $\phi \left(x\right)⪯\phi \left(y\right)$ and $\phi \left(y\right)⪯\phi \left(z\right)$. By transitivity of ⪯, we have $\phi \left(x\right)⪯\phi \left(z\right)$. So, $(x,z)\in \sigma$.

Now, let $(x,y)\in \sigma$ and $z\in R$. Then, $\phi \left(x\right)⪯\phi \left(y\right)$. Since T is an ordered hyperring, we have

$$\phi \left(x\right)\oplus \phi \left(z\right)⪯\phi \left(y\right)\oplus \phi \left(z\right).$$

Thus, ${\displaystyle \bigcup _{\begin{array}{c}u\in x+z\end{array}}}\phi \left(u\right)⪯{\displaystyle \bigcup _{\begin{array}{c}v\in y+z\end{array}}}\phi \left(v\right)$. So, for every $u\in x+z$ there exists $v\in y+z$ such that $\phi \left(u\right)⪯\phi \left(v\right)$, i.e., $(u,v)\in \sigma$. Hence, $x+z\overrightarrow{\sigma }y+z$. Similarly, we have

$$z+x\overrightarrow{\sigma }z+y,$$

$$x·z\overrightarrow{\sigma }y·z,$$

$$z·x\overrightarrow{\sigma }z·y.$$

If $(x,y)\in \sigma$ and $(y,x)\in \sigma$, then $\phi \left(x\right)⪯\phi \left(y\right)$ and $\phi \left(y\right)⪯\phi \left(x\right)$. So, $\phi \left(x\right)=\phi \left(y\right)$. This implies that $\phi \left(x\right)\oplus \phi \left(z\right)=\phi \left(y\right)\oplus \phi \left(z\right)$, i.e., ${\displaystyle \bigcup _{\begin{array}{c}u\in x+z\end{array}}}\phi \left(u\right)={\displaystyle \bigcup _{\begin{array}{c}v\in y+z\end{array}}}\phi \left(v\right)$. So, for every $u\in x+z$ there exists $v\in y+z$ such that $\phi \left(u\right)=\phi \left(v\right)$. It follows that $\phi \left(u\right)⪯\phi \left(v\right)$ and $\phi \left(v\right)⪯\phi \left(u\right)$. Thus $(u,v)\in \sigma$ and $(v,u)\in \sigma$. On the other hand, for every $v^{\prime }\in y+z$ there exists $u^{\prime }\in x+z$ such that $\phi \left(u^{\prime }\right)=\phi \left(v^{\prime }\right)$. So, $\phi \left(u^{\prime }\right)⪯\phi \left(v^{\prime }\right)$ and $\phi \left(v^{\prime }\right)⪯\phi \left(u^{\prime }\right)$. Hence $(u^{\prime },v^{\prime })\in \sigma$ and $(v^{\prime },u^{\prime })\in \sigma$. Therefore, $x+z\tilde{\sigma }y+z$. Similarly, we have

$$z+x\tilde{\sigma }z+y,$$

$$x·z\tilde{\sigma }y·z,$$

$$z·x\tilde{\sigma }z·y.$$

Hence, the theorem is proved. □

Let $(R,+,·,\le )$ be an ordered hyperring, $\sigma ,\theta$ be weak pseudoorders on R such that $\sigma \subseteq \theta$. We define a relation $\theta /\sigma$ on $R/{\sigma }^{*}$ as follows:

$$\theta /\sigma :=\{({\sigma }^{*}\left(a\right),{\sigma }^{*}\left(b\right))\in R/{\sigma }^{*}\times R/{\sigma }^{*}\mid \exists x\in {\sigma }^{*}\left(a\right),\exists y\in {\sigma }^{*}\left(b\right)$$

$$\mathrm{such}\mathrm{that}(x,y)\in \theta \}.$$

Then, we can see that

$$({\sigma }^{*}\left(a\right),{\sigma }^{*}\left(b\right))\in \theta /\sigma \iff (a,b)\in \theta .$$

Theorem 3.

Let $(R,+,·,\le )$ be an ordered hyperring, $\sigma ,\theta$ be weak pseudoorders on R such that $\sigma \subseteq \theta$. Then,

(1)

$\theta /\sigma$ is a weak pseudoorder on $R/{\sigma }^{*}$.

(2)

$(R/{\sigma }^{*})/{(\theta /\sigma )}^{*}\cong R/{\theta }^{*}$.

Proof. 

(1) Clearly, $\theta /\sigma$ is a weak pseudoorder on $R/{\sigma }^{*}$.

(2) We assert that the mapping $\psi :R/{\sigma }^{*}\to R/{\theta }^{*}|{\sigma }^{*}\left(a\right)\mapsto {\theta }^{*}\left(a\right)$ is a homomorphism. We first show that $\psi$ is well-defined. Let ${\sigma }^{*}\left(a\right)={\sigma }^{*}\left(b\right)$. Then $(a,b)\in {\sigma }^{*}$. Hence, by the definition of ${\sigma }^{*}$, $(a,b)\in \sigma \subseteq \theta$ and $(b,a)\in \sigma \subseteq \theta$. This implies that $(a,b)\in {\theta }^{*}$ and so ${\theta }^{*}\left(a\right)={\theta }^{*}\left(b\right)$. Therefore, $\psi$ is well-defined. Now, let ${\sigma }^{*}\left(x\right),{\sigma }^{*}\left(y\right)\in R/{\sigma }^{*}$. We have

$$\begin{array}{cc}\psi \left({\sigma }^{*}\left(x\right){\oplus }_{\sigma }{\sigma }^{*}\left(y\right)\right)\hfill & ={\displaystyle \bigcup _{\begin{array}{c}u\in x+y\end{array}}}\psi \left({\sigma }^{*}\left(u\right)\right)\hfill \\ \\ & ={\displaystyle \bigcup _{\begin{array}{c}u\in x+y\end{array}}}{\theta }^{*}\left(u\right)\hfill \\ \\ & ={\theta }^{*}\left(x\right){\oplus }_{\theta }{\theta }^{*}\left(y\right)\hfill \\ \\ & =\psi \left({\sigma }^{*}\left(x\right)\right){\oplus }_{\theta }\psi \left({\sigma }^{*}\left(y\right)\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\psi \left({\sigma }^{*}\left(x\right){\odot }_{\sigma }{\sigma }^{*}\left(y\right)\right)\hfill & ={\displaystyle \bigcup _{\begin{array}{c}v\in x·y\end{array}}}\psi \left({\sigma }^{*}\left(v\right)\right)\hfill \\ \\ & ={\displaystyle \bigcup _{\begin{array}{c}v\in x·y\end{array}}}{\theta }^{*}\left(v\right)\hfill \\ \\ & ={\theta }^{*}\left(x\right){\odot }_{\theta }{\theta }^{*}\left(y\right)\hfill \\ \\ & =\psi \left({\sigma }^{*}\left(x\right)\right){\odot }_{\theta }\psi \left({\sigma }^{*}\left(y\right)\right).\hfill \end{array}$$

Furthermore, if ${\sigma }^{*}\left(x\right){⪯}_{\sigma }{\sigma }^{*}\left(y\right)$, then $(x,y)\in \sigma \subseteq \theta$ and this implies that ${\theta }^{*}\left(x\right){⪯}_{\theta }{\theta }^{*}\left(y\right)$, i.e., $\psi$ is isotone. Hence, $\psi$ is a homomorphism. Also, we have

$$\begin{array}{c}Im\psi =\left\{\psi \left({\sigma }^{*}\left(a\right)\right)\right|a\in R\}=\left\{{\theta }^{*}\left(a\right)\right|a\in R\}=R/{\theta }^{*}.\hfill \end{array}$$

Now, let

$$\begin{array}{c}k:=\left\{({\sigma }^{*}\left(x\right),{\sigma }^{*}\left(y\right))\right|\psi \left({\sigma }^{*}\left(x\right)\right){⪯}_{\theta }\psi \left({\sigma }^{*}\left(y\right)\right)\}\hfill \end{array}$$

Then,

$$\begin{array}{cc}({\sigma }^{*}\left(x\right),{\sigma }^{*}\left(y\right))\in k\hfill & \iff \psi \left({\sigma }^{*}\left(x\right)\right){⪯}_{\theta }\psi \left({\sigma }^{*}\left(y\right)\right)\hfill \\ \\ & \iff {\theta }^{*}\left(x\right){⪯}_{\theta }{\theta }^{*}\left(y\right)\hfill \\ \\ & \iff (x,y)\in \theta \hfill \\ \\ & \iff ({\sigma }^{*}\left(x\right),{\sigma }^{*}\left(y\right))\in \theta /\sigma .\hfill \end{array}$$

So, $k=\theta /\sigma$ and thus $Ker\psi ={(\theta /\sigma )}^{*}$. This completes the proof. □

We continue this section with the following definition.

Definition 2.

A subsemihypergroup K of an ordered Γ-semihypergroup $(S,\mathsf{\Gamma },\le )$ is called a left (resp. right) weak interior hyperideal of S if

(1) 

$S\mathsf{\Gamma }K\mathsf{\Gamma }K\subseteq K$ (resp. $K\mathsf{\Gamma }K\mathsf{\Gamma }S\subseteq K$);

(2) 

$\left(K\right]\subseteq K$.

A non-empty subset K of an ordered hyperstructure S is said to be weak interior hyperideal if K is a left and a right weak interior hyperideal of S.

Lemma 1.

Every interior hyperideal of an ordered hyperstructure S is a left weak interior hyperideal of S.

Proof. 

Let K be an interior hyperideal of an ordered $\mathsf{\Gamma }$-semihypergroup S. Then,

$$S\mathsf{\Gamma }K\mathsf{\Gamma }K\subseteq S\mathsf{\Gamma }K\mathsf{\Gamma }S\subseteq K.$$

So, K is a left weak interior hyperideal of S. □

In the following example, we show that the converse of Lemma 1 is not true in general.

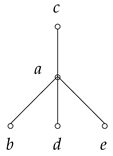
Example 1.

Consider the set $S=\{a,b,c,d,e\}$, where $\mathsf{\Gamma }=\{\circ \}$, with

$$\begin{array}{cccccc}\circ & a& b& c& d& e\\ a& a& \{a,b\}& \{a,c\}& \{a,d\}& e\\ b& a& \{a,b\}& \{a,c\}& \{a,d\}& e\\ c& a& \{a,b\}& \{a,c\}& \{a,d\}& e\\ d& a& \{a,b\}& \{a,c\}& \{a,d\}& e\\ e& a& \{a,b\}& \{a,c\}& \{a,d\}& e\end{array}$$

$$\begin{array}{cc}\le \hfill & :=\left\{\right(a,a),(a,c),(b,a),(b,b),(b,c),(c,c),\hfill \\ & (d,a),(d,c),(d,d),(e,a),(e,c),(e,e)\}.\hfill \end{array}$$

Then $(S,\circ ,\le )$ is an ordered semihypergroup. The covering relation and the figure of S are given by:

$$\begin{array}{c}\prec =\left\{\right(a,c),(b,a),(d,a),(e,a\left)\right\}.\hfill \end{array}$$

Put $K=\{a,b,d,e\}$. Clearly, K is a subsemihypergroup of S. We have

$$S\circ K\circ K=\{a,b,d,e\}\subseteq K,$$

$$\left(K\right]=K.$$

Therefore, K is a left weak interior hyperideal of S. On the other hand,

$$S\circ K\circ S=S⊈K.$$

Hence, K is not an interior hyperideal of S.

The intersection of any family of left weak interior hyperideals of an ordered hyperstructure S is a left weak interior hyperideal of S.

Lemma 2.

Let $(S,\mathsf{\Gamma },\le )$ be an ordered Γ-semihypergroup. If M is a left weak interior hyperideal and N is a left hyperideal of S, then $L=M\cap N$ is a left weak interior hyperideal of S. If $\mathsf{\Gamma }=\{\circ \}$, then $(S,\mathsf{\Gamma },\le )$ is an ordered semihypergroup.

Proof. 

By hypothesis, we get

$$S\mathsf{\Gamma }L\mathsf{\Gamma }L\subseteq S\mathsf{\Gamma }M\mathsf{\Gamma }M\subseteq M,$$

and

$$S\mathsf{\Gamma }L\mathsf{\Gamma }L\subseteq S\mathsf{\Gamma }N\mathsf{\Gamma }N\subseteq N\mathsf{\Gamma }N\subseteq N.$$

It means that

$$S\mathsf{\Gamma }L\mathsf{\Gamma }L\subseteq M\cap N=L.$$

Now, let $x\in L$, $y\in S$ and $y\le x$. Then $x\in M$ and $x\in N$. Since $\left(M\right]\subseteq M$ and $\left(N\right]\subseteq N$, we have $y\in M$ and $y\in N$. Hence, $y\in M\cap N=L$. Thus, $\left(L\right]\subseteq L$. Therefore, L is a left weak interior hyperideal of S. □

Let K be a left weak interior hyperideal of an ordered $\mathsf{\Gamma }$-semihypergroup S. If $S=\left(S\mathsf{\Gamma }a\right]$ for all $a\in S$, then K is a quasi-hyperideal of S. Indeed: let $x\in K$. Then $S\mathsf{\Gamma }x\subseteq S\mathsf{\Gamma }K$. So, $\left(S\mathsf{\Gamma }x\right]\subseteq \left(S\mathsf{\Gamma }K\right]$. By hypothesis, $\left(S\mathsf{\Gamma }x\right]=S$. Thus, $S\subseteq \left(S\mathsf{\Gamma }K\right]\subseteq S$ and so $S=\left(S\mathsf{\Gamma }K\right]$. Since K is a left weak interior hyperideal of S, we get $S\mathsf{\Gamma }K\mathsf{\Gamma }K\subseteq K$. Thus $\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]\subseteq \left(K\right]=K$. On the other hand,

$$\begin{array}{cc}\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]\hfill & =\left(\right(S\mathsf{\Gamma }K\left)\mathsf{\Gamma }K\right]\hfill \\ \\ & =\left(\right(S\mathsf{\Gamma }K\left]\mathsf{\Gamma }\right(K\left]\right]\hfill \\ \\ & =\left(S\mathsf{\Gamma }K\right]\hfill \\ \\ & =S.\hfill \end{array}$$

So, $S\subseteq K$ and hence $S=K$. Now,

$$\left(K\mathsf{\Gamma }S\right]\cap \left(S\mathsf{\Gamma }K\right]=\left(K\mathsf{\Gamma }S\right]\cap S=\left(K\mathsf{\Gamma }S\right]\cap K\subseteq K.$$

Therefore, K is a quasi-hyperideal of S.

Theorem 4.

Let K be a left hyperideal of the left hyperideal L of an ordered Γ-semihypergroup S. Then K is a left weak interior hyperideal of S.

Proof. 

Since K is a left hyperideal of L, we get $L\mathsf{\Gamma }K\subseteq K$. As $S\mathsf{\Gamma }L\subseteq L$, we have

$$S\mathsf{\Gamma }K\mathsf{\Gamma }K\subseteq S\mathsf{\Gamma }L\mathsf{\Gamma }K\subseteq L\mathsf{\Gamma }K\subseteq K.$$

Now, let $a\in K\subseteq L$ and $x\in S$ such that $x\le a$. Since L is a left hyperideal of S, it follows that $x\in L$. By hypothesis, K is a left hyperideal of L. So, $x\in K$. Hence, $\left(K\right]\subseteq K$. Therefore, K is a left weak interior hyperideal of S. □

Theorem 5.

Let $(S,\mathsf{\Gamma },\le )$ be a commutative ordered Γ-semihypergroup. Then S is regular if and only if $\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]=K$ for every left weak interior hyperideal K of S.

Proof. 

Necessity. Let K be a left weak interior hyperideal of S. Then $S\mathsf{\Gamma }K\mathsf{\Gamma }K\subseteq K$. So, $\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]\subseteq \left(K\right]=K$. Take any $x\in K$. Since S is regular, there exist $y\in S$ and $\alpha ,\beta \in \mathsf{\Gamma }$ such that

$$\begin{array}{cc}x\hfill & \le x\alpha y\beta x\hfill \\ \\ & =y\alpha x\beta x\hfill \\ \\ & \subseteq S\mathsf{\Gamma }K\mathsf{\Gamma }K.\hfill \end{array}$$

Hence, $x\le u$ for some $u\in S\mathsf{\Gamma }K\mathsf{\Gamma }K$. This means that $x\in \left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]$. So, $K\subseteq \left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]$. Therefore, $\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]=K$ for every left weak interior hyperideal K of S.

Sufficiency. Let $\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]=K$ for every left weak interior hyperideal K of S. If $M,N$ are right and left hyperideals of S, respectively, then $M\cap N$ is a left weak interior hyperideal of S. So,

$$\begin{array}{cc}M\cap N\hfill & =\left(S\mathsf{\Gamma }\right(M\cap N\left)\mathsf{\Gamma }\right(M\cap N\left)\right]\hfill \\ \\ & \subseteq \left(S\mathsf{\Gamma }N\mathsf{\Gamma }M\right]\hfill \\ \\ & \subseteq \left(N\mathsf{\Gamma }M\right]\hfill \\ \\ & =\left(M\mathsf{\Gamma }N\right].\hfill \end{array}$$

On the other hand,

$$\left(M\mathsf{\Gamma }N\right]\subseteq \left(M\mathsf{\Gamma }N\right]\subseteq \left(M\right]=M.$$

Similarly, $\left(M\mathsf{\Gamma }N\right]\subseteq N$. Hence, $\left(M\mathsf{\Gamma }N\right]\subseteq M\cap N$. Thus $M\cap N=\left(M\mathsf{\Gamma }N\right]$ for any right hyperideal M and left hyperideal N of S. Now, by Theorem 1, S is a regular ordered $\mathsf{\Gamma }$-semihypergroup. □

Corollary 1.

Let $(S,\mathsf{\Gamma },\le )$ be a commutative ordered Γ-hypergroup. Then $\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]=K$ for every left weak interior hyperideal K of S.

Proof. 

Clearly, every ordered $\mathsf{\Gamma }$-hypergroup is a regular ordered $\mathsf{\Gamma }$-semihypergroup. Now, by Theorem 5, $\left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]=K$ for every left weak interior hyperideal K of S. □

An ordered hyperstructure S is said to be left (resp. right) weak interior simple if S has no proper left (resp. right) weak interior hyperideals. Also, S is said to be weak interior simple if it does not contain proper weak interior hyperideals, i.e., for any weak interior hyperideal $\varnothing \ne K\subseteq S$, we have $K=S$. If S is a left (right) weak interior simple ordered hyperstructure, then S is a weak interior simple ordered hyperstructure.

Example 2. 

(1) 

Define the symmetrical hyperoperation $\mathsf{\Gamma }=\{\circ \}$ and (partial) order relation ≤ on $S=\{e,a,b,c\}$ as follows:

$$\begin{array}{ccccc}\circ & e& a& b& c\\ e& c& \{a,b\}& \{a,b\}& c\\ a& \{a,b\}& c& c& \{a,b\}\\ b& \{a,b\}& c& c& \{a,b\}\\ c& c& \{a,b\}& \{a,b\}& c\end{array}$$

$$\begin{array}{cc}\le \hfill & :=\left\{\right(e,e),(e,c),(a,a),(a,b),(b,b),(c,c\left)\right\}.\hfill \end{array}$$

Then $(S,\circ ,\le )$ is an ordered semihypergroup. We can easily verify that S is a left weak interior simple ordered semihypergroup.

(2) 

Let $(R,+,·,\le )$ be an ordered hyperring with the following symmetrical tables and (partial) order relation ≤:

$$\begin{array}{cccc}+& u& v& w\\ u& \{u,v\}& \{u,v\}& R\\ v& \{u,v\}& \{u,v\}& R\\ w& R& R& R\end{array}\begin{array}{cccc}·& u& v& w\\ u& R& R& R\\ v& R& \{v,w\}& \{v,w\}\\ w& R& \{v,w\}& \{v,w\}\end{array}$$

$$\le =\left\{\right(u,u),(u,v),(u,w),(v,v),(v,w),(w,w\left)\right\}.$$

It is not difficult to verify that R is a weak interior simple ordered hyperring.

Theorem 6.

Let $(S,\mathsf{\Gamma },\le )$ be an ordered Γ-semihypergroup. Then, S is left weak interior simple if and only if $\left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]=S$ for all $x\in S$.

Proof. 

Necessity. Let S be a left weak interior simple ordered $\mathsf{\Gamma }$-semihypergroup and $x\in S$. We assert that $\left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$ is a left weak interior hyperideal of S. Let $a\in S$ and $y\in \left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$. Then $y\le u$ for some $u\in S\mathsf{\Gamma }x\mathsf{\Gamma }x$. Since $u\in S\mathsf{\Gamma }x\mathsf{\Gamma }x$, we get $u\in z\alpha x\beta x$ where $z\in S$ and $\alpha ,\beta \in \mathsf{\Gamma }$. By hypothesis, we obtain

$$\begin{array}{cc}a\gamma y\hfill & \le a\gamma u\hfill \\ \\ & \subseteq a\gamma \left(z\alpha x\beta x\right)\hfill \\ \\ & =\left(a\gamma z\right)\alpha x\beta x\hfill \\ \\ & \subseteq S\mathsf{\Gamma }x\mathsf{\Gamma }x.\hfill \end{array}$$

So, $a\gamma y\subseteq \left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$. It means that $S\mathsf{\Gamma }\left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]\subseteq \left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$. Now, let $a\in \left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$, $b\in S$ and $b\le a$. Since $a\in \left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$, it follows that $a\le u$ for some $u\in S\mathsf{\Gamma }x\mathsf{\Gamma }x$. As ≤ is transitive, we get $b\le u$. So, $b\in \left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$. Therefore, $\left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$ is a left hyperideal of S. Clearly, every left hyperideal is a left weak interior hyperideal of S. Hence, $\left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]$ is a left weak interior hyperideal of S. Since S is simple, we get $\left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]=S$ for all $x\in S$.

Sufficiency. Suppose that $\left(S\mathsf{\Gamma }x\mathsf{\Gamma }x\right]=S$ for all $x\in S$. Let K be a left weak interior hyperideal of S and $a\in K$. Then,

$$S=\left(S\mathsf{\Gamma }a\mathsf{\Gamma }a\right]\subseteq \left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right]\subseteq \left(K\right]=K.$$

So, $S\subseteq K$ and hence $K=S$. Therefore, S is a left weak interior simple ordered $\mathsf{\Gamma }$-semihypergroup. □

Proposition 1.

A left weak interior hyperideal K of S is said to be minimal if K does not properly contain any left weak interior hyperideal of S. Assume that K is a left weak interior hyperideal of an ordered Γ-semihypergroup $(S,\mathsf{\Gamma },\le )$. Then, K is a left weak interior simple subsemihypergroup of S if and only if K is a minimal left weak interior hyperideal of S.

Proof. 

Necessity. Let C be a left weak interior hyperideal of S and $C\subseteq K$. Then,

$$K\mathsf{\Gamma }C\mathsf{\Gamma }C\subseteq S\mathsf{\Gamma }C\mathsf{\Gamma }C\subseteq C.$$

Hence, C is a left weak interior hyperideal of K. As K is simple, we have $C=K$. Thus, K is a minimal left weak interior hyperideal of S.

Sufficiency. Suppose that K is a minimal left weak interior hyperideal of S. Let L be a left weak interior hyperideal of K. Then $K\mathsf{\Gamma }L\mathsf{\Gamma }L\subseteq L$. Put $\mathcal{C}={\left(K\mathsf{\Gamma }L\mathsf{\Gamma }L\right]}_L$. Then $\varnothing \ne \mathcal{C}\subseteq L\subseteq K$. We assert that $\mathcal{C}$ is a left weak interior hyperideal of S. Let $c_1,c_2\in \mathcal{C}$. Then $c_1\le a_1{\alpha }_1{l}_1{\beta }_1{l}_1^{\prime }$ and $c_2\le a_2{\alpha }_2{l}_2{\beta }_2{l}_2^{\prime }$ for some $a_1,a_2\in A$, $l_1,l_1^{\prime },l_2,l_2^{\prime }\in L$ and ${\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2\in \mathsf{\Gamma }$. So,

$$\begin{array}{cc}{c}_1\gamma c_2\hfill & =\left(a_1{\alpha }_1{l}_1{\beta }_1{l}_1^{\prime }\right)\gamma \left(a_2{\alpha }_2{l}_2{\beta }_2{l}_2^{\prime }\right)\hfill \\ \\ & \subseteq \left(K\mathsf{\Gamma }L\mathsf{\Gamma }L\right)\mathsf{\Gamma }\left(K\mathsf{\Gamma }L\mathsf{\Gamma }L\right)\hfill \\ \\ & \subseteq L\mathsf{\Gamma }L\hfill \\ \\ & \subseteq L.\hfill \end{array}$$

where $\gamma \in \mathsf{\Gamma }$. Thus $c_1\gamma c_2\subseteq {\left(K\mathsf{\Gamma }L\mathsf{\Gamma }L\right]}_L=\mathcal{C}$. Therefore, $\mathcal{C}$ is a subsemihypergroup of S. Now, let $x\in S$ and $\lambda ,\mu \in \mathsf{\Gamma }$. Then,

$$\begin{array}{cc}x\lambda c_1\mu c_2\hfill & \le x\lambda \left(a_1{\alpha }_1{l}_1{\beta }_1{l}_1^{\prime }\right)\mu \left(a_2{\alpha }_2{l}_2{\beta }_2{l}_2^{\prime }\right)\hfill \\ \\ & =\left(x\lambda a_1{\alpha }_1{l}_1\right){\beta }_1{l}_1^{\prime }\mu \left(a_2{\alpha }_2{l}_2{\beta }_2{l}_2^{\prime }\right)\hfill \\ \\ & \subseteq \left(S\mathsf{\Gamma }K\mathsf{\Gamma }K\right)\mathsf{\Gamma }L\mathsf{\Gamma }\left(K\mathsf{\Gamma }L\mathsf{\Gamma }L\right)\hfill \\ \\ & \subseteq K\mathsf{\Gamma }L\mathsf{\Gamma }L\hfill \\ \\ & \subseteq L.\hfill \end{array}$$

Since L is a left weak interior hyperideal of K and

$$x\lambda c_1\mu c_2\subseteq S\mathsf{\Gamma }\mathcal{C}\mathsf{\Gamma }\mathcal{C}\subseteq S\mathsf{\Gamma }K\mathsf{\Gamma }K\subseteq K,$$

we get $x\lambda c_1\mu c_2\subseteq L$. It implies that $x\lambda c_1\mu c_2\subseteq {\left(K\mathsf{\Gamma }L\mathsf{\Gamma }L\right]}_L=\mathcal{C}$. So, $S\mathsf{\Gamma }\mathcal{C}\mathsf{\Gamma }\mathcal{C}\subseteq \mathcal{C}$.

Now, let $u\in \left(\mathcal{C}\right]$. Then $u\le v$ for some $v\in \mathcal{C}$. Since $v\in \mathcal{C}$, there exist $l,l^{\prime }\in L$, $a\in K$ and $\gamma ,\delta \in \mathsf{\Gamma }$ such that

$$\begin{array}{cc}v\hfill & \le a\gamma l\delta l^{\prime }\hfill \\ \\ & \subseteq K\mathsf{\Gamma }L\mathsf{\Gamma }L\hfill \\ \\ & \subseteq L\hfill \\ \\ & \subseteq K.\hfill \end{array}$$

As K is a left weak interior hyperideal of S, we get $v\in K$. Since $u\le v\in K$ and $\left(K\right]\subseteq K$, we obtain $u\in K$. Hence, $K\ni u\le v$ for some $v\in L$. Since L is a left weak interior hyperideal of K, it follows that $u\in L$. It implies that $u\in {\left(K\mathsf{\Gamma }L\mathsf{\Gamma }L\right]}_L=\mathcal{C}$. Thus, $\left(\mathcal{C}\right]\subseteq \mathcal{C}$. Hence, $\mathcal{C}$ is a left weak interior hyperideal of S. As K is a minimal left weak interior hyperideal of S, we get $\mathcal{C}=K$. It implies that $L=K$. Therefore, K is a left weak interior simple subsemihypergroup of S. □

4. Conclusions

In this paper, we have proved some results on weak pseudoorders in quotient ordered hyperrings. Also, we have studied some properties of left weak interior hyperideals of ordered hyperstructures. A characterization of a regular ordered hyperstructure via a left weak interior hyperideal is given. We finished our study with the characterization of weak interior simple ordered $\mathsf{\Gamma }$-semihypergroups in terms of left weak interior hyperideals in order to other ordered hyperstructures such as ordered hyperrings can be discussed in a similar way. For future work, it will be interesting to study fuzzy (left) weak interior hyperideals of ordered hyperstructures. Also, we plan to study uni-soft weak interior hyperideals in ordered hyperstructures. Our purpose in the future is to establish a connection between almost weak interior hyperideals and weak interior hyperideals in ordered hyperstructures.