Abstract
In our investigation on quantum gravity, we introduce an infinite dimensional complex Lie algebra that extends . It is defined through a symmetric Cartan matrix of a rank 12 Borcherds algebra. We turn into a Lie superalgebra with no superpartners, in order to comply with the Pauli exclusion principle. There is a natural action of the Poincaré group on , which is an automorphism in the massive sector. We introduce a mechanism for scattering that includes decays as particular resonant scattering. Finally, we complete the model by merging the local into a vertex-type algebra.
1. Introduction
This is the second of two papers—see also [1]—describing an algebraic model of quantum gravity.
Our guiding idea was to exploit the most fundamental principles of quantum mechanics and general relativity as we believe they should apply in the extreme conditions of a hot dense universe in its early stages.
We started from two very intuitive physical principles:
- there is no classical observable to be quantized: one has to think directly in terms of quantum objects and states of the system;
- there is no spacetime geometry to start with.
As to the first point, the model departs from the conventional view that quantum gravity ought to be realized as the quantization of gravity with its renormalization, with the four fundamental forces unifying at the Planck scale. We are at the Plank scale: the dynamics only depends on the quantum charges of the constituents and they are indeed symmetrical. Gravity is identified with the way spacetime is created and evolves. It is quantum because spacetime is created via quantum interactions, producing curvature, and quantum expansion, as they both occur with complex probability amplitudes.
Although everything looks symmetrical, diversity comes from quantum theory itself, and from the initial conditions.
As to the second point, the absence of spacetime to start with leaves us with the sole interactions that we assume to be tree-like, as physical observations at very high temperature suggest. The basic blocks involve therefore three objects, and this has led us to consider algebraic models, with the algebra product playing the role of the building blocks of all interactions. A mechanism for the quantum creation of spacetime suggested the inclusion of momenta within the charges (roots) of the algebra, thus achieving charge and energy-momentum conservation as well. The evolution of the universe, its quantum interactions and quantum expansion from a chosen initial state of a finite set of generators, can be turned into an algorithm in which all physical quantities are, in principle, calculable. We would need a huge powerful computer to do that, but this is not the point of our two papers. Our point is: trying to think outside the box by going back to the basic physical principles, and by building a consistent model that can accommodate the physics we know.
In this respect, we would like to emphasize that our main object is a superalgebra. Again we were led to it by fundamental physics, the Pauli principle in particular. The way we define it does not leave room for superpartners. Superparticles have not been observed and we can describe all the physical interactions without any need of supersymmetry for renormalization purposes: our theory is finite.
It also turns out, by construction, that spacetime in our model is discrete, simply because, if we start, at say , with a finite set of generators, the number of interactions will stay finite at and spacetime will be created in finite chunks, with certain probability amplitudes, see [1]. What we have denoted here by t is an order parameter for the succession of interactions, and is interpreted as universal time. Nevertheless we show that there is a natural action of the Poincaré group in our model. This is crucial for its relationship with the concept of spin and with relativity. Since the model has an intrinsic notion of universal time, how do we compare future observers measurements? Where is relativity of time and space? If a particle has a certain intrinsic momentum included in a root of the algebra, how do we describe an interaction in the rest frame of a massive particle? These are crucial questions coming from the physics we know and experiment. To answer these questions we show that a local action of the Poincaré group is defined and has the right properties as a Wigner representation, even though spacetime is discrete.
As a final remark on this preliminary conceptual outline, let us focus on the interactions. Their building blocks involve three objects and are mathematically described by the multiplication law of the algebra. A generator in the algebra is related to a particle, with certain charges coming from the algebra roots, but it is also related to a quantum field, since new generators are produced by multiplication in the algebra: a generator expands in spacetime with complex quantum amplitudes but locally interacts, and disappears and contributes to the creation of new generators. This local action can be considered as a vertex, made of generators obeying the rules of an algebra. There is no vacuum since space points exist only where generators are. We see therefore that we do have an algebra at the core of the model, that we denote , but the expansion of spacetime embeds it into a larger picture: that of a vertex-type algebra describing quantum interactions and a quantum generated spacetime.
We believe the above considerations are plausible and strongly based on fundamental physics. Their concrete, calculable realization is what we have achieved with our model, which has no claim other than being physically consistent and mathematically rigorous.
In the first paper we have described the basic principles of our model and we have investigated the mathematical structures that may suit our purpose. In particular, we have focused on rank-12 infinite dimensional Kac-Moody, [2], and Borcherds algebras, [3,4], and we have given physical and mathematical reasons why the latter are preferable.
In our model for the expansion of quantum early Universe, [1,5], the need for an infinite dimensional Lie algebra stems from the unlimited number of possible 4-momenta, but at each fixed cosmological time the number of generators and roots involved is finite. There is a known algorithm of Lie algebra theory that allows to determine the structure constants among a finite number of generators of a Borcherds algebra [3,4]. Let us grade the commutators by levels, by saying that the commutators involving n simple roots have level . A consistent set of structure constants is calculable level by level, and once the structure constants are calculated at level n, they will not be affected by the calculation at any level . There are computer programs that apply this algorithm and give the explicit structure constants level by level, see for instance the package LieRing of GAP, developed by S. Cicalò and W.A. de Graaf [6].
However, for the sake of simplicity, in [1] we have chosen to deal with a simpler Lie algebra, that extends and . In the present paper, we will start investigating a physical model for quantum gravity based on this particular rank-12 algebra . We will start by focussing on local aspects of the algebraic model: in Section 2, we recall , which is then turned into a Lie superalgebra in Section 3. Section 4 will then discuss interactions, scattering processes and decays, whereas the role of the Poincaré group is analyzed in Section 5. Finally, in Section 6 and Section 7 we will define the quantum states, and then we will merge the algebra into a vertex-type algebra, representing the quantum early Universe with its expanding spacetime.
2. The Lie Algebra
We start and consider , the Lie subalgebra of the rank-12 Borcherds algebra introduced in [1] and generated by the Chevalley generators corresponding to positive roots. A further simplification will then give rise to , the Lie algebra that acts locally on the quantum state of the Universe [1].
We recall from [1] that the generalized Cartan matrix for the Borcherds algebra , with simple roots denoted by , is
By defining
the 4-momentum vector can be written as
Then, we restrict to the subalgebra of , namely to positive roots , , with . Consequently, the 4-momentum (3) becomes
with , implying
namely p either lightlike or timelike. In particular (),
Remark 1.
Notice that the mass of a particle cannot be arbitrary small, since there is a lower limit, .
Hence, we extend the possible values of the 4-momentum by including those with opposite 3-momentum , as explained in [1], so that
The algebra extends the 1 + 1-dimensional toy model based on discussed in [1]; it is defined as the algebra generated by and , such that , satisfying the following commutation relations:
where is the Euclidean scalar product in , the function is the asymmetry function [1,2,7], and
in order to have an antisymmetric algebra.
Moreover, for consistency, we require that
Notice that implies .
Remark 2.
Notice also that imply . Thus, there is a subalgebra of with the same commutation relations (10), but with generators and such that (only massive particles).
The proof is in Appendix A.
The algebra has a natural 2-grading inherited by that of , due to the decomposition into the subalgebra and its Weyl spinor, [1]. The generators are fermionic (resp. bosonic) if is fermionic (resp. bosonic), whereas the generators are bosonic, due to the commutation relations (10).
3. The Lie Superalgebra
In order to turn the Lie algebra into a Lie superalgebra, we exploit the Grassmann envelope of ,
where is the boson subalgebra of , its fermionic part, and are the even, odd parts of a Grassmann algebra with infinitely many generators. More precisely, we map each generator X of to the generator of , where is even if X is bosonic, odd if X is fermionic, and if . Then the graded Jacobi identity is satisfied, [8], and one obtains, by linearity, a Lie superalgebra, that we denote by .
Let us show this straightforward calculation explicitly.
Let be generators of of degree respectively. We remind, from [1], that the generators have degree 0, whereas the generators have degree if is bosonic and degree if is fermionic.
Let still denote the product of in and the corresponding product in . Then:
and the graded Jacobi identity is satisfied:
where is the Jacobi identity for .
Remark 3.
The product in the Lie superalgebra is effectively the same as in the Lie algebra but its symmetry property is crucial for the elements of the universal enveloping algebra, that appear point by point in the model for the expanding Universe. The universal enveloping algebra is indeed the tensor algebra modulo the relations for all , embedded in the tensor algebra, of degree respectively. In particular this makes the fermions comply with the Pauli exclusion principle: , for x fermionic, whereas the same relation is trivial, , if x is bosonic.
Remark 4.
The Lie superalgebradoes not involve superpartners. The elements are exactly the same as those of the algebra . The importance we attribute to this algebra is solely due to the fulfillment of the Pauli exclusion principle.
Remark 5.
We also notice that the use of the Grassmann envelope produces zero divisors in the algebra whenever the same fermionic root, with the same momentum, is in two interacting particles. This is the precise mathematical statement we need in order to apply the previous two remarks to our model. The Pauli principle is therefore fulfilled.
4. Interaction Graphs
As mentioned in the Introduction of [1], the interactions have a tree structure whose building blocks involve only three particles, and they are expressed by the product in the underlying algebra. The scattering amplitudes are proportional, up to normalization, to the structure constants of the related products. An ordering of the roots has to be a priori set, so that the commutator between two generators is taken according to that order. Quantum interference is obviously independent from the ordering choice.
In this section, we set up a correspondence between graphs and products in the algebra spanned by the generators
and the procedure can then be trivially extended to by Remark 3.
We include the decays among the possible scatterings as resonance interactions, a well known and studied phenomenon in many physical processes, as we now explain. Suppose that two particles, one with charge and momentum , the other with charge and momentum , are present at the same space point and are such that and ; then, a decay occurs, with a certain amplitude, producing the outgoing particles of charges , with momenta and respectively, whereas the particle with charge and momentum shifts in space according to the expansion rule, see [1]. The amplitude for the decay is proportional, up to normalization, to the structure constant of the commutator between the outgoing particles (we will comment on this viewpoint on the decays at the end of this section).
The possible situations for an elementary interaction are depicted in the following graphs, given by Figure 1, Figure 2 and Figure 3 (the resonant particle is also shown in case of a decay). In the graphs we use wiggly lines for the neutral particles and straight lines for the charged particles . Red lines indicate outgoing particles and blue lines incoming ones.
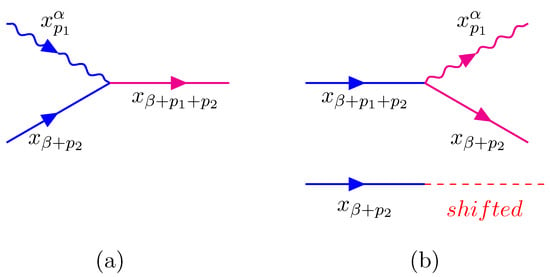
Figure 1.
; (a): absorption by ; (b): emission by (similarly for and interchanged).
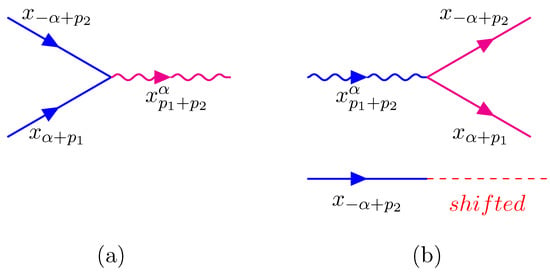
Figure 2.
; (a): annihilation; (b): pair creation (similarly for and interchanged).
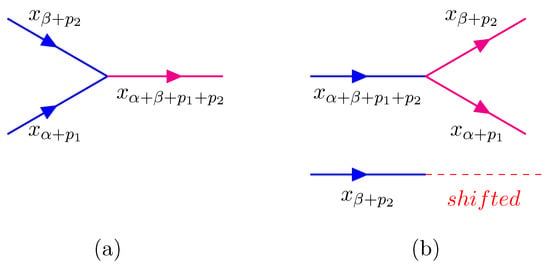
Figure 3.
; (a): scattering; (b): decay into and (similarly for and interchanged).
We would like to stress that the orientation of the graphs is not significant; these are not Feynmann diagrams, although they resemble them: only the distinction between incoming and outgoing particles matters; it complies with 4-momentum and charge conservation.
A particular case represented by Figure 3 is the interaction among gluons.
Notice that for each interaction as in (a) of Figure 1, Figure 2 and Figure 3 there is an amplitude for a shift of the two particles without interaction. This allows for an interaction as in (b) of the same Figure at a later time.
These graphs represent the building blocks of the interactions and make the model effective and calculable, being the amplitudes for each process and for the space expansion well determined. We stress again that the overall picture is that of particles associated to generators that interact while they expand in the same fashion as the wave function spreads out in standard quantum mechanics. The expansion occurs however in a discrete space at discrete time intervals. The graphs in the figures of this section show what happens locally to the component of the expanded particle in a point where it is located at a certain instant of the universal time, [1], with a certain amplitude.
We recall from reference [1] that our concept of a geometrical point in space reverses that of locality: a point is where an interaction occurs. The initial set of generators are all allowed to interact with each other, with a certain amplitude proportional up to normalization to the structure constants of the algebra, at what we call time 0 of the universal clock. This is equivalent to saying that at time 0 all particles are in the same point. The outcome of the first interactions, plus the creation of space, which is a consequence of the momentum part of the root associated with each generator, leads to a second set of interactions, and so on. What we call universal time is this order parameter of the interactions.
5. The Poincaré Group
We refer to Section 2.3 of our previous paper [1], in particular we denote by the roots and respectively.
We have a complex Lie algebra generated by , and the corresponding Cartan generators , .
The spin subalgebra is the compact form of the subalgebra with generators , and , namely is generated by , and .
We denote by w the Pauli-Lubanski vector and we classify the generators or with respect to and , the two Casimir invariants of the Poincaré group. We use the shorthand notation , (resp. ) when k has an even (resp. odd) number of + signs.
Let be the extension of that includes all timelike and lightlike momenta (not necessarily with integer component), and let the subalgebra of massive particles, namely the extension of the subalgebra introduced in Remark 2. We regard the following proposition as fundamental for the relativistic behavior of our model.
Proposition 2.
There is a natural action of the Poincaré group . Let be an element of , where Λ is a Lorentz transformation and a a translation.
The action extends by linearity the following action on the generators and of .
- If , fix a transformation such that and let be the Wigner rotation induced by Λwhere is the adjoint action of the generator of the Wigner rotation .
- If and the action reduces towhere is the helicity of α and θ is the angle of the rotation along the direction of , analogous to the Wigner rotation of the massive case.
The Poincaré group is a subgroup of the automorphism group of.
Proof.
The action on each generator with a certain mass and spin/helicity acts as the irreducible induced representation, introduced by Wigner, [9].
We only need to prove that it is an automorphism of , namely that is non-singular and preserves the Lie product (10). Part of the proof is similar to the classical one, see Lemma 4.3.1 in [10].
The fact that is non-singular comes from the obvious existence of its inverse transformation. We are left with the proof that .
Let us consider in particular in (18). Since R is an generator then is nilpotent, namely for some r and
We have
and also that for implies
Let and . We get:
Similarly for the other commutators in (10). □
The action can be easily extended to by acting accordingly on the Grassmann variable in order to get the variable associated to the transformed generators of .
6. Initial Quantum State
The initial quantum state of our model of the expanding early Universe is an element of the universal enveloping algebra of , namely an element of the tensor algebra built on the generators of modulo the relations defining the product in the algebra itself. The initial generators are all in pairs with opposite helicity and opposite 3-momentum, [1], and have a phase or amplitude associated to each of them as a complex coefficient. The interactions and expansions starting from the initial state are such that locally the quantum state is an element of the universal enveloping algebra. Interference plays the crucial role in the quantum behavior of the model, including repulsive versus attractive forces. The quantum nature of gravity appears through the quantum nature of spacetime: at every cosmological instant, a point in space has an amplitude which is the sum of the amplitudes for particles to be at that point.
The initial state has the mean energy of the Universe concentrated on the generators that interact with each other at . The choice of the initial state is crucial in determining the likelihood for the existence of particles and of an eventual symmetry breaking. It is beyond the scope of this paper to investigate this subject in depth; an algorithm based on the algebra and the expansion rule that we have introduced can be the basis for computer calculations, which should shed some light on the physical consequences of the choice of the initial quantum state.
7. Vertex-Type Algebra and Gravitahedra
Space expansion leads to an enrichment of the algebra. The locality of interactions suggests to embed the algebra in a vertex-type operator algebra, in which the generators of act as vertex operators on a discrete space that is being built up, step by step, by driven interactions.
The tree structure of the interactions allows for a description of scattering amplitudes in terms of associahedra or permutahedra,11,12,13,14,15,16,17,18,19], with structure constants attached to each vertex; see Figure 4 for the interaction of four particles, producing the associahedron . A vertex is interpreted as an interaction with universal time flowing from top to bottom in the trees of Figure 4. However, if one includes the gravitational effect of space expansion, one should describe the interactions through permutahedra rather than associahedra; see Figure 5 for the interaction of four particles, producing the permutahedron .
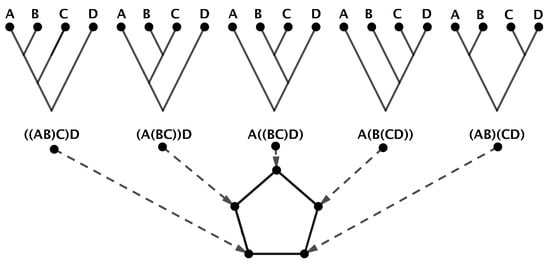
Figure 4.
Associahedron . Adjacent vertices , for sub-words .
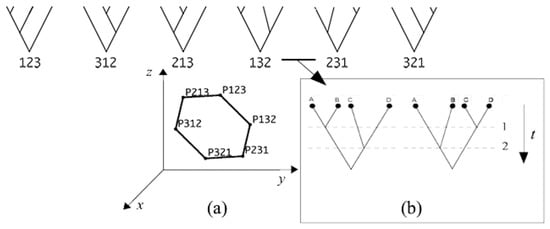
Figure 5.
(a): whose; (b): renders a magnification, shows the permutahedron , pertaining to the interaction of 4 particles.
The two trees in Figure 5b are different due to the spreading of particles in space, because the same interactions occur at different times (represented by the horizontal lines).
A complete graphical description of the interactions, including the spacetime effects, hence gravity, can be quite complicated and needs a deep study. A research program with this goal has initiated, and the name gravitahedra has been coined for the polytopes that will eventually, and hopefully, describe such interactions.
The fact that locally the quantum state is an element of the universal enveloping algebra means that we can assign to it labels q of space Q, which are triples of rational numbers, due to the expansion by , where are integers, [1]. The vertex-type algebra is therefore the algebra , whose relations have been extended in order to include the commutation of elements with different space-labels.
8. Conclusions
In the pair of papers given by [1] and the present paper, we have presented an intrinsically quantum and relativistic theory of the creation of spacetime starting from a quantum state as cosmological boundary condition, which we conceive to play a key role in any fundamental theory of Quantum Gravity. We have discussed the general framework of a workable model, based on a rank-12 infinite dimensional Lie superalgebra, which can be applied to the quantum era of the first cosmic evolution. Our model can accommodate the degrees of freedom of the particles we know, without superpartners, namely spin- fermions and spin-0 and spin-1 bosons obeying the proper statistics.
The seed of quantum gravity has to be searched at the big bang era. In the algebraic realm there is no need to have the whole set of generators at the big bang, since a proper choice of a (finite) number of them can produce all generators in the algebra. The use of Serre’s theorem, for instance, states this fact in the proper and elegant mathematical language in the case of a Lie algebra. The same is true for infinite dimensional Kac-Moody and Borcherds algebras.
In our model a proper finite set of generators is suitable to represent the initial state, but as soon as time starts flowing the state necessarily becomes a fully entangled pure state—one may start with few generators of a much simpler algebra than ours, to deduce this fact from our rules. It is intuitive to say that the state stays this way, a pure entangled state, until the first observations, supposedly occurring after the universe has cooled down a lot and undergone a large expansion. The measurement by an apparatus that entangles with the observed object, changes the pure state of the universe: namely it disentangles a very tiny part from it and eventually, after subsequent observations, turns that pure state into a mixture. Quasi-classical phenomena may thus appear in a very small part of the universe—locally, we may say. The density matrix of the universe changes a little tiny bit, some information is lost and the entropy increases.
The quantum nature of gravity is intrinsically unobservable, because observation implies the destruction of the entanglement and the collapse of the wavefunction.
This is the reason why objects that are expected to be intrinsically quantum, such as black holes or the rapid expansion characterizing inflation in early Universe, can effectively be described by (semi)classical structures, such as a Riemannian metric and a potential with flat directions, respectively.
Thus, the deal in Quantum Gravity is the following: the intrinsically quantum and relativistic description of an intrinsically unobservable regime should be made consistent with the existence of a macroscopic observer, and thus of a (semi)classical observational symmetry, emerging in the thermodynamical/macroscopic limit in which the entanglement becomes irrelevant. Our model, by exploiting Occam’s razor, tackles this crucial issue of Quantum gravity, providing an elegant solution, which can be regarded as a “third way”, alternative to both supersting/M- theory and loop quantum gravity: indeed, the Poincaré group emerges from both the “spin” sector () and the kinematical sector (complementary of in ) of the Lie superalgebra . Besides the absence of superpartners and the implementation of the Pauli exclusion principle, the emergence of the Poincaré group is a crucial feature of our model. We should stress that, of course, the Poincaré group can be defined only in the thermodynamical limit in which the observer can be consistently decoupled from the evolutive dynamics of the Universe, given in toto by . Especially in an early Universe, the back-reaction of the observer on the object of the observation should be relevant, and thus the abstraction of a decoupled and distinct observer is not totally consistent during the early stages of the Universe.
Many physical properties have still to be verified and/or fulfilled, like the proton decay, the confinement of quarks, the attractive nature of gravity on the large scale. The general framework of the model leaves however a great freedom of choice, and this is to be regarded as a benefit for those who believe this is a promising approach and wish to explore it.
There is much left for future work, to start with the definition of a particular quantum initial state allowing to perform some preliminary computer calculations that may give an idea of how the model effectively works. In particular, the density matrix, von Neumann entropy, mean energy, scattering amplitudes can be explicitly calculated according to our model.
We end this series of two papers by recapitulating what we consider the main physical features of our approach:
- (I)
- spacetime is the outcome of the interactions driven by an infinite-dimensional Lie superalgebra ; it is discrete, finite and expanding;
- (II)
- the algebra incorporates 4-momentum and charge conservation; it involves fermions and bosons, with fermions fulfilling the Pauli exclusion principle;
- (III)
- is a Lie superalgebra without any supersymmetry forcing the existence of superpartners for the particles of the Standard Model;
- (IV)
- every particle has positive energy and it is either timelike or lightlike;
- (V)
- the initial state is an element of the universal enveloping algebra of ;
- (VI)
- the interactions are local, and the whole algebraic structure is a vertex-type algebra, due to a mechanism for the expansion of space (in fact, an expansion of matter and radiation);
- (VII)
- the emerging spacetime inherits the quantum nature of the interactions, hence Quantum Gravity is an expression for quantum spacetime—in particular, there is no spin-2 particle;
- (VIII)
- the Poincaré group has a natural action on the local algebra;
- (IX)
- once an initial state is fixed, the model can be viewed as an algorithm for explicit computer calculations of physical quantities, like scattering amplitudes, density matrix, partition function, mean energy, von Neumann entropy, etc.
Author Contributions
Conceptualization, P.T., A.M., M.R. and K.I.; methodology, P.T. and A.M.; formal analysis, P.T., A.M. and M.R.; investigation, P.T.; writing—original draft preparation, P.T.; writing—review and editing, P.T., A.M. and M.R.; supervision, K.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We prove Proposition 1.
The algebra with relations (10)–(12) is obviously infinite dimensional, and its product is antisymmetric. We only need to prove that it fulfills the Jacobi identity.
Throughout the proof we strongly rely on the following standard results, see [1] and Refs. therein.
Proposition A1.
For each the scalar product ; ( respectively ) is a root if and only if (respectively ); if both and are not in then .
For if is a root then is not a root.
Proposition A2.
The asymmetry function ε satisfies, for α, β, γ ∈ :
By linearity it is sufficient to prove that the Jacobi identity holds for the generators of the algebra. For each triple of generators we write
We want to prove that .
For we call the generators of type 0 and of type 1.
We consider the various cases.
- (a)
- At least one of is of type-0
- (a1)
- If are all of the type-0 then Jacobi holds trivially.
- (a2)
- If are of type 0 and is of type 1 then , and , hence .
- (a3)
- If is of type 0 and are of type 1, then , and , . We have 3 cases:
- (a3.i)
- then ;
- (a3.ii)
- then ;
- (a3.iii)
- then , and , hence .
- (b)
- None of is of type-0. Let be all of type 1. For any two roots of , say without loss of generality, we have three cases:
- (b1)
- :
- (b1.i)
- if both then trivially;
- (b1.ii)
- if and then . Since both then hence if , then and . On the other hand if then . But and imply hence ;
- (b1.iii)
- if and then and . If then hence . If then . Since , we get and, from Proposition A2, and , implying and . Finally if then and would be a root, contradicting the hypothesis.
- (b1.iv)
- if and then and . But hence and .
- (b1.v)
- If and then and , imply hence therefore and .
- (b1.vi)
- If and thenand, being , implying .
- (b1.vii)
- If and then and and .
- (b1.viii)
- If and then ; since and , therefore and .From now on .
- (b2)
- :
- (b2.i)
- If then hence . Then , , . Since , , see (13), we get .
- (b2.ii)
- If and then which is impossible.
- (b2.iii)
- If and then which is impossible.
- (b2.iv)
- If and then which is impossible.
- (b3)
- :
- (b3.i)
- If then ; we can only have implying , that contradicts .
- (b3.ii)
- If then ; we can only have implying that contradicts .
- (b3.iii)
- If both and then which contradicts .
This ends the proof. □
References
- Truini, P.; Marrani, A.; Rios, M.; Irwin, K. Space, Matter and Interactions in a Quantum Early Universe. Part I: Kac-Moody and Borcherds Algebras. arXiv 2020, arXiv:2012.10227. [Google Scholar]
- Kac, V.G. Infinite Dimensional Lie Algebras; Third Edition Reprinted with Corrections; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Borcherds, R.E. Generalized Kac-Moody algebras. J. Algebra 1988, 115, 501–512. [Google Scholar] [CrossRef] [Green Version]
- Borcherds, R.E. Monstrous moonshine and monstrous Lie superalgebras. Invent. Math. Invent. Math. 1992, 109, 405–444. [Google Scholar] [CrossRef] [Green Version]
- Truini, P. Vertex operators for an expanding universe. In Proceedings of the Symmetries and Order: Algebraic Methods in Many Body Systems, Francesco Iachello, Yale, 5–6 October 2018; Volume 2150, p. 040005. [Google Scholar]
- The GAP Group. GAP—Groups, Algorithms, and Programming, Version 4.10.2. 2019. Available online: https://www.gap-system.org (accessed on 12 September 2021).
- de Graaf, W.A. Lie Algebras: Theory and Algorithms; North-Holland Mathematical Library 56; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Shestakov, I.P. Prime Malcev Superalgebras. Mat. Sb. Mat. Sb. 1993, 74, 101–110. [Google Scholar] [CrossRef]
- Wigner, E.P. On unitary representations of the inhomogeneous Lorentz group. Ann. Math. Ann. Math. 1939, 40, 149. [Google Scholar] [CrossRef]
- Carter, R.W. Simple Groups of Lie Type; Wiley-Interscience: New York, NY, USA, 1989. [Google Scholar]
- Sheppeard, M.D. Gluon Phenomenology and a Linear Topos. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2007. [Google Scholar]
- Arkani-Hamed, N.; Trnka, J. The Amplituhedron. J. High Energy Phys. J. High Energy Phys. 2014, 10, 030. [Google Scholar] [CrossRef] [Green Version]
- Mizera, S. Combinatorics and topology of Kawai-Lewellen-Tye relations. J. High Energy Phys. J. High Energy Phys. 2017, 8, 97. [Google Scholar] [CrossRef] [Green Version]
- Arkani-Hamed, N.; Bai, Y.; Lam, T.J. Positive Geometries and Canonical Forms. J. High Energy Phys. J. High Energy Phys. 2017, 11, 39. [Google Scholar] [CrossRef] [Green Version]
- Stasheff, J.D. Homotopy associativity of H-spaces. I. Trans. Am. Math. Soc. I. Trans. Am. Math. Soc. 1963, 108, 275–292. [Google Scholar]
- Stasheff, J.D. Homotopy associativity of H-spaces. II. Trans. Am. Math. Soc. II. Trans. Am. Math. Soc. 1963, 108, 293–312. [Google Scholar]
- Stasheff, J.D. From operads to physically inspired theories. In Operads: Proceedings of Renaissance Conferences (Hartford, Connecticut/Luminy, France, 4–5 March 1995); American Mathematical Soc.: Providence, RI, USA, 1997; Volume 202, p. 53. [Google Scholar]
- Tonks, A. Relating the associahedron and the permutohedron. In Operads: Proceedings of Renaissance Conferences (Hartford, Connecticut/Luminy, France, 4–5 March 1995); American Mathematical Soc.: Providence, RI, USA, 1997; Volume 202, pp. 33–36. [Google Scholar]
- Loday, J.L. Realization of the Stasheff polytope. Arch. Math. Arch. Math. 2004, 83, 267. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).