1. Introduction
Failure Mode and Effect Analysis (FMEA) was proposed by the military of the United States of America in 1949 as a standard operational procedure [
1,
2]. Then, the technique was developmented as a formal methodology in the aerospace industry by NASA in 1963 to improve reliability requirements. The Apollo space mission was his first application where the impacts of the systems and the failures of the equipment, personnel and security systems were evaluated, as well as the maintainability and performance of the system [
3,
4]. In 1977, the Ford Motor Company adopted FMEA technique within the automotive industry to evaluate the security, reliability and to comply with regulations of the production processes and product design [
5]. In addition, FMEA helps to, and to document potential failures of the system before the failure as an appropiate procedure of prevention before reaching the end customer. In the 1980s, FMEA became a military standard of the Department of Defense of the United States of America under the title “procedure for performing a failure mode, effects and criticality analysis”. In the 1990s, Ford, Chrysler, and General Motors developmented the first FMEA manual that was revised by the Automotive Industry Action Group (AIAG) in the following editions (second, third, and fourth edition). Nowadays, a new FMEA handbook was developed by the AIAG and Verband der Automobilindustrie (VDA) and published in June 2019 [
2].
In addtion, according to Zavadskas et al. [
6] multi-criteria decision-making are considered as complexity tools to symmetry the goals, risks, and constraints regard a problem. Besides, symmetry and asymmetry between fuzzy sets are common notions in decision-making problems [
7,
8]. In this mode, the symmetry related to the assesment obtained from MCDM method can be modelling [
9]. In the same time, according to Liu [
10], for the traditional FMEA, the risk associated with identified failure modes can be assessed and prioritized for proactive intervention and corrective actions, especially for the more serious aspects identified to improve reliability and security of a system, product, process, design or services thought the appraisal of the risk parameters of severity (S), occurrence (O), and detection (D) of failure to calculate the risk priority number (RPN) or criticality index [
11], where the highest value is the most important risk, and so on. Therefore, we can consider the risk factors as decision criteria, possible causes of failure as decision alternatives, and the priority ranking of failure causes as decision goal as mentioned Liu [
10] in his book to evaluate a problem.
Public transportation service: Experience has also shown that the application of the FMEA method is non-exclusive of private industry for automotive or aeronautical companies. This method can also be used to analyze the public policies in the cities with high population density through a mathematical methodology to avoid ambiguities in decision-making [
12].
Despite the complex environment about the public transportation service, it can be deployed in failure modes and potential risks to facilitate the problem visualization and propose priority recommendations for the implementation of improvements the quality of service for captive users and attract potential users. Likewise the failure modes and potential risks describe the problems that must be addressed to improve the quality of service for captive users and attract potential users, suchs as the readiness can affect the user’s opinion (cualitative information) about the public transportation service when the route is modified outside the residential area, however, frequency low, the time travel increase and the accesibility is reduced as a consequence [
13].
Nowadays, according to Tirachini and Cats [
14], hygiene and sanitary protocols have gained importance within buses as a measure to protect people and mitigate the spread of the coronavirus disease (COVID-19) pandemic. One user may consider the bus clean if there is no garbage, however for another user the cleaning should consider strict cleaning and disinfection protocols in every space and seat inside the bus. Furthermore, higher fares are not usually well accepted and users express complaints about the service in opposition to the new prices, in most cases they are mainly linked to the comfort, punctuality and convenience criteria [
13,
15].
On the other hand, according to literature review, there are three relevant gaps in traditional FMEA method that need to be addressed:
It assumes that the relative importance of the severity, occurrence and detection parameters are equal affecting the evaluation of failure modes [
4,
16].
The combination of the risk parameters produces the same value of RPN, as example of
and
according to [
4,
16].
It assumes that the level of knowledge is the same because the degree of knowledge of the decision-makers is not specified [
16], and
The evaluation of the RPN parameters is limited to a quantitative (crisp) information [
5].
The motivation of this work is to find a model that is able to take into consideration subjectivity that may exist among the criteria (failure modes) involved in FMEA method, and at the same time handle information related to stimate RPN parameters. In order to tackle the gaps mentioned above, in this study, we propose FMEA and the Combinative Distance-Based Assessment (CODAS) method under Pythagorean Fuzzy environment. The main contributions in this study are presented as following:
We develop a hybridization between FMEA method and the Combinative Distance-Based Assessment (CODAS) method under Pythagorean Fuzzy environment.
We calculate the vector of weights of the risk parameters with the mathematical model of the Pythagorean Fuzzy CODAS methods.
We introduce the linguistic terms based on the Pythagorean fuzzy numbers are the best to evaluate every failure mode for severity, occurence, and detection.
The remainder of this paper is organized as follows. In
Section 2 introduces a brief literature review on MCDM based FMEA techniques. The proposed methodology is detailed in
Section 3. In
Section 4 a numerical case concludes to illustrate its applicability of the proposed methodology. In
Section 5 the dicussiones are presented. Finally,
Section 6 summarizes our work and provides some directions for future research.
2. A Brief Literature Review on MCDM Based FMEA Techniques
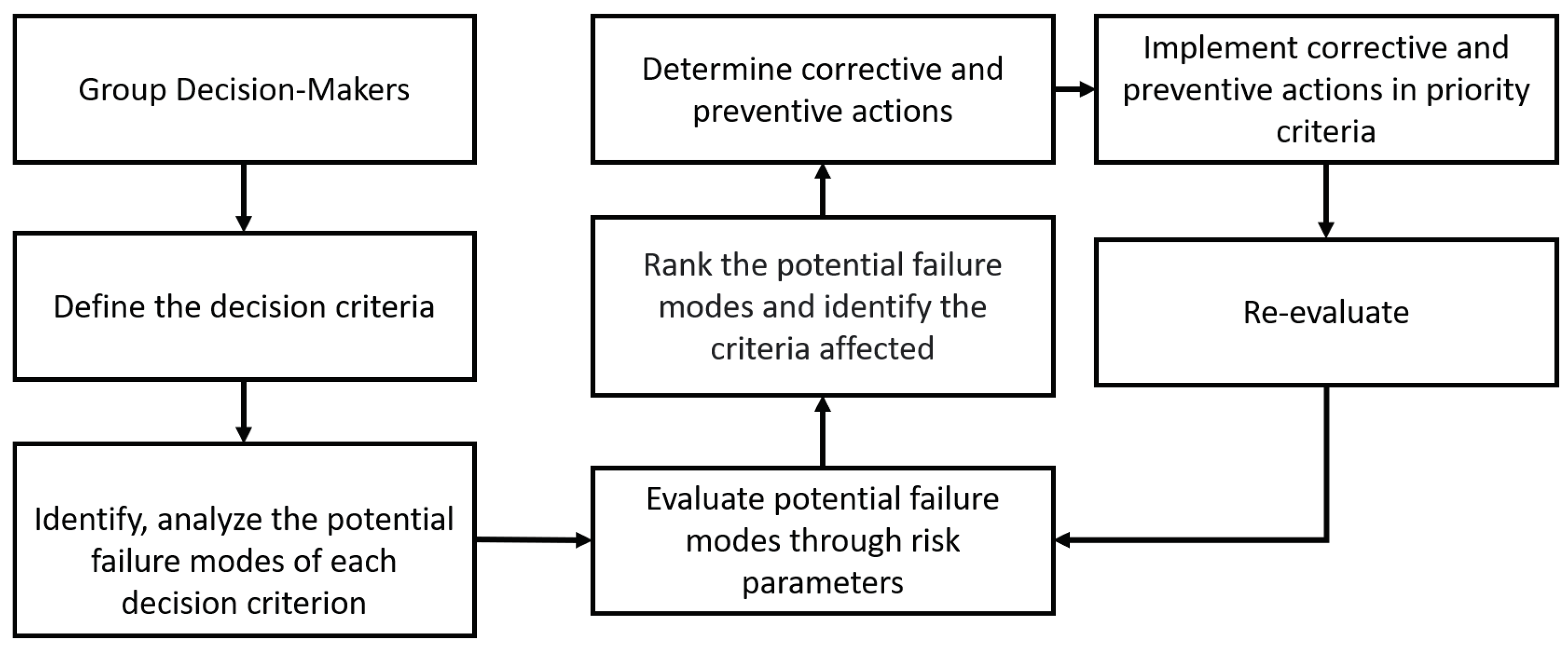
In general, traditional FMEA procedure consists in: (1) define the scope of the analysis, (2) integrate a multidisciplinary team, (3) understand the system to be analyzed, (4) design brainstorms of the failure modes of each item and their effects, (5) determine the scores of the parameters severity, occurrence, and detection for failure modes, (6) calculate the RPN, (7) rank failure modes, (8) prepare the report of FMEA with a resume of the analysis with results, and (9) calculate the RPN revised with the failure modes that were reduced or eliminated [
17].
The relative importance of the parameters of severity, occurrence, and detection is considered equal which causes the combination of the parameters can give the same results of the RPN affecting the adequate evaluation of failure modes [
4]. This way of calculating the RPN generates uncertainty in the results which can vary and generate error (or omissions) of the failure modes, and therefore implement unnecessary actions. The correct application of the quality tools can affect the results of the project, especially the importance of the degree of knowledge of the team combined with the reliability of the information that will be managed.
In this sense, the traditional FMEA tends to respond positive based on a good team integration that will define, analyze and evaluate the failure modes and their potential effects. The traditional FMEA is basically a technique of prevention of the risks that can make failure in a product, design, service, or process. This technique allows to clarify all the ways in which a potential failure can occur in a real case through the conventional RPN that is a crisp number as the result of the multiplication between the risk parameters of severity (S), occurrence (O), and detection (D). But Liu et al. [
18], applied the fuzzy set theory into a FMEA, it means that the evaluation of the risk parameters were evaluated using intuitionistic fuzzy hybrid TOPSIS approach because the fuzzy logic models the uncertain, imprecise, unspecific, and fuzzy situations [
3]. Liu et al. [
18] calculate the relative importance of the risk parameters when FMEA team give their opinions to aggregated them using the IFWA operator, then the IFW-TOPSIS calculates which fault is closest to the ideal point.
In this regard, it is advisable to adopt decision makers, experts in the areas of interest and the opinion of the client or users specifying the level of knowledge, from each area of the project within the risk analysis and analyze the problem under a Pythagorean fuzzy (PF) environment to manage uncertainty and improve the definition of projects. Also, multi-criteria decision-making (MCDM) can bring certainty for FMEA, and which consider the relative importance of risk factors and prioritize the identified failure modes using mathematical models to reduce the error of the calculation [
19].
Albeit, a team of four experts in [
5] documented and identified failure modes and effects of reheat valve system in nuclear steam turbine using fuzzy weighted TOPSIS with triangular fuzzy numbers to approach the solution; also, the vector of weights of the risk parameter were calculated with entropy method. Likewise, Liu et al. [
16] proposed a novel approach for FMEA using fuzzy AHP in the evaluations of FMEA team to calculate the vector of weights of risk factors, likewise, they applied entropy method for objective weights of risk parameters. Then, they applied fuzzy VIKOR evaluation of each failure mode integrated on the vector of weights. Liu et al. [
3] used an extension of VIKOR method under fuzzy environment with trapezoidal fuzzy numbers to capture the vagueness of the information of the general anesthesia process in FMEA of 5 decision makers. Nazam et al. [
20] proposed a combination between fuzzy AHP to calculate the criteria weights and fuzzy TOPSIS to assessment the compromised criteria level with subcriteria of a green initiative in supply chain in the textile industry.
4. Numerical Case
Step 1. Integrate a team of experts (DMs). Two decision makers are the FMEA team to evaluate potential failure mode. Two decision makers are considered for evaluation. The set of DMs are shown in
Table 3.
Step 2. List and screening criteria of the passenger transportation system. The criteria is shown in
Figure 2. Criteria decision describe the main characteristics of passenger transport systems (public transportation) from the user’s point of view with the perspective of readiness, timeliness, comfortable service, convenience, safety and security, and tariff.
Step 3. Determine the importance of risk parameters. The importance of risk parameters is the best contribution to get better analysis of the public transportation or another application of FMEA method because the traditional FMEA method considered the severity, occurrence, and detection equal. This causes uncertainty about how and where to solve a specific problem. The DM’s evaluated the risk parameters as shown in
Table 4. It is also important to consider the contribution in knowledge and experiences of the decision makers in this evaluation as can see in
Table 4.
Step 4. Record the potential failure mode for every criteria.
In addition, in
Table 5 the failure modes are presented.
Step 5. Assessment of each potential failure mode. Decision Makers evaluates the potential risk modes using the Linguistic Terms of the
Table 2, theses terms will later be converted to numerical variables composed of Fuzzy Pythagorean Numbers.
Step 6. Construct the Pythagorean fuzzy decision matrix for potential failure mode assessment as shown in the
Table 6. This table is expresed by Linguistic Terms, however, we can convert this terms into PFNs and express them in a matrix to do the calculations.
Step 7. Calculate Aggregated Pythagorean Fuzzy decision Matrix (APFDM). The individual opinion of DMs in linguistic terms are transformed using the linguistic variables to integrate the evaluations of both decision makers in the APFDM that is shown in
Table 7.
Step 8. Calculate the Pythagorean Fuzzy Normalized Matrix using lineal normalization using Equations (10) and (11), then construct the Matrix with the result as shown in
Table 8.
Step 9. Using Equation (13) calculate the Pythagorean Fuzzy Weighted Normalized Decision Matrix as shown in
Table 9. This part integrate the contribution of the risk parameters with the normalization of the potential failure mode evaluated.
Step 10. Calculate with the Equations (16) and (17) the Pythagorean fuzzy negative ideal solution to define the reference of the worst solution. Results are shown in
Table 10.
Step 11. Euclidean and Taxicab distances are calculated using Equations (18) and (19), respectively. From step 10, We calculate the distance for each risk parameter: severity (S), occurence (O), detection (D), then sum the calculated of the Euclidean Distance and the Taxicab Distance are shown in
Table 11.
Step 12. The Sum of the Euclidean and Taxicab distances (See “Distance Sum” in
Table 11) is necessary to construct the relative assessment matrix using the Equation (21) as shown in
Table 12, also the threshold parameter (
) is to compare the Euclidean distance as a primary measure, then Taxicab distance is used as a secondary measure.
Step 13. Using the relative assessment matrix, calculate the assessment score of each potential failure mode with the Equation (23). The results are shown in the
Table 13.
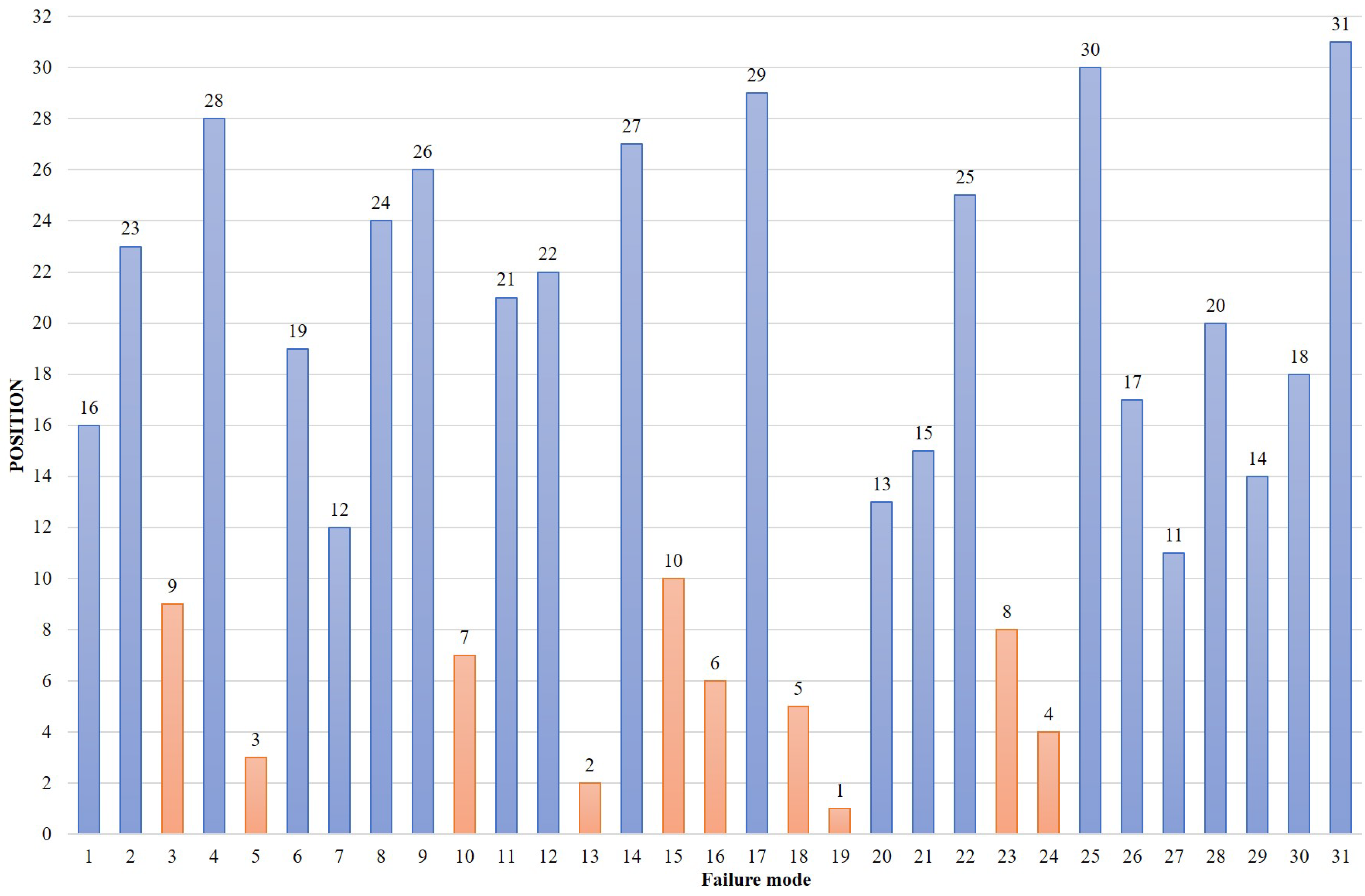
Step 14. Finally, the relative assesment is ordered from highest to lowest, that is, in descending order with the objective of detect priority potential failure modes. In the same way that the results are observed in the
Table 13, ranking of potential failure modes can be observed in the following
Figure 3.
Comparisons
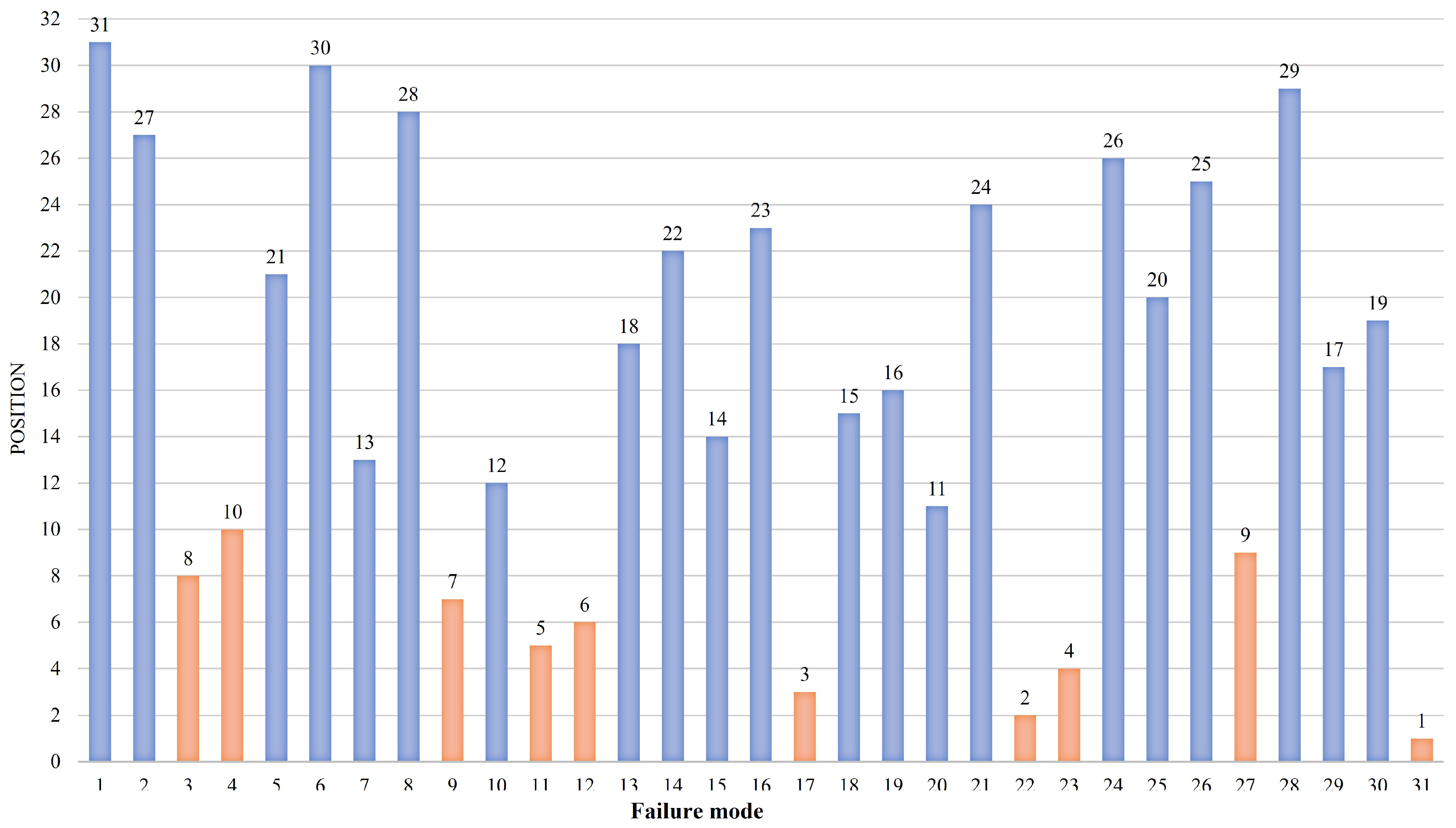
To compare the results versus the proposal, a variation with Multi-Objective Optimization Method by Ratio Analysis (MOORA) presented by Pérez-Domínguez et al. [
41] was developmented for the same 31 failure modes under the same conditions and values, only the mathematics’ for convergence the analysis is different, the
Table 14 and the
Figure 4 shows the results for variation with Pythagorean Fuzzy MOORA.
5. Discussions
It is important to remember that FMEA is, in essence, a tool for the prevention of risks and their effects. Then, the first failure modes are listed:
(MF19) Bad driving makes the operation risky for the driver, the user and the general public. The recommendation is to implement defensive bus driving training programs.
(MF13) Buses do not comply with international standard (polluting gases). The recommendation is to adopt the most current international standards when designing tenders or bus acquisitions. That the main requirement is to introduce policies of care to the environment.
(MF05) ecrease in the required operational fleet is a result of the design of the itineraries. It is recommended to include parameters according to the demand of users measured in the attention of the Origin-Destiny Matrix, also include the fleet with reliable available and the traffic rules allowed locally and within the organization.
(MF24) Reduce the number of buses arbitrarily over a significant period of time. This failure mode response to the realiability or maintability of the buses and the schedule program.
(MF18) Users in wheelchairs or with reduced mobility cannot access the bus. The bus configuration is not adequate in dimensions this responds to the accesibility criterion in the senses of having characteristics (dimensions) of the adequate buses that permits to the people in wheelchairs into the buses without assistant.
While the variation with PF MOORA is based on the normalization of your data, the results are measured comparando los valores of the Euclidean distance between them, and the proposed method which is based on PF-CODAS, uses the Taxicab distance allowing to measure the response closest to the ideal that is the reason of their differences position in ranking.
The development of the numerical case make allowed to visualize how FMEA was integrated into Pythagorean Fuzzy CODAS method to prioritize failure modes through the calculation of the vector of weights of the risk parameters (severity, occurrence and detection), compared with traditional method where the risk parameters are equal, which generates uncertainty when multiplying the risk parameters to calculate the Risk Priority Number.
Also, the introduction of Pythagorean fuzzy sets helps the multidisciplinary team to express their opinions and assessments due to the introduction of labels or linguistic terms based on natural language.
The results of the method applied help to detect using the ranking, priorities in the failure modes evaluated to improve the performance of the transport service with technical recommendations and to eliminate arbitrariness when making decisions