Abstract
Given a graph G, the zero forcing number of G, , is the smallest cardinality of any set S of vertices on which repeated applications of the forcing rule results in all vertices being in S. The forcing rule is: if a vertex v is in S, and exactly one neighbor u of v is not in S, then u is added to S in the next iteration. Zero forcing numbers have attracted great interest over the past 15 years and have been well studied. In this paper, we investigate the largest size of a set S that does not force all of the vertices in a graph to be in S. This quantity is known as the failed zero forcing number of a graph and will be denoted by . We present new results involving this parameter. In particular, we completely characterize all graphs G where , solving a problem posed in 2015 by Fetcie, Jacob, and Saavedra.
1. Introduction
Given a graph G, the zero forcing number of G, , is the smallest cardinality of any set S of vertices on which repeated applications of the forcing rule results in all vertices being in S. The forcing rule is: if a vertex v is in S, and exactly one neighbor u of v is not in S, then u is added to S in the next iteration. Zero forcing numbers have attracted great interest over the past 15 years and have been well studied [1]. In this paper, we investigate the largest size of a set S that does not force all of the vertices in a graph to be in S. This quantity is known as the failed zero forcing number of a graph and will be denoted by [2,3]. Shitov [4], proved that determining the failed zero forcing number of a graph is NP-complete. Independently, a closely related property called the zero blocking number of a graph was introduced in 2020 by Beaudouin-Lafona, Crawford, Chen, Karst, Nielsen, and Sakai Troxell [5] and Karst, Shen, and Vu [6]. The zero blocking number of a graph G equals .
We will use , , , to denote the complete graph, path, and cycle on n vertices, respectively. The complete bipartite graph with r vertices in one part and t in the other part will be denoted . The disjoint union of graphs G and H will be denoted by . Following the terminology of [7], we will refer to an induced as a “cherry”. A vertex v is a cut-vertex of a graph G if has more components than G. We will refer to a subgraph that contains a cut-vertex v of degree 3 that is adjacent to vertices u and w, which are adjacent to each other and have degree 2, as a pendant .
Throughout the paper, we will use colorings to describe our failed zero forcing sets where the vertex in S will be colored blue (or referred to as filled) and the vertices not in S will be colored white (or referred to as uncolored). A vertex will be called true blue if it is colored blue and all of its neighbors are colored blue. A vertex that is not a true blue vertex will be referred to as non true blue.
Failed zero forcing numbers were introduced by Fetcie, Jacob, and Saavedra [2] where they established numerous results. In particular they proved that for any connected graph and gave a characterization of all graphs G where . They showed that the only graphs where are either or and the only graphs where are , , , or . It was also shown that if and only if G contains an isolated vertex. In addition, if and only if G contains a module of order 2, where a module is defined as follows. A set X of vertices in is a module if all vertices in X have the same set of neighbors among vertices not in X. They gave examples of some graphs where and posed the problem of characterizing all graphs with this property. We provide a complete solution to this problem in Section 2.
2. Graphs with a Failed Zero Forcing Number of 2
We provide a characterization of all graphs with a failed zero forcing number of 2. We first examined all graphs with between 3 and 6 vertices and identified all graphs with . These 15 graphs are shown in Figure 1i–xv with larger vertices indicating the failed zero forcing set of size 2. Later we show that no other graphs exist. We will show that if G has at least 7 vertices then .
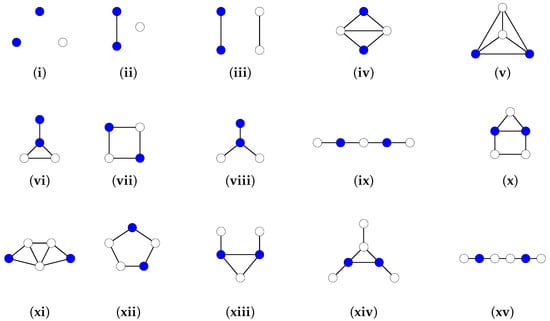
Figure 1.
All 15 graphs with .
It is not difficult to verify that each of these graphs has a failed zero forcing number of 2. For the sake of completeness, we include the details. For each graph, the larger vertices give a lower bound for the failed zero forcing number of 2. For the disconnected graphs (i)–(iii), the upper bound for follows since coloring any three vertices blue forces all of the vertices to be colored blue. For the five connected graphs with four vertices (iv)–(viii) the upper bound follows since . For the two paths (ix) and (xv), the coloring of any three vertices blue will result in either a vertex of degree 1 being colored blue or two adjacent vertices colored blue, both of which will force all of the vertices in the graph to be blue. For the graph of coloring any three vertices blue will mean that two adjacent vertices were colored blue, which will force the remaining vertices in the graph. For the house graph (x) note that coloring any three of the vertices in the graph blue will either include two vertices of the triangle or three vertices in the both of which will force all vertices in the graph to be blue. For the gem fan graph (xii) with five vertices, coloring three vertices blue will either include the vertex of degree four and two other vertices, or three vertices of degree two or three, both of which will force all vertices in the graph to be blue. For the graph consisting of a triangle and two pendant edges (xiii) note that coloring any three vertices blue will either include the three vertices of degree greater than 1, one vertex of degree 1, and two vertices of degree greater than 1, or two vertices of degree 1, all of which will force all vertices to be colored blue. Finally for the triangle with three pendant edges (xiv), coloring any three vertices blue will either include all three vertices of degree greater than 1, or at least one vertex of degree 1 and two other vertices that are either degree 1 or greater than 1, all of which will force all vertices to be blue.
We examined all connected graphs on six vertices [8] and found that all but two graphs have a failed zero forcing number of at least 3. The two graphs the corona and (graphs (xiv) and (xv) in Figure 1) have a failed zero forcing number of 2. Adding an additional vertex v and any number of edges between v and other vertices of the graph results in a graph with a failed zero forcing number of 3 (This is verified later in Section 2.2). The above suggests that any graph with 7 or more vertices has a failed zero forcing number of at least 3, which we will prove.
The following theorem guarantees that our list of 15 graphs with is complete.
Theorem 1.
Let G be a graph with at least 7 vertices. Then .
It is tempting to think that if you have a graph G where , then for any supergraph H of G we have . However, it can be the case that and in fact we can construct graphs where is arbitrarily large. In Figure 2 we give an example of a graph G where and a supergraph H of G where .

Figure 2.
Adding a single edge to G to create a supergraph H.
Theorem 2.
There exist graphs G with a supergraph H where is arbitrarily large.
Proof.
Let G be a graph with vertices with edges and . Here .
Now add the edge to create a supergraph H. Since H is a cycle with a pendant vertex we can obtain a maximum-sized failed zero forcing set by selecting the pendant vertex and vertices along the cycle (including the neighbor of the pendant vertex). Hence . Since this difference can be made arbitrarily large, by choosing a graph with a sufficiently large number of vertices. □
We next present a series of lemmas that will be used to prove Theorem 1.
A characterization of disconnected graphs with a failed zero forcing number k was given by Fetcie, Jacob, and Saavedra [2].
Lemma 1.
Let G be a disconnected graph with maximal connected components. Let be the k maximal connected components of G. Then .
This theorem can be applied to determine all disconnected graphs with a particular failed zero forcing number. We show the result for the case where .
Lemma 2.
For a disconnected graph G, if and only if G equals , , or .
Proof.
If G consists of three components the only possibility is for G to equal , since if any component contained vertices we would have . If G has two components one component must contain exactly two vertices, and the other component must have a failed zero forcing number of 0 which are either or . We note that if G contains a component with more than 2 vertices then we could color the vertices in this component blue and vertices in other component white and obtain a failed zero forcing set with more than 2 vertices. □
Now that we have identified all disconnected graphs with , we next consider the case of connected graphs.
We will next show that every graph with at least 7 vertices has a failed zero forcing number of at least 3. The approach will be as follows. A sketch is shown in Figure 3.
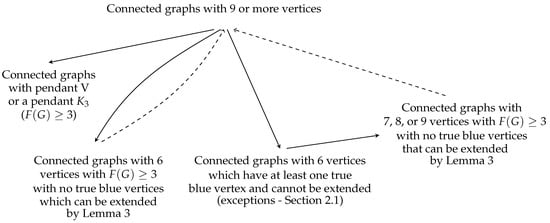
Figure 3.
Dotted arrows indicate extensions by Lemma 3.
We provide a sketch of the approach here. A complete proof appears in Section 2.2. We start with a connected graph with 9 or more vertices that does not contain a pendant V or a pendant and reduce it to a graph with 6 vertices by removing vertices and incident edges. We note we can maintain a connected graph by successively removing a leaf from a spanning tree of the graph. We will show in Lemmas 6 and 7 that the reduced graphs will not contain a pendant V or a pendant . As a result when we consider various cases in reducing the graph we can ignore cases where we have a pendant V or a pendant . If the resulting graph on six vertices does not have any true blue vertices, then we apply Lemma 3 add back vertices and edges to obtain the original graph which will have a failed zero forcing set of size at least 3. If the resulting graph on six vertices has at least one true blue vertex then we consider all possible extensions to supergraphs with 7 vertices. We show that all of these graphs have . If these graphs on 7 vertices do not have any true blue vertices then we can apply Lemma 3 and extend the graph to the original graph which will a failed zero forcing set of size at least 3. If the extensions to graphs with 7 vertices have at least one true blue vertex then we consider all possible extensions to 8 vertices. By showing that all of these graphs do not have any true blue vertices, they can be extended back to the original graph showing that .
In our next lemma we show that if a graph G can be extended to contain an additional vertex v and if the extended graph has a failed zero forcing set S where v is not in S then any number of edges can be added between v and vertices of G and S will still be a failed zero forcing set of any of these new graphs.
Lemma 3.
Let G be a connected graph with a set of S of blue vertices. If each vertex in S is adjacent to two vertices not in S, then for any supergraph H of G, we have that .
Proof.
We can add any number of vertices and edges G to create a supergraph H. Then color all of the vertices in white. Then since white vertices cannot force any other vertices and the blue vertices are still adjacent to two white vertices, no vertices in the graph will be forced. Hence . □
Lemma 4.
If a connected graph G has a pendant . Then .
Proof.
We can color the two vertices of degree 2 in the white and all other vertices blue. Then each blue vertex will either be true blue or will be adjacent to two white vertices. Hence this is a failed zero forcing set of size . □
In the next three lemmas we identify families of graphs that have a failed zero forcing number of at least 3. These will be used to prove Theorem 1.
Lemma 5.
Let G be a graph with 5 or more vertices and contains a cut-vertex v such that has at least three components, at least two of which are paths. Then .
Proof.
We consider two cases.
Case (i) G has a cut-vertex v such that consists of three disjoint paths , , and . Then either i, j, or k must be at least 2. Without loss of generality suppose . Then v along with the vertices of form a failed zero forcing set of at least 3. To see this note that v will be adjacent to two white vertices, and all other vertices in the graph can be colored blue.
Case (ii) G is a graph with 5 or more vertices and has a cut-vertex v such that consists of a subgraph H with at least two vertices and two disjoint paths. Then we color v and all vertices in H blue, and the remaining vertices white. This creates a failed zero forcing set of at least 3. Note that all of the blue vertices in this coloring all vertices in H are true blue and v is adjacent to two white vertices. □
A pendant V is a subgraph containing a cut-vertex v of degree at least 3 whose removal results in at least two paths in different components. In our next two lemmas, we prove that if a graph G does not contain a pendant V or a pendant then it can be reduced to a subgraph by removing vertices and edges, so that does not contain a pendant V or a pendant .
Lemma 6
(pendant V). Let G be a connected graph with at least five vertices that does not contain a pendant V. Then vertices of G can be successively removed (along with incident edges) to create a graph that does not have a pendant V.
Proof.
We will show that if a graph G does not have a pendant V, then there is some vertex we can remove from G so that the resulting graph does not have a pendant V. Let G be a graph that is not a cycle and does not have a pendant V subgraph. We will show that there is always some vertex v whose removal does not leave a subgraph with a pendant V. We use to denote the smallest degree of a vertex in a graph G. We can assume that since we could remove a vertex of degree 1 and not create a pendant V subgraph. Since , G must contain a cycle C that has no pendant paths. Since the cycle C must contain a vertex w with degree at least 3. Removing a vertex on C that has degree 2 is adjacent to w will not leave a pendant V since the part of the graph in will not contain a pendant V. □
Lemma 7
(pendant ). Let G be a connected graph with at least five vertices that does not contain a pendant . Then vertices of G can be successively removed (along with incident edges) to create a graph that does not have a pendant .
Proof.
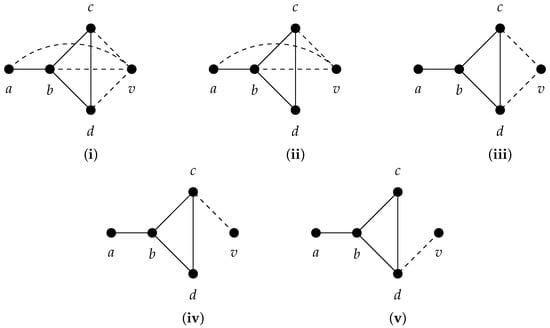
We will show that if G does not contain a pendant , there is always some vertex we can remove so that the resulting graph does not contain a pendant . Let G be a graph without a pendant , but contains a pendant with vertices a, b, c, and d where a and b are adjacent, and b, c, and d are all mutually adjacent, and c and d are not adjacent to a. Furthermore assume that b, c, and d are not adjacent to any other vertices. Since G has at least 5 vertices we can assume that either or . We will consider cases (i)–(iv) and show in each case that a different vertex can be removed from G that will not result in a pendant . It may be helpful to refer to Figure 4.

Figure 4.
In each case removing v leaves a pendant , but we can always remove a different vertex so that we do not have a pendant .
Case (i): v is adjacent to a, b, c, and d. Removing d leaves an induced (a complete graph on 4 vertices with one edge removed) on vertices a, v, b, and c.
Case (ii): v is adjacent to a, b, and c only. Then removing b results in a path on vertices a, v, c, and d.
Case (iii): v is adjacent to c and d only. Then removing c results in a path on vertices v, d, b, and a.
Case (iv): v is adjacent to c only. Then removing d results in a path on vertices v, c, b, and a.
Case (v): v is adjacent to d only. Then removing c results in a path on vertices v, d, b, and a. □
2.1. Graphs with Six Vertices: Exception Cases
We will consider the 112 connected graphs with six vertices. We will refer to the table and numbering found in [8]. For convenience, we explicitly show each graph in each of the individual cases.
Out of 112 different graphs, there were 16 cases where there does not exist three blue vertices, none of which are true blue. We will refer to these as our exception cases. We will show that each of the exception cases with six vertices can either be extended to graphs with seven, eight, or nine vertices where there are three blue vertices with none of which are true blue, or the extension includes a pendant V, which would be ruled out by Lemma 6. In each of the cases below when identifying the three blue vertices, none of which are true blue, it can be assumed that all other vertices can be colored white.
This will not only show that they have a failed zero forcing number of at least 3, but they can be extended indefinitely by adding vertices and edges and the resulting supergraph will also have a failed zero forcing number of at least 3.
These graphs are the exceptions: 54, 58, 59, 60, 76, 77, 80, 85, 86, 87, 96, 98, 102, 103, 105, and 112, each of which we will present individually. Graph 54: Please refer to Figure 5.
Figure 5.
Graph 54.
We begin by extending graph 54 by one vertex v and connecting it to each vertex in G. Notice there will be no case where v is adjacent to or . This is because connecting a vertex to either one will create a cherry structure and that case is covered by our cherry lemma. Our goal with extending is to find no true blue vertex within the graph. It is also important to notice that in each case, we are able to find a failed zero forcing number of three.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue. If v is adjacent to , then and can be colored blue. If v is adjacent to , then and can be colored blue.
If v is adjacent to only then G contains a pendant cherry and is removed from consideration by Lemma 6.
If v is adjacent to only then G contains a pendant cherry and is removed from consideration by Lemma 6.
If v is adjacent to and then and can be colored blue.
Since all cases can be extended indefinitely, this implies that graph 54 can be extended indefinitely without being forced with . Graph 58: Please refer to Figure 6.
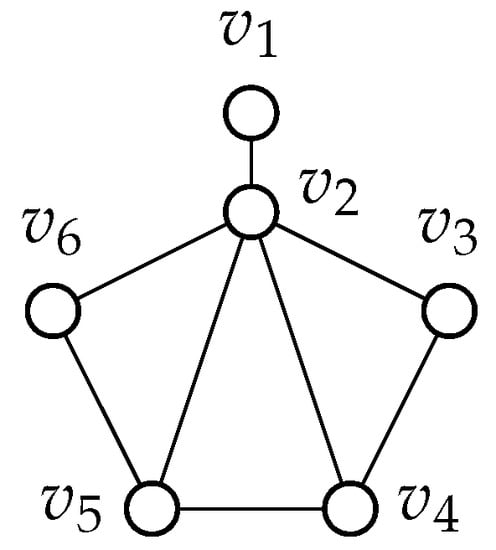
Figure 6.
Graph 58.
Let be the vertex of degree 1 and let be the neighbor of ; is the vertex of degree 3 that is adjacent to , , and . Let be the vertex of degree 3 that is adjacent to ; vertices and both have degree 2. We consider extending the graph by adding a new vertex v.
If v is adjacent to then and can be colored blue.
If v is adjacent to then and can be colored blue.
If v is adjacent to then and can be colored blue.
If v is adjacent to and then and can be colored blue.
In all of the above cases, we are left without any true blue vertices and thus we can extend these graphs indefinitely with .
If v is adjacent to only then the graph contains a cherry and is removed from consideration by Lemma 6.
The only problem cases is where v is adjacent to or (but not both). Here we can find a failed zero forcing set S of size 3 by selecting , , and , however we may not be able to extend S to larger graphs. Without loss of generality assume that v is adjacent to . We consider adding a new vertex u with possible neighbors. We note that u cannot have degree 1 and be adjacent to or since this would create a cherry and this case would be ruled out by Lemma 6. If u is adjacent to both or then we can color u, , and blue. If u is adjacent to v then we could color v, , and blue. If u is adjacent to then we could color , , and blue. If u is adjacent to then we could color , and blue. If u is adjacent to then we could color , and blue. If u is adjacent to then we could color , and blue. Graph 59: Please refer to Figure 7.
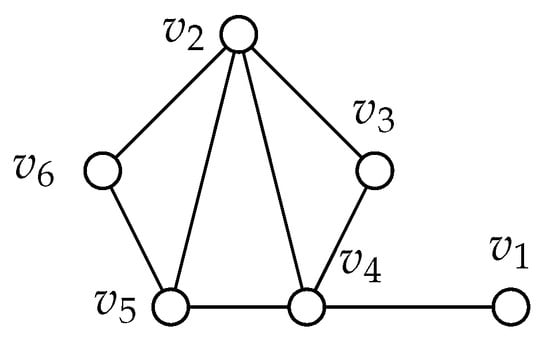
Figure 7.
Graph 59.
Let be the vertex of degree 1, be the vertex of degree 4 that is adjacent to , be the vertex of degree 2 that is adjacent to , be the other vertex of degree 4, be the vertex of degree 3 that is adjacent to and , and be the vertex of degree 2 that is adjacent to and . Graph 59 follows with the case of graph 58. We can extend along any vertex without any true blue vertices with the only exception being when a new vertex is adjacent to vertex . Similarly to graph 58 however, upon any additional extension, there are no issues arising when all the vertices are reshuffled.
For the sake of completeness we include the details. We consider adding a new vertex v and possible neighbors of v. The vertex v cannot have degree 1 and be adjacent to since this would create a cherry. In each case of the remaining cases we can find a coloring with 3 blue vertices, none of which are true blue vertices, and all of the remaining vertices including v will be colored white. If v is adjacent to , then , and can be colored blue. If v is adjacent to , then , and can be colored blue. If v is adjacent to then and can be colored blue. If v is adjacent to , then , and can be colored blue. The only problem case is if v is adjacent to . Here we can find a failed zero forcing set S of size 3 with vertices , , and , but we many not be able to extend this graph. Here we consider adding another vertex u. The vertex u cannot have degree 1 and be adjacent to either or since this would create a cherry and we can remove it from consideration by Lemma 2.6. If u is adjacent to v, then we color v, , and blue. If u is adjacent to , then we color , , and blue. If u is adjacent to , then we color , , and blue. If u is adjacent to , then we color , , and blue. If u is adjacent to , then we color , , and blue. If u is adjacent to both and then we color u, , and blue. Graph 60: Please refer to Figure 8.
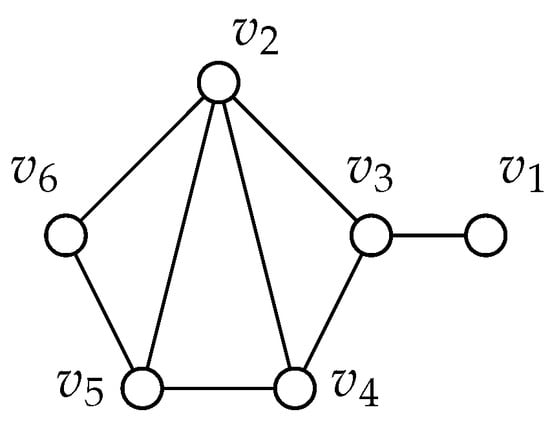
Figure 8.
Graph 60.
Graph 60 has at least one true blue vertex but all extensions along graph 60 result in and no true blue vertices. Let be the vertex of degree 1, be the neighbor of , be the vertex of degree 4, be the vertex of degree 3 that is adjacent to and , be the vertex of degree 3 adjacent to , and let be the vertex of degree 2. We consider adding another vertex v and possible neighbors of v. First if v has degree 1 then it cannot be adjacent to since this would create a cherry. In each of the remaining cases we can find a coloring with 3 blue vertices, none of which are true blue vertices, and all of the remaining vertices including v will be colored white. If v is adjacent to then we can color , , and blue, if v is adjacent to then , , and can be colored blue. If v is adjacent to then , and can be colored blue and if v is adjacent to then , and can be colored blue, and if v is adjacent to then , and can be colored blue. Graph 76: Please refer to Figure 9.
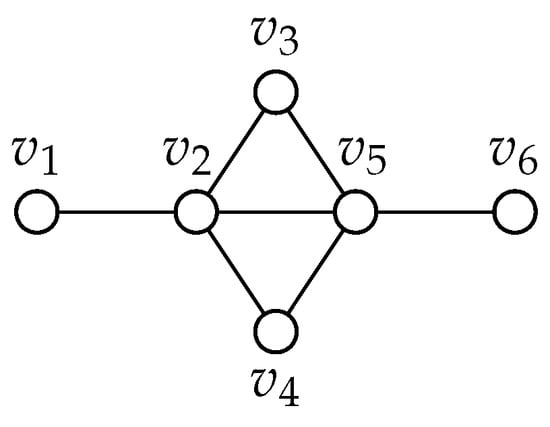
Figure 9.
Graph 76.
We will show that all but two extensions of G to a graph with 7 vertices will have no true blue vertex of degree 1. Let v denote the new vertex. Note that extensions that would result in a cherry are neglected as those cases are resolved by Lemma 6. We have the following cases
If v is adjacent to only, we color , , and blue and v, , and white.
We consider cases of adding a new vertex v.
If v is adjacent to , we color , , and blue.
If v is adjacent to , we color , , and blue.
If v is adjacent to or only, then this case can be removed by Lemma 6.
If v is adjacent to both and only, then color v, , and blue.
The only problem cases is where v is adjacent to or .
Without loss of generality, we assume v is adjacent to . Then we consider adding another vertex u.
If u is adjacent to v then color v, , and blue.
If u is adjacent to then color , , and blue.
If u is adjacent to then color , , and blue.
If u is adjacent to then color , , and blue.
If u is adjacent to , , or only then this case can be removed by Lemma 6.
If u is adjacent to , , and then we can color , , and blue.
If u is adjacent to and only then we can color , , and blue.
If u is adjacent to and only then we can color u, , and blue.
If u is adjacent to and only then we can color , , and blue.
Since in each of these extensions we have three blue vertices none of which are true blue, we can extend these graphs indefinitely. Graph 77: Please refer to Figure 10. Suppose we add a new vertex called v.
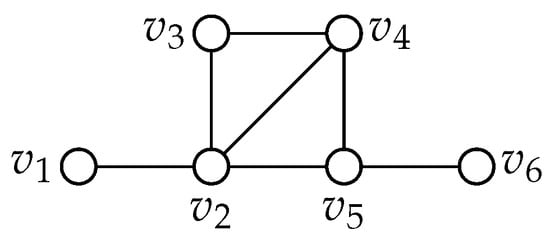
Figure 10.
Graph 77.
If v is adjacent to or only then we can remove this case by Lemma 6. Our goal with extending is to find no true blue vertex. If we do have a true blue, we must then extend further.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
There are two cases in which we cannot not obtain three non-true blue vertices. The first is when v is adjacent to and the second is when v is adjacent to both and .
Case 1. If v is adjacent to , then and v can be filled. For this case, we must extend further since there is a true blue vertex. Suppose we add a second vertex called u.
If u is adjacent to v then , and can be colored blue.
If u is adjacent to then , and can be colored blue.
If u is adjacent to then , and can be colored blue.
If u is adjacent to then , and can be colored blue.
If u is adjacent to , or only then we can remove this case by Lemma 6.
If u is adjacent to and then , and can be colored blue.
If u is adjacent to and then , and can be colored blue.
If u is adjacent to and then , and ccan be colored blue.
Case 2. If v is adjacent to both and then we consider adding another vertex w.
If w is adjacent to v then , and can be colored blue.
If w is adjacent to then , and can be colored blue.
If w is adjacent to then , and can be colored blue.
If w is adjacent to then , and can be colored blue.
If w is adjacent to then , and can be colored blue.
The cases where w is adjacent to or only can be removed from consideration by Lemma 6.
If w is adjacent to and then , and can be colored blue.
Thus, we can extend all cases indefinitely without ever forcing G. Since each case is extendable, then graph 77 is extendable.
Notice there is no case where v is adjacent to or . This is because connecting a vertex to either one would create a cherry structure and that case is covered elsewhere. It is also important to notice that in each case, we are able to find a failed zero forcing number of three.
Every blue vertex has two white neighbors, so we can add any number of edges or vertices to any of these graphs without forcing G. This is because the three blue vertices will always be adjacent to two white neighbors and cannot force any other vertex. Thus, for graph 77.
Graph 80: Please refer to Figure 11. It will be helpful to refer to Figure 11. Let the vertex on the far left be . Let the vertex adjacent to be . Let the top vertex adjacent to be and the bottom be . Let the vertex that is adjacent to both and on the right be . Furthermore, finally, let the vertex on the far right side be . We begin by extending graph 80 by one vertex, v and connecting v to every vertex in G. We can rule out the case where v is adjacent to or only by Lemma 6. If v is adjacent to both and then then we can color vertices v, , and blue and all other vertices white. This is because connecting a vertex to either would create a cherry structure and that case is covered elsewhere.
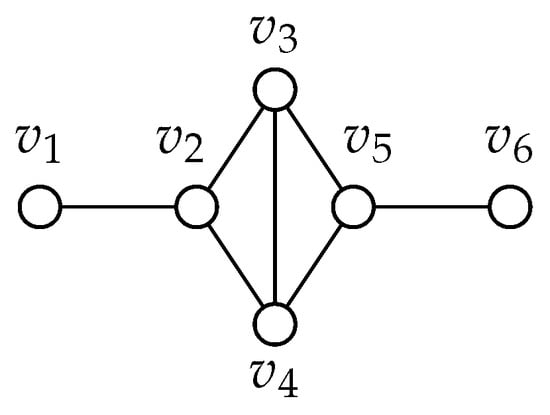
Figure 11.
Graph 80.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then , and can be colored blue.
In all cases, there are no true blue vertices. Thus, all cases are extendable and this implies graph 80 can be extended indefinitely. It is also important to notice that in each case, we are able to find a failed zero forcing number of three. Graph 85: Please refer to Figure 12.
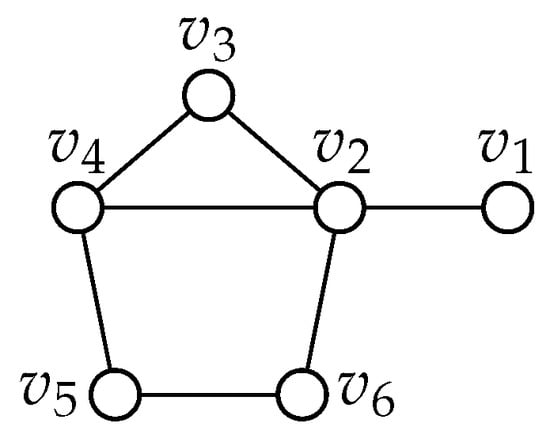
Figure 12.
Graph 85.
We will show that all but two extensions of G to a graph with 7 vertices have no true blue vertex of degree 1. Let v denote the new vertex. Note that extensions that would result in a cherry are neglected as those cases are resolved by Lemma 6. We consider the following cases.
If v is adjacent to only, we color , , and blue.
If v is adjacent to only, we color , , and blue.
If v is adjacent to only, then , , and can be colored blue.
If v is adjacent to only then this case can be removed by Lemma 2.6.
The only problems are where v is adjacent to or .
First, we consider the case where v is adjacent to .
Then we add another vertex u.
If u is adjacent to or only then this case can be removed by Lemma 2.6.
If u is adjacent to and , then u, , and can be colored blue.
If u is adjacent to v, then v, , and can be colored blue.
If u is adjacent to , then , , and can be colored blue.
If u is adjacent to , then , , and can be colored blue.
If u is adjacent to , then , , and can be colored blue.
If u is adjacent to , then , , and can be colored blue.
First, we consider the case where v is adjacent to .
Then we add another vertex w.
If w is adjacent to v, then v, , and can be colored blue.
If w is adjacent to , then , , and can be colored blue.
If w is adjacent to , then , , and can be colored blue.
If w is adjacent to , then , , and can be colored blue.
If w is adjacent to , then , , and can be colored blue.
If w is adjacent to or only then this case can be removed by Lemma 2.6.
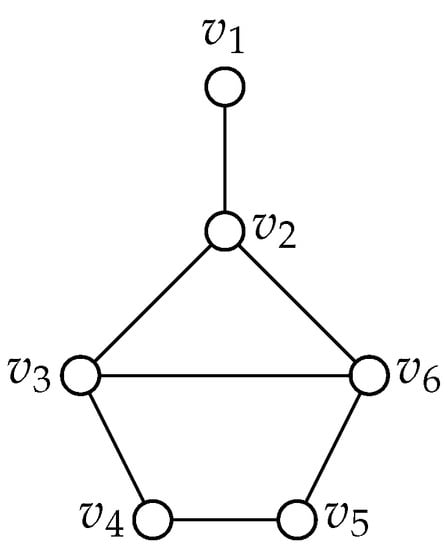
Figure 13.
Graph 86.
We will show that all extensions of G to a graph with 7 vertices have no true blue vertices of degree 1. Let v be the new vertex. Let be the vertex of degree 1, be the vertex of degree 2 that is adjacent to , be the vertex of degree 3 that is adjacent to and on the left of , be the vertex of degree 2 that is adjacent to , be the vertex of degree 2 that is adjacent to , and be the vertex of degree 3 that is adjacent to . We have the following cases.
If v is adjacent to only, we color , , and blue.
If v is adjacent to only, the resulting graph contains a cherry. So we color v, white, and color the remaining vertices blue.
If v is adjacent to only, we color , , and blue.
If v is adjacent to only, we color , , and blue.
The remaining cases of connecting v to G are analogous to one of the previous four. Furthermore, note that in each case where the resulting graph does not contain a cherry, we can always color v white and add edges between v and any subset of the remaining vertices without affecting the number of blue vertices. Graph 87: Please refer to Figure 14.
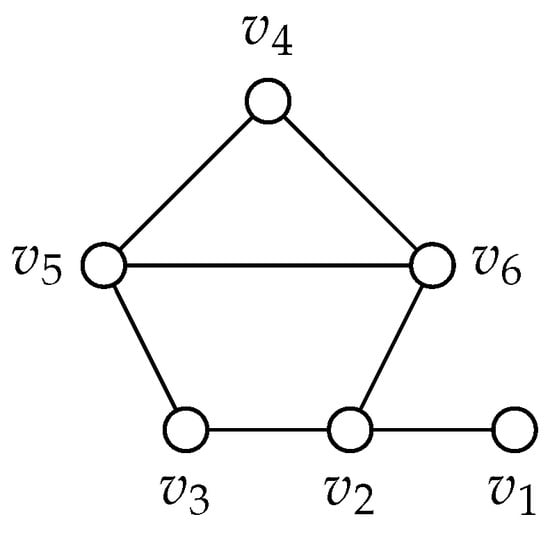
Figure 14.
Graph 87.
All but one of the single vertex extensions of G is either a cherry or suitable for extension by Lemma 3. Let be the only vertex of degree one that is adjacent to ; is adjacent to and ; will be adjacent to and and will be adjacent to and .
If v is adjacent to , we can fill in , , and .
If v is adjacent to , it creates a cherry and this case can be discarded.
If v is adjacent to , we can fill in , , and .
If v is adjacent to , we can fill in , , and .
If v is adjacent to , we can fill in , , and .
If v is adjacent to , we must have a true blue vertex and thus this graph must be extended further. We can then add in an additional vertex, u.
If u is adjacent to , we can fill in , , and .
If u is adjacent to , it again creates a cherry and we can discard this case.
If u is adjacent to , we can fill in , , and .
If u is adjacent to , we can fill in , , and .
If u is adjacent to , we get another cherry and thus another discarded case.
If u is adjacent to , we can fill in , , and .
If u is adjacent to v, then we can fill v, , and .
In every case, we see a suitable coloring for extension by Lemma 3. Thus, we may extend graph 87 to a super-graph H, and by Lemma 3, . Graph 96: Please refer to Figure 15.
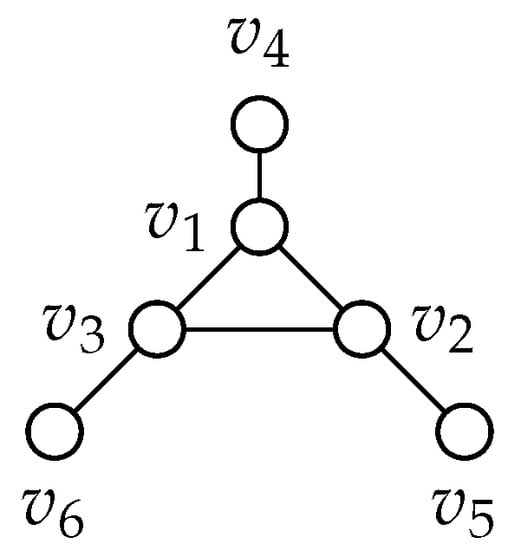
Figure 15.
Graph 96.
We will show that any extension of G to a graph with 7 vertices will have at most one true blue vertex. Let the vertices of the triangle be and which are adjacent to vertices of degree 1, and , respectively.
Consider the addition of a new vertex v. We first consider if v is adjacent to or . Without loss of generality assume v is adjacent to . Then we color and blue and and white. If v is adjacent to one of the vertices or only then we apply Lemma 6. If v is adjacent to all of the vertices and then we can color and blue. The only case that is a problem is where v is adjacent to exactly two of the vertices and . Without loss of generality we assume that v is adjacent to and .
Here we add another vertex u.
If u is adjacent to , , and then these cases are similar to the previous cases involving v,
If u is adjacent to v then we can color v, , and blue.
If u is adjacent to exactly one of , , and then this case can be removed by Lemma 6.
If u is adjacent to and only then we can color u, v, and blue.
If u is adjacent to and only then we can color , , and blue.
If u is adjacent to and only then we can color , , and blue.
If u is adjacent to , , and then we can color , , and blue. Graph 98: Please refer to Figure 16.
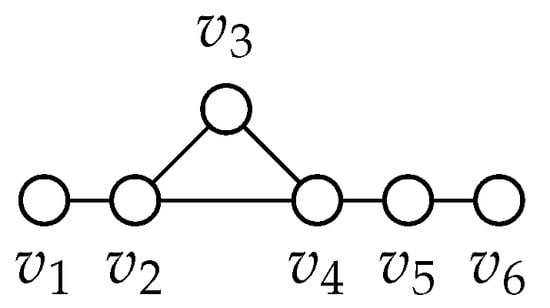
Figure 16.
Graph 98.
We begin by extending graph 98 by one vertex, v and connecting v to every vertex in G.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
The case where v is adjacent to , , or only can be removed by Lemma 6.
If v is adjacent to and , then and can be colored blue.
If v is adjacent to and , then and can be colored blue.
If v is adjacent to and , then and can be colored blue.
We can see in all cases there are no true blue vertices. Thus, all cases are extendable and this implies graph 98 can be extended indefinitely. It is also important to notice that in each case, we are able to find a failed zero forcing set of size three. Graph 102: Please refer to Figure 17.
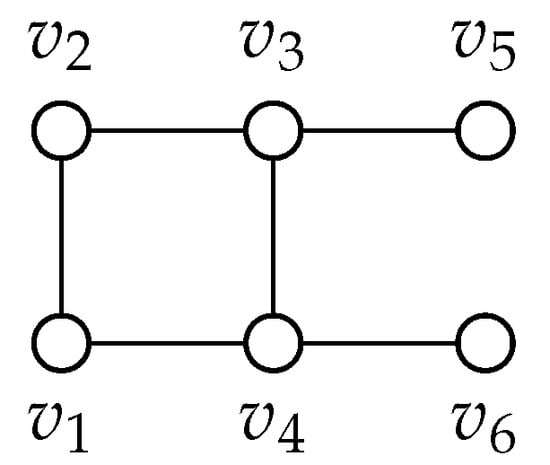
Figure 17.
Graph 102.
We begin by extending graph 102 by one vertex, v and connecting v to every vertex in G. Due to the symmetry of the graph, we can ignore the case where v is adjacent to . Notice there will be no case where v is adjacent to or . This is because connecting a vertex to either one will create a cherry structure, and this is covered by Lemma 6.
We have to consider the case where v is adjacent to both and . In this case, we have to add a new vertex u.
If u is adjacent to v, then , and can be colored blue.
If u is adjacent to , then , and can be colored blue.
If u is adjacent to , then and can be colored blue. If u is adjacent to , then and can be colored blue. If u is adjacent to , then and can be colored blue. If u is adjacent to or only then this can be removed by Lemma 6.
If u is adjacent to and then and can be colored blue.
If v is adjacent to , then and can be colored blue. Due to the symmetry of the graph, this case is the same as when v is adjacent to . So it can be ignored. However, this case has a true blue and so it must be extended. Suppose we add a new vertex u.
If u is adjacent to , then and can be filled.
If u is adjacent to , then and can be filled. Here vertex u is true blue, so we must extend further. Suppose we add another vertex called w.
If w is adjacent to , then and can be filled.
The only problem case left is if w is adjacent to only. This would create a with a pendant edge at each vertex.
Here we can add another vertex x.
If x is adjacent to v, then and can be colored blue.
If x is adjacent to w, then and can be colored blue. If x is adjacent to , then and can be colored blue.
If x is adjacent to , then and can be colored blue.
If x is adjacent to , , , and only then this case can be removed by Lemma 6.
If x is adjacent to and , then and can be colored blue.
If x is adjacent to and , then and can be colored blue.
If x is adjacent to and , then and can be colored blue.
If x is adjacent to and , then and can be colored blue.
Notice there are no true blue vertices and that in all cases. Since there are no true blue vertices, then this case is now extendable. Since each case is extendable, then graph 102 can be extended indefinitely without being forced.
Graph 103: Please refer to Figure 18. We begin by extending graph 103 by one vertex, v, and connecting v to every vertex in G. Notice there will be no case where v is adjacent to or . This is because connecting a vertex to either would create a cherry structure and that case is covered by the cherry lemma. It is also important to notice that in each case and sub-case, we are able to find a failed zero forcing number of three. Our goal with extending is to find no true blue vertex within the graph. Due to the symmetry of the graph, we can ignore the cases where v is adjacent to and .
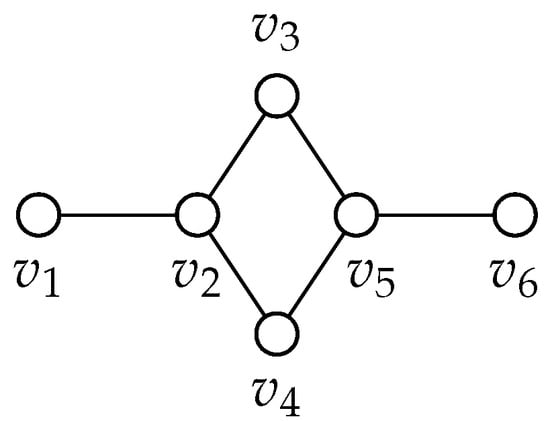
Figure 18.
Graph 103.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then this reverts to the extension of Graph 102 where the added vertex v is adjacent to .
Since there are no more true blue vertices, then this case is resolved and can be extended indefinitely. Since each case is extendable, this implies that graph 103 can also be extended indefinitely without being forced. Graph 105: Please refer to Figure 19.
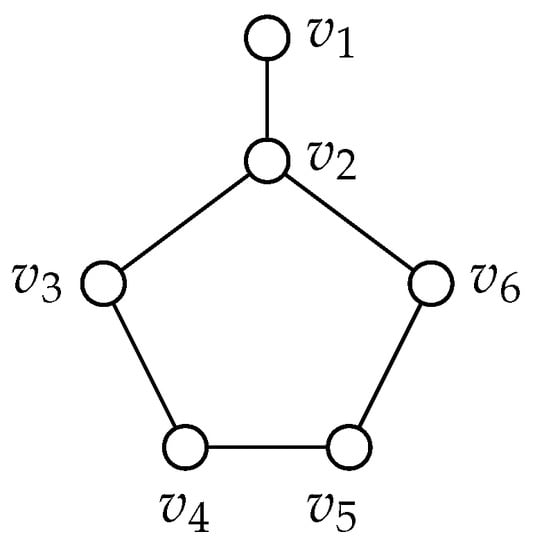
Figure 19.
Graph 105.
We begin by extending graph 105 by one vertex, v and connecting v to every vertex in G. Notice there will be no case where v is adjacent to . This is because adding an extension to would create a cherry structure and this case is covered by the cherry lemma. It is also important to notice that in each case, we are able to find a failed zero forcing number of three. Our goal with extending is to find no true blue vertex within the graph.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be colored blue.
If v is adjacent to , then and can be filled.
Notice the last two cases have a true blue vertex. Without loss of generality assume that v is adjacent to .
Suppose we add a new vertex u.
If u is adjacent to or only then this case can be removed by Lemma 6.
If u is adjacent to v, then and can be colored blue.
If u is adjacent to , then and can be colored blue.
If u is adjacent to , then and can be colored blue.
If u is adjacent to and , then and can be colored blue.
If u is adjacent to , then and can be colored blue.
If u is adjacent to , then and can be colored blue.
Since there are no more true blue vertices in these sub-cases, then this case is resolved and can be extended indefinitely. Since each case is extendable, this implies that graph 105 can be extended indefinitely without being forced and .
Graph 112: Please refer to Figure 20.
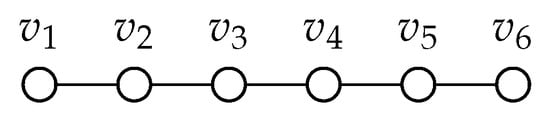
Figure 20.
Graph 112.
: Any extension of to a graph with 7 vertices will have at most one true blue vertex.
We consider adding a vertex v to this graph. If v is adjacent to then we can color vertex v white and color vertices and blue to create a failed zero forcing set of size 3. If v is adjacent to then we can color vertex v white and color vertices and blue to create a failed zero forcing set of size 3. If v is not adjacent to either or then v must be adjacent to one or more of the vertices or . We consider different cases, each showing that we can create a failed zero forcing set of size 3 with at most one true blue vertex. We consider a series of different cases.
If v is adjacent to only one of the vertices , , , or then this creates a pendant V which can be removed from consideration by Lemma 6.
If v is adjacent to and only then we color and blue.
If v is adjacent to and only then we color and blue.
If v is adjacent to and only then we color and blue.
If v is adjacent to and only then we color and blue.
If v is adjacent to and only then we color , and blue.
If v is adjacent to and only then we color and blue.
If v is adjacent to and only, then we color , and blue.
The only problem case is where v is adjacent to both and . In this case we add a new vertex u.
If u is adjacent to v then we color and blue.
If u is adjacent to then we color and blue.
If u is adjacent to then we color and blue.
If u is adjacent to then we color and blue.
If u is adjacent to then we color and blue.
If u is adjacent to or only then this case can be removed from consideration by Lemma 6.
If u is adjacent to and then we color u, v, and blue.
2.2. Proof of the Main Theorems
We now prove Theorem 1. Let G be a graph with at least 7 vertices. Then .
Proof.
The graphs with six vertices fall into three different groups (i) graphs where has at least three blue vertices, none of which are true blue, (ii) graphs where has three blue vertices, but one is true blue (which we will call exceptions), and (iii) graphs that contain a pendant V or a pendant triangle. The strategy is as follows. We start with a graph H with at least 8 vertices and remove vertices (along with incident edges) to obtain a reduced graph G with 6 vertices. We note we can maintain a connected graph by successively removing a leaf from a spanning tree of the graph. If G is in group (i) then , and since each blue vertex has two white neighbors we can extend G by Lemma 3 by adding vertices and edges to obtain the original graph H, so that . If G is in group (ii) then , but since G contains a true blue vertex it may not be able to be extended to obtain H. These are the exception cases. Here we consider all extensions of G to graphs with 7, 8, or 9 vertices so that there can be three blue vertices, none of which are true blue. Then we can extend G by Lemma 3 by adding vertices and edges (if necessary) to obtain the original graph H, so that . If G is in group (iii) then it contains a pendant V or a pendant triangle. By Lemmas 6 and 7 if every reduction of G results in a graph G with a pendant triangle or pendant V then H must have had a pendant triangle or pendant V. By Lemmas 4 and 5, . This shows that any graph with at least 8 vertices has a failed zero forcing number of at least 3. However, examining the exception cases from Section 2.1, we note that any extension of graphs with six vertices to seven vertices still have a failed zero forcing number of at least 3. Hence any graph with at least 7 vertices has a failed zero forcing number of at least 3. □
We have now proved our main theorem that gives us a characterization of all graphs with .
Theorem 3.
The graphs with are precisely those shown in Figure 1.
3. Conclusions
In this paper, we have investigated failed zero forcing sets, which not only provided new theoretical results but also have practical implications. Applications of zero forcing lie in the area of social networks in which a person knows a particular piece of information and if they share it with all but one of their friends, in the interest of unity, they share the information with their remaining friend. For failed zero forcing we are seeking the largest number of people that could know a piece of information so that it does not spread across the entire network. This is also relevant in the spreading of disease in a pandemic where we seek the maximum number of people that can be infected, yet the infection does not spread to the entire population.
We have completely characterized all graphs with a failed zero forcing number of 2. We pose the following problem.
Problem 1.
Characterize all graphs with a failed zero forcing number of 3.
Our investigations into this problem revealed a much larger number of graphs with a failed zero forcing number of 3 and the methods used in this paper will require investigation of a much larger number of exception cases.
We also showed that all graphs with at least 7 vertices have a failed zero forcing number of 3. As an extension of this result, we pose the following problem.
Problem 2.
Determine the smallest n such that all graphs with at least n vertices have a failed zero forcing number of size k.
Author Contributions
Conceptualization, L.G., K.R., J.T. and D.A.N., Formal analysis, L.G., K.R., J.T. and D.A.N., Funding acquisition, D.A.N., Writing—original draft, L.G., K.R., J.T. and D.A.N., Writing—review and editing, D.A.N., All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by a National Science Foundation Research Experiences for Undergraduates grant, No. 1950189.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable as the study did not report any data.
Acknowledgments
We are grateful to three anonymous referees for carefully reviewing our paper and for providing recommendations that greatly improved the presentation of the paper. In particular, one reviewer provided excellent feedback on both the original manuscript and the revision. This research was supported by the National Science Foundation Research for Undergraduates Award 1950189.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fallat, S.M.; Hogben, L. The minimum rank of symmetric matrices described by a graph: A survey. Linear Algebra Appl. 2007, 426, 558–582. [Google Scholar] [CrossRef] [Green Version]
- Fetcie, K.; Jacob, B.; Saavedra, D. The Failed Zero-Forcing Number of a Graph. Involve 2015, 8, 99–117. [Google Scholar] [CrossRef]
- Adams, A.; Jacob, B. Failed zero forcing and critical sets on directed graphs. arXiv 2019, arXiv:1911.06705. [Google Scholar]
- Shitov, Y. On the complexity of failed zero forcing. Theor. Comput. Sci. 2017, 660, 102–104. [Google Scholar] [CrossRef] [Green Version]
- Beaudouin-Lafona, M.; Crawford, M.; Chen, S.; Karst, N.; Nielsen, L.; Troxell, D.S. On the zero blocking number of rectangular, cylindrical, and Möbius grids. Discret. Appl. Math. 2020, 285, 380–396. [Google Scholar] [CrossRef]
- Karst, N.; Shen, X.; Vu, M. Blocking zero forcing processes in Cartesian products of graphs. Discret. Appl. Math. 2020, 285, 380–396. [Google Scholar] [CrossRef]
- Erdos, P.; Rényi, A. Asymmetric Graphs. Acta Math. Acad. Sci. Hungar. 1963, 14, 295–315. [Google Scholar] [CrossRef]
- Cvetković, D.; Petrić, M. A table of connected graphs on six vertices. Discret. Math. 1984, 50, 37–48. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).