An Ordinal Consistency Indicator for Pairwise Comparison Matrix
Abstract
1. Introduction
2. Literature Review
3. The Proposed Indicator SDR
4. Comparisons
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thurstone, L.L. A law of comparative judgment. Psychol. Rev. 1927, 34, 273–286. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Kuo, T. A modified TOPSIS with a different ranking index. Eur. J. Oper. Res. 2017, 260, 152–160. [Google Scholar] [CrossRef]
- Smith, J.E.; von Winterfeldt, D. Anniversary article: Decision analysis in management science. Manag. Sci. 2004, 50, 561–574. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Marra, M. The state of the art development of AHP (1979–2017): A literature review with a social network analysis. Int. J. Prod. Res. 2017, 55, 6653–6675. [Google Scholar] [CrossRef]
- Ishizaka, A.; Labib, A. Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 2011, 38, 14336–14345. [Google Scholar] [CrossRef]
- Koczkodaj, W.W.; Mikhailov, L.; Redlarski, G.; Soltys, M.; Szybowski, J.; Tamazian, G.; Wajch, E.; Yuen, K.K.F. Important Facts and Observations about Pairwise Comparisons. Fundam. Inform. 2016, 144, 291–307. [Google Scholar] [CrossRef]
- Dong, Y.; Xu, Y.; Li, H.; Dai, M. A comparative study of the numerical scales and the prioritization methods in AHP. Eur. J. Oper. Res. 2008, 186, 229–242. [Google Scholar] [CrossRef]
- Ma, D.; Zheng, X. 9/9-9/1 scale method of AHP. In Proceedings of the 2nd International Symposium on the AHP, Pittsburgh, PA, USA, 11–14 August 1991; Volume 1, pp. 197–202. [Google Scholar]
- Salo, A.A.; Hämäläinen, R.P. On the measurement of preferences in the analytic hierarchy process. J. Multi-Criteria Decis. Anal. 1997, 6, 309–319. [Google Scholar] [CrossRef]
- Cavallo, B.; D’Apuzzo, L. A general unified framework for pairwise comparison matrices in multicriterial methods. Int. J. Intell. Syst. 2009, 24, 377–398. [Google Scholar] [CrossRef]
- Koczkodaj, W.W.; Szybowski, J. The limit of inconsistency reduction in pairwise comparisons. Int. J. Appl. Math. Comput. Sci. 2016, 26, 721–729. [Google Scholar] [CrossRef]
- Saaty, T.L. Axiomatic foundation of the analytic hierarchy process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Rehman, N.; Faizi, S.; Sałabun, W. On the Analytic Hierarchy Process Structure in Group Decision-Making Using Incomplete Fuzzy Information with Applications. Symmetry 2021, 13, 609. [Google Scholar]
- Grzybowski, A.Z. New results on inconsistency indices and their relationship with the quality of priority vector estimation. Expert Syst. Appl. 2016, 43, 197–212. [Google Scholar] [CrossRef][Green Version]
- Barzilai, J. Deriving weights from pairwise comparison matrices. J. Oper. Res. Soc. 1997, 48, 1226–1232. [Google Scholar] [CrossRef]
- Choo, E.U.; Wedley, W.C. A common framework for deriving preference values from pairwise comparison matrices. Comput. Oper. Res. 2004, 31, 893–908. [Google Scholar] [CrossRef]
- Crawford, G.B. The geometric mean procedure for estimating the scale of a judgement matrix. Math. Model. 1987, 9, 327–334. [Google Scholar] [CrossRef]
- Golany, B.; Kress, M. A multicriteria evaluation of methods for obtaining weights from ratio-scale matrices. Eur. J. Oper. Res. 1993, 69, 210–220. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Comparison of eigenvalue, logarithmic least squares and least squares methods in estimating ratios. Math. Model. 1984, 5, 309–324. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision-making with the AHP: Why is the principal eigenvector necessary. Eur. J. Oper. Res. 2003, 145, 85–91. [Google Scholar] [CrossRef]
- Siraj, S.; Mikhailov, L.; Keane, J.A. Preference elicitation from inconsistent judgments using multi-objective optimization. Eur. J. Oper. Res. 2012, 220, 461–471. [Google Scholar] [CrossRef]
- Aguaròn, J.; Moreno-Jiménez, J.M. The geometric consistency index: Approximated thresholds. Eur. J. Oper. Res. 2003, 147, 137–145. [Google Scholar] [CrossRef]
- Barzilai, J. Consistency measures for pairwise comparison matrices. J. Multi-Criteria Decis. Anal. 1998, 7, 123–132. [Google Scholar] [CrossRef]
- Brunelli, M.; Canal, L.; Fedrizzi, M. Inconsistency indices for pairwise comparison matrices: A numerical study. Ann. Oper. Res. 2013, 211, 493–509. [Google Scholar] [CrossRef]
- Brunelli, M. Recent Advances on Inconsistency Indices for Pairwise Comparisons—A Commentary. Fundam. Inform. 2016, 144, 321–332. [Google Scholar] [CrossRef]
- Koczkodaj, W.W. A new definition of consistency of pairwise comparisons. Math. Comput. Model. 1993, 18, 79–84. [Google Scholar] [CrossRef]
- Koczkodaj, W.W.; Szwarc, R. On axiomatization of inconsistency indicators for pairwise comparisons. Fundam. Inform. 2014, 132, 485–500. [Google Scholar] [CrossRef]
- Lamata, M.T.; Peláez, J.I. A method for improving the consistency of judgements. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 677–686. [Google Scholar] [CrossRef]
- Peláez, J.I.; Lamata, M.T. A new measure of consistency for positive reciprocal matrices. Comput. Math. Appl. 2003, 46, 1839–1845. [Google Scholar] [CrossRef]
- Golden, B.L.; Wang, Q. An alternate measure of consistency. In The Analytic Hierarchy Process; Springer: Berlin/Heidelberg, Germany, 1989; pp. 68–81. [Google Scholar]
- Stein, W.E.; Mizzi, P.J. The harmonic consistency indicator for the analytic hierarchy process. Eur. J. Oper. Res. 2007, 177, 488–497. [Google Scholar] [CrossRef]
- Brunelli, M.; Fedrizzi, M. Boundary properties of the inconsistency of pairwise comparisons in group decisions. Eur. J. Oper. Res. 2015, 240, 765–773. [Google Scholar] [CrossRef]
- Brunelli, M. Studying a set of properties of inconsistency indices for pairwise comparisons. Ann. Oper. Res. 2017, 248, 143–161. [Google Scholar] [CrossRef]
- Yang, W.E.; Ma, C.Q.; Han, Z.Q.; Chen, W.J. Checking and adjusting order-consistency of linguistic pairwise comparison matrices for getting transitive preference relations. OR Spectr. 2016, 38, 769–787. [Google Scholar] [CrossRef]
- Siraj, S.; Mikhailov, L.; Keane, J.A. A heuristic method to rectify intransitive judgments in pairwise comparison matrices. Eur. J. Oper. Res. 2012, 216, 420–428. [Google Scholar] [CrossRef]
- Bozóki, S.; Rapcsak, T. On Saaty’s and Koczkodaj’s inconsistencies of pairwise comparison matrices. J. Glob. Optim. 2008, 42, 157–175. [Google Scholar] [CrossRef]
- Kwiesielewicz, M.; Van Uden, E. Inconsistent and contradictory judgements in pairwise comparison method in the AHP. Comput. Oper. Res. 2004, 31, 713–719. [Google Scholar] [CrossRef]
- Siraj, S.; Mikhailov, L.; Keane, J.A. Contribution of individual judgments toward inconsistency in pairwise comparisons. Eur. J. Oper. Res. 2015, 242, 557–567. [Google Scholar] [CrossRef]
- Akarte, M.M.; Surendra, N.V.; Ravi, B.; Rangaraj, N. Web based casting supplier evaluation using analytical hierarchy process. J. Oper. Res. Soc. 2001, 52, 511–522. [Google Scholar] [CrossRef]
- Forman, E.H.; Gass, S.I. The analytic hierarchy process—An exposition. Oper. Res. 2001, 49, 469–486. [Google Scholar] [CrossRef]
- Golden, B.L.; Wasil, E.A.; Harker, P.T. The Analytic Hierarchy Process: Applications and Studies; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Ho, W. Integrated analytic hierarchy process and its applications–A literature review. Eur. J. Oper. Res. 2008, 186, 211–228. [Google Scholar] [CrossRef]
- Shim, J.P. Bibliographical research on the analytic hierarchy process (AHP). Socio-Econ. Plan. Sci. 1989, 23, 161–167. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Vargas, L.G. An overview of the analytic hierarchy process and its applications. Eur. J. Oper. Res. 1990, 48, 2–8. [Google Scholar] [CrossRef]
- Zahedi, F. The analytic hierarchy process—a survey of the method and its applications. Interfaces 1986, 16, 96–108. [Google Scholar] [CrossRef]
- Sugden, R. Why be consistent? A critical analysis of consistency requirements in choice theory. Economica 1985, 52, 167–183. [Google Scholar] [CrossRef]
- Alonso, J.A.; Lamata, M.T. Consistency in the analytic hierarchy process: A new approach. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2006, 14, 445–459. [Google Scholar] [CrossRef]
- Ergu, D.; Kou, G.; Peng, Y.; Shi, Y. A simple method to improve the consistency ratio of the pair-wise comparison matrix in ANP. Eur. J. Oper. Res. 2011, 213, 246–259. [Google Scholar] [CrossRef]
- Ishizaka, A.; Lusti, M. An expert module to improve the consistency of AHP matrices. Int. Trans. Oper. Res. 2004, 11, 97–105. [Google Scholar] [CrossRef]
- Kou, G.; Ergu, D.; Shang, J. Enhancing data consistency in decision matrix: Adapting Hadamard model to mitigate judgment contradiction. Eur. J. Oper. Res. 2014, 236, 261–271. [Google Scholar] [CrossRef]
- Li, H.L.; Ma, L.C. Detecting and adjusting ordinal and cardinal inconsistencies through a graphical and optimal approach in AHP models. Comput. Oper. Res. 2007, 34, 780–798. [Google Scholar] [CrossRef]
- Vargas, L.G. The consistency index in reciprocal matrices: Comparison of deterministic and statistical approaches. Eur. J. Oper. Res. 2008, 191, 454–463. [Google Scholar] [CrossRef]
- Xu, W.J.; Dong, Y.C.; Xiao, W.L. Is It Reasonable for Saaty’s Consistency Test in the Pairwise Comparison Method? In Proceedings of the 2008 ISECS International Colloquium on Computing, Communication, Control, and Management, Guangzhou, China, 3–4 August 2008; Volume 3, pp. 294–298. [Google Scholar]
- Genest, C.; Zhang, S.S. A graphical analysis of ratio-scaled paired comparison data. Manag. Sci. 1996, 42, 335–349. [Google Scholar] [CrossRef]
- Gower, J.C. The analysis of asymmetry and orthogonality. In Recent Developments in Statistics; Barra, J.-R., Brodeau, F., Romier, G., Van Cutsem, B., Eds.; North-Holland: Amsterdam, The Netherlands, 1977; pp. 109–123. [Google Scholar]
- Kuo, T. An Ordinal Consistency Indicator for Pairwise Comparison Matrix. In Proceedings of the 2018 NTCB Conference for International Management Practices, National Taipei University of Business, Taipei, Taiwan, 21 December 2018; pp. 49–50. [Google Scholar]
- Saaty, T.L.; Peniwati, K. Group Decision Making: Drawing Out and Reconciling Differences; RWS Publications: Pittsburgh, PA, USA, 2013. [Google Scholar]

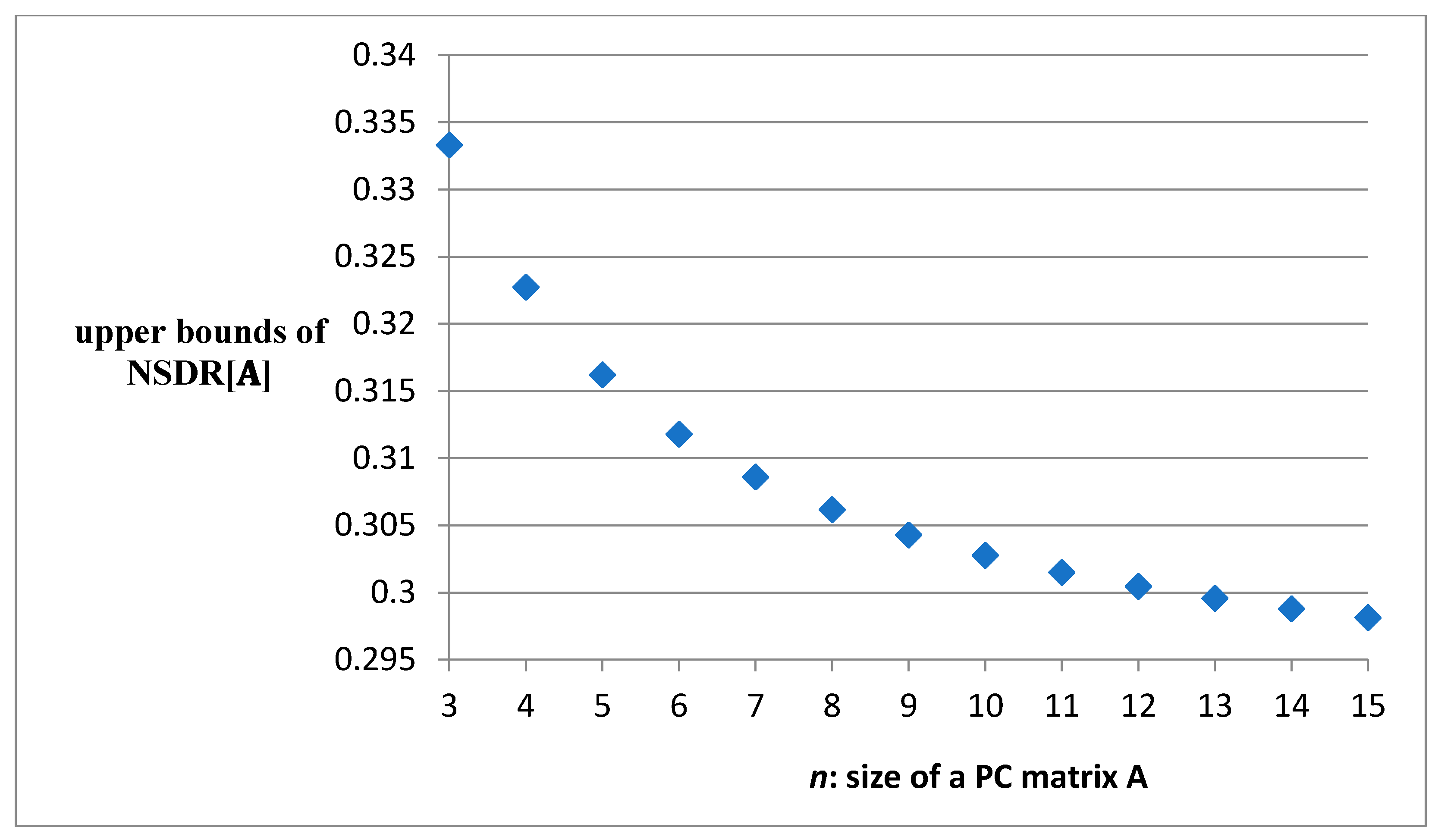

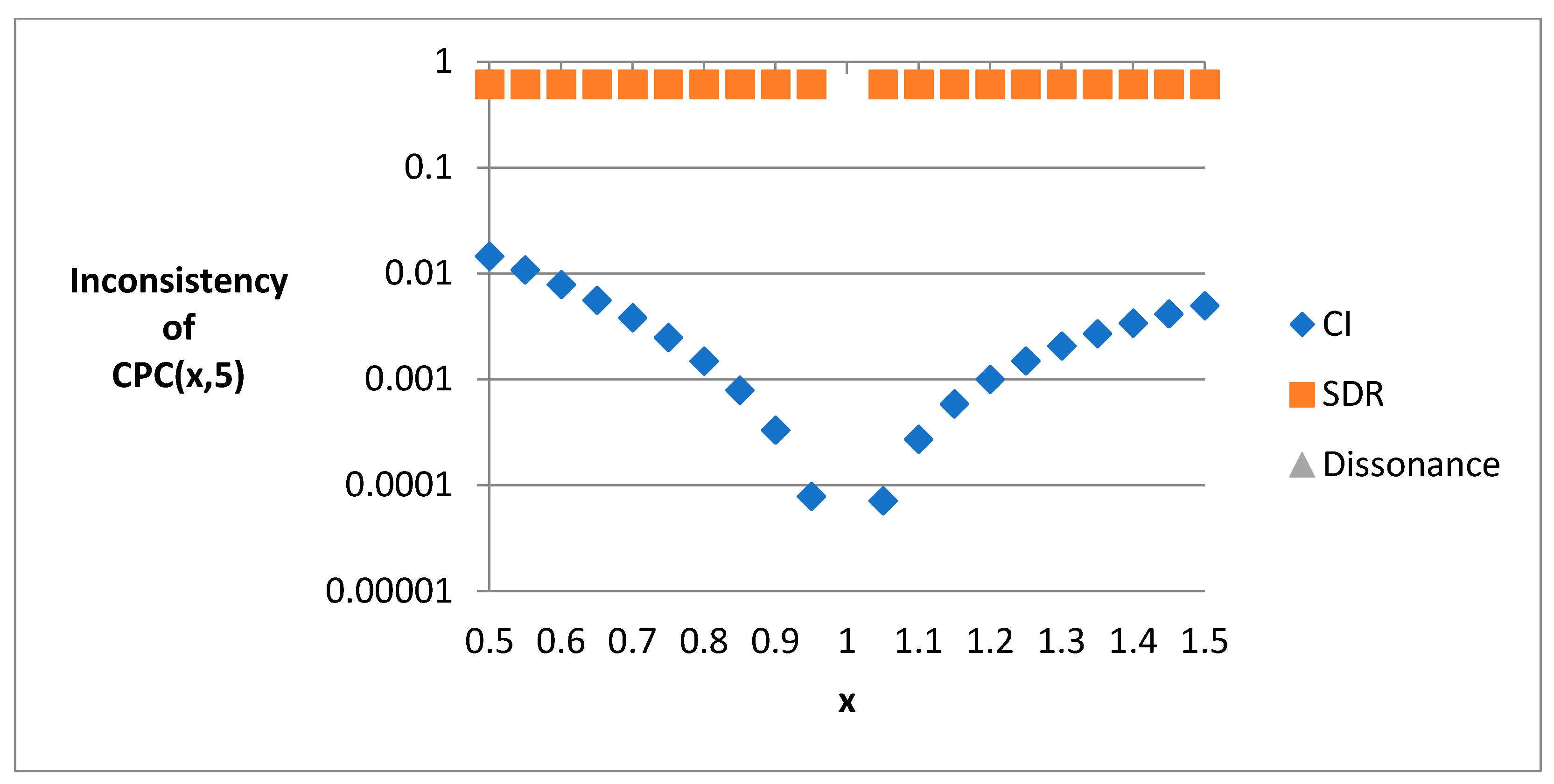
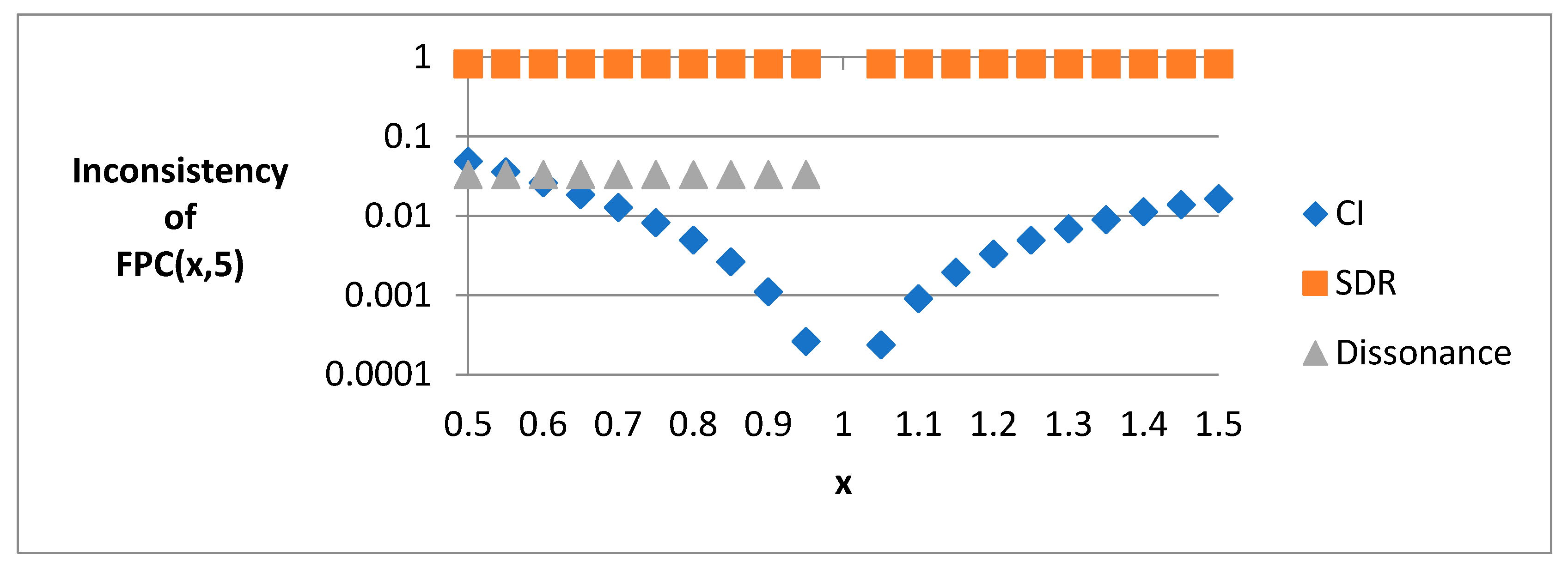
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.29 | 1.58 | 1.87 | 2.16 | 2.45 | 2.74 | 3.03 | 3.32 | 3.61 | 3.89 | 4.18 | 4.47 |
| 0.01 | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
|---|---|---|---|---|---|---|---|---|
| 3-scales 4-scales 5-scales 6-scales 7-scales 8-scales 9-scales | S | 0.00 | 0.00 | 0.00 | 0.19 | 0.19 | 0.39 | 0.53 |
| I | 0.00 | 0.00 | 0.00 | 0.19 | 0.19 | 0.39 | 0.53 | |
| B | 0.00 | 0.00 | 0.00 | 0.19 | 0.19 | 0.39 | 0.53 |
| CI | SDR | CI* | GCI | HCI | RE | GW | KI | ICD | |
|---|---|---|---|---|---|---|---|---|---|
| CI | 1 | 0.743 | 0.967 | 0.998 | 0.933 | 0.798 | 0.924 | 0.713 | 0.946 |
| SDR | 0.743 | 1 | 0.619 | 0.772 | 0.705 | 0.855 | 0.845 | 0.829 | 0.705 |
| CI* | 0.967 | 0.619 | 1 | 0.951 | 0.9 | 0.716 | 0.839 | 0.61 | 0.882 |
| GCI | 0.998 | 0.772 | 0.951 | 1 | 0.93 | 0.813 | 0.938 | 0.744 | 0.943 |
| HCI | 0.933 | 0.705 | 0.9 | 0.93 | 1 | 0.765 | 0.937 | 0.646 | 0.89 |
| RE | 0.798 | 0.855 | 0.716 | 0.813 | 0.765 | 1 | 0.842 | 0.696 | 0.734 |
| GW | 0.924 | 0.845 | 0.839 | 0.938 | 0.937 | 0.842 | 1 | 0.803 | 0.867 |
| KI | 0.713 | 0.829 | 0.61 | 0.744 | 0.646 | 0.696 | 0.803 | 1 | 0.619 |
| ICD | 0.946 | 0.705 | 0.882 | 0.943 | 0.89 | 0.734 | 0.867 | 0.619 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, T. An Ordinal Consistency Indicator for Pairwise Comparison Matrix. Symmetry 2021, 13, 2183. https://doi.org/10.3390/sym13112183
Kuo T. An Ordinal Consistency Indicator for Pairwise Comparison Matrix. Symmetry. 2021; 13(11):2183. https://doi.org/10.3390/sym13112183
Chicago/Turabian StyleKuo, Ting. 2021. "An Ordinal Consistency Indicator for Pairwise Comparison Matrix" Symmetry 13, no. 11: 2183. https://doi.org/10.3390/sym13112183
APA StyleKuo, T. (2021). An Ordinal Consistency Indicator for Pairwise Comparison Matrix. Symmetry, 13(11), 2183. https://doi.org/10.3390/sym13112183






