Abstract
Important aspects of QED-corrections to hadronic decays are reviewed with emphasis on conceptual points such as infrared divergences and structure dependence. These matter are illustrated for the , the leptonic decay and the semileptonic decay . Aspects of structure dependence include the (non)-cancellation of hard-collinear logs (e.g., and ) of charged final states.
1. Introduction
Quantum electrodynamics (QED) can be regarded as the oldest and possibly most accurate and successful quantum field theory (QFT) there is. The renormalisation of QED, by the pioneers Dyson, Feynman, Schwinger, Tomonaga and others [1], gave birth to the successful application of quantum field theory to all of particle physics culminating in the Standard Model (SM) in the 1960s [2,3,4] and finally the Higgs-boson discovery in 2012 [5,6]. Since the QED coupling constant is small perturbation theory is a reliable tool for many cases. A topical example is the anomalous magnetic moment of the muon with the theory average [7] very close to the experimental average [8], currently with some tension.
The application of QED to particle decays comes with additional subtleties that can be traced back to two idealisations, infinite space and infinitely precise measurement apparatuses, which do not hold in practice leading to infrared- (IR) divergences and IR-sensitive terms. In well-defined observables, IR-divergences cancel and the understanding thereof is based on cancellation-theorems [9,10,11] relying on principles such as unitarity. IR-sensitivity, leading to large logs, can invalidate the naive counting in perturbation theory. In for example, one will find to all orders in perturbation theory.
In reporting experimental results in flavour physics the QED-radiation is regarded as a background and is removed by using Monte-Carlo programs such as PHOTOS [12]. Such tools are based on versions of scalar QED (point-like approximations). The cross-validation of these programs seems essential in assuring precision extraction of CKM matrix elements (e.g., ) or the testing of lepton flavour universality [13] (e.g., ). This topic certainly deserves further discussion and study. However, we will not do so in this text and focus instead on theoretical aspects. (Let us add that one needs to distinguish kaon physics from D- and B-physics in this respect. In the former case the situation is better as the logs are not that large, structure-dependent analyses in chiral perturbation theory exist and experiment is more inclusive in the photon such that Monte-Carlo tools are not indispensable in principle.)
We will not comment on the infrared problems of quantum chromodynamics (QCD) but refer the reader to an excellent list of text books [14,15,16,17,18] and review articles [19,20]. We content ourselves emphasising that QCD is conceptually very different from QED in that there is a mass gap for the observable hadronic spectrum. All particle masses are proportional to a non-perturbative scale with the exception of the pion for which due to its pseudo-goldstone nature. The challenge in QCD is to establish factorisation theorems whereby collinear divergences arising from a hard kernel, computed with quarks and gluons, are absorbed in a meaningful way into hadronic objects such as the parton distribution functions or jets.
These short notes are organised as follows. In Section 2, we describe the origin of infrared divergences and the cancellation thereof in observables. Three examples, , and in increasing complexity are reviewed in Section 3 at the level of the point-like approximation. Aspects of going beyond this approximation are discussed in Section 4 and we end with conclusions in Section 5. Aspects of infrared physics such as the Low-theorem, the KLN-theorem, coherent states, infrared singularities of one-loop diagrams and terminology are briefly discussed in Appendices Appendix A–Appendix F, respectively.
2. Infrared Divergences and Infrared-Sensitivity
IR-divergences are associated with massless particles and there are two known mechanisms for enforcing massless particles, goldstone bosons and gauge bosons (without confinement and unbroken gauge symmetry). (The fermion mass in QCD can be put to zero and remains zero in perturbation theory due to chiral symmetry but the zero value in itself does not stand out by any mechanism.) The goldstone effective theory, chiral perturbation theory in QCD, is largely free from IR-divergences as the shift symmetry enforces derivative interactions which tame the IR-behaviour. Now, the only gauge boson of the type mentioned is our well-known photon and this places QED as a unique laboratory for IR-problems. (To some extent this also applies to the graviton and gravity as already studied by Weinberg [21,22] for renewed interest.) Before venturing any deeper it is advisable to review the basics of IR-divergences. Since real and virtual photon radiation are connected by cancellation theorems it is sufficient, at first, to consider real radiation only.
Disregarding ultraviolet (UV) divergences the only type of divergences that can arise are from propagators going on-shell which are of the IR-type. At leading order this is particularly simple as we may just consider real emission of a photon from a charged particle, e.g., a lepton ℓ, as depicted in Figure 1. The propagator denominator, for on-shell p, behaves like
where , , , and the angle between the unit vector and the z-axis. The propagator is singular if either the photon energy or the angle approach zero (and ). These divergences are known as soft and collinear, respectively. In they lead to logarithmic singularities and . (A photon mass is introduced to regulate the soft divergence, in addition to (1), which in dimensional regularisation would map into . Note that the photon mass also regularises the collinear divergences.) In certain regions of phase space these divergences combine and lead to soft-collinear divergences . Generally, at n-loops there are terms of the order with and .
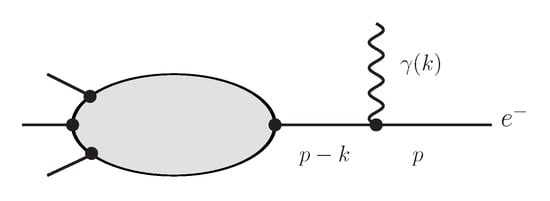
Figure 1.
Photon-emission from an external electron in a generic process.
It seems worthwhile to briefly digress on the collinear term . For finite lepton mass this is a physical effect, see for example the previously mentioned sizeable -terms in . (At a technical level the problem reoccurs when computing with massless quarks and gluons in which case the collinear divergences are absorbed into hadronic quantities such as distribution amplitudes, parton distribution functions or jets in the context of what is known as factorisation theorems.) The question of whether QED is well-defined for zero lepton masses gave rise to the KLN-theorem (cf. Appendix B for further comments). We shall assume leptons masses to be non-zero and special emphasis will be given to -terms to which we refer to as hard-collinear logs. In what follows we use the terms IR-divergences and soft-divergences as done in much of the literature.
Observables are Infrared Finite
Of course physical observables have to be free of divergences and this is where one expects deep physical principles to dictate cancellations. Cancellations segregate observable from non-observable quantities. (In his book on string theory, Joe Polchinski refers to IR-divergences as follows in his glossary: “ ...if you encounter IR-divergences you have not asked the right question.”)
There are essentially two approaches to deal with the IR-problems. The fixed particle Fock-space is abandoned in favour of the coherent states which take into account that charged particles are surrounded by a soft photon-cloud [23,24,25,26,27]. This was first made rigorous by Faddeev and Kulish for QED in 1970. In this approach the S-matrix is well-defined, e.g. unitary and gauge invariant, and this is important for the studying more formal aspects of the theory. The second approach is more relevant to experiment as in colliders physics one does not deal with coherent states. Namely, one defines observables which are inclusive enough such that these divergences cancel. This approach was pioneered by Bloch and Nordsieck 1937 [9], extended by the KLN-theorem [10,11] to include collinear singularities in the sixties and applied to correlation functions in form of the Kinoshita–Poggio–Quinn-theorem [10,28,29]. As a rule of thumb, the more inclusive a quantity is, the fewer divergences or IR-sensitive terms there are. Despite their apparent different motivation, the second approach can be seen as a limit of the first one by expanding in powers of the .
Thinking a little bit about it, one notices that the IR-divergences are interlinked with the very definition of what a particle is and the measurement process itself. How can one distinguish a single electron from an electron with an ultrasoft photon or an electron with a photon emitted at an infinitesimally small angle? That is also indeed where the resolution lies, what is measurable needs to be assessed carefully. One needs to come back to the idealisation mentioned in the introduction: infinite space and infinite detector resolution.
In view of it being more general we consider it worthwhile to discuss the coherent state approach. The presentation is largely based on the excellent presentation in Duncan’s book [30]. The first thing to realise is that detectors cannot resolve or measure the energy of incoming photons to an arbitrary precision. We may assume that the detector can only capture photons with an energy above and reject photons with energies above that threshold. (In practice one may of course increase but not decrease it.) Thus, it is advisable to replace the electron state, to which we adhere for illustration, by a state with any number of photons with energies smaller than the detector cut-off
and is the coherent state, with appropriate , which can be written as an exponential of an integral over the creation operators cf. Appendix C. Denoting by the probability of n-soft photon emission, the total probability is a sum of all possibilities . Kulish and Faddeev [27] showed that this leads to a finite S-matrix in QED, which is gauge invariant and a separable Hilbert space. The QCD-version is dealt with in [31] but hardly relevant in practice because of the mass gap and factorisation theorems.
Let us briefly digress and motivate the abandonment of the fixed-number Fock space from a different viewpoint. The S-matrix of the fixed-number Fock space does not exist as it turns out to be zero. The IR-divergences, caused by the absence of a mass gap, can be seen as an indication for the ill-defined fixed number Fock space S-matrix. This can be understood in two different ways. First the IR-divergences exponentiate such that the in the limit of zero photon mass. Thus, the asymptotic completeness of the in and out Hilbert space ceases to make sense as there is no S-matrix connecting the two. (Whereas the S-matrix is gauge invariant in perturbation theory this is not the whole story. It has been shown recently, in an interesting paper and stream of work, that the reason the S-matrix vanishes is that it is not gauge invariant under so-called large gauge transformations of asymptotic symmetries on what is known as the celestial sphere by now [32].) Another way to look at it is to realise that due to the massless photons the single particle pole, assumed by the LSZ-formalism, is softened by the presence of radiative corrections into a branch cut [33]. This makes the particle of mass m disappear from the S-matrix when multiplied by the LSZ-factor upon taking the on-shell limit . In fact Buchholz has shown, using very general arguments, that a charged particle obeying Gauss’ law cannot be a discrete eigenstate of the momentum squared operator [34].
Advocates of the Bloch–Nordsieck and KLN approach would simply point to the fact that the S-matrix is not an observable but rather an intermediate auxiliary quantity. However, as stated above, a scattering theory can be formulated between the coherent states of the type (2) with well-defined S-matrix [27]. When the total transition probability of all n-states (2) is considered, the momentum space integrals are cut-off below at and are thus manifestly IR-finite (no soft-divergences). The S-matrix is well-defined and the IR-divergences are absorbed into the definition of the states. It seems worthwhile to point out that this bears some resemblance with the absorption of the UV divergences into the parameters of the theory which in turn also originates from an idealisation, namely that space-time is a continuum. Reassuringly, upon expanding to finite order in one recovers the Bloch–Nordsieck solution. For example, at correspond to the non-radiative (virtual) and radiative (real) part. More concretely, in order to compute the corrections to a decay process one has to consider its radiative counterpart . In the total transition probability one can show that the IR-divergences cancel diagram by diagram—as beautifully illustrated in many textbooks, e.g., for in [16]. These cancellations have been shown to hold to all orders in QED by exponentiation [21,35]. (The case of QCD, which is beyond the scope of these notes, is complicated as the simple combinatorics in QED are spoiled by zero mass charged particles (the gluons) and the colour structure. The Bloch–Nordsieck mechanism is replaced in perturbation theory by the KLN-theorem, whose features are briefly discussed in Appendix B, and for the more involved case of hadrons in final states we refer to the textbooks [14,18].) In conclusion in practice the infrared problem of QED is bypassed in the pragmatic approach by IR-regularisation (e.g., ) and removing the regulator () in observable such as decay rates. In practice, for a number of reasons (e.g., no additional scale) dimensional regularisation is the choice of most authors.
3. Decay Rates and Their Infrared-Effects
Following the discussion of the origin of IR-divergences and why they disappear from observables we discuss the mechanisms in three practical examples with decreasing level of inclusiveness and increasing level of IR-effects. Namely, the (inclusive) cross section, the leptonic decay and the semileptonic case . In the latter two cases, the hadrons will be treated in the point-like approximation with comments beyond this treatment deferred to Section 4.
For most practical applications first order is sufficient. At the amplitudes level we therefore need , denoted , corresponding to tree, real and virtual. We refer to and as the non-radiative and to as the radiative amplitude. The cancellation of IR-divergences is then a result of vs. when properly integrated over phase space. Let us rephrase this in terms of a generic decay at the level of the rates
where is the phase space measure, i a small mass of a final state particle (e.g., an electron mass) and stands for either or . The subscripts V and R denote virtual and real and A, B and C stand for soft, soft-collinear and hard-collinear divergences. Integrating over the entire photon phase space
with all the soft-divergences cancelling and the collinear logs cancel,
depending on the differential variables with further comments below. The further statement of the cancellation-theorems (Bloch–Nordsieck and KLN) is that that if one integrates over the remaining phase space , then (in the total rate)
all IR-divergences are absent, schematically: . This picture broken in practice by two sources.
- (i)
- The experiment is not fully photon-inclusive and rejects hard photons with where is the previously discussed threshold which is (slightly) larger than the actual detector resolution. (If one if the final state particles is very light then a cut has to be placed on the angular resolution as well.) This leads to the replacementswhere generically independent on whether the differential variables are IR-safe or not.
- (ii)
- The rate can be differential in some final state kinematics and therefore not a total rate as in (4). In this case the unitarity argument, on which the cancellation is based, does not necessarily hold since the kinematics make the sum too restrictive. The (non)-cancellation needs to be reassessed and depending on the kinematic variables hard-collinear effects do not cancel.
3.1. A Classic Example of Infrared Finiteness:
Here we briefly deviate from the QED-course as we consider finiteness under correction in the strong coupling constant to . An analogue in QED would be the somewhat exotic . By the optical theorem the total cross-section
is related to the imaginary part of the vacuum polarisation
where is the electromagnetic current and the electromagnetic charge. On the non-perturabative level there is no question as to whether this quantity is well-defined because of the mass gap. In particular, in the large- limit with the vector meson decay constants and most importantly is the lowest mass exhibiting the mass gap. The question we would like to address is whether it is finite to all orders in perturbation theory using quarks and gluons as degrees of freedom.
According to the cancellation-theorems and the discussion outlined in the beginning of this section this must be the case since this is a fully inclusive observable (and conditions (i) and (ii) are not met). Alternatively, this can be established on grounds of the Kinoshita–Poggio–Quinn-theorem [10,28,29] which states: In massless renormalisable theories the one-particle irreducible correlation functions are IR-finite for non-exceptional (external) Euclidean momenta. (Non-exceptional momenta configurations are such that no subset of momenta adds to zero.) Renormalisability is important as it settles power counting for the proof and the Euclidean momenta condition avoids particles going on-shell. This applies to the case at hand since and the effectively count as off-shell (or Euclidean in practice). Hence must be IR-finite (in perturbation theory) as found in many explicit computations for any in particular.
One can learn a fair amount considering the one-loop corrections since the imaginary part is proportional to the discontinuity and the latter is proportional to the sum of all cuts by the Cutkosky rules (e.g., [14]) as shown in Figure 2. The different types of cuts include the radiative and non-radiative parts cf. figure caption. Each one of these cuts is IR-divergent but they cancel in the sum as dictated by the arguments given above. That individual contributions behave very different from the total contribution is not restricted to IR effects but can also appear in the power-behaviour of a heavy quark mass or an external momentum in case they are assumed to be large.
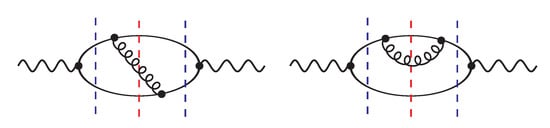
Figure 2.
Corrections to the strong coupling to the vacuum polarisation (9), at , which necessarily involves quarks and gluons (partons). As its imaginary part corresponds to the total cross Section (8) the cuts give rise to various subprocesses which include the virtual and real parts. The dashed or blue cuts and the dotted or red cuts correspond to the virtual and the real parts, respectively.
3.2. Leptonic Decay of Type
We now turn to a simple example of an exclusive decay, the pion decay . The photon energy cut-off will introduce the log-terms as in (7). The hard-collinear logs (C-type in (3)) are a bit peculiar in this decay in the SM that the amplitude is and therefore automatically finite in the limit . This helicity suppression is relieved for interactions and we thus include them along the structure in order to illustrate the straightforward nature of the hard-collinear logs in this example. The real photon emission will be treated with an energy cut-off in the pion restframe. This will lead to soft- and soft-collinear terms as indicated in Table 1. Hard-collinear logs, , can only be present for the case with photon energy cut-off and have to disappear in the photon-inclusive limit

Table 1.
Types of observables considered where diff. is short for differential in or f (final states) and (i) and (ii) refer to the itemised conditions above.
The four-Fermi effective Lagrangian, including - and -interactions, reads
where and in the SM . The LO amplitude is given by
where the leptonic matrix elements read
with and and the hadronic matrix elements are
with , and the adjoint -representation matrix corresponding to (with (u)p and (d)own quarks). Note that use of the equation of motion was made for the -part in (11) which makes the -suppression factor explicit. The LO decay rate is given by
where the lepton velocity, in the pion’s restframe, is
and denotes the Källèn function. Notably , a non-perturbative parameter of QCD known as the pion decay constant, is the order parameter of the spontaneous breaking of chiral symmetry (in the limit). When QED-corrections are considered it ceases to be an observable and it is essentially degraded to the status of a wave function renormalisation constant. This can be seen from the explicit results in the review [36] where is found to be gauge dependent and divergent in the limit. Unlike in QCD, in QED the chiral logs are not protected by powers in the pion mass since is not an observable. This is a point we will come back to at the end of the section.
Next we discuss how to incorporate radiative corrections in the point-like approximation. This is a straightforward exercise in effective field theory. The hadronic operator are matched to pions ()
such that the LO matrix element (13) is reproduced. The leading radiative amplitude is given by
where , in order to be more general, and the conventions are the same as in [37]: () and for out(in)-going states. The last term in (17), and centre of Figure 3, is the so-called contact term, only present from since it originates from the photon in . Additionally, the following compact notation has been introduced
likewise for . The terms of the Low-theorem (cf. Appendix A) are explicit which include the eikonal term
and the -term related to the angular momentum can be seen in the leptonic parts. Gauge invariance amounts to which does hold provided which is nothing but charge conservation. The latter has to be imposed in gauge-fixed perturbation theory but would be automatic in a manifestly gauge invariant formalism as the path-integral used in lattice computations. Hence the radiative amplitude is gauge invariant and thus the virtual (or non-radiative) amplitude must be as well. In particular in the virtual amplitude the gauge dependence of the pion decay constant cancels against the lepton–pion and lepton radiative corrections. (In fact in the virtual case one finds that the covariant gauge-fixing parameter appears in the form and is again effectively absent because of charge conservation [37]. This time the charge condition is quadratic of course.) As previously said, we present the S-P and V-A interaction separately as they both have different features.
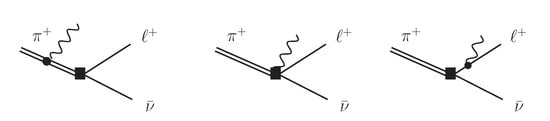
Figure 3.
Real emission diagram of the pion decay. The diagram in the centre is the so-called contact term and does appear for the V-A but not the S-P interaction. The real amplitude is given in (17).
3.2.1. Leading Logs with S-P Interaction
For the S-P interaction () we may parametrise the rate as follows (In the case where the LO rate is differential the form below does hold for the soft but not for the collinear part. An example of which is the semileptonic decay considered in the next section.)
where “non-log” stands for anything that is neither a soft, soft-collinear or hard-collinear log. Hatted quantities, except charges, are understood to be divided by the pion mass in this section. The quantity is the previously introduced photon energy cut-off and its photon-inclusive limit is . Below we discuss both and without resorting to the full computation.
- The soft and soft-collinear terms are universal and given byand its exponentiation is a well established [21,35]where and are IR and UV cut-offs. These are to be replaced with and the largest scale in the problem beyond that are undetermined by the nature of the leading log approximation. (We will have more to say on how this happens in computation in Section 3.3 as the breaking of Lorentz-invariance by introducing a photon energy cut-off in a specific frame introduces a practical challenge.) Now, the factor A has a pleasing formwhere the sum is over the charged particles in the decay andis the relativistic addition of the velocities of the -particles in the -restframe. With for (since the relative velocities are zero) and one recovers (21). The integral definition of the summand in (23) is given a few lines below. Furthermore, note that the second formula in (24) is often more useful in practice as it makes use of Lorentz invariance in a manifest way.It is instructive to reproduce the leading term from the eikonal part (19) which is of course what the original papers did. Following [37], we denote the decay rate aswhere and stand for the non-radiative and the radiative part, respectively, and is the relative correction, not to be confused with the photon energy cut-off, which is a function of the non-trivial differential variables (with and in the leptonic and semileptonic case, respectively). After making use of gauge invariance, by choosing the Feynman gauge , performing the polarisation sum over the eikonal part one getswhere “non-soft” stands for finite non-logarithmic regularisation dependent terms. The -term is the regularisation dependent energy integrals and an angular integral. In the leading log approximation and are separately Lorentz invariant [37]. This is non-trivial since the introduction of photon energy cut-off introduces a preferred frame and complicates the analytic evaluation of the non-approximated integrals. More concretely,given in dimensional regularisation and photon mass regularisation (cf. Appendix D [37] for some more detail). The angular integral produces a termwhich matches the expression in (23) and thus reproduces (21) as outlined earlier.
- The hard-collinear logs can be obtained from the splitting function which has been verified in [37] for the more advanced semileptonic case. The formula for the collinear logs reads(and thus ) with fermion splitting functionand the plus distribution . For the leptonic case the formula is trivial since there are no phase space variables. Crucially, in the photon-inclusive limit the hard-collinear logs cancel in accordance with the KLN-theorem. This has to hold since which in turn follows from the conservation of the electromagnetic current.
3.2.2. Leading Order Result with V-A Interaction as in the Standard Model
The Standard Model computation () has of course been obtained a long time ago [38,39] and we quote
and comment on the various terms further below. In (20) incorporates the matching to the -scale [39]. The explicit radiative function is given by [40]
In the photon-inclusive case, , the radiative function assumes the form
Let us now turn to the logs as previously discussed.
- The soft and soft-collinear terms are universal and is indeed the same function as in (21).
- Hard-collinear logs, of the type , are not present. The LO V-A amplitude is -suppressed. and this is enough to guarantee the absence of the latter at which can be seen as follows. In the real radiation rate the -terms arise from the eikonal part (19) that are proportional the LO amplitude which is and thus the logs can be at worst of the form in the rate. Since the -terms in the virtual and the real part of the rate have to cancel the virtual rate cannot contain them either. We are to conclude that are the leading logs of this type. Since the limit is not divergent these logs do not have to cancel. Inspection of (33) shows that they do indeed not cancel since . This does not apply to the interaction, which we have taken for granted in Section 3.2.1 by using the splitting function to obtain the -terms. The moral of the story is that collinear logs only cancel if they have to due to the principle of unitarity which underlies the KLN-theorem. The reason the terms do not cancel in the V-A case is that there are regions in phase space, different from the collinear region, where the suppression is relieved.
- A different type of collinear log: We may however turn the tables and consider the decay and regard as a collinear log. The amplitude which is identical to the one for the leptonic decay is not -suppressed, thus there will be terms in the real and the virtual part of the rate and they have to cancel in the total rate. (There are some differences in the integration over phase space for the radiative part but not for the relevant eikonal terms.) Inspecting (33) taking the limit and adding the log in (20), one collects and it is seen that the logs do cancel as they should.
3.3. Semileptonic Decay of the Type
The new element in the semileptonic decay is the extra meson in the final state leading to two non-trivial kinematic variables. They can be chosen to be the Dalitz-plot variables or the more commonly used lepton momentum squared and the angle of a lepton to the decay axis in the q-restframe (as depicted in Figure 4). Hence the LO decay is differential unlike in the leptonic case (cf. for instance Appendix B.1 in [37] for the explicit result).
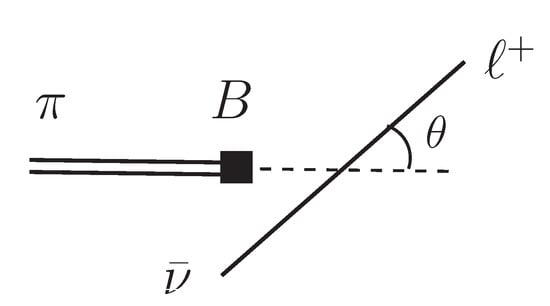
Figure 4.
Sketch of semileptonic decay with the definition of the lepton angle (and ). The definition of these variables need to be revised when the photon emission is considered in addition (35).
In many ways the QED-treatment of the semileptonic decay in the point-like approximation is similar to the leptonic decay and we shall be brief on those matters. There are also new aspects which bring in a certain amount of complication which we identify and examine more closely:
- (1)
- The role of the pion decay constant is taken by two form factors ,Often in the literature the form factor is taken to be a constant, which is a good approximation in but less so for . Expanding the form factor in , as in [37], leads to a more involved effective theory which goes beyond the point-like approximation. The effect of the expansion is most prominent when the photon energy cut is large for which refer the reader to the plots in Appendix A in [37]. (The FCNC case is peculiar in that for the form factor expansion amounts to the replacement fo the constant form factor by , whereas in the charged case the expansion is necessary and can be quite relevant because of the migration of radiation in conjunction with resonance-contributions entering non-resonant bins.)
- (2)
- For the radiative matrix element the -variables have to be adapted because of the additional photon. We follow the discussion in [37] (replacing the kaon by the pion) where the following kinematic variablesare defined with and denoting the q and restframes, respectively. The -variables are difficult to measure at a hadron collider where the components of the B-momentum are unknown.
- (3)
- The leading order amplitude is not -suppressed and it is only the total rate which is well-defined in the photon-inclusive limit for . (For finite as in real world this leads to a sizeable and measurable effect.) This raises the interesting question as to whether this property remains intact in any of the differential variables in the photon inclusive case.
- (4)
- The photon interacts with many particle-pairs and this complicates the analytic evaluation of the phase-space integrals as one can choose the restframe only once. As previously discussed, the energy- and soft-integrals (28) are separately Lorentz-invariant in the soft-limit and can therefore each be evaluated using a preferred frame [37].
Point 1. is of a technical nature, we refer the reader to reference [37]. Point 4. is covered by Appendix E. Provided a constant form factor is assumed the computation of the real and virtual amplitude is very similar to the leptonic case albeit more involved. In the case of charged meson(s) a non-constant form factor complicates the computation with each order in the Taylor expansion around . Gauge invariance works out in the same way, namely as an interplay between contact and non-contact terms and total charge conservation. The points raised in 1. and 2. deserve a closer look.
(Non)-Cancellation of Hard-Collinear Logs
The soft-divergences which have to cancel at the differential level, can of course be derived using the same techniques as for the lepton case (22) with relevant practical remarks deferred to Appendix E. The hard-collinear divergences have been isolated using the phase space slicing technique. They cancel charge by charge in the photon-inclusive total rate in accordance with (6).
Let us now turn to the question, phrased in point 3., whether or not these logs cancel in the differential variables defined in (35). It is found by explicit computation that the -terms cancel in the - but not the -variables [37].
We wish to discuss this result from a physical point of view. The cancellation of soft-divergences at the differential level is quite plausible since the soft photon does not make a difference to the radiative versus the non-radiative decay topology. For the (energetic) collinear photon this is not the case. The topologies of the radiative and non-radiative amplitude are rather different and a priori one would not expect cancellations. In the total rate these cancellations are non-trivial and based on unitarity. Thus, it is natural to ask whether it can be understood from this viewpoint. The answer is affirmative. The -variable is the four momentum of the total lepton-photon system and for fixed one may interpret it as a decay of a boson of mass into the two leptons and the photon. Essentially this corresponds to the leptonic case which is not differential and thus the terms have to cancel. Alternatively, one may regard as the analogue of a jet where radiative and non-radiative parts are not distinguished and the problem of discerning the lepton from the lepton with a photon emitted at an infinitesimally small angle does not pose itself.
4. Structure-Dependent QED-Corrections—Resolving the Hadrons
4.1. Summary on Status of Structure-Dependent QED-Corrections
The field of QED-corrections to hadronic decays including structure-dependent corrections (i.e., going beyond the point-like approximation) is not yet at a mature stage. The physical picture is well-motivated from the hydrogen atom where the proton and electron make up a charge neutral object but photonic interaction plays an important role. Thus, it cannot be expected that a photon does not interact with a neutral B-meson composed of b- and d-valence quark. It is precisely for this meson that one can expect the largest effects as it is composed of a heavy and a light quark. There are various reasons why this is a difficult task. One of them is of course the cancellations of IR-divergences which enforces to consider real radiation. A task which goes beyond standard flavour physics and interferes with confinement at shorter distance.
Amongst the continuum methods there is chiral perturbation theory and light-cone approaches such as soft-collinear effective theory (SCET). QED in Chiral perturbation is well established [41,42], and presumably the main challenge is the determination of the counterterms (which seem to follow the pattern of vector resonance saturation as in QCD). In SCET the leptonic FCNC decay has been investigated in [43,44] with the main parametric uncertainty coming from the QCD B-meson distribution amplitude. Hadronic decays of the type have been investigated in [45] and the definition of the charged light-meson distribution amplitudes is non-trivial. A remarkable aspect is that so far in SCET only virtual contributions have been considered. Real radiation is only incorporated via the universal soft-photon part (22). Lattice QCD + QED comes with its own challenges such as containing the massless photon in a finite box (cf. [46] for a review). A program has been proposed in [40] where currently only virtual corrections are computed and for the real correction the point-like approximation is proposed which is a good enough approach for . First results have been reported in [47,48] for these decays. Notably this formalism uses gauge-variant interpolating operators. A fully gauge invariant approach to lattice QCD, building upon ideas from Dirac and others, has been proposed for determining hadron masses [49]. Decays have so far not been attacked in this formalism.
4.2. Cancellation of Hard-Collinear Logs for Structure Dependent Contribution
Technicalities aside, one may in particular be concerned that hard-collinear logs , originating from structure-dependent corrections, which do lead to large uncertainties as currently unknown. Fortunately a rigorous result can be established forbidding those logs [37], based on gauge invariance. The basic idea of the proof is that when one considers a light particle like the electron and photon then in the collinear region which lends itself to the use of gauge invariance. We will sketch some more detail by decomposing the radiative amplitude ( for brevity)
such that the entire eikonal term of the electron is in . Squaring this matrix element, summing over polarisation in the Feynman gauge (cf. Section 3.2.1) and integrating over the photon phases space one gets three terms
The first is by construction finite in the collinear region of the lepton . The second has no hard collinear logs since it is proportional to
in the collinear region. The third one gives raise to the collinear logs. Firstly, we learn that the -terms are necessarily proportional to . Second, and more importantly there cannot be any further hard collinear logs in the structure dependent part. This is the case since the addition of structure dependent term will just change where is itself gauge invariant and will be finite in the first term and not change the conclusions in the second either.
Hence the result is: any gauge invariant addition (to the point-like approximation) can at most lead to logs of the form . These terms are not sizeable and in particular vanish in the chiral limit . This result has been verified in the derivative expansion of the form factor which is a particular approach that goes beyond the point-like approximation. This is fortunate as it puts , or more generally tests in the lepton universality, on much firmer grounds since Monte Carlo tools such as PHOTOS do not incorporate structure-dependence.
5. Discussions ans Conclusions
QED-corrections have a long history. In particular electromagnetic corrections have been the vehicle to the development of quantum mechanics and QFT. The massless photon leads to IR-effects which have a high degree of universality. The Bloch–Nordsieck cancellation mechanism from 1937, predates the solid development of QED in the 1940s, and is a strong indication of the universality of the IR-domain. The IR-effects are interlinked with the measurement process and govern the largest QED-corrections.
We have reviewed the very basic of IR-divergences in Section 2 along with the connection to the elegant coherent states formalism. How IR-effects affect predictions was the topic of Section 3 including three examples of increasing IR-sensitivity: the (inclusive) cross section, the leptonic decay and the semileptonic case in Section 3.1–Section 3.3, respectively. We have highlighted the peculiarity of the leading collinear logs in the leptonic decay in the Standard Model and clarified the importance of the choice of kinematic variables in the differential distribution of the semileptonic decay types. Going beyond the point-like approximation, taking into account structure dependence, is the next step in the precision physics program of weak decays and the topic of Section 4. We have given a brief summary of the different methods and approaches in Section 4.1. The text ends in Section 4.2 with the model-independent demonstration, based on gauge invariance, that the structure dependent part does not lead to new hard-collinear logs. This is fortunate as it will considerably reduce the uncertainty in many important observables such as the precision determination of heavy-light CKM-elements and tests of lepton flavour universality. However, the implementation of these corrections in experiment will necessitate the development or extension of Monte-Carlo tools. This demands a joint effort of theory experiment.
Funding
This research was funded by STFC Consolidated Grant, ST/P0000630/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
I am grateful to Saad Nabeebaccus and Matt Rowe for careful reading of the notes and valuable comments.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IR | infrared |
| LO | leading order |
| QCD | quantum chromodynamics |
| QED | quantum electrodynamics |
| QFT | quantum field theory |
| SCET | soft collinear effective theory |
| SM | Standard Model |
| UV | ultraviolet |
Appendix A. Low-Theorem
By the physical picture of the multipole expansion of electrodynamics a soft photon should be sensitive to the charge (monopole) and dipole distribution in the next approximation. One thus expects low energy theorems. In field theory such low energy theorems are connected Ward identities. The circle of ideas closes as Ward identities derive from gauge invariance which in turn allows for the massless photon. Somewhat coincidentally this theorem was put forward by a scientist to the name of Low and extended by others and is known as the Low–Burnett–Kroll–Goldberger–Gell–Mann theorem [50,51,52,53]. The statement is that adding a real photon to an amplitude , the two first terms in an -expansion are universal
where the monopole and dipole term of and , respectively, are given by
where Above is the orbital angular momentum operator and square brackets denoting antisymmetrisation in indices as usual. Hatted quantities have the same meaning as described below (17).
The derivation is rather straightforward. Parametrising the amplitude
with the additional convenient notation which resolves the issue of in- and out-going states. Now, (A1) is obtained by making an ansatz for the the Ward identity and solving it to the appropriate order. We may write the ansatz as follows
where R stands for the remainder. The QED Ward identity reads
and the essential step is to Taylor expand, as appropriate for a low-energy theorem in k
Note that, one will not be able to make a statement about as this probes the structure dependent part of the of the process. Equating terms one gets
charge conservation at . To make the equation useful one needs to uncontract the k. This is allowed since no information is lost. This can be seen as follows. Assume then the only non-trivial solution appears for two external vectors with . Hence
Low’s theorem (A1) in the notation used here. This theorem does not receive any non-perturbative corrections. The only argument against it is that QED is possibly not well-defined because of the Landau pole in the UV but that is outside of any concerns for practitioners. Analogous theorems in QCD do receive corrections, at least when coloured external particles are considered, as then some loop contributions have non-local corrections and this is where the analogous derivation, as given above, falls short.
Appendix B. KLN-Theorem
Whether QED with massless matter is well-defined is a question that was asked in the mid-1960s by Kinosthita [10] and Lee and Nauenberg [11]. The statement of the theorem is: S-matrix elements squared are finite if one sums over energy-degenerate initialandfinal states. Schematically
which relies on unitarity and involves the use of time-ordered or old-fashioned perturbation theory. We refer the reader to Weinberg’s book for an alternative proof closer to the coherent state approach [15]. A few remarks are in order
- One might be inclined to ask what the infinites mean in the context of massless QED. The point is that no detector apparatus can distinguish an electron from an electron with a photon at (nearly) zero angle. Again the divergences are associated with an idealisation. For remarks on QCD and collider physics cf. Appendix F under IR safety.
- The requirement of the summation over degenerate energy states does invalidate some differential decay rates or cross section as observables. Cf. the discussion in Section 3.3.
- The KLN-theorem was established before the advent of QCD in the late seventies but is often referred to in the context of QCD (when ignoring hadronisation). The problem with QCD or non-abelian gauge theories, confined or not, is that coloured states are not valid asymptotic states since the colour of any state can always be changed by emitting a soft gluon, e.g., [17]. The KLN-theorem reduces to the Bloch–Nordsieck mechanism when the states are direct product states of fixed number of charged particles cf. chapter 13.4. in [15]. It is the fixed number of charged particle assumption which fails in the case of massless lepton QED. Historically the first counterexample to the Bloch–Nordsieck mechanism was found in at the 2-loop level [54].
- If one sums over either all initial or all final states then the S-matrix elements squared are of course finite: by unitarity () of the S-matrix. It is by selecting exclusive (final) states that IR-sensitivity appears.
- The KLN-theorem is reminiscent of a theorem in CP-violation that states that if one sums over all final states that can rescatter into each other under the strong force, then the rate of particle and anti-particle process are the same () [55]. Not only the flair of the theorem but also its method of proof, namely unitarity, is the same.
Appendix C. Brief Synopsis of Coherent States
In this brief appendix we sketch some elements of coherent states following the excellent exposition in [30]. The coherent state can be seen as the state maximising the number-phase uncertainty relation. One can derive analogues of the Heisenberg uncertainty relation for the particle number and the phase. Searching for a solution thereof, and justifiably truncating the Hilbert space, one arrives at the condition that this state is to be an eigenstate of the annihilation operator. This makes it clear that this state must be a coherent sum over the infinite series of all excitation modes.
Starting with the standard harmonic oscillator (, , ) and imposing the eigenvalue equation for a generic ansatz, a set of recursion relation emerges which is solved by the coherent state
Or alternatively where and the prefactor assures (since ). This state saturates the number-phase inequality and can be regarded as a state close to a classical state. In particular follows a Poisson distribution. In QED each n corresponds to the emission of n undetectable soft photons. In QED the prefactor is the analogue of the (divergent) virtual amplitude.
For a (scalar) quantum field theory the analogue of the operator S is given by where , Fourier transform of , is the momentum distribution defining the wave packet. The state f is then given by and the omitted normalisation factor above is the analogue of the virtual amplitude defined without emission of extra soft-particles created by . The coherent states used in the IR-definition of the S-matrix then comes with .
Appendix D. Heuristic Discussion of Infrared Divergences in One-Loop Diagrams
We consider it worthwhile to briefly give the essence of how IR-singularities are identified in one-loop diagrams paralleling the real-emission discussion in Section 2.
The collinear-divergences are simpler than the soft ones in the sense that one does not need to involve power counting arguments based on the dimension of spacetime. Collinear-divergences occur when a massless particles is emitted from another massless particle and the two momenta are collinear. If either of the particles has a (small) mass m then the divergence is regulated by cf. (1).
The soft-divergences are more subtle as the inverse power in the photon energy . The criteria is that two external momenta are to be on-shell with a photon propagating in the loop. The relevant power counting then assumes
where and were dropped in the second step. We see that this integral is logarithmically divergent for when as previously stated.
There are algorithms to extract soft and collinear-divergences at one-loop [56] and two loops [57]. An approach that works more generically is to realise that IR-singularities are associated with singularities in the complex plane which in turn can be studied in perturbation theory by the Landau equations. This involves though two further non-trivial steps. First, one needs to check whether the singularity in question is on the first sheet. Second, not every singularity or branch points leads to a IR-singularity. For example, has a branch cut starting at but is not singular at that point itself. The second topic is discussed in detail in Sterman’s book chapter 13 [14] as well as in his lecture notes [19,20]. The systematic development of singularities in terms of effective Lagrangians is the theory of soft-collinear effective theory [58] with the advantage of the systematic use of the equation of motion and a renormalisation program.
Appendix E. How to Handle Non-Analytic Decay Rates Numerically
It seems relevant to briefly mention the practical problem of dealing with IR-divergences numerically. For the leptonic decay (in the point-like approximation) everything can be done analytically and then matters are straightforward. For the semileptonic case it is already more challenging but since there is just one non-trivial phase space integral, namely when the photon couples to the pion and the lepton, it is still doable [59]. In the generic case, if we take all particles to be charged [37], it is maybe possible but the effort is not worthwhile. At higher loops in QCD this becomes totally unfeasible and people resort to so-called subtraction schemes (e.g., dipole, antenna or Carani–Seymour subtraction). The idea is simple, one decomposes
where is doable analytically and the term in bracket is free from IR-divergences. Preferably, it is also free from large logs in order to avoid numerical instabilities. It is for this reason that the evaluation of the phase space integral in (26) in the leading log approximation is valuable in practice. It is fortunate that in this approximation both integrals can be shown to be separately Lorentz invariant!
Appendix F. Terminology
Whereas terminology can always be a hurdle for people learning a subject, QED-corrections are riddled with multiple expressions meaning the same thing and are historic or context based rather than logical. This short appendix ought to help clarifying a few of these matters.
- When hadrons are treated as point-like particles one often refers to this approach as scalar-QED presumably in the context of scalar mesons such as the pion. Of course one can also treat a baryon as point-like but it being a fermion then makes the term scalar-QED seem inappropriate. Going beyond the point-like approximation, resolving the hadrons beyond the monopole approximation, is referred to as a structure-dependent contribution which is the context of Section 4.
- IR-divergences are often synonymous with soft-divergences which includes soft-collinear-divergences. Collinear terms, referred to as in the text where f stands for final states, are referred to as collinear-divergences if (when computing with massless quarks in QCD) or (hard-)collinear logs (if ). It should usually be clear from the context but it is useful to be aware of the potential of confusion.
- The concept of IR-safety has been introduced by Sterman and Weinberg [60] and means the following. An observable computed with quark and gluons is IR-safe if the quark masses can be taken to zero without encountering singularities (i.e., avoiding hard-collinear singularities of the -type). As previously stated, In the context of QCD this amounts to either defining inclusive enough quantities or legitimately absorbing collinear logs into hadronic objects (jets or parton distribution functions) at the expense of introducing a factorisation scale.
- In the context of computations and the use of the Bloch–Nordsieck and KLN cancellations of IR-divergences (6) one refers to and as the non-radiative and radiative rate, respectively. Often the terms virtual and real are used synonymously since those correspond to the precise -terms.
References
- Schweber, S.S. QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Glashow, S.L. Partial Symmetries of Weak Interactions. Nucl. Phys. 1961, 22, 579–588. [Google Scholar] [CrossRef]
- Weinberg, S. A Model of Leptons. Phys. Rev. Lett. 1967, 19, 1264–1266. [Google Scholar] [CrossRef]
- Salam, A. Weak and Electromagnetic Interactions. Conf. Proc. C 1968, 680519, 367–377. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Calame, C.M.C.; Cè, M.; Colangelo, G.; et al. The anomalous magnetic moment of the muon in the Standard Model. Phys. Rept. 2020, 887, 1–166. [Google Scholar] [CrossRef]
- Abi, B.; Albahri, T.; Al-Kilani, S.; Allspach, D.; Alonzi, L.P.; Anastasi, A.; Anisenkov, A.; Azfar, F.; Badgley, K.; Baeßler, S.; et al. Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef] [PubMed]
- Bloch, F.; Nordsieck, A. Note on the Radiation Field of the electron. Phys. Rev. 1937, 52, 54–59. [Google Scholar] [CrossRef]
- Kinoshita, T. Mass singularities of Feynman amplitudes. J. Math. Phys. 1962, 3, 650–677. [Google Scholar] [CrossRef]
- Lee, T.D.; Nauenberg, M. Degenerate Systems and Mass Singularities. Phys. Rev. 1964, 133, B1549–B1562. [Google Scholar] [CrossRef]
- Davidson, N.; Przedzinski, T.; Was, Z. PHOTOS interface in C++: Technical and Physics Documentation. Comput. Phys. Commun. 2016, 199, 86–101. [Google Scholar] [CrossRef]
- Bifani, S.; Descotes-Genon, S.; Romero Vidal, A.; Schune, M.H. Review of Lepton Universality tests in B decays. J. Phys. G 2019, 46, 023001. [Google Scholar] [CrossRef]
- Sterman, G.F. An Introduction to Quantum Field Theory; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields. Vol. 1: Foundations; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Muta, T. Foundations of Quantum Chromodynamics, 2nd ed.; World Scientific: Singapore, 1998; Volume 57. [Google Scholar]
- Smilga, A.V. Lectures on Quantum Chromodynamics; WSP: Singapore, 2001. [Google Scholar]
- Collins, J. Foundations of Perturbative QCD; Cambridge University Press: Cambridge, UK, 2013; Volume 32. [Google Scholar]
- Sterman, G.F. Partons, Factorization and Resummation, TASI 95. Theoretical Advanced Study Institute in Elementary Particle Physics (TASI 95): QCD and Beyond. 1995, pp. 327–408. Available online: https://arxiv.org/abs/hep-ph/9606312 (accessed on 16 June 2021).
- Sterman, G.F. QCD and Jets. Theoretical Advanced Study Institute in Elementary Particle Physics: Physics in D ≧ 4. 2004, pp. 67–145. Available online: https://www.worldscientific.com/doi/abs/10.1142/9789812773579_0003 (accessed on 16 June 2021).
- Weinberg, S. Infrared photons and gravitons. Phys. Rev. 1965, 140, B516–B524. [Google Scholar] [CrossRef]
- Cachazo, F.; Strominger, A. Evidence for a New Soft Graviton Theorem. arXiv 2014, arXiv:1404.4091. [Google Scholar]
- Chung, V. Infrared Divergence in Quantum Electrodynamics. Phys. Rev. 1965, 140, B1110–B1122. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Coherent soft-photon states and infrared divergences. ii. mass-shell singularities of green’s functions. Phys. Rev. 1968, 173, 1527–1535. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Coherent soft-photon states and infrared divergences. iii. asymptotic states and reduction formulas. Phys. Rev. 1968, 174, 1882–1901. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Coherent soft-photon states and infrared divergences. iv. the scattering operator. Phys. Rev. 1968, 175, 1624–1640. [Google Scholar] [CrossRef]
- Kulish, P.P.; Faddeev, L.D. Asymptotic conditions and infrared divergences in quantum electrodynamics. Theor. Math. Phys. 1970, 4, 745. [Google Scholar] [CrossRef]
- Poggio, E.C.; Quinn, H.R. The Infrared Behavior of Zero-Mass Green’s Functions and the Absence of Quark Confinement in Perturbation Theory. Phys. Rev. D 1976, 14, 578. [Google Scholar] [CrossRef]
- Sterman, G.F. Kinoshita’s Theorem in Yang-Mills Theories. Phys. Rev. D 1976, 14, 2123–2125. [Google Scholar] [CrossRef]
- Duncan, A. The Conceptual Framework of Quantum Field Theory; Oxofrd University Press: Oxofrd, UK, 2012. [Google Scholar]
- Giavarini, G.; Marchesini, G. IR Finite S Matrix in the QCD Coherent State Basis. Nucl. Phys. B 1988, 296, 546–556. [Google Scholar] [CrossRef]
- Kapec, D.; Perry, M.; Raclariu, A.M.; Strominger, A. Infrared Divergences in QED, Revisited. Phys. Rev. D 2017, 96, 085002. [Google Scholar] [CrossRef]
- Schroer, B. Infraparticles in quantum field theory. Fortsch. Phys. 1963, 11, 1–31. [Google Scholar] [CrossRef]
- Buchholz, D. Gauss’ Law and the Infraparticle Problem. Phys. Lett. B 1986, 174, 331–334. [Google Scholar] [CrossRef]
- Yennie, D.R.; Frautschi, S.C.; Suura, H. The infrared divergence phenomena and high-energy processes. Annals Phys. 1961, 13, 379–452. [Google Scholar] [CrossRef]
- Gasser, J.; Zarnauskas, G. On the pion decay constant. Phys. Lett. B 2010, 693, 122–128. [Google Scholar] [CrossRef]
- Isidori, G.; Nabeebaccus, S.; Zwicky, R. QED corrections in B¯→K¯ℓ+ℓ- at the double-differential level. JHEP 2020, 12, 104. [Google Scholar] [CrossRef]
- Kinoshita, T. Radiative corrections to pi-e decay. Phys. Rev. Lett. 1959, 2, 477. [Google Scholar] [CrossRef]
- Marciano, W.J.; Sirlin, A. Radiative corrections to pi(lepton 2) decays. Phys. Rev. Lett. 1993, 71, 3629–3632. [Google Scholar] [CrossRef]
- Carrasco, N.; Lubicz, V.; Martinelli, G.; Sachrajda, C.T.; Tantalo, N.; Tarantino, C.; Testa, M. QED Corrections to Hadronic Processes in Lattice QCD. Phys. Rev. 2015, D91, 074506. [Google Scholar] [CrossRef]
- Cirigliano, V.; Knecht, M.; Neufeld, H.; Rupertsberger, H.; Talavera, P. Radiative corrections to K(l3) decays. Eur. Phys. J. 2002, C23, 121–133. [Google Scholar] [CrossRef]
- Cirigliano, V.; Giannotti, M.; Neufeld, H. Electromagnetic effects in K(l3) decays. JHEP 2008, 11, 006. [Google Scholar] [CrossRef]
- Beneke, M.; Bobeth, C.; Szafron, R. Enhanced electromagnetic correction to the rare B-meson decay Bs,d→μ+μ-. arXiv 2017, arXiv:1708.09152. [Google Scholar]
- Beneke, M.; Bobeth, C.; Szafron, R. Power-enhanced leading-logarithmic QED corrections to Bq→μ+μ-. JHEP 2019, 10, 232. [Google Scholar] [CrossRef]
- Beneke, M.; Böer, P.; Toelstede, J.N.; Vos, K.K. QED factorization of non-leptonic B decays. JHEP 2020, 11, 081. [Google Scholar] [CrossRef]
- Patella, A. QED Corrections to Hadronic Observables. arXiv 2017, arXiv:1702.03857. [Google Scholar]
- Giusti, D.; Lubicz, V.; Martinelli, G.; Sachrajda, C.T.; Sanfilippo, F.; Simula, S.; Tantalo, N.; Tarantino, C. First lattice calculation of the QED corrections to leptonic decay rates. Phys. Rev. Lett. 2018, 120, 072001. [Google Scholar] [CrossRef]
- Di Carlo, M.; Giusti, D.; Lubicz, V.; Martinelli, G.; Sachrajda, C.T.; Sanfilippo, F.; Simula, S.; Tantalo, N. Light-meson leptonic decay rates in lattice QCD+QED. Phys. Rev. D 2019, 100, 034514. [Google Scholar] [CrossRef]
- Hansen, M.; Lucini, B.; Patella, A.; Tantalo, N. Gauge invariant determination of charged hadron masses. JHEP 2018, 5, 146. [Google Scholar] [CrossRef]
- Low, F.E. Scattering of light of very low frequency by systems of spin 1/2. Phys. Rev. 1954, 96, 1428–1432. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Goldberger, M.L. Scattering of low-energy photons by particles of spin 1/2. Phys. Rev. 1954, 96, 1433–1438. [Google Scholar] [CrossRef]
- Low, F.E. Bremsstrahlung of very low-energy quanta in elementary particle collisions. Phys. Rev. 1958, 110, 974–977. [Google Scholar] [CrossRef]
- Burnett, T.H.; Kroll, N.M. Extension of the low soft photon theorem. Phys. Rev. Lett. 1968, 20, 86. [Google Scholar] [CrossRef]
- Doria, R.; Frenkel, J.; Taylor, J.C. Counter Example to Nonabelian Bloch-Nordsieck Theorem. Nucl. Phys. B 1980, 168, 93–110. [Google Scholar] [CrossRef]
- Bigi, I.I.; Sanda, A.I. CP Violation; Cambridge University Press: Cambridge, UK, 2009; Volume 9. [Google Scholar]
- Dittmaier, S. Separation of soft and collinear singularities from one loop N point integrals. Nucl. Phys. B 2003, 675, 447–466. [Google Scholar] [CrossRef][Green Version]
- Anastasiou, C.; Sterman, G. Removing infrared divergences from two-loop integrals. JHEP 2019, 7, 56. [Google Scholar] [CrossRef]
- Becher, T.; Broggio, A.; Ferroglia, A. Introduction to Soft-Collinear Effective Theory; Springer: Berlin/Heidelberg, Germany, 2015; Volume 896. [Google Scholar]
- Ginsberg, E.S. Radiative corrections to the k-l-3 +- dalitz plot. Phys. Rev. 1967, 162, 1570. [Google Scholar] [CrossRef]
- Sterman, G.F.; Weinberg, S. Jets from Quantum Chromodynamics. Phys. Rev. Lett. 1977, 39, 1436. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).