Determination of Spinel Content in Cycled Li1.2Ni0.13Mn0.54Co0.13O2 Using Three-Dimensional Electron Diffraction and Precession Electron Diffraction
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Effect of the Electron Beam on the Spinel Ratio in LR-NMC Battery Cathode Materials When Using Electron Diffraction
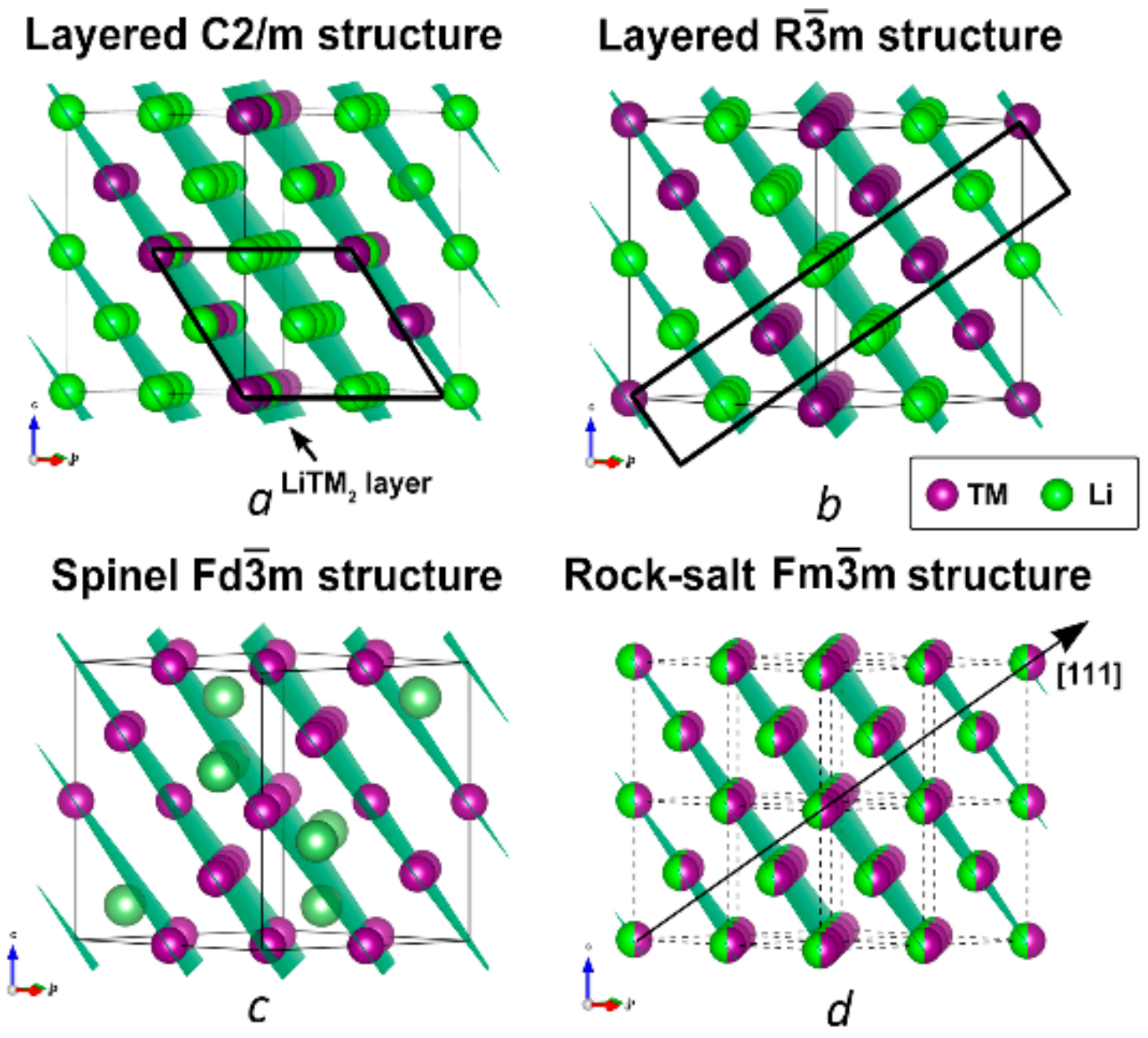
3.2. Determination of the Amount of Spinel in a LR-NMC Submicron-Sized Crystal
3.3. Application to Experimental Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Genevois, C.; Koga, H.; Croguennec, L.; Ménétrier, M.; Delmas, C.; Weill, F. Insight into the atomic structure of cycled lithium-rich layered oxide Li1.20Mn0.54Co0.13Ni0.13O2 using HAADF STEM and electron nanodiffraction. J. Phys. Chem. C 2015, 119, 75–83. [Google Scholar] [CrossRef]
- Kleiner, K.; Strehle, B.; Baker, A.R.; Day, S.J.; Tang, C.C.; Buchberger, I.; Chesneau, F.-F.; Gasteiger, H.A.; Piana, M. Origin of High Capacity and Poor Cycling Stability of Li-Rich Layered Oxides: A Long-Duration in Situ Synchrotron Powder Diffraction Study. Chem. Mater. 2018, 30, 3656–3667. [Google Scholar] [CrossRef]
- Zhan, C.; Wu, T.; Lu, J.; Amine, K. Dissolution, migration, and deposition of transition metal ions in Li-ion batteries exemplified by Mn-based cathodes-A critical review. Energy Environ. Sci. 2018, 11, 243–257. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, W.; Zhao, Y.; Guo, Z.; Cai, Q. Fundamental understanding and practical challenges of lithium-rich oxide cathode materials: Layered and disordered-rocksalt structure. Energy Storage Mater. 2021, 40, 51–71. [Google Scholar] [CrossRef]
- Pimenta, V.; Sathiya, M.; Batuk, D.; Abakumov, A.M.; Giaume, D.; Cassaignon, S.; Larcher, D.; Tarascon, J.M. Synthesis of Li-Rich NMC: A Comprehensive Study. Chem. Mater. 2017, 29, 9923–9936. [Google Scholar] [CrossRef]
- McCalla, E.; Abakumov, A.M.; Saubanere, M.; Foix, D.; Berg, E.J.; Rousse, G.; Doublet, M.-L.M.L.; Gonbeau, D.; Novak, P.; Van Tendeloo, G.; et al. Visualization of O-O peroxo-like dimers in high-capacity layered oxides for Li-ion batteries. Science 2015, 350, 1516–1521. [Google Scholar] [CrossRef]
- Mauger, A.; Julien, C. Surface modifications of electrode materials for lithium-ion batteries: Status and trends. Ionics 2014, 20, 751–787. [Google Scholar] [CrossRef]
- Lu, P.; Yan, P.; Romero, E.; Spoerke, E.D.; Zhang, J.G.; Wang, C.M. Observation of electron-beam-induced phase evolution mimicking the effect of the charge-discharge cycle in Li-rich layered cathode materials used for Li ion batteries. Chem. Mater. 2015, 27, 1375–1380. [Google Scholar] [CrossRef]
- Lin, F.; Markus, I.M.; Nordlund, D.; Weng, T.-C.; Asta, M.D.; Xin, H.L.; Doeff, M.M. Surface reconstruction and chemical evolution of stoichiometric layered cathode materials for lithium-ion batteries. Nat. Commun. 2014, 5, 3529. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Markus, I.M.; Doeff, M.M.; Xin, H.L. Chemical and structural stability of lithium-ion battery electrode materials under electron beam. Sci. Rep. 2014, 4, 5694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shukla, A.K.; Ramasse, Q.M.; Ophus, C.; Duncan, H.; Hage, F.; Chen, G. Unravelling structural ambiguities in lithium- and manganese-rich transition metal oxides. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarvis, K.A.; Wang, C.C.; Knight, J.C.; Rabenberg, L.; Manthiram, A.; Ferreira, P.J. Formation and effect of orientation domains in layered oxide cathodes of lithium-ion batteries. Acta Mater. 2016, 108, 264–270. [Google Scholar] [CrossRef] [Green Version]
- Jarvis, K.A.; Deng, Z.; Allard, L.F.; Manthiram, A.; Ferreira, P.J. Understanding structural defects in lithium-rich layered oxide cathodes. J. Mater. Chem. 2012, 22, 11550–11555. [Google Scholar] [CrossRef]
- Gemmi, M.; Mugnaioli, E.; Gorelik, T.E.; Kolb, U.; Palatinus, L.; Boullay, P.; Hovmöller, S.; Abrahams, J.P. 3D electron diffraction: The nanocrystallography revolution. ACS Cent. Sci. 2019, 5, 1315–1329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palatinus, L.; Corrêa, C.A.; Steciuk, G.; Jacob, D.; Roussel, P.; Boullay, P.; Klementová, M.; Gemmi, M.; Kopeček, J.; Domeneghetti, M.C.; et al. Structure refinement using precession electron diffraction tomography and dynamical diffraction: Tests on experimental data. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2015, 71, 740–751. [Google Scholar] [CrossRef] [PubMed]
- Karakulina, O.M.; Demortière, A.; Dachraoui, W.; Abakumov, A.M.; Hadermann, J. In Situ Electron Diffraction Tomography Using a Liquid-Electrochemical Transmission Electron Microscopy Cell for Crystal Structure Determination of Cathode Materials for Li-Ion batteries. Nano Lett. 2018, 18, 6286–6291. [Google Scholar] [CrossRef]
- Hadermann, J.; Abakumov, A.M. Structure solution and refinement of metal-ion battery cathode materials using electron diffraction tomography. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2019, 75, 485–494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hadermann, J.; Abakumov, A.; Van Rompaey, S.; Perkisas, T.; Filinchuk, Y.; Van Tendeloo, G. Crystal structure of a lightweight borohydride from submicrometer crystallites by precession electron diffraction. Chem. Mater. 2012, 24, 3401–3405. [Google Scholar] [CrossRef]
- Orlova, E.D.; Savina, A.A.; Abakumov, S.A.; Morozov, A.V.; Abakumov, A.M. Comprehensive Study of Li+/Ni2+ Disorder in Ni-Rich NMCs Cathodes for Li-Ion Batteries. Symmetry 2021, 13, 1628. [Google Scholar] [CrossRef]
- Zhao, H.; Krysiak, Y.; Hoffmann, K.; Barton, B.; Molina-Luna, L.; Neder, R.B.; Kleebe, H.-J.; Gesing, T.M.; Schneider, H.; Fischer, R.X.; et al. Elucidating structural order and disorder phenomena in mullite-type Al4B2O9 by automated electron diffraction tomography. J. Solid State Chem. 2017, 249, 114–123. [Google Scholar] [CrossRef]
- Krysiak, Y.; Barton, B.; Marler, B.; Neder, R.B.; Kolb, U. Ab initio structure determination and quantitative disorder analysis on nanoparticles by electron diffraction tomography. Acta Crystallogr. Sect. A Found. Adv. 2018, 74, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Brázda, P.; Palatinus, L.; Klementová, M.; Buršík, J.; Knížek, K. Mapping of reciprocal space of La0.30CoO2 in 3D: Analysis of superstructure diffractions and intergrowths with Co3O4. J. Solid State Chem. 2015, 227, 30–34. [Google Scholar] [CrossRef]
- Lanza, A.; Margheritis, E.; Mugnaioli, E.; Cappello, V.; Garau, G.; Gemmi, M. Nanobeam precession-assisted 3D electron diffraction reveals a new polymorph of hen egg-white lysozyme. IUCrJ 2019, 6, 178–188. [Google Scholar] [CrossRef]
- Paulus, A.; Hendrickx, M.; Bercx, M.; Karakulina, O.M.; Kirsanova, M.A.; Lamoen, D.; Hadermann, J.; Abakumov, A.M.; Van Bael, M.K.; Hardy, A. An in-depth study of Sn substitution in Li-rich/Mn-rich NMC as a cathode material for Li-ion batteries. Dalt. Trans. 2020, 49, 10486–10497. [Google Scholar] [CrossRef]
- Proffen, T.; Neder, R.B. DISCUS: A program for diffuse scattering and defect-structure simulation. J. Appl. Crystallogr. 1997, 30, 171–175. [Google Scholar] [CrossRef] [Green Version]
- Neder, R.B.; Proffen, T. Diffuse Scattering and Defect Structure Simulations: A Cook Book Using the Program DISCUS; Oxford University Press: Oxford, UK, 2008; Volume 11, ISBN 9780191715563. [Google Scholar]
- Palatinus, L. PETS—Program for Analysis of Electron Diffraction Data. Available online: http://pets.fzu.cz/ (accessed on 1 August 2021).
- Palatinus, L.; Brázda, P.; Jelínek, M.; Hrdá, J.; Steciuk, G.; Klementová, M. Specifics of the data processing of precession electron diffraction tomography data and their implementation in the program PETS2.0. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2019, 75, 512–522. [Google Scholar] [CrossRef]
- Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Krist. Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Wojdyr, M. Fityk: A general-purpose peak fitting program. J. Appl. Crystallogr. 2010, 43, 1126–1128. [Google Scholar] [CrossRef]
- Karakulina, O.M.; Khasanova, N.R.; Drozhzhin, O.A.; Tsirlin, A.A.; Hadermann, J.; Antipov, E.V.; Abakumov, A.M. Antisite Disorder and Bond Valence Compensation in Li2FePO4F Cathode for Li-Ion Batteries. Chem. Mater. 2016, 28, 7578–7581. [Google Scholar] [CrossRef]
- Drozhzhin, O.A.; Sumanov, V.D.; Karakulina, O.M.; Abakumov, A.M.; Hadermann, J.; Baranov, A.N.; Stevenson, K.J.; Antipov, E.V. Switching between solid solution and two-phase regimes in the Li1-xFe1-yMnyPO4 cathode materials during lithium (de)insertion: Combined PITT, in situ XRPD and electron diffraction tomography study. Electrochim. Acta 2016, 191, 149–157. [Google Scholar] [CrossRef]
- Mikhailova, D.; Karakulina, O.M.; Batuk, D.; Hadermann, J.; Abakumov, A.M.; Herklotz, M.; Tsirlin, A.A.; Oswald, S.; Giebeler, L.; Schmidt, M.; et al. Layered-to-Tunnel Structure Transformation and Oxygen Redox Chemistry in LiRhO2 upon Li Extraction and Insertion. Inorg. Chem. 2016, 55, 7079–7089. [Google Scholar] [CrossRef]
- Fedotov, S.S.; Khasanova, N.R.; Samarin, A.S.; Drozhzhin, O.A.; Batuk, D.; Karakulina, O.M.; Hadermann, J.; Abakumov, A.M.; Antipov, E.V. AVPO4F (A = Li, K): A 4 V Cathode Material for High-Power Rechargeable Batteries. Chem. Mater. 2016, 28, 411–415. [Google Scholar] [CrossRef] [Green Version]
- Plana-Ruiz, S.; Krysiak, Y.; Portillo, J.; Alig, E.; Estradé, S.; Peiró, F.; Kolb, U. Fast-ADT: A fast and automated electron diffraction tomography setup for structure determination and refinement. Ultramicroscopy 2020, 211, 112951. [Google Scholar] [CrossRef]
- Cichocka, M.O.; Ångström, J.; Wang, B.; Zou, X.; Smeets, S. High-throughput continuous rotation electron diffraction data acquisition via software automation. J. Appl. Crystallogr. 2018, 51, 1652–1661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, B.; Zou, X.; Smeets, S. Automated serial rotation electron diffraction combined with cluster analysis: An efficient multi-crystal workflow for structure determination. IUCrJ 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Gemmi, M.; La Placa, M.G.I.; Galanis, A.S.; Rauch, E.F.; Nicolopoulos, S. Fast electron diffraction tomography. J. Appl. Crystallogr. 2015, 48, 718–727. [Google Scholar] [CrossRef]
- Gruene, T.; Wennmacher, J.T.C.; Zaubitzer, C.; Holstein, J.J.; Heidler, J.; Fecteau-Lefebvre, A.; De Carlo, S.; Müller, E.; Goldie, K.N.; Regeni, I.; et al. Rapid Structure Determination of Microcrystalline Molecular Compounds Using Electron Diffraction. Angew. Chemie—Int. Ed. 2018, 57, 16313–16317. [Google Scholar] [CrossRef] [Green Version]
- Palatinus, L.; Brázda, P.; Boullay, P.; Perez, O.; Klementová, M.; Petit, S.; Eigner, V.; Zaarour, M.; Mintova, S. Hydrogen positions in single nanocrystals revealed by electron diffraction. Science 2017, 355, 166–169. [Google Scholar] [CrossRef]
- Kolb, U.; Gorelik, T.E.; Mugnaioli, E.; Stewart, A. Structural Characterization of Organics Using Manual and Automated Electron Diffraction. Polym. Rev. 2010, 50, 385–409. [Google Scholar] [CrossRef]
- Kodjikian, S.; Klein, H. Low-dose electron diffraction tomography (LD-EDT). Ultramicroscopy 2019, 200, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Steciuk, G.; David, A.; Petříček, V.; Palatinus, L.; Mercey, B.; Prellier, W.; Pautrat, A.; Boullay, P. Precession electron diffraction tomography on twinned crystals: Application to CaTiO3 thin films. J. Appl. Crystallogr. 2019, 52, 626–636. [Google Scholar] [CrossRef]
- Mohanty, D.; Huq, A.; Payzant, E.A.; Sefat, A.S.; Li, J.; Abraham, D.P.; Wood, D.L.; Daniel, C. Neutron Diffraction and Magnetic Susceptibility Studies on a High-Voltage Li1.2Mn0.55Ni0.15Co0.10O2 Lithium Ion Battery Cathode: Insight into the Crystal Structure. Chem. Mater 2013, 25. [Google Scholar] [CrossRef]
- Mosbah, A.; Verbaere, A.; Tournoux, M. Phases LixMnO2λ rattachees au type spinelle. Mater. Res. Bull. 1983, 18, 1375–1381. [Google Scholar] [CrossRef]
- Simancas, J.; Simancas, R.; Bereciartua, P.J.; Jorda, J.L.; Rey, F.; Corma, A.; Nicolopoulos, S.; Pratim Das, P.; Gemmi, M.; Mugnaioli, E. Ultrafast Electron Diffraction Tomography for Structure Determination of the New Zeolite ITQ-58. J. Am. Chem. Soc. 2016, 138, 10116–10119. [Google Scholar] [CrossRef] [Green Version]
- Smeets, S.; Wang, B.; Cichocka, M.O.; Ångström, J.; Wan, W. Instamatic. Available online: http://doi.org/10.5281/zenodo.1090389 (accessed on 1 August 2021).









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintelier, M.; Perkisas, T.; Poppe, R.; Batuk, M.; Hendrickx, M.; Hadermann, J. Determination of Spinel Content in Cycled Li1.2Ni0.13Mn0.54Co0.13O2 Using Three-Dimensional Electron Diffraction and Precession Electron Diffraction. Symmetry 2021, 13, 1989. https://doi.org/10.3390/sym13111989
Quintelier M, Perkisas T, Poppe R, Batuk M, Hendrickx M, Hadermann J. Determination of Spinel Content in Cycled Li1.2Ni0.13Mn0.54Co0.13O2 Using Three-Dimensional Electron Diffraction and Precession Electron Diffraction. Symmetry. 2021; 13(11):1989. https://doi.org/10.3390/sym13111989
Chicago/Turabian StyleQuintelier, Matthias, Tyché Perkisas, Romy Poppe, Maria Batuk, Mylene Hendrickx, and Joke Hadermann. 2021. "Determination of Spinel Content in Cycled Li1.2Ni0.13Mn0.54Co0.13O2 Using Three-Dimensional Electron Diffraction and Precession Electron Diffraction" Symmetry 13, no. 11: 1989. https://doi.org/10.3390/sym13111989
APA StyleQuintelier, M., Perkisas, T., Poppe, R., Batuk, M., Hendrickx, M., & Hadermann, J. (2021). Determination of Spinel Content in Cycled Li1.2Ni0.13Mn0.54Co0.13O2 Using Three-Dimensional Electron Diffraction and Precession Electron Diffraction. Symmetry, 13(11), 1989. https://doi.org/10.3390/sym13111989






