On the Controllability of a System Modeling Cell Dynamics Related to Leukemia
Abstract
:1. Introduction
1.1. Biological Background
1.2. Mathematical Model and Approach
2. Controllability of a Fixed Point Equation
2.1. A General Controllability Principle
2.2. Stability of the General Control Problem
- (a)
- For each solution and there exists such that
- (b)
- For each solution and there exists such thatThen, the control problem (2) is -stable.
3. First Control Problem for the Normal–Leukemic System
3.1. Solving of the Control Problem
- (a)
- (control regularity) In case one has
- (b)
- (continuous dependence) If and as uniformly on and then as in
3.2. Stability of the Control Problem
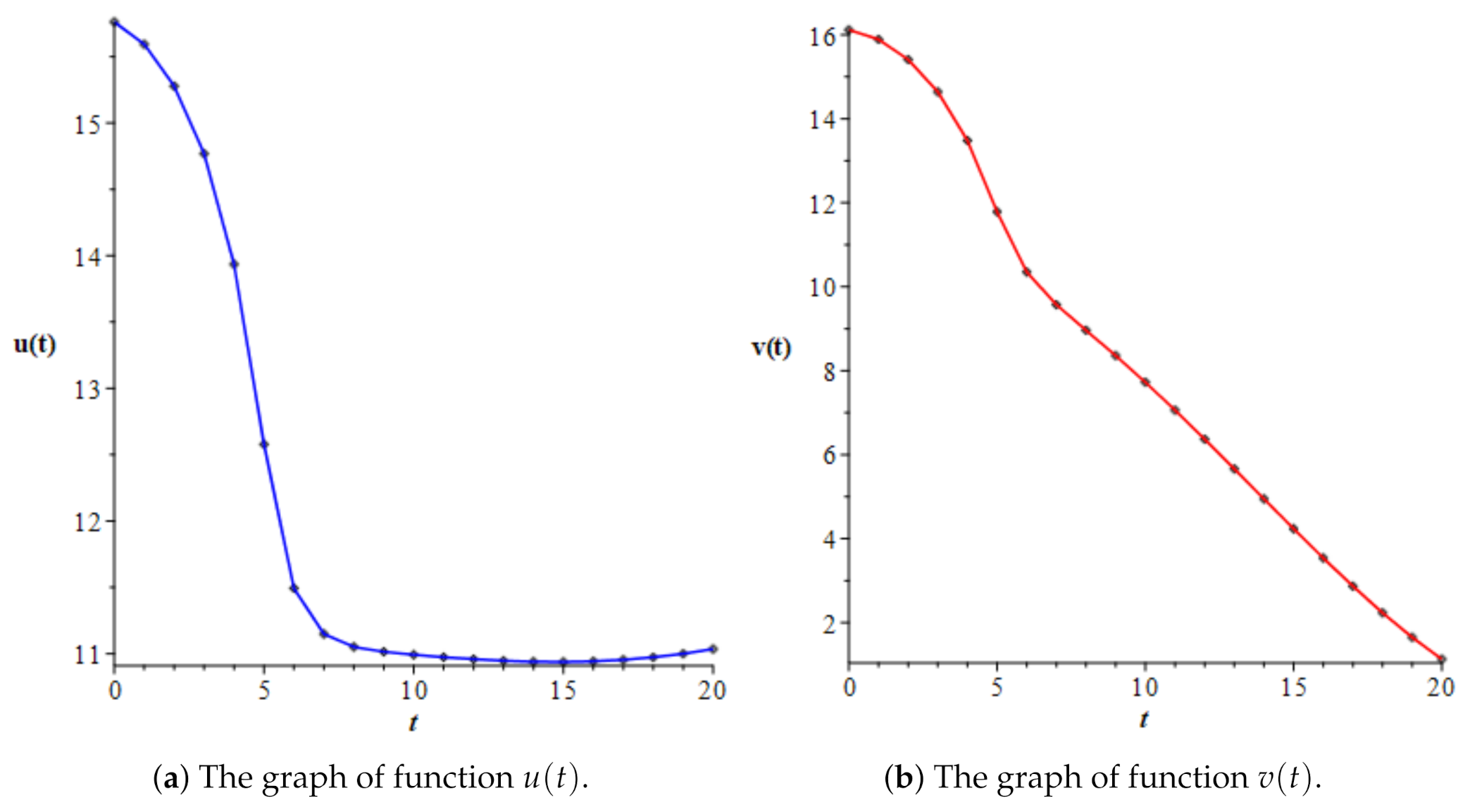
3.3. Numerical Simulations
3.4. A Different Objective Condition
4. Second Control Problem for the Normal–Leukemic System
4.1. Solving of the Control Problem
4.2. Stability of the Control Problem
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DeVita, V.T., Jr.; Chu, E. A History of cancer chemotherapy. Cancer Res. 2008, 68, 8643–8653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steensma, D.P.; Kyle, R.A. Hematopoietic stem cell discoverers. Mayo Clin. Proc. 2021, 96, 830–831. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, D. Leukemic stem cells show the way. Folia Histochem. Cytobiol. 2005, 43, 183–186. [Google Scholar] [PubMed]
- Schättler, H.; Ledzewicz, U. Optimal Control for Mathematical Models of Cancer Therapies: An Application of Geometric Methods; Springer: New York, NY, USA, 2015. [Google Scholar]
- Friberg, L.E.; Henningsson, A.; Maas, H.; Nguyen, L.; Karlsson, M.O. Model of chemotherapy-induced myelosuppression with parameter consistency across drugs. J. Clin. Oncol. 2002, 20, 4713–4721. [Google Scholar] [CrossRef]
- Arimoto, M.K.; Nakamoto, Y.; Nakatani, K.; Ishimori, T.; Yamashita, K.; Takaori-Kondo, A.; Togashi, K. Increased bone marrow uptake of 18F-FDG in leukemia patients: Preliminary findings. SpringerPlus 2015, 4, 521. [Google Scholar] [CrossRef] [Green Version]
- Ohanian, M.; Faderl, S.; Ravandi, F.; Pemmaraju, N.; Garcia-Manero, G.; Cortes, J.; Estrov, Z. Is acute myeloid leukemia a liquid tumor? Int. J. Cancer 2013, 133, 534. [Google Scholar] [CrossRef]
- Weaver, B.A. How Taxol/Paclitaxel kills cancer cells. Mol. Biol. Cell 2014, 25, 2677–2681. [Google Scholar] [CrossRef]
- Engelhardt, D.; Michor, F. A quantitative paradigm for decision-making in precision oncology. Trends Cancer 2021, 7, 293–300. [Google Scholar] [CrossRef]
- Afenya, E.K. Using mathematical modeling as a resource in clinical trials. Math. Biosci. Eng. 2005, 3, 421–436. [Google Scholar] [CrossRef]
- Afenya, E.K.; Bentil, D.E. Some perspectives on modeling leukemia. Math. Biosci. 1998, 150, 113–130. [Google Scholar] [CrossRef]
- Berezansky, L.; Bunimovich-Mendrazitsky, S.; Shklyar, B. Stability and controllability issues in mathematical modeling of the intensive treatment of leukemia. J. Optim. Theory Appl. 2015, 167, 326–341. [Google Scholar] [CrossRef]
- Bratus, A.S.; Fimmel, E.; Todorov, Y.; Semenov, Y.S.; Nuernberg, F. On strategies on a mathematical model for leukemia therapy. Nonlinear Anal. Real World Appl. 2012, 13, 1044–1059. [Google Scholar] [CrossRef]
- Crowell, H.L.; MacLean, A.L.; Stumpf, M.P.H. Feedback mechanisms control coexistence in a stem cell model of acute myeloid leukaemia. J. Theor. Biol. 2016, 401, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Cucuianu, A.; Precup, R. A hypothetical-mathematical model of acute myeloid leukaemia pathogenesis. Comput. Math. Methods Med. 2010, 11, 49–65. [Google Scholar] [CrossRef]
- Dingli, D.; Michor, F. Successful therapy must eradicate cancer stem cells. Stem. Cells 2006, 24, 2603–2610. [Google Scholar] [CrossRef] [Green Version]
- Djulbegovic, B.; Svetina, S. Mathematical model of acute myeloblastic leukaemia: An investigation of the relevant kinetic parameters. Cell Prolif. 1985, 18, 307–319. [Google Scholar] [CrossRef]
- Foley, C.; Mackey, M.C. Dynamic hematological disease: A review. J. Math. Biol. 2009, 58, 285–322. [Google Scholar] [CrossRef]
- Kim, P.S.; Lee, P.P.; Levy, D. Modeling regulation mechanisms in the immune system. J. Theor. Biol. 2007, 246, 33–69. [Google Scholar] [CrossRef]
- Mac Lean, A.L.; Lo Celso, C.; Stumpf, M.P.H. Population dynamics of normal and leukaemia stem cells in the haematopoietic stem cell niche show distinct regimes where leukaemia will be controlled. J. R. Soc. Interface 2013, 10, 20120968. [Google Scholar] [CrossRef] [Green Version]
- Moore, H.; Li, N.K. A mathematical model for chronic myelogenous leukemia (CML) and T cell interaction. J. Theor. Biol. 2004, 227, 513–523. [Google Scholar] [CrossRef]
- Parajdi, L.G.; Precup, R.; Bonci, E.A.; Tomuleasa, C. A mathematical model of the transition from normal hematopoiesis to the chronic and accelerated-acute stages in myeloid leukemia. Mathematics 2020, 8, 376. [Google Scholar] [CrossRef] [Green Version]
- Precup, R. Mathematical understanding of the autologous stem cell transplantation. Ann. Tiberiu Popoviciu Semin. Funct. Equ. Approx. Convexity 2012, 10, 155–167. [Google Scholar]
- Precup, R.; Serban, M.A.; Trif, D.; Cucuianu, A. A planning algorithm for correction therapies after allogeneic stem cell transplantation. J. Math. Model. Algorithms 2012, 11, 309–323. [Google Scholar] [CrossRef]
- Rubinow, S.I.; Lebowitz, J.L. A mathematical model of the acute myeloblastic leukemic state in man. Biophys. J. 1976, 16, 897–910. [Google Scholar] [CrossRef] [Green Version]
- Sharp, J.A.; Browning, A.P.; Mapder, T.; Baker, C.M.; Burrage, K.; Simpson, M.J. Designing combination therapies using multiple optimal controls. J. Theor. Biol. 2020, 497, 110277. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef]
- Barbu, V. Mathematical Methods in Optimization of Differential Systems; Springer Science+Business Media: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Becker, L.C.; Wheeler, M. Numerical and Graphical Solutions of Volterra Equations of the Second Kind; Maple Application Center: Waterloo, ON, Canada, 2005. [Google Scholar]
- Burton, T.A. Volterra Integral and Differential Equations, 2nd ed.; Mathematics in Science & Engineering; Elsevier: Amsterdam, The Netherlands, 2005; Volume 202. [Google Scholar]
- Linz, P. Analytical and Numerical Methods for Volterra Equations; Studies in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1985; Volume 7. [Google Scholar]



| t | u(t) | v(t) | v(t)/u(t) | |
|---|---|---|---|---|
| 0.0 | 15.76142 | 16.11810 | 1.02263 | 1.03667861 |
| 1.0 | 15.74559 | 16.04691 | 1.01914 | 1.82681929 |
| 2.0 | 15.69218 | 15.82858 | 1.00869 | 2.72096808 |
| 3.0 | 15.60090 | 15.46682 | 0.99141 | 3.73208846 |
| 4.0 | 15.47141 | 14.96789 | 0.96745 | 4.88700566 |
| 5.0 | 15.30324 | 14.34054 | 0.93709 | 6.21220861 |
| 6.0 | 15.09671 | 13.59667 | 0.90064 | 7.72168000 |
| 7.0 | 14.85444 | 12.75238 | 0.85849 | 9.42156274 |
| 8.0 | 14.58279 | 11.82826 | 0.81111 | 11.31917081 |
| 9.0 | 14.29297 | 10.84895 | 0.75904 | 13.40181913 |
| 10.0 | 14.00196 | 9.84183 | 0.70289 | 15.58459339 |
| 11.0 | 13.73138 | 8.83391 | 0.64334 | 17.68482475 |
| 12.0 | 13.50188 | 7.84645 | 0.58114 | 19.48688614 |
| 13.0 | 13.32522 | 6.89067 | 0.51712 | 20.85563950 |
| 14.0 | 13.20103 | 5.96906 | 0.45217 | 21.77786674 |
| 15.0 | 13.12077 | 5.08115 | 0.38726 | 22.31403995 |
| 16.0 | 13.07384 | 4.22854 | 0.32343 | 22.53852452 |
| 17.0 | 13.05129 | 3.41688 | 0.26180 | 22.51022240 |
| 18.0 | 13.04694 | 2.65569 | 0.20355 | 22.26679888 |
| 19.0 | 13.05703 | 1.95760 | 0.14993 | 21.82786481 |
| 20.0 | 13.07965 | 1.33756 | 0.10226 | 21.19948845 |
| t | u(t) | v(t) | v(t)/u(t) | |
|---|---|---|---|---|
| 0.0 | 15.76142 | 16.11810 | 1.02263 | 3.15804 |
| 1.0 | 15.59321 | 15.89161 | 1.01914 | 6.05741 |
| 2.0 | 15.27793 | 15.41073 | 1.00869 | 9.93469 |
| 3.0 | 14.76795 | 14.64103 | 0.99141 | 16.19792 |
| 4.0 | 13.93492 | 13.48141 | 0.96745 | 29.76677 |
| 5.0 | 12.57768 | 11.78644 | 0.93709 | 57.07073 |
| 6.0 | 11.49280 | 10.35085 | 0.90064 | 66.27579 |
| 7.0 | 11.14817 | 9.57058 | 0.85849 | 66.82106 |
| 8.0 | 11.05090 | 8.96350 | 0.81111 | 67.63740 |
| 9.0 | 11.01412 | 8.36017 | 0.75904 | 68.47741 |
| 10.0 | 10.99174 | 7.72598 | 0.70289 | 69.17105 |
| 11.0 | 10.97355 | 7.05969 | 0.64334 | 69.69562 |
| 12.0 | 10.95824 | 6.36825 | 0.58114 | 70.06188 |
| 13.0 | 10.94651 | 5.66061 | 0.51712 | 70.28064 |
| 14.0 | 10.93937 | 4.94642 | 0.45217 | 70.35631 |
| 15.0 | 10.93770 | 4.23573 | 0.38726 | 70.28740 |
| 16.0 | 10.94224 | 3.53910 | 0.32343 | 70.06809 |
| 17.0 | 10.95364 | 2.86770 | 0.26180 | 69.68924 |
| 18.0 | 10.97248 | 2.23344 | 0.20355 | 69.13897 |
| 19.0 | 10.99933 | 1.64909 | 0.14993 | 68.40266 |
| 20.0 | 11.03477 | 1.12845 | 0.10226 | 67.46265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haplea, I.Ş.; Parajdi, L.G.; Precup, R. On the Controllability of a System Modeling Cell Dynamics Related to Leukemia. Symmetry 2021, 13, 1867. https://doi.org/10.3390/sym13101867
Haplea IŞ, Parajdi LG, Precup R. On the Controllability of a System Modeling Cell Dynamics Related to Leukemia. Symmetry. 2021; 13(10):1867. https://doi.org/10.3390/sym13101867
Chicago/Turabian StyleHaplea, Ioan Ştefan, Lorand Gabriel Parajdi, and Radu Precup. 2021. "On the Controllability of a System Modeling Cell Dynamics Related to Leukemia" Symmetry 13, no. 10: 1867. https://doi.org/10.3390/sym13101867
APA StyleHaplea, I. Ş., Parajdi, L. G., & Precup, R. (2021). On the Controllability of a System Modeling Cell Dynamics Related to Leukemia. Symmetry, 13(10), 1867. https://doi.org/10.3390/sym13101867






