Two-Dimensional Numerical Model for Stability Analysis of Tunnel Face Based on Particle Flow Code
Abstract
1. Introduction
2. Numerical Model and Procedure
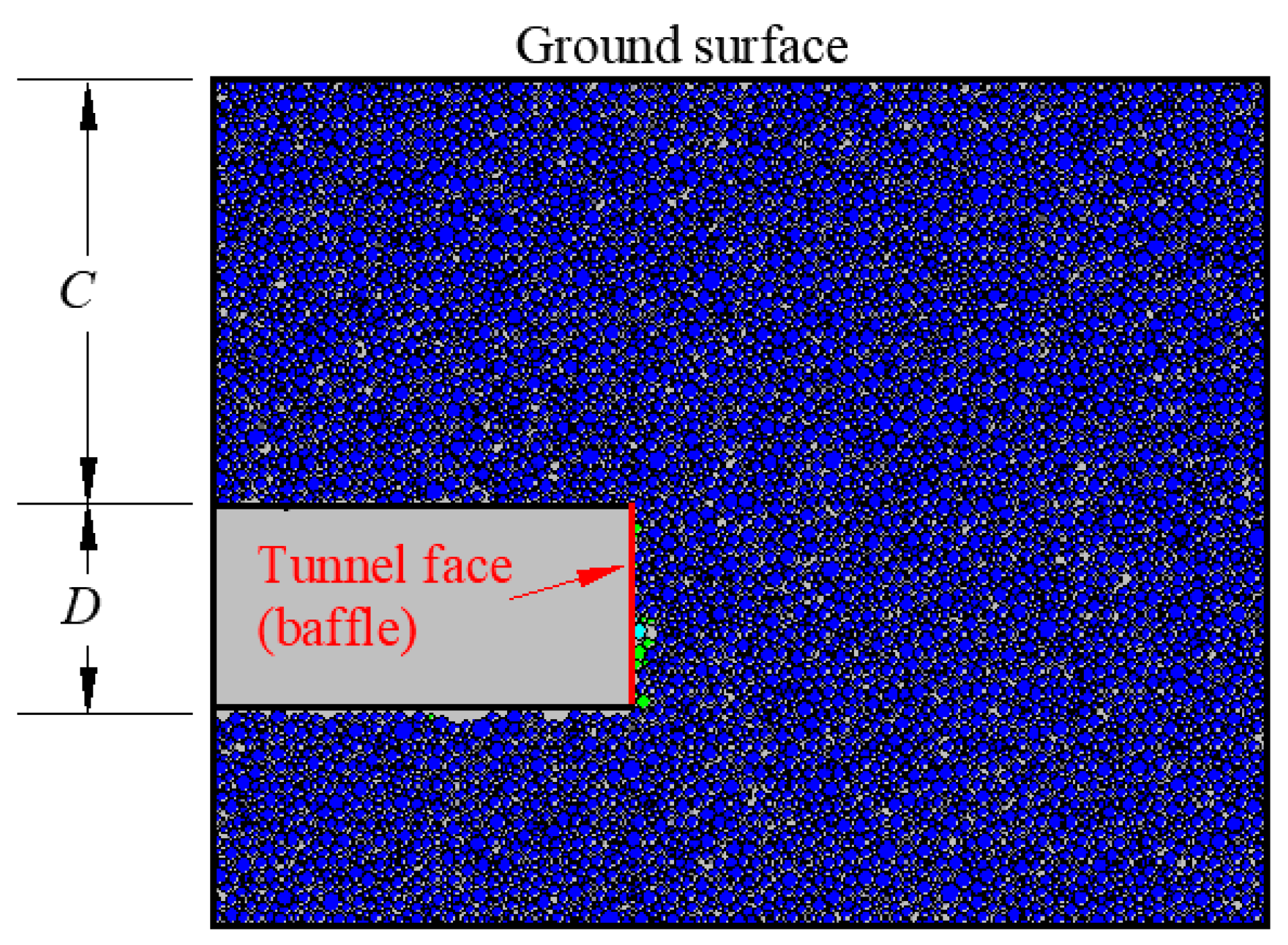
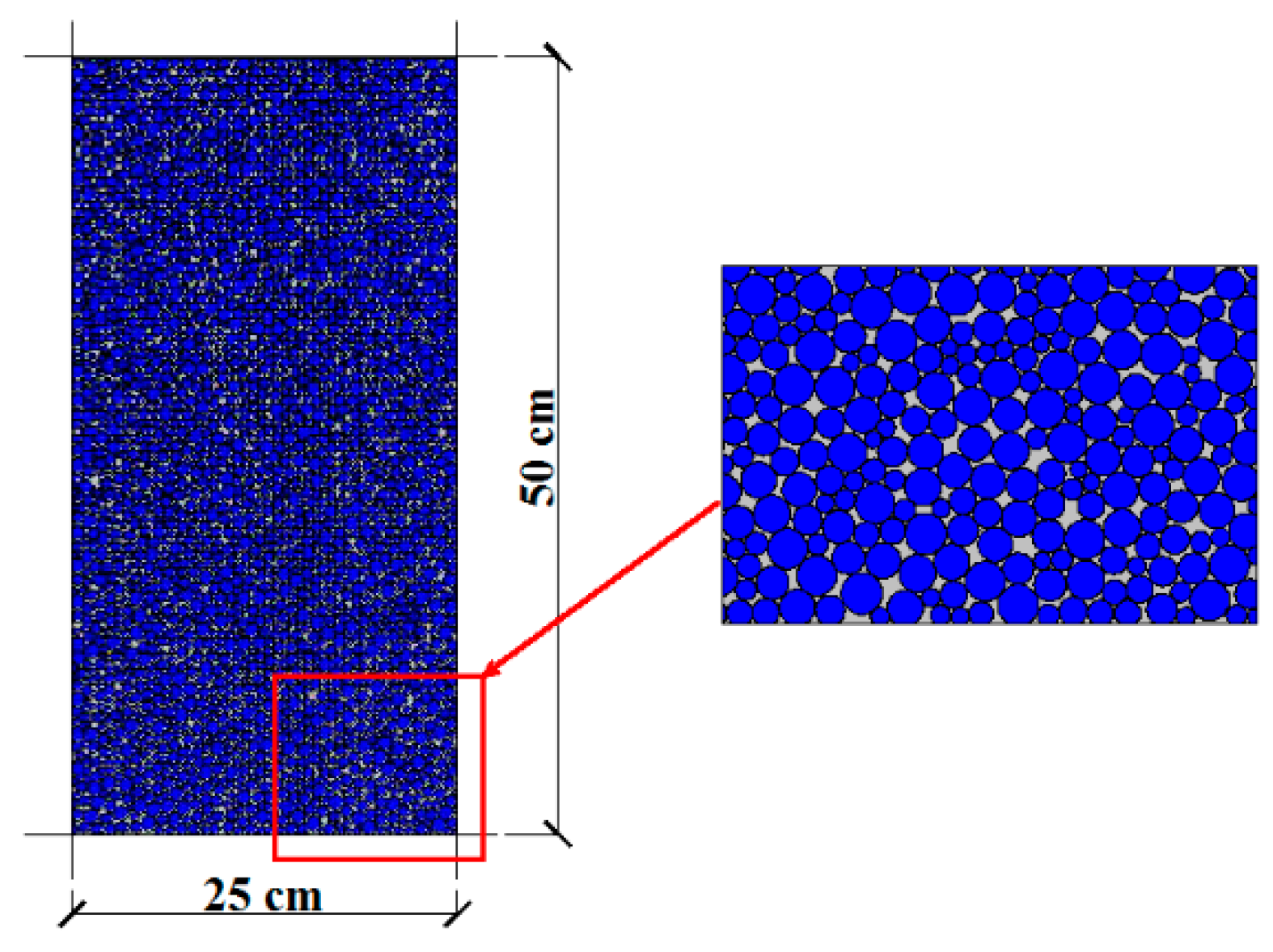
2.1. Dimensions of the Numerical Model
2.2. Numerical Procedure
- Through the biaxial test of the sample, the parameters were calibrated and the microscopic parameters used in the numerical simulation are obtained;
- The boundary of the model wall was formed, and the aggregate of the particles was formed by using the radius expansion method according to the particle gradation and the particle pore ratio. The first stable equilibrium state was achieved by applying gravity to the model. Then the soil particle were given the friction coefficient and the connection strength to reach the second stable state under the gravity stress field.
- The instability failure of tunnel face was investigated according to the method of displacement control, and the parameters of lining were given after parameter calibration. The lining adopted the parallel connection model, and the specific parameters are shown in Table 1.
- Progressive instability of the tunnel face was achieved through the withdrawal of the baffle used to simulate the tunnel face. Retreating displacement of the tunnel face was denoted by δ. The monitoring points and measuring rings were arranged. After the retaining wall and supporting force were added to the model, the modeling process of all models was completed, and then the calculation was carried out through the set time step.
- In the post-processing stage, data extraction was conducted to investigate the evolution laws of the contact force chain, particle displacement and ground surface settlement.
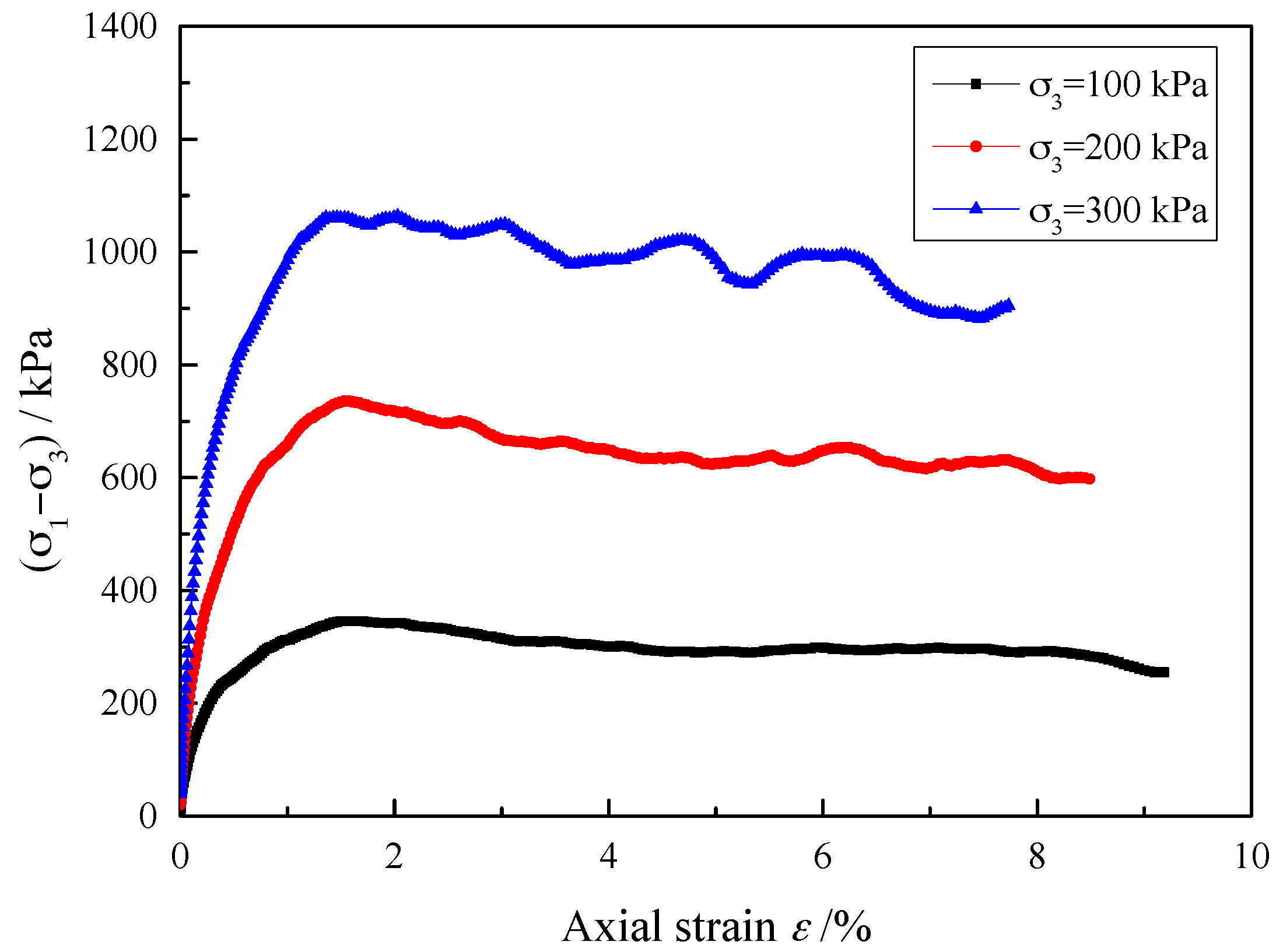
2.3. Parameter Calibration
3. Numerical Results and Analyses
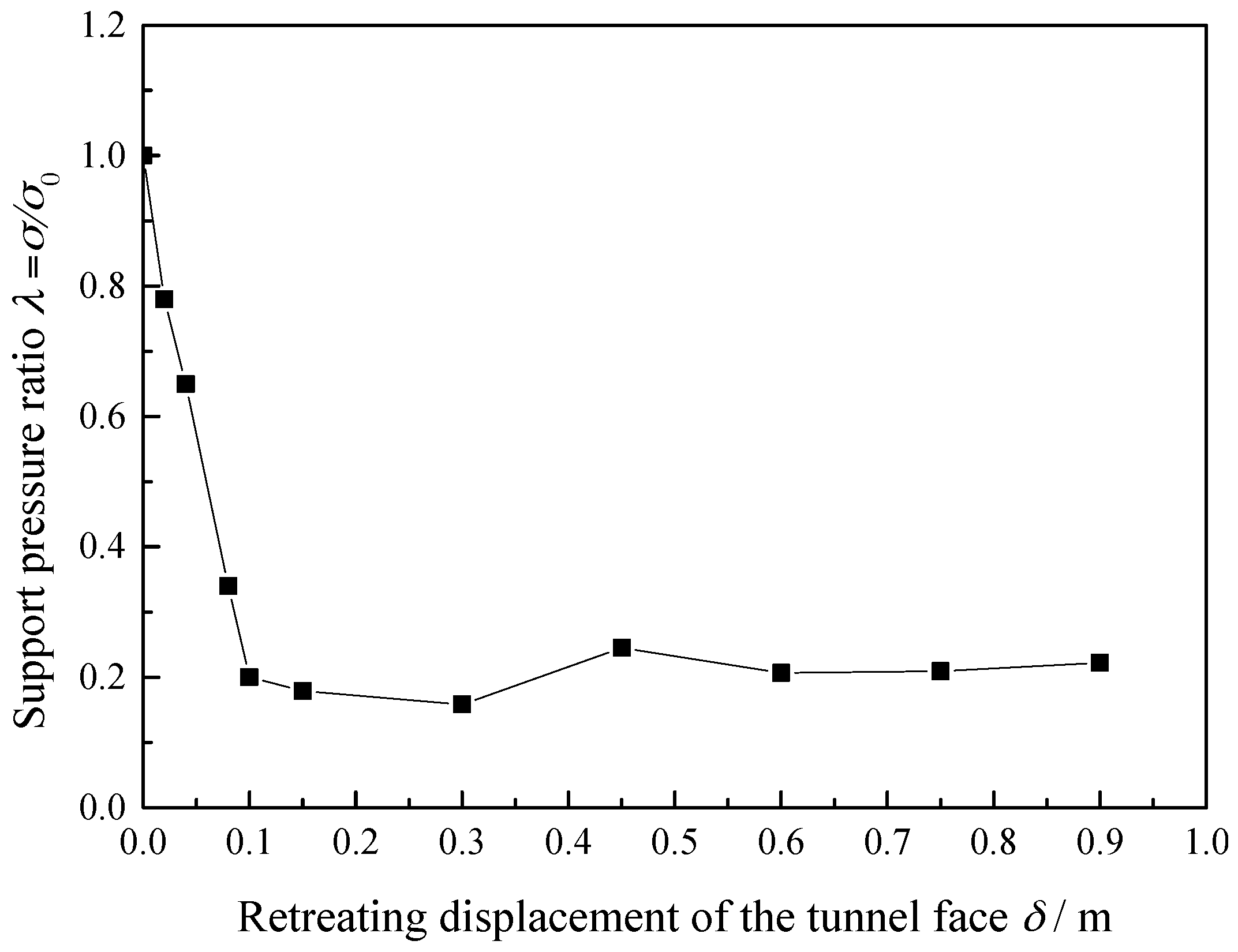
3.1. Analysis of Limit Support Pressure
- The first stage (rapid decline stage). When the tunnel face is retreating slightly, the support pressure on the tunnel face will decrease rapidly, and the curve of the support pressure and the displacement of the excavated surface is close to linear.
- The second stage (minimum stage). As the tunnel face continues to retreat, the downward trend of the support pressure on the tunnel face gradually slows down, and the support pressure gradually reaches the minimum value, which is called the limit value p.
- The third stage (slow rising stage). As the tunnel face continues to withdraw, the support pressure on tunnel face slowly rises.
- The fourth stage (horizontal stability stage). The loose zone continues to develop to the surface and eventually forms the penetrating surface. The support pressure on the tunnel face remains unchanged.
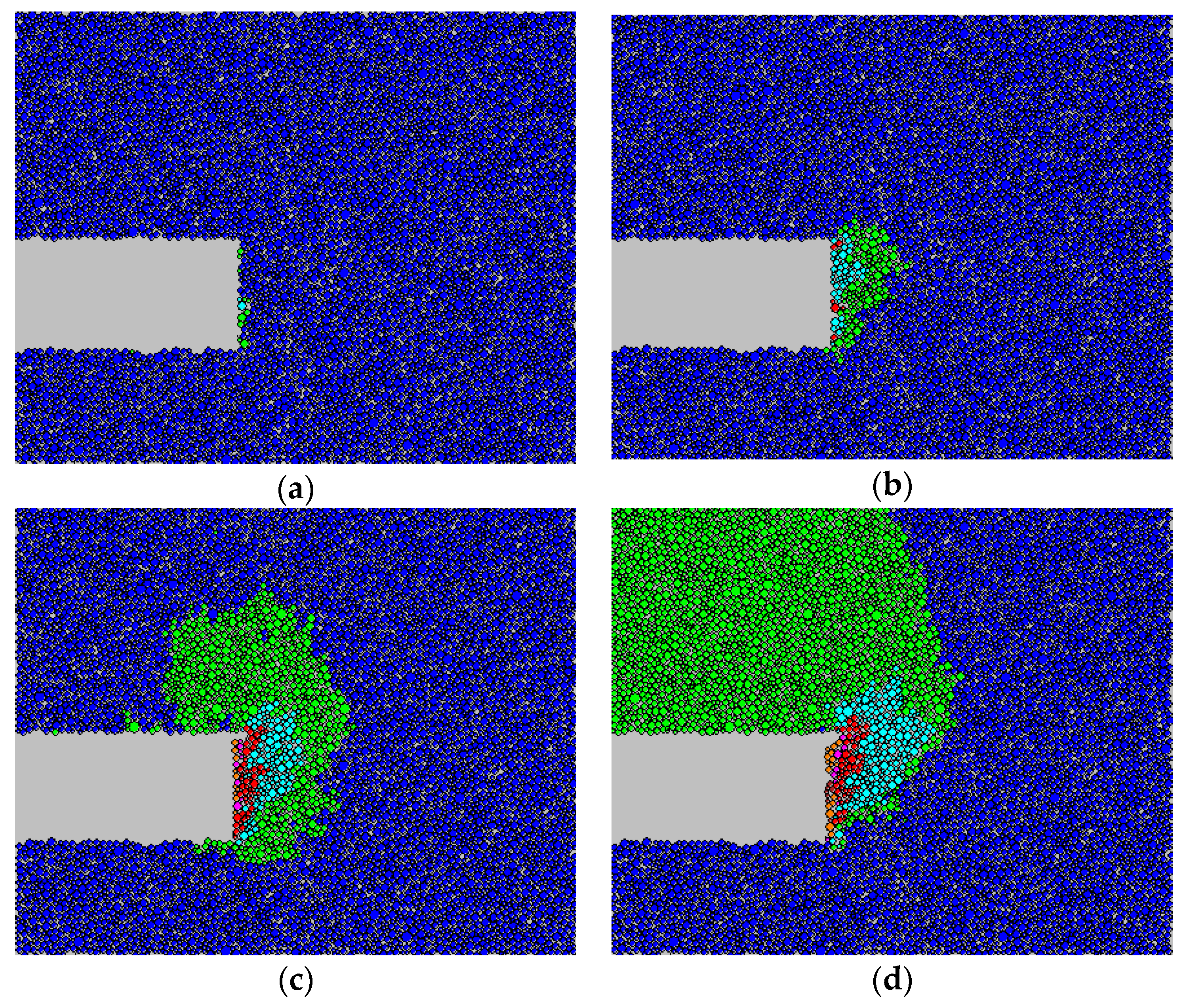
3.2. Analysis of Displacement of the Particles
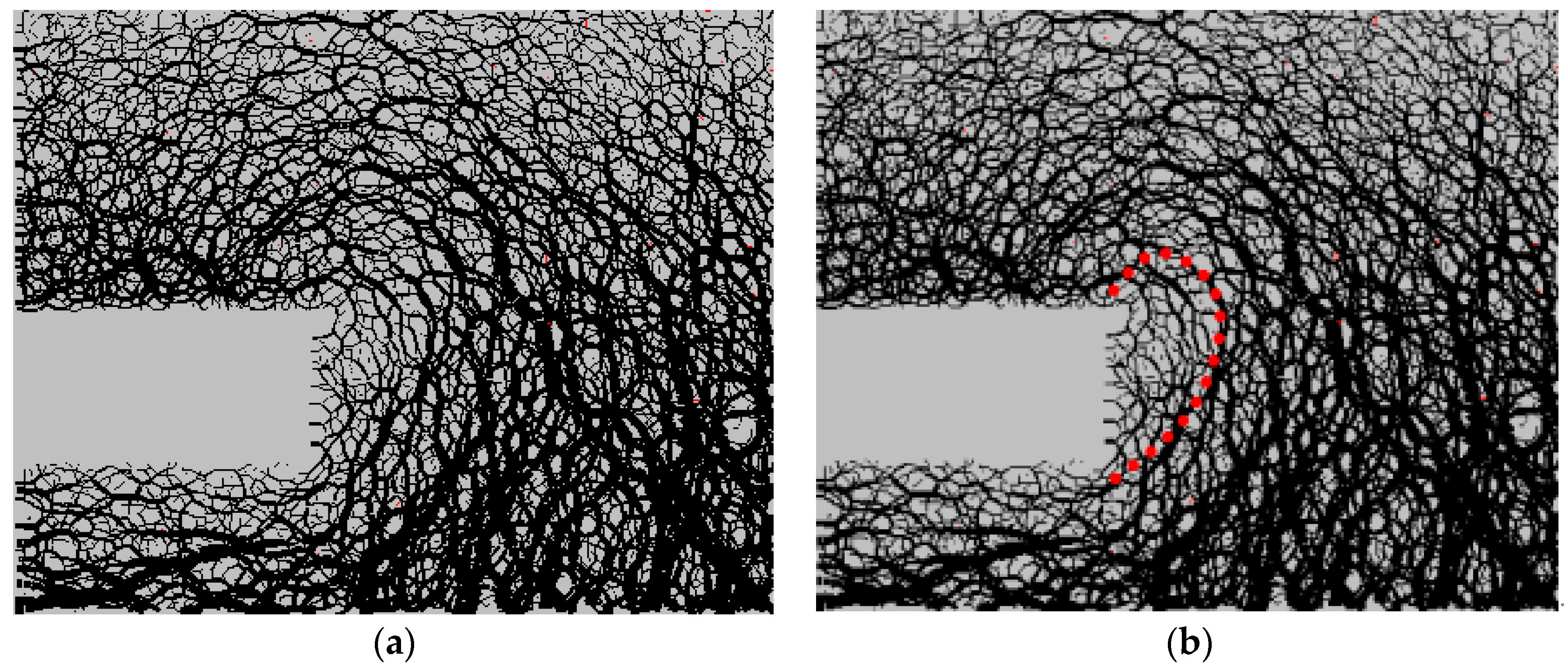
3.3. Analysis of Contact Force Chains of the Particles
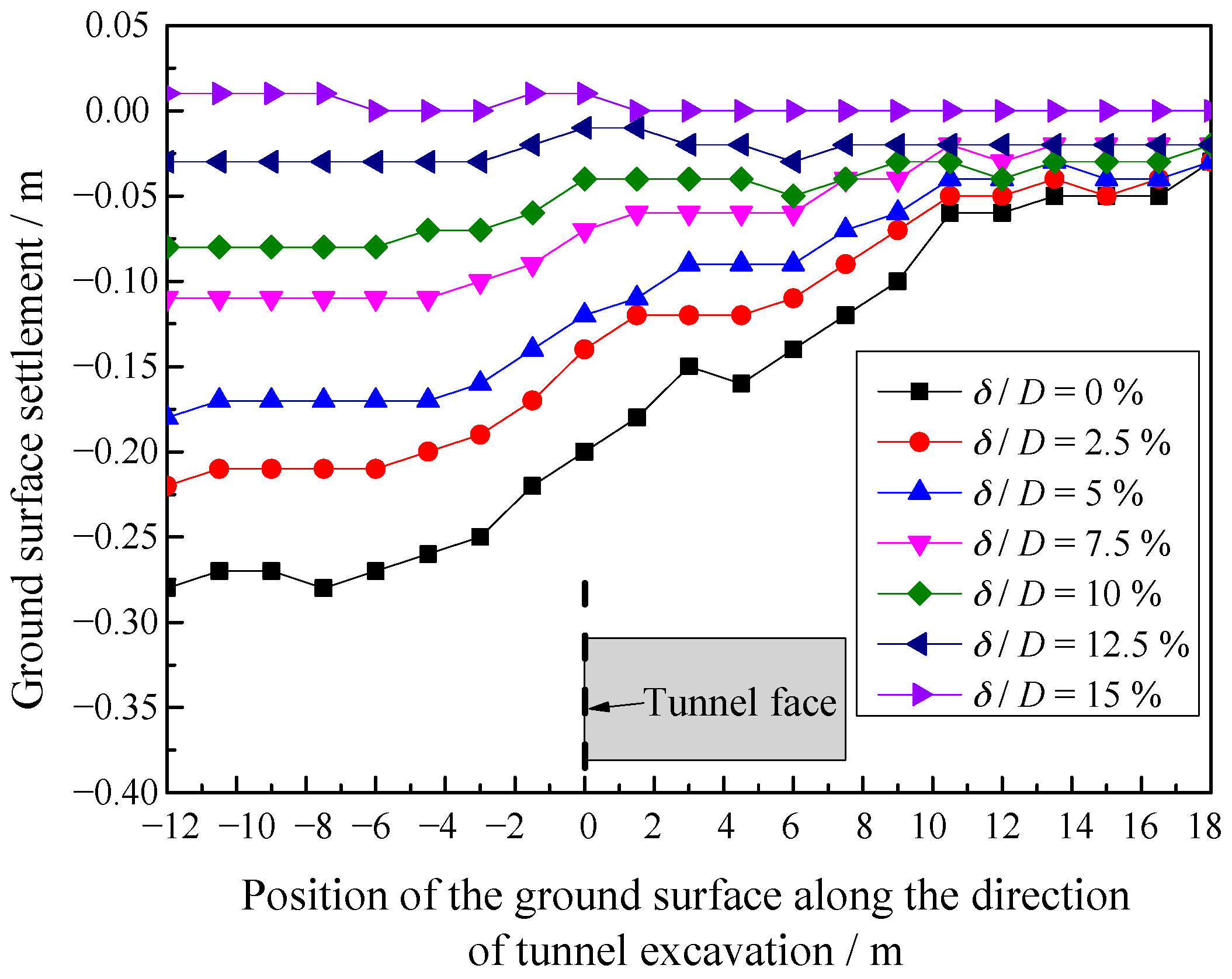
3.4. Analysis of Settlement Curve of Ground Surface
3.5. Analysis of Discriminant Criterion on of Failure Zones at Tunnel Face
4. Conclusions
- With the withdrawal of the tunnel face, the support pressure on the tunnel face can be divided into four stages, namely, the rapid decline stage, the minimum stage, the slow rising stage, and the horizontal stability stage.
- When the retreating displacement of the tunnel face grows gradually, the ranges and magnitudes of the the ground surface settlement, particle displacement and contact force chains of the particles increase. Moreover, with the increase of the retreating displacement of the tunnel face, the horizontal contact force chains near the tunnel face decrease, and the loose zone is formed. The contact force chain of the loose zone boundary forms a ring, and the stress increases gradually, which indicates that the horizontal and vertical arch become increasingly stable.
- For the discrete element codes PFC2D, the innermost obvious contact force chain under the limit state can be directly taken as the discriminant criterion for the failure zone.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Han, K.; Xie, T.; Luo, J. Calculation of Limit Support Pressure for EPB Shield Tunnel Face in Water-Rich Sand. Symmetry 2019, 11, 1102. [Google Scholar] [CrossRef]
- Mi, B.; Xiang, Y. Analysis of the Limit Support Pressure of a Shallow Shield Tunnel in Sandy Soil Considering the Influence of Seepage. Symmetry 2020, 12, 1023. [Google Scholar] [CrossRef]
- Li, X.; Wang, T.; Yang, Y. An Investigation into the Tunnel-Soil-Pipeline Interaction by in Situ Measured Settlements of the Pipelines. Adv. Civ. Eng. 2020, 2020, 18. [Google Scholar]
- Li, X.; Yuan, D.; Jin, D.; Yu, J.; Li, M. Twin neighboring tunnel construction under an operating airport runway. Tunn. Undergr. Sp. Technol. 2018, 81, 534–546. [Google Scholar] [CrossRef]
- De Buhan, P.; Cuvillier, A.; Dormieux, L.; Maghous, S. Face stability of shallow circular tunnels driven under the water table: A numerical analysis. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 79–95. [Google Scholar] [CrossRef]
- Vermeer, P.; Ruse, N.; Marcher, T. Tunnel heading stability in drained ground. Felsbau 2002, 20, 8–18. [Google Scholar]
- Kamata, H.; Mashimo, H. Centrifuge model test of tunnel face reinforcement by bolting. Tunn. Undergr. Space Technol. 2003, 18, 205–212. [Google Scholar] [CrossRef]
- Chen, R.P.; Tang, L.J.; Ling, D.S.; Chen, Y.M. Face stability analysis of shallow shield tunnels in dry sandy ground using the discrete element method. Comput. Geotech. 2011, 38, 187–195. [Google Scholar] [CrossRef]
- Dias, D.; Janin, J.-P.; Soubra, A.-H.; Kastner, R. Three-Dimensional Face Stability Analysis of Circular Tunnels by Numerical Simulations. In Proceedings of the GeoCongress 2008: Characterization, Monitoring, and Modeling of GeoSystems, New Orleans, Louisiana, 9–12 March 2008; pp. 886–893. [Google Scholar]
- Cundall, P.A. Particle Flow Code in 2 Dimensions Command and Fish Reference Summary; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 1999. [Google Scholar]
- Fakhimi, A.; Carvalho, F.; Ishida, T.; Labuz, J.F. Simulation of failure around a circular opening in rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 507–515. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Hu, X.Y.; Scott, K.D. A discrete numerical approach for modeling face stability in slurry shield tunnelling in soft soils. Comput. Geotech. 2011, 38, 94–104. [Google Scholar] [CrossRef]
- Funatsu, T.; Hoshino, T.; Sawae, H.; Shimizu, N. Numerical analysis to better understand the mechanism of the effects of ground supports and reinforcements on the stability of tunnels using the distinct element method. Tunn. Undergr. Space Technol. 2008, 23, 561–573. [Google Scholar] [CrossRef]
- Wang, P.; Cai, M.; Ren, F. Anisotropy and directionality of tensile behaviours of a jointed rock mass subjected to numerical Brazilian tests. Tunn. Undergr. Space Technol. 2018, 73, 139–153. [Google Scholar] [CrossRef]
- Saadat, M.; Taheri, A. A cohesive discrete element based approach to characterizing the shear behavior of cohesive soil and clay-infilled rock joints. Comput. Geotech. 2019, 114, 103109. [Google Scholar] [CrossRef]



| Density | Normal Stiffness | Shear Stiffness | Normal Contact Strength | Tangential Contact Strength | Contact Radius | Friction Coefficient |
|---|---|---|---|---|---|---|
| 3000/(kg/m3) | 7 × 109/(N m−1) | 2.8 × 109/(N m−1) | 1.57 × 107/(N m−1) | 1.57 × 107/(N m−1) | 1.0 | 0.5 |
| Name of Name | Symbol | Value |
|---|---|---|
| Spherical density | ρ/(kg/m3) | 1940 |
| porosity | ρ0 | 0.15 |
| Minimum radius of the ball | Rmin/m | 0.05 |
| Ratio of maximum radius to minimum radius of sphere | Rmax/Rmin | 1.5 |
| Spherical contact stiffness | Kn/Pa | 5.6 × 108 |
| Spherical contact stiffness ratio | Kn/Ks | 10 |
| Spherical contact modulus | Ec/Pa | 5 × 109 |
| Spherical friction coefficient | μp | 0.5 |
| Normal contact bond strength | σc-bond/Pa | 2 × 104 |
| Ratio of contact bond strength | σc-bond/τc-bond | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, T.; Han, K. Two-Dimensional Numerical Model for Stability Analysis of Tunnel Face Based on Particle Flow Code. Symmetry 2021, 13, 94. https://doi.org/10.3390/sym13010094
Xie T, Han K. Two-Dimensional Numerical Model for Stability Analysis of Tunnel Face Based on Particle Flow Code. Symmetry. 2021; 13(1):94. https://doi.org/10.3390/sym13010094
Chicago/Turabian StyleXie, Tingwei, and Kaihang Han. 2021. "Two-Dimensional Numerical Model for Stability Analysis of Tunnel Face Based on Particle Flow Code" Symmetry 13, no. 1: 94. https://doi.org/10.3390/sym13010094
APA StyleXie, T., & Han, K. (2021). Two-Dimensional Numerical Model for Stability Analysis of Tunnel Face Based on Particle Flow Code. Symmetry, 13(1), 94. https://doi.org/10.3390/sym13010094






