An Improved Whale Optimization Algorithm for the Traveling Salesman Problem

Abstract

The whale optimization algorithm is a new type of swarm intelligence bionic optimization algorithm, which has achieved good optimization results in solving continuous optimization problems. However, it has less application in discrete optimization problems. A variable neighborhood discrete whale optimization algorithm for the traveling salesman problem (TSP) is studied in this paper. The discrete code is designed first, and then the adaptive weight, Gaussian disturbance, and variable neighborhood search strategy are introduced, so that the population diversity and the global search ability of the algorithm are improved. The proposed algorithm is tested by 12 classic problems of the Traveling Salesman Problem Library (TSPLIB). Experiment results show that the proposed algorithm has better optimization performance and higher efficiency compared with other popular algorithms and relevant literature.

1. Introduction

In order to solve optimization problems in many fields, swarm intelligence-based optimization algorithms have attracted much attention [1,2,3,4,5,6] in recent years. The whale optimization algorithm (WOA) [7] is a new type of swarm intelligence optimization algorithm proposed by Mirjalili and Lewis in 2016 which is inspired by the unique predation behavior of humpback whales. The algorithm simulated the whales foraging behavior of encircling and bubbles attacking for optimization. Because the advantages of simple principle, simple operation, easy implementation, few adjustment parameters, and strong robustness, the WOA algorithm has received extensive attention and has obtained many valuable research results since it has been proposed.

The WOA algorithm is mostly used for continuous function optimization problems up to now. Research results show that it is superior to other optimization algorithms such as differential evolution and gravitational search in terms of solution accuracy and algorithm stability [7]. However, like other meta-heuristic algorithms, the classic WOA algorithm has defects like low solution accuracy, slow convergence speed, and easy to fall into local optimum [8]. Therefore, scholars study to improve the classic WOA algorithm.

Literature [9,10,11,12,13,14,15,16] studied the function optimization problem by the WOA algorithm. Trivedi et al. (2016) [9] introduced an adaptive strategy and proposed a new global optimization adaptive WOA algorithm. To increase diversity of the population, Ling et al. (2017) [10] designed an improved LWOA by introduced the Levy flight strategy. To balance the capabilities of exploration and exploitation of the algorithm, Kaur and Arora (2018) [11] introduced the chaos principle into WOA. In order to improve the global search ability of the algorithm, Wu and Song (2019) [12] adopted the opposite learning strategy to initialize the population, and the normal mutation operator is used to interfere with the whales. Chen et al. (2019) [13] introduced a dual-adaptive weighting strategy which improved the exploration ability in the early stage of the algorithm and the exploitation ability in the later stage. Huang et al. (2020) [14] proposed an improved WOA algorithm based on chaotic weights and elite guidance strategies. They adopted the evolutionary feedback information of elite individuals to timely adjust the search direction of the population so that the global search ability of the algorithm is improved, and then the chaotic dynamic weight factor is introduced to enhance the local search ability. Ding et al. (2019) [15] combined the WOA with adaptive weight and simulated annealing. The former is used to adjust the convergence speed and later is used to improve the global optimization ability of the WOA algorithm. Bozorgi and Yazdani (2019) [16] introduced a differential evolution algorithm to improve the local search ability of the algorithm.

For discrete optimization problems, there are relatively few studies using the WOA algorithm. For example, Aziz et al. (2017) [17] applied the WOA to solve the multi-threshold image segmentation problems. Prakash et al. (2017) [18] applied the WOA to solve the location problem of radial network capacitors. Aljarah et al. (2018) [19] used the WOA algorithm for the weight optimization problem of the neural network. Ya Li et al. (2020) [20] applied the improved WOA to solve the Knapsack problem. Majdi et al. (2017) [21] combined the WOA with the simulated annealing algorithm for the feature selection problem. Oliva et al. (2017) [22] combined the WOA with chaotic mapping strategy to predict the solar cell parameters.

For the traveling salesman problem, Ahmed and Kahramanli (2018) [23] used the classic WOA and the gray wolf optimization algorithm to solve smaller-scale problems, respectively. They found that the WOA was mostly better than the gray wolf optimization algorithm. Yan and Ye (2018) [24] adopted a hybrid stochastic quantum whale optimization algorithm (HSQWOA) to solve smaller-scale problems, and verified the good performance of the algorithm through data comparison.

Based on the characteristics of the traveling salesman problem (TSP) [25] and the optimization mechanism of the WOA, a discrete whale optimization algorithm with variable neighborhood search (VDWOA) for solving larger-scale TSP is designed in this paper. Adaptive weight strategy is introduced to update position of the population and the variable neighborhood idea and Gaussian perturbation is used for local search. Twelve classic problems in the TSPLIB standard library [26] is tested and compared with the bat algorithm (BA), discrete whale optimization algorithm (DWOA), grey wolf optimizer (GWO), moth-flame optimization (MFO), and particle swarm optimization (PSO), etc. Experimental results are analyzed to verify the effectiveness of the proposed VDWOA algorithm.

2. Basic Theory of WOA

The WOA algorithm is inspired by the special hunting method of humpback whales. Their foraging behavior is called bubble-net attacking method which include following special behavior: encircling prey, spiraling update position, and searching for the prey. The algorithm performs the exploitation phase based on the first two behaviors and the other is the exploration phase. During the search procedure, the whales gradually obtain relevant position of the prey by enclosing and spiraling and capture it finally.

2.1. Encircling Prey

The whales need to decide the position of the prey to surround and capture it when they are foraging. The best search whale assumes that the current optimal candidate solution is the position of the prey or close to the target. The other whales will update their positions according to the optimal candidate solution. This behavior can be described as Equations (1)–(4):

$$D=\left|C\cdot X^{\ast }(t)-X(t)\right|$$

(1)

$$X(t+1)=X^{\ast }(t)-A\cdot D$$

(2)

$$A=2a\cdot r-a$$

(3)

$$C=2\cdot r$$

(4)

where t is the current iteration number, X* is the position vector of current optimal solution, X is the position vector of the whales, D is the distance vector between the whales and current optimal solution, C(C$\in$[0, 2]) and A(A$\in$[−a, a]) are the adjustment coefficient, a is an adjustment parameter whose value decreases linearly from 2 to 0 as the number of iterations increases, | | is the absolute value, r is a random number in [0, 1].

2.2. Bubble-Net Attacking Method

The WOA algorithm adopted shrinking encirclement and spiraling strategy to update positions of the whales.

The shrinking encirclement behavior is realized by adjusting the value of a by Equation (3). If |A| ≤ 1, the whales will approach to the optimal solution from their original position. The position of the whales will be updated by Equation (2) to realize the shrinking encirclement. In the process of spiraling, a mathematical model is constructed by simulating the spiral behavior of the whales shown as Equations (5) and (6):

$$D^{’}=\left|X^{\ast }(t)-X(t)\right|,$$

(5)

$$X(t+1)=D^{’}\cdot e^{bl}\cdot \cos (2\pi l)+X^{\ast }(t),$$

(6)

where D’ is the distance vector between the whales and the prey (current optimal solution), b is a constant coefficient of the spiral shape, l is a random number in [−1, 1].

The whales adopt two strategies of shrinking encirclement and spiral update at the same time to update their locations. The WOA executes these two location update strategies by the value of the probability parameter p, which is shown as Equation (7):

$$X(t+1)=\{\begin{array}{ll}{X}^{\ast }(t)-A\cdot D& if\hspace{0.17em}p<0.5\\ D^{’}\cdot e^{bl}\cdot \cos (2\pi l)+X^{\ast }(t)& if\hspace{0.17em}p\ge 0.5\end{array},$$

(7)

where p is a random number in [0, 1].

2.3. Searching for Prey

In the process of foraging, the variation of adjustment coefficient A is used to search for prey. If |A| ≤ 1, the whales will approach to the prey (exploitation). If |A| > 1, the whales do not choose the best whale to update their positions, but select a random whale to be the best position (exploration). The whales update their positions by Equations (8) and (9) in the exploration phase. This mechanism of foraging allows the WOA algorithm to perform a global search:

$$D=\left|C\cdot X_{rand}-X\right|,$$

(8)

$$X(t+1)=X_{rand}-A\cdot D,$$

(9)

where X_rand represents the position vector of a whale randomly selected from the current whale population. The pseudo-code of the WOA algorithm is as Algorithm 1.

Algorithm 1. The pseudo-code of the WOA algorithm

1. Begin

2.  Initialize the relevant parameters of the WOA and the positions of whales;

3.  Calculate the fitness of each whale;

4.  Find the best whale (X*);

5.  While (t < maximum iteration)

6.    for each whale

7.      Update a, A, C, l and p;

8.      if 1 (p < 0.5)

9.       if 2 (|A| < 1)

10.        Update the position of the current whale by Equation (2);

11.      else if 2 (|A| ≥ 1)

12.       Select a random whale (Xrand);

13.       Update the position of the current whale by Equation (9);

14.      end if 2

15.     else if 1 (p ≥ 0.5)

16.      Update the position of the current search by Equation (6);

17.     end if 1

18.    end for

19.    Check if any whale goes beyond the search space and amend it;

20.    Calculate the fitness of each whale;

21.    Update X* if there is a better solution;

22.    t = t + 1;

23.   end while

24.   return X*.

25. End

3. DWOA for the TSP Problem

The TSP is a widespread concerned combinatorial optimization problem, which can be described as: The salesman should pay a visit to m cities in his region and coming back to the start point. Each city should be visited and only once. The challenging issue is to find a shortest route to complete the tour. Since TSP belongs to NP-hard [27], heuristic algorithms are usually used to find approximate results.

To solve this problem, this paper designed a discrete coding form, which can be described as follows: Assuming that there with m cities and the coding of the solution is represented by the sequence of city numbers should be visited. Each component in the solution corresponds to a city number, so the code of solution X is:

X = (c₁,c₂,…,c_m),

where m is the code length, and c_i represents the number of the i-th client to be visited (c_i$\in$[1, m], and any c_i ≠ c_j).

The fitness function is defined as f that can be expressed by Equation (10):

$$f={\displaystyle \sum _{i=1}^{m-1}{d}_{c_i,c_{i+1}}+d_{c_m,c_1}},$$

(10)

where $d_{c_i,c_{i+1}}$ is the distance between c_i and c_i+1.

3.1. DWOA Improvement Strategy

Due to the lack of disturbance mechanism, the classical WOA has some defects, such as slow convergence in the later stage and easy to fall into local optimum [28]. Two improved strategies are introduced in this paper.

3.1.1. Adaptive Weight Strategy

For the classical WOA, the position of each whale is quite different and the search space is considerably wide in the initial stage. According to the increasing of iteration numbers, the distribution scope of whales continues to shrink which results in reduction of the search space. The algorithm will fall into the local optimum due to the reduced population diversity. In order to increase the diversity of the population and make the algorithm jump out of the local optimum, this paper introduces an adaptive weight factor w_i, and the calculation method is shown in Equation (11):

$$w_i=\exp ( Nite{r}_i/ Nite{r}_{max}-1),$$

(11)

where w_i stands for the weight at the i-th iteration, Niter_max is the maximum number of iterations, Niter_i is the current number of iterations and Niter_i ≤ Niter_max.

The location update mode of the improved WOA is shown in Equations (12)–(14):

$$X(t+1)=X^{\ast }(t)-w_i\cdot A\cdot D,$$

(12)

$$X(t+1)=w_i\cdot D^{’}\cdot e^{bl}\cdot \cos (2\pi l)+X^{\ast }(t),$$

(13)

$$X(t+1)=X_{rand}-w_i\cdot A\cdot D,$$

(14)

3.1.2. Gaussian Disturbance

Since the WOA algorithm has strong local search ability, it will fall into local optimum easily during the later stage. This paper introduced a Gaussian disturbance strategy to make the whales deviate from the local optimum to a certain extent so that the local search range and the global search ability of the algorithm can be improved. The Gaussian disturbance method is shown in Equation (15)

$$X(t+1)=X^{\ast }(t)+\epsilon \cdot {\delta }_t\cdot \left(Nite{r}_{\max }-t\right)/Nite{r}_{\max },$$

(15)

where ε$\in$(0, 1) is a constant which indicating the weight of Gaussian disturbance, δ is a random vector of the same dimension as X^*, and is standard normal distribution δ∼N(0, 1), Niter_max is the maximum number of iterations. This equation can make the disturbance scope gradually smaller when the whales are closer to the prey during the search process.

The pseudo code of the DWOA is similar to the VDWOA described later except for the procedure of variable neighborhood search. That is to say, codes between lines 15–18 and lines 29–32 of VDWOA are not included in the DWOA.

3.2. Description of VDWOA

3.2.1. Variable Neighborhood Search

The classical WOA algorithm mainly relies on the interaction between whales to solve the optimization problems. The algorithm will easily fall into local optimum because of the simple neighborhood structure and the lack of disturbance between whales. Variable neighborhood search is introduced to further increase diversity of the neighborhood in this paper.

Variable neighborhood search (VNS) [29] is a well-known meta-heuristic algorithm proposed by Mladenović and Hansen in 1997. The VNS algorithm based on principle of systematically changing neighborhoods to escape from local optimum, which has a good effect on solving large-scale combinatorial optimization problems. The premise of this algorithm is that the local optimum of a neighborhood structure may be the global optimal. Local optimum of different neighborhood structures may be different. The VNS algorithm systematically searches the solution space through multiple different neighborhood structures to increase the disturbance to expand the search scope.

This paper defines the idea of combining variable neighborhood search and a neighborhood set n_k (k$\in${1, 2, 3}) which contain three neighborhood structures.

2-opt neighborhood structure named as n₁: Select any two nodes randomly from the path and swap them to get a new one, so that the diversity of path search is increased and the local search ability of the algorithm is improved. For example: assuming that there have seven customer points that were labeled as 1, 2, 3, 4, 5, 6, and 7. Suppose that s is the current optimal solution, which is {1, 2, 3, 4, 5, 6, 7}. Select two non-adjacent nodes 2 and 5 randomly from s, the partial paths before node 2 and after node 5 remain the same and are added to the new path, while the partial path between node 2 and 5 are flipped and added to the new path, so the new path s’ is {1, 5, 4, 3, 2, 6, 7}.

3-opt neighborhood structure named as n₂: Select any three nodes randomly from the path and swap to get a new one. Suppose s is the current optimal solution which is {1, 2, 3, 4, 5, 6, 7}. Select three non-adjacent nodes 1, 4, and 6 randomly, and then perform 2-opt on (1, 4), (1, 6), and (4, 6) separately. After the above operations, solution s₁, s₂, and s’ can be obtained successively, where s₁ is {4, 3, 2, 1, 5, 6, 7}, s₂ is {4, 3, 2, 6, 5, 1, 7}, and the new path s’ is {6, 2, 3, 4, 5, 1, 7}.

Nodes interchange neighborhood structure named as n3: Select any two nodes from the path and interchange their positions. The other nodes will remain in their original positions and a new solution will generate. Suppose that s is the current optimal solution which is {1, 2, 3, 4, 5, 6, 7}. Two non-adjacent nodes 2 and 6 are selected randomly and their position is interchanged, so the new path’s will be {1, 6, 3, 4, 5, 2, 7}.

The procedure of variable neighborhood search of this paper is defined as Proc_VNS, whose pseudo-code is as Algorithm 2.

Algorithm 2. The pseudo-code of Proc_VNS

1. Begin

2.  Set the current optimal solution as the initial solution x;

3.  while (termination condition not met)

4.    k = 1;

5.    while (k ≤ 3)

6.     Generate the neighborhood solution x’ for x by the nk;

7.     Produce a new local optimal x″ for x’ by local search;

8.     if (the fitness value of x″ is better than x)

9.      x = x″;

10.       k = 1;

11.     else k = k + 1;

12.     end if

13.   end while

14.  end while

15. End

3.2.2. Pseudo-Code of the VDWOA

The pseudo-code of the VDWOA for the TSP problem is as Algorithm 3.

Algorithm 3. The pseudo-code of the VDWOA for the TSP

1. Begin

2.  Initialize the relevant parameters of the WOA algorithm and the positions of whales;

3.  Calculate the fitness of each whale according to Equation (10);

4.  Find the best whale(X*);

5.  while (t < maximum iteration)

6.   for each whale

7.    Update a, A, C, l and p;

8.    if1 (p < 0.5)

9.     if2 (|A| < 1)

10.      if3 (current r < 0.5)

11.       Update the position of the whale by Equation (15);

12.      else

13.       Update the position of the current whale by Equation (12);

14.      end if3

15.      if4 (current r > 0.5)

16.       Call Proc_VNS for the current optimal whale;

17.       Update the local optimal solution;

18.      end if4

19.     else if2 (|A| ≥ 1)

20.      Select a random whale(Xrand);

21.      Update the position of the current whale by Equation (14);

22.     end if2

23.    else if1 (p ≥ 0.5)

24.       if5 (current r < 0.5)

25.        Update the position of the whale by Equation (15);

26.       else

27.        Update the position of the current whale by Equation (13);

28.       end if5

29.       if6 (current r > 0.5)

30.        Call Proc_VNS for the current optimal whale;

31.        Update the local optimal solution;

32.       end if6

33.    end if1

34.   end for

35.   Check if any whale goes beyond the search space and amend it;

36.   Calculate the fitness of each whale;

37.   Update X* if there is a better solution;

38.   t = t + 1;

39.  end while

40.  return X*;

41. End.

4. Experiment and Results

The algorithm is programmed in MATLAB R2016a and implemented on Intel (R) Core (TM) i5-7500 CPU, 3.4GHz frequency, 8GB memory, and Windows 10 (64-bit) operating system.

Twelve classic problems of the TSPLIB standard library is selected and test by BA, GWO, MFO, PSO, DWOA, and VDWOA separately. Each algorithm is performed 50 times on the 12 problems, and uses the minimum value as the optimal solution obtained by the algorithm. In the VDWOA and DWOA algorithm, the constant-coefficient b of the spiral shape of is 1. ε is 0.35. In BA, the maximum and minimum values of pulse frequency are 1 and 0, respectively, the attenuation coefficient of sound loudness is 0.9, the search frequency the enhancement factor of is 0.9, the loudness of the sound is between (0, 1), and the pulse emission rate is between (0, 1). In GWO, the distance adjustment parameter is between (0, 2). In MFO, the spiral shape parameter of is 1. The inertia weight factor of PSO is 0.2, and the acceleration factor is 2. The Euclidian distance is used for computing the distance between each two cities.

Table 1. Calculation and comparison results of six algorithms for 1000 iterations.

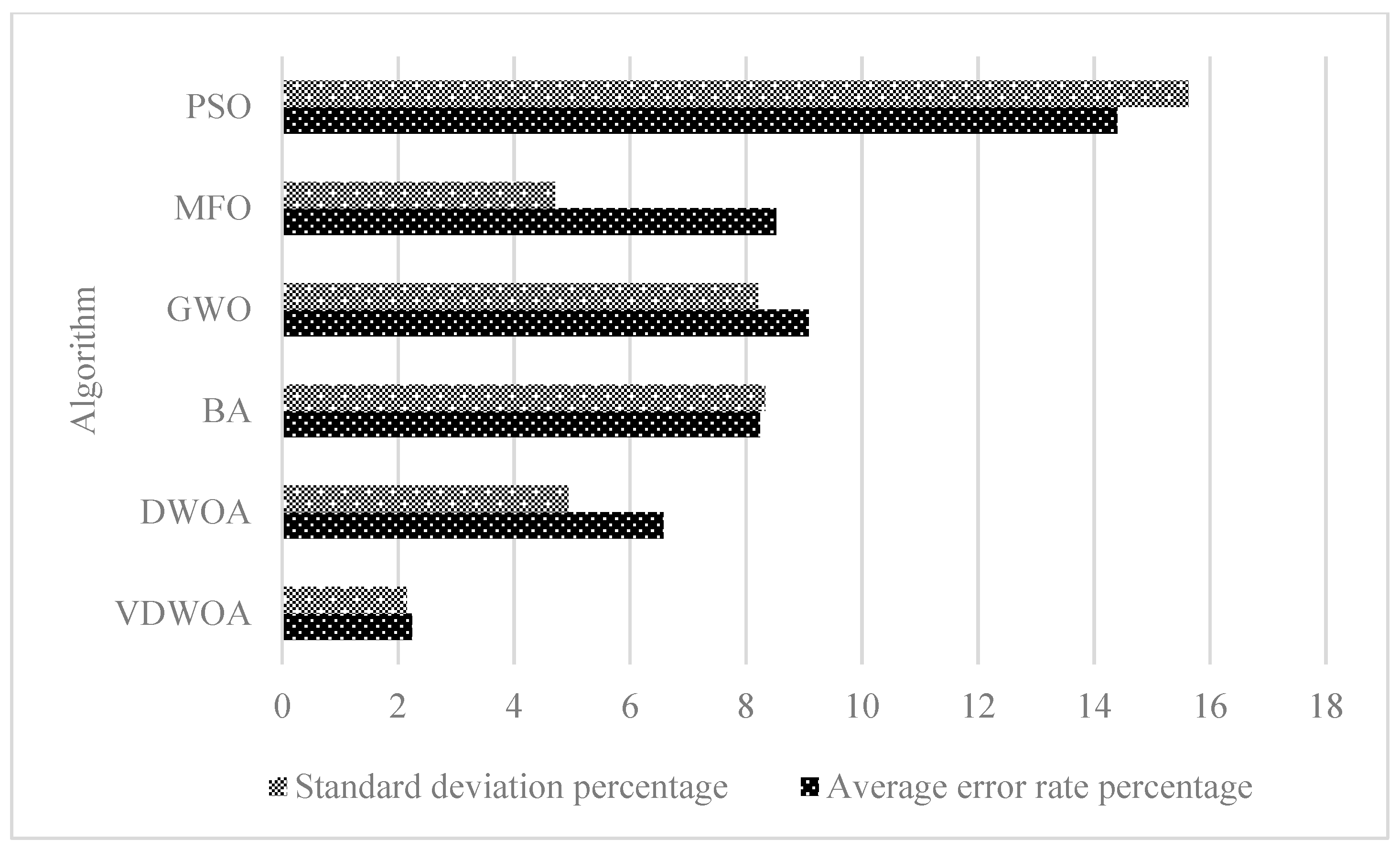
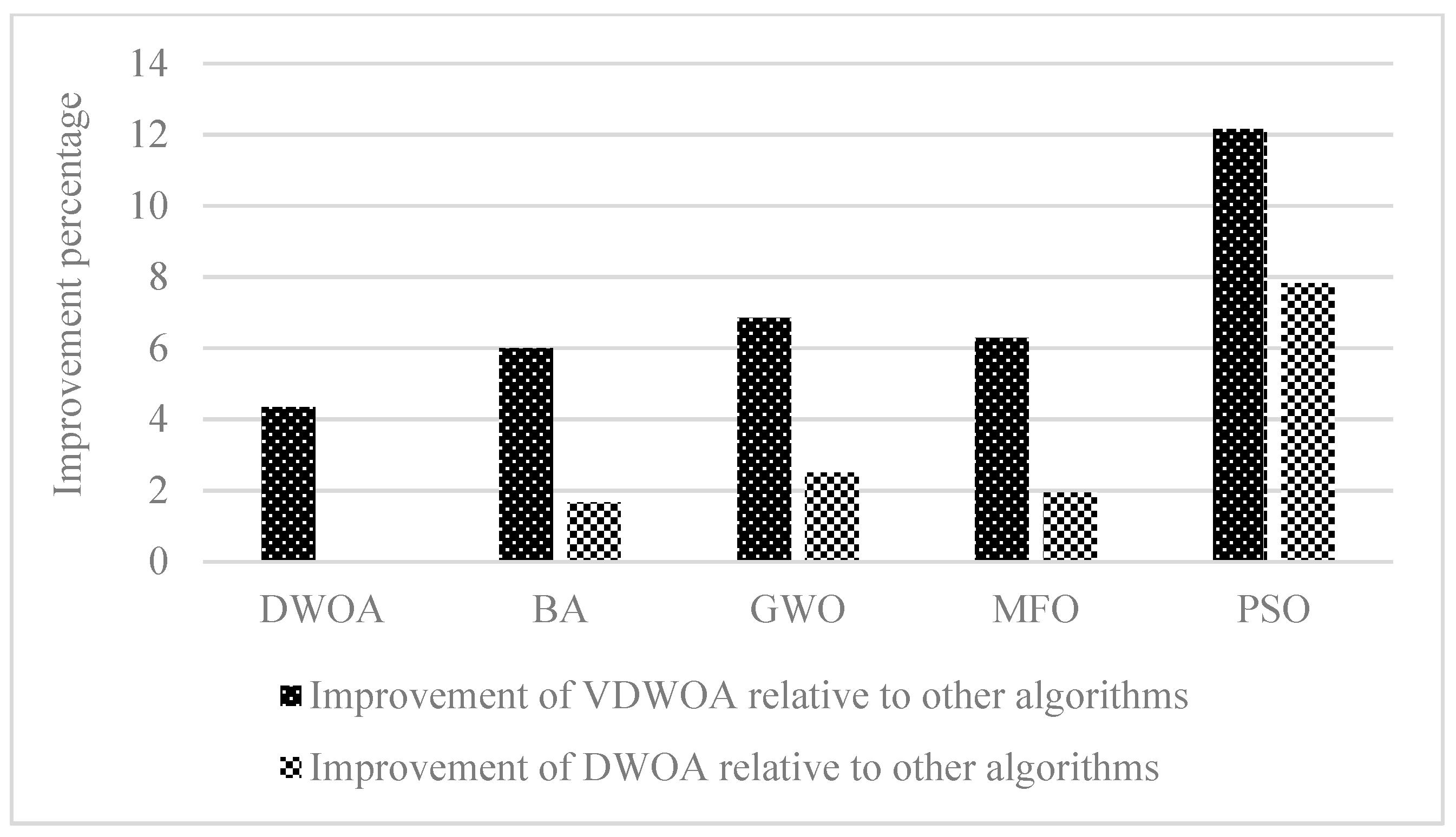
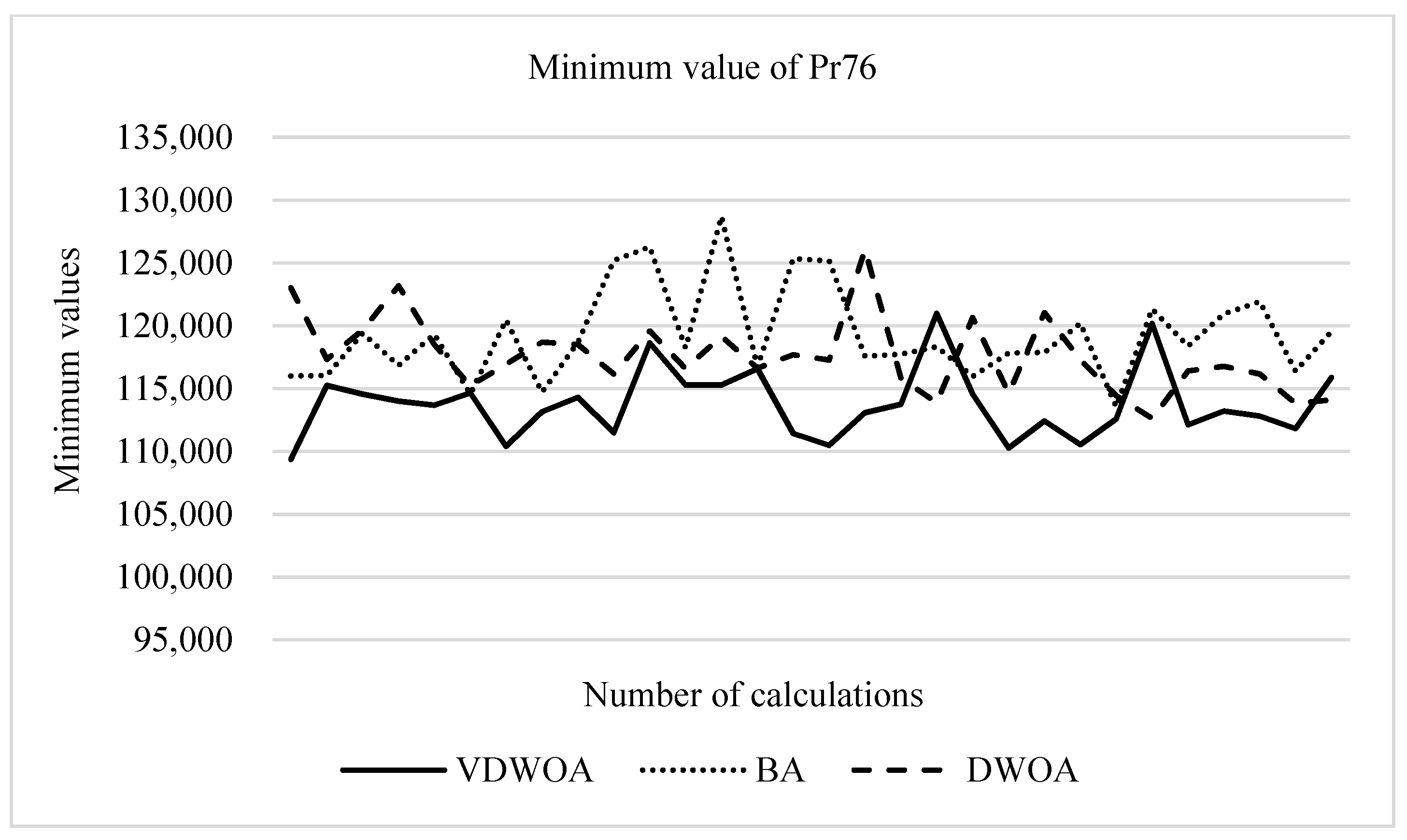
Problem (Known Optimal Solution)	Algorithm	Optimal Solution	Average Time (Unit: Second)	Er (%)
Oliver30(420)	VDWOA	420	4.74	0
	DWOA	420	2.08	0
	BA	420	2.21	0
	GWO	422	1.42	0.48
	MFO	423	2.24	0.71
	PSO	424	2.08	0.95
Eil51(426)	VDWOA	429	10.47	0.7
	DWOA	445	3.73	4.46
	BA	439	4.27	3.05
	GWO	441	3.42	3.52
	MFO	449	4.4	5.4
	PSO	445	3.91	4.46
Berlin52(7542)	VDWOA	7542	10.79	0
	DWOA	7727	3.78	2.45
	BA	7694	4.28	2.02
	GWO	7898	3.6	4.72
	MFO	8184	4.39	8.51
	PSO	7862	3.93	4.24
St70(675)	VDWOA	676	17.69	0.15
	DWOA	712	5.31	5.48
	BA	718	6.38	6.37
	GWO	726	5.59	7.56
	MFO	710	6.57	5.19
	PSO	732	5.72	8.44
Eil76(538)	VDWOA	554	20.5	2.97
	DWOA	579	5.81	7.62
	BA	561	7	4.28
	GWO	565	6.23	5.02
	MFO	577	7.29	7.25
	PSO	595	6.3	10.59
Pr76(108159)	VDWOA	108,353	20.52	0.18
	DWOA	111,511	5.85	3.1
	BA	111,989	6.96	3.54
	GWO	114,261	6.19	5.64
	MFO	114,377	7.18	5.75
	PSO	115,265	6.14	6.57
KroA100(21282)	VDWOA	21,721	35.24	2.06
	DWOA	22,471	8.12	5.59
	BA	23,424	10.24	10.06
	GWO	22,963	8.77	7.9
	MFO	23,456	10.52	10.22
	PSO	23,480	8.72	10.33
Pr107(44303)	VDWOA	45,030	38.09	1.64
	DWOA	45,780	8.72	3.33
	BA	46,419	11.39	4.78
	GWO	46,083	9.62	4.02
	MFO	47,437	11.69	7.07
	PSO	46,919	9.48	5.9
Ch150(6528)	VDWOA	6863	77.37	5.13
	DWOA	7329	13.87	12.27
	BA	7440	19.59	13.97
	GWO	7384	15.26	13.11
	MFO	7329	19.57	12.27
	PSO	7833	15.1	19.99
D198(15780)	VDWOA	16,313	145.24	3.38
	DWOA	16,603	20.56	5.22
	BA	16,849	32.41	6.77
	GWO	17,109	22.48	8.42
	MFO	16,911	30.86	7.17
	PSO	18,130	22.52	14.89
Tsp225(3916)	VDWOA	4136	195.54	5.62
	DWOA	4399	25	12.33
	BA	4427	41.63	13.05
	GWO	4620	27.41	17.98
	MFO	4469	38.3	14.12
	PSO	5049	27.44	28.93
Fl417(11861)	VDWOA	12,462	2485.61	5.07
	DWOA	13,886	276.12	17.07
	BA	15,532	363.01	30.95
	GWO	15,492	286.92	30.61
	MFO	14,087	411.23	18.55
	PSO	18,688	321.63	57.56

shows the optimal solution and average time consuming of these algorithms when the initial population number is equal to the problem scale and the number of iterations is 1000. The error rate (%) is calculated by Equation (16), which is the difference between the optimal solution (denoted as OpS) obtained by the algorithm and the known optimal solution (denoted as KopS) of TSPLIB:

$$Er=(\frac{OpS-KopS}{KopS})\times 100.$$

(16)

From Table 1, it can be seen that for the 12 problems, the average error rate of VDWOA, DWOA, BA, GWO, MFO, and PSO is 2.24%, 6.58%, 8.24%, 9.08%, 8.52%, and 14.40%, respectively. The DWOA has improved 1.66%, 2.5%, 1.94%, and 7.82% compared to BA, GWO, MFO, and PSO, respectively, in terms of solution accuracy. The VDWOA has the best solution, which has improved 4.34%, 6%, 6.84%, 6.28%, and 12.16%, respectively, compared to DWOA, BA, GWO, MFO, and PSO. The standard deviation of VDWOA, DWOA, BA, GWO, MFO, and PSO is 2.15%, 4.94%, 8.33%, 8.21%, 4.71%, and 15.63%, respectively.

For these 12 problems, Figure 1 is a bar chart of the average error rate and the standard deviation percentage of six algorithms. Figure 2 is the bar chart of the average improvement percentage of VDWOA and DWOA relative to other algorithms.

From Figure 1 and Figure 2, and the above analysis results, it can be seen that the optimal values obtained by the VDWOA are better than the other comparison algorithms. The average error rate of the VDWOA is the best, the DWOA algorithm is the second, and the BA algorithm is the third. In terms of average time consumption, the DWOA algorithm is faster. With the increase of the problem scale, the time advantage of this algorithm become more obvious. Time consuming of the VDWOA algorithm is slightly more than the comparison algorithms, but the results of the algorithm have obvious advantages, which shows that when a faster response time is required, the DWOA algorithm should be selected, while the VDWOA algorithm should be selected when required for better accuracy.

For the 12 problems, Figure 3a,b shows the maximum, minimum, and average bar chart of the VDWOA algorithm calculated 50 times in order to verify the stability of the algorithm.

Figure 3 shows that for the 12 problems, the difference between the maximum, minimum, and average values obtained by the VDWOA algorithm is relatively small in addition to the Pr76 problem, which shows that the algorithm has good stability.

For the Pr76 problem, Figure 4 shows the line chart of the minimum value calculated 30 times obtained by the top three algorithms of VDWOA, BA, and DWOA. It can be seen that the stability of the VDWOA and DWOA algorithms is better than that of the BA algorithm for the Pr76 problem.

The above figures and data show that the VDWOA algorithm designed in this paper has a better solution effect than other algorithms, and the solution effect of the DWOA algorithm is second.

To verify the performance of the proposed algorithm further, this paper compared with the above-mentioned algorithm for solving the TSP problem in the literature review. Since the above algorithms do not consider the time cost, this paper selects the VDWOA algorithm for comparison.

Table 2. Optimal solution compared with other literature.

Instance (Known Optimal Solution)	Algorithm	Optimal Solution	Er (%)
Oliver30(420)	VDWOA	420	0
	Min_GWO_WOA	423	0.71
	HSQWOA	-	-
Eil51(426)	VDWOA	429	0.7
	Min_GWO_WOA	429	0.7
	HSQWOA	429	0.7
Berlin52(7542)	VDWOA	7542	0
	Min_GWO_WOA	7661	1.58
	HSQWOA	-	-
St70(675)	VDWOA	676	0.15
	Min_GWO_WOA	679	0.59
	HSQWOA	677	0.3
Eil76(538)	VDWOA	554	2.97
	Min_GWO_WOA	569	5.76
	HSQWOA	-	-
KroA100(21282)	VDWOA	21,721	2.06
	Min_GWO_WOA	21,954	3.16
	HSQWOA	-	-

shows the optimal value of the proposed VDWOA algorithm, the optimal value of WOA and GWO (denoted as Min_WOA_GWO) in literature [23], and the optimal value of HSQWOA in literature [24] (We choose problems involved in the former and that use the same distance formula in the later). The symbol “-” in the table indicates that the example is not calculated in the literature.

From Table 2, it can be seen that for the six problems, the optimal solution obtained by the proposed VDWOA algorithm and the error rate are better than that of the references. Therefore, the proposed VDWOA is superior to other algorithms in terms of solution accuracy.

5. Conclusions

The TSP problem is a classic combinatorial optimization problem, and the basic WOA is not suitable for such discrete problems. Therefore, this paper designed a VDWOA for solving the TSP problem. The adaptive weight, Gaussian disturbance, and variable neighborhood search strategy are introduced to improve the performance of the algorithm. Experimental results show that the designed algorithm can effectively solve the TSP problem. Further research will consider designing WOA algorithms for solving more complex combinational optimization problems such as various vehicle routing problems, so as to further enhance the application scope of this algorithm.