Abstract
Linear programming was used to assess the ability of polarized infrared absorption, Raman scattering, and visible–infrared sum-frequency generation to correctly identify the composition of a mixture of molecules adsorbed onto a surface in four scenarios. The first two scenarios consisted of a distribution of species where the polarity of the orientation distribution is known, both with and without consideration of an arbitrary scaling factor between candidate spectra and the observed spectra of the mixture. The final two scenarios have repeated the tests, but assuming that the polarity of the orientation is unknown, so the symmetry-breaking attributes of the second-order nonlinear technique are required. The results indicate that polarized Raman spectra are more sensitive to orientation and molecular identity than the other techniques. However, further analysis reveals that this sensitivity is not due to the high-order angle dependence of Raman, but is instead attributed to the number of unique projections that can be measured in a polarized Raman experiment.
1. Introduction
The structural characterization of ordered systems has been a cornerstone of chemistry. Understanding the orientation of molecules with respect to each other, and with respect to a macroscopic entity such as a crystal structure, material profile, or surface can inform on the physical and chemical properties of the system. Molecular arrangements have been studied by X-ray and neutron scattering, nuclear magnetic resonance, and optical spectroscopy. Among the optical methods [1], vibrational techniques are of particular interest due to their ability to access sub-molecular information from the characteristic vibrational frequencies associated with specific chemical functional groups, thereby providing local bond-level orientation information, in addition to revealing markers of molecular conformation. The general idea exploits the relationship between transition dipole moment and electric field, as the strength of the interaction depends on the angle between these two vector quantities [2]. Combining these ideas, the use of polarized light in vibrational spectroscopy has long been used to qualitatively and quantitatively assess the identity and orientation of molecules [3].
The theory of polarized infrared (IR) absorption [4,5,6,7,8,9,10,11,12] and polarized Raman scattering [13,14,15,16,17,18,19,20] to elucidate the orientation of molecules in bulk materials, thin films, and on surfaces has been well-established. When dealing with monolayers on surfaces, infrared absorption experiments in either transmission or reflection geometry are challenging due to the low value of absorbance (in the range), but are possible. Spontaneous Raman scattering from such a low number density is more of a challenge but has been addressed, primarily through the use of resonance Raman techniques [21,22,23,24]. Visible-infrared sum-frequency generation (SFG) spectroscopy [25,26,27,28,29,30,31,32], on the other hand, is ideally suited for the study of surfaces since sufficient signal may be detected even for monolayers. The niche application of SFG is the study of surfaces whose constituent molecules are the same as those in the bulk—for example the water vapour–liquid interface [33,34]. In such cases, only molecules at the surface contribute to the measured signal as a result of the inversion symmetry-breaking requirement of SFG [25,35]. In the present discussion, however, we can keep the application general, exploring the ability of these techniques to discriminate between different molecules in different orientations regardless of whether the assembly is two- or three-dimensional. Typical sample and experimental conditions will often limit the applicability of these three techniques but, in an idealized comparison, we can assess their sensitivity based on the nature of the response functions alone. In this work, we consider a mixture of six molecules with varying composition and orientations. This would, for example, describe a surface that is exposed to a solution of molecules. Even if we know the proportion of molecules in the bulk solution state, we cannot know in advance the composition of the surface due to variability in the surface preference. Furthermore, each species may adsorb with a preferred orientation; there are of course bulk analogies as well. As the assessment of molecular specificity and orientation requires the evaluation of thousands of combinations of spectra in a highly multi-dimensional parameter space, we employ linear programming to be guaranteed of the exact solution to the spectral unmixing problem that encodes the structural information we seek.
2. Background
2.1. Molecular and Ensemble Response Functions
When light with a time-varying j-polarized electric field interacts with a molecule, the element of the linear polarizability determines the magnitude and phase of the resulting time-varying induced dipole moment, whose Cartesian component i is given by . In general, higher order polarizabilities (the so-called hyperpolarizabilities) can contribute through the expansion [35,36]
where we have used Einstein notation for implicit summation over repeated indices. It is simplest to describe the above interactions when the induced dipole moment, electric fields, and polarizability tensors are all in the same coordinate system. We will use the indices as placeholders for any of the molecule-fixed Cartesian coordinates as shown in Figure 1.
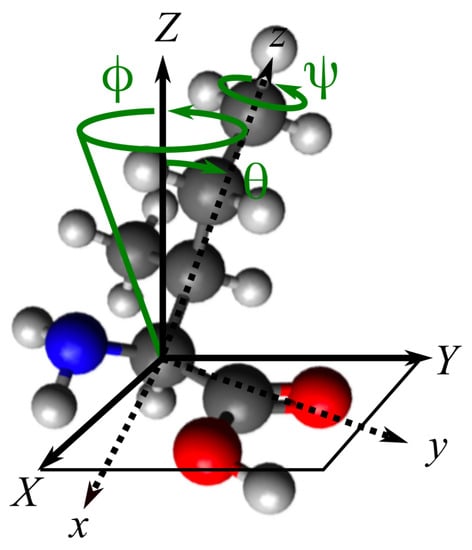
Figure 1.
Illustration of the molecule-fixed and laboratory frame coordinates, related through three Euler angles. Here is the tilt angle that projects the molecular long axis z onto the surface normal Z, is the azimuthal angle that describes rotation about Z and is the twist angle that describes rotation about z. The surface is represented by the -plane.
However, this is not a practical description in reality, since the input and measured fields are in the laboratory frame. Now using as placeholders for any of the lab frame coordinates, we can write an expression for the polarization (dipole moment per unit volume)
These expressions are related by the molecular number density N and the average over participating molecular orientations. For example, in a molecular dynamics simulation where the orientation of each molecule can be tracked independently, . In an experiment, we do not have access to such information, and instead work with the ensemble average
The point to note is that, before the ensemble average can be considered in Equation (3), it is required to project from the molecular frame in which it is defined into the laboratory frame to arrive at , thereby encoding the molecular orientation. The manner in which these projections are performed is related to the light–matter interaction accompanying each of the processes. As a result, different spectroscopic techniques have different symmetry properties, sensitivity to molecular orientation, and fingerprinting abilities.
Figure 2 provides energy level and double-sided Feynman diagrams illustrating the interactions associated with the three spectroscopic techniques that we consider in this comparison. The first case illustrates that IR absorption spectroscopy is a probe of the linear polarizability . Absorption of an IR photon causes a transition from the ground vibrational state to an excited vibrational state . The emitted photon has the same frequency, polarization, and wavevector as the exciting photon, and hence this self-heterodyne experiment provides direct access to Ⅱm. In visible–infrared sum-frequency generation, a broadband or tuneable IR beam is spatially and temporally overlapped with a typically fixed frequency visible beam. In the absence of inversion symmetry, this generates light at the sum of the two input frequencies, proportional to the second-order susceptibility , through interaction with a non-resonant electronic virtual state . Intensity-only detection schemes measure a signal proportional to , while phase-sensitive detection provides access to Ⅱm [37,38,39,40,41,42]. Of the large family of Raman scattering probes, we consider the case of spontaneous Raman scattering where the Stokes-shifted wavelengths are detected. Although the intensity of the detected light (frequency in Figure 2) is linearly proportional to the intensity of the pump beam (frequency ) [43], the observables commonly associated with Raman spectroscopy reveal that this is in fact a probe of Ⅱm, and is associated with four light-matter interactions [44,45].
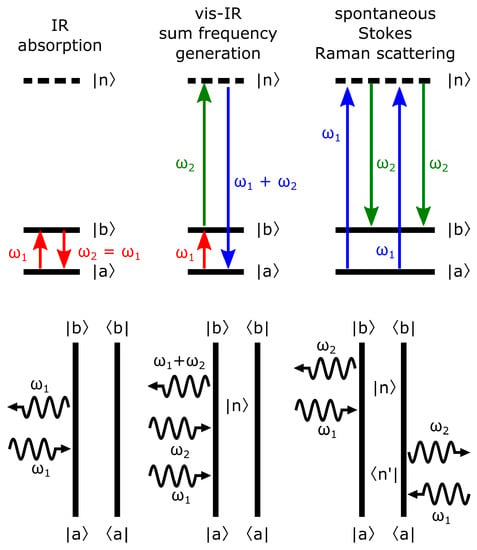
Figure 2.
Energy level and double-sided Feynman diagrams of the IR absorption, visible–infrared sum-frequency generation, and spontaneous Stokes Raman scattering processes.
2.2. Accessing Elements of the Response Functions Using Polarized Light
IR absorption. In an infrared absorption experiment, one measures diagonal elements of the rank-2 tensor Ⅱm that originates from a sum and orientational average over Ⅱm. As shown in Figure 3, these quantities have nine elements, but can almost always be diagonalized into three principle components. This is the origin of the typically single-subscripted refractive index and absorption coefficient. If we consider to be the direction cosine matrix (DCM) incorporating the Euler angles , , and defined in Figure 1, we can then carry out the projection [26,46]
If we were to use the contracted version, such as the 3-element transition dipole moment vector, we would use
where is the dipole moment operator. Note that, even though we are now using a single application of the the direction cosine matrix to transform a vector (tensor of rank 1) from the molecule-fixed to the laboratory-fixed coordinate system, the square results in the same angle-dependence. For the present demonstration, we assume an isotropic distribution of azimuthal angles and twist angles (see Figure 1) so the the only orientation is that between the molecular reference axis and the laboratory z-axis. In the case of molecules adsorbed to surfaces, this is the often-encountered situation in which there is no preferred orientation in the plane of the surface, and is the polar angle between the molecular long axis and the surface normal . This may be realized by integrating over and to obtain
The main point is that, regardless of whether we use the rank 2 tensor , or the vector , the -dependence of the resulting function is the same. Furthermore, when this integration is carried out over all Cartesian coordinates, we find that there are only two unique elements; these are (due to azimuthal symmetry of the surface) and . A polarized IR absorption experiment is therefore carried out with a single polarizer placed before the sample. Owing to the symmetry of specific normal modes of vibration, the molecular frame may have a simple form, for example for a methyl symmetric stretch. In general, however, we can consider , as these molecular values will be determined from electronic structure calculations. Regardless of any inherent symmetries in , we can always write the result as
which, in turn, enables the polarized IR absorption spectra to be expressed in terms of an order parameter derived from the second-order Legendre polynomial [47].
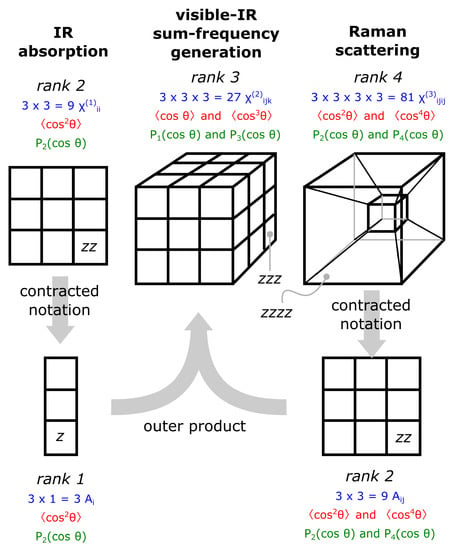
Figure 3.
The tensoral nature of the IR absorption, visible–infrared sum-frequency generation, and Raman scattering processes illustrated. In the top row, the material response is arranged according to the rank of the process. In the bottom row, the most-often used contracted notation for an absorption process and Raman scattering are illustrated.
Sum frequency generation. In a vibrational SFG experiment, we can independently control the polarization of the incoming visible and infrared beams, and select a component of the emitted SFG field polarization. This enables measurement of all non-zero components of the 27-element rank-3 tensor . From the molecular response, we can again project into the laboratory frame to obtain
this time employing three direction cosine matrix elements to compute each element of as this is a rank 3 tensor. We are interested in the result
We note that, unlike the case of IR absorption, this function has odd symmetry with respect to . We can therefore express the solution in terms of the order parameters and . Among the methods we discuss, SFG is the only technique that is capable of distinguishing molecules oriented in the quadrant from those in the quadrant . That is, Ⅱm. In the most commonly-encountered case of electronic non-resonance, this integration results in only seven non-zero elements, of which three are unique. These are , , and .
Raman scattering. The Raman scattering process is the most complex and interesting among the techniques we compare, owing to the four-dimension response function. In a spontaneous Raman experiment, although we probe components of the 81-element rank-3 tensor , only the elements are accessible. This readily lends itself to the contracted notation as shown in Figure 3, where the transition polarizability (a rank 2 tensor with dimensions are used. In analogy to our description of the IR absorption experiment, we note that the transformation from molecular to laboratory coordinates can then be carried out on directly [48]:
If we were to use the contracted version corresponding to the the transition polarizability matrix, we would use
Once again, we emphasize that, regardless of whether the rank 4 or rank 2 representation of the Raman response is used, the same angle dependence results, noting that the square of the transition polarizability must be used when determining the orientational average. Integrating over the angles that we consider to be uniformly distributed provides the tilt angle dependence
The resulting functional form shares the same symmetry characteristics as IR absorption (insensitive to the polarity of the tilt angle distribution), but now includes a higher-order contribution as we can probe the average , and therefore also have access to the order parameter . Further symmetry and electronic non-resonance reduce the probed elements to , , , and . In practice, all of the above-mentioned tensor elements are obtained using one or more polarization schemes, but those experimental details are not relevant to the current discussion. Instead, we focus on the maximum information content available from each experiment as a consequence of the symmetry of the relevant susceptibility tensor.
3. Methods
3.1. Generation of the Candidate Spectra
Methods for the calculation of infrared transition dipole moments , Raman transition polarizabilities , and their coupling to estimate vibrational hyperpolarizabilties (direct product as illustrated in Figure 3) have been previously described [26,49]. In brief, calculations were carried out using GAMESS [50] at the B3LYP/6-31G(d,p) level, using a finite difference approach to determine the transition matrix elements from the dipole moment frequency dependent polarizability variation with respect to the normal mode coordinates. It has been established this basis set reproduces vibrational spectra of amino acids [51]. A polarizable continuum model was used to simulate adsorbed states in an aqueous solution. A frequency scaling factor of 0.96 has been applied [52]. We consider the six amino acids methionine (Met), leucine (Leu), isoleucine (Ile), alanine (Ala), threonine (Thr) and valine (Val). We have previously demonstrated the manner in which the spectral lineshape is calculated from these quantum mechanical properties [46]. In the case of infrared spectroscopy, the absorbance is proportional to
where and are the frequency and homogeneous linewidth of the qth normal mode. For a mixture of molecules each oriented at a different angle according to the weighting factor , the overall IR spectrum of the mixture, hereafter referred to as the target spectrum, is given by
imposing the normalization condition
The lineshape for the polarized heterodyne-detected SFG spectrum of a single molecule at a single tilt angle is given by
and the collection of molecules has the target spectrum
The Raman spectra of individual candidate molecules are obtained from
where is the Stokes shift with respect to the incident light frequency. We assume that the mixture of molecules then has an overall measured Raman spectrum given by
Note that, with the exception of the hyperpolarizabilities and susceptibilities , we will not explicitly specify the nth order quantities with superscripts and instead rely on the Cartesian coordinates in subscripts such as to indicate that this is an element of rank 4 tensor representing a third-order response function.
3.2. Linear Programming
Linear programming (LP) belongs to the class of convex optimization techniques that is known to provide exact solutions to problems that are challenging to solve using other methods, either due to the inherent complexity of the function to be minimized, or due to the number of local minima in the multidimensional parameter/error space [53,54,55,56]. In addition, LP can provide solutions in time, compared to traditional techniques [57,58,59] that can require time. An example of a small LP problem that is convenient to visualize is minimization of the two-dimensional objective function
subject to the constraints
The region of the solution space is illustrated as the shaded region in Figure 4. The fundamental theorem of LP states that the minimum exists at the boundary of the convex polyhedron that defines the feasible region of the solution space. It can be shown that the solution is further restricted to the vertices of this polyhedron. In this simple two-dimensional example, there are only four vertices at , , and . It is straightforward to evaluate the value of the function at each of these locations to select the vertex with the minimum value. In practice, for more difficult problems, the task of vertex finding and evaluation may be performed by algorithms such as simplex [60], and there are existing packages for this task. We used the GNU linear programming toolkit [61] to identify the LP solutions.
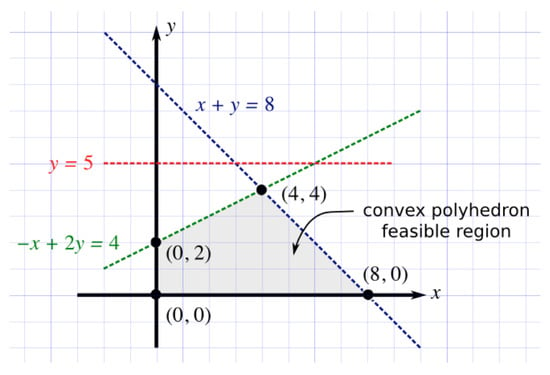
Figure 4.
A two-dimensional example of a minimization problem subject to constraints whose linear programming solution can be visualized graphically.
In order to apply LP to spectroscopy problems, we need to have an appropriate formulation of the objective function to be minimized. For each polarization of the IR spectrum, we can a component of the objective function as
where are the unknown fractions of the candidate, the decision variables returned by the LP solver; p is the number of points selected along the wavenumber axis, both for candidates and target spectra; c is the number of candidates. We can then include both projections that come from the two unique polarization schemes identified in our problem by combining them in
Further details on the formulation of the objective function and its solution are given in Ref. [62]. In brief, the absolute residual between the target spectrum and the one composed by the decision variables is calculated for each data point. The objective function minimizes the sum of the absolute residuals over all the data points. Note that the LP model exactly describes our problem to be solved, yielding the target composition if we can provide precise enough data. Recall that if the solution space of an LP instance is feasible and bounded, then there is a unique optimum solution.
Analogous versions of the objective function in Equation (22) exist for the SFG data as , from which
is calculated, and for the Raman spectra from which
may be determined.
3.3. Construction of Test Cases
IR (2 polarizations), SFG (3 polarizations), and Raman (4 polarizations) spectra for each molecule were calculated as a function of tilt angle from to with a step size of and stored, so subsequent calculations and spectra of mixtures could be computed quickly. A random number generator was then used to determine the composition of the mixture, and the result is normalized so the fraction of all candidates together does not exceed 100%. An independently-seeded random number generator determined the tilt angle of each amino acid in the mixture. An example of the semi-discrete parameter space is shown in Figure 5. Linear programming is then used to decipher the composition of the mixture, using all available polarization data, but possibly a subset of the experimental techniques in the following cases: IR data only, SFG data only, Raman data only, IR and SFG data combined, IR and SFG, SFG and Raman, and the combination of all data employing IR and SFG and Raman spectra. Each test case was then run 100 times in order to remove potential bias that may result from insufficient statistics.
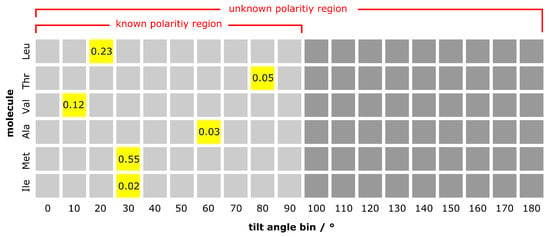
Figure 5.
An illustration of the semi-discrete parameter space that comprises a single mixture. In the case of molecules with known polarity, we consider the range to in discrete steps of . In the case of unknown polarity, the tilt angles in the range to may be selected for each molecule. A fraction of each molecule (yellow squares) is then chosen as a weighting factor to generate the mixture. The mixture in the example shown contains 55% methionine tilted at as its largest component, and 2% isoleucine tilted at as its smallest component.
4. Results and Discussion
The results of all test cases are summarized in Table 1. Instead of describing individual outcomes (that would appear as indicated in Figure 5) corresponding to a randomly selected distribution of molecules, we report on whether LP was able to determine the correct composition of the mixture (molecular identity of the species and tilt angle of each component) from data obtained in all trials. The advantage of LP is that we can be assured of finding the global minimum solution. In cases where we were not able to recover the target composition, the local minima and global minimum have identical scores S.

Table 1.
A summary of the evaluated test cases indicating the ability of the spectral data to reveal the target composition in terms of the identity and orientation of the constituent molecules. An ✗ indicates that the data set was insufficient to determine the target composition. A ✓ indicates that sufficient data was available for spectral unmixing, while a parenthetical (✓) indicates success, but a data set that is unnecessary since a subset of the data has been shown to be sufficient.
4.1. Known Scaling Factors
The first set of cases we considered corresponds to the scenario in which the absolute intensity scaling (absorbance in the case of IR, and intensity with respect to a reference sample in the case of SFG and Raman, or expressed in terms of absolute units of and ) is known. Although this is certainly possible, it is not common practice to go through this effort, especially for Raman data. Nevertheless, it is an important set of data for us to discuss first, as it represents the simplest case where all techniques can readily be compared on equal footing. We further divide this data set into cases where the polarity of the orientation of each molecule is known in advance (whether the tilt angle lies in the range or ) or is unknown () and therefore needs to be resolved through the spectral interpretation. For simplicity, we can consider the known polarity as corresponding to tilt angles restricted to the quadrant , since it is always possible to redefine the orientation of the molecular long axis to suit this definition. From an experimental perspective, this is equivalent to using chemical intuition to identify which end of the molecule is closest to the surface. In this case, column a of Table 1 indicates that IR data taken alone can return the correct composition of the mixture, but either SFG or Raman are able to do this. Immediately, two conclusions come to mind: SFG and Raman contain higher order response functions, sensitive to and , and more unique polarization schemes compared to the sensitivity of IR spectra and the two unique polarizations it offers. We will further comment on the origins of the molecular specificity and orientation sensitivity below. We note that determinations using combinations of the methods are moot within this set, as the results are predictable from the success of individual methods. This is indicated by the parenthetical (✓) in Table 1 representing successful spectral unmixing from an unnecessary combination of data.
We next consider the interesting case where each molecule in the mixture can lie in any of the two quadrants covered by the tilt angle cones. These results, summarized in column b of Table 1. The fact that IR and Raman data, either alone or in combination, cannot resolve the tilt angle is expected, since the even powers of cosine are symmetric about (the plane of the surface). We therefore anticipate requiring SFG data to answer any question that requires such symmetry breaking. It is interesting to see, however, that SFG spectra alone cannot consistently return the correct target composition, and so we label its data as insufficient. When SFG is combined with either IR or Raman data, the spectral unmixing then succeeds. We will return to the discussion of this result after considering the remaining cases.
4.2. Arbitrary Scaling Factors
In the data described above, we have used electronic structure calculations to determine the spectra of various molecules at particular tilt angles, created a linear combination of these results, and then evaluated the ability of different spectroscopic data to aid in the unmixing. We therefore had significant help from the fact that the candidate spectra and the target spectrum were on the same scale. In a real experiment, there are two factors that prevent such information from being available in most cases. One is that the response in SFG and particularly Raman is typically not calibrated through the use of a reference material. Furthermore, since we are not dealing with isotropic mixtures, it would be difficult to obtain oriented samples in order to know the response from each species. Hence the use of electronic structure calculations is valuable. This, however, poses the second challenge: the spectra predicted by any calculation will necessarily be on a different scale from the measured target spectrum. Furthermore, the arbitrary scaling factor differs in the case of IR absorption, SFG, and Raman scattering. Fortunately, linear programming enables us to readily consider such scaling factors by introducing slack variables. A detailed example on the use of slack variables with application to unmixing Raman data is provided in Ref. [62]. Here we introduce separate slack variables for IR, SFG, and Raman data thereby acknowledging that the scaling factors are constant within an experiment when changing only the beam/detector polarization (which still requires calibration, but is easy to achieve in practice), but is not related across the techniques. This is obviously a more challenging problem to solve, with the results indicated in column c of Table 1. In the case of molecular orientations restricted to a single known quadrant of the tilt angle, now only Raman data (and no longer SFG alone) can accurately reveal the molecular identities and orientations. Naturally, any combination with Raman also works, but provides no additional benefit. When we increase the complexity of the problem by lifting the polarity restriction, column d shows that the needed SFG data must now be combined with Raman data (as an IR complement to SFG is no longer sufficient).
4.3. Exploring the Origins of Orientation Sensitivity
As we have noted, many of the results presented above have displayed the trend Raman > SFG > IR in terms of the abilities of the techniques to resolve the components of the mixture including proper identification of the tilt angles of each component. Based on this information alone, one is curious about the origins of displayed sensitivities. On the one hand, this sequence follows from being more sensitive than which is in turn more sensitive to small differences in the tilt angle than . On the other hand, the techniques based on higher-order response functions necessarily have more unique elements of the response tensor that can be probed with different polarizations. The two features are intrinsically linked through the transformations between molecular and laboratory coordinates as illustrated. Nevertheless, in an attempt to further comment on the relative utility of multiple projections compared to higher angle sensitivity of individual spectroscopies, we have performed a separate comparison using only z-polarized version of each technique. In other words, the response from IR absorption with a z-polarized input light field; the element of the SFG response (that typically needs to be separated from a combination of terms when all beams are p-polarized), and that is measured in a Raman experiment with a z-polarized input field and the selection of the z-polarized scattered light for detection. For this evaluation, we consider all pairs of neighbouring angles that are separated by , for example , , up to . The specific angle is avoided since it results in zero intensity for SFG due to the isotropy of the twist and azimuthal distributions. We then compute the pairwise Pearson’s correlation coefficient
where refers to in the case of IR and SFG spectra, and to the Stokes shift in the case of Raman spectra. When results from all pairs of angles were averaged over all six molecules, we obtained the result for the set of z-polarized IR spectra, for the set of z-polarized SFG spectra, and for the z-polarized Raman spectra. These coefficients are invariant to scale, so we can compare across techniques without normalizing the spectra. We anticipate in all cases, as the spectral features for the same molecule tilted by an additional are small. Nevertheless, the result is counter-intuitive as the largest difference (smallest ) is not seen for the Raman spectra. There is in fact no trend in this data that is consistent with the results from LP that we have reported.
Further insight into this result may be obtained by plotting the spectrum obtained by averaging over all tilt angles (blue traces in Figure 6) along with the standard deviation about the mean (grey trace in Figure 6. Vector normalized spectra are used to allow for comparison between the three techniques. Visual inspection alone suggests that for all molecules the SFG spectra display the highest spectral variation across all tilt angles. This is numerically highlighted with the spectral deviation averaged over all frequencies , where SFG is the highest in all cases. Otherwise, the averaged standard deviation does not reveal any consistent trend between IR and Raman. For example, for the case of isoleucine (Ile) we obtain for the set of z-polarized IR spectra, for the set of z-polarized SFG spectra, and for the z-polarized Raman spectra. In this case we may conclude that spectral variation follows the trend of SFG > Raman > IR. For methionine (Met), this changes to SFG > IR > Raman, indicating that there is no general trend. Regardless, the point is that the largest variation is not observed in the Raman spectra, supporting the conclusion made using the Pearson’s correlation coefficient.
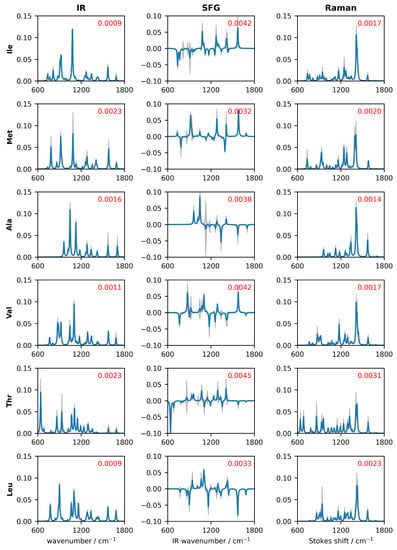
Figure 6.
Average spectra (blue) computed from all tilt angles in the range – and the standard deviation (grey) about the mean. The extent of the vertical axis is the same in all plots, as the spectra are vector normalized for this comparison only. The standard deviation averaged over all frequencies is indicated in red in the inset of each panel.
We now return to the earlier result revealed by LP that, in the case where molecules can lie in any of the two tilt angle quadrants, SFG is needed but SFG alone is not sufficient to return the complete mixture composition for all 100 randomly chosen samples. In the case where no additional scaling factor was introduced, the SFG data needed to be combined with either IR or Raman data to ensure success in all tests. It was intriguing that IR could complement the SFG data since it is, in theory, less sensitive to changes in tilt angle. This was an early indication that the additional projections in form of unique polarized spectra are potentially more valuable than higher-order response functions, a point that is now confirmed through the examination of these spectral differences.
A final point concerns the utility of higher-order techniques for molecular orientation determination. In the cases we have considered in this work, all molecules are assumed to be aligned at a fixed angle , with no spread in angles. In other words, we have considered an orientation distribution described by . A more realistic system has a spread of tilt angles, and the goal of any complete orientation analysis is to reconstruct the orientation distribution from experimental data. In the next simplest case, where it is assumed that the distribution is Gaussian, experimental data must then provide the value of the mean tilt angle and the width of the tilt distribution . Data from IR absorption alone cannot provide even these two parameters, regardless of whether the polarity of the orientation is known. In such cases, one exploits the true power of higher-order spectroscopies [63,64,65]. Nevertheless, many experimental systems are either too complex for detailed analysis, or have too many undermined parameters. In such cases, it is common to assume a narrow distribution of tilt angles. This work has demonstrated how information obtained from different experiments can aid in these pursuits.
5. Conclusions
This work has addressed the challenging problem of a mixture of molecules in solution whose component molecules may preferentially adsorb to a surface and adopt a preferential orientation in their adsorbed state. We have theoretically investigated the ability of three spectroscopic techniques to unmix the spectral signatures in order to determine the composition and structure of the system. These included IR absorption spectroscopy, based on the rank 2 response function derived from the linear susceptibility; visible-infrared sum-frequency spectroscopy that is based on the rank 3 response of the second-order susceptibility; spontaneous Raman scattering that, although linear in its dependence on the incident light intensity, encodes information characteristic of a rank 4 third-order response function. Linear programming is ideally suited to this investigation as it is a convex optimization technique and hence can return the global minimum. The results indicate that polarized Raman scattering is always the preferred technique that is capable of returning the correct distribution of species and orientations, provided that there is no ambiguity in the polarity of the orientation. In cases where polarity resolution is required, one must incorporate a technique with an even-order response function (such as sum-frequency generation), but SFG alone cannot accurately describe complex mixtures without the aid of IR and, in the most general case, Raman data. Our analysis of these results indicates that it is the additional projections afforded by the unique elements of the response tensors that are responsible for the sensitivity of Raman spectroscopy.
Author Contributions
Conceptualization, U.S. and D.K.H.; methodology, F.C., K.-K.H. and L.G.; software, F.C. and L.G.; writing, L.G., U.S., and D.K.H.; funding acquisition, U.S. and D.K.H. All authors have read and agreed to the published version of the manuscript.
Funding
We thank the Natural Sciences and Engineering Research Council of Canada (NSERC) for support of this science with Discovery Grants to D.K.H. and U.S. F.C. is grateful to the University of Victoria for a graduate fellowship. LG is partially supported by an NSERC Canada Graduate Scholarship, and a Chemistry Graduate Award for Research Excellence.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| DCM | direction cosine matrix |
| IR | infrared |
| LP | linear programming |
| SFG | sum-frequency generation |
References
- Ward, I.M. Determination of Molecular Orientation by Spectroscopic Techniques. Adv. Poly. Sci. 1985, 66, 81–115. [Google Scholar]
- McHale, J.L. Molecular Spectroscopy; Pearson Education: New York, NY, USA, 2008. [Google Scholar]
- Kliger, D.S.; Lewis, J.W.; Randal, C.E. Polarized Light in Optics and Spectroscopy; Academic Press, Inc.: San Diego, CA, USA, 1990. [Google Scholar]
- Pelletier, I.; Laurin, I.; Buffeteau, T.; Pézolet, M. Determination of Molecular Orientation in Biaxially Oriented Ultrathin Films. J. Phys. Chem. B 2004, 108, 7162–7169. [Google Scholar] [CrossRef]
- Umemura, J.; Kamata, T.; Kawai, T.; Takenaka, T. Quantitative Evaluation of Molecular Orientation in Thin Langmuir–Blodgett Films by FT-IR Transmission and Reflection-Absorption Spectroscopy. J. Phys. Chem. 1990, 94, 62–67. [Google Scholar] [CrossRef]
- Brunner, H.; Mayer, U.; Hoffmann, M. External Reflection Infrared Spectroscopy of Aniostropic Adsorbate Layers on Dielectric Substrates. Appl. Spectrosc. 1997, 51, 209–217. [Google Scholar] [CrossRef]
- Chollet, P.A.; Messier, J.; Rosilio, C. Infrared Determination of the Orientation of Molecules in Stearamide Monolayers. J. Chem. Phys. 1976, 64, 1042–1050. [Google Scholar] [CrossRef]
- Debe, M.K. Extracting Physical Structure Information from Thin Film Organic Films with Reflection Absorption Infrared Spectroscopy. J. Appl. Phys. 1984, 55, 3354–3366. [Google Scholar] [CrossRef]
- Dluhy, R.A. Quantitative External Reflection Infrared Spectroscopic Analysis of Insoluble Monolayers Spread at the Air–Water Interface. J. Phys. Chem. 1986, 90, 1373–1379. [Google Scholar] [CrossRef]
- Greenler, R.G. Infrared study of adsorbed molecules on metal surfaces by reflection techniques. J. Chem. Phys. 1966, 44, 310–315. [Google Scholar] [CrossRef]
- Hasegawa, T.; Takeda, S.; Kawaguchi, A.; Umemura, J. Quantitative Analysis of Uniaxial Molecular Orientation in Langmuir-Blodgett Films by Infrared Reflection Spectroscopy. Langmuir 1995, 11, 1236–1243. [Google Scholar] [CrossRef]
- Mendelson, R.; Brauner, J.W.; Gericke, A. External Infrared Absorption Spectrometry of Monolayer Films at the Air-Water Interface. Annu. Rev. Phys. Chem. 1995, 46, 305–333. [Google Scholar] [CrossRef]
- Sourisseau, C. Polarization Measurements in Macro- and Micro-Raman Spectoscopies: Molecular Orientations in Thin Films and Azo-Dye Polymer Systems. Chem. Rev. 2004, 104, 3851–3892. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, M.; Young, R.J. Polarised Raman Spectroscopy for the Study of Molecular Orientation Distributions in Polymers. J. Mater. Sci. 2006, 41, 963–991. [Google Scholar] [CrossRef]
- Bower, D.I. Investigation of Molecular Orientation Distributions by Polarized Raman Scattering and Polarized Fluorescence. J. Poly. Sci. 1972, 10, 2135–2153. [Google Scholar] [CrossRef]
- Lagugné Labarthet, F. Polarized Measurements in Raman Microscopy. Annu. Rep. Prog. Chem. 2007, 103, 326–350. [Google Scholar] [CrossRef]
- Richard-Lacroix, M.; Pellerin, C. Novel Method for Quantifying Molecular Orientation by Polarized Raman Spectroscopy: A Comparative Simulations Study. Appl. Spectrosc. 2013, 67, 409–419. [Google Scholar] [CrossRef] [PubMed]
- Richard-Lacroix, M.; Pellerin, C. Accurate New Method for Molecular Orientation Quantification Using Polarized Raman Spectroscopy. Macromolecules 2013, 46, 5561–5569. [Google Scholar] [CrossRef]
- Tsuboi, M.; Benevides, J.M.; Tomas, G.J., Jr. Raman Tensors and their Application in Structural Studies of Biological Systems. Proc. Jpn. Acad. Ser. B 2009, 85, 83–97. [Google Scholar] [CrossRef]
- Yang, S.; Michielsen, S. Orientation Distribution Functions Obtained via Polarized Raman Spectroscopy of Poly(ethylene terephthalate) Fibers. Macromolecules 2003, 36, 6484–6492. [Google Scholar] [CrossRef]
- Takenaka, T.; Fukuzaki, H. Resonance Raman Spectra of Insoluble Monolayers Spread on a Water Surface. J. Raman Spectrosc. 1979, 8, 151–154. [Google Scholar] [CrossRef]
- Takenaka, T.; Nakanaga, T. Resonance Raman Spectra of Monolayers Adsorbed at the Interface between Carbon Tetrachloride and an Aqueous Solution of a Surfactant and a Dye. J. Phys. Chem. 1976, 80, 475–480. [Google Scholar] [CrossRef]
- Takenaka, T. Effect of Electrolyte on the Molecular Orientation in Monolayers Adsorbed at the Liquid–Liquid Interface: Studies by Resonance Raman Spectra. Chem. Phys. Lett. 1978, 55, 515–518. [Google Scholar] [CrossRef]
- Nakanaga, T.; Takenaka, T. Resonance Raman Spectra of Monolayers of a Surface–Active Dye Adsorbed at the Oil–Water Interface. J. Phys. Chem. 1977, 81, 645–649. [Google Scholar] [CrossRef]
- Morita, A. Theory of Sum Frequency Generation Spectroscopy; Springer: Singapore, 2018. [Google Scholar]
- Hall, S.A.; Jena, K.C.; Covert, P.A.; Roy, S.; Trudeau, T.G.; Hore, D.K. Molecular-Level Surface Structure from Nonlinear Vibrational Spectroscopy Combined with Simulations. J. Phys. Chem. B 2014, 118, 5617–5636. [Google Scholar] [CrossRef] [PubMed]
- Richmond, G.L. Molecular Bonding and Interactions at Aqueous Surfaces as Probed by Vibrational Sum Frequency Spectroscopy. Chem. Rev. 2002, 102, 2693–2724. [Google Scholar] [CrossRef] [PubMed]
- Bain, C.D. Sum-Frequency Vibrational Spectroscopy of the Solid/Liquid Interface. J. Chem. Soc. Faraday Trans. 1995, 91, 1281–1296. [Google Scholar] [CrossRef]
- Lambert, A.G.; Davies, P.B.; Neivandt, D.J. Implementing the Theory of Sum Frequency Generation Vibrational Spectroscopy: A Tutorial Review. Appl. Spectrosc. Rev. 2005, 40, 103–145. [Google Scholar] [CrossRef]
- Vidal, F.; Tadjeddine, A. Sum-Frequency Generation Spectroscopy of Interfaces. Rep. Prog. Phys. 2005, 68, 1095–1127. [Google Scholar] [CrossRef]
- Buck, M.; Himmelhaus, M. Vibrational Spectroscopy of Interfaces by Infrared-Visible Sum Frequency Generation. J. Vac. Sci. Technol. A 2001, 19, 2717–2736. [Google Scholar] [CrossRef]
- Shen, Y.R. Basic Theory of Surface Sum-Frequency Generation. J. Phys. Chem. C 2012, 116, 15505–15509. [Google Scholar] [CrossRef]
- Pezzotti, S.; Serva, A.; Gaigeot, M.P. 2D-HB Network at the Air–Water Interface: A Structural and Dynamical Characterization by Means of ab initio and Classical Molecular Dynamics Simulations. J. Chem. Phys. 2018, 148, 174701. [Google Scholar] [CrossRef]
- Ojha, D.; Kühne, T.D. “On-The-Fly” Calculation of the Vibrational Sum-Frequency Generation Spectrum at the Air-Water Interface. Molecules 2020, 25, 3939. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.R. Surfaces Probed by Nonlinear Optics. Surf. Sci. 1994, 299–300, 551–562. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 2nd ed.; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Superfine, R.; Huang, J.Y.; Shen, Y.R. Phase Measurement For Surface Infrared-Visible Sum-Frequency Generation. Opt. Lett. 1990, 15, 1276–1278. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.R.; Ostroverkhov, V. Sum-frequency Vibrational Spectroscopy on Water Interfaces: Polar Orientation of Water Molecules at Interfaces. Chem. Rev. 2006, 106, 1140–1154. [Google Scholar] [CrossRef] [PubMed]
- Mondal, J.; Nihonyanagi, S.; Yamaguchi, S.; Tahara, T. Structure and Orientation of Water at Charged Lipid Monolayer/Water Interfaces Probed by Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy. J. Am. Chem. Soc. 2010, 132, 10656–10657. [Google Scholar] [CrossRef] [PubMed]
- Nihonyanagi, S.; Yamaguchi, S.; Tahara, T. Direct Evidence for Orientational Flip–Flop of Water Molecules at Charged Interfaces: A Heterodyne-Detected Vibrational Sum Frequency Generation Study. J. Chem. Phys. 2009, 130, 204704. [Google Scholar]
- Jena, K.; Hung, K.K.; Schwantje, T.; Hore, D.K. Methyl groups at dielectric and metal surfaces studied by sum-frequency generation in co- and counter-propagating configurations. J. Chem. Phys. 2011, 135, 044704. [Google Scholar] [CrossRef]
- Jena, K.C.; Covert, P.A.; Hore, D.K. Phase Measurement in Non-Degenerate Three-Wave Mixing Spectroscopy. J. Chem. Phys. 2011, 134, 044712. [Google Scholar] [CrossRef]
- Long, D.A. The Raman Effect: A Unified Treatment of The Theory of Raman Scattering by Molecules; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Potma, E.O.; Mukamel, S. Coherent Raman Scattering Microscopy; CRC Press: Boca Raton, FL, USA, 2013; Chapter 1; pp. 3–42. [Google Scholar]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Hung, K.K.; Stege, U.; Hore, D.K. IR Absorption, Raman Scattering, and IR-Vis Sum-Frequency Generation Spectroscopy as Quantitative Probes of Surface Structure. Appl. Spectrosc. Rev. 2015, 50, 351–376. [Google Scholar] [CrossRef]
- Lagugné Labarthet, F.; Buffeteau, T.; Sourisseau, C. Orientation Distribution Functions in Uniaxial Systems Centered Perpendicularly to a Constraint Direction. Appl. Spectrosc. 2000, 54, 699–705. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, Z.F.; Wang, H.F. Experimental Observables and Macroscopic Susceptibility/Microscopic Polarizability Tensors for Third and Fourth-Order Nonlinear Spectroscopy of Ordered Molecular System. Chin. J. Chem. Phys. 2007, 20, 449–460. [Google Scholar] [CrossRef]
- Hall, S.A.; Hickey, A.D.; Hore, D.K. Structure of Phenylalanine Adsorbed on Polystyrene From Nonlinear Vibrational Spectroscopy Measurements and Electronic Structure Calculations. J. Phys. Chem. C 2010, 114, 9748–9757. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Linder, R.; Nispeal, M.; Häber, T.; Kleinermanns, K. Gas-phase FT-IR spectra of natural amino acids. Chem. Phys. Lett. 2005, 409, 260–264. [Google Scholar] [CrossRef]
- Merrick, J.R.; Moran, D.; Radom, L. An Evaluation of Harmonic Vibrational Frequency Scale Factors. J. Phys. Chem. A 2007, 111, 11683–11700. [Google Scholar] [CrossRef]
- Matousek, J.; Gärtner, B. Understanding and Using Linear Programming; Springer: Heidelberg/Berlin, Germany, 2007. [Google Scholar]
- Dantzig, G.B. Reminiscences about the origins of linear programming. Oper. Res. Lett. 1982, 1, 43–48. [Google Scholar] [CrossRef]
- Karmarkar, N. A new polynomial-time algorithm for linear programming. Combinatorica 1984, 4, 373–395. [Google Scholar] [CrossRef]
- Chvatal, V. Linear Programming; W. H. Freeman and Company: New York, NY, USA, 1983. [Google Scholar]
- Roy, R.; Sevick-Muraca, E. Truncated Newton’s Optimization Scheme for Absorption and Fluorescence Optical Tomography: Part I Theory and Formulation. Opt. Exp. 1999, 4, 353–371. [Google Scholar] [CrossRef]
- Partovi-Azar, P.; Kühne, T.D.; Kaghazchi, P. Evidence for the Existence of Li2S2 clusters in Lithium-Sulfur Batteries: ab initio Raman spectroscopy simulation. Phys. Chem. Chem. Phys. 2015, 17, 22009–22014. [Google Scholar] [CrossRef]
- Li, D.H.; Fukushima, M. A Modified BFGS Method and its Global Convergence in Nonconvex Minimization. J. Comput. Appl. Math. 2001, 129, 15–35. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Livest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA; McGraw-Hill: New York, NY, USA, 2001; Chapter The Simplex Algorithm; pp. 790–804. [Google Scholar]
- GNU Linear Programming Kit, Version 4.64. 2017. Available online: http://www.gnu.org/software/glpk/glpk.html (accessed on 19 February 2015).
- Chen, F.; Hung, K.K.; Stege, U.; Hore, D.K. Linear Programming Applied to Polarized Raman Data for Elucidating Molecular Structure at Surfaces. Chemometr. Intell. Lab. 2020, 196, 103898. [Google Scholar] [CrossRef]
- Buffeteau, T.; Lagugné Labarthet, F.; Sourisseau, C.; Kostromine, S.; Bieringer, T. Biaxial orientation induced in a photoaddressable azopolymer thin film as evidenced by polarized UV-visible, infrared, and Raman spectra. Macromolecules 2004, 37, 2880–2889. [Google Scholar] [CrossRef]
- Lagugné-Labarthet, F.; Sourisseau, C.; Schaller, R.D.; Saykally, R.J.; Rochon, P. Chromophore orientations in a nonlinear optical azopolymer diffraction grating: Even and odd order parameters from far-field Raman and near-field second harmonic generation microscopies. J. Phys. Chem. B 2004, 108, 17059–17068. [Google Scholar] [CrossRef]
- Rodriguez, V.; Lagugné Labarthet, F.; Sourisseau, C. Orientation Distribution Functions based upon both ⟨P1⟩, ⟨P3⟩ Order Parameters and upon the Four ⟨P1⟩ up to ⟨P4⟩ Values: Application to an Electrically Poled Nonlinear Optical Azopolymer Film. Appl. Spectrosc. 2005, 59, 322–328. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).