Inflation inside Non-Topological Defects and Scalar Black Holes
Abstract
1. Introduction
2. Model
3. Results
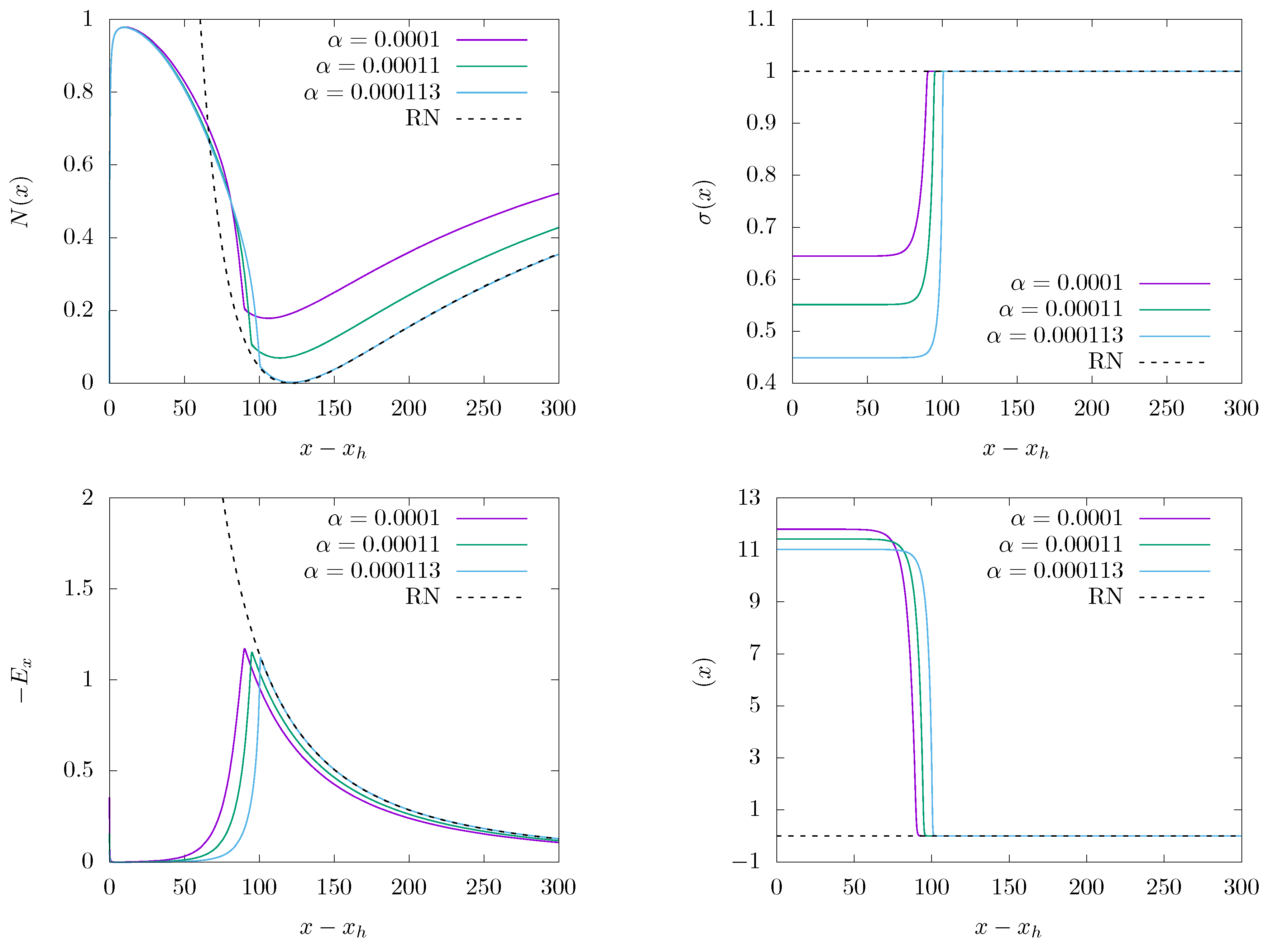
3.1. Black Hole Solutions
3.1.1. Solutions without Scalar Fields
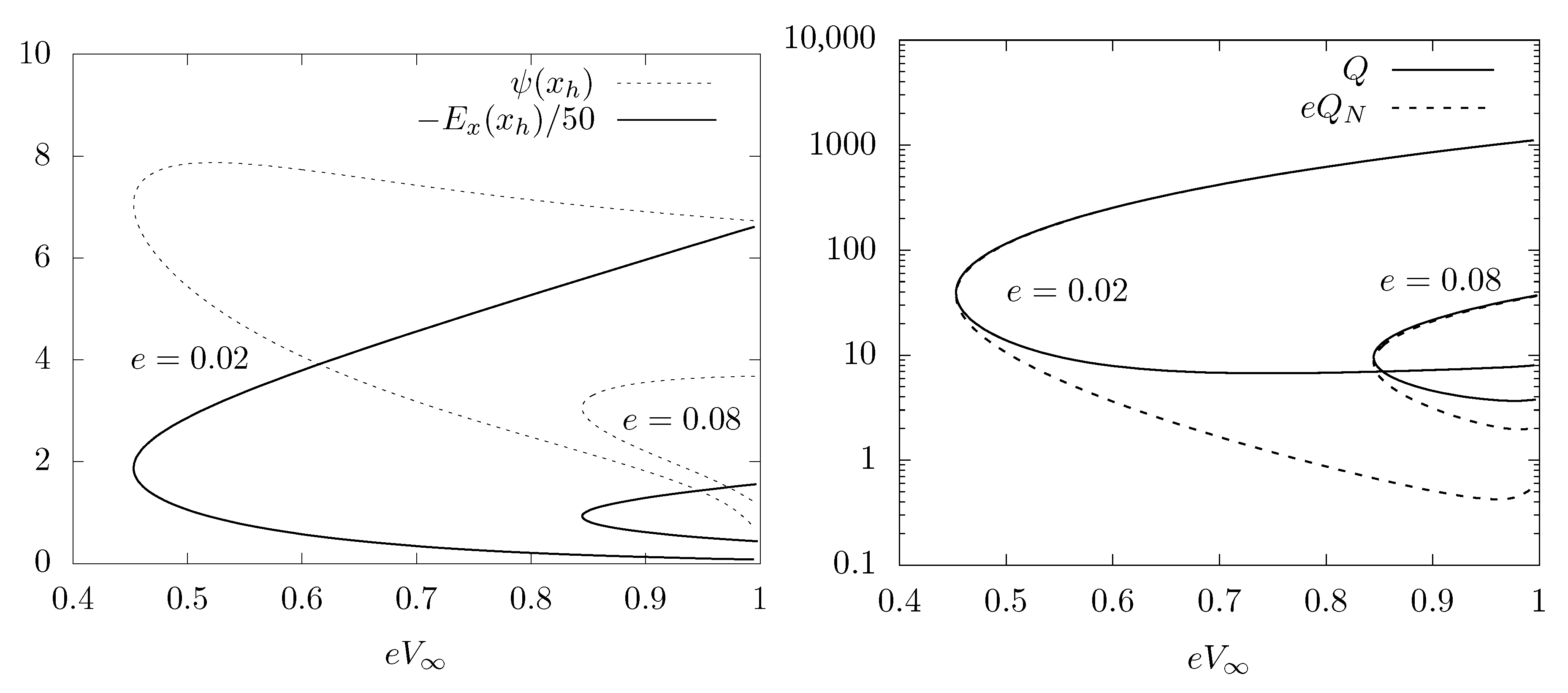
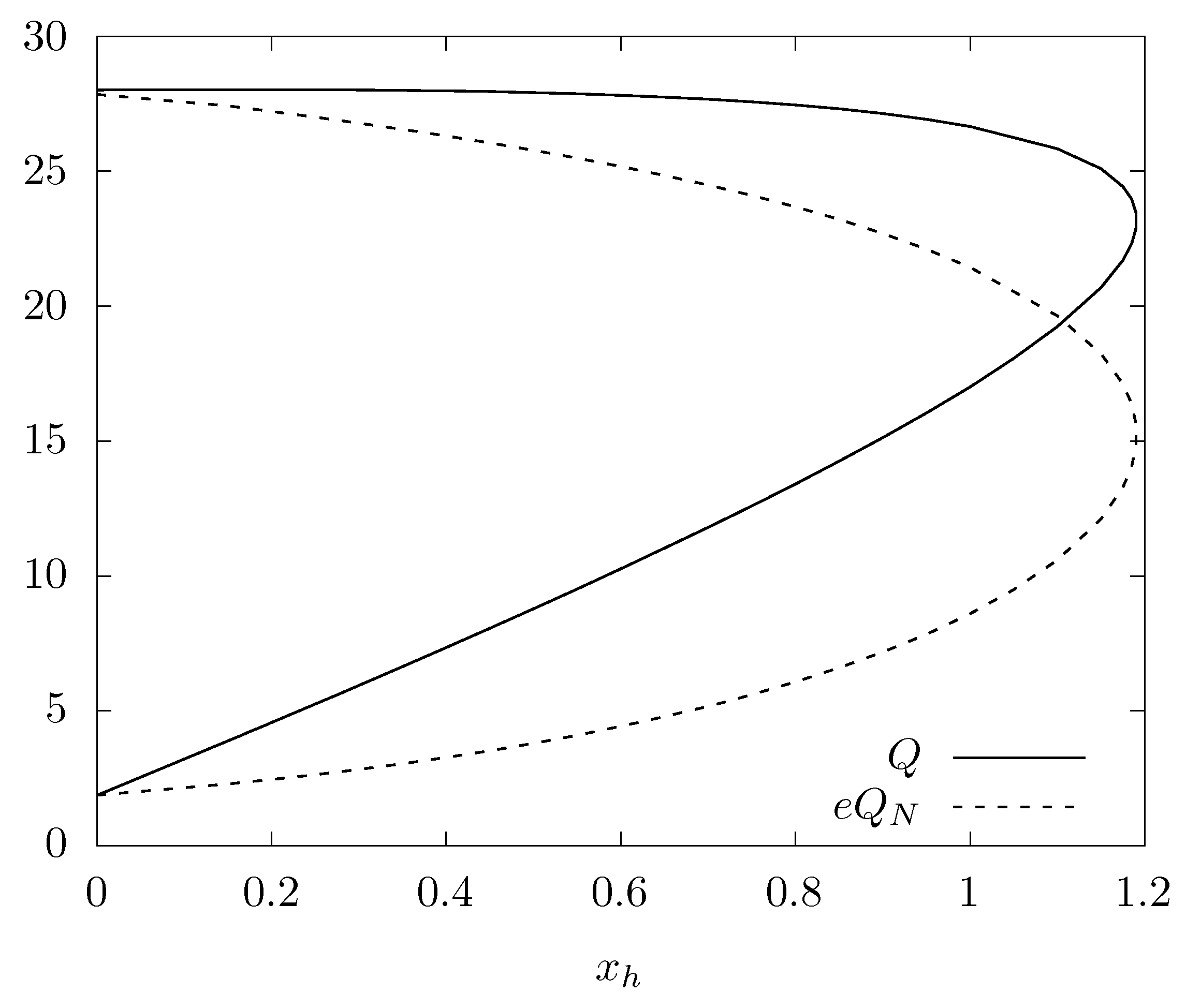
3.1.2. Q-Clouds on Schwarzschild Black Holes
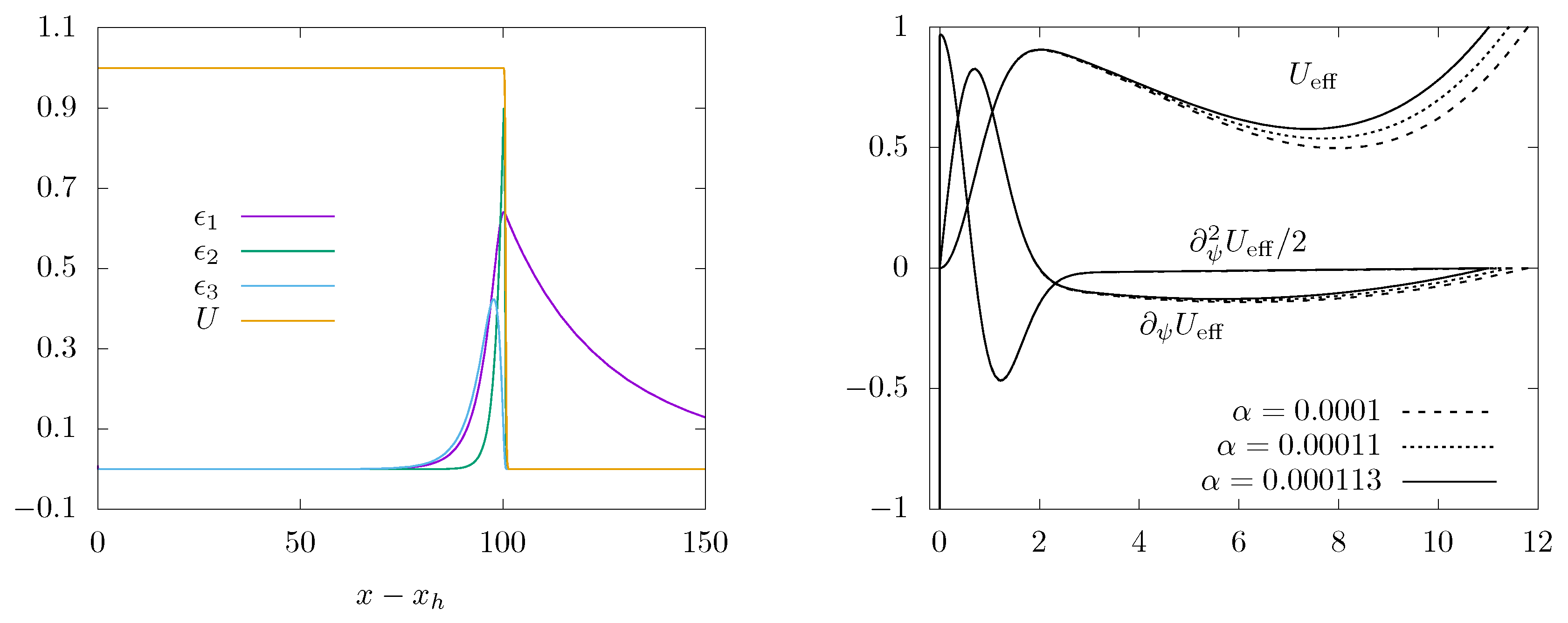
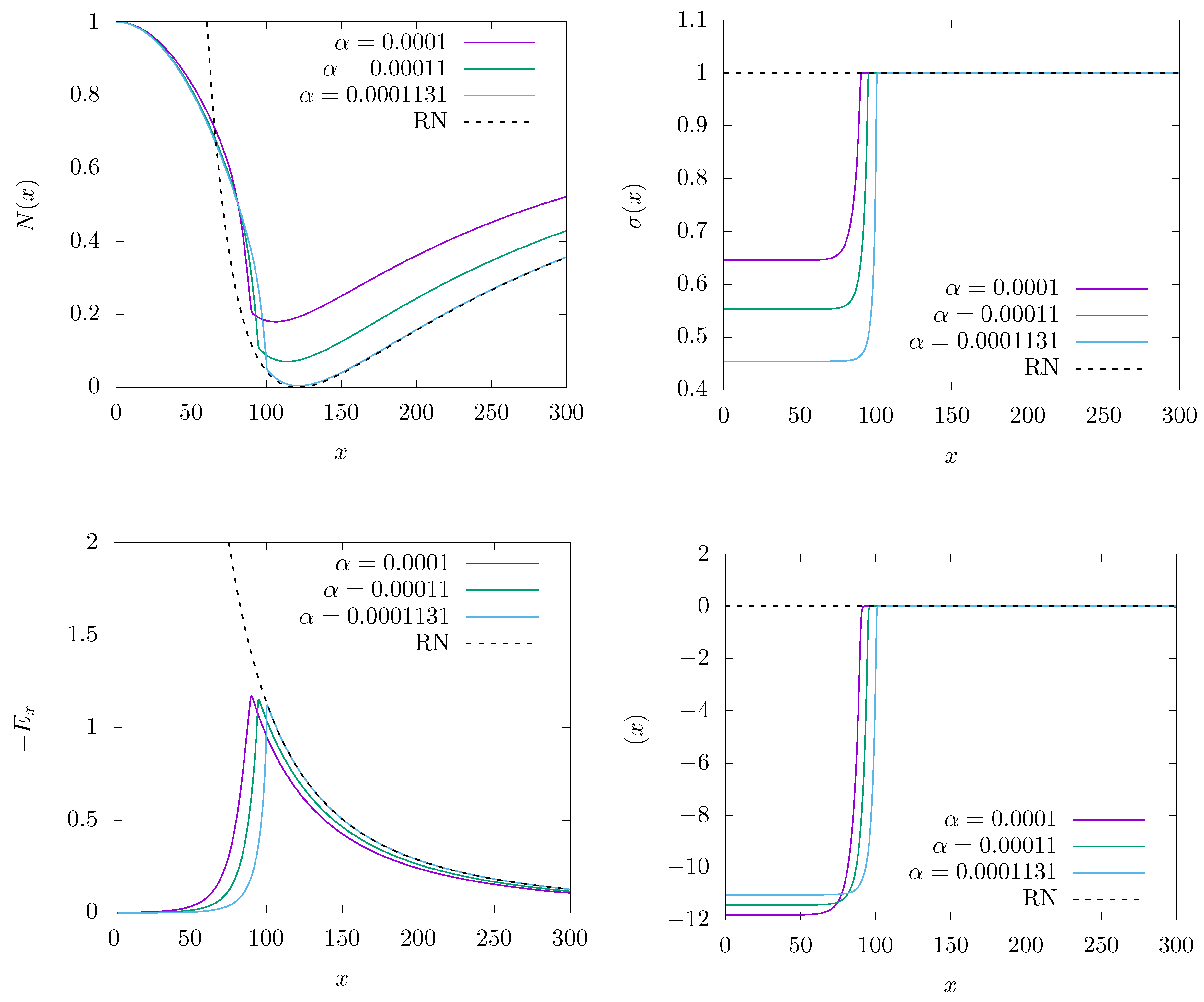
3.1.3. Backreaction of Q-Clouds
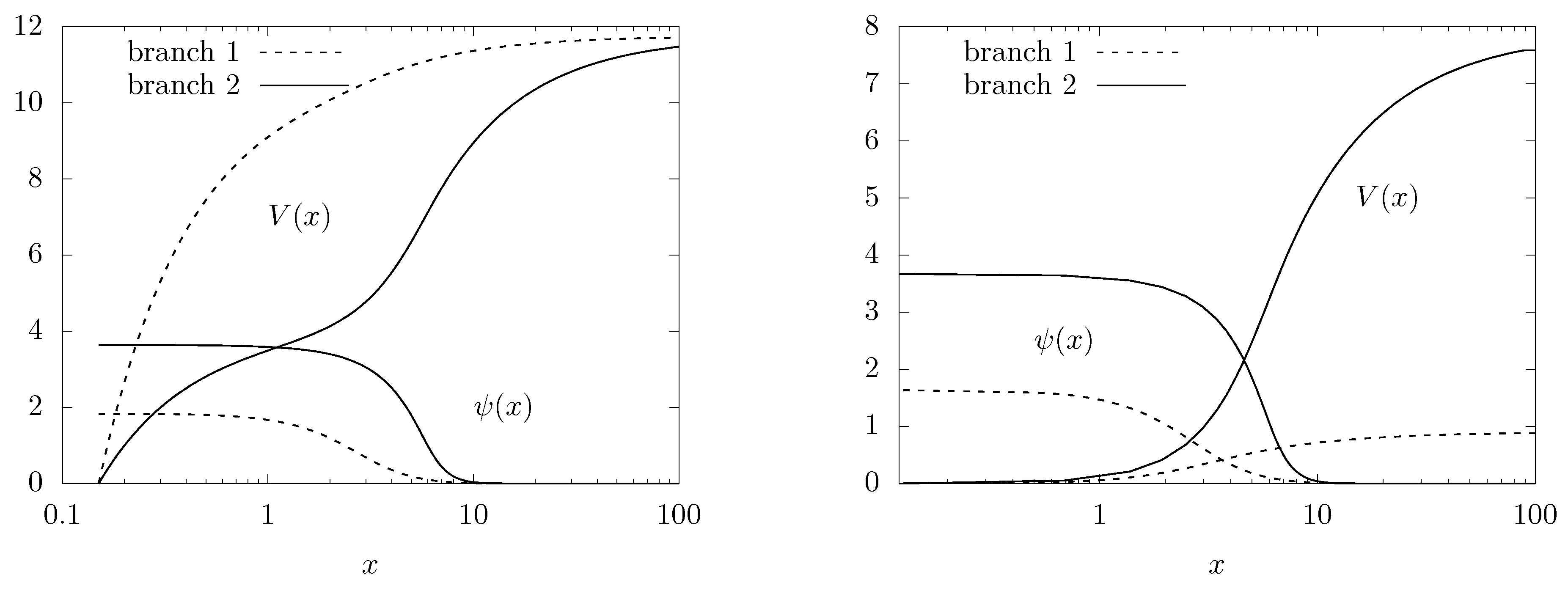
3.2. Globally Regular Solutions
3.2.1. (Un)Charged Q-Balls
3.2.2. Charged Boson Stars
4. Discussion
5. Materials and Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BH | Black Hole |
| BS | Boson Star |
| NS | Neutron Star |
| RN | Reissner–Nordström |
References
- Ruffini, R.; Wheeler, J.A. Introducing the black hole. Phys. Today 1971, 24, 30. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Radu, E. Asymptotically flat black holes with scalar hair: A review. Int. J. Mod. Phys. D 2015, 24, 1542014. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Nonperturbative strong field effects in tensor-scalar theories of gravitation. Phys. Rev. Lett. 1993, 70, 2220. [Google Scholar] [CrossRef] [PubMed]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss-Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef]
- Hod, S. Stationary Scalar Clouds Around Rotating Black Holes. Phys. Rev. D 2012, 86, 104026. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Radu, E. Kerr black holes with scalar hair. Phys. Rev. Lett. 2014, 112, 221101. [Google Scholar] [CrossRef]
- Coleman, S.R. Q-Balls. Nucl. Phys. B 1985, 262, 263. [Google Scholar] [CrossRef]
- Schunck, F.E.; Mielke, E.W. General relativistic boson stars. Class. Quant. Grav. 2003, 20, R301. [Google Scholar] [CrossRef]
- Eby, J.; Kouvaris, C.; Nielsen, N.G.; Wijewardhana, L.C.R. Boson Stars from Self-Interacting Dark Matter. JHEP 2016, 02, 028. [Google Scholar] [CrossRef]
- Guzman, F.S.; Rueda-Becerril, J.M. Spherical boson stars as black hole mimickers. Phys. Rev. D 2009, 80, 084023. [Google Scholar] [CrossRef]
- Macedo, C.F.B.; Pani, P.; Cardoso, V.; Crispino, L.C.B. Astrophysical signatures of boson stars: Quasinormal modes and inspiral resonances. Phys. Rev. D 2013, 88, 064046. [Google Scholar] [CrossRef]
- Brihaye, Y.; Diemer, V.; Hartmann, B. Charged Q-balls and boson stars and dynamics of charged test particles. Phys. Rev. D 2014, 89, 084048. [Google Scholar] [CrossRef]
- Campanelli, L.; Ruggieri, M. Supersymmetric Q-balls: A Numerical study. Phys. Rev. D 2008, 77, 043504. [Google Scholar] [CrossRef]
- Copeland, E.J.; Tsumagari, M.I. Q-balls in flat potentials. Phys. Rev. D 2009, 80, 025016. [Google Scholar] [CrossRef]
- Hartmann, B.; Riedel, J. Supersymmetric Q-balls and boson stars in (d+1) dimensions. Phys. Rev. D 2013, 87, 044003. [Google Scholar] [CrossRef]
- Hartmann, B.; Kleihaus, B.; Kunz, J.; Schaffer, I. Compact Boson Stars. Phys. Lett. B 2012, 714, 120. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Radu, E. Spherical electro-vacuum black holes with resonant, scalar Q-hair. Eur. Phys. J. C 2020, 80, 390. [Google Scholar] [CrossRef]
- Brihaye, Y.; Hartmann, B. Strong gravity effects of charged Q-clouds and inflating black holes. arXiv 2020, arXiv:2009.08293. [Google Scholar]
- Breitenlohner, P.; Forgacs, P.; Maison, D. Gravitating monopole solutions. Nucl. Phys. B 1992, 383, 357. [Google Scholar] [CrossRef]
- Breitenlohner, P.; Forgacs, P.; Maison, D. Gravitating monopole solutions 2. Nucl. Phys. B 1995, 442, 126. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kahlen, S.; Kunz, J. Critical solutions in scalarized black holes. arXiv 2020, arXiv:2011.01326. [Google Scholar]
- Vilenkin, A. Topological inflation. Phys. Rev. Lett. 1994, 72, 3137. [Google Scholar] [CrossRef] [PubMed]
- Linde, A.D. Monopoles as big as a universe. Phys. Lett. B 1994, 327, 208. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brihaye, Y.; Console, F.; Hartmann, B. Inflation inside Non-Topological Defects and Scalar Black Holes. Symmetry 2021, 13, 2. https://doi.org/10.3390/sym13010002
Brihaye Y, Console F, Hartmann B. Inflation inside Non-Topological Defects and Scalar Black Holes. Symmetry. 2021; 13(1):2. https://doi.org/10.3390/sym13010002
Chicago/Turabian StyleBrihaye, Yves, Felipe Console, and Betti Hartmann. 2021. "Inflation inside Non-Topological Defects and Scalar Black Holes" Symmetry 13, no. 1: 2. https://doi.org/10.3390/sym13010002
APA StyleBrihaye, Y., Console, F., & Hartmann, B. (2021). Inflation inside Non-Topological Defects and Scalar Black Holes. Symmetry, 13(1), 2. https://doi.org/10.3390/sym13010002



