Forecasting Model and Related Index of Pig Population in China
Abstract
1. Introduction
2. Model Building
2.1. Pig Type and Growth Stage
2.2. Derivation and Establishment of the Recursive Model of Pig population and Estimation Model of Pork Supply
- The recurrence formula of the distribution of the number of new born piglets by months of age is as follows:
- The recurrence formula for the distribution of sows by months of age is as follows: is the number of artificially retained.
- 3.
- The recurrence formula for the distribution of boars by months of age is as follows:
- 4.
- The recurrence formula for the distribution of the number of pork pigs per month of age is as follows:
2.3. Estimation Method for New Kept Gilts and Breeding Sows
2.3.1. Estimation of the Sum of Monthly Mortality and Culling Rate of Breeding Sows
2.3.2. Calculation Method for New Gilts in Each Month
Construction of the Relationship Model between New Kept Gilts and Pork Prices
Parameter Calculation of the Relationship Model between New Kept Gilts and Pork Prices
2.3.3. Estimation of Breeding Sows at Each Month of Age
2.4. Estimate of the Initial Condition of the Pig Population
2.5. Population Index
- (1)
- Number of breeding sows at the end of the year:
- (2)
- Inventory of pigs at the end of the year:
- (3)
- Number of slaughtered fattened hogs
- (4)
- Pork production in the current year:
- (5)
- Number of sows per month at time t:
- (6)
- Number of boars per month age at time t
- (7)
- The number of boars at time t
- (8)
- The total number of slaughter pigs at time t is as follows:
3. Example Calculations
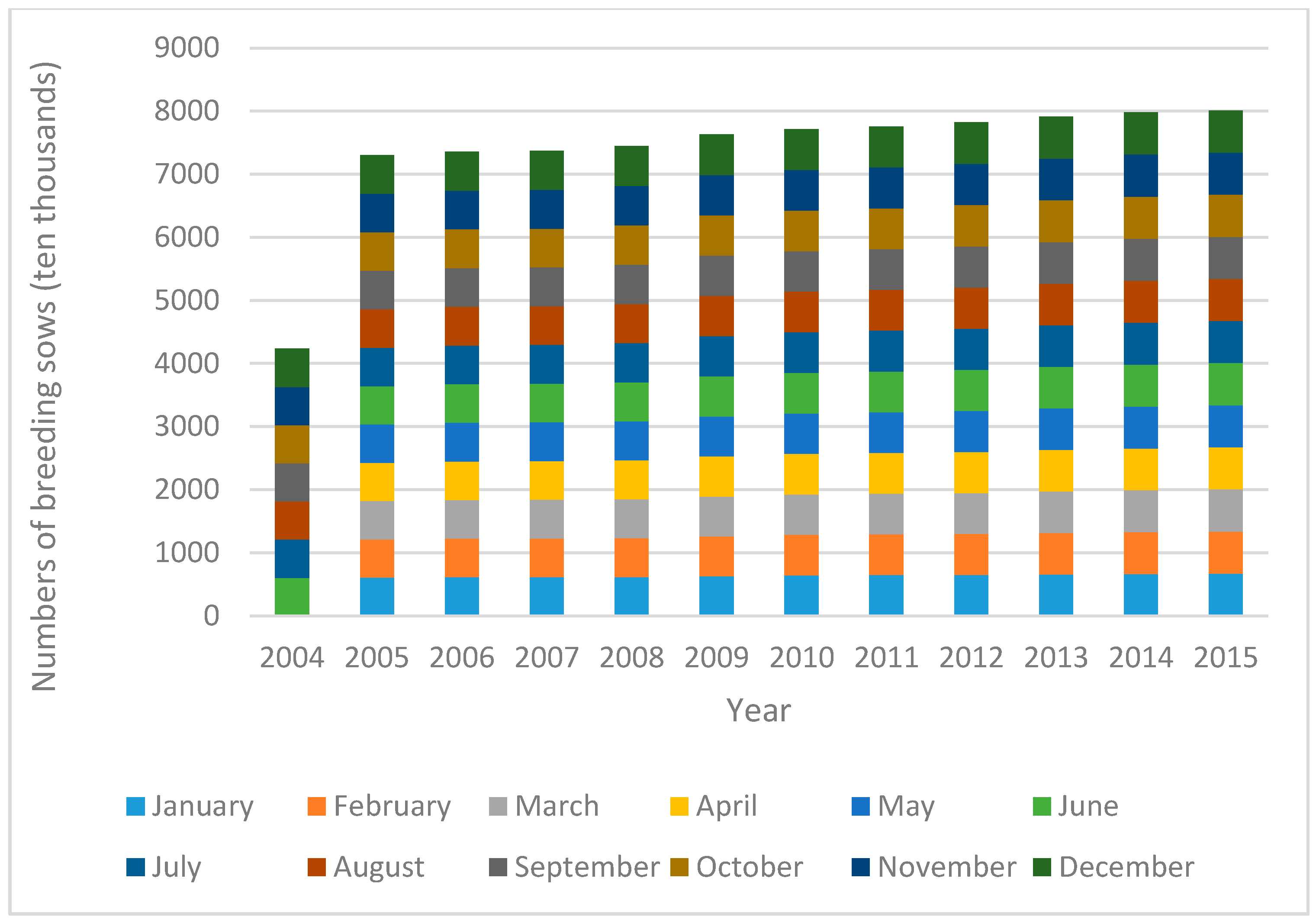
3.1. Data Source and Description
3.2. Examples and Results Evaluation
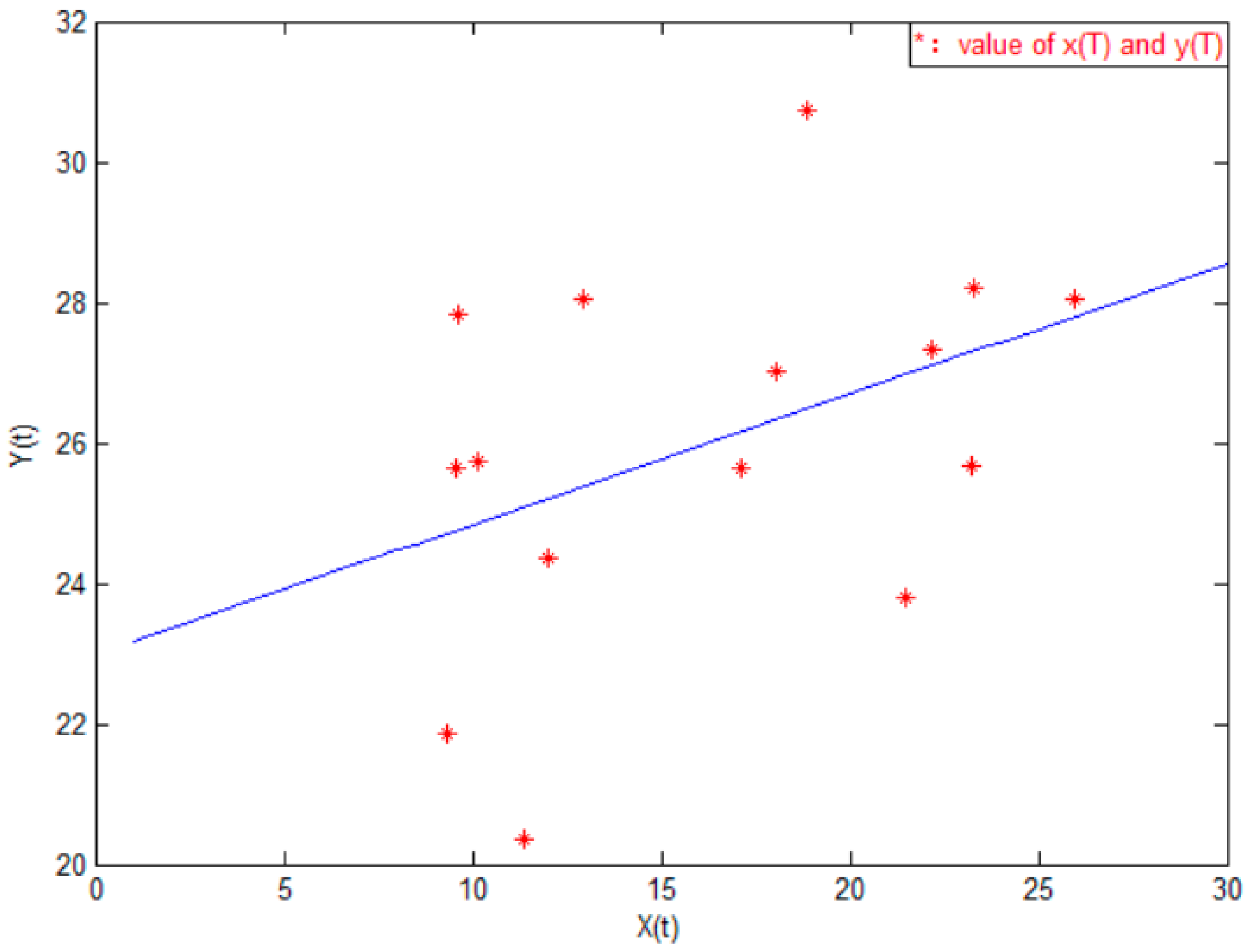
3.2.1. Estimation of New Gilts and Breeding Sows
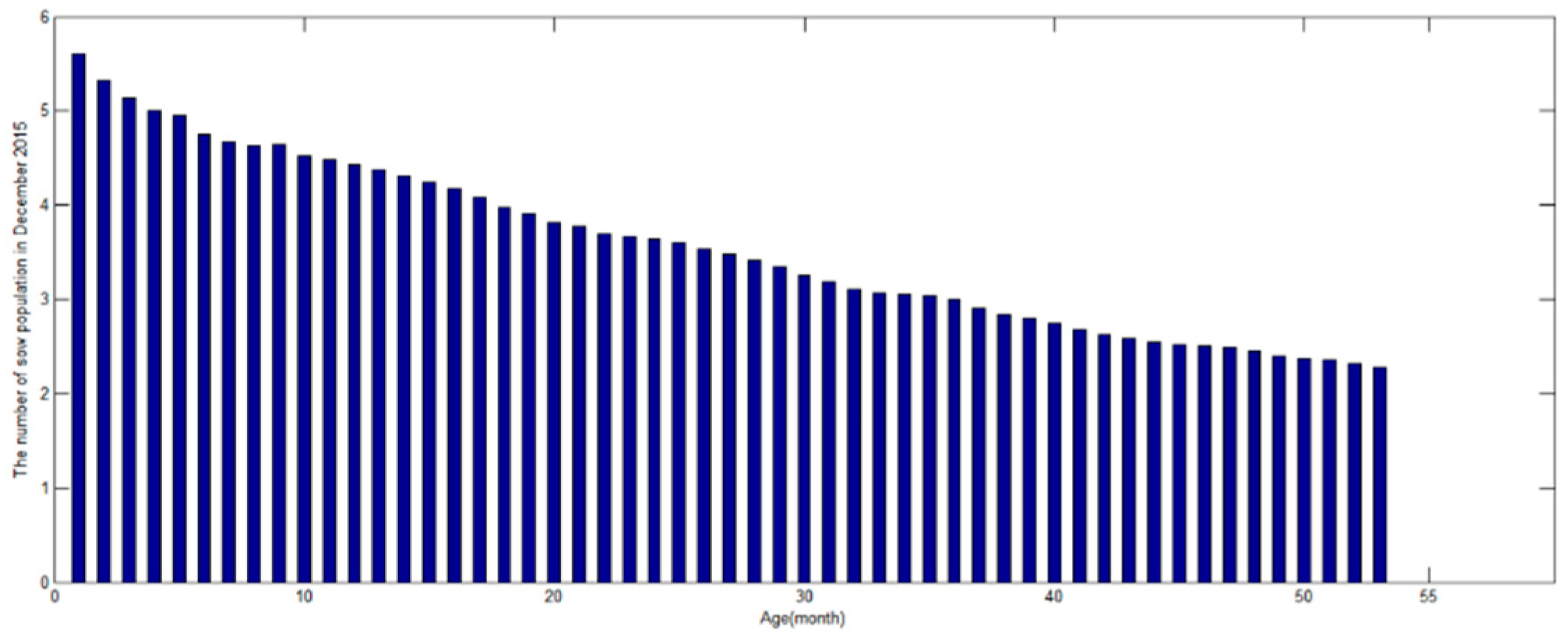
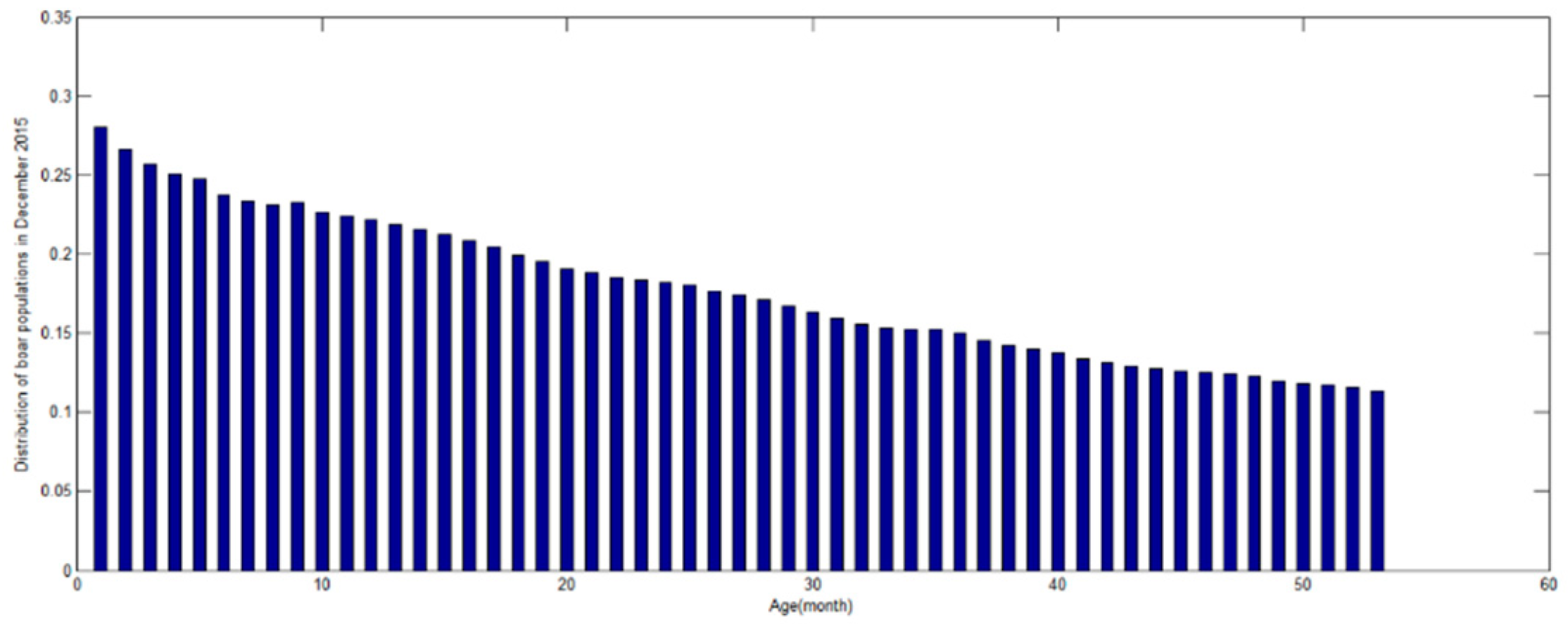
3.2.2. The Estimation of Initial Pig Population State
3.2.3. Predict the Distribution of Pig Population in China in the Future
3.2.4. The Prediction of the Pig Population Index in China in 2017
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, L.; Duan, D.M.; Lu, F.B.; Xu, W.; Wang, S.Y. Integration forecast of Chinese pork consumption demand-empirical based on Arima var and Vec models. Syst. Eng. Theory Pract. 2013, 33, 918–925. [Google Scholar]
- Liu, Y.; Duan, Q.; Wang, D.; Zhang, Z.; Liu, C. Prediction for hog prices based on similar sub-series search and support vector regression. Comput. Electron. Agric. 2019, 157, 581–588. [Google Scholar] [CrossRef]
- Sun, J. Pork price forecast based on breeding sow stocks and hog-grain price ratio. Trans. Chin. Soc. Agric. Eng. 2013, 29, 1–6. [Google Scholar]
- Tao, X.; Chong, L.I.; Yukun, B. An improved EEMD-based hybrid approach for the short-term forecasting of hog price in China. Agric. Econ. 2017, 63, 136–148. [Google Scholar] [CrossRef]
- Zhou, D.; Yu, X.; Herzfeld, T. Dynamic food demand in urban China. China Agric. Econ. Rev. 2015, 7, 27–44. [Google Scholar] [CrossRef]
- Trujillo-Barrera, A.; Garcia, P.; Mallory, M.L. Short-term price density forecasts in the lean hog futures market. Eur. Rev. Agric. Econ. 2017, 45, 121–142. [Google Scholar] [CrossRef]
- Jaile-Benitez, J.M.; Ferrer-Comalat, J.C.; Linares-Mustarós, S. Determining the influence variables in the pork price, based on expert systems. Sci. Methods Treat. Uncertain. Soc. Sci. 2015, 377, 81–92. [Google Scholar]
- Wu, H.; Qi, Y.; Chen, D. A dynamic analysis of influencing factors in price fluctuation of live pigs-based on statistical data in Sichuan province of China. Asian Soc. Sci. 2012, 8, 256. [Google Scholar] [CrossRef]
- Jia, W.; Yang, Y.; Qin, F. The study on China’s pork industry chain price transmission mechanism: Based on province comparison. Stat. Inf. Forum 2013, 3, 49–55. [Google Scholar]
- Zhou, D.; Dieter, K. Price transmission in hog and feed markets of china. J. Integr. Agric. 2015, 6, 1122–1129. [Google Scholar] [CrossRef]
- Jumah, A.; Kunst, R.M. Seasonal prediction of European cereal prices: Good forecasts using bad models? J. Forecast. 2008, 27, 391–406. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.X.; Tian, M.; Zhang, S.Y.; Liu, J.; Zhu, D. Application of the Arima models in drought forecasting using the standardized precipitation index. Appl. Math. Comput. 2012, 392, 352–358. [Google Scholar]
- Yercan, M.; Adanacioglu, H. An analysis of tomato prices at wholesale level in turkey: An application of sarima model. Custos E Agronegocio 2012, 8, 52–75. [Google Scholar]
- Gan, L.I.; Shi-Wei, X.U.; Zhe-Min, L.I.; Yi-Guo, S.; Xiao-Xia, D. Using quantile regression approach to analyze price movements of agricultural products in China. J. Integr. Agric. 2012, 11, 674–683. [Google Scholar]
- Saengwong, S.; Jatuporn, C.; Roan, S.W. An analysis of Taiwanese livestock prices: Empirical time series approaches. J. Anim. Vet. Adv. 2012, 11, 4340–4346. [Google Scholar]
- Gloria, H. Forecasting pseudo-periodic seasonal patterns in agricultural prices. Agric. Econ. 2012, 43, 531–544. [Google Scholar]
- Wu, L.; Liu, S.; Yang, Y. Grey double exponential smoothing model and its application on pig price forecasting in china. Appl. Soft Comput. 2016, 39, 117–123. [Google Scholar] [CrossRef]
- Tian, F.; Peng, Y. Machine vision system of nondestructive real-time prediction of live-pig meat yield. Trans. Chin. Soc. Agric. Eng. 2016, 32, 230–235. [Google Scholar]
- Zhang, J.H.; Li, Z.M.; Kong, F.T.; Dong, X.X.; Chen, W.; Wang, S.W. Prediction of pork prices based on SVM. In Proceedings of the 2013 World Agricultural Outlook Conference, Beijing, China, 6–7 June 2013; Springer: Berlin/Heidelberg, Germany, 2014; pp. 173–178. [Google Scholar]
- Delgado, C.L.; Rosegrant, M.W.; Steinfeld, H.; Ehui, S.K.; Courbois, C. Livestock to 2020: The next food revolution. Vis. Discuss. Pap. 2001, 30, 27–29. [Google Scholar] [CrossRef]
- Jurknait, N.; Djuric, I. Impact of the Russian trade bans on Lithuanian pork sector. Econstor Open Access Artic. 2018, 40, 481–491. [Google Scholar] [CrossRef]
- Meng, Z.; Nan, Z. Lean meat percentage prediction of pig carcass based on radial basis function neural network. J. Agric. Mech. Res. 2017, 6, 38. [Google Scholar]
- Lumogdang, C.F.D.; Wata, M.G.; Loyola, S.J.S.; Angelia, R.E.; Angelia, H.L.P. Supervised Machine Learning Approach for Pork Meat Freshness Identification. In Proceedings of the International Conference on Bioinformatics Research and Applications, Seoul, Korea, 19–21 June 2019; pp. 1–6. [Google Scholar]
- Shih, M.L.; Huang, B.W.; Chiu, N.H.; Chiu, C.; Hu, W.Y. Farm price prediction using case-based reasoning approach—A case of broiler industry in Taiwan. Comput. Electron. Agric. 2009, 66, 70–75. [Google Scholar] [CrossRef]
- Ribeiro, C.O.; Oliveira, S.M. A hybrid commodity price-forecasting model applied to the sugar–alcohol sector. Aust. J. Agric. Resour. Econ. 2011, 55, 180–198. [Google Scholar] [CrossRef]
- Jha, G.K.; Sinha, K. Time-delay neural networks for time series prediction: An application to the monthly wholesale price of oilseeds in India. Neural Comput. Appl. 2014, 24, 563–571. [Google Scholar] [CrossRef]
- Xin, S.; Yi, W.; Duan, S.; Ma, J.H. Detecting chaos from agricultural product price time series. Entropy 2014, 16, 6415–6433. [Google Scholar]
- Liu, T.H.; Li, Z.; Teng, G. Prediction of pig weight based on radical basis function neural network. J. Agric. Mach. 2013, 44, 245–249. [Google Scholar]
- Li, Z.; Xu, S.; Cui, L.; Li, G.; Dong, X.; Wu, Z. The Short-Term Forecast Model of Pork Price Based on CNN-GA. Trans. Tech. Publ. 2013, 628, 350–358. [Google Scholar] [CrossRef]
- Zou, P.; Yang, J.; Fu, J.; Liu, G.; Li, D. Artificial neural network and time series models for predicting soil salt and water content. Agric. Water Manag. 2010, 97, 2009–2019. [Google Scholar] [CrossRef]
- Jang, I.; Lee, S.Y.; Choe, Y.C. Weighted sampling method for improving performance prediction: The case of pig management system. Adv. Sci. Technol. Lett. 2015, 95, 73–77. [Google Scholar] [CrossRef]
- Piewthongngam, K.; Vijitnopparat, P.; Pathumnakul, S.; Chumpatong, S.; Duangjinda, M. System dynamics modelling of an integrated pig production supply chain. Biosyst. Eng. 2014, 127, 24–40. [Google Scholar] [CrossRef]
- Xu, B.; Shi, L.; Liu, Y. Prediction and empirical study of pig price in China. Agric. Econ. Issues 2014, 35, 25–32. (In Chinese) [Google Scholar]
- Zhan, L. Regularity waveform, cause and control of pig price time series. Agric. Mod. Res. 2014, 35, 25–28. (In Chinese) [Google Scholar]
- Song, J. Population Prediction and Population Control; People’s Publishing: Beijing, China, 1982. [Google Scholar]
- Zawadzka, D. The history of research on the “pig cycle”. Probl. Agric. Econ. Zagadnienia Ekonomiki Rolnej 2010, 1, 208–214. [Google Scholar]



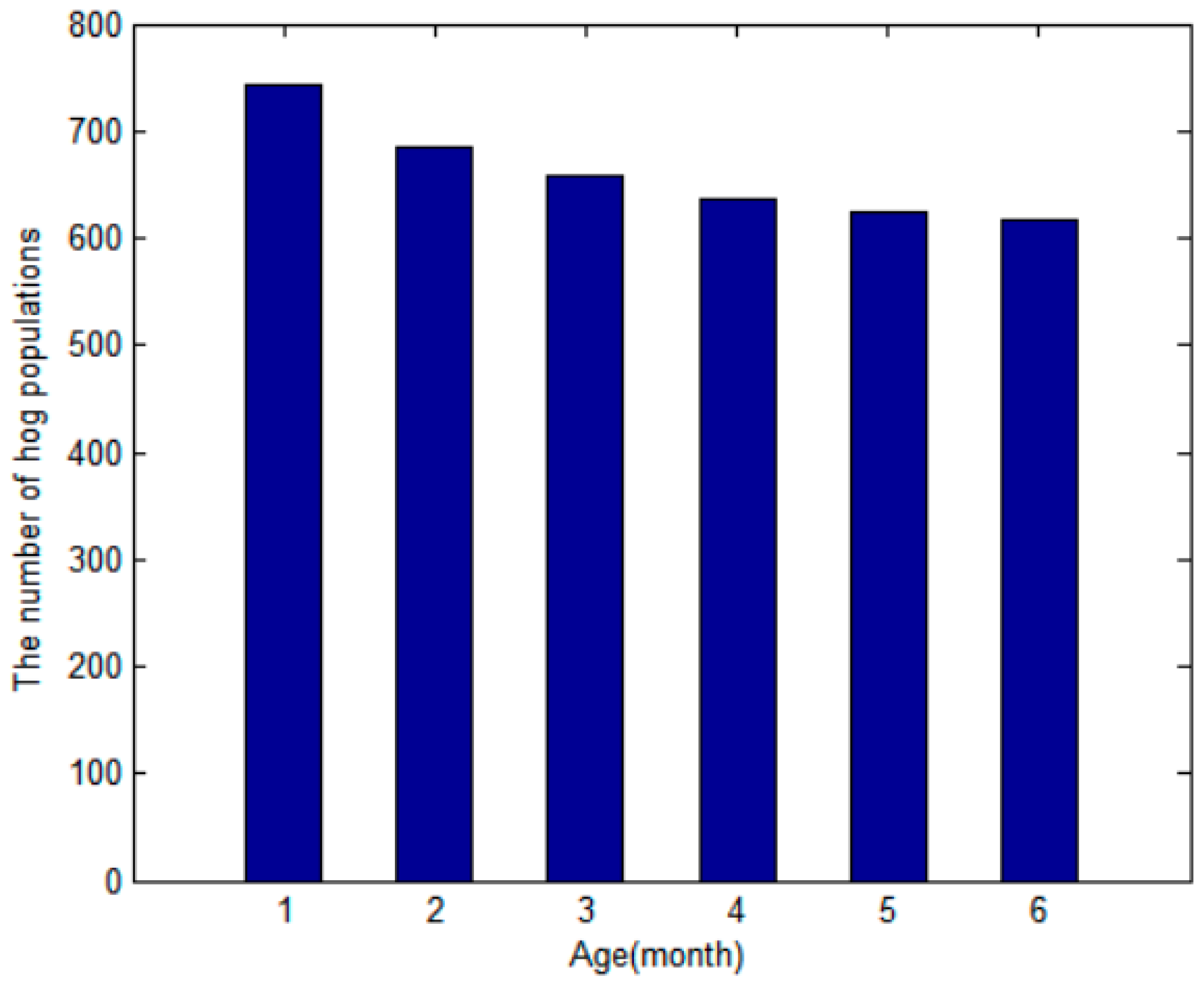
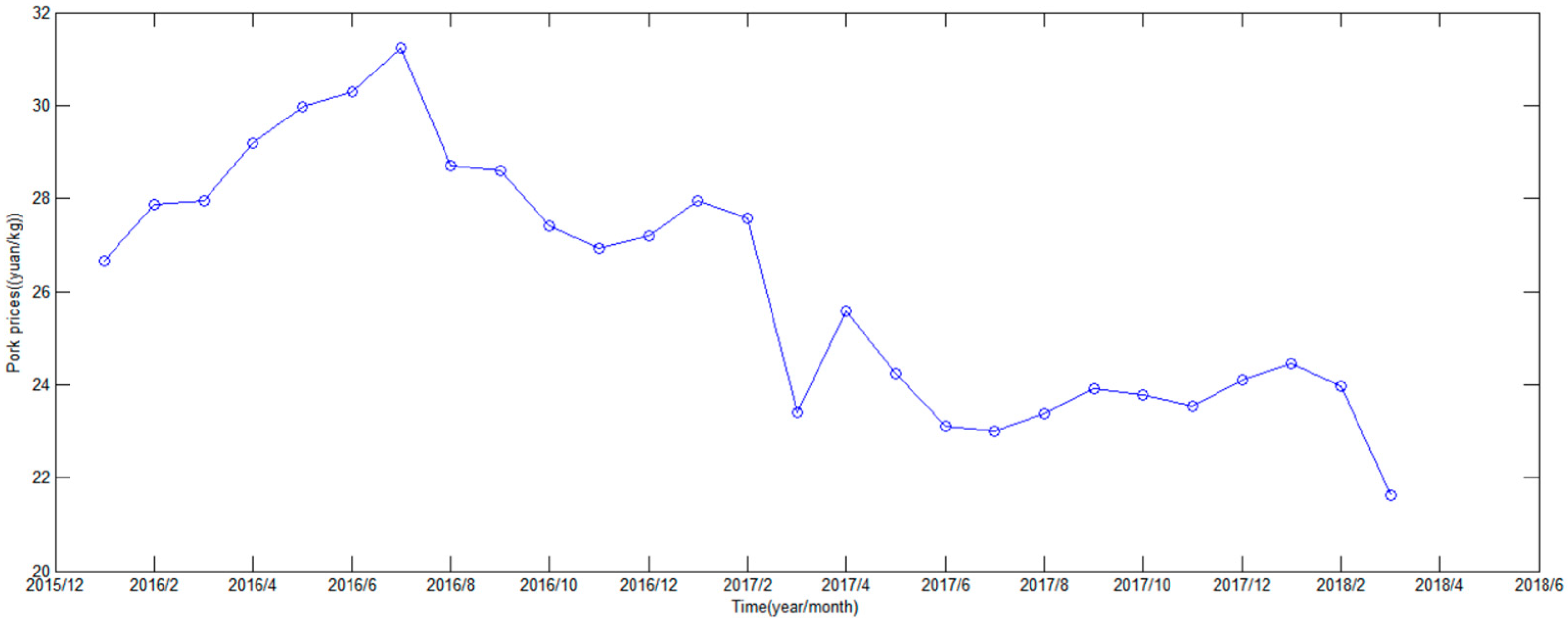
| Year | Predictive Value (Ten Thousand) | Actual Value (Ten Thousand) | Relative Error |
|---|---|---|---|
| 2004 | 566 | 566 | |
| 2005 | 570.9614574 | 589 | 0.030625709 |
| 2006 | 573.4566575 | 570 | 0.006064311 |
| 2007 | 574.9350511 | 523 | 0.099302201 |
| 2008 | 585.8609814 | 587 | 0.001940406 |
| 2009 | 598.6894485 | 595 | 0.006200754 |
| 2010 | 603.0519213 | 585 | 0.030857985 |
| 2011 | 605.5471426 | 591 | 0.024614455 |
| 2012 | 613.1236142 | 604 | 0.015105322 |
| 2013 | 618.7693569 | 613 | 0.009411675 |
| 2014 | 624.2275925 | 596 | 0.047361732 |
| 2015 | 622.1858153 | 569 | 0.093472435 |
| Year | Predictive Value (Ten Thousand) | Actual Value (Ten Thousand) | Relative Error |
|---|---|---|---|
| 2006 | 7105.02 | 6780.717945 | 0.047827097 |
| 2007 | 7471.41 | 6804.190631 | 0.098060064 |
| 2008 | 6360.7 | 6809.446693 | 0.06590061 |
| 2009 | 6431.4 | 6961.360612 | 0.076128884 |
| 2010 | 6915.5 | 7108.225114 | 0.027112973 |
| 2011 | 7178.28 | 7149.174708 | 0.00407114 |
| 2012 | 7002.6 | 7180.25797 | 0.024742561 |
| 2013 | 7170.7 | 7276.110933 | 0.014487263 |
| 2014 | 7314.1 | 7344.67785 | 0.004163266 |
| 2015 | 7445 | 7404.611788 | 0.005454467 |
| Time | Number (Ten Thousand) | Time | Number (Ten Thousand) | Time | Number (Ten Thousand) |
|---|---|---|---|---|---|
| January 2016 | 27.9298 | October 2016 | 28.0708 | July 2017 | 27.2512 |
| February 2016 | 28.1523 | November 2016 | 27.9799 | August 2017 | 27.3216 |
| March 2016 | 28.1672 | December 2016 | 28.0318 | September 2017 | 27.4218 |
| April 2016 | 28.4008 | January 2017 | 28.1690 | October 2017 | 27.3939 |
| May 2016 | 28.5436 | February 2017 | 28.0986 | November 2017 | 27.3531 |
| June 2016 | 28.6029 | March 2017 | 27.3272 | December 2017 | 27.4570 |
| July 2016 | 28.7791 | April 2017 | 27.7314 | January 2018 | 27.5219 |
| August 2016 | 28.3081 | May 2017 | 27.4792 | February 2018 | 27.4329 |
| September 2016 | 28.2896 | June 2017 | 27.2716 | March 2018 | 26.9971 |
| Time | Number (Ten Thousand) | Time | Number (Ten Thousand) | Time | Number (Ten Thousand) |
|---|---|---|---|---|---|
| January 2016 | 665.2360 | October 2016 | 665.3340 | July 2017 | 672.4522 |
| February 2016 | 664.3963 | November 2016 | 665.8391 | August 2017 | 673.1802 |
| March 2016 | 663.9295 | December 2016 | 666.4881 | September 2017 | 673.8585 |
| April 2016 | 663.4213 | January 2017 | 667.2831 | October 2017 | 674.4909 |
| May 2016 | 663.0983 | February 2017 | 668.0141 | November 2017 | 675.0584 |
| June 2016 | 663.0819 | March 2017 | 668.9140 | December 2017 | 675.6828 |
| July 2016 | 663.7822 | April 2017 | 669.9261 | January 2018 | 676.1457 |
| August 2016 | 664.3333 | May 2017 | 670.8922 | February 2018 | 675.9240 |
| September 2016 | 664.8637 | June 2017 | 671.8684 | March 2018 | 676.0462 |
| Time | Number (Ten Thousand) | Time | Number (Ten Thousand) | Time | Number (Ten Thousand) |
|---|---|---|---|---|---|
| January 2016 | 579.3772 | October 2016 | 575.9535917 | July 2017 | 579.6922849 |
| February 2016 | 579.65269 | November 2016 | 575.5439568 | August 2017 | 580.9896057 |
| March 2016 | 579.7294325 | December 2016 | 575.4801702 | September 2017 | 581.4689223 |
| April 2016 | 579.7225285 | January 2018 | 576.3562409 | October 2017 | 582.5915294 |
| May 2016 | 597.6500583 | February 2017 | 576.8695025 | November 2017 | 583.6358593 |
| June 2016 | 122.7583752 | March 2017 | 577.5293108 | December 2017 | 584.5347175 |
| July 2016 | 577.9820714 | April 2017 | 578.0292742 | January 2018 | 585.0040278 |
| August 2016 | 577.0397165 | May 2017 | 578.4427404 | February 2018 | 585.5790734 |
| September 2016 | 576.6056677 | June 2017 | 578.9158294 | March 2018 | 586.2149126 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Wang, F.; Wang, F. Forecasting Model and Related Index of Pig Population in China. Symmetry 2021, 13, 114. https://doi.org/10.3390/sym13010114
Zhang F, Wang F, Wang F. Forecasting Model and Related Index of Pig Population in China. Symmetry. 2021; 13(1):114. https://doi.org/10.3390/sym13010114
Chicago/Turabian StyleZhang, Fan, Fulin Wang, and Fulin Wang. 2021. "Forecasting Model and Related Index of Pig Population in China" Symmetry 13, no. 1: 114. https://doi.org/10.3390/sym13010114
APA StyleZhang, F., Wang, F., & Wang, F. (2021). Forecasting Model and Related Index of Pig Population in China. Symmetry, 13(1), 114. https://doi.org/10.3390/sym13010114




