Abstract
Trust prediction is essential to enhancing reliability and reducing risk from the unreliable node, especially for online applications in open network environments. An essential fact in trust prediction is to measure the relation of both the interacting entities accurately. However, most of the existing methods infer the trust relation between interacting entities usually rely on modeling the similarity between nodes on a graph and ignore semantic relation and the influence of negative links (e.g., distrust relation). In this paper, we proposed a relation representation learning via signed graph mutual information maximization (called SGMIM). In SGMIM, we incorporate a translation model and positive point-wise mutual information to enhance the relation representations and adopt Mutual Information Maximization to align the entity and relation semantic spaces. Moreover, we further develop a sign prediction model for making accurate trust predictions. We conduct link sign prediction in trust networks based on learned the relation representation. Extensive experimental results in four real-world datasets on trust prediction task show that SGMIM significantly outperforms state-of-the-art baseline methods.
1. Introduction
Graph representation learning (GRL), as one of the most popular and promising machine learning techniques on graphs, has been successfully applied to diverse graph analysis tasks, such as link prediction [1,2,3], node classification [4,5,6], molecular generation [7,8,9], community detection [10,11], and demonstrated to be quite useful. GRL aims to learn a low-dimensional latent vector representation of nodes or edges while making the vector preserve as much more structure and feature information as possible. However, most of the GRL approaches focus more on the vector representation of nodes, in which abundant edge information has not been well captured and used, especially in social networks with complex relationships.
Recently, with the growth of online social networks, signed networks are becoming increasingly ubiquitous. A singed network is a classic directed graph with two kinds of edges (positive or negative), where the positive edges are usually seen as similarity or collaboration, while negative edges represent opposites and differences [12]. For example, in the Epinions network, positive edges mean trust, while negative edges represent distrust. Recent works demonstrated that negative edges are also as crucial as positive edges for a lot of graph analysis tasks [13], such as trust prediction [14], link prediction [15], and recommendation systems [16]. Most trust prediction problems can be regarded as sign predictions on the signed graph, to be more specific. Figure 1 shows an example to illustrate the sign prediction problem in the trust network.
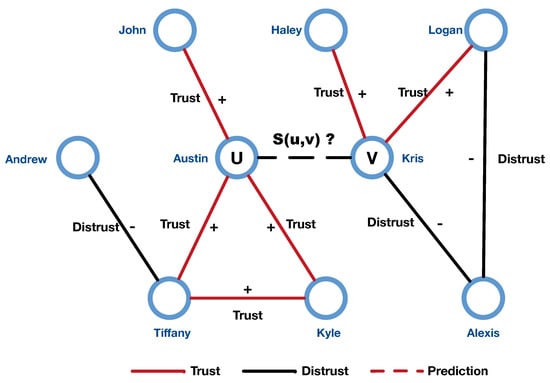
Figure 1.
An illustration of sign prediction problem in trust network.
For unsigned graph analysis tasks, graph neural networks (GNNs) [17] exhibit more robust performance in recent years, such as Graph Convolutional Networks (GCN) [18], GraphSAGE [19], Graph Attention Networks (GAT) [20], Gated Graph Neural Networks (GGNN) [21]. These methods in unsigned networks assume that directly connected nodes have a similar preference. However, this assumption is not suitable for signed networks due to the existence of negative links. Moreover, the transitivity property of unsigned networks is not always effective for the negative links in the signed networks. Hence, existing graph representation learning approaches designed for unsigned networks cannot be directly applied to the signed networks.
To deal with this problem, a great number of representation learning approaches on the signed graph were proposed [22,23,24,25]. SiNE [22] incorporates structural balance theory into a deep neural network to learn the relationship between the user for the signed social networks. SNE [23] employ a random walk to generate short nodes sequence on a signed network, and then use the log-bilinear algorithm to learn the representation of the nodes along the edge. Moreover, SNEA [24] and SignedFS [25] resort attributes of node to improve the performance for signed graph analysis.
Although many efforts were made for signed graph representation learning, there are still some challenges: (1). How to effectively capture the semantic and structural features on the signed graph with the negative edges to obtain a high-quality node or relation representation. (2). How to better measure the correlation between entities in different semantic spaces to generate a robust relation representation for signed graph analysis tasks. (3). We cannot merely treat the negative edges the same as positive edges because the semantic meaning and properties are completely different.
In this paper, in order to further overcome the problem of insufficient capture of latent features and semantic information of negative edges while learning the relation representation model in a unified semantic space, we propose a signed graph representation learning framework via signed graph mutual information maximization (SGMIM). SGMIM learns signed graph embedding and requires only the network information and a small percentage of signed label. the main contribution of this paper can be summarized as follows.
- We propose a novel relation representation learning model via maximizing mutual information between the signed graph and entity relation representation, which is preferable and suitable for trust networks modeling.
- We first introduce translation principle to signed graph to explore abundant feature and semantic information of edges on the signed graph.
- We develop a trust prediction algorithm that takes the learned relation representation vector to complete the trust prediction tasks.
- Experiments with four real-world datasets show that SGMIM can obtain efficient accuracy.
The rest of the paper is organized as follows. In Section 2 we briefly review related work regarding trust prediction and signed graph representation. Section 3 formally defines the problems of relation representation learning on the signed graph. Section 4 introduces our proposed method’s framework and discusses the building and training of SGMIM model for relation representation learning on the signed graph. Section 5 provides experimental settings and the analysis of results. Finally, we conclude this paper with a summary and future research directions.
2. Related Work
There has been much numerous research on relationship learning and trust learning in recent years. in this section, we review several main methods for relation learning, including traditional social network-based trust measure approaches, GNNs-based approaches, and signed graph-based approaches.
2.1. Approaches Based on Social Network Analysis
Traditional approaches to trust evaluation based on social network analysis mainly rely on trust transitivity and aggregation mechanisms, structural balance theory, and centrality theory. For P2P file-sharing systems, EigenTrust [26] uses multiplication and weighted mean to propagate and aggregates trust correspondingly to measures trust according to satisfied and unsatisfied experiences. Jsang considers trust as an uncertain probability and proposed a Subjective Logic model [27], which uses a discount strategy to propagate trust from the source node to the target node and then to aggregation. To improve accuracy, Golbeck presents TidalTrust [28], a trust management system, which combines trust by weighted mean trust values from multiple paths only from trusted neighbors. At the same time, the resulting trust value is not less than a set threshold. Due to trust’s nondeterministic characteristics, many works use fuzzy logic to measure trust. Unlike traditional binary logic measures, fuzzy logic is usually used to solve the partial between completely true and completely false [29]. Hao, Min et al. proposed MobiFuzzyTrust [30] combines familiarity-base trust, prestige-based trust, and similarity-based trust to calculate trust value, which represents trust with linguistic terms and defined fuzzy membership function to transform trust value from number to linguistic terms. Kant and Bharadwaj [31] proposed a fuzzy calculation approach of trust or distrust for recommendations through knowledge factors and similarity based on linguistic expressions. To avoid a lot of potential coordinated malicious attacks on nodes, Rasmussen et al. [32] introduced trust as soft security to help participants for social control. For the naive attack and whitewashing attack, TidalTrust [28] is robust because it uses a weighted mean to aggregate the trust value. However, the traitor attack does not contain any defense strategy. For a cold-start participant, Massa [33] proposed MoleTrust model that uses one continuous value to represent trust. It is robust to the whitewashing and naive attack because it only accepts trustworthy paths. For each type of attack, not all models are robust, and only a few models focus on the traitor attack. Combining trust transitivity and aggregation to reinforcement learning, Kim and Song [34] propose a reinforcement learning method to measure trust. Some works employ the matrix factorization method to generate a trust matrix for trust prediction, such as hTrust [35], which factorizes a low-rank matrix to model the trust relationship between the nodes. Moreover, it considers the homogeneity effect. Another matrix factorization method is Matri [36] that regards trust aspects as latent factors: trustor and trustee.
2.2. Approaches Based on GNNs
To model the relation between nodes, most methods based on GNNs usually first learn latent node representations and then learn relation representations by calculating the similarity of the nodes. Early graph representation learning is based on matrix eigenvector, such as Laplace Eigenmap (LE) [37,38], Locally Linear Embedding (LLE) [39,40], directed graph embedding [41]. in this kind of models, graphs are constructed offline by calculating similarity between the nodes. LLE assumes that the node embedding is locally linear, i.e., a node on the graph can be linearly represented by its neighbor nodes. the key of LLE algorithm is to find the linear relation of K nearest neighbors of each node and generate the linear relation weight matrix. Finally, the optimization problem of the objective is converted to a relational matrix eigenvector decomposition problem. Similar to LLE, LEE [37,38] algorithm believes that the representations of two connected nodes in a low-dimensional space should also be similar. the similarity between nodes is defined as the Euclidean distance of node vectors, and the optimization problem is also converted into the decomposition of Laplace eigenvectors. Inspired by Word2vec, DeepWalk [42] algorithm is the first to introduce the natural language processing approach into the graph embedding, which treats the node sequence generated by truncated random walk as sentences of language model and nodes as words, and then use Skip-gram and hierarchical Softmax to learn the node embedding by maximizing the likelihood probability of the random walk sequence. To further improve the performance of embedding, Node2Vec [43] algorithm presents a search strategy based on DeepWalk. Unlike the random sampling of DeepWalk, Node2vec adopts different search strategies to balance capturing local or global features. Another work, LINE [44], develops a network embedding approach that can model both first-order and second-order proximity and can be used in large-scale information networks. However, these relation representation learning model variants mainly rely on similarity modeling between nodes, and the mutual information aspect of signed graph relationship representation is not thoroughly investigated. Many research works on the mutual information have attracted a lot of attention based on GNN (graph neural networks [45]). For the molecule property prediction tasks, Ref. [46] proposed an approach that maximize mutual information between edge states and transforms parameters. In [47], the author learned the student model from the teacher model via mutual information maximization between intermediate representation. However, the methodology of mutual information maximization on the signed graph has not yet been used for the analysis tasks for trust prediction. Our proposed method in this paper is mainly inspired by the Graph InfoMax (GIM) and explores a trust relationship representation model suitable for trust networks.
2.3. Approaches Based on Signed Graph
Guha et al. [48] first investigated the sign prediction problem in the trust network and used a mathematical formula to describe the propagation behavior for trust and distrust relationships. They took into account two distrust propagation mechanisms: one is to assume that the distrust relationship is only propagated once, the other is to propagate the distrust relationship continuously. Experiments proved that the former mechanism is more concise and effective. However, the models have a limitation on the chain’s length. Mishara et al. [49] designed signed indicators on the trust networks to identify users’ trust preferences and influence. They believe that if a user always trusts or distrusts other users, his trust preference is regarded as biased, and his trust score will be reduced. in addition to network structure information as features, the content attributes and context features of nodes can also be used in sign prediction of trust networks. Zolfaghar et al. [50] proposed a classification system to predict the relationship between trust and distrust based on user behavior context feature and network structure feature information.
3. Preliminaries
This section begins with problem formulation and a brief introduction of graph mutual information. the common notations needed in the following sections are shown in Table 1.

Table 1.
Common notations.
3.1. Problem Formulation
Definition 1 (Signed Trust Network).
A Signed Trust Network is denoted as the signed graph , where is the set of vertexes, and each vertex represent a trust entity such as social media user, software service, recommendation item and network node, and are the sets of positive, negative links respectively. Please note that , . the associated graph adjacency matrix of signed graph G is denoted as
For each edge, is an ordered pair where u represents trustor and v represents trustee and is associated with a signed label or , which indicates trust or distrust. Please note that the trust relationship cannot have both a positive and negative sign simultaneously.
Definition 2
(Relation Representation Learning). Given a signed trust network G, relation representation learning aims to learn a function
where is a d-dimensional vector space, and . the structural features of trust networks and semantic relationship features will be preserved as much as possible in space .
Definition 3 (Trust Prediction).
The trust prediction problem to be addressed is to predict the sign of the relationship of node pairs (positive or negative).
3.2. Mutual Information
Mutual information (MI) is a useful information measure in information theory, which refers to the dependence between the two random variables. in particular, MI quantifies the amount of information obtained about one random variable by observing the other random variable. According to the information theory, given two discrete random variables and , the MI between U and V is defined as
where is a joint distribution of u and v, and and are the marginal distributions of u and v. According to the relationship between entropy H and MI, is also rewritten as:
Thus, the MI can be understood as the reduction in the uncertainty of U due to the knowledge of V. Consider U and V to be different views of the input data (e.g., a node and its neighborhood context, subgraph partitions of a graph), maximizing mutual information can effectively improve the performance of graph representation learning. However, Maximizing MI directly is intractable for GNNs. To tackle this problem, some approaches such Deep InfoMax (DIM), Deep Graph Infomax (DGI [51]), and Graph Mutual Information (GMI [52]) resort to mutual information neural estimation (MINE) [53] by training a statistics neural network as a classifier to differentiate samples from the joint distribution of two random variables and their product of marginals. Formally, can be written as:
where is a representation of the KL-divergence [54], and the supremum is taken over all functions T such that the two expectations are finite. Parameterize T into a neural network to find a tighter lower bound of mutual information: , and then use gradient update to continuously raise the lower bound while increasing the mutual information between U and V.
Another particular lower bound based on Noise Contrastive Estimation (NCE) [55] is InfoNCE [56], which has been proved to work well in real world practice. It is defined as:
where u and v are two distinct views from the input data, and is defined as a function with parameter . For example, the inner product of encoded embedding of a vertex and its neighbor context or inner product of encoded embedding of a graph and the subgraph of the graph, and is a sample set drawn from a proposal distribution that contains negative sample and positive sample v. Since infoNCE can be regarded as a special cross-entropy, when contains all possible values of Y, maximizing infoNCE loss is equivalent to minimizing the cross-entropy loss follow as:
Follow with this idea, we can use specific U, V to maximize the MI between two different views of the input data (e.g., a node and its neighborhood nodes on the graph, or different space representation of nodes and edges).
4. Proposed Method
Existing Semi-supervised GNNs mainly resort to the message passing mechanism to aggregate neighbor node features to learn the low-dimension representation with both labeled and unlabeled data. However, the transitivity assumption of the messages is not always valid due to the existence of negative edges. Inspired by recent self-learning work with MI maximization [57,58] and knowledge graph embedding (KGE) [59,60,61], we propose a relation representation learning framework via signed graph mutual information maximization, and then use learned vector representation as the input of neural networks to perform the task of trust prediction.
4.1. Framework
This section discusses in detail the general framework of our proposed method, which consists of two main parts: semantic relation encoder and structure feature learning. the semantic learning part employs the knowledge graph embedding approach to encode semantic information and maximize mutual information for model training, while the structure learning part captures structural features by factorizing PPMI matrix (positive point-wise mutual information matrix). Figure 2 shows the framework of SGMIM. in detail, we initialize the head entity u, relation r, and tail entity v for relation triplet to one-hot embedding vectors, and then design two objectives: semantic relation encoder captured semantic features and PPMI matrix factory extracted structural features. Finally, we jointly optimize the two objectives to learn a robust relation representation.
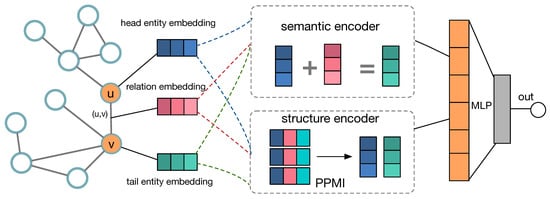
Figure 2.
Framework of SGMI.
As shown in Figure 2, SGMIM consists of two critical parts, the encoder part and relation representation construction part. in the following parts, we first give a detailed introduction of building encoder in SGMIM. Afterward, we describe how to construct the relation representations. At lash, we give the overall objective function of SGMIM.
4.2. Encoding Semantic Relation
How to encode more relation features between entities is crucial for predicting the relations precisely. the traditional signed network representation models simply use the inner product of the representation vector of node u and the representation vector of neighborhood node v. Obviously, in this way, the sign information has not been well captured and used. Motivated by translation mechanisms in knowledge graph representation learning (KGRL) fields [59,60], we assume that the interactions between entities in trust networks can also be portrayed as translations in the representation space. For each edge and its corresponding sign, the relations are represented as translations in the representation space. We introduce two vectors and for each entity, corresponding to its head representation and tail representation. For the same representation space , the translation mechanism among , can be formalized as
where is the relation embedding vector. Moreover, we define a triplet () as the semantic relationship from u to v. For example, a triple () in trust networks represent entity u trust (distrust) entity v. in most practical scenarios, entity representation space and relational representation space are different. Therefor, For each triplet () and its entity embedding and relation embedding , we define a score function follow as:
where , , and ,, (relation space), and is a projection matrix . Most existing of knowledge graph representation approaches [59,60] employ margin-base score function as objective for training:
where is the margin, S is the set of positive samples triples, and is the set of samples from a proposal triples (shuffle the original triple). Rather than a margin-based objective, In this work, we develop a loss function based on contrastive learning framework, which maximizes the MI between both entity and relation view. Following Equation (6), we minimize the following loss:
4.3. Learning Structure Information
The second part of our proposed approach SGMI is how to learn structural information on signed graphs. As we mentioned in Section 1, the message passing assumptions in unsigned graphs are invalid in signed graphs due to the existence of negative links. Hence, we use to maximize the Point-wise Mutual Information (PMI) [62] between node and neighbor context to learn the structured information on the signed network.
For a signed graph , the vectors , and are the representation corresponding to entity u, v, and relation r respectively. Specifically, the PMI is defined as:
where is the joint distribution of node pair (i, j), and is the product of marginal distribution. Based on statistics of global co-occurrence counts, we can compute the joint probability and the marginal probability.
where is the number of occurrences of node pair (i, j), and an represent the number of occurrences of node i and node j, respectively, and , so also can be:
where is the sign value of edge , denote the out-degree of node and denote the in-degree of node . in order to avoid cause by some is not in D, we set each negative value as 0, and then derive the following matrix formula:
where Z is PPMI matrix.
Afterward, we develop a probability matrix factorization model that learns the relation embedding between the nodes on the signed graph preserves rich edge structure information and contextual feature. Let denote as a matrix of the embedding vector of head entity (e.g., trustor entity in trust networks), and denote as a matrix of the embedding of tail entity (e.g., trustee entity in trust networks). Hence, we define the conditional probability of the observed Z (PPMI) as follows:
where is a Gaussian distribution with mean and variance , and is defined as the indicator function which is equal to 1 if i link j and equal to 0 otherwise. the function is the sigmoid function , which bounds the range of within [0,1]. Moreover, zero-mean Gaussian priors are assumed for head entity and tail entity vectors:
Through a Bayesian inference, the posterior probability of the random variables U and V can be defined as follows:
4.4. Model Training
In this subsection, we detail the training process of our proposed model. As we mentioned in Section 3, maximizing mutual information is intractable. A typical way is to employ MINE [53] to classify samples from the joint distribution and the product of marginals. However, an essential aspect of contrastive learning is how to construct positive and negative samples. For different types of data, how to reasonably define which samples should be regarded as positive samples and which should be regarded as negative samples. Moreover, the number of negative samples is also a factor that affects the performance of the model. Therefore, designing a reasonable positive and negative example pair and improving the coverage of semantic relation can aid the model to learn an effective representation for the downstream tasks. Recent work such as short random walks, node-anchored sampling, and curriculum-based negative sampling provide different sampling alternatives. in this work, for the positive sample, we directly use the triple from training data as positive sample triplet set S. Meanwhile, we adopt random pairs sampling strategies to draw the negative sample triplet set . in other words, we first fix the head entities u and relations r of the positive triplet set S (, and then shuffle the tail entities v to generate the negative sample triplet set (. in the same way, we fix the relations and tail entities and shuffle the head entity to generate another negative sample set (. Finally, Combine and into (i.e., ).
To preserve the semantic information among node and edge embedding as well as the structural features of edge on the signed graph, we combine both the objectives in Equations (9) and (15) into an overall objective function. in term of each triplet and its negative sample , we jointly optimize the following objective functions:
where is a hyper-parameter to trade-off the weights of different parts, in order to avoid model overfitting, we also use the dropout layer to optimize the parameters. Moreover, we adopt the optimization function Adam to minimize the objective in Equation (16). A More detailed training process and steps are shown in Algorithm 1 below.
| Algorithm 1Traning process of SGMIM model |
| Require:G: ; A: adjacency matrix; S: sign set of edges; k: dimension of node embedding vector; m: dimension of edge embedding vector; : hyper-parameter; epoches: iterate number. |
| Ensure:U: head entity representation; V: tail entity representation; R: relation representation. |
| 1: Initialization U, V, R |
| 2: Calculate PPMI Z |
| 3: for iter in range(epoches) |
| 4: Sample positive triple (u, r, v) |
| 5: Generate embedding U, R, V |
| 6: Sample negative triple (u’, r, v’) |
| 7: Generate embedding U’, R, V’ |
| 8: |
| 9: score = Discriminator(, ) |
| 10: Loss1 = BCEWithLogicLoss(score, S) |
| 11: Loss2 = CrossEntropyLoss(, Z) |
| 12: Loss = Loss1+(1−Loss2 |
| 13: Update U, R, V |
| 14: Loss Backforward |
| 15: end for |
5. Experiments
In order to evaluate the effectiveness of SGMIM on learning relation representation between the nodes on the signed graph, we compare the accuracy and efficiency of SGMIM model to the state-of-the-art baseline methods on sign prediction with four standard real-world datasets (Epinions, Slashdot and WikiElec, and WikiRfa) for trust prediction tasks and link prediction tasks. In this work, all the algorithms are written in Python3.7. In addition, we also use deep learning util package pytorch1.5 (https://pytorch.org/) and complex network analysis library networkx2.3 (http://networkx.github.io/) and achieve execution. We conduct the experiments are on an Intel (R) Core (TM) i7-8700U with 16Gb RAM running desktop computer. We use Macro-F1 score and Area Under Curve (AUC) to evaluate the accuracy of the prediction task.
5.1. Datasets
We use four publicly datasets: Epinions, Slashdot, WikiElec, WikiRfa. The statistical characteristics of the four datasets are summarized in Table 2, and the degree distribution of the dataset see Figure 3.

Table 2.
Statistics information of the datasets.
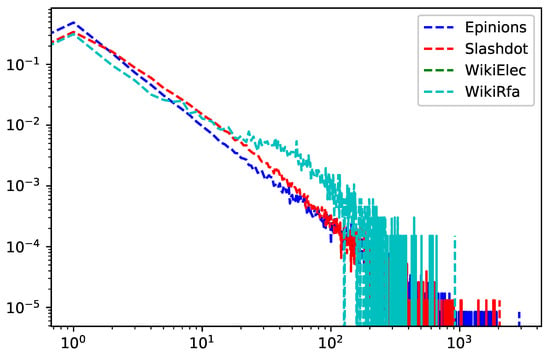
Figure 3.
Degree Distribution of Datasets (Epinions, Slashdot, WikiElec, WikiRfa).
1. Epinions (http://www.trustlet.org/epinions.html). Epinions is an online review website where users can review any products. Users can register for free and write reviews for many different types of products such as music, software hardware. In Epinions, users can be allowed to other users to their “Web of Trust.“ Epinions datasets contain the ratings given by users to the item and the trust statements issued by users. It was collected by Paolo Massa crawl from the Epinions website in a five-week, which contains 49,290 users who rated a total of 139,738 different products at least once and writing 664,824 reviews, and 487,181 issued trust statements. The dataset consists of two data files: Ratings data and Trust data, in which trust data contains the trust statements issued by users, and every line has the following format: source-user-id, target-user-id, trust-statement-value. For example, line 10,572 11,715 −1 represents user 10,572 has expressed a negative trust statement on user 11,715. The value of the trust-statement is only 1 or −1, and 1 means positive trust, and −1 means negative ones (distrust). The detailed statistics about the Epinions dataset see Table 2.
2. Slashdot (https://www.slashdot.org). Slashdot is a technology-related news website know for its specific user community, which features editor-evaluated and user-submitted current primarily technology-oriented news. The interesting part of Slashdot is its reader comments. Generally, each news item has hundreds or even thousands of reader comments. The system will automatically randomly select moderators from active users. The selected moderator can give a score to each comment, and positive comments add 1 point and negative comments minus 1 point. Slashdot uses the SlashdotZoo feature, which allows user to tag each other as friends or foes. The User network contains friend/foe links between the users of Slashdot. Slashdot network contains nodes 82,168 and edges 948,464. See Table 2 for detailed statistics on Slashdot datasets.
3. WikiElec and WikiRfa (http://snap.stanford.edu/data/wiki-Elec.html). Wikipedia is a free encyclopedia website maintained by volunteers from all over the world. To manage the administrator, Wikipedia develops a voting network (WikiElec) to decide whom to promote to the administrator via a public vote for the adminship elections, and WikiRfa is a new version of WikiElec. Both WikiElec and WikiRfa contain positive, negative, and neutral votes. According to the statistical results, we find that the average sparsity of WikiElec is larger than WikiRfa. WikiElec network contains 7194 nodes and 114,040 edges, and WikiRfa contains 10,885 nodes and 137,966 edges. See Table 2 for detailed statistics on WikiElec and WikiRfa datasets.
5.2. Baselines
We compare with the following baseline methods.
(1) Signed Spectral Clustering [63] is a spectral clustering method based on eigenvalue decomposition. It takes the eigenvector of the k smallest eigenvalues obtained by the signed spectral decomposition as the node’s representation vector. The spectral method’s performance in real tasks would be affected by the dimension of the eigenvector, and it is more suitable for undirected graphs.
(2) SiNE [64]: SiNE incorporates the structural balance theory into deep learning model for learning the node embedding on the signed graph. It assumes the signed graph is an undirected graph.
(3) SNE [23]: SNE is a signed graph representation learning method based on random walk. It extracts many short node paths by random walk along with the graph, and then further adopts the log-bilinear model to learn the node representation.
(4) nSNE [65]: nSNE is a neural network signed network embedding method. It learns both node embedding and edge embedding by modeling first-order proximity and second-order between the nodes on the signed graph with negative link.
5.3. Evaluation Metric
We consider using macro F1-score and AUC (Area Under Curve) as the metric for evaluating our model. Most machine learning methods for multi-classification problems usually use macro F1-score as the final evaluation metric to assess the quality of problems. In particular, macro F1-score is also the balance average of precision and recall. The maximum value of F1-score is 1, and the minimum value is 0. The formula for the -score is:
where presents the proportion of true positive samples in the sample predicted to be positive, refers to the proportion of samples predicted to be correct in the sample predicted to be positive. We define Precision and Recall as follows:
AUC (Area Under Curve) is another most frequently used classification measurement at various threshold settings. ROC (Receiver Operating Characteristic) curve can help us set a threshold for a classifier that minimizes the false positives while maximizing the true positives and evaluating the performance of the classifier over entire operating range. AUC represents the measure or degree of separability. It tells us how many nodes may distinguishing the classes. The higher the AUC, the better the model is at distinguishing between nodes with the positive or negative. We can draw the ROC curve with TPR as the x-axis and FPR as the y-axis, where TPR (True Positive Rate) is equal to Recall, and FPR (False Positive Rate) is defined as:
In this work, we use the leave-one-out strategy for evaluation and reserve 20% of the datasets for test and the remaining 80% for model training through cross-validation.
5.4. Experimental Results
This section shows and analyzes the experimental results for different baseline methods on four real datasets, as shown Table 3. According to the experimental results, we can find:

Table 3.
Experiments Results on Sign Prediction Task.
Compared with the traditional signed graph embedding methods based on spectral decomposition, the neural network representation learning methods perform more better on most datasets because the neutral network has the powerful capacity to extract the complex non-linear features, such as SNE, iSNE, and nSNE. Besides, we also find that for large-scale sparse datasets, the computational efficiency of the spectral method is significantly reduced because of the time-consuming spectral feature decomposition.
As for neural network representation methods on the signed graph, SNE employs social balance theory to enhance the second-order approximate between nodes and perform better than the spectral decomposition method. However, its generalization ability on the signed graph containing more negative edges is insufficient than that of signed graphs containing fewer negative edges. The main reason is that the balance theory enhances local features and ignores global features.
Table 3 demonstrates Macro-F1 and AUC metrics for different baselines on four datasets. Please note that the dimension of the relation representation is also a critical parameter that affects the experimental result. As the dimension size increases, Macro-F1 and AUC also increase accordingly, especially when the dimension is greater than 120, Macro-F1 and AUC reach the maximum value. The best experimental results in Table 3 are shown in Bold numbers.
Finally, the statistical analysis results show that our proposed SGMIM method has a good result by calculating Frieman’s rank and Wilcoxon’s signed-rank [66] of each baseline method on every dimension setting and the dataset. In contrast to these baseline methods, we incorporate the knowledge graph relation embedding and positive point-wise mutual information by maximizing graph mutual information between signed graph and latent representation to learn a robust relation representation. The experiment results demonstrate that mutual information maximization can effectively improve the performance of signed graph relation representation learning for trust prediction tasks.
5.5. Parameter Sensitivity
This section discusses the sensitivity of parameters in the trust prediction task on four datasets (WikiElec, WikiRfa, Epinions, and Slashdot) for our proposed method SGMIM. In particular, we discuss the sensitivity of several critical parameters in SGMIM model, such as node representation dimension , and relation representation dimension , and hyper-parameter on SGMIM model.
5.5.1. Dimension
To evaluate the effect of node embedding dimension and relation embedding dimension in sign prediction task for our model, we uniformly set parameter and as same value () and then set parameter as 0.2, the number of train epochs as 200 and learning rate as 0.015. After that, we change the dimension parameters K from 20 to 120 with an interval of 20. Figure 4 shows the performance of the SGMIM model on the trust prediction task of different dimensions K on four real-world datasets. Figure 4a,b show AUC and Macro-F1 score on Epinions dataset, Figure 4c,d show AUC and Macro-F1 score on Slashdot dataset, Figure 4e,f show AUC and Macro-F1 score on WikiElec dataset, and Figure 4g,h show AUC and Macro-F1 score on WikiRfa dataset. As shown in the performance in Figure 4, we find that the AUC (Macro-F1) score keeps increasing when the value of K ranges from 20 to 120, and the performance tends to be stable when K is 100. In summary, the experimental results show that the trend of the parameters in SGMIM model is smooth in different dimension values. Specifically, the embedding dimension is not sensitive to SGMIM model.
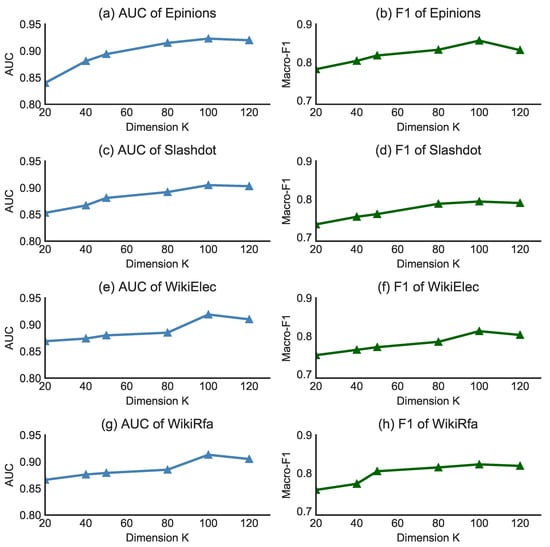
Figure 4.
Performance (Macro-F, AUC) comparison w.r.t different size of dimension on Epinions, Slashdot and WikiRra datasets.
5.5.2. Hyper-Parameters
Hyper-parameter trade-off the weight of semantic encoder loss and positive point-wise mutual information loss. In this experiment, we set as 0.05, and experiment results demonstrate that increasing the weight ratio of the semantic encoder can improve the effect of entity embedding. On the contrary, increasing the weight ratio of the structural encoder can enhance the embedding effect of relation representation. For training parameters, we set the learning rate to 0.015 and the epochs to 300. The results show that the model loss tends to decrease, and the accuracy tends to increase when epochs are taken from 50 to 300. Please note that after epochs reach 300, the accuracy of the model tends to stabilize. Accordingly, SGMIM can be well trained and optimized in sign prediction tasks because of the insensitivity of hyper-parameter.
6. Conclusions
In this paper, we proposed a relation embedding approach on the signed graph base on mutual information maximization (SGMIM). In SGMIM, we incorporate the knowledge graph representation method into signed graph relation representation learning to learn a robust node and relation representation. We can capture the semantic correlations on the signed graph with negative links by maximizing mutual information between head entity, relation, and tail entity. Moreover, we devise an objective by factorizing the PPMI Matrix to learn the signed graph’s structural features. The experiments demonstrate SGMIM performs better than existed several baseline methods on trust prediction task and has better robustness for signed graphs with negative links.
There are many challenges for large-scale complex trust networks with the attribute, segment, and multi relation. We will further investigate and optimize our proposed method’s performance in large-scale complex networks and improve the efficiency of the model in real scenarios in future works.
Author Contributions
Conceptualization, writing—original draft preparation and supervision, Y.J.; Formal analysis, methodology, H.W., Y.J.; Data validation and visualization, K.S., X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by the National Natural Science Foundation of China (61572167).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors are grateful to the editor and referees for their valuable comments and suggestions for improving the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kipf, T.N.; Welling, M. Variational Graph Auto-Encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. In Advances in Neural Information Processing Systems; 2018; pp. 5171–5181. Available online: https://papers.nips.cc/paper/2018/file/53f0d7c537d99b3824f0f99d62ea2428-Paper.pdf (accessed on 11 January 2021).
- Qu, M.; Bengio, Y.; Tang, J. GMNN: Graph Markov Neural Networks. arXiv 2019, arXiv:1905.06214. [Google Scholar]
- Wu, J.; He, J.; Xu, J. DEMO-Net: Degree-specific Graph Neural Networks for Node and Graph Classification. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 406–415. [Google Scholar]
- Zhang, Y.; Pal, S.; Coates, M.; Ustebay, D. Bayesian Graph Convolutional Neural Networks for Semi-Supervised Classification. Proc. AAAI Conf. Artif. Intell. 2019, 33, 5829–5836. [Google Scholar] [CrossRef]
- Bjerrum, E.J.; Threlfall, R. Molecular Generation with Recurrent Neural Networks (RNNs). arXiv 2017, arXiv:1705.04612. [Google Scholar]
- Bresson, X.; Laurent, T. A Two-Step Graph Convolutional Decoder for Molecule Generation. arXiv 2019, arXiv:1906.03412. [Google Scholar]
- Chen, C.; Ye, W.; Zuo, Y.; Zheng, C.; Ong, S.P. Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals. Chem. Mater. 2019, 31, 3564–3572. [Google Scholar] [CrossRef]
- Wang, X.; Cui, P.; Wang, J.; Pei, J.; Yang, S. Community Preserving Network Embedding. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Cao, S.; Wei, L.; Xu, Q. GraRep: Learning Graph Representations with Global Structural Information. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, Melbourne, Australia, 19–23 October 2015. [Google Scholar]
- Tang, J.; Chang, Y.; Aggarwal, C.; Liu, H. A Survey of Signed Network Mining in Social Media. ACM Comput. Surv. 2016, 49, 42. [Google Scholar] [CrossRef]
- Tang, J.; Hu, X.; Liu, H. Is distrust the negation of trust? The value of distrust in social media. In Proceedings of the 25th ACM Conference on Hypertext and Social Media, Santiago, Chile, 1–4 September 2014; pp. 148–157. [Google Scholar]
- Somu, N.; Raman, M.R.G.; Kalpana, V.; Kirthivasan, K.; Sriram, V.S.S. An improved robust heteroscedastic probabilistic neural network based trust prediction approach for cloud service selection. Neural Netw. 2018, 108, 339–354. [Google Scholar] [CrossRef]
- Leskovec, J.; Huttenlocher, D.; Kleinberg, J. Predicting positive and negative links in online social networks. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 641–650. [Google Scholar]
- Victor, P.; Cornelis, C.; Cock, M.D.; Teredesai, A.M. Trust- and Distrust-Based Recommendations for Controversial Reviews. IEEE Intell. Syst. 2011, 26, 48–55. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation Learning on Graphs: Methods and Applications. IEEE Data (Base) Eng. Bull. 2017, 40, 52–74. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. ICLR (Poster). arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hamilton, W.L.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1024–1034. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated Graph Sequence Neural Networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Wang, S.; Tang, J.; Aggarwal, C.C.; Chang, Y.; Liu, H. Signed network embedding in social media. In Proceedings of the 17th SIAM International Conference on Data Mining, Houston, TX, USA, 27–29 April 2017; pp. 327–335. [Google Scholar]
- Yuan, S.; Wu, X.; Xiang, Y. SNE: Signed Network Embedding. In Proceedings of the Pacific-asia Conference on Knowledge Discovery & Data Mining, Jeju, Korea, 23–26 May 2017; pp. 183–195. [Google Scholar]
- Wang, S.; Aggarwal, C.; Tang, J.; Liu, H. Attributed Signed Network Embedding. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 137–146. [Google Scholar]
- Cheng, K.; Li, J.; Liu, H. Unsupervised Feature Selection in Signed Social Networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 777–786. [Google Scholar]
- Kamvar, S.D.; Schlosser, M.T.; Garcia-Molina, H. The Eigentrust algorithm for reputation management in P2P networks. In Proceedings of the International Conference on World Wide Web, Budapest, Hungary, 20–24 May 2003; pp. 640–651. [Google Scholar]
- Josang, A. A logic for uncertain probabilities. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2001, 9, 279–311. [Google Scholar] [CrossRef]
- Golbeck, J.A. Computing and Applying Trust in Web-Based Social Networks; University of Maryland at College Park: College Park, MD, USA, 2005. [Google Scholar]
- Novák, V.; Perfilieva, I.; Močkoř, J. Mathematical Principles of Fuzzy Logic; Kluwer Academic: Dordrecht, The Netherlands, 1999; pp. 1–5. [Google Scholar]
- Hao, F.; Min, G.; Lin, M.; Luo, C.; Yang, L.T. MobiFuzzyTrust: An Efficient Fuzzy Trust Inference Mechanism in Mobile Social Networks. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2944–2955. [Google Scholar] [CrossRef]
- Kant, V.; Bharadwaj, K.K. Fuzzy Computational Models of Trust and Distrust for Enhanced Recommendations. Int. J. Intell. Syst. 2013, 28, 332–365. [Google Scholar] [CrossRef]
- Rasmusson, L.; Jansson, S. Simulated social control for secure Internet commerce. In Proceedings of the 1996 Workshop on New Security Paradigms, Lake Arrowhead, CA, USA, 17–20 September 1996; pp. 18–25. [Google Scholar]
- Massa, P.; Avesani, P. Controversial Users Demand Local Trust Metrics: An Experimental Study on Epinions.com Community. In Proceedings of the AAAI-05, Pittsburgh, PA, USA, 9–13 July 2005; pp. 121–126. [Google Scholar]
- Kim, Y.A.; Song, H.S. Strategies for predicting local trust based on trust propagation in social networks. Knowl. Based Syst. 2011, 24, 1360–1371. [Google Scholar] [CrossRef]
- Tang, J.; Gao, H.; Hu, X.; Liu, H. Exploiting homophily effect for trust prediction. In Proceedings of the ACM International Conference on Web Search and Data Mining, Rome, Italy, 4–8 February 2013; pp. 53–62. [Google Scholar]
- Yao, Y.; Tong, H.; Lu, J.; Lu, J.; Lu, J. MATRI: A multi-aspect and transitive trust inference model. In Proceedings of the 22nd International Conference on World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1467–1476. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural Inf. Process. Syst. 2001, 14, 585–591. [Google Scholar]
- Tang, L.; Liu, H. Leveraging social media networks for classification. Data Min. Knowl. Discov. 2011, 23, 447–478. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Saul, L.K.; Roweis, S.T. An introduction to locally linear embedding. J. Mach. Learn. Res. 2008, 7. Available online: http://www.cs.columbia.edu/~jebara/6772/papers/lleintro.pdf (accessed on 11 January 2021).
- Yang, Q.; Chen, M.; Tang, X. Directed graph embedding. In IJCAI; 2009; pp. 2707–2712. Available online: https://www.aaai.org/Papers/IJCAI/2007/IJCAI07-435.pdf (accessed on 11 January 2021).
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online learning of social representations. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–17 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable Feature Learning for Networks. In Proceedings of the ACM Sigkdd International Conference on Knowledge Discovery & Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale Information Network Embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks. arXiv 2018, arXiv:1810.00826. [Google Scholar]
- You, J.; Liu, B.; Ying, R.; Pande, V.; Leskovec, J. Graph convolutional policy network for goal-directed molecular graph generation. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31, pp. 6412–6422. [Google Scholar]
- Sun, F.Y.; Hoffman, J.; Verma, V.; Tang, J. InfoGraph: Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization. arXiv 2020, arXiv:1908.01000. [Google Scholar]
- Guha, R.; Kumar, R.; Raghavan, P.; Tomkins, A. Propagation of trust and distrust. In Proceedings of the International Conference on World Wide Web, New York, NY, USA, 17–20 May 2004; pp. 403–412. [Google Scholar]
- Mishra, A.; Bhattacharya, A. Finding the bias and prestige of nodes in networks based on trust scores. In Proceedings of the 20th International Conference on World Wide Web (WWW 2011), Hyderabad, India, 28 March–1 April 2011. [Google Scholar]
- Zolfaghar, K.; Aghaie, A. Mining trust and distrust relationships in social Web applications. In Proceedings of the 2010 IEEE 6th International Conference on Intelligent Computer Communication and Processing (ICCP10), Cluj-Napoca, Romania, 26–28 August 2010; pp. 73–80. [Google Scholar] [CrossRef]
- Velikovi, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep Graph Infomax. In Proceedings of the 2018 International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Peng, Z.; Huang, W.; Luo, M.; Zheng, Q.; Rong, Y.; Xu, T.; Huang, J. Graph Representation Learning via Graphical Mutual Information Maximization. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020. [Google Scholar]
- Belghazi, I.; Rajeswar, S.; Baratin, A.; Hjelm, R.D.; Courville, A. MINE: Mutual Information Neural Estimation. ArXiv 2018, arXiv:1801.04062. [Google Scholar]
- Donsker, M.D.; Varadhan, S.S. Asymptotic evaluation of certain markov process expectations for large time. IV. Commun. Pure Appl. Math. 1983, 36, 183–212. [Google Scholar] [CrossRef]
- Gutmann, M.U.; Hyvärinen, A. Noise-Contrastive Estimation of Unnormalized Statistical Models, with Applications to Natural Image Statistics. J. Mach. Learn. Res. 2012, 13, 307–361. [Google Scholar]
- Logeswaran, L.; Lee, H. An efficient framework for learning sentence representations. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April 30–3 May 2018. [Google Scholar]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. arXiv 2018, arXiv:1808.06670. [Google Scholar]
- Zhou, K.; Wang, H.; Zhao, W.; Zhu, Y.; Wang, S.; Zhang, F.; Wang, Z.; Wen, J.R. S3-Rec: Self-Supervised Learning for Sequential Recommendation with Mutual Information Maximization. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Galway, Ireland, 19–23 October 2020. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Durán, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-Relational Data. In Proceedings of the 26th International Conference on Neural Information Processing Systems (NIPS’13), Lake Tahoe, NV, USA, 5–8 December 2013; Curran Associates Inc.: Red Hook, NY, USA, 2013; Volume 2, pp. 2787–2795. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning Entity and Relation Embeddings for Knowledge Graph Completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI’15), Austin, TX, USA, 25–30 January 2015; pp. 2181–2187. [Google Scholar]
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. arxiv 2019, arXiv:1902.10197. [Google Scholar]
- Bullinaria, J.A.; Levy, J.P. Extracting semantic representations from word co-occurrence statistics: A computational study. Behav. Res. Methods 2007, 39, 510–526. [Google Scholar] [CrossRef]
- Kunegis, J.; Schmidt, S.; Lommatzsch, A.; Lerner, J.; Albayrak, S. Spectral Analysis of Signed Graphs for Clustering, Prediction and Visualization. In Proceedings of the Siam International Conference on Data Mining, Columbus, OH, USA, 29 April–1 May 2010. [Google Scholar]
- Leskovec, J. Signed Networks in Social Media. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Atlanta, GA, USA, 10–15 April 2010. [Google Scholar]
- Song, W.; Wang, S.; Yang, B.; Lu, Y.; Zhao, X.; Liu, X. Learning Node and Edge Embeddings for Signed Networks. Neurocomputing 2018, 319, 42–54. [Google Scholar] [CrossRef]
- Demiar, J.; Schuurmans, D. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).